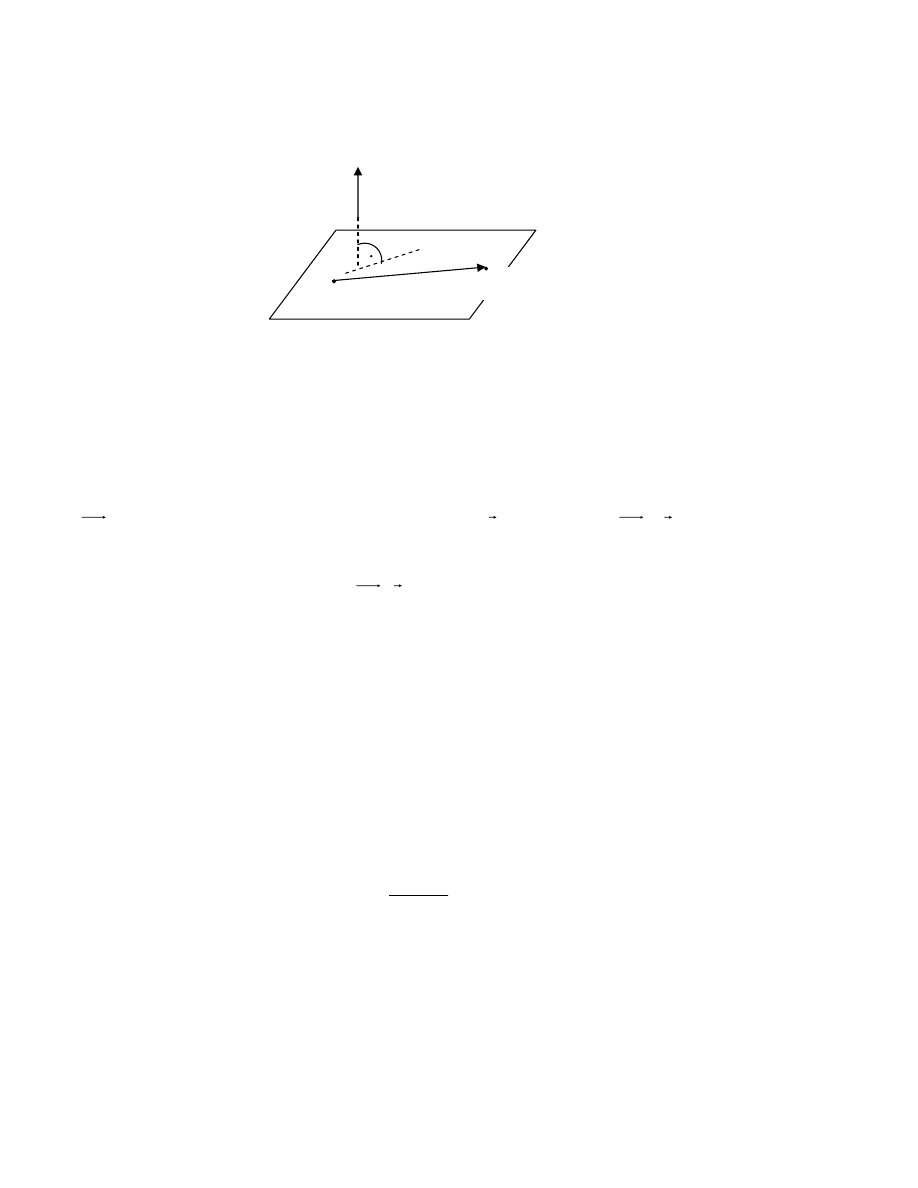
1. Pùaszczyzna
Wektor
0
,
,
C
B
A
n
,kt
óry jest
wektorem prostopad
ùym do pùaszczyzny
,
nazywamy
wektorem normalnym pùaszczyzny
.
Niech
0
0
0
z
,
y
,
x
M
ustalony punkt na p
ùaszczyênie.
Obieramy dowolny punkt
z
,
y
,
x
P
nale
¿¹cy do pùaszczyzny, wtedy wektor
0
0
0
,
,
z
z
y
y
x
x
MP
jest prostopad
ùy do wektora
n
(symbolicznie:
n
MP
)
mamy zatem:
0
n
MP
czyli
0
0
0
0
C
,
B
,
A
z
z
,
y
y
,
x
x
0
0
0
0
z
z
C
y
y
B
x
x
A
0
0
0
0
Cz
By
Ax
Cz
By
Ax
oznaczaj
¹c
0
0
0
Cz
By
Ax
D
otrzymujemy
równanie ogólne pùaszczyzny
0
D
Cz
By
Ax
K¹t
miêdzy pùaszczyznami
o wektorach normalnych
1
n
,
2
n
obliczamy ze wzoru
|
||
|
|
|
cos
2
1
2
1
n
n
n
n
wektor normalny
p
ùaszczyzny
r
ównanie ogólne
p
ùaszczyzny
k
¹t pomiêdzy
p
ùaszczyznami
C
B
A
n
,
,
)
,
,
(
0
0
0
z
y
x
M
)
,
,
(
z
y
x
P
id3838093 pdfMachine by Broadgun Software - a great PDF writer! - a great PDF creator! - http://www.pdfmachine.com http://www.broadgun.com

2. Prosta
Wektor
0
,
,
c
b
a
u
, kt
óry
jest wektorem r
ównolegùym do prostej
, nazywamy
wektorem kierunkowym prostej
.
Niech
)
,
,
(
0
0
0
z
y
x
M
ustalony punkt na prostej.
Obieramy dowolny punkt
)
,
,
(
z
y
x
P
nale
¿¹cy
do
prostej,
wtedy
wekt
or
0
0
0
,
,
z
z
y
y
x
x
MP
jest r
ównolegùy do wektora
u
(symbolicznie:
MP
u
)
zatem wektor
MP
mo
¿na przedstawiã w postaci:
MP
u
t
gdzie
t
jest pewn
¹ liczb¹ rzeczywist¹ czyli
c
b
a
t
z
z
y
y
x
x
,
,
,
,
0
0
0
st
¹d
c
t
z
z
b
t
y
y
a
t
x
x
0
0
0
st
¹d otrzymujemy
równania prostej w postaci parametrycznej
c
t
z
z
b
t
y
y
a
t
x
x
0
0
0
,
t
- parametr
Wyliczaj
¹c
parametr
t
z ka
¿dego
r
ównania powy¿szego ukùadu mamy
c
z
z
t
b
y
y
t
a
x
x
t
0
0
0
wektor
kierunkowy
prostej
r
ównania
parametryczne
prostej
c
b
a
u
,
,
)
,
,
(
0
0
0
z
y
x
M
)
,
,
(
z
y
x
P

po przyr
ównaniu prawych stron równañ otrzymujemy
równania kanoniczne prostej
c
z
z
b
y
y
a
x
x
0
0
0
Dwie nier
ównolegùe
p
ùaszczyzny
0
1
1
1
1
D
z
C
y
B
x
A
,
0
2
2
2
2
D
z
C
y
B
x
A
przecinaj
¹ siê wzdùu¿ prostej, której równania mo¿na zapiaã w postaci:
0
0
2
2
2
2
1
1
1
1
D
z
C
y
B
x
A
D
z
C
y
B
x
A
s
¹ to tzw.
równania krawêdziowe prostej
.
K¹t
miêdzy prostymi
o wektorach kierunkowych
1
u
,
2
u
obliczamy ze wzoru:
|
||
|
|
|
cos
2
1
2
1
u
u
u
u
r
ównania
kanoniczne
prostej
r
ównania
kraw
êdziowe
prostej
k
¹t pomiêdzy
prostymi
..........................................................................................
PRZYK£AD 1
Dane s
¹ punkty A
(3,-2,0) i
B
(-5,3,7). Znale
êã równanie pùaszczyzny przechodz¹cej przez punkt
A
i prostopad
ùej do wektora AB
.
Rozwi
¹zanie
Wektor
]
7
,
5
,
8
[
AB
jest wektorem normalnym p
ùaszczyzny, a p
unkt
A
(3,-2,0) nale
¿y do
p
ùaszczyzny.
Obieramy dowolny punkt
)
,
,
(
z
y
x
P
nale
¿¹cy do pùaszczyzny,
wtedy wektor
7
,
5
,
8
z
y
x
AP
jest prostopad
ùy do wektora AB
mamy zatem:
0
AB
AP
czyli
0
7
,
5
,
8
7
,
5
,
8
z
y
x
0
)
7
(
7
)
5
(
5
)
8
(
8
z
y
x
0
34
7
5
8
z
y
x
Odpowied
ê
R
ównanie pùaszczyzny ma postaã:
0
34
7
5
8
z
y
x
.
..........................................................................................

PRZYK£AD 2
Znale
êã
równanie
pùaszczyzny
przechodz¹cej
przez
punkt
)
7
,
1
,
4
(
M
i r
ównolegùej do pùaszczyzny
0
1
5
2
3
z
y
x
.
Rozwi
¹zanie
Punkt
)
7
,
1
,
4
(
M
jest ustalonym punktem szukanej p
ùaszczyzny. Poszukujemy wektora
normalnego tej p
ùaszczyzny. Wektor normalny
]
5
,
2
,
3
[
n
podanej w tre
œci zadania pùaszczyzny
jest jednocze
œnie wektorem normalnym szukanej pùaszczyzny.
Obieramy dowolny punkt
)
,
,
(
z
y
x
P
nale
¿¹cy do szukanej pùaszczyzny, wtedy wektor
7
,
1
,
4
z
y
x
MP
jest prostopad
ùy do wektora
n
mamy zatem:
0
n
MP
czyli
0
5
,
2
,
3
7
,
1
,
4
z
y
x
0
)
7
(
5
)
1
(
2
)
4
(
3
z
y
x
0
49
5
2
3
z
y
x
R
ównanie pùaszczyzny ma postaã:
0
49
5
2
3
z
y
x
.
..........................................................................................
PRZYK£AD 3
Znale
êã równanie pùaszczyzny przechodz¹cej przez punkt
)
2
,
1
,
3
(
M
i r
ównolegùej do dwóch
wektor
ów:
]
5
,
4
,
2
[
u
,
]
3
,
2
,
1
[
v
.
Rozwi
¹zanie
Punkt
)
2
,
1
,
3
(
M
jest ustalonym punktem p
ùaszczyzny. Szukamy wektora normalnego tej
p
ùaszczyzny. Wektor
]
8
,
11
,
2
[
v
u
jest prostopad
ùy jednoczeœnie do wektora
u
i do wektora
v
,
a wi
êc jest prostopadùy do pùaszczyzny.
Jest wi
êc jej wektorem normalnym.
Obieramy dowolny punkt
)
,
,
(
z
y
x
P
nale
¿¹cy do pùaszczyzny,
wtedy wektor
2
,
1
,
3
z
y
x
MP
jest prostopad
ùy do wektora
v
u
st
¹d
mamy
0
)
(
v
u
MP
czyli
0
8
,
11
,
2
2
,
1
,
3
z
y
x
0
)
2
(
8
)
1
(
11
)
3
(
2
z
y
x
0
11
8
11
2
z
y
x

R
ównanie pùaszczyzny ma postaã:
0
11
8
11
2
z
y
x
.
..........................................................................................
PRZYK£AD 4
Znale
êã równanie pùaszczyzny przechodz¹cej przez dwa punkty
)
1
,
3
,
0
(
A
,
)
5
,
2
,
3
(
B
i r
ównolegùej
do wektora:
]
1
,
3
,
2
[
u
.
Rozwi
¹zanie
Ustalonym punktem p
ùaszczyzny jest np. punkt
)
1
,
3
,
0
(
A
. Szukamy wektora normalnego tej
p
ùaszczyzny. Wektor
]
19
,
5
,
17
[
AB
u
jest prostopad
ùy jednoczeœnie do wektora
u
i do wektora
]
4
,
5
,
3
[
AB
, a wi
êc jest prostopadùy do pùaszczyzny. Jest wiêc jej wektorem normalnym.
Obieramy dowolny punkt
)
,
,
(
z
y
x
P
nale
¿¹cy do pùaszczyzny, wtedy wektor
1
,
3
,
z
y
x
AP
jest
prostopad
ùy do wektora
AB
u
st
¹d mamy
0
)
(
AB
u
AP
czyli
0
19
,
5
,
17
1
,
3
,
z
y
x
0
)
1
(
19
)
3
(
5
17
z
y
x
0
34
19
5
17
z
y
x
R
ównanie pùaszczyzny ma postaã:
0
34
19
5
17
z
y
x
.
..........................................................................................
PRZYK£AD 5
Znale
êã równanie pùaszczyzny przechodz¹cej przez punkt
)
3
,
1
,
2
(
M
i prostopad
ùej do pùaszczyzn
0
2
3
4
z
y
x
,
0
4
2
3
z
y
x
.
Rozwi
¹zanie
Punkt
)
3
,
1
,
2
(
M
jest ustalonym punktem p
ùaszczyzny. Poszukujemy wektora
normalnego tej
p
ùaszczyzny. Wektory normalne danych pùaszczyzn to:
]
3
,
1
,
4
[
1
n
,
]
1
,
2
,
3
[
2
n
. Szukamy
p
ùaszczyzny prostopadùej do danych pùaszczyzn
, a wi
êc równolegùej do ich wektorów normalnych.
Zadanie sprowadza si
ê wiêc do
problemu rozwi
¹zanego w Przykùadzie 3.
Wektor
]
11
,
13
,
5
[
2
1
n
n
jest prostopad
ùy jednoczeœnie do wektora
1
n
i do wektora
2
n
a wi
êc
jest prostopad
ùy do szukanej pùaszczyzny. Jest wiêc jej wektorem normalnym. Obiera
my dowolny
punkt
)
,
,
(
z
y
x
P
nale
¿¹cy do szukanej pùaszczyzny,
wtedy wektor
3
,
1
,
2
z
y
x
MP
jest
prostopad
ùy do wektora
2
1
n
n
st
¹d mamy
0
)
(
2
1
n
n
MP
czyli
0
11
,
13
,
5
3
,
1
,
2
z
y
x
0
)
3
(
11
)
1
(
13
)
2
(
5
z
y
x
0
10
11
13
5
z
y
x
R
ównanie szukanej pùaszczyzny ma postaã:
0
10
11
13
5
z
y
x
.
..........................................................................................
PRZYK£AD 6
Znale
êã równanie pùaszczyzny przechodz¹cej przez trzy punkty
)
2
,
3
,
1
(
A
,
)
1
,
2
,
5
(
B
,
)
2
,
1
,
4
(
C
.
Rozwi
¹zanie
Ustalonym punktem p
ùaszczyzny jest np. punkt
)
2
,
3
,
1
(
A
. Maj
¹c trzy punkty na pùaszczyênie
mo
¿emy utworzyã dwa wektory AB
,
AC
le
¿¹ce na pùaszczyênie a wiêc równolegùe do niej.
Zadanie sprowadza si
ê wiêc do problemu rozwi¹zanego w Przykùadzie 3.
Szukamy wektora normalnego p
ùaszczyzny. Wektor
]
27
,
3
,
4
[
AC
AB
jest prostopad
ùy
jednocze
œnie do wektora AB
i do wektora
AC
a wi
êc jest prostopadùy do pùaszczyzny. Jest wiêc
jej wektorem normalnym. Obieramy dowolny punkt
)
,
,
(
z
y
x
P
nale
¿¹cy do pùaszczyzny, wtedy
wektor
2
,
3
,
1
z
y
x
AP
jest prostopad
ùy do wektora
AC
AB
st
¹d mamy
0
)
(
AC
AB
AP
czyli
0
]
27
,
3
,
4
[
2
,
3
,
1
z
y
x
0
)
2
(
27
)
3
(
3
)
1
(
4
z
y
x
0
41
27
3
4
z
y
x
R
ównanie pùaszczyzny ma postaã:
0
41
27
3
4
z
y
x
.
..........................................................................................
PRZYK£AD 7
Obliczy
ã k¹t pomiêdzy pùaszczyznami
0
11
3
4
z
y
x
,
0
4
2
3
z
y
x
.
Rozwi
¹zanie
Wektor normalny pierwszej p
ùaszczyzny
to
]
1
,
3
,
4
[
1
n
, wektor normalny drugiej p
ùaszczyzny
to
]
2
,
3
,
1
[
2
n
. St
¹d
11
2
1
n
n
26
|
|
1
n

14
|
|
2
n
Oznaczmy k
¹t pomiêdzy pùaszczyznami przez
wtedy
91
2
11
14
26
|
11
|
cos
Zatem
91
2
11
cos
,
gdzie
to k
¹t pomiêdzy pùaszczyznami.
..........................................................................................
PRZYK£AD 8
Poda
ã równania kanoniczne i parametryczne prostej przechodz¹cej przez punkt
)
2
,
1
,
3
(
M
i r
ównolegù
ej do wektora
]
2
,
5
,
4
[
u
.
Rozwi
¹zanie
R
ównania kanoniczne prostej:
2
2
5
1
4
3
z
y
x
.
R
ównania parametryczne prostej:
t
z
t
y
t
x
2
2
5
1
4
3
,
t
- parametr.
..........................................................................................
PRZYK£AD 9
Znale
êã równania kanoniczne i parametryczne prostej przechodz¹cej przez dwa punkty
)
3
,
2
,
6
(
A
,
)
1
,
2
,
3
(
B
.
Rozwi
¹zanie
Wektor
]
4
,
0
,
3
[
AB
jest wektorem le
¿¹cym na prostej (jes
t wi
êc równolegùy do niej). Jest zatem
jej wektorem kierunkowym. Ustalonym punktem prostej niech b
êdzie punkt
)
3
,
2
,
6
(
A
.
R
ównania kanoniczne prostej
4
3
0
2
3
6
z
y
x
.
UWAGA.
W r
ównaniach kanonicznych prostej mo¿na umieœciã zero w mian
owniku. Nie oznacza to
dzielenia przez zero, informuje jedynie o tym,
¿e drug¹ skùadow¹ wektora kierunkowego jest zero.
R
ównania parametryczne prostej:
t
z
y
t
x
4
3
2
3
6
,
t
- parametr.
..........................................................................................
PRZYK£AD 10
Prost
¹ w
postaci
krawêdziowej
0
2
2
3
0
3
5
3
z
y
x
z
y
x
przedstawi
ã
w postaci kanonicznej
i parametrycznej.
Rozwi
¹zanie
Sposób I
Rozwi
¹¿emy ukùad równañ
2
2
3
3
5
3
z
y
x
z
y
x
.
Skoro te p
ùaszczyzn
y maj
¹ przecinaã siê wzdùu¿ prostej, to w rozwi¹zaniu powinien wyst¹piã
jeden parametr zgodnie z og
óln¹ postaci¹ równañ parametrycznych prostej.
Macierz rozszerzona
uk
ùadu ma postaã
2
2
1
3
3
5
3
1
.
1
2
3w
w
7
13
8
0
3
5
3
1
7
13
8
3
5
3
z
y
z
y
x
8
7
8
13
3
5
3
z
y
z
y
x
8
7
8
13
3
5
)
8
7
8
13
(
3
z
y
z
z
x
8
7
8
13
3
5
8
21
8
39
z
y
z
z
x
8
7
8
13
8
21
3
8
39
5
z
y
z
z
x
8
7
8
13
8
3
8
1
z
y
z
x
z jest parametrem. Oznaczmy
t
z
.
Mamy r
ównania parametryczne prostej

t
z
t
y
t
x
8
7
8
13
8
3
8
1
gdzie
t
- parametr.
Z r
ównañ parametrycznych odczytujemy wektor kierunkowy
]
1
,
8
13
,
8
1
[
u
prostej oraz ustalony
punkt
)
0
,
8
7
,
8
3
(
M
tej prostej.
Podajemy r
ównania kanoniczne
prostej:
1
8
13
8
7
8
1
8
3
z
y
x
.
Mo
¿na
podaã
równania
kanoniczne
i
parametryczne
prostej
bez
u
ùamków.
Z postaci parametrycznej wyznaczmy inny punkt prostej. Gdy
3
t
otrzymujemy
3
4
0
z
y
x
Mamy zatem punkt o wsp
óùrzêdnych
)
3
,
4
,
0
(
nale
¿¹cy do prostej.
Wektorem kierunkowym tej prostej jest ka
¿dy niezerowy wektor równolegùy do wektora
]
1
,
8
13
,
8
1
[
u
, a wi
êc np.
]
8
,
13
,
1
[
.
Podajemy r
ównania parametryczne
t
z
t
y
t
x
8
3
13
4
,
t
- parametr.
Podajemy r
ównania kanoniczne prostej:
8
3
13
4
1
z
y
x
.
Wida
ã, ¿e równania te ró¿ni¹ siê od wczeœniej podanych ale mimo to opisuj¹ t¹ sam¹ prost¹.
Sposób II
Maj
¹c równania pùaszczyzn
0
3
5
3
z
y
x
i
0
2
2
3
z
y
x
znamy wektory normalne tych
p
ùaszczyzn
5
3
1
1
,
,
n
(wektor normalny pierwszej p
ùaszczyzny) i
2
1
3
2
,
,
n
(wektor normalny
drugiej p
ùaszczyzny)
, do kt
órych jest prostopadùy wektor kierunkowy szukanej prostej, tj.
8
13
1
2
1
3
5
3
1
2
1
,
,
k
j
i
n
n
u

Z wcze
œniejszych obliczeñ wiemy, ¿e punkt
)
3
,
4
,
0
(
nale
¿y do prostej. St¹d mamy
r
ównania
parametryczne szukanej prostej :
t
z
t
y
t
x
8
3
13
4
, (
t
- parametr) oraz r
ównania kanoniczne
8
3
13
4
1
z
y
x
.
..........................................................................................
PRZYK£AD 11
Poda
ã 5 punktów nale¿¹cych do prostej
2
1
1
3
4
2
z
y
x
.
Rozwi
¹zanie
Z r
ównañ
parametrycznych
prostej
wynika,
¿e
ka¿dy
punkt
prostej
ma
postaã:
)
2
1
,
3
,
4
2
(
t
t
t
gdzie
R
t
:
dla
0
t
otrzymujemy punkt prostej
)
1
,
3
,
2
(
,
dla
1
t
otrzymujemy punkt prostej
)
1
,
2
,
6
(
,
dla
2
t
otrzymujemy punkt prostej
)
3
,
1
,
10
(
,
dla
1
t
otrzymujemy punkt prostej
)
3
,
4
,
2
(
,
dla
2
t
otrzymujemy punkt prostej
)
5
,
5
,
6
(
.
..........................................................................................
PRZYK£AD 12
Znale
êã punkt przebicia pùaszczyzny
0
4
4
3
z
y
x
prost
¹
4
2
2
3
3
1
z
y
x
.
Rozwi
¹zanie
Dla u
ùatwienia rachunków prost¹ przedstawiamy w postaci parametrycznej
t
z
t
y
t
x
4
2
2
3
3
1
,
t
- parametr
i rozwi
¹
zujemy uk
ùad równañ:
t
z
t
y
t
x
z
y
x
4
2
2
3
3
1
0
4
4
3
t
z
t
y
t
x
t
t
t
4
2
2
3
3
1
0
4
4
2
)
2
3
(
4
)
3
1
(
3

t
z
t
y
t
x
t
4
2
2
3
3
1
1
2
1
2
1
z
y
x
t
.
St
¹d p
unkt
)
2
,
1
,
2
(
jest punktem wsp
ólnym prostej i pùaszczyzny (punktem przebicia
p
ùaszczyzny prost¹)
.
..........................................................................................
PRZYK£AD 13
Znale
êã rzut
prostok
¹tny
punktu
)
4
,
0
,
7
(
M
na prost
¹
2
5
3
1
2
z
y
x
.
Rozwi
¹zanie
W podanym zadaniu chodzi o rzut prostok
¹tny
dlatego pomocniczo wyznaczymy r
ównanie
p
ùaszczyzny
prostopad
ùej
do danej prostej przechodz
¹cej przez punkt
M
. Punkt wsp
ólny
pomocniczej p
ùaszczyzny i danej prostej jest szukanym rzutem punktu
M
na dan
¹
prost
¹.
Wektor
kierunkowy prostej
]
2
,
3
,
1
[
u
b
êdzie wektorem normalnym pomocniczej pùaszczyzny
, a punkt
)
4
,
0
,
7
(
M
nale
¿y do pomocniczej pùaszczyzny.
Obieramy dowolny punkt
)
,
,
(
z
y
x
P
nale
¿¹cy do pomocniczej pùaszczyzny,
wtedy wektor
4
,
,
7
z
y
x
MP
jest prostopad
ùy do wektora normalnego
]
2
,
3
,
1
[
u
p
ùaszczyzny.
Mamy
zatem
0
u
MP
czyli
0
2
,
3
,
1
4
,
,
7
z
y
x
0
)
4
(
2
3
7
z
y
x
0
1
2
3
z
y
x
- r
ównanie p
omocniczej
p
ùaszczyzny
Punkt wsp
ólny
pomocniczej p
ùaszczyzny i danej prostej
wyznaczymy podobnie jak w Przyk
ùadzie
12.
Prost
¹ przedstawiamy w postaci parametrycznej:
t
z
t
y
t
x
2
5
3
1
2
,
t
- parametr
i rozwi
¹zujemy ukùad równañ:
t
z
t
y
t
x
z
y
x
2
5
3
1
2
0
1
2
3
3
2
1
1
z
y
x
t
.
Stad punkt
)
3
,
2
,
1
(
jest rzutem punktu
M
na prost
¹
2
5
3
1
2
z
y
x
.
..........................................................................................
PRZYK£AD 14
Znale
êã odlegùoœã punktu
)
1
,
2
,
4
(
M
od prostej
3
3
2
4
z
y
x
.
Rozwi
¹zanie
Wyznaczymy rzut punktu
)
1
,
2
,
4
(
M
na prost
¹
3
3
2
4
z
y
x
. Otrzymany punkt oznaczmy
przez
A
. Obliczymy d
ùugoœã odcinka AM
. Otrzymana liczba jest odleg
ùoœci¹ punktu
)
1
,
2
,
4
(
M
od
prostej
3
3
2
4
z
y
x
.
Punkt
A
czyli rzut punktu
M
na prost
¹ wyznaczymy w taki sam sposób jak w przykùadzie 13.
Pomocniczo wyznaczymy r
ównanie pùaszczyzny prostopadùej do danej prostej przechodz¹cej
przez punkt
M
.
Wektor kierunkowy prostej
]
1
,
3
,
2
[
u
b
êdzie wektorem nor
malnym pomocniczej p
ùaszczyzny, a
punkt
)
1
,
2
,
4
(
M
nale
¿y do pomocniczej pùaszczyzny.
Obieramy dowolny punkt
)
,
,
(
z
y
x
P
nale
¿¹cy do pomocniczej pùaszczyzny,
wtedy wektor
1
,
2
,
4
z
y
x
MP
jest prostopad
ùy do wektora normalnego
]
1
,
3
,
2
[
u
p
ùaszczyzny.
Mamy
zatem
0
u
MP
czyli
0
]
1
,
3
,
2
[
1
,
2
,
4
z
y
x
0
1
)
2
(
3
)
4
(
2
z
y
x
0
3
3
2
z
y
x
- r
ównanie pomocniczej
p
ùaszczyzny
Punkt wsp
ólny pomocniczej pùaszczyzny i danej prostej jest szukanym punktem
A
czyli rzutem
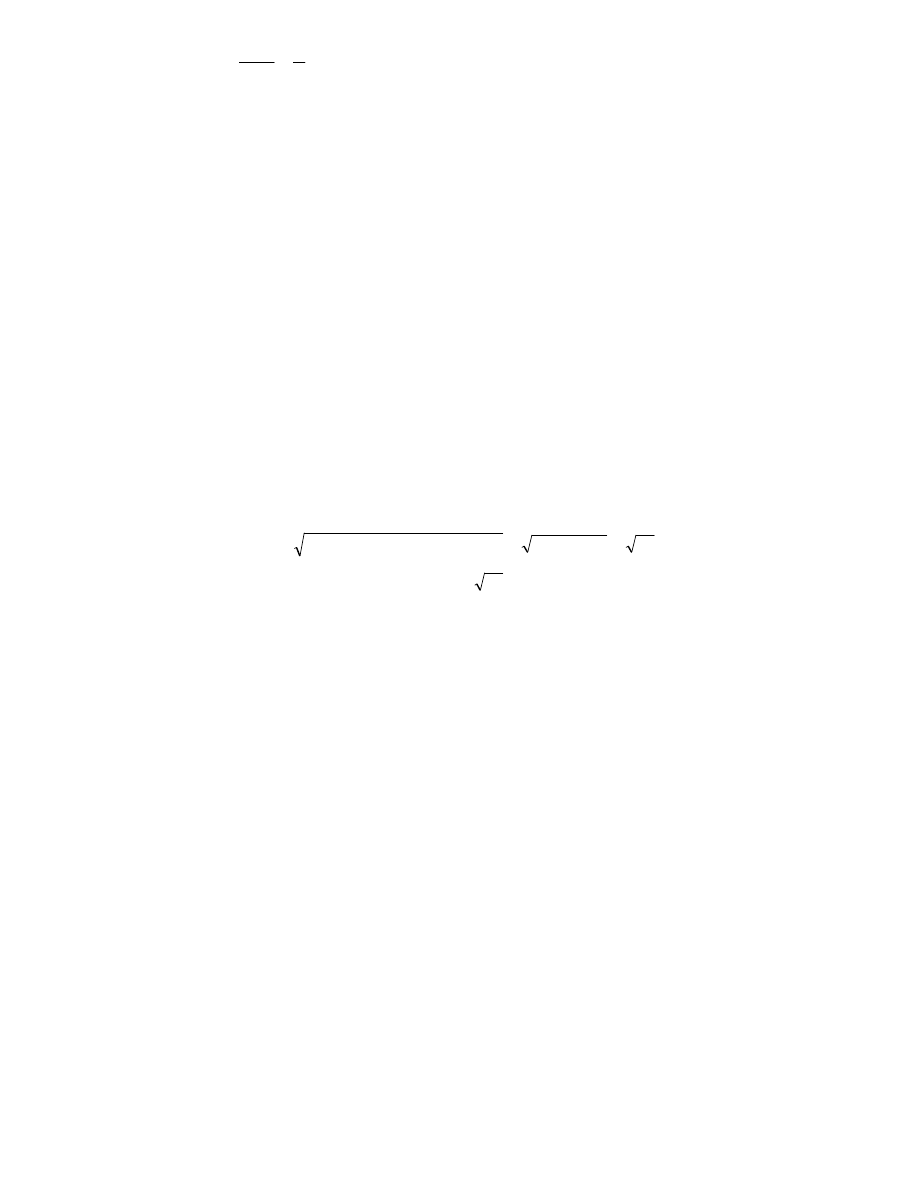
punktu
M
na prost
¹
3
3
2
4
z
y
x
. Punkt wsp
ólny wyznaczymy podobnie jak w przykùadzie
12. Prost
¹ przedstawiamy w postaci parametrycznej:
t
z
t
y
t
x
3
3
2
4
,
t
- parametr
i rozwi
¹zujemy ukùad równañ:
t
z
t
y
t
x
z
y
x
3
3
2
4
0
3
3
2
2
3
2
1
z
y
x
t
St
¹d
)
2
,
3
,
2
(
A
jest rzutem punktu
M
na prost
¹.
Obliczamy d
ùugoœã odcinka
AM
70
9
25
36
)
2
1
(
)
3
2
(
)
2
4
(
|
|
2
2
2
AM
Ostatecznie odleg
ùoœã punktu
M
od prostej wynosi
70
.
..........................................................................................

RZYK£AD 15
Znale
êã
punkt
symetryczny
do
punktu
)
0
,
1
,
2
(
M
wzgl
êdem
prostej
2
1
2
2
3
z
y
x
.
Rozwi
¹zanie
Aby wyznaczy
ã punkt symetryczny do punktu
M
wzgl
êdem prostej najpierw
wyznaczymy rzut punktu
M
na prost
¹. Otrzymany punkt oznaczymy
przez
A
.
Nast
êpnie punkt A
przesuniemy o wektor
MA
. Otrzymany punkt b
êdzie
symetryczny
do punktu
)
0
,
1
,
2
(
M
wzgl
êdem danej prostej.
Aby wyznaczy
ã p
unkt
A
czyli rzut
punktu
M
na prost
¹ postêpujemy tak jak w przykùadzie 13.
Pomocniczo
wyznaczamy r
ównanie pùaszczyzny
prostopad
ùej do danej prostej przechodz¹cej
przez punkt
M
. Po prostych obliczeniach otrzymujemy r
ównanie pomocniczej
p
ùaszczyzny w postaci:
0
3
2
2
z
y
x
. Punkt wsp
ólny pomocniczej pùaszczyzny
i danej prostej, czyli rzut punktu
M
na prost
¹
, ma wsp
óùrzêdne
)
1
,
3
,
1
(
A
.Punkt
A
przesuwamy o wektor
]
1
,
4
,
3
[
MA
i otrzymujemy punkt o wsp
óùrzêdnych
)
2
,
7
,
4
(
jest to punkt symetryczny do punktu
M
wzgl
êdem prostej.
Ostatecznie punkt symetryczny do punktu
M
wzgl
êdem prostej to punkt
)
2
,
7
,
4
(
.
..........................................................................................
PRZYK£AD 16
Znale
êã
rzut prostok
¹tny
punktu
)
2
,
3
,
6
(
M
na p
ùaszczyznê
0
6
3
z
y
x
.
Rozwi
¹zanie
Pomocniczo wyznaczymy r
ównanie prostej
prostopad
ùej
do danej p
ùaszczyzny
przechodz
¹cej przez punkt
M
. Punkt wsp
ólny pomocniczej
prostej i danej
p
ùaszczyzny jest szukanym rzutem punktu
M
na dan
¹
p
ùaszczyznê.
Wektor
normalny
p
ùaszczyzny
]
1
,
3
,
1
[
n
b
êdzie
wektorem
kierunkowym
pomocniczej prostej, a punkt
)
2
,
3
,
6
(
M
nale
¿y do pomocniczej
prostej.
Mamy zatem r
ównania parametryczn
e pomocniczej prostej w postaci
t
z
t
y
t
x
2
3
3
6
,
t
- parametr.
Aby wyznaczy
ã punkt wspólny pomocniczej prostej i danej pùas
zczyzny rozwi
¹¿emy
uk
ùad równañ

t
z
t
y
t
x
z
y
x
2
3
3
6
0
6
3
zatem
1
0
7
1
z
y
x
t
.
Ostatecznie rzutem punktu
M
na p
ùaszczyznê jest punkt
)
1
,
0
,
7
(
.
..........................................................................................
PRZYK£AD 17
Znale
êã
rzut
prostok
¹tn
y
prostej
2
3
1
4
2
z
y
x
na
p
ùaszczyznê
0
3
2
7
z
y
x
.
Rozwi
¹zanie
Rzutem prostej na p
ùaszczyznê jest prosta, któr¹ podamy w postaci krawêdziowej
jako przeci
êcie danej pùaszczyzny oraz pomocniczej pùaszczyzny prostopadùej do
danej p
ùasz
czyzny i zawieraj
¹cej dan¹ prost¹.
Punkt prostej
)
0
,
1
,
2
(
nale
¿y równie¿
do pomocniczej p
ùaszczyzny.
Aby wyznaczy
ã równanie pomocniczej pùaszczyzny
potrzebujemy jeszcze jej wektora normalnego.
Mamy wektor kierunkowy prostej
]
2
,
3
,
4
[
u
oraz wektor normalny p
ùaszczyzny
]
3
,
2
,
1
,
7
[
n
. Wektor
]
17
,
6
,
4
[
n
u
jest wektorem normalnym pomocniczej
p
ùaszczyzny.
Obieramy
dowolny
punkt
)
,
,
(
z
y
x
P
nale
¿¹cy
do
pomocniczej
p
ùaszczyzny,
wtedy wektor
z
y
x
MP
,
1
,
2
jest prostopad
ùy do wektora
normalnego
]
17
,
6
,
4
[
n
u
pomocniczej p
ùaszczyzny.
Mamy zatem:
0
)
(
n
u
MP
czyli
0
]
17
,
6
,
4
[
,
1
,
2
z
y
x
0
17
)
1
(
6
)
2
(
4
z
y
x
0
2
17
6
4
z
y
x
0
2
17
6
4
z
y
x
- r
ównanie pomocniczej
p
ùaszczyzny

Otrzymujemy prost
¹ w postaci krawêdziowej
0
2
17
6
4
0
3
2
7
z
y
x
z
y
x
, kt
óra jest
szukanym rzutem prostej na p
ùaszczyznê.
..........................................................................................
Wyszukiwarka
Podobne podstrony:
Leczenie prostaty id 264608 Nieznany
Leczenie prostaty id 264608 Nieznany
Abolicja podatkowa id 50334 Nieznany (2)
4 LIDER MENEDZER id 37733 Nieznany (2)
katechezy MB id 233498 Nieznany
metro sciaga id 296943 Nieznany
perf id 354744 Nieznany
interbase id 92028 Nieznany
Mbaku id 289860 Nieznany
Probiotyki antybiotyki id 66316 Nieznany
miedziowanie cz 2 id 113259 Nieznany
LTC1729 id 273494 Nieznany
D11B7AOver0400 id 130434 Nieznany
analiza ryzyka bio id 61320 Nieznany
pedagogika ogolna id 353595 Nieznany
Misc3 id 302777 Nieznany
cw med 5 id 122239 Nieznany
więcej podobnych podstron