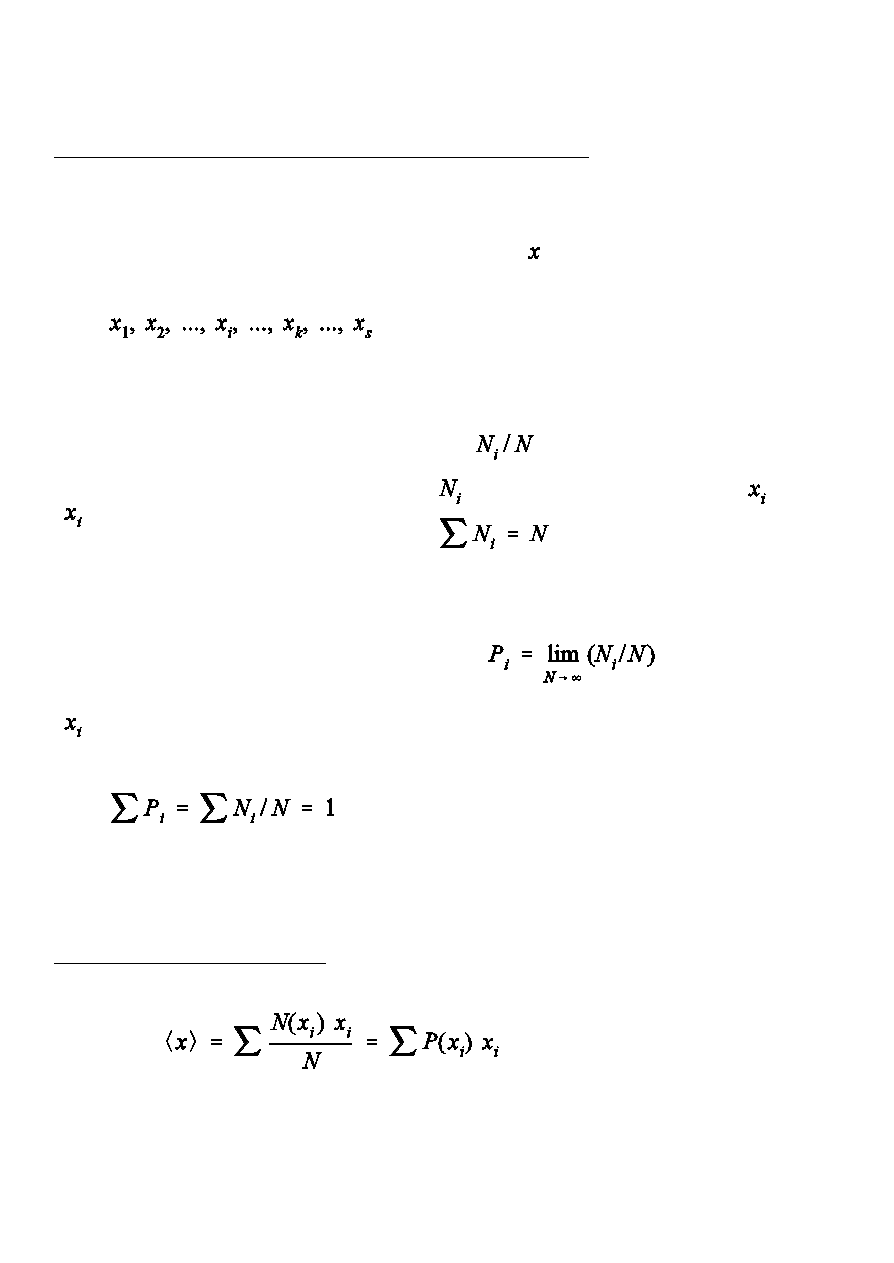
Fizyka s tatystycz na 1

FIZYKA STATYSTYCZNA

Wybrane zagadnienia z rachunku prawdopodobie½stwa

Rozwaómy uk»ad makroskopowy znajdujcy si“ w danym stanie. Za»óómy, óe

pewna charakterystyczna dla uk»adu wielkoу   moóe przyjmowaƒ dyskretne

wartoÑci

.

Wzgl“dna cz“stoу

pojawiania si“ wyniku

-

wielkoу 

 - liczba pomiarów o wyniku 

    - liczba wszystkich

pomiarów

Prawdopodobie½stwo

pojawienia si“ wyniku

-

wielkoу   

Suma prawdopodobie½sw wszystkich moóliwych

wyników pomiaru jest równa jednoÑci.

Ðrednia wyników pomiarów

Fizyka s tatystycz na 2

Przypadek cig»ego widma wartoÑci wyników pomiaru

Uogólnijmy otrzymane wyniki na przypadek, kiedy wielkoу   moóe przyjmowaƒ

w sposób  cig»y wartoÑci rzeczywiste od 0 do 4.

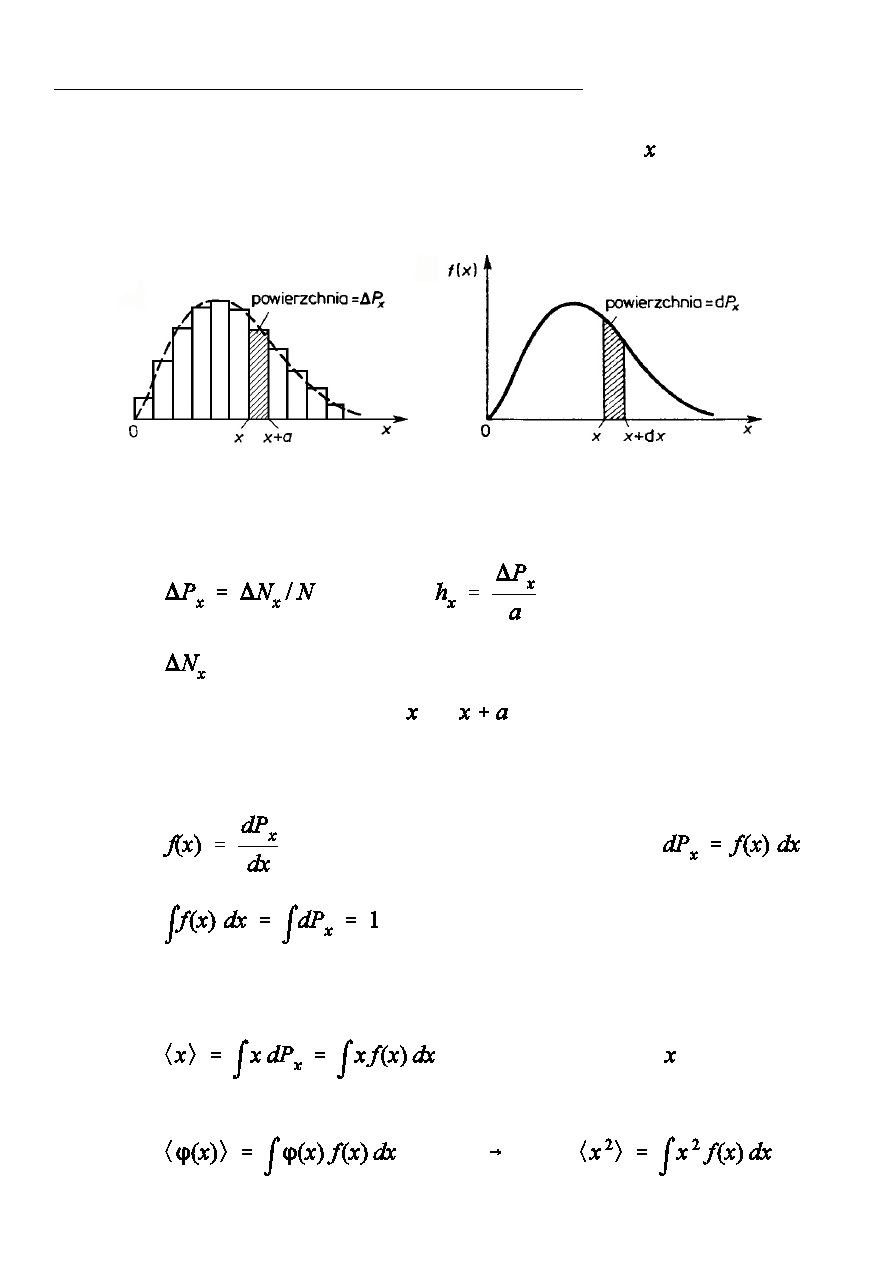
  Histogram

Funkcja rozk»adu

  - wysokoу paska,

   -

liczba pomiarów, dla których wynik pomiaru jest zawarty w

przedziale od   do 

.

Pole powierzchni ca»ego histogramu jest równe jednoÑci.

   - g“stoу prawdopodobie½stwa, 

  

warunek normalizacji prawdopodo-

bie½stwa

-  Ñrednia wartoу 

np. 

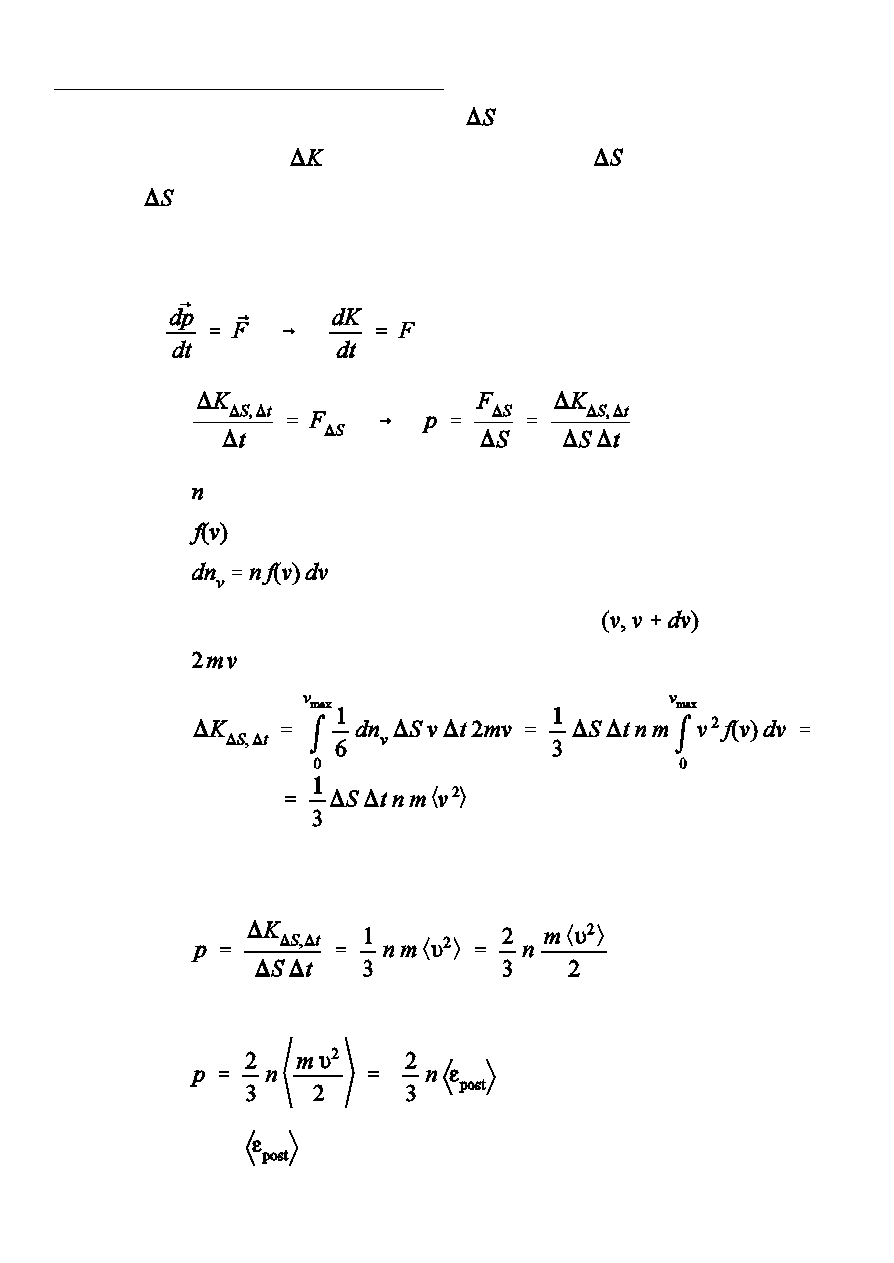
Fizyka s tatystycz na 3

CiÑnienie gazu (obliczenia uproszczone)

W wyniku uderze½ czsteczek elementowi 

 Ñcianki naczynia w jednostce czasu

przekazywany jest p“d 

 równy sile dzia»ajcej na 

. Stosunek tej si»y do

wartoÑci 

 jest ciÑnieniem gazu na Ñciank“ naczynia.

Przyjmiemy oznaczenie K dla p“du, óeby si“ nie myli»o z oznaczeniem p dla

ciÑnienia.

          

  

 

          

 

        -   liczba czsteczek w jednostce obj“toÑci

 

        -   funkcja rozk»adu modu»u pr“dkoÑci czsteczek

  -   liczba czsteczek w jednostce obj“toÑci majcych

    pr“dkoÑci z przedzia»u 

        -   zmiana p“du czsteczki przy odbiciu

Std ciÑnienie gazu

Przyjmujc, óe masa wszystkich czstek jest taka sama, otrzymujemy

    - Ñrednia energia ruchu post“powego czsteczki.

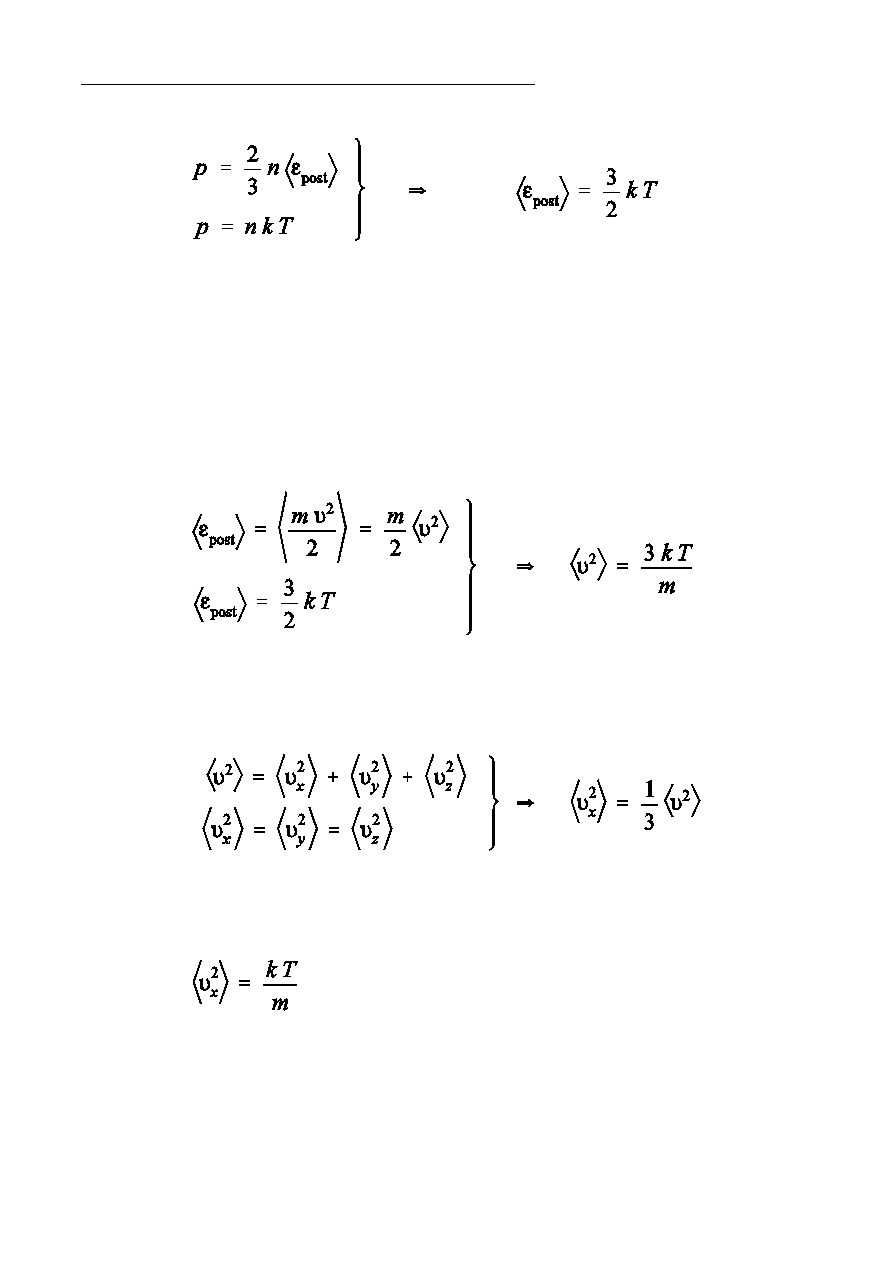
Fizyka s tatystycz na 4

Ðrednia energia ruchu post“powego czsteczek

Z zaleónoÑci tej wynika, óe temperatura bezwzgl“dna jest proporcjonalna do

Ñredniej energii kinetycznej ruchu post“powego czsteczek.  (Sprawdza si“ to w

przypadku gazów, natomiast ze wzgl“du na wyst“powanie efektów kwantowych

nie dotyczy to cieczy i cia» sta»ych.)

Fizyka s tatystycz na 5

Zasada ekwipartycji energii

Wynik 

 wióe si“ z prawem ekwipartycji energii (zasad

równego rozk»adu energii na stopnie swobody czsteczek). 

Na kaódy rodzaj ruchu  (stopie½ swobody) przypada - Ñrednio - taka sama

energia kinetyczna 

.

Liczb stopni swobody uk»adu mechanicznego nazywamy liczb“

niezaleónych wspó»rz“dnych, za pomoc których moóe byƒ opisane

po»oóenie uk»adu.

Punkt materialny ma trzy stopnie swobody (do opisu jego po»oóenia w

przestrzeni potrzebne s trzy wspó»rz“dne)

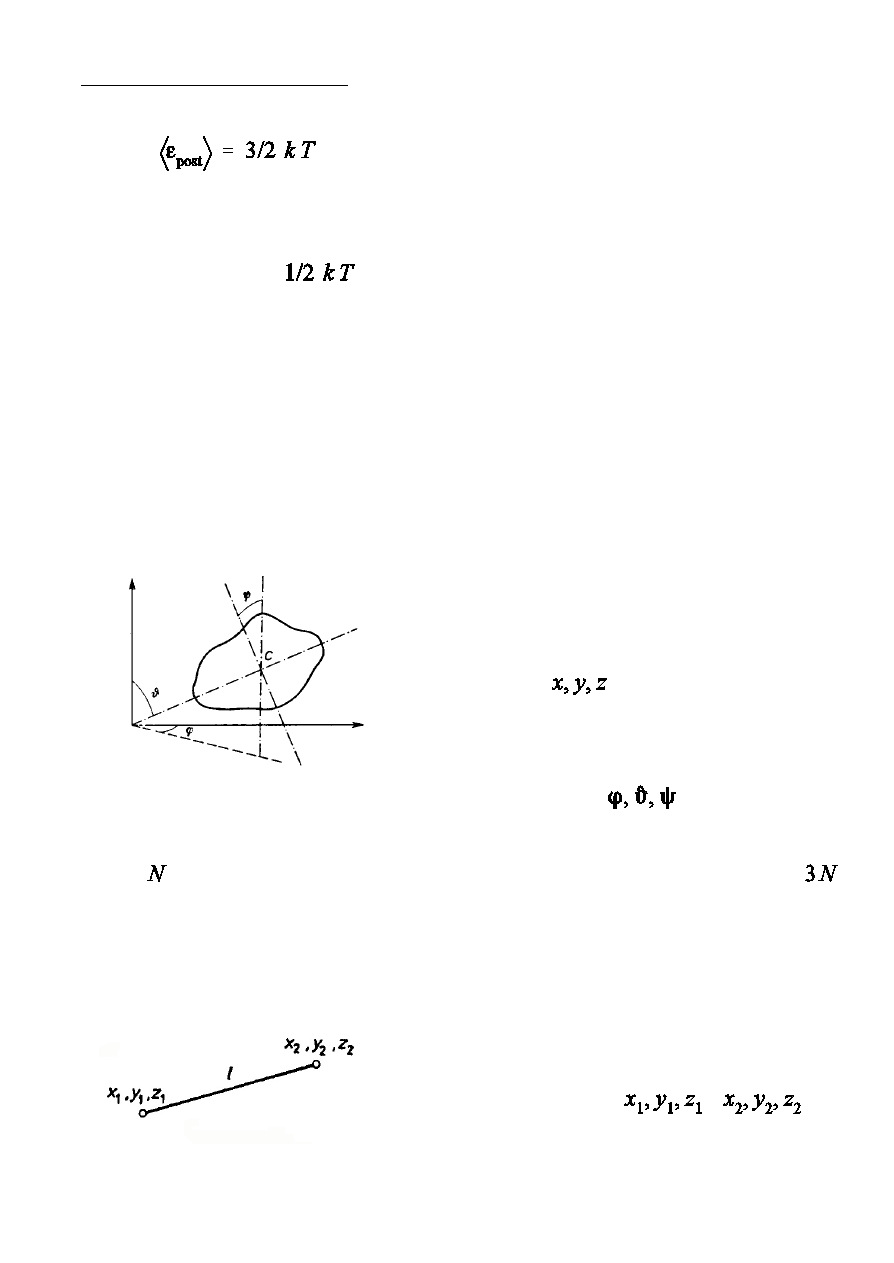
Bry»a sztywna ma szeу stopni swobody:

  -

t r z y  p o s t “ powe (t ran slac yjne) ,

zwizane z opisem po»oóenia Ñrodka

masy (

),

  -

trzy obrotowe (rotacyjne), zwizane

opisem po»oóenia osi bry»y w

przestrzeni (

).

Uk»ad   punktów materialnych, które nie s ze sob sztywno zwizane ma 

stopni swobody. Kaóde sztywne wizanie mi“dzy dwoma punktami zmniejsza

liczb“ stopni swobody o jeden.

Uk»ad dwóch punktów materialnych o sta»ej

wzajemnej odleg»oÑci posiada pi“ƒ stopni

swobody. (Wspó»rz“dne 

 i 

 nie

s ca»kowicie niezaleóne)

Fizyka s tatystycz na 6

Zasada ekwipartycji energii, cd.

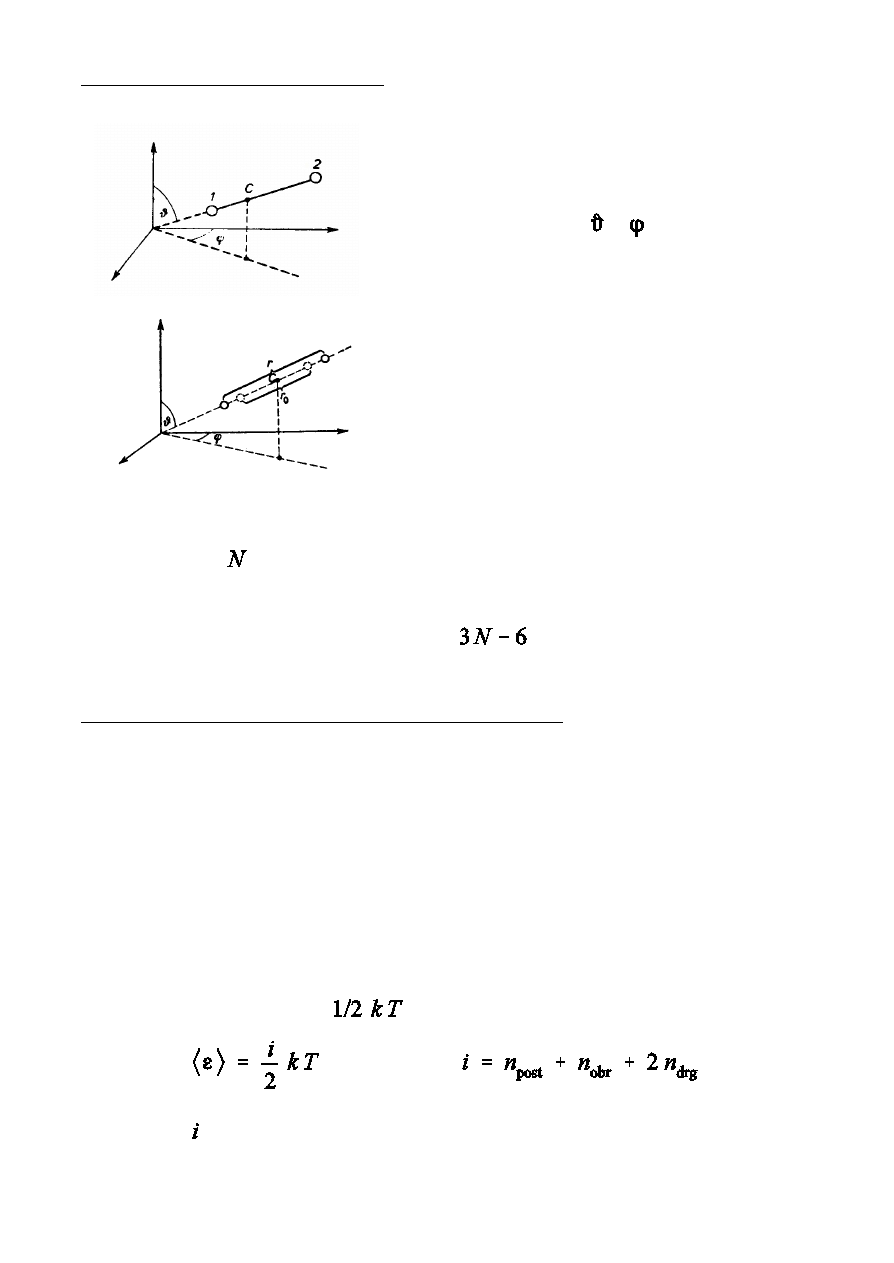
Do opisu po»oóenia uk»adu dwóch punktów

materialnych o sta»ej wzajemnej odleg»oÑci

potrzeba pi“ƒ wspó»rz“dnych, trzy wspó»rz“dne

Ñrodka masy oraz kty   i  .

Uk»ad dwóch punktów materialnych po»czonych

wizaniem, które nie jest sztywne, ma szeу

stopni swobody

 -

trzy translacyjne,

 -

dwa rotacyjne,

 -

jeden oscylacyjny (drganiowy).

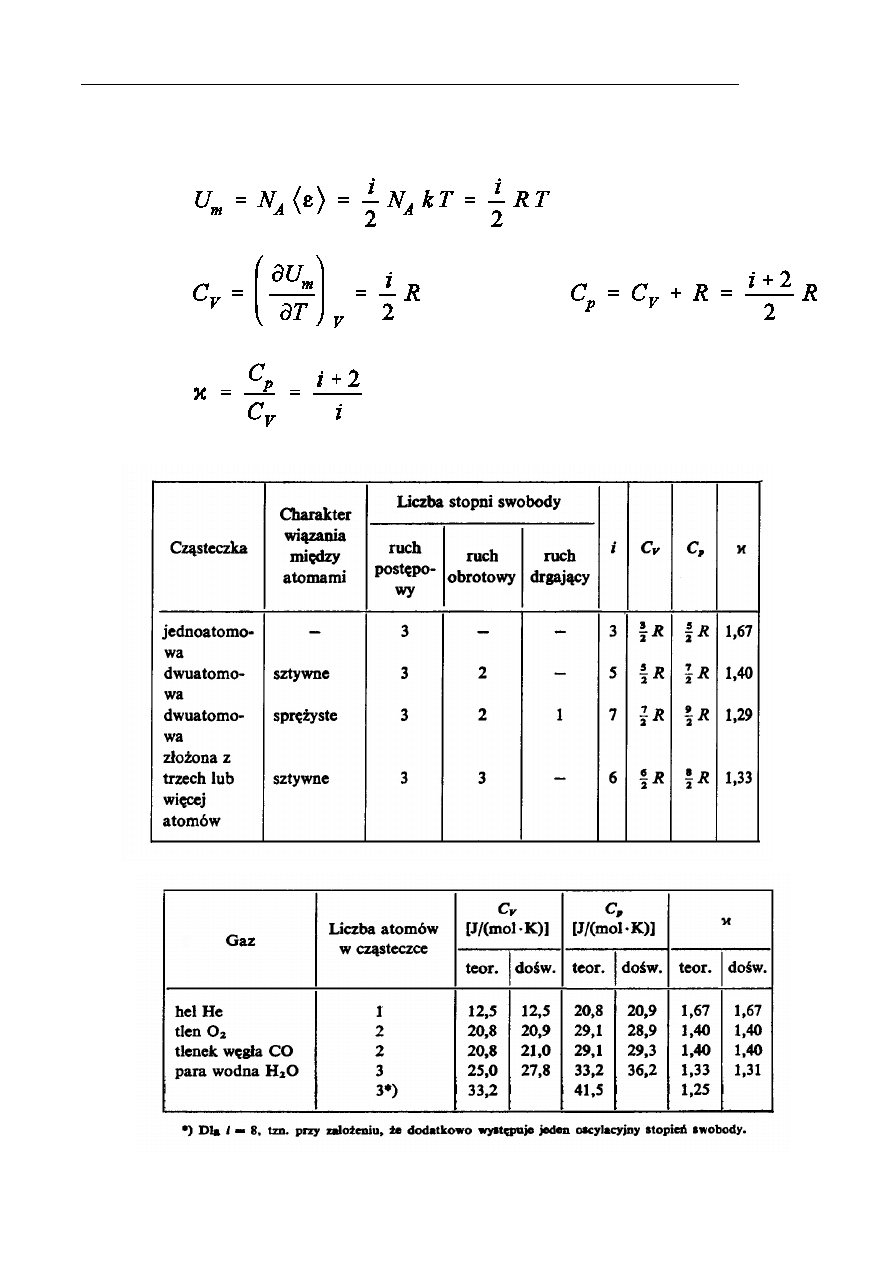
Dla  uk»adu 

 spr“óyÑcie powizanych punktów materialnych (przy

równowagowych po»oóeniach punktów nie leócych na jednej prostej) liczba

oscylacyjnych stopni swobody wynosi 

.

Obliczanie Ñredniej energii kinetycznej czsteczki

 -

przy obliczaniu iloÑci stopni swobody czsteczki atomy traktuje si“ jak

punkty materialne,

 -

oscylacyjnym stopniom swobody przypisuje si“ podwojon energi“

translacyjnego (lub rotacyjnego) stopnia swobody. (Ruchy post“powe lub

obrotowe zwizane s tylko z energi kinetyczn, natomiast ruchy

oscylacyjne z energi kinetyczn i potencjaln, których Ñrednie wartoÑci z

osobna wynosz po 

).

 - liczba stopni swobody czsteczki.

Fizyka s tatystycz na 7

Energia wewn“trzna i ciep»o w»aÑciwe czsteczek gazu doskona»ego

Czsteczki gazu doskona»ego nie oddzia»ywuj ze sob. Std

,

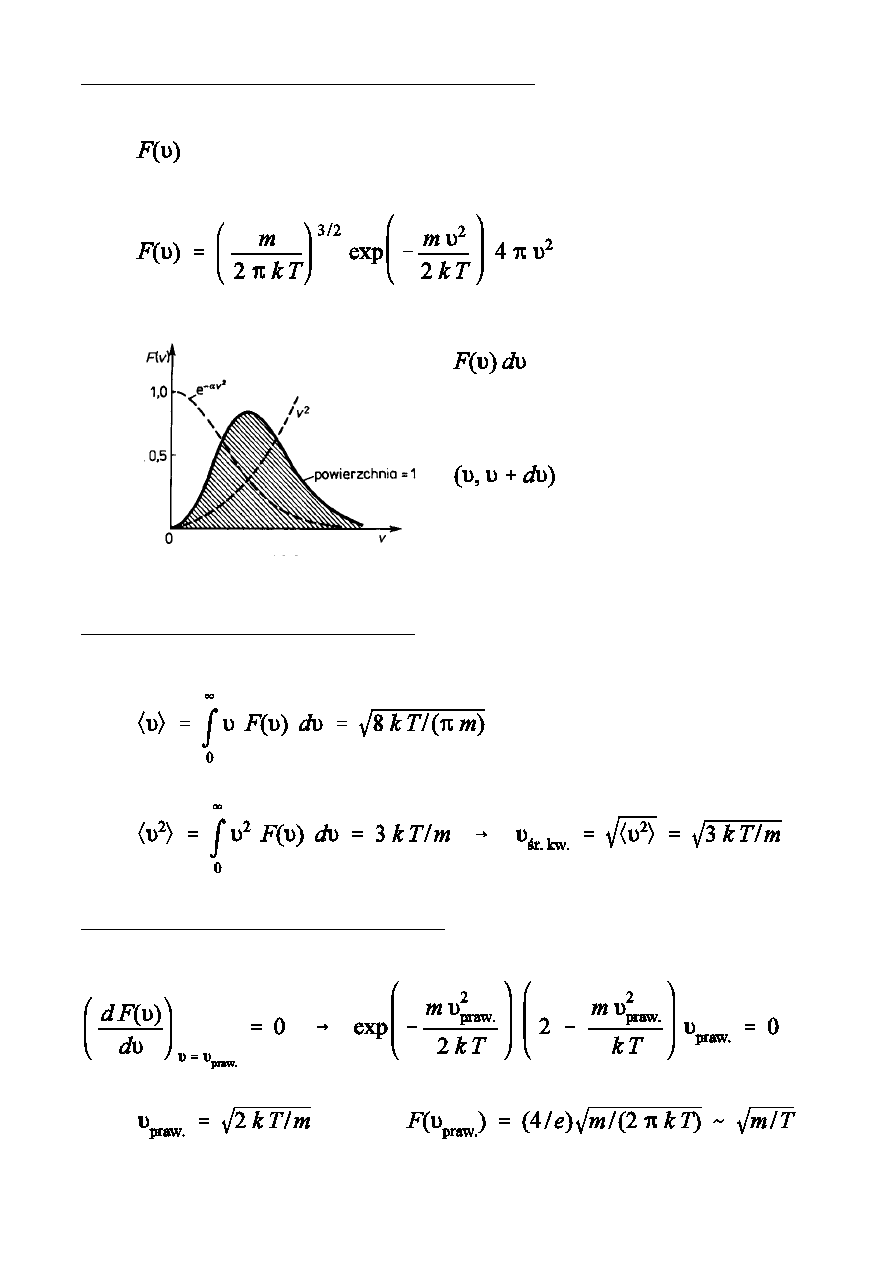
Fizyka s tatystycz na 8

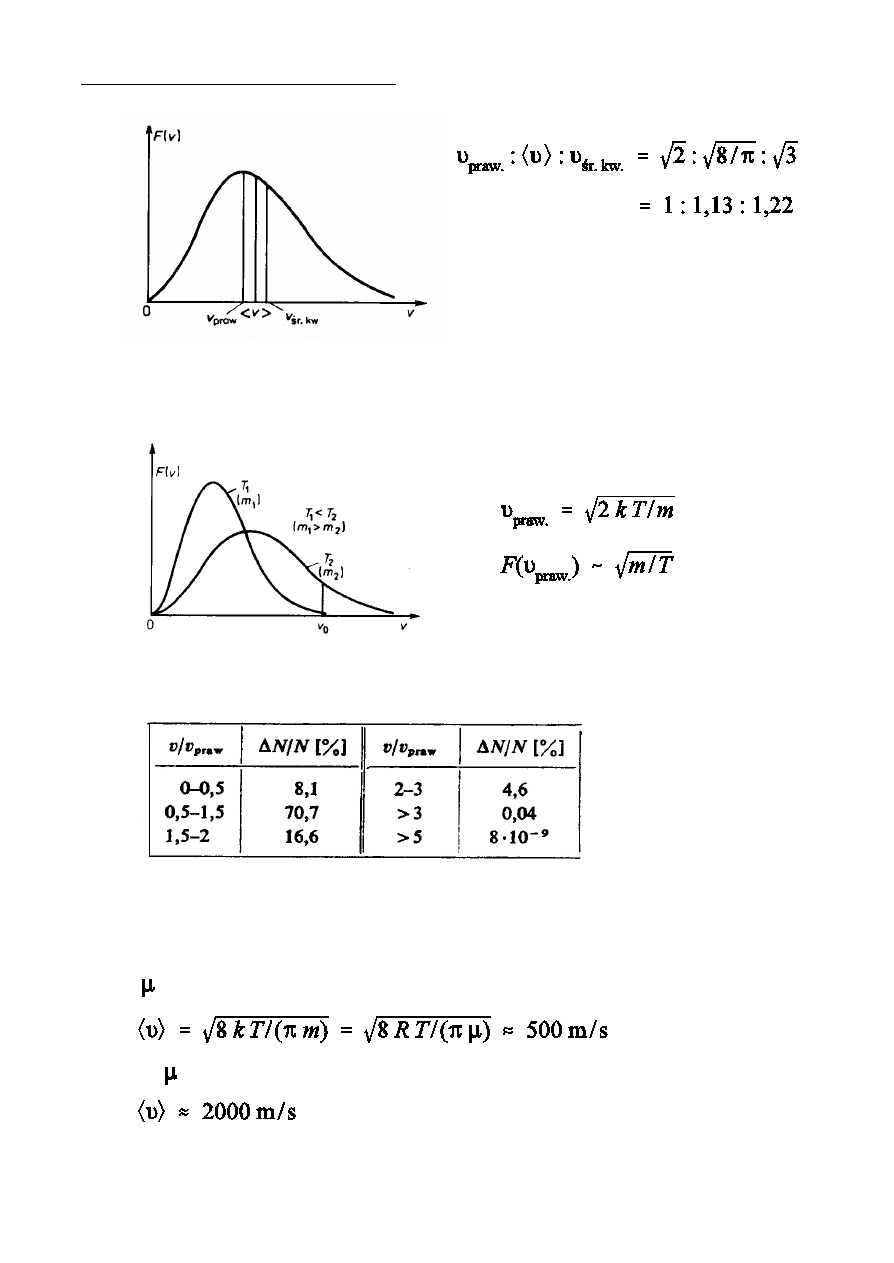
Rozk»ad Maxwella (rozk»ad pr“dkoÑci czstek)

   -

funkcja rozk»adu pr“dkoÑci czsteczek gazu.

    (rozk»ad Maxwella)

 ma znaczenie prawdopodo-

bie½stwa tego, óe dana czsteczka ma

modu» pr“dkoÑci zawarty w przedziale

Ðrednie pr“dkoÑci czsteczek gazu

   

Pr“dkoу najbardziej prawdopodobna

    

,

Fizyka s tatystycz na 9

W»aÑciwoÑci rozk»adu Maxwella

   

Tlen (  = 32 g/mol, T = 300 K )

Wodór ( = 2 g/mol, T = 300 K )

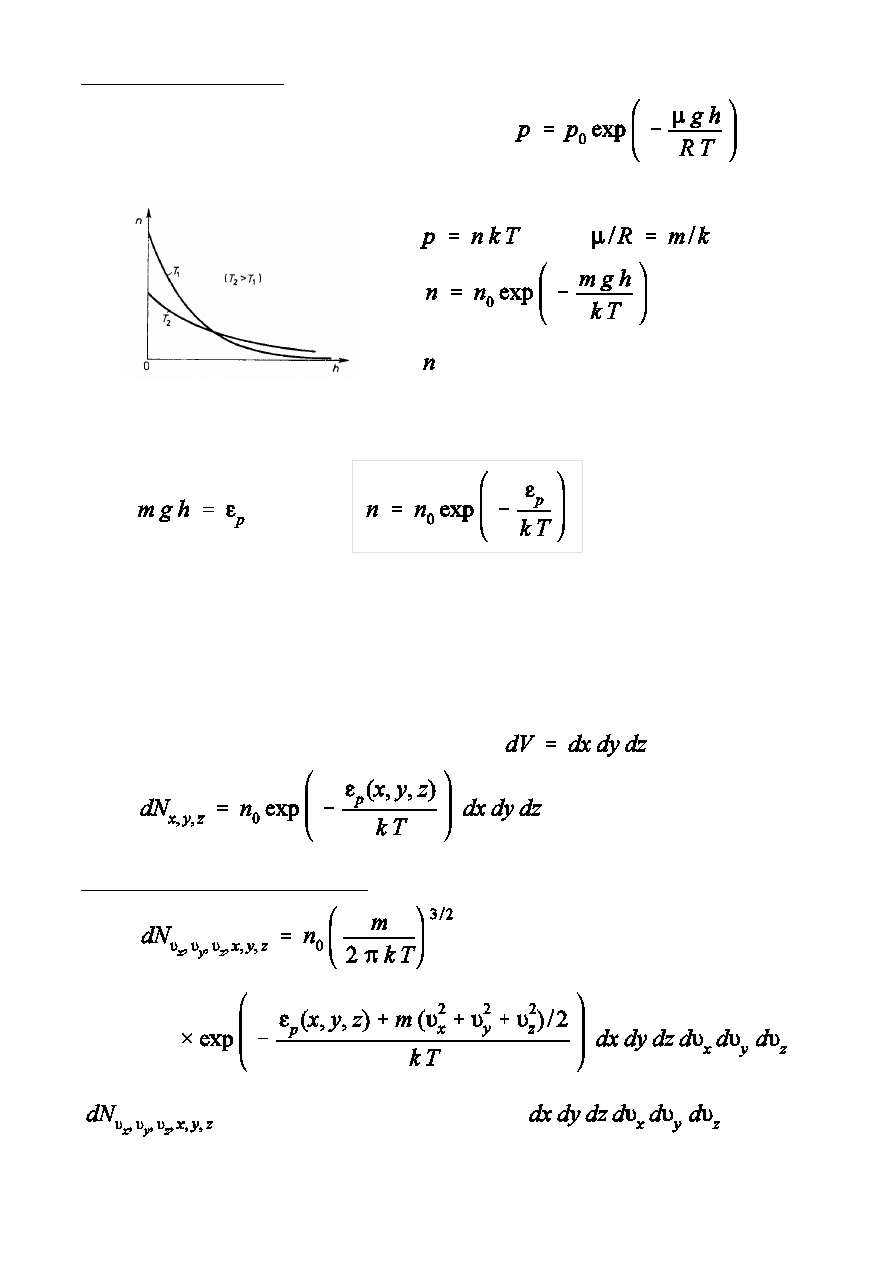
Fizyka statystyczna 10

Rozk»ad Boltzmanna

Wzór barometryczny

,

 

   - liczba czstek w jednostce obj“toÑci

(koncentracja czstek)

         

Rozk»ad Boltzmanna. 

Rozk»ad Boltzmanna jest to rozk»ad koncentracji czsteczek w dowolnym

potencjalnym polu si», o ile mamy do czynienia ze zbiorem jednakowych czstek

poruszajcych si“ chaotycznym ruchem cieplnym.

Liczba czstek w elemencie obj“toÑci 

Prawo Maxwella-Boltzmanna

         

       

 - liczba czstek w elemencie 

 przestrzeni

szeÑciowymiarowej.