Politechnika Świętokrzyska
Wydział Mechatroniki i Budowy Maszyn
Centrum Laserowych Technologii Metali PŚk i PAN
Zakład Informatyki i Robotyki
Przedmiot: Teoria Sterowania - laboratorium, rok IV, sem. VII,
Specjalność: Zastosowanie Informatyki, 2003÷2004.
Ćwiczenie nr 5
Badanie układu regulacji temperatury – symulacja komputerowa
1. Wstęp
Stosuje się kilka podziałów klasyfikacyjnych układów automatycznej regulacji (UAR). Do
najczęściej stosowanych należą podział ze względu na zadanie układu oraz podział ze względu
na sposób działania elementów układu.
Ze względu na sposób działania UAR można podzielić na:
‒
układy o działaniu ciągłym,
‒
układy o działaniu nieciągłym.
W układach o działaniu ciągłym wszystkie elementy układu działają w sposób
ciągły w czasie i poziomie. Oznacza to, że wszystkie sygnały są funkcjami ciągłymi i mogą
przybierać każdą wartość (od najmniejszej do największej), znajdującą się w normalnym
obszarze ich zmienności.
Układy o działaniu nieciągłym (dyskretnym) zawierają przynajmniej jeden element
o działaniu dyskretnym w czasie lub poziomie. Sygnały wyjściowe (lub wejściowe) tych
elementów mogą przyjmować tylko niektóre, wybrane wartości lub występują tylko w
wybranych chwilach czasu. Przykładem układów o działaniu nieciągłym są układy
regulacji dwustawnej.
Wielkość wyjściowa regulatora w dwustawnych UAR może przyjmować tylko
dwie wartości: maksymalną i minimalną. Taki regulator nazwano regulatorem
dwustawnym. Prostota i taniość regulatorów dwustawnych zadecydowały o ich
powszechnym zastosowaniu, ograniczonym jednak do obiektów, w których dopuszczalne
1
są periodyczne zmiany wielkości regulowanej, wynikające z dwustawnego działania
regulatora. Regulacja dwustawna jest najczęściej stosowana w układach regulacji
temperatury.
2. Budowa dwustawnych regulatorów temperatury
Regulatory dwustawne można podzielić pod względem konstrukcji na dwie grupy.
Pierwsza grupa to regulatory ze stykami przełączanymi bezpośrednio przez czujnik
(termometry stykowe). Drugą grupę stanowią regulatory dwustawne z pośrednim
przełączaniem styków.
2.1. Regulatory dwustawne ze stykami przełączanymi bezpośrednio przez czujnik
Przykładem regulatora dwustawnego z zestykiem przełączanym bezpośrednio
przez czujnik jest termometr rtęciowy kontaktowy (rys.2.1.). Do zbiornika rtęci 1
zatopiono na trwałe elektrodę 2. W rurce 3 znajduje się ruchoma elektroda 4 połączona z
nakrętką 5. Pokręcając śrubą 6 za pomocą magnesu zewnętrznego 7, przesuwamy
elektrodę 4, co zmienia wartość zadaną. Ze względu na małą obciążalność styku, elektroda
4 – rtęć, termometr kontaktowy współpracuje zwykle z przekaźnikiem pośredniczącym.
Zetknięcie słupka rtęci z elektrodą nastawną 4 powoduje zamknięcie obwodu zasilania
przekaźnika. Wówczas jego styk rozwierny wyłączy uzwojenie grzejne, np. pieca
elektrycznego. W innych konstrukcjach styki mogą być uruchamiane bimetalem,
dylatometrem itp.
Rys. 2.1.1 Termometr kontaktowy rtęciowy
2.2 Regulatory elektroniczne
Współczesne regulatory elektroniczne są urządzeniami mikroprocesorowymi.
Przykładem takiego regulatora jest mikroprocesorowy regulator RE54 produkowany
2
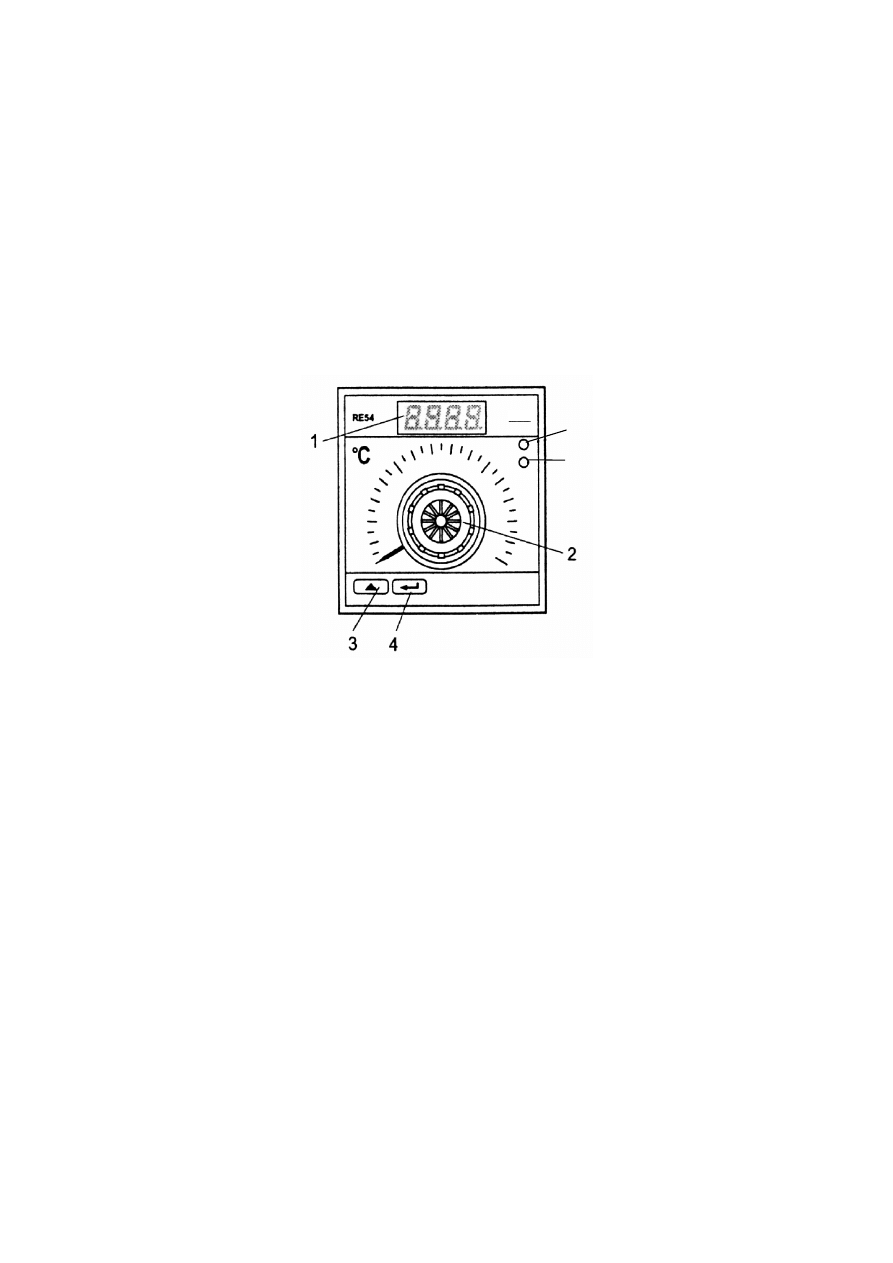
przez „LUMEL” Zielona Góra. Płytę czołową tego regulatora pokazano na rys. 2.2.1
Regulator RE54 wyposażony jest w cyfrowy wskaźnik wartości wielkości regulowanej 1 i
analogowy nastawnik wartości zadanej 2. Oprogramowanie regulatora umożliwia
wybranie różnych wariantów pracy tego regulatora np.: wariant podstawowy - regulator
dwustawny lub warianty, w których regulator dwustawny ma własności zbliżone do
regulatorów typu P, PD lub PID. Przyciski 3 i 4, oznaczone symbolami , służą do
wybór wariantu algorytmu regulatora jego nastaw. Diody 5 i 6 sygnalizują stany wyjść
regulatora. Schemat obsługi regulatora przedstawia rys. 2.2.
3. Charakterystyka statyczna regulatora dwustawnego
Charakterystykę statyczną regulatora dwustawnego z histerezą dodatnią
przedstawiono na rys. 3.1. Jeżeli odchyłka e = y – y
z
jest zawarta w przedziale –H/2 < e <
+H/2, to możliwe są dwa stany wyjściowe: u = U
max
lub U
min
. Charakterystyka jest w tym
przedziale niejednoznaczna. Zmiana stanu wyjściowego regulatora z U
max
na U
min
następuje wówczas, gdy odchyłka przekroczy wartość e = H/2 i odwrotnie: z U
min
na U
max
,
gdy odchyłka zmaleje poniżej wartości e = – H/2. H jest szerokością strefy histerezy i
zależy od konstrukcji regulatora. W niektórych regulatorach szerokość strefy histerezy
można zmieniać w pewnym zakresie.
3
Rys. 2.2.1 Mikroprocesorowy regulator RE54
5
6
LUMEL
Rys. 3.1. Charakterystyka statyczna regulatora dwustawnego
4. Układ regulacji dwustawnej
Schemat blokowy układu regulacji dwustawnej pokazano na rys. 4.1, a
charakterystykę skokową obiektu regulacji przedstawiono na rys. 4.2. Jeżeli na wejście
obiektu załączymy U
max
, to w czasie t sygnał wyjściowy osiągnie wartość y
max
.
Odpowiednio dla u = U
min
otrzymamy wartość y
min
. Z charakterystyki skokowej obiektu
wyznaczono:
‒
T
m
– czas martwy obiektu (charakterystyczna właściwość obiektu polegająca na
przedłużeniu stanu istniejącego przed wymuszeniem),
‒
T
0
– opóźnienie zastępcze obiektu,
‒
T
z
– zastępcza stała czasowa obiektu.
Wykres przebiegu temperatury w układzie regulacji dwustawnej pokazano na
rys. 4.3. W chwili t
0
na wejście obiektu jest załączone napięcie U
max
, temperatura y w
obiekcie narasta. W chwili t
1
temperatura obiektu osiągnęła wartość y
z
+ H/2. W tym
momencie regulator wyłączy grzanie (u = U
min
). Pomimo to temperatura obiektu nadal
narasta przez czas T
m
, po czym zaczyna maleć. W chwili t
2
temperatura zmalała do
wartości y
z
– H/2. Regulator załączył grzanie (U
max
). Jednak temperatura nadal maleje i
dopiero po czasie T
m
nastąpi w obiekcie ponowny jej wzrost. Omówiony cykl powtarza
się.
4
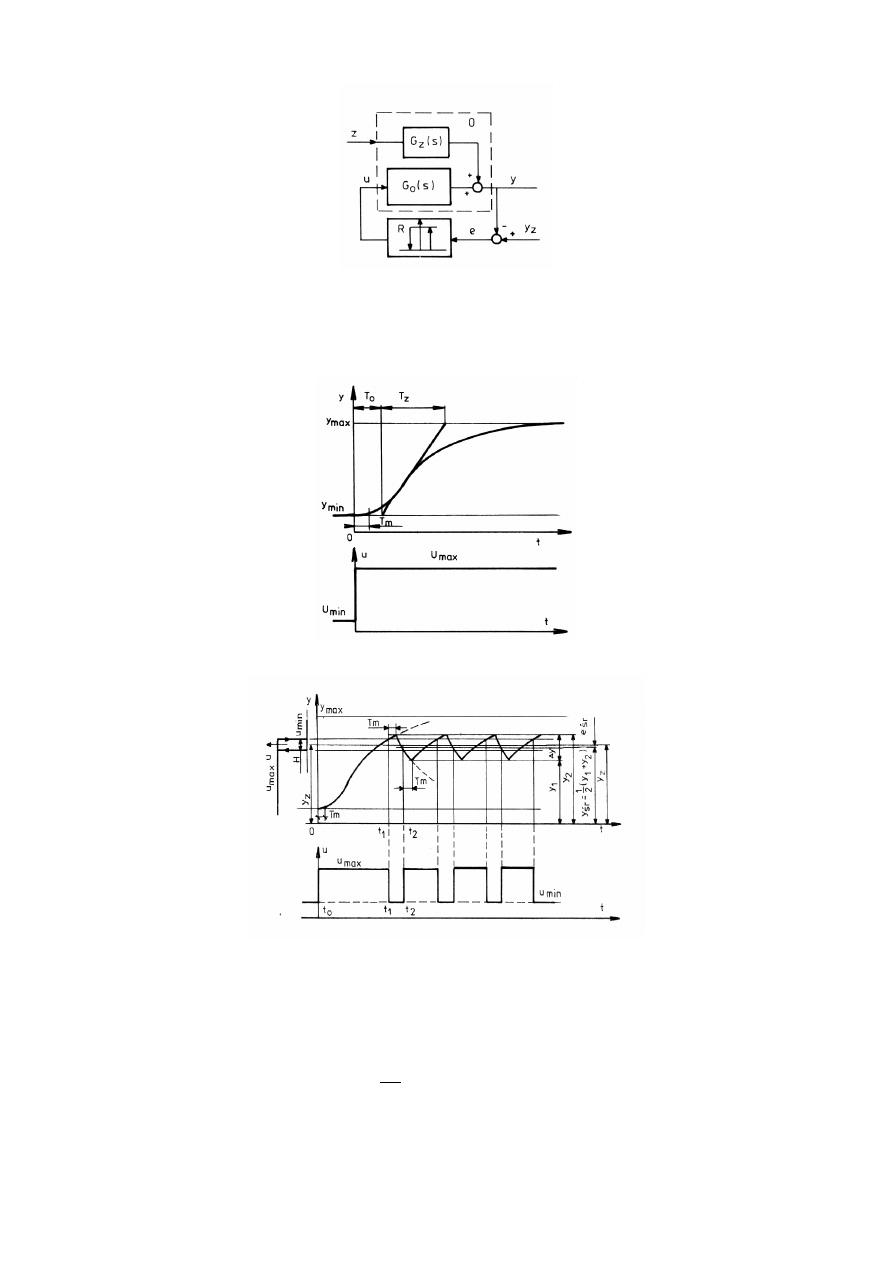
Rys. 4.1. Schemat blokowy układu regulacji dwustawnej
Rys. 4.2. Charakterystyka skokowa obiektu
Rys. 4.3. Przebieg wielkości regulowanej w układzie regulacji dwustawnej
Wielkość regulowana oscyluje między y
1
i y
2
z amplitudą y = y
2
– y
1
. Amplitudę
oscylacji wyznacza w przybliżeniu zależność:
)
(
min
max
y
y
T
T
H
y
z
m
(4.1)
5
Jak widać, jedną z wielkości decydujących o amplitudzie, jest stosunek T
m
/T
z
. W
praktyce jako kryterium stosowalności regulacji dwustawnej przyjęto:
)
2
,
0
(
1
,
0
0
z
T
T
(4.2)
Amplitudę oscylacji można zmniejszyć dobierając: y
max
i y
min
, regulator o małej
strefie histerezy lub z histerezą ujemną oraz regulatory z członami korekcyjnymi. Wartość
średnia przebiegu y
śr
= y
2
+ y
1
/2, różni się od wartości zadanej y
z
o odchyłkę
œr
z
œr
y
y
e
(4.3)
Wielkość tej odchyłki można określić wzorem przybliżonym
z
m
z
œr
T
T
y
y
y
e
)
2
(
min
max
(4.4)
Odchyłka e
śr
jest więc równa zeru tylko dla przypadku
z
y
y
y
)
(
2
1
min
max
(4.5)
Ze wzoru (4.4) można wywnioskować, iż zakłócenie z (zmieniające wartości y
max
lub y
min
)
będzie miało T
z
/T
m
razy mniejszy wpływ niż w układzie bez regulatora. Układ zachowuje
się więc jak proporcjonalny. Przedstawione rozważania oparto na założeniu, że amplituda
oscylacji jest niewielka, a właściwości dynamiczne obiektu zbliżone do właściwości członu
inercyjnego pierwszego rzędu z opóźnieniem. Otrzymane zależności (4.1) i (4.4) są więc
jedynie przybliżeniem rzeczywistych zależności i można je stosować dla obiektów z
inercyjnością pierwszego i drugiego rzędu.
5. Regulatory dwustawne z korekcją
Zmniejszenie amplitudy oscylacji wielkości regulowanej, w układzie regulacji
dwustawnej, można uzyskać dzięki zastosowaniu regulatora z korekcyjnym sprzężeniem
zwrotnym. Schemat blokowy układu regulacji dwustawnej z inercyjnym sprzężeniem
zwrotnym pokazano na rys. 5.1.
6
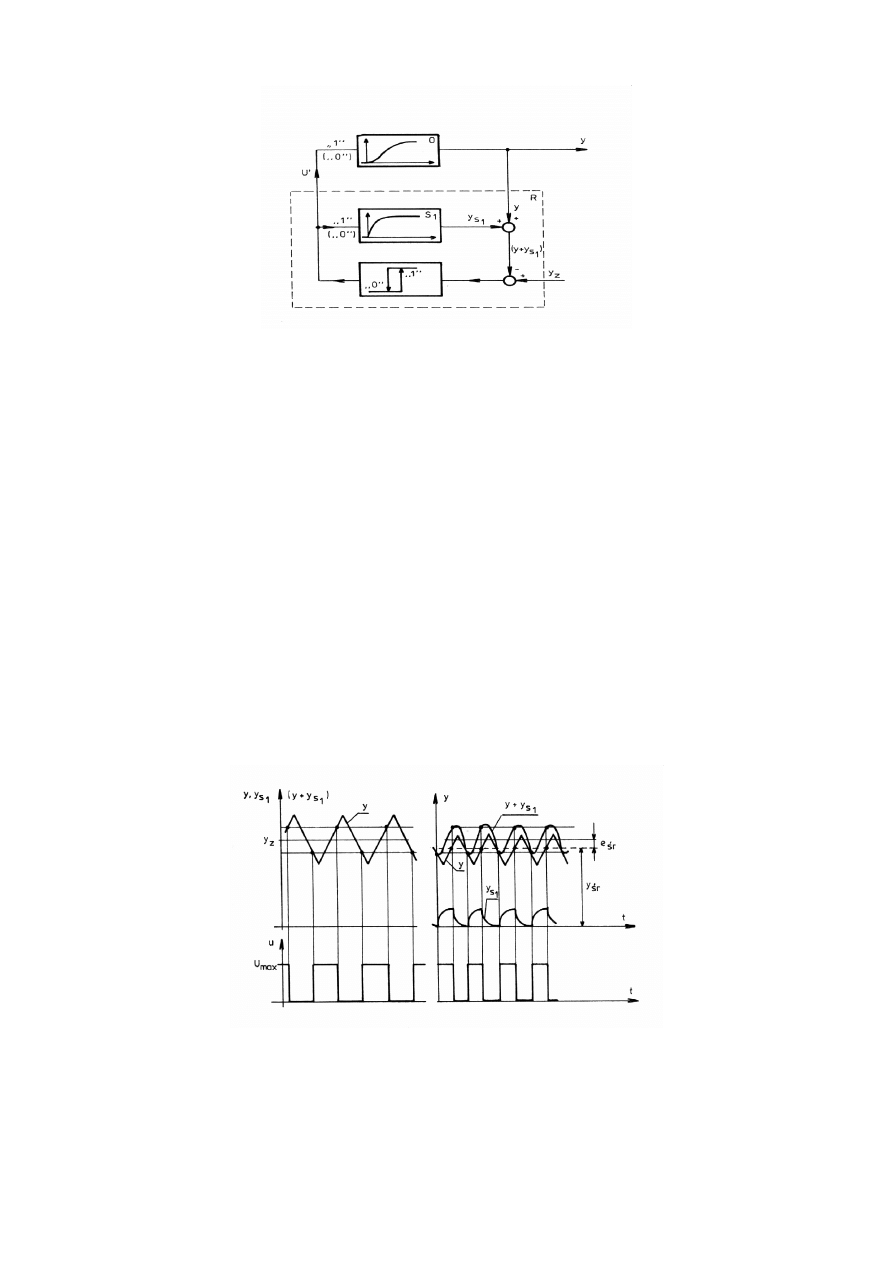
Rys. 5.1. Schemat blokowy układu regulacji dwustawnej ze sprzężeniem zwrotnym
Stała czasowa T członu w sprzężeniu zwrotnym powinna być znacznie mniejsza
od zastępczej stałej czasowej T
z
obiektu regulacji. Przebieg regulacji w tym układzie na
rys. 5.2. Jak widać, po zastosowaniu pojedynczego sprzężenia zwrotnego wzrosła
częstotliwość oscylacji, zmalała amplituda wahań, wystąpiła natomiast różnica między
wartością średnią y
śr
a zadaną y
z
. Odchyłkę tę można zmniejszyć przez zastosowanie
drugiego inercyjnego sprzężenia zwrotnego (rys. 5.3). Regulator dwustawny z
pojedynczym inercyjnym sprzężeniem zwrotnym ma właściwości zbliżone do regulatora
PD. Regulator z dwoma członami inercyjnymi w sprzężeniu ma natomiast charakter
zbliżony do PID. Za wielkość wyjściową regulatora uważa się wówczas wartość średnią
przebiegu u(t).
Rys. 5.2. Porównanie przebiegu regulacji w układzie regulacji dwustawnej bez sprzężenia
zwrotnego z przebiegami w układzie z pojedynczym sprzężeniem zwrotnym
7
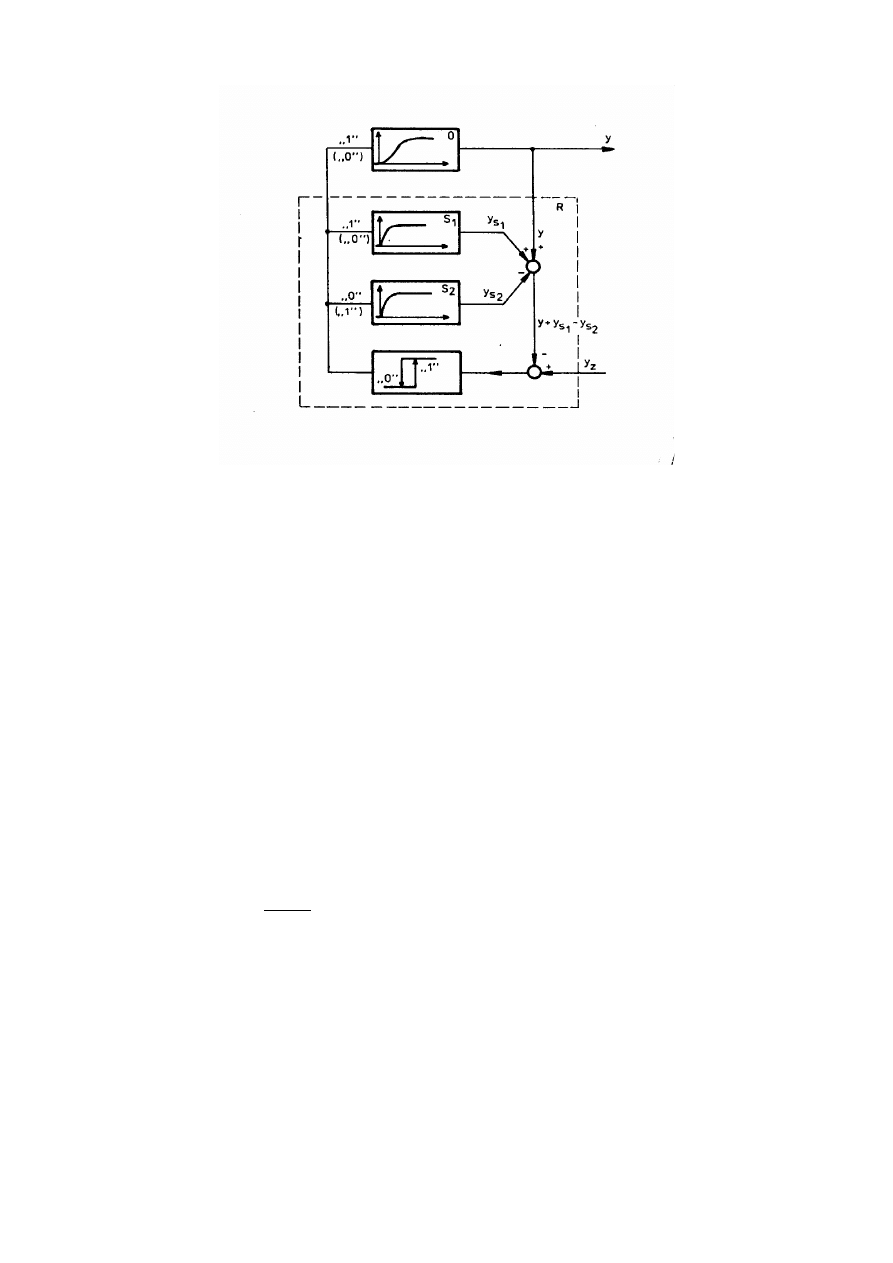
Rys. 5.3. Schemat blokowy układu regulacji dwustawnej z podwójnym sprzężeniem
zwrotnym
6. Ćwiczenia
a) otworzyć okno robocze (polecenie File/New), uwaga: parametr Max Step
Size (opcja Simulation) należy ustawić tak, aby otrzymać dostatecznie dużą
liczbę wartości sygnału w oknie oscyloskopu (np. przy ustawieniu parametru
Scope/Horizontal Range = 1, aby otrzymać w oknie obraz złożony ze 100
wartości sygnału należy przyjąć Max Step Size = 0:01).
b) zamodelować układ regulacji dwupołożeniowej z obiektem inercyjnym I-szego
rzędu z opóźnieniem przyjmując następujące dane:
–
transmitancja obiektu:
G
0
s=
e
−T
0
s
T s1
,
T
0
=0.1
, T=10 ,
–
poziomy przełączeń przekaźnika:
Y
off
=0
,
Y
on
=2
,
–
strefa histerezy:
H=±0.5 ,
–
wymuszenie: jednostkowe.
8
c) uruchomić symulację układu i przeprowadzić obserwacje sygnałów uchybu
regulacji, zmiennej regulowanej i sygnału sterującego, zbadać wpływ zmian
parametrów
T
0,
T , H ,Y
on
i wymuszenia na przebiegi regulacji.
d) zamodelować układ z regulatorem dwupołożeniowym z korekcyjnym
sprzężeniem zwrotnym:
G
0
s=
k
T s1
, k=0.5 , T=0.005 ,
e) przeprowadzić obserwację przebiegów regulacji i zbadać wpływ zmian
parametrów sprzężenia korekcyjnego na te przebiegi.
f) jakie sprzężenie należy zastosować, aby regulator miał właściwości zbliżone do
regulatora liniowego ciągłego typu PID - sprawdzić symulacyjnie.
g) uzasadnić wyniki symulacji otrzymane w e) i f).
Spis treści
1. Wstęp...............................................................................................................................................1
2. Budowa dwustawnych regulatorów temperatury..................................................................2
2.1. Regulatory dwustawne ze stykami przełączanymi bezpośrednio przez czujnik.............2
2.2 Regulatory elektroniczne............................................................................................................2
3. Charakterystyka statyczna regulatora dwustawnego............................................................3
4. Układ regulacji dwustawnej...................................................................................................... 4
5. Regulatory dwustawne z korekcją............................................................................................ 6
6. Ćwiczenia....................................................................................................................................... 8
9