Krzysztof Donten
Zakład Konstrukcji Betonowych
1
Warszawa, 20.03.2006 r
KONSTRUKCJE BETONOWE SPECJALNE
PROJEKT ZBIORNIKA NA WODĘ
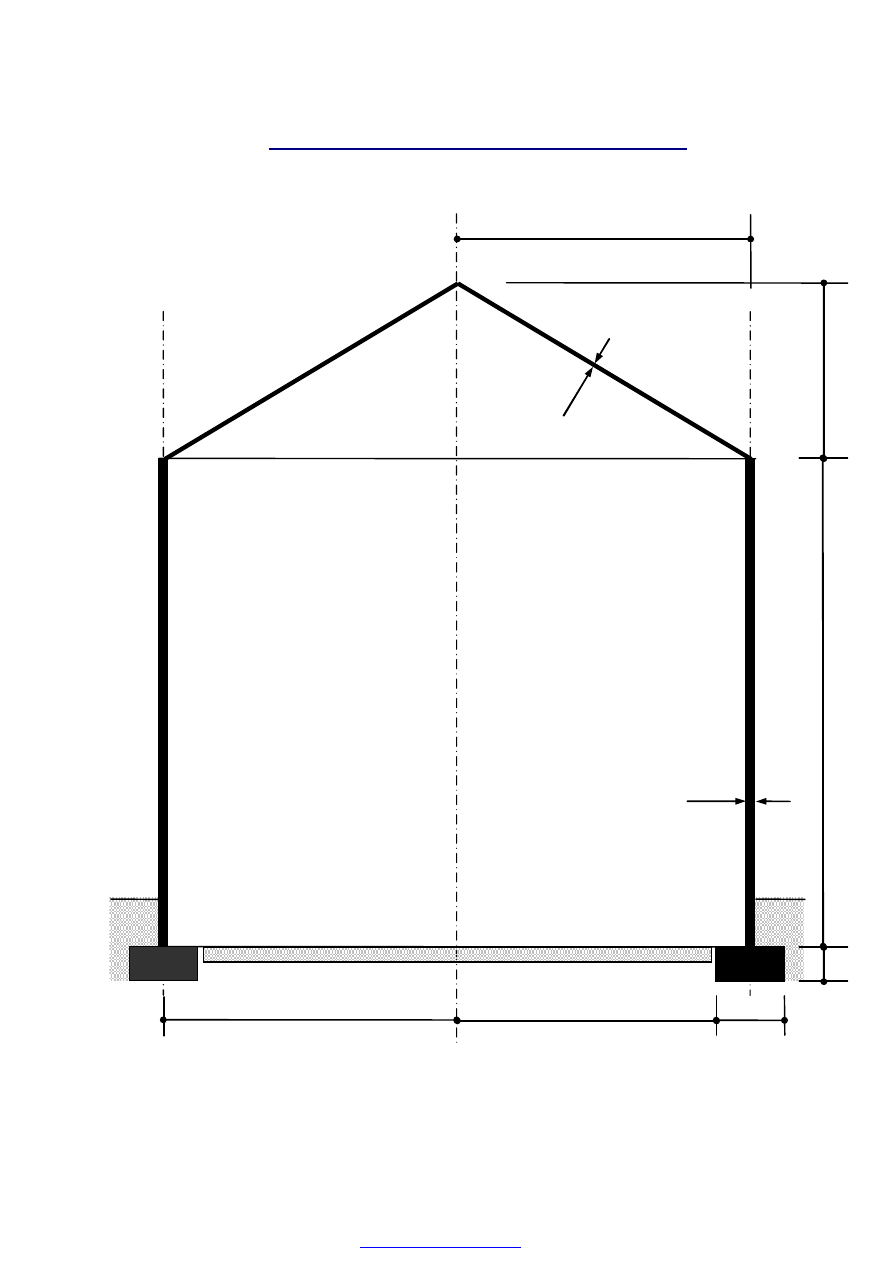
1
0
0
0
0
6000
7
0
0
1400
3
6
0
0
6000
5300
200
80
PDF created with pdfFactory trial version
Krzysztof Donten
Zakład Konstrukcji Betonowych
2
1.
Założenia konstrukcyjne i obliczeniowe.
1.1. Materiały konstrukcyjne.
−
Beton konstrukcyjny B37:
MPa.
MPa,
MPa,
MPa,
MPa,
MPa,
32000
33
1
0
.
20
90
.
2
00
2
0
30
=
=
=
=
=
=
cm
ctd
cd
ctm
ctk
ck
E
.
f
f
f
.
f
.
f
−
Zbrojenie ściany walcowej i ławy kołowej zbiornika - stal A-II (18G2):
.
200000
,
310
,
355
MPa
MPa
MPa
=
=
=
s
yd
yk
E
f
f
−
Zbrojenie kopuły; strzemiona w ławie - stal A-I (St3S):
MPa.
MPa,
MPa,
200000
210
240
=
=
=
s
yd
yk
E
f
f
−
Otulina zbrojenia głównego:
(
)
(
)
mm
mm,
wa
fundamento
ława
mm,
mm,
c
:
XC4
środowiska
klasa
cowa
ściana wal
mm,
mm,
:
XC3
środowiska
klasa
kopuła
min
60
10
50
50
:
30
5
25
25
25
5
20
20
min
min
min
min
min
=
+
=
+
=
=
−
=
+
=
+
=
=
−
=
+
=
+
=
=
−
Δc
c
c
c
Δc
c
c
Δc
c
c
c
nom
nom
nom
1.2. Wymagania konstrukcyjne.
•
Graniczna szerokość rozwarcia rys:
.
1
.
0
lim
mm
=
w
2.
Obciążenia.
2.1. Obciążenia powłoki przekrycia.
•
Zestawienie obciążeń stałych na 1 m
2
powłoki stożkowej:
lp. Zestawienie obciążeń kN/m
2
powierzchni powłoki,
q
Sk
γ
f
q
Sd
1. papa bitumiczna klejona na gorąco,
0.20
1.200
0.24
2. gładź cementowa zbrojona 5 cm,
0.05
×
24.0=
1.20
1.300
1.56
3. folia budowlana,
0.05
1.200
0.06
4. wełna mineralna,
0.08
×
0.50=
0.04
1.200
0.05
5. kopuła żelbetowa 8 cm,
0.08
×
25.0=
2.00
1.100
2.20
razem obciążenie stałe g
s
=
3.49
1.178
4.11
•
Obciążenie śniegiem I strefa:
.
08
.
1
50
.
1
72
.
0
,
72
.
0
80
.
0
90
.
0
2
2
kN/m
kN/m
=
⋅
=
=
=
⋅
=
f
s
Sk
s
Sd
s
Sk
p
p
p
γ
2.2. Obciążenia ściany walcowej.
•
Zestawienie obciążeń pionowych na 1 m
2
ściany.
lp. Zestawienie obciążeń kN/m
2
powierzchni ściany,
q
Sk
γ
f
q
Sd
1. blacha fałdowa na listwach,
0.20
1.200
0.24
2. wełna mineralna 10 cm,
0.10
×
5.0=
0.05
1.200
0.06
3.
ściana żelbetowa 20 cm,
0.20
×
25.0=
5.00
1.100
5.50
razem obciążenie stałe.
5.25
1.105
5.80
•
Ciężar wody:
.
0
.
11
0
.
10
10
.
1
,
0
.
10
2
2
kN/m
kN/m
=
⋅
=
=
=
f
Sk
Sd
Sk
γ
γ
γ
γ
PDF created with pdfFactory trial version

Krzysztof Donten
Zakład Konstrukcji Betonowych
3
3.
Obliczenia statyczne zbiornika.
3.1. Dane geometryczne i parametry sztywnościowe elementów zbiornika.
•
powłoka przekrycia (stożkowa):
−
grubość kopuły stożkowej:
m,
0.08
s
=
t
−
promień oparcia powierzchni środkowej:
,
00
.
6
m
=
s
r
−
kąt oparcia powłoki:
,
9638
.
30
600
.
0
00
.
6
60
.
3
tan
o
=
→
=
=
α
α
−
długość powierzchni środkowej:
m,
0
.
7
997
.
6
60
.
3
00
.
6
2
2
≈
=
+
=
s
l
−
parametry obliczeniowe:
(
)
(
)
(
)
(
)
m.
m
m
kNm,
m
kN
66
.
4
742
.
0
2
2
0
.
7
,
742
.
0
2
.
0
1
3
1
600
.
0
08
.
0
0
.
7
1
3
1
tan
10
42
.
1
2
.
0
1
12
08
.
0
32000000
1
12
,
10
56
.
2
08
.
0
32000000
4
2
2
2
2
4
2
2
2
2
3
2
3
2
3
6
=
⋅
=
>
=
=
−
⋅
⋅
=
−
⋅
=
×
=
−
⋅
⋅
=
−
=
×
=
⋅
=
=
π
π
ν
α
ν
s
s
s
s
s
s
cm
s
s
cm
s
L
l
t
l
L
t
E
D
t
E
F
Kopuła spełnia warunki obliczeniowe dla powłok długich.
•
powłoka cylindryczna:
−
grubość powłoki cylindrycznej:
m,
0.20
c
=
t
−
wysokość powłoki:
,
00
.
10
m
=
c
H
−
promień powierzchni środkowej:
,
00
.
6
m
=
c
r
−
parametry obliczeniowe:
(
)
(
)
(
)
(
)
.
28
.
5
841
.
0
2
2
00
.
10
,
841
.
0
2
.
0
1
3
20
.
0
00
.
6
1
3
10
2
.
22
2
.
0
1
12
20
.
0
32000000
1
12
,
10
40
.
6
20
.
0
32000000
4
2
2
2
4
2
2
2
3
2
3
2
3
6
m
m
m
kNm,
m
kN
=
⋅
=
>
=
=
−
⋅
=
−
=
×
=
−
⋅
=
−
=
×
=
⋅
=
=
π
π
ν
ν
c
c
c
c
c
c
cm
c
c
cm
c
L
H
t
r
L
t
E
D
t
E
F
Powłoka cylindryczna spełnia warunki obliczeniowe dla powłok długich.
•
ława fundamentowa:
−
moduł podatności podłoża:
,
20000
3
m
kN
=
C
−
wymiary geometryczne:
,
00
.
6
2
40
.
1
30
.
5
m
m,
0.70
m,
1.4
=
+
=
=
=
L
L
L
r
h
b
−
pole przekroju ławy:
,
98
.
0
70
.
0
40
.
1
2
m
=
×
=
=
L
L
L
h
b
A
−
sztywności ławy:
kN,
m
kN
kN,
2
3
3
3
;
6
3
6
3
6
6
10
57
.
4
12
40
.
1
20000
12
,
10
28
.
1
12
70
.
0
40
.
1
10
0
.
32
12
10
4
.
31
98
.
0
10
0
.
32
×
=
⋅
=
=
⋅
×
=
⋅
⋅
×
=
=
=
×
=
⋅
×
=
=
L
F
L
L
L
cm
L
cm
L
L
cm
L
b
C
J
C
t
b
E
J
E
D
A
E
F
Moment bezwładności podstawy ławy J
L;F
(w ostatnim wzorze) jest obliczany na jednostkę długo-
ści obwodu środkowego ławy i ma wymiar [m
4
/m]
PDF created with pdfFactory trial version
Krzysztof Donten
Zakład Konstrukcji Betonowych
4
3.2. Równania równowagi węzła górnego.
Równania zgodności przemieszczeń węzła:
(
)
.
P
X
δ
δ
c
s
=
⋅
+
Jednostkowe przemieszczenia krawędziowe kopuły i powłoki walcowej
oblicza się ze wzorów:
.
2
2
,
2
sin
sin
sin
2
2
2
2
=
−
−
=
c
c
c
c
c
s
s
s
s
s
s
L
L
L
D
L
L
L
L
D
L
c
δ
δ
α
α
α
Prawe strony układu równań są określone zależnościami:
,
cos
,
0
21
11
0
0
0
0
0
0
0
0
α
δ
δ
s
H
c
c
c
c
s
s
s
N
r
r
+
Ψ
∆
+
Ψ
∆
−
=
P
gdzie:
(
)
(
)
(
)
(
)
(
)
(
)
.
,
1
tan
1
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
=
=
−
−
−
=
−
−
−
⋅
+
−
−
=
c
s
s
h
c
c
c
c
c
c
c
c
c
H
h
s
s
s
s
s
s
s
s
s
s
s
s
N
ν
R
dh
d
N
ν
R
F
r
Ψ
Δr
N
ν
R
dh
d
h
N
R
ν
N
ν
R
h
F
Ψ
Δr
α
Po podstawieniu podanych w pkt. 3.1 wielkości geometrycznych i parametrów sztywnościowych
otrzymuje się:
.
10
0379
.
0
0159
.
0
0159
.
0
0134
.
0
2
841
.
0
841
.
0
841
.
0
10
2
.
22
2
841
.
0
,
10
5225
.
0
0997
.
0
0997
.
0
0381
.
0
2
5145
.
0
742
.
0
5145
.
0
742
.
0
5145
.
0
742
.
0
10
42
.
1
2
742
.
0
3
2
3
3
2
2
3
−
−
×
+
+
+
+
=
+
+
+
+
×
⋅
=
×
+
−
−
+
=
+
⋅
−
⋅
−
⋅
+
×
⋅
=
c
s
δ
δ
Ostatecznie macierz układu równań przybierze postać:
.
10
5604
.
0
0838
.
0
0839
.
0
0515
.
0
10
0379
.
0
5225
.
0
0159
.
0
0997
.
0
0159
.
0
0997
.
0
0134
.
0
0381
.
0
3
3
−
−
×
+
−
−
+
=
×
+
+
+
−
+
−
+
+
=
+
c
s
δ
δ
Wielkości krawędziowe przemieszczeń w powłoce stożkowej (brzeg h
s
=H
s
=3.6 m;
α=30.9638
o
)
(
)
(
)
(
)
(
)
(
)
(
)
(
) (
)
[
]
.
10
0433
.
0
1
.
13
60
.
3
3
.
34
4
.
50
2
.
0
1
6000
.
0
10
56
.
2
1
1
tan
1
10
1020
.
0
3
.
34
2
.
0
4
.
50
6000
.
0
10
56
.
2
60
.
3
tan
,
1
.
13
5145
.
0
2
04
.
5
2
.
0
6000
.
0
04
.
5
sin
2
tan
,
4
.
29
8575
.
0
3
.
34
cos
,
3
.
34
5145
.
0
2
60
.
3
04
.
5
sin
2
,
4
.
50
6000
.
0
60
.
3
04
.
5
tan
,
04
.
5
8575
.
0
08
.
1
11
.
4
cos
3
6
0
0
0
,
0
,
0
3
6
0
;
0
;
0
2
2
2
2
0
0
0
,
2
2
0
;
2
2
0
;
−
=
−
=
=
=
×
+
=
⋅
−
+
−
⋅
+
⋅
⋅
×
−
=
=
−
+
−
⋅
+
−
=
Ψ
×
−
=
⋅
+
−
⋅
⋅
×
=
−
=
∆
−
=
⋅
+
−
=
−
=
−
−
=
⋅
−
=
−
=
⋅
⋅
−
=
=
−
=
⋅
−
=
=
−
=
⋅
−
−
=
+
=
s
s
s
s
s
s
s
s
s
s
s
s
s
s
s
s
s
H
h
s
s
s
s
H
s
H
s
s
H
s
H
s
H
s
s
s
H
s
s
s
H
h
s
s
s
H
s
H
h
s
s
H
s
H
h
s
s
H
s
s
s
s
N
R
dh
d
H
N
R
F
N
R
F
H
r
q
q
N
R
dh
d
N
h
q
N
h
q
R
p
g
q
ν
ν
α
ν
α
α
ν
α
ν
α
α
α
α
m,
m
kN
m
kN
m
kN
m
kN
m
kN
2
2
Wielkości krawędziowe przemieszczeń w powłoce cylindrycznej (h
c
=0.0 m):
(
)
(
)
,
6
.
17
5145
.
0
3
.
34
0
80
.
5
sin
,
0
.
0
0
.
0
0
.
6
0
.
11
0
,
0
0
0
;
0
0
0
;
m
kN
m
kN
−
=
⋅
−
⋅
−
=
+
=
=
⋅
⋅
=
=
=
=
α
γ
s
c
c
H
s
h
c
c
c
h
c
c
c
c
N
h
g
N
h
r
R
α
cos
0
p
N
UKŁAD RÓWNAŃ
g
X
1
g
X
1
g
X
2
g
X
2
PDF created with pdfFactory trial version
Krzysztof Donten
Zakład Konstrukcji Betonowych
5
(
)
(
)
(
)
(
)
,
10
0630
.
0
2
.
67
10
40
.
6
00
.
6
,
10
0033
.
0
6
.
17
2
.
0
0
10
40
.
6
00
.
6
,
2
.
67
80
.
5
2
.
0
00
.
6
0
.
11
3
6
0
0
0
0
0
3
6
0
0
;
0
0
;
0
0
0
0
0
−
=
−
=
×
−
=
⋅
×
−
=
−
−
=
Ψ
×
=
⋅
+
⋅
×
=
−
=
∆
=
⋅
+
⋅
=
+
=
−
c
c
h
c
c
c
c
c
c
c
c
c
c
c
c
c
c
h
c
c
c
N
R
dh
d
F
r
N
R
F
r
r
g
r
N
R
dh
d
ν
ν
ν
γ
ν
2
m
kN
Prawe strony układu równań:
,
10
3612
.
0
4993
.
0
10
4
.
29
0159
.
0
0630
.
0
0433
.
0
4
.
29
0134
.
0
0033
.
0
1020
.
0
cos
cos
3
3
0
,
21
0
0
0
0
0
,
11
0
0
0
0
−
−
×
=
×
⋅
+
−
−
⋅
+
+
+
=
⋅
−
Ψ
+
Ψ
−
⋅
−
∆
+
∆
−
=
α
δ
α
δ
s
s
H
s
c
c
s
H
s
c
c
s
N
N
r
r
P
Ostatecznie układ równań przybierze postać:
,
3612
.
0
4993
.
0
5604
.
0
0839
.
0
0839
.
0
0515
.
0
2
1
+
+
=
×
+
−
−
+
g
g
X
X
Rozwiązaniem układu są wielkości niewiadomych:
,
m
kNm
,
m
kN
78
2
2
14
2
1
.
X
.
X
g
g
=
=
3.3. Równania równowagi węzła dolnego.
Równania zgodności przemieszczeń węzła:
[
] [
]
,
L
c
L
c
P
P
X
δ
δ
+
=
⋅
+
Jednostkowe przemieszczenia krawędziowe kopuły i powłoki wal-
cowej oblicza się ze wzorów:
.
J
C
r
D
k
e
e
e
F
k
r
k
L
L
L
D
L
L;F
L
L
L
g
g
g
L
L
L
L
c
c
c
c
c
+
=
+
=
−
−
=
2
2
2
2
1
,
1
,
2
2
:
gdzie
L
c
δ
δ
Prawe strony układu równań są określone zależnościami:
(
)
(
)
(
)
,
1
0
,
,
0
0
0
0
0
0
L
c
H
c
g
L
H
h
c
c
c
c
c
c
c
H
c
H
c
r
r
N
e
k
N
R
dh
d
N
R
F
r
r
c
c
c
c
c
−
−
=
−
−
−
=
Ψ
∆
=
=
L
c
P
P
ν
ν
Wymiary przekroju ławy b
L
×
h
L
=1.50
×
0.70 m. Moduł podatności podłoża C=15000 kN/m
4
. Na pod-
stawie poz. 3.1 dane geometryczne i parametry sztywnościowe ławy wynoszą:
,
10
57
.
4
,
10
28
.
1
10
4
.
31
3
;
2
6
6
kN
kNm
kN,
×
=
×
=
×
=
F
L
L
L
J
C
D
F
Macierz sztywności wieńca:
,
10
0249
.
0
0087
.
0
0087
.
0
0042
.
0
10
1
35
.
0
35
.
0
35
.
0
4
.
31
9
.
24
00
.
6
9
.
24
1
35
.
0
2
70
.
0
2
,
1
10
9
.
24
10
57
.
4
0
.
6
10
28
.
1
1
1
3
6
2
2
;
;
2
;
2
;
6
3
2
6
;
2
−
−
−
×
=
×
+
⋅
⋅
=
+
=
=
=
=
×
=
×
+
×
=
+
=
g
L
g
L
g
L
L
L
L
L
L
g
L
F
L
L
L
L
e
e
e
F
k
r
k
h
e
CJ
r
D
k
L
δ
m,
kN
Macierz sztywności powłoki cylindrycznej na podstawie poz. 3.2 wynosi:
,
10
0379
.
0
0159
.
0
0159
.
0
0134
.
0
3
−
×
+
−
−
+
=
c
δ
Ostatecznie wyrazy macierzy głównej dla węzła dolnego przybiorą wartości:
,
10
0628
.
0
0072
.
0
0072
.
0
0176
.
0
10
0249
.
0
0379
.
0
0087
.
0
0159
.
0
0087
.
0
0159
.
0
0042
.
0
0134
.
0
3
3
−
−
×
+
−
−
+
=
×
+
+
+
−
+
−
+
+
=
+
L
c
δ
δ
d
X
1
UKŁAD RÓWNAŃ
0
, H
c
N
H
L
M
L
∆σ
X
d
X
2
d
X
1
d
X
2
PDF created with pdfFactory trial version

Krzysztof Donten
Zakład Konstrukcji Betonowych
6
Wielkości krawędziowe przemieszczeń w powłoce cylindrycznej:
(
)
(
)
(
)
(
)
(
)
(
)
,
10
0630
.
0
2
.
67
10
40
.
6
0
.
6
,
10
6329
.
0
6
.
75
2
.
0
0
.
660
10
40
.
6
0
.
6
,
2
.
67
80
.
5
2
.
0
0
.
6
0
.
11
,
6
.
75
5145
.
0
3
.
34
0
.
10
80
.
5
sin
,
0
.
660
0
.
10
00
.
6
0
.
11
1
3
6
0
0
0
3
6
0
;
0
;
0
0
0
0
,
0
;
0
;
−
−
=
−
=
=
=
×
−
=
⋅
×
−
=
−
−
=
Ψ
×
=
⋅
+
⋅
×
=
−
=
∆
=
⋅
+
⋅
=
+
=
−
−
=
⋅
−
⋅
−
=
+
=
=
⋅
⋅
=
=
m
m
m
kN
m
kN
m
kN
2
c
c
c
c
c
c
c
c
c
c
c
c
H
h
c
c
c
c
c
H
c
H
c
H
c
c
c
H
c
c
c
c
H
h
c
c
c
H
s
H
h
c
c
H
c
H
h
c
c
c
H
c
N
R
dh
d
F
r
N
R
F
r
r
g
r
N
R
dh
d
N
h
g
N
h
r
R
ν
ν
ν
γ
ν
α
γ
Wektor prawych stron od obciążeń powłoki cylindrycznej:
,
10
0630
.
0
6329
.
0
3
0
0
−
×
+
−
=
Ψ
∆
−
=
H
c
H
c
r
c
P
Wektor prawych stron od obciążeń pionowych działających na ławę będzie wektorem zerowym:
(
)
,
0
0
0
=
→
=
−
L
P
L
c
r
r
Ostatecznie układ równań przybierze postać:
,
0630
.
0
6329
.
0
0628
.
0
0072
.
0
0072
.
0
0176
.
0
2
1
+
−
=
×
+
−
−
+
d
d
X
X
Rozwiązaniem układu są wielkości niewiadomych:
,
m
kNm
,
m
kN
28
.
3
3
.
37
2
1
−
=
−
=
d
d
X
X
PDF created with pdfFactory trial version

Krzysztof Donten
Zakład Konstrukcji Betonowych
7
3.4. Siły wewnętrzne w zbiorniku.
3.4.1. Powłoka stożkowa.
•
Siły wewnętrzne w stanie błonowym (bezmomentowym):
−
obciążenie ciężarem własnym g
s
kN/m
2
i obciążenie powierzchniowe p
s
kN/m
2
rzutu:
,
04
.
5
8575
.
0
08
.
1
11
.
4
cos
2
m
kN
−
=
⋅
−
−
=
+
=
α
s
s
s
p
g
q
−
siły wewnętrzne:
,
52
.
9
5145
.
0
2
04
.
5
sin
2
,
0
.
14
6000
.
0
04
.
5
tan
2
2
0
2
2
0
s
s
s
s
s
s
s
s
s
s
h
h
h
q
N
h
h
h
q
R
⋅
=
⋅
−
=
=
⋅
=
−
=
=
α
α
•
Siły wewnętrzne w stanie zgięciowym.
−
dodatnie zwroty sił krawędziowych:
(
)
,
sin
α
s
s
h
h
s
−
=
−
wzory ogólne na wpływ zaburzeń brzegowych:
( )
(
)
(
)
( )
( )
( )
(
)
(
)
( )
,
,
cos
cos
,
sin
2
sin
8
,
sin
2
,
sin
sin
,
sin
tan
1
2
,
cos
cos
2
,
cos
sin
2
2
,
cos
2
,
,
4
2
,
4
,
,
4
4
2
s
M
x
s
so
s
s
M
s
H
x
so
s
s
H
s
s
M
x
s
s
s
H
x
s
s
M
s
s
H
s
so
s
s
M
s
s
so
s
H
s
L
s
M
e
r
L
M
M
M
e
r
L
H
M
e
M
M
e
L
H
M
e
L
M
N
e
H
N
e
r
L
M
R
e
L
r
H
R
=
+
⋅
⋅
−
=
+
+
⋅
⋅
=
+
⋅
⋅
−
=
⋅
⋅
=
⋅
⋅
+
=
+
⋅
⋅
=
+
⋅
⋅
−
=
⋅
⋅
=
−
−
−
−
−
−
−
−
η
ν
η
α
ν
η
α
η
η
α
η
α
η
α
η
α
η
η
ϑ
π
η
ϑ
π
η
η
η
π
η
π
η
η
−
wielkości zaburzeń brzegowych (dolnych):
,
m
kNm
,
m
kN
78
.
2
2
.
14
2
1
=
=
=
=
g
s
g
s
X
M
X
H
−
czynniki stałe wzorów na wpływ zaburzeń na krawędzi podparcia powłoki stożkowej:
,
2948
.
0
8575
.
0
00
.
6
742
.
0
78
.
2
cos
,
4065
.
0
8824
.
0
8
0
.
6
742
.
0
2
.
14
2
sin
8
,
932
.
3
2
78
.
2
2
,
421
.
5
5145
.
0
742
.
0
2
.
14
sin
,
49
.
12
6000
.
0
742
.
0
2
78
.
2
tan
2
,
22
.
17
8575
.
0
2
2
.
14
cos
2
,
6
.
166
5145
.
0
00
.
6
742
.
0
8
78
.
2
sin
8
,
6
.
229
742
.
0
00
.
6
2
2
.
14
2
2
2
2
2
=
⋅
⋅
=
⋅
=
⋅
⋅
⋅
=
⋅
=
⋅
=
⋅
=
⋅
⋅
=
⋅
=
⋅
⋅
=
⋅
=
⋅
⋅
=
⋅
=
⋅
⋅
=
⋅
=
⋅
⋅
=
⋅
α
α
α
α
α
α
so
s
s
so
s
s
s
s
s
s
s
s
so
s
s
s
so
s
r
L
M
r
L
H
M
L
H
L
M
H
r
L
M
L
r
H
−
związki na siły wewnętrzne w powłoce stożkowej:
( )
(
)
[
]
(
)
( )
[
]
( )
(
)
[
]
(
)
( )
[
]
,
,
cos
2948
.
0
sin
4065
.
0
,
sin
932
.
3
sin
421
.
5
,
sin
49
.
12
cos
22
.
17
,
cos
6
.
166
cos
6
.
229
4
,
4
;
4
0
4
0
s
x
s
x
s
s
s
s
s
L
s
M
e
M
e
M
e
N
N
e
R
R
=
+
⋅
⋅
−
+
⋅
=
⋅
+
⋅
−
⋅
=
⋅
⋅
+
+
⋅
+
=
⋅
+
⋅
−
⋅
+
=
−
−
−
−
η
ν
η
η
η
η
η
η
η
η
η
π
ϑ
η
π
η
π
η
π
:
gdzie
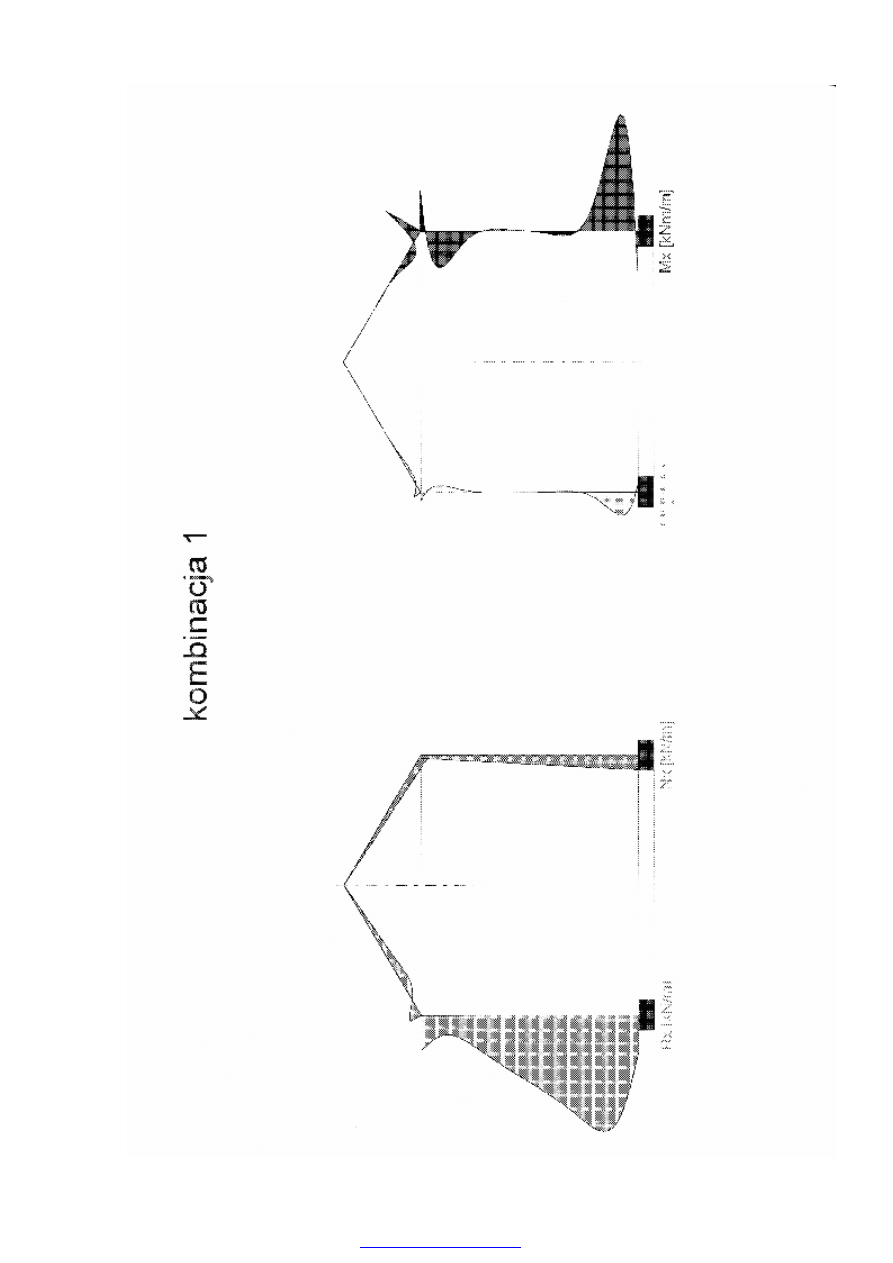
Obliczenia sił wewnętrznych w powłoce stożkowej wykonano za pomocą programu Excell. Wyniki
obliczeń przedstawiono w tablicy 3.4.1 oraz na wykresie 3.4.
ZAŁOŻENIA
s
H
s
M
s
r
so
α
PDF created with pdfFactory trial version
Krzysztof Donten
Zakład Konstrukcji Betonowych
8
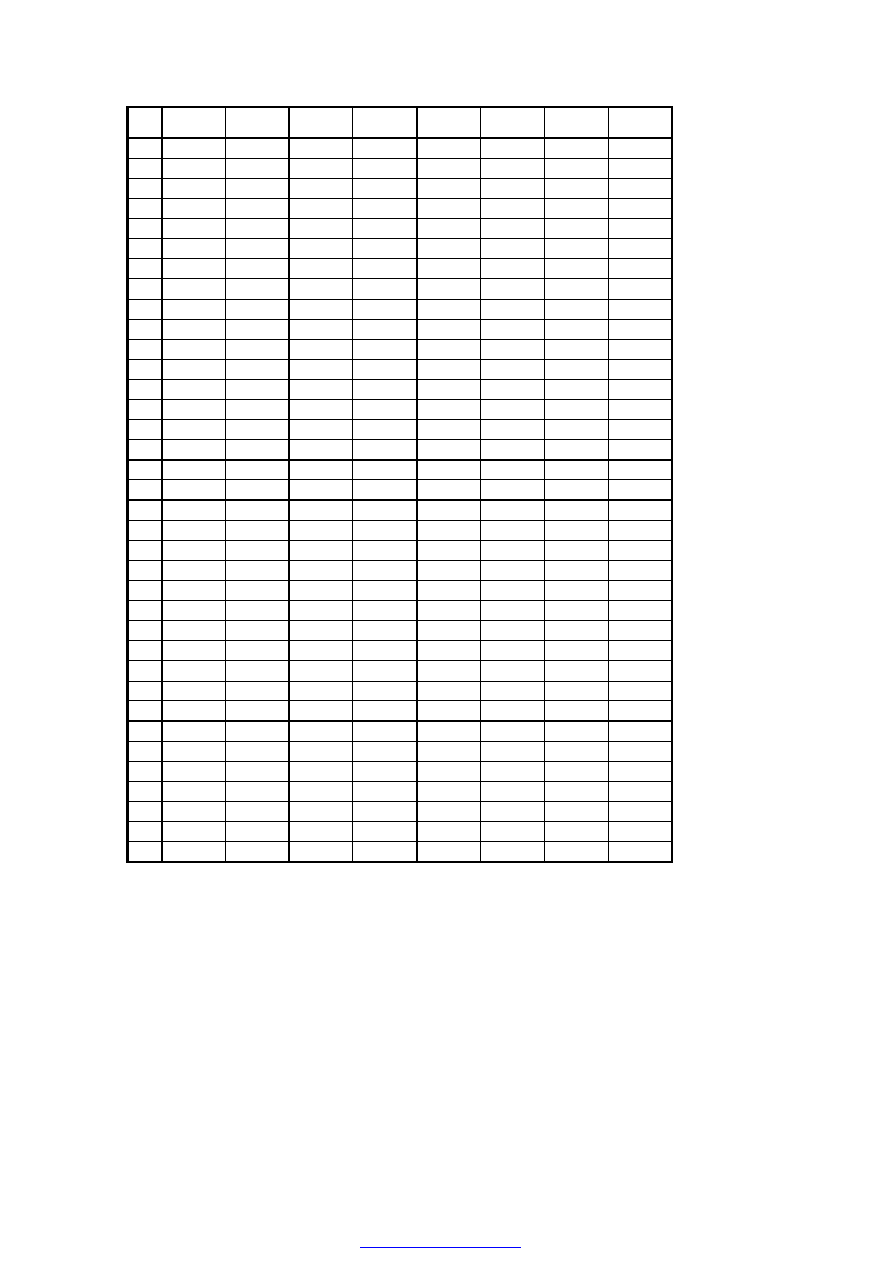
Tablica 3.4.1. Siły wewnętrzne w powłoce stożkowej.
lp.
s
η
0
s
R
0
s
N
ϕ
,
s
R
ϕ
,
s
N
ϕ
,
s
M
ϑ
,
s
M
0
7.000
9.434
0.0
0.0
0.0
0.0
0.00
0.00
1
6.800
9.164
-1.4
-1.0
-1.4
-1.0
0.00
0.00
2
6.600
8.895
-2.9
-2.0
-2.9
-2.0
0.00
0.00
3
6.400
8.625
-4.3
-2.9
-4.3
-2.9
0.00
0.00
4
6.200
8.356
-5.8
-3.9
-5.8
-3.9
0.00
0.00
5
6.000
8.086
-7.2
-4.9
-7.2
-4.9
0.00
0.00
6
5.800
7.817
-8.6
-5.9
-8.6
-5.9
0.00
0.00
7
5.600
7.547
-10.1
-6.9
-10.0
-6.9
0.00
0.00
8
5.400
7.278
-11.5
-7.8
-11.4
-7.8
0.00
0.00
9
5.200
7.008
-13.0
-8.8
-12.8
-8.8
0.00
0.00
10
5.000
6.739
-14.4
-9.8
-14.2
-9.8
0.00
0.00
11
4.800
6.469
-15.8
-10.8
-15.6
-10.8
0.00
0.00
12
4.600
6.199
-17.3
-11.8
-17.1
-11.7
-0.01
0.00
13
4.400
5.930
-18.7
-12.7
-18.6
-12.7
-0.01
0.00
14
4.200
5.660
-20.2
-13.7
-20.1
-13.7
-0.01
0.00
15
4.000
5.391
-21.6
-14.7
-21.7
-14.7
-0.02
0.00
16
3.800
5.121
-23.0
-15.7
-23.4
-15.6
-0.02
-0.01
17
3.600
4.852
-24.5
-16.7
-25.3
-16.6
-0.02
-0.01
18
3.400
4.582
-25.9
-17.6
-27.3
-17.7
-0.02
-0.01
19
3.200
4.313
-27.4
-18.6
-29.4
-18.7
-0.02
-0.01
20
3.000
4.043
-28.8
-19.6
-31.6
-19.7
-0.01
-0.01
21
2.800
3.774
-30.3
-20.6
-33.9
-20.8
0.02
0.00
22
2.600
3.504
-31.7
-21.6
-36.1
-21.9
0.05
0.01
23
2.400
3.235
-33.1
-22.5
-37.9
-23.0
0.10
0.02
24
2.200
2.965
-34.6
-23.5
-39.2
-24.1
0.17
0.04
25
2.000
2.695
-36.0
-24.5
-39.4
-25.2
0.25
0.06
26
1.800
2.426
-37.5
-25.5
-38.1
-26.3
0.34
0.08
27
1.600
2.156
-38.9
-26.4
-34.7
-27.2
0.43
0.11
28
1.400
1.887
-40.3
-27.4
-28.6
-28.0
0.51
0.14
29
1.200
1.617
-41.8
-28.4
-19.5
-28.5
0.55
0.17
30
1.000
1.348
-43.2
-29.4
-6.9
-28.6
0.51
0.17
31
0.800
1.078
-44.7
-30.4
8.6
-28.3
0.34
0.15
32
0.600
0.809
-46.1
-31.3
26.2
-27.5
0.00
0.09
33
0.400
0.539
-47.5
-32.3
43.7
-26.1
-0.60
-0.04
34
0.200
0.270
-49.0
-33.3
57.3
-24.3
-1.51
-0.25
35
0.000
0.000
-50.4
-34.3
61.4
-22.1
-2.78
-0.56
W tablicach sił wewnętrznych dodatnie znaki sił odnoszą się do rozciągania, ujemne do ściskania. Z
kolei dodatnie znaki momentów oznaczają rozciąganie włókien wewnętrznych; ujemne – rozciąganie
włókien zewnętrznych.
PDF created with pdfFactory trial version

Krzysztof Donten
Zakład Konstrukcji Betonowych
9
3.4.2. Powłoka walcowa.
•
siły wewnętrzne w stanie błonowym (bezmomentowym):
−
obciążenia ciężarem własnym g
c
kN/m
2
powierzchni:
,
80
.
5
6
.
17
sin
,
0
0
;
0
0
x
x
g
N
N
R
c
H
s
c
c
s
⋅
+
=
⋅
+
+
=
=
α
−
obciążenie parciem cieczy
γ
c
kN/m
3
,
0
,
0
.
66
00
.
6
0
.
11
0
0
=
⋅
=
⋅
⋅
=
+
=
c
c
c
c
N
x
x
x
r
R
γ
•
Siły wewnętrzne w stanie zgięciowym.
−
dodatnie zwroty sił krawędziowych:
ZAŁOŻENIA
g
c
H
g
c
M
d
c
H
d
c
M
x
’
x
−
wzory ogólne na wpływ zaburzeń brzegowych:
( )
(
)
( )
(
)
,
,
,
sin
2
,
sin
,
0
,
0
,
cos
2
2
,
cos
2
,
,
,
,
4
,
,
4
2
M
x
c
M
c
H
x
c
H
c
M
x
c
c
H
x
c
M
c
H
c
c
c
M
c
c
c
H
c
M
M
M
M
e
M
M
e
L
H
M
N
N
e
r
L
M
R
e
L
r
H
R
ν
ν
η
η
η
η
ϑ
ϑ
π
η
η
π
η
η
+
=
+
=
+
⋅
⋅
±
=
⋅
⋅
+
=
=
=
+
⋅
⋅
±
=
⋅
⋅
+
=
−
−
−
−
W powyższych wzorach znaki górne odnoszą się do węzła górnego; natomiast znaki dolne do
węzła dolnego.
−
wielkości zaburzeń brzegowych (górnych i dolnych):
,
m
kNm
,
m
kN
,
m
kNm
,
m
kN
28
.
3
3
.
37
78
.
2
2
.
15
4
.
29
2
.
14
cos
2
1
2
0
,
1
−
=
=
−
=
=
−
=
−
=
=
+
−
=
−
−
=
d
d
c
d
d
c
g
g
c
H
s
g
g
c
X
M
X
H
X
M
N
X
H
s
α
−
czynniki stałe wzorów na wpływ zaburzeń brzegowych na krawędzi górnej:
,
93
.
3
2
78
.
2
2
,
78
.
12
841
.
0
2
.
15
,
7
.
66
0
.
6
841
.
0
2
2
78
.
2
2
2
,
9
.
216
841
.
0
00
.
6
2
2
.
15
2
2
2
=
⋅
=
⋅
=
⋅
=
⋅
=
⋅
⋅
=
⋅
=
⋅
⋅
=
⋅
g
c
c
g
c
c
c
g
c
c
c
g
c
M
L
H
r
L
M
L
r
H
−
czynniki stałe wzorów na wpływ zaburzeń brzegowych na krawędzi dolnej:
,
64
.
4
2
28
.
3
2
,
37
.
31
841
.
0
3
.
37
,
7
.
78
0
.
6
841
.
0
2
2
28
.
3
2
2
,
2
.
532
841
.
0
00
.
6
2
3
.
37
2
2
2
=
⋅
=
⋅
=
⋅
=
⋅
=
⋅
⋅
=
⋅
=
⋅
⋅
=
⋅
d
c
c
d
c
c
c
d
c
c
c
d
c
M
L
H
r
L
M
L
r
H
−
związki na siły wewnętrzne w powłoce cylindrycznej:
( )
(
)
[
]
( )
(
)
[
]
( )
(
)
[
]
( )
(
)
[
]
,
,
,
,
sin
64
.
4
sin
37
.
31
sin
93
.
3
sin
78
.
12
,
,
cos
7
.
78
cos
2
.
532
cos
7
.
66
cos
9
.
216
;
;
4
4
;
0
4
4
0
η
η
η
ν
η
η
η
η
η
η
η
η
ϑ
η
π
η
π
η
π
η
π
−
=
′
=
=
⋅
+
′
⋅
+
⋅
+
⋅
+
⋅
+
⋅
=
=
⋅
+
′
⋅
+
⋅
+
⋅
+
⋅
+
⋅
+
=
′
−
−
′
−
−
c
c
c
x
c
c
x
c
c
c
c
c
L
H
L
x
M
M
e
e
M
N
N
e
e
R
R
:
gdzie
Obliczenia sił wewnętrznych w powłoce cylindrycznej wykonano za pomocą programu Excell.
Wyniki obliczeń przedstawiono w tablicy 3.4.2 oraz na wykresie 3.4.
PDF created with pdfFactory trial version
Krzysztof Donten
Zakład Konstrukcji Betonowych
10
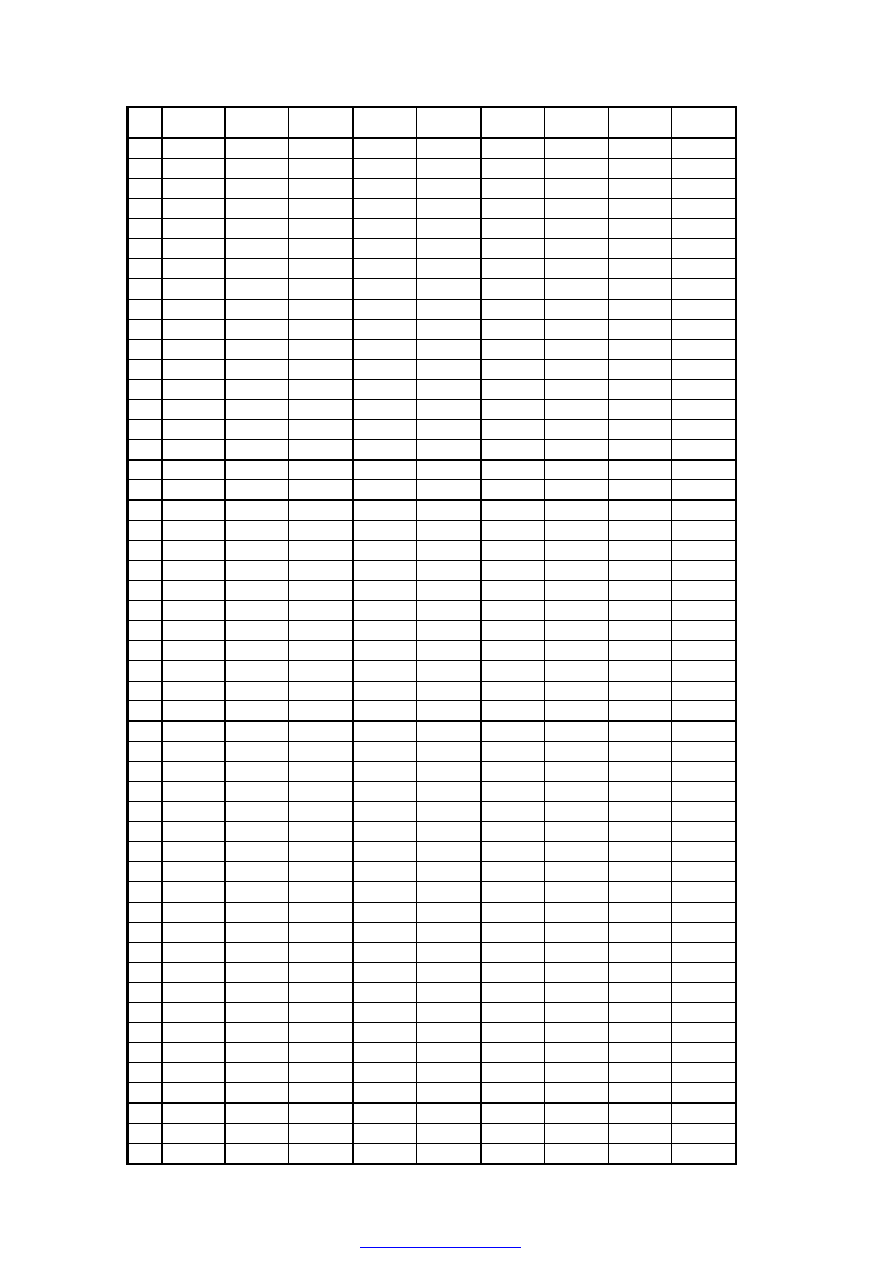
Tablica 3.4.2. Siły wewnętrzne w powłoce cylindrycznej.
lp.
x
η
[rd]
η
’
[rd]
0
c
R
0
c
N
x
c
R
;
x
c
N
;
x
c
M
;
ϑ
;
c
M
0
0.00
0.000 11.891
0.0
-17.6
169.7
-17.6
-2.78
-0.56
1
0.20
0.238 11.653
13.2
-18.8
152.0
-18.8
-0.27
-0.05
2
0.40
0.476 11.415
26.4
-19.9
133.6
-19.9
1.31
0.26
3
0.60
0.713 11.177
39.6
-21.1
117.6
-21.1
2.18
0.44
4
0.80
0.951 10.939
52.8
-22.2
105.7
-22.2
2.52
0.50
5
1.00
1.189 10.702
66.0
-23.4
98.6
-23.4
2.51
0.50
6
1.20
1.427 10.464
79.2
-24.6
96.3
-24.6
2.28
0.46
7
1.40
1.665 10.226
92.4
-25.7
98.3
-25.7
1.93
0.39
8
1.60
1.902
9.988
105.6
-26.9
104.0
-26.9
1.55
0.31
9
1.80
2.140
9.750
118.8
-28.0
112.7
-28.0
1.17
0.23
10
2.00
2.378
9.512
132.0
-29.2
123.7
-29.2
0.83
0.17
11
2.20
2.616
9.275
145.2
-30.4
136.2
-30.4
0.54
0.11
12
2.40
2.854
9.037
158.4
-31.5
149.8
-31.5
0.32
0.06
13
2.60
3.092
8.799
171.6
-32.7
164.1
-32.7
0.15
0.03
14
2.80
3.329
8.561
184.8
-33.8
178.6
-33.8
0.03
0.01
15
3.00
3.567
8.323
198.0
-35.0
193.1
-35.0
-0.05
-0.01
16
3.20
3.805
8.086
211.2
-36.2
207.6
-36.2
-0.10
-0.02
17
3.40
4.043
7.848
224.4
-37.3
221.9
-37.3
-0.12
-0.02
18
3.60
4.281
7.610
237.6
-38.5
235.9
-38.5
-0.12
-0.02
19
3.80
4.518
7.372
250.8
-39.6
249.8
-39.6
-0.12
-0.02
20
4.00
4.756
7.134
264.0
-40.8
263.4
-40.8
-0.10
-0.02
21
4.20
4.994
6.897
277.2
-42.0
276.8
-42.0
-0.08
-0.02
22
4.40
5.232
6.659
290.4
-43.1
290.0
-43.1
-0.06
-0.01
23
4.60
5.470
6.421
303.6
-44.3
303.2
-44.3
-0.04
-0.01
24
4.80
5.707
6.183
316.8
-45.4
316.2
-45.4
-0.01
0.00
25
5.00
5.945
5.945
330.0
-46.6
329.2
-46.6
0.02
0.00
26
5.20
6.183
5.707
343.2
-47.8
342.3
-47.8
0.05
0.01
27
5.40
6.421
5.470
356.4
-48.9
355.5
-48.9
0.09
0.02
28
5.60
6.659
5.232
369.6
-50.1
368.8
-50.1
0.14
0.03
29
5.80
6.897
4.994
382.8
-51.2
382.4
-51.2
0.19
0.04
30
6.00
7.134
4.756
396.0
-52.4
396.4
-52.4
0.25
0.05
31
6.20
7.372
4.518
409.2
-53.6
410.9
-53.6
0.30
0.06
32
6.40
7.610
4.281
422.4
-54.7
425.9
-54.7
0.34
0.07
33
6.60
7.848
4.043
435.6
-55.9
441.6
-55.9
0.35
0.07
34
6.80
8.086
3.805
448.8
-57.0
457.9
-57.0
0.33
0.07
35
7.00
8.323
3.567
462.0
-58.2
474.9
-58.2
0.25
0.05
36
7.20
8.561
3.329
475.2
-59.4
492.3
-59.4
0.07
0.01
37
7.40
8.799
3.092
488.4
-60.5
509.9
-60.5
-0.21
-0.04
38
7.60
9.037
2.854
501.6
-61.7
527.0
-61.7
-0.64
-0.13
39
7.80
9.275
2.616
514.8
-62.8
542.9
-62.8
-1.24
-0.25
40
8.00
9.512
2.378
528.0
-64.0
556.3
-64.0
-2.02
-0.40
41
8.20
9.750
2.140
541.2
-65.2
565.9
-65.2
-2.99
-0.60
42
8.40
9.988
1.902
554.4
-66.3
569.7
-66.3
-4.12
-0.82
43
8.60 10.226
1.665
567.6
-67.5
565.6
-67.5
-5.35
-1.07
44
8.80 10.464
1.427
580.8
-68.6
551.2
-68.6
-6.56
-1.31
45
9.00 10.702
1.189
594.0
-69.8
524.2
-69.8
-7.57
-1.51
46
9.20 10.939
0.951
607.2
-71.0
482.8
-71.0
-8.10
-1.62
47
9.40 11.177
0.713
620.4
-72.1
426.0
-72.1
-7.79
-1.56
48
9.60 11.415
0.476
633.6
-73.3
354.5
-73.3
-6.18
-1.24
49
9.80 11.653
0.238
646.8
-74.4
271.3
-74.4
-2.70
-0.54
50
10.00 11.891
0.000
660.0
-75.6
183.5
-75.6
3.28
0.66
PDF created with pdfFactory trial version
Krzysztof Donten
Zakład Konstrukcji Betonowych
11
PDF created with pdfFactory trial version
Krzysztof Donten
Zakład Konstrukcji Betonowych
12
4.
Wymiarowanie konstrukcji.
4.1. Kopuła stożkowa przekrycia.
4.1.1. Zbrojenie południkowe powłoki stożkowej.
−
zbrojenie południkowe powłoki stożkowej w połączeniu powłok (mimośrodowe ściskanie):
m,
m
cm,
5.2
cm,
mm
m
m
kN
m
kNm
024
.
0
028
.
0
052
.
0
138
.
0
028
.
0
2
08
.
0
126
.
0
2
8
.
2
0
.
8
8
.
2
28
2
6
25
2
,
126
.
0
1
.
22
78
.
2
,
1
.
22
,
78
.
2
0
1
2
1
0
,
,
=
−
=
−
>
=
−
+
=
−
+
=
=
−
=
−
=
=
=
+
=
+
=
=
=
=
=
=
=
=
=
=
a
d
a
h
e
e
a
h
d
c
a
a
a
N
M
e
R
N
M
M
s
nom
Sd
Sd
s
Sd
s
Sd
φ
ϕ
ϑ
Duży mimośród.
,
68
.
0
2
.
5
0
.
100
0013
.
0
,
82
.
1
2
.
5
0
.
100
00350
.
0
,
003
.
0
0048
.
0
0013
.
0
0035
.
0
,
0013
.
0
,
0013
.
0
00350
.
0
00202
.
0
00552
.
0
,
00202
.
0
210
052
.
0
0
.
1
0221
.
0
,
00552
.
0
210
0
.
20
058
.
0
,
50
.
0
058
.
0
056
.
0
0
.
20
052
.
0
0
.
1
138
.
0
0221
.
0
2
2
1
1
2
1
min
2
min
1
lim
,
*
lim
,
2
*
2
1
2
2
cm
cm
=
⋅
⋅
=
=
=
⋅
⋅
=
=
>
=
+
=
+
=
=
=
>
=
−
=
−
=
→
<
=
⋅
⋅
=
=
=
⋅
=
=
=
<
=
→
=
⋅
⋅
⋅
=
=
d
b
A
d
b
A
f
d
b
N
f
f
f
d
b
e
N
s
s
s
s
s
s
s
s
N
s
eff
yd
Sd
N
yd
cd
eff
cd
s
Sd
c
ρ
ρ
ρ
ρ
ρ
ρ
ρ
ρ
ρ
ρ
ξ
ξ
ρ
ξ
ρ
ξ
ξ
Przyjęto zbrojenie południkowe w strefie połączenia z powłoką cylindryczną górą i dołem
φ
6 co
150 mm o przekroju A
s
=1.89 cm
2
; poza strefą połączenia rozstaw prętów należy zwiększyć do 20 cm.
4.1.2. Zbrojenie równoleżnikowe powłoki stożkowej.
−
zbrojenie w strefie rozciągań brzegowych (mimośrodowe rozciąganie):
,
0031
.
0
034
.
0
2
08
.
0
0091
.
0
2
006
.
0
034
.
0
2
08
.
0
2
0091
.
0
6
.
4
4
.
3
0
.
8
34
6
5
.
1
25
5
.
1
,
0091
.
0
4
.
61
56
.
0
,
4
.
61
,
56
.
0
0
1
0
2
1
0
,
,
m
mimośród,
duży
m
cm,
cm,
3.4
mm
m
m
kN
m
kNm
=
+
−
=
+
−
=
→
=
−
=
−
>
=
=
−
=
−
=
=
=
⋅
+
=
+
=
=
=
=
=
=
=
=
=
=
a
h
e
e
a
h
e
a
h
d
c
a
a
a
N
M
e
R
N
M
M
s
nom
Sd
Sd
s
Sd
s
Sd
φ
ϕ
ϑ
,
68
.
0
4
.
3
0
.
100
002
.
0
12
.
3
,
12
.
3
92
.
2
20
.
0
10
210
0614
.
0
10
210
046
.
0
98
.
0
0031
.
0
0614
.
0
,
98
.
0
0045
.
0
0
.
20
046
.
0
0
.
1
0031
.
0
0614
.
0
min
min
,
1
2
4
4
1
2
2
1
2
2
cm
cm
cm
=
⋅
⋅
=
=
>
=
=
+
=
×
+
×
⋅
⋅
⋅
=
+
=
=
→
=
⋅
⋅
⋅
=
=
d
b
A
A
f
N
f
d
e
N
A
f
d
b
e
N
s
s
s
yd
Sd
yd
s
Sd
s
cd
s
Sd
c
ρ
ζ
ζ
Przyjęto w strefie rozciągań górą zbrojenie #6/100 mm o As=2.83 cm
2
dodatkowo wzmocnione
1#12 o As=1.13 cm
2
w przekroju oparcia powłoki stożkowej na ścianie walcowej.
−
zbrojenie równoleżnikowe dołem oraz górą poza strefą rozciągań brzegowych konstrukcyjne
φ
6/200 o A
s
=1.42 cm
2
.
−
zarysowanie przekroju podporowego:
,
1
.
52
138
08
.
0
1
00107
.
0
0091
.
0
10
90
.
2
1
,
00107
.
0
6
08
.
0
0
.
1
,
0
.
1
08
.
0
0091
.
0
,
1
.
52
178
.
1
4
.
61
3
2
0
m
kN
m
kN
m
m
m,
m
kN
3
2
=
>
=
+
×
=
−
=
=
⋅
=
⋅
=
=
=
=
≈
=
Sk
c
c
ctm
cr
c
c
f
Sd
Sk
N
A
W
e
f
N
W
A
e
e
N
N
γ
Obwodowy przekrój podporowy powłoki stożkowej nie jest zarysowany.
PDF created with pdfFactory trial version

Krzysztof Donten
Zakład Konstrukcji Betonowych
13
4.2. Powłoka cylindryczna.
4.2.1. Zbrojenie równoleżnikowe powłoki cylindrycznej.
−
zbrojenie minimalne ściany zbiornika (po każdej stronie ściany):
,
52
.
4
,
250
12
#
0
.
4
200
100
002
.
0
2
1
min
min
;
m
cm
mm
m
cm
2
przyjęto
2
=
=
→
=
⋅
⋅
=
=
s
s
s
A
A
h
b
A
ρ
−
osiowa siła rysująca ścianę zbiornika:
,
518
10
.
1
570
580
10
00
.
1
20
.
0
90
.
2
max
;
max
;
3
m
kN
m
kN
=
=
=
>
=
×
⋅
⋅
=
=
f
Sd
Sk
c
ctm
cr
N
N
A
f
N
γ
Na całej wysokości ściany siły rzeczywiste są mniejsze od siły rysującej
•
strefa I (górna - przy połączeniu z powłoką stożkową; x=0.0÷3.0 m).
−
Zbrojenie ze względu na nośność:
,
05
.
4
2
09
.
8
09
.
8
10
310
193
.
0
3
.
1
,
193
2
1
4
2
1
0
.
3
;
2
2
cm
cm
m
kN
=
=
=
→
=
×
⋅
=
=
+
=
=
=
s
s
yd
Sd
s
s
h
c
Sd
A
A
f
R
m
A
A
R
R
c
Przyjęto zbrojenie obustronne (minimalne) 2#12/250 mm o przekroju A
s
=2
×
4.52 cm
2
.
•
strefa II (x=3.0÷7.0 m).
−
Zbrojenie ze względu na nośność:
,
96
.
9
2
92
.
19
92
.
19
10
310
475
.
0
3
.
1
,
475
2
1
4
2
1
0
.
7
;
2
2
cm
cm
m
kN
=
=
=
→
=
×
⋅
=
=
+
=
=
=
s
s
yd
Sd
s
s
h
c
Sd
A
A
f
R
m
A
A
R
R
c
Przyjęto zbrojenie obustronne 2#16/200 mm o przekroju A
s
=2
×
10.05 cm
2
.
•
strefa III (dolna - przy połączeniu z ławą fundamentową x=7.0÷10.0 m).
−
Zbrojenie ze względu na nośność:
,
95
.
11
2
9
.
23
9
.
23
10
310
570
.
0
3
.
1
,
570
2
1
4
2
1
4
.
8
;
2
2
cm
cm
m
kN
=
=
=
→
=
×
⋅
=
=
+
=
=
=
s
s
yd
Sd
s
s
h
c
Sd
A
A
f
R
m
A
A
R
R
c
Przyjęto obustronnie po #16/150 mm o przekroju A
s
=2
×
13.4=26.8 cm
2
.
4.2.2. Zbrojenie pionowe powłoki cylindrycznej.
Miarodajna do obliczeń zbrojenia pionowego jest strefa połączenia powłoki cylindrycznej z ławą
fundamentową. Do wymiarowania przyjęto maksymalną wielkość mimośrodu w strefie i największą
wielkość siły pionowej (węzłową).
,
6
.
75
,
112
.
0
1
.
72
10
.
8
20
.
9
max
,
,
max
,
max
m
kN
m
m
0
=
=
=
=
=
=
→
=
x
c
Sd
x
c
x
c
N
N
e
N
M
e
x
−
zbrojenie ze względu na nośność (mimośrodowe ściskanie):
m,
m
cm,
cm,
3.6
mm
128
.
0
036
.
0
164
.
0
176
.
0
036
.
0
2
20
.
0
112
.
0
2
4
.
16
6
.
3
0
.
20
36
2
12
30
2
0
1
2
1
=
−
=
−
>
=
−
+
=
−
+
=
=
−
=
−
=
=
=
+
=
+
=
=
=
a
d
a
h
e
e
a
h
d
c
a
a
a
s
nom
φ
Duży mimośród.
,
52
.
4
250
/
12
#
,
36
.
3
4
.
16
0
.
100
00205
.
0
,
00205
.
0
036
.
0
164
.
0
176
.
0
00149
.
0
,
00149
.
0
310
164
.
0
0
.
1
0756
.
0
,
439
.
0
4
.
16
6
.
3
2
2
026
.
0
025
.
0
0
.
20
164
.
0
0
.
1
176
.
0
0756
.
0
%,
15
.
0
2
3
.
0
003
.
0
000037
.
0
310
0756
.
0
15
.
0
15
.
0
2
1
2
1
min
1
2
1
2
*
2
1
min
min
cm
mm,
cm
2
=
→
=
⋅
⋅
=
=
=
>
=
−
⋅
=
−
=
=
=
⋅
⋅
=
=
=
⋅
=
<
=
→
=
⋅
⋅
⋅
=
=
=
=
→
<
=
⋅
=
=
∑
s
s
s
s
s
N
s
s
yd
Sd
N
cd
s
Sd
c
yd
Sd
A
d
b
A
A
a
d
e
f
d
b
N
d
a
f
d
b
e
N
s
f
N
ρ
ρ
ρ
ρ
ρ
ρ
ξ
ρ
ρ
Przyjęto zbrojenie standardowe 4#12 obustronnie, po wewnętrznej stronie prętów obwodowych.
PDF created with pdfFactory trial version
Krzysztof Donten
Zakład Konstrukcji Betonowych
14
−
zarysowanie przekroju:
,
4
.
67
246
20
.
0
1
00667
.
0
112
.
0
10
90
.
2
1
,
00667
.
0
6
2
.
0
0
.
1
,
0
.
1
2
.
0
,
4
.
67
05
.
1
0
.
58
178
.
1
6
.
17
max
3
2
max
m
kN
m
kN
m
m
m
kN
3
2
=
>>
=
−
×
=
−
=
=
⋅
=
⋅
=
=
+
=
Sk
c
c
ctm
cr
c
c
Sk
N
A
W
e
f
N
W
A
N
Przekroje równoleżnikowe ściany nie są zarysowane.
4.3. Ława fundamentowa.
−
Kąt obrotu ławy i odpór podłoża pod ławą (od obrotu ławy):
(
)
[
]
[
]
,
b
C
σ
r
r
N
X
e
X
k
L
M
L
L
c
H
c
d
g
L
d
L
M
L
L
c
L
2
m
kN
70
.
5
10
2
40
.
1
20000
10
407
2
,
10
407
0
28
.
3
35
.
0
3
.
37
10
9
.
24
3
6
0
6
6
0
;
2
;
1
0
=
×
⋅
⋅
×
=
Ψ
=
∆
×
=
+
−
⋅
−
×
−
=
−
+
+
−
=
Ψ
−
−
−
−
Siły zewnętrzne działające na ławę:
(
)
,
5
.
14
6
40
.
1
70
.
5
28
.
3
35
.
0
3
.
37
0
6
,
3
.
37
2
2
2
,
1
0
;
1
m
kNm
m
kN
=
⋅
−
+
⋅
+
−
=
∆
−
−
−
−
−
=
+
=
−
=
L
g
L
L
c
o
c
L
L
b
X
e
X
r
r
N
M
X
H
σ
−
Siła rozciągająca wieniec i moment zginający:
m,
kNm
kN
388
.
0
224
87
87
00
.
6
5
.
14
224
00
.
6
3
.
37
0
=
=
=
→
=
⋅
=
=
=
⋅
=
=
Sd
Sd
L
L
Sd
L
L
Sd
N
M
e
r
M
M
r
H
N
Przekrój mimośrodowo rozciągany – silniej rozciągana jest strefa górna ławy.
m,
m
cm,
cm,
6.8
mm
564
.
0
068
.
0
632
.
0
670
.
0
068
.
0
2
70
.
0
388
.
0
2
2
.
63
8
.
6
0
.
70
68
2
16
60
2
0
1
2
1
=
−
=
−
>
≈
−
+
=
−
+
=
=
−
=
−
=
=
=
+
=
+
=
=
=
a
d
a
h
e
e
a
h
d
c
a
a
a
s
nom
φ
Duży mimośród.
,
70
.
17
2
.
63
0
.
140
002
.
0
04
.
15
,
04
.
15
22
.
7
82
.
7
10
310
224
.
0
10
310
632
.
0
98
.
0
670
.
0
224
.
0
,
98
.
0
013
.
0
0
.
20
632
.
0
4
.
1
670
.
0
224
.
0
min
min
,
1
2
4
4
1
2
2
1
2
2
cm
cm
cm
=
⋅
⋅
=
=
<
=
=
+
=
×
+
×
⋅
⋅
⋅
=
+
=
=
→
=
⋅
⋅
⋅
=
=
d
b
A
A
f
N
f
d
e
N
A
f
d
b
e
N
s
s
s
yd
Sd
yd
s
Sd
s
cd
s
Sd
c
ρ
ζ
ζ
Przyjęto zbrojenie górą 9#16/~160 mm o A
s
=18.09 cm
2
; Dołem (ze względu na minimalny
stopień zbrojenia) przyjęto również 9#16/160 o A
s
=18.09 cm
2
. Dodatkowo przy powierzchniach
bocznych ławy przyjęto po 2#16 (pomiędzy prętami w narożach ławy).
−
zarysowanie przekroju (współczynnik obciążenia
γ
f
=1.10 jak dla parcia wody):
,
204
408
98
.
0
1
08000
.
0
487
.
0
10
90
.
2
1
,
0800
.
0
6
7
.
0
4
.
1
,
98
.
0
4
.
1
7
.
0
,
204
10
.
1
224
3
0
2
kN
kN
m
m
kN
3
2
=
>
=
+
×
=
+
=
=
⋅
=
=
⋅
=
=
≈
=
Sk
c
c
ctm
cr
c
c
f
Sd
Sk
N
A
W
e
f
N
W
A
N
N
γ
Przekrój ławy nie jest zarysowany.
PDF created with pdfFactory trial version
Wyszukiwarka
Podobne podstrony:
Abolicja podatkowa id 50334 Nieznany (2)
4 LIDER MENEDZER id 37733 Nieznany (2)
katechezy MB id 233498 Nieznany
metro sciaga id 296943 Nieznany
perf id 354744 Nieznany
interbase id 92028 Nieznany
Mbaku id 289860 Nieznany
Probiotyki antybiotyki id 66316 Nieznany
miedziowanie cz 2 id 113259 Nieznany
LTC1729 id 273494 Nieznany
D11B7AOver0400 id 130434 Nieznany
analiza ryzyka bio id 61320 Nieznany
pedagogika ogolna id 353595 Nieznany
Misc3 id 302777 Nieznany
cw med 5 id 122239 Nieznany
D20031152Lj id 130579 Nieznany
mechanika 3 id 290735 Nieznany
więcej podobnych podstron