
Prawo wielkich liczb Bernoulliego i centralne tw. graniczne
Podstawowe poj ˛ecia wnioskowania statystycznego
PODSTAWY WNIOSKOWANIA
STATYSTYCZNEGO – cze¸ ´s ´c I
Agnieszka Rossa
Agnieszka Rossa

Prawo wielkich liczb Bernoulliego i centralne tw. graniczne
Podstawowe poj ˛ecia wnioskowania statystycznego
Szkic wykładu
1
2
Prawo wielkich liczb Bernoulliego i centralne tw.
graniczne
3
Podstawowe poj ˛ecia wnioskowania statystycznego
4
Agnieszka Rossa

Prawo wielkich liczb Bernoulliego i centralne tw. graniczne
Podstawowe poj ˛ecia wnioskowania statystycznego
Przykład wprowadzaj ˛
acy
W Polsce ró˙zne głosowania odbywaj ˛
a si ˛e co kilka lat,
a pytanie o preferencje wyborcze jest jednym z cz ˛esto
zadawanych w badaniach sonda˙zowych.
Sonda˙z PGB przeprowadzony w´sód 1018 osób tu˙z przed
wyborami parlamentarnymi w 2007 r. wskazywał m.in., ˙ze
na kandydatów PiS głosowa´c b ˛edzie 35% wyborców.
Zgodnie z oficjalnymi wynikami wyborów, rzeczywisty
odsetek głosów oddanych na PiS w tych wyborach był
równy 32,11%.
Wynik sonda˙zu był zatem zbli˙zony do rzeczywistego pomi-
mo, ˙ze próba 1018 respondentów była relatywnie bardzo
mała wobec populacji ponad 30,6 mln osób uprawnionych
do głosowania (czy te˙z ok. 16,5 mln faktycznie głosuj ˛
a-
cych).
Agnieszka Rossa

Prawo wielkich liczb Bernoulliego i centralne tw. graniczne
Podstawowe poj ˛ecia wnioskowania statystycznego
Przykład wprowadzaj ˛
acy
W Polsce ró˙zne głosowania odbywaj ˛
a si ˛e co kilka lat,
a pytanie o preferencje wyborcze jest jednym z cz ˛esto
zadawanych w badaniach sonda˙zowych.
Sonda˙z PGB przeprowadzony w´sód 1018 osób tu˙z przed
wyborami parlamentarnymi w 2007 r. wskazywał m.in., ˙ze
na kandydatów PiS głosowa´c b ˛edzie 35% wyborców.
Zgodnie z oficjalnymi wynikami wyborów, rzeczywisty
odsetek głosów oddanych na PiS w tych wyborach był
równy 32,11%.
Wynik sonda˙zu był zatem zbli˙zony do rzeczywistego pomi-
mo, ˙ze próba 1018 respondentów była relatywnie bardzo
mała wobec populacji ponad 30,6 mln osób uprawnionych
do głosowania (czy te˙z ok. 16,5 mln faktycznie głosuj ˛
a-
cych).
Agnieszka Rossa

Prawo wielkich liczb Bernoulliego i centralne tw. graniczne
Podstawowe poj ˛ecia wnioskowania statystycznego
Przykład wprowadzaj ˛
acy
W Polsce ró˙zne głosowania odbywaj ˛
a si ˛e co kilka lat,
a pytanie o preferencje wyborcze jest jednym z cz ˛esto
zadawanych w badaniach sonda˙zowych.
Sonda˙z PGB przeprowadzony w´sód 1018 osób tu˙z przed
wyborami parlamentarnymi w 2007 r. wskazywał m.in., ˙ze
na kandydatów PiS głosowa´c b ˛edzie 35% wyborców.
Zgodnie z oficjalnymi wynikami wyborów, rzeczywisty
odsetek głosów oddanych na PiS w tych wyborach był
równy 32,11%.
Wynik sonda˙zu był zatem zbli˙zony do rzeczywistego pomi-
mo, ˙ze próba 1018 respondentów była relatywnie bardzo
mała wobec populacji ponad 30,6 mln osób uprawnionych
do głosowania (czy te˙z ok. 16,5 mln faktycznie głosuj ˛
a-
cych).
Agnieszka Rossa

Prawo wielkich liczb Bernoulliego i centralne tw. graniczne
Podstawowe poj ˛ecia wnioskowania statystycznego
Przykład wprowadzaj ˛
acy
W Polsce ró˙zne głosowania odbywaj ˛
a si ˛e co kilka lat,
a pytanie o preferencje wyborcze jest jednym z cz ˛esto
zadawanych w badaniach sonda˙zowych.
Sonda˙z PGB przeprowadzony w´sód 1018 osób tu˙z przed
wyborami parlamentarnymi w 2007 r. wskazywał m.in., ˙ze
na kandydatów PiS głosowa´c b ˛edzie 35% wyborców.
Zgodnie z oficjalnymi wynikami wyborów, rzeczywisty
odsetek głosów oddanych na PiS w tych wyborach był
równy 32,11%.
Wynik sonda˙zu był zatem zbli˙zony do rzeczywistego pomi-
mo, ˙ze próba 1018 respondentów była relatywnie bardzo
mała wobec populacji ponad 30,6 mln osób uprawnionych
do głosowania (czy te˙z ok. 16,5 mln faktycznie głosuj ˛
a-
cych).
Agnieszka Rossa

Prawo wielkich liczb Bernoulliego i centralne tw. graniczne
Podstawowe poj ˛ecia wnioskowania statystycznego
Uwagi do przykładu
Uwaga 1:
Wylosowana próba respondentów nie daje peł-
nej gwarancji, ˙ze udział głosów na dan ˛
a parti ˛e w tej próbie
b ˛edzie taki sam, jak w całej populacji. Istnieje jednak pew-
na zale˙zno´s´c mi ˛edzy liczno´sci ˛
a próby a dokładno´sci ˛
a
oszacowania danego wska´znika, do czego wrócimy.
Uwaga 2:
Wskazane byłoby, aby oprócz pojedycznej licz-
by poda´c tak˙ze ´sredni bł ˛
ad oszacowania lub te˙z poda´c
przedział liczbowy, który zawierałby, ze znanym prawdopo-
dobie ´nstwem, rzeczywist ˛
a warto´s´c szukanego wska´znika.
Uwaga 3:
Zauwa˙zymy, ˙ze gdyby´smy osobom głosuj ˛
acym
na PiS przyporz ˛
adkowali warto´s´c 1, a pozostałym warto´s´c
0, to udział głosuj ˛
acych na t ˛e parti ˛e b ˛edzie równy ´sredniej
arytmetycznej ze zbioru zer i jedynek (tak ˛
a ´sredni ˛
a mo˙ze-
my zdefiniowa´c zarówno dla próby, jak i dla populacji).
Agnieszka Rossa

Prawo wielkich liczb Bernoulliego i centralne tw. graniczne
Podstawowe poj ˛ecia wnioskowania statystycznego
Uwagi do przykładu
Uwaga 1:
Wylosowana próba respondentów nie daje peł-
nej gwarancji, ˙ze udział głosów na dan ˛
a parti ˛e w tej próbie
b ˛edzie taki sam, jak w całej populacji. Istnieje jednak pew-
na zale˙zno´s´c mi ˛edzy liczno´sci ˛
a próby a dokładno´sci ˛
a
oszacowania danego wska´znika, do czego wrócimy.
Uwaga 2:
Wskazane byłoby, aby oprócz pojedycznej licz-
by poda´c tak˙ze ´sredni bł ˛
ad oszacowania lub te˙z poda´c
przedział liczbowy, który zawierałby, ze znanym prawdopo-
dobie ´nstwem, rzeczywist ˛
a warto´s´c szukanego wska´znika.
Uwaga 3:
Zauwa˙zymy, ˙ze gdyby´smy osobom głosuj ˛
acym
na PiS przyporz ˛
adkowali warto´s´c 1, a pozostałym warto´s´c
0, to udział głosuj ˛
acych na t ˛e parti ˛e b ˛edzie równy ´sredniej
arytmetycznej ze zbioru zer i jedynek (tak ˛
a ´sredni ˛
a mo˙ze-
my zdefiniowa´c zarówno dla próby, jak i dla populacji).
Agnieszka Rossa

Prawo wielkich liczb Bernoulliego i centralne tw. graniczne
Podstawowe poj ˛ecia wnioskowania statystycznego
Uwagi do przykładu
Uwaga 1:
Wylosowana próba respondentów nie daje peł-
nej gwarancji, ˙ze udział głosów na dan ˛
a parti ˛e w tej próbie
b ˛edzie taki sam, jak w całej populacji. Istnieje jednak pew-
na zale˙zno´s´c mi ˛edzy liczno´sci ˛
a próby a dokładno´sci ˛
a
oszacowania danego wska´znika, do czego wrócimy.
Uwaga 2:
Wskazane byłoby, aby oprócz pojedycznej licz-
by poda´c tak˙ze ´sredni bł ˛
ad oszacowania lub te˙z poda´c
przedział liczbowy, który zawierałby, ze znanym prawdopo-
dobie ´nstwem, rzeczywist ˛
a warto´s´c szukanego wska´znika.
Uwaga 3:
Zauwa˙zymy, ˙ze gdyby´smy osobom głosuj ˛
acym
na PiS przyporz ˛
adkowali warto´s´c 1, a pozostałym warto´s´c
0, to udział głosuj ˛
acych na t ˛e parti ˛e b ˛edzie równy ´sredniej
arytmetycznej ze zbioru zer i jedynek (tak ˛
a ´sredni ˛
a mo˙ze-
my zdefiniowa´c zarówno dla próby, jak i dla populacji).
Agnieszka Rossa

Prawo wielkich liczb Bernoulliego i centralne tw. graniczne
Podstawowe poj ˛ecia wnioskowania statystycznego
Prawo wielkich liczb i centralne twierdzenie graniczne
W dalszych rozwa˙zaniach przedstawimy słabe prawo wielkich
liczb, b ˛ed ˛
ace jednym z podstawowych zasad rachunku prawdo-
podobie ´nstwa oraz centralne twierdzenie graniczne, które wy-
korzystamy w zagadnieniach szacowania nieznanych wska´z-
ników (parametrów) populacji.
Prawo wielkich liczb zostało sformułowane po raz pierwszy
przez Jakuba Bernoulliego, ˙zyj ˛
acego na przełomie XVII i XVIII
wieku, ale opublikowane zostało dopiero w 1913 r., tj. 200 lat po
´smierci jego twórcy. Bernoulli nazwał je
”złotym twierdzeniem”
.
Z prawdopodobie ´nstwem dowolnie bliskim 1 mo˙zna si ˛e spo-
dziewa´c, i˙z przy dostatecznie wielkiej liczbie powtórze ´n ekspe-
rymentu losowego, z których ka˙zdy ko ´nczy si ˛e sukcesem lub
pora˙zk ˛
a, cz ˛esto´s´c wyst ˛
apienia sukcesu w serii eksperymentów
b ˛edzie si ˛e dowolnie mało ró˙zniła od jego prawdopodobie ´nstwa.
Agnieszka Rossa

Prawo wielkich liczb Bernoulliego i centralne tw. graniczne
Podstawowe poj ˛ecia wnioskowania statystycznego
Prawo wielkich liczb i centralne twierdzenie graniczne
W dalszych rozwa˙zaniach przedstawimy słabe prawo wielkich
liczb, b ˛ed ˛
ace jednym z podstawowych zasad rachunku prawdo-
podobie ´nstwa oraz centralne twierdzenie graniczne, które wy-
korzystamy w zagadnieniach szacowania nieznanych wska´z-
ników (parametrów) populacji.
Prawo wielkich liczb zostało sformułowane po raz pierwszy
przez Jakuba Bernoulliego, ˙zyj ˛
acego na przełomie XVII i XVIII
wieku, ale opublikowane zostało dopiero w 1913 r., tj. 200 lat po
´smierci jego twórcy. Bernoulli nazwał je
”złotym twierdzeniem”
.
Z prawdopodobie ´nstwem dowolnie bliskim 1 mo˙zna si ˛e spo-
dziewa´c, i˙z przy dostatecznie wielkiej liczbie powtórze ´n ekspe-
rymentu losowego, z których ka˙zdy ko ´nczy si ˛e sukcesem lub
pora˙zk ˛
a, cz ˛esto´s´c wyst ˛
apienia sukcesu w serii eksperymentów
b ˛edzie si ˛e dowolnie mało ró˙zniła od jego prawdopodobie ´nstwa.
Agnieszka Rossa

Prawo wielkich liczb Bernoulliego i centralne tw. graniczne
Podstawowe poj ˛ecia wnioskowania statystycznego
Prawo wielkich liczb i centralne twierdzenie graniczne
W dalszych rozwa˙zaniach przedstawimy słabe prawo wielkich
liczb, b ˛ed ˛
ace jednym z podstawowych zasad rachunku prawdo-
podobie ´nstwa oraz centralne twierdzenie graniczne, które wy-
korzystamy w zagadnieniach szacowania nieznanych wska´z-
ników (parametrów) populacji.
Prawo wielkich liczb zostało sformułowane po raz pierwszy
przez Jakuba Bernoulliego, ˙zyj ˛
acego na przełomie XVII i XVIII
wieku, ale opublikowane zostało dopiero w 1913 r., tj. 200 lat po
´smierci jego twórcy. Bernoulli nazwał je
”złotym twierdzeniem”
.
Z prawdopodobie ´nstwem dowolnie bliskim 1 mo˙zna si ˛e spo-
dziewa´c, i˙z przy dostatecznie wielkiej liczbie powtórze ´n ekspe-
rymentu losowego, z których ka˙zdy ko ´nczy si ˛e sukcesem lub
pora˙zk ˛
a, cz ˛esto´s´c wyst ˛
apienia sukcesu w serii eksperymentów
b ˛edzie si ˛e dowolnie mało ró˙zniła od jego prawdopodobie ´nstwa.
Agnieszka Rossa

Prawo wielkich liczb Bernoulliego i centralne tw. graniczne
Podstawowe poj ˛ecia wnioskowania statystycznego
Prawo wielkich liczb Bernoulliego
Przykład.
Załó˙zmy, ˙ze przeprowadzamy seri ˛e eksperymentów pole-
gaj ˛
acych na rzucaniu monet ˛
a.
Niech sukcesem b ˛edzie wyrzucenie orła w pojedynczym
rzucie. Je´sli moneta jest symetryczna, to prawdopodo-
bie ´nstwo sukcesu w ka˙zdym eksperymencie wynosi
1
2
.
Załó˙zmy, ˙ze po ka˙zdym rzucie obliczamy cz ˛esto´s´c wyrzu-
conych orłów w serii dotychczas wykonanych rzutów (czyli
iloraz liczby orłów do liczby rzutów).
Prawo Bernoulliego mówi, ˙ze szansa na to, by obliczona
cz ˛esto´s´c była bardzo bliska prawdopodobie ´nstwu
1
2
(a dokładniej – aby ró˙zniła si ˛e od niego dowolnie mało),
zmierza do 1 wraz ze zwi ˛ekszaniem liczby rzutów.
Agnieszka Rossa

Prawo wielkich liczb Bernoulliego i centralne tw. graniczne
Podstawowe poj ˛ecia wnioskowania statystycznego
Prawo wielkich liczb Bernoulliego
Przykład.
Załó˙zmy, ˙ze przeprowadzamy seri ˛e eksperymentów pole-
gaj ˛
acych na rzucaniu monet ˛
a.
Niech sukcesem b ˛edzie wyrzucenie orła w pojedynczym
rzucie. Je´sli moneta jest symetryczna, to prawdopodo-
bie ´nstwo sukcesu w ka˙zdym eksperymencie wynosi
1
2
.
Załó˙zmy, ˙ze po ka˙zdym rzucie obliczamy cz ˛esto´s´c wyrzu-
conych orłów w serii dotychczas wykonanych rzutów (czyli
iloraz liczby orłów do liczby rzutów).
Prawo Bernoulliego mówi, ˙ze szansa na to, by obliczona
cz ˛esto´s´c była bardzo bliska prawdopodobie ´nstwu
1
2
(a dokładniej – aby ró˙zniła si ˛e od niego dowolnie mało),
zmierza do 1 wraz ze zwi ˛ekszaniem liczby rzutów.
Agnieszka Rossa

Prawo wielkich liczb Bernoulliego i centralne tw. graniczne
Podstawowe poj ˛ecia wnioskowania statystycznego
Prawo wielkich liczb Bernoulliego
Przykład.
Załó˙zmy, ˙ze przeprowadzamy seri ˛e eksperymentów pole-
gaj ˛
acych na rzucaniu monet ˛
a.
Niech sukcesem b ˛edzie wyrzucenie orła w pojedynczym
rzucie. Je´sli moneta jest symetryczna, to prawdopodo-
bie ´nstwo sukcesu w ka˙zdym eksperymencie wynosi
1
2
.
Załó˙zmy, ˙ze po ka˙zdym rzucie obliczamy cz ˛esto´s´c wyrzu-
conych orłów w serii dotychczas wykonanych rzutów (czyli
iloraz liczby orłów do liczby rzutów).
Prawo Bernoulliego mówi, ˙ze szansa na to, by obliczona
cz ˛esto´s´c była bardzo bliska prawdopodobie ´nstwu
1
2
(a dokładniej – aby ró˙zniła si ˛e od niego dowolnie mało),
zmierza do 1 wraz ze zwi ˛ekszaniem liczby rzutów.
Agnieszka Rossa

Prawo wielkich liczb Bernoulliego i centralne tw. graniczne
Podstawowe poj ˛ecia wnioskowania statystycznego
Prawo wielkich liczb Bernoulliego
Przykład.
Załó˙zmy, ˙ze przeprowadzamy seri ˛e eksperymentów pole-
gaj ˛
acych na rzucaniu monet ˛
a.
Niech sukcesem b ˛edzie wyrzucenie orła w pojedynczym
rzucie. Je´sli moneta jest symetryczna, to prawdopodo-
bie ´nstwo sukcesu w ka˙zdym eksperymencie wynosi
1
2
.
Załó˙zmy, ˙ze po ka˙zdym rzucie obliczamy cz ˛esto´s´c wyrzu-
conych orłów w serii dotychczas wykonanych rzutów (czyli
iloraz liczby orłów do liczby rzutów).
Prawo Bernoulliego mówi, ˙ze szansa na to, by obliczona
cz ˛esto´s´c była bardzo bliska prawdopodobie ´nstwu
1
2
(a dokładniej – aby ró˙zniła si ˛e od niego dowolnie mało),
zmierza do 1 wraz ze zwi ˛ekszaniem liczby rzutów.
Agnieszka Rossa

Prawo wielkich liczb Bernoulliego i centralne tw. graniczne
Podstawowe poj ˛ecia wnioskowania statystycznego
Słabe prawo wielkich liczb
Podobne prawo mo˙zna tak˙ze sformułowa´c w odniesienu do
´sredniej z próby losowej (w szczególnym przypadku, cz ˛esto´s´c
wyst ˛
apienia sukcesu w serii n eksperymentów mo˙zemy trak-
towa´c jak ´sredni ˛
a z n-elementowej próby składaj ˛
acej si ˛e z zer
i jedynek – zob. Uwaga 3). Prawo to nazywamy
słabym
prawem wielkich liczb
:
Je´sli z dowolnej populacji wylosuje si ˛e próbk˛e o liczno´sci n
i je´sli dla takiej próbki obliczy si ˛e ´sredni ˛
a arytmetyczn ˛
a, to
prawdopodobie ´nstwo tego, ˙ze ´srednia próbkowa b ˛edzie ró˙zni´c
si ˛e dowolnie mało od ´sredniej dla całej populacji, zbli˙za si ˛e do 1
wraz ze wzrostem n.
Jest to tzw. zbie˙zno´s´c wg prawdopodobie ´nstwa. Mówi ˛
ac
w uproszczeniu, zwi ˛ekszanie liczebno´sci próby, zwi ˛eksza
szans ˛e, ˙ze ´srednia z takiej próby ”trafi” w ´sredni ˛
a z populacji.
Agnieszka Rossa

Prawo wielkich liczb Bernoulliego i centralne tw. graniczne
Podstawowe poj ˛ecia wnioskowania statystycznego
Słabe prawo wielkich liczb
Podobne prawo mo˙zna tak˙ze sformułowa´c w odniesienu do
´sredniej z próby losowej (w szczególnym przypadku, cz ˛esto´s´c
wyst ˛
apienia sukcesu w serii n eksperymentów mo˙zemy trak-
towa´c jak ´sredni ˛
a z n-elementowej próby składaj ˛
acej si ˛e z zer
i jedynek – zob. Uwaga 3). Prawo to nazywamy
słabym
prawem wielkich liczb
:
Je´sli z dowolnej populacji wylosuje si ˛e próbk˛e o liczno´sci n
i je´sli dla takiej próbki obliczy si ˛e ´sredni ˛
a arytmetyczn ˛
a, to
prawdopodobie ´nstwo tego, ˙ze ´srednia próbkowa b ˛edzie ró˙zni´c
si ˛e dowolnie mało od ´sredniej dla całej populacji, zbli˙za si ˛e do 1
wraz ze wzrostem n.
Jest to tzw. zbie˙zno´s´c wg prawdopodobie ´nstwa. Mówi ˛
ac
w uproszczeniu, zwi ˛ekszanie liczebno´sci próby, zwi ˛eksza
szans ˛e, ˙ze ´srednia z takiej próby ”trafi” w ´sredni ˛
a z populacji.
Agnieszka Rossa

Prawo wielkich liczb Bernoulliego i centralne tw. graniczne
Podstawowe poj ˛ecia wnioskowania statystycznego
Słabe prawo wielkich liczb
Podobne prawo mo˙zna tak˙ze sformułowa´c w odniesienu do
´sredniej z próby losowej (w szczególnym przypadku, cz ˛esto´s´c
wyst ˛
apienia sukcesu w serii n eksperymentów mo˙zemy trak-
towa´c jak ´sredni ˛
a z n-elementowej próby składaj ˛
acej si ˛e z zer
i jedynek – zob. Uwaga 3). Prawo to nazywamy
słabym
prawem wielkich liczb
:
Je´sli z dowolnej populacji wylosuje si ˛e próbk˛e o liczno´sci n
i je´sli dla takiej próbki obliczy si ˛e ´sredni ˛
a arytmetyczn ˛
a, to
prawdopodobie ´nstwo tego, ˙ze ´srednia próbkowa b ˛edzie ró˙zni´c
si ˛e dowolnie mało od ´sredniej dla całej populacji, zbli˙za si ˛e do 1
wraz ze wzrostem n.
Jest to tzw. zbie˙zno´s´c wg prawdopodobie ´nstwa. Mówi ˛
ac
w uproszczeniu, zwi ˛ekszanie liczebno´sci próby, zwi ˛eksza
szans ˛e, ˙ze ´srednia z takiej próby ”trafi” w ´sredni ˛
a z populacji.
Agnieszka Rossa
Prawo wielkich liczb Bernoulliego i centralne tw. graniczne
Podstawowe poj ˛ecia wnioskowania statystycznego
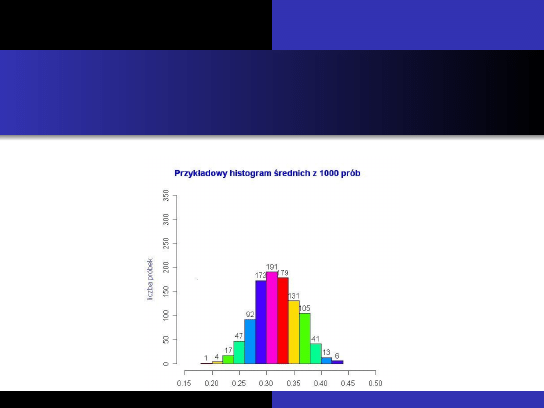
Gdyby ´smy posiadali wiele n-elementowych próbek, to histogram
´srednich z tych próbek przybli˙załby tzw.
rozkład ´sredniej z próby
.
Przykład histogramu dla 1000 próbek (ka˙zda o liczno ´sci n = 150)
przybli˙zaj ˛
acego rozkład ´sredniej z próby przedstawia wykres.
Copyright Giorgio Krenkel and Alex Sandri, GNU Free Documentation License, Low Resolution
Agnieszka Rossa
Prawo wielkich liczb Bernoulliego i centralne tw. graniczne
Podstawowe poj ˛ecia wnioskowania statystycznego
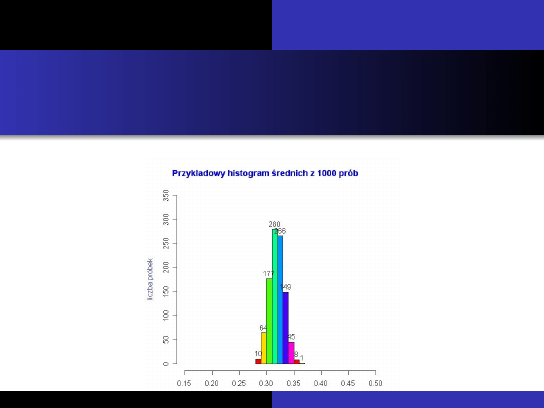
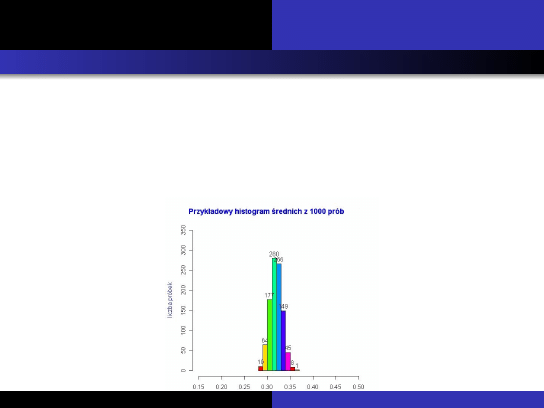
Je ´sli zwi ˛ekszymy liczebno ´s ´c ka˙zdej próbki, np. do n = 1000,
wówczas histogram ´srednich obliczonych z tych próbek b ˛edzie
bardziej ”skupiony” wokół ´sredniej z populacji (tu ´srednia z
populacji= 0,32). Histogram poni˙zej wykonano dla 1000 próbek.
Copyright Giorgio Krenkel and Alex Sandri, GNU Free Documentation License, Low Resolution
Agnieszka Rossa
Prawo wielkich liczb Bernoulliego i centralne tw. graniczne
Podstawowe poj ˛ecia wnioskowania statystycznego
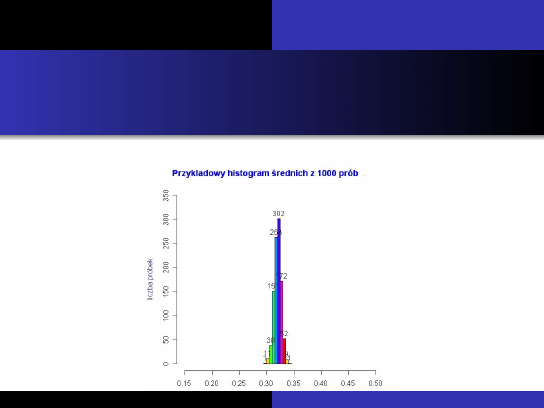
Załó˙zmy teraz, ˙ze n = 5000. Koncentracja ´srednich z próbek wokół
´sredniej z populacji jest tu jeszcze bardziej wyra´zna. W tym
przypadku ´srednie dla wi ˛ekszo ´sci próbek s ˛
a bardzo bliskie war-
to ´sci ´sredniej dla całej populacji (równej nadal 0,32).
Copyright Giorgio Krenkel and Alex Sandri, GNU Free Documentation License, Low Resolution
Agnieszka Rossa

Prawo wielkich liczb Bernoulliego i centralne tw. graniczne
Podstawowe poj ˛ecia wnioskowania statystycznego
Centralne twierdzenie graniczne – ilustracja na przykładzie
Wró´cmy do wykresu histogramu ´srednich z próbek
licz ˛
acych po n = 1000 elementów.
Na wykresie tym na osi pionowej odło˙zone s ˛
a liczby
próbek, dla których ´srednie nale˙zały do poszczególnych
podprzedziałów liczbowych, ka˙zdy o długo´sci 0,01
(podprzedziały te s ˛
a okre´slone przez podstawy słupków).
Wykre´slimy teraz podobny histogram, odkładaj ˛
ac na osi
pionowej liczebno´sci wzgl ˛edne, przeliczone na jednostk˛e
długo´sci przedziałów (tj. cz ˛esto´sci podzielone przez dłu-
go´sci podprzedziałów).
Na tym samym wykresie umie´s´cmy dodatkow ˛
a krzyw ˛
a,
który przybli˙za kształt histogramu sporz ˛
adzonego na
podstawie ´srednich z bardzo wielu próbek (w tym przy-
padku z 1000 próbek, zob. nast ˛epny wykres).
Agnieszka Rossa

Prawo wielkich liczb Bernoulliego i centralne tw. graniczne
Podstawowe poj ˛ecia wnioskowania statystycznego
Centralne twierdzenie graniczne – ilustracja na przykładzie
Wró´cmy do wykresu histogramu ´srednich z próbek
licz ˛
acych po n = 1000 elementów.
Na wykresie tym na osi pionowej odło˙zone s ˛
a liczby
próbek, dla których ´srednie nale˙zały do poszczególnych
podprzedziałów liczbowych, ka˙zdy o długo´sci 0,01
(podprzedziały te s ˛
a okre´slone przez podstawy słupków).
Wykre´slimy teraz podobny histogram, odkładaj ˛
ac na osi
pionowej liczebno´sci wzgl ˛edne, przeliczone na jednostk˛e
długo´sci przedziałów (tj. cz ˛esto´sci podzielone przez dłu-
go´sci podprzedziałów).
Na tym samym wykresie umie´s´cmy dodatkow ˛
a krzyw ˛
a,
który przybli˙za kształt histogramu sporz ˛
adzonego na
podstawie ´srednich z bardzo wielu próbek (w tym przy-
padku z 1000 próbek, zob. nast ˛epny wykres).
Agnieszka Rossa

Prawo wielkich liczb Bernoulliego i centralne tw. graniczne
Podstawowe poj ˛ecia wnioskowania statystycznego
Centralne twierdzenie graniczne – ilustracja na przykładzie
Wró´cmy do wykresu histogramu ´srednich z próbek
licz ˛
acych po n = 1000 elementów.
Na wykresie tym na osi pionowej odło˙zone s ˛
a liczby
próbek, dla których ´srednie nale˙zały do poszczególnych
podprzedziałów liczbowych, ka˙zdy o długo´sci 0,01
(podprzedziały te s ˛
a okre´slone przez podstawy słupków).
Wykre´slimy teraz podobny histogram, odkładaj ˛
ac na osi
pionowej liczebno´sci wzgl ˛edne, przeliczone na jednostk˛e
długo´sci przedziałów (tj. cz ˛esto´sci podzielone przez dłu-
go´sci podprzedziałów).
Na tym samym wykresie umie´s´cmy dodatkow ˛
a krzyw ˛
a,
który przybli˙za kształt histogramu sporz ˛
adzonego na
podstawie ´srednich z bardzo wielu próbek (w tym przy-
padku z 1000 próbek, zob. nast ˛epny wykres).
Agnieszka Rossa

Prawo wielkich liczb Bernoulliego i centralne tw. graniczne
Podstawowe poj ˛ecia wnioskowania statystycznego
Centralne twierdzenie graniczne – ilustracja na przykładzie
Wró´cmy do wykresu histogramu ´srednich z próbek
licz ˛
acych po n = 1000 elementów.
Na wykresie tym na osi pionowej odło˙zone s ˛
a liczby
próbek, dla których ´srednie nale˙zały do poszczególnych
podprzedziałów liczbowych, ka˙zdy o długo´sci 0,01
(podprzedziały te s ˛
a okre´slone przez podstawy słupków).
Wykre´slimy teraz podobny histogram, odkładaj ˛
ac na osi
pionowej liczebno´sci wzgl ˛edne, przeliczone na jednostk˛e
długo´sci przedziałów (tj. cz ˛esto´sci podzielone przez dłu-
go´sci podprzedziałów).
Na tym samym wykresie umie´s´cmy dodatkow ˛
a krzyw ˛
a,
który przybli˙za kształt histogramu sporz ˛
adzonego na
podstawie ´srednich z bardzo wielu próbek (w tym przy-
padku z 1000 próbek, zob. nast ˛epny wykres).
Agnieszka Rossa
Prawo wielkich liczb Bernoulliego i centralne tw. graniczne
Podstawowe poj ˛ecia wnioskowania statystycznego
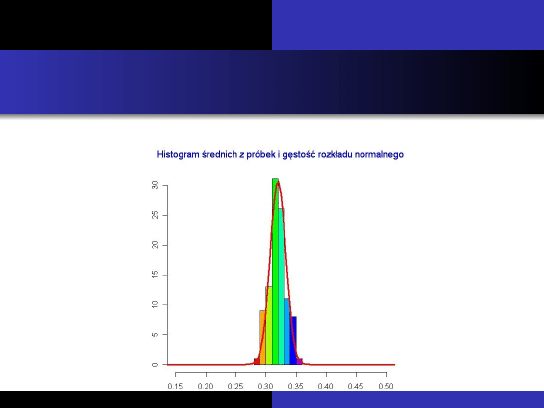
Zauwa˙zymy, ˙ze wykre ´slona krzywa przypomina krzyw ˛
a g ˛esto ´sci
rozkładu normalnego. Wykres ten ilustruje w uproszczeniu sens
centralnego twierdzenia granicznego
przedstawionego dalej.
Copyright Giorgio Krenkel and Alex Sandri, GNU Free Documentation License, Low Resolution
Agnieszka Rossa

Prawo wielkich liczb Bernoulliego i centralne tw. graniczne
Podstawowe poj ˛ecia wnioskowania statystycznego
Centralne twierdzenie graniczne
Centralne twierdzenie graniczne
jest kolejnym, wa˙znym
twierdzeniem rachunku prawdopodobie ´nstwa.
W skócie mówi ono, i˙z
rozkład standaryzowanej ´sredniej
arytmetycznej z próby d ˛
a˙zy do rozkładu normalnego N(0, 1),
gdy liczebno´s´c n próby d ˛
a˙zy do niesko ´nczono´sci
(o standa-
ryzacji była mowa przy okazji omawiania rozkładów).
Upraszczaj ˛
ac nieco, mo˙zemy powy˙zsze sformułowanie wy-
ja´sni´c nast ˛epuj ˛
aco. Je´sli wylosujemy z populacji bardzo wiele
n-elementowych próbek i obliczymy dla ka˙zdej z nich ´sredni ˛
a
arytmetyczn ˛
a to:
histogram liczebno´sci wzgl ˛ednych (w przeliczeniu na jed-
nostk˛e długo´sci) dla ´srednich próbkowych b ˛edzie przybie-
ra´c
kształt zbli˙zony do krzywej g ˛esto ´sci rozkładu
normalnego
, o ile liczno´sci n próbek b ˛ed ˛
a du˙ze.
Agnieszka Rossa

Prawo wielkich liczb Bernoulliego i centralne tw. graniczne
Podstawowe poj ˛ecia wnioskowania statystycznego
Centralne twierdzenie graniczne
Centralne twierdzenie graniczne
jest kolejnym, wa˙znym
twierdzeniem rachunku prawdopodobie ´nstwa.
W skócie mówi ono, i˙z
rozkład standaryzowanej ´sredniej
arytmetycznej z próby d ˛
a˙zy do rozkładu normalnego N(0, 1),
gdy liczebno´s´c n próby d ˛
a˙zy do niesko ´nczono´sci
(o standa-
ryzacji była mowa przy okazji omawiania rozkładów).
Upraszczaj ˛
ac nieco, mo˙zemy powy˙zsze sformułowanie wy-
ja´sni´c nast ˛epuj ˛
aco. Je´sli wylosujemy z populacji bardzo wiele
n-elementowych próbek i obliczymy dla ka˙zdej z nich ´sredni ˛
a
arytmetyczn ˛
a to:
histogram liczebno´sci wzgl ˛ednych (w przeliczeniu na jed-
nostk˛e długo´sci) dla ´srednich próbkowych b ˛edzie przybie-
ra´c
kształt zbli˙zony do krzywej g ˛esto ´sci rozkładu
normalnego
, o ile liczno´sci n próbek b ˛ed ˛
a du˙ze.
Agnieszka Rossa

Prawo wielkich liczb Bernoulliego i centralne tw. graniczne
Podstawowe poj ˛ecia wnioskowania statystycznego
Centralne twierdzenie graniczne
Centralne twierdzenie graniczne
jest kolejnym, wa˙znym
twierdzeniem rachunku prawdopodobie ´nstwa.
W skócie mówi ono, i˙z
rozkład standaryzowanej ´sredniej
arytmetycznej z próby d ˛
a˙zy do rozkładu normalnego N(0, 1),
gdy liczebno´s´c n próby d ˛
a˙zy do niesko ´nczono´sci
(o standa-
ryzacji była mowa przy okazji omawiania rozkładów).
Upraszczaj ˛
ac nieco, mo˙zemy powy˙zsze sformułowanie wy-
ja´sni´c nast ˛epuj ˛
aco. Je´sli wylosujemy z populacji bardzo wiele
n-elementowych próbek i obliczymy dla ka˙zdej z nich ´sredni ˛
a
arytmetyczn ˛
a to:
histogram liczebno´sci wzgl ˛ednych (w przeliczeniu na jed-
nostk˛e długo´sci) dla ´srednich próbkowych b ˛edzie przybie-
ra´c
kształt zbli˙zony do krzywej g ˛esto ´sci rozkładu
normalnego
, o ile liczno´sci n próbek b ˛ed ˛
a du˙ze.
Agnieszka Rossa

Prawo wielkich liczb Bernoulliego i centralne tw. graniczne
Podstawowe poj ˛ecia wnioskowania statystycznego
Centralne twierdzenie graniczne
Centralne twierdzenie graniczne
jest kolejnym, wa˙znym
twierdzeniem rachunku prawdopodobie ´nstwa.
W skócie mówi ono, i˙z
rozkład standaryzowanej ´sredniej
arytmetycznej z próby d ˛
a˙zy do rozkładu normalnego N(0, 1),
gdy liczebno´s´c n próby d ˛
a˙zy do niesko ´nczono´sci
(o standa-
ryzacji była mowa przy okazji omawiania rozkładów).
Upraszczaj ˛
ac nieco, mo˙zemy powy˙zsze sformułowanie wy-
ja´sni´c nast ˛epuj ˛
aco. Je´sli wylosujemy z populacji bardzo wiele
n-elementowych próbek i obliczymy dla ka˙zdej z nich ´sredni ˛
a
arytmetyczn ˛
a to:
histogram liczebno´sci wzgl ˛ednych (w przeliczeniu na jed-
nostk˛e długo´sci) dla ´srednich próbkowych b ˛edzie przybie-
ra´c
kształt zbli˙zony do krzywej g ˛esto ´sci rozkładu
normalnego
, o ile liczno´sci n próbek b ˛ed ˛
a du˙ze.
Agnieszka Rossa

Prawo wielkich liczb Bernoulliego i centralne tw. graniczne
Podstawowe poj ˛ecia wnioskowania statystycznego
Własno ´sci ´srednich próbkowych
W uzupełnieniu do przedstawionego wyja´snienia warto jeszcze
przedstawi´c dwie własno´sci ´srednich próbkowych, z których
korzysta si ˛e m.in. przy
standaryzacji ´sredniej arytmetycznej
z próby
(o czym jest mowa w centralnym tw. granicznym):
Własno ´s ´c 1.
Gdyby´smy wylosowali bardzo du˙zo n-ele-
mentowych próbek (teoretycznie zakłada si ˛e niesko ´ncz-
nie wiele próbek losowanych z niesko ´nczonej populacji)
i obliczyli dla ka˙zdej z nich ´sredni ˛
a arytmetyczn ˛
a, czyli
´srednie próbkowe, a nast ˛epnie ´sredni ˛
a ze ´srednich, to
okazałoby si ˛e, ˙ze wielko´s´c ta jest
równa ´sredniej badanej
cechy w całej populacji
. ´
Sredni ˛
a dla populacji b ˛edziemy
dalej oznacza´c przez
µ
.
W j ˛ezyku formalnym przedstawion ˛
a własno´s´c zapisujemy:
E( ¯
X ) = µ.
Agnieszka Rossa

Prawo wielkich liczb Bernoulliego i centralne tw. graniczne
Podstawowe poj ˛ecia wnioskowania statystycznego
Własno ´sci ´srednich próbkowych
W uzupełnieniu do przedstawionego wyja´snienia warto jeszcze
przedstawi´c dwie własno´sci ´srednich próbkowych, z których
korzysta si ˛e m.in. przy
standaryzacji ´sredniej arytmetycznej
z próby
(o czym jest mowa w centralnym tw. granicznym):
Własno ´s ´c 1.
Gdyby´smy wylosowali bardzo du˙zo n-ele-
mentowych próbek (teoretycznie zakłada si ˛e niesko ´ncz-
nie wiele próbek losowanych z niesko ´nczonej populacji)
i obliczyli dla ka˙zdej z nich ´sredni ˛
a arytmetyczn ˛
a, czyli
´srednie próbkowe, a nast ˛epnie ´sredni ˛
a ze ´srednich, to
okazałoby si ˛e, ˙ze wielko´s´c ta jest
równa ´sredniej badanej
cechy w całej populacji
.
´
Sredni ˛
a dla populacji b ˛edziemy
dalej oznacza´c przez
µ
.
W j ˛ezyku formalnym przedstawion ˛
a własno´s´c zapisujemy:
E( ¯
X ) = µ.
Agnieszka Rossa

Prawo wielkich liczb Bernoulliego i centralne tw. graniczne
Podstawowe poj ˛ecia wnioskowania statystycznego
Własno ´sci ´srednich próbkowych
W uzupełnieniu do przedstawionego wyja´snienia warto jeszcze
przedstawi´c dwie własno´sci ´srednich próbkowych, z których
korzysta si ˛e m.in. przy
standaryzacji ´sredniej arytmetycznej
z próby
(o czym jest mowa w centralnym tw. granicznym):
Własno ´s ´c 1.
Gdyby´smy wylosowali bardzo du˙zo n-ele-
mentowych próbek (teoretycznie zakłada si ˛e niesko ´ncz-
nie wiele próbek losowanych z niesko ´nczonej populacji)
i obliczyli dla ka˙zdej z nich ´sredni ˛
a arytmetyczn ˛
a, czyli
´srednie próbkowe, a nast ˛epnie ´sredni ˛
a ze ´srednich, to
okazałoby si ˛e, ˙ze wielko´s´c ta jest
równa ´sredniej badanej
cechy w całej populacji
. ´
Sredni ˛
a dla populacji b ˛edziemy
dalej oznacza´c przez
µ
.
W j ˛ezyku formalnym przedstawion ˛
a własno´s´c zapisujemy:
E( ¯
X ) = µ.
Agnieszka Rossa

Prawo wielkich liczb Bernoulliego i centralne tw. graniczne
Podstawowe poj ˛ecia wnioskowania statystycznego
Własno ´sci ´srednich próbkowych
W uzupełnieniu do przedstawionego wyja´snienia warto jeszcze
przedstawi´c dwie własno´sci ´srednich próbkowych, z których
korzysta si ˛e m.in. przy
standaryzacji ´sredniej arytmetycznej
z próby
(o czym jest mowa w centralnym tw. granicznym):
Własno ´s ´c 1.
Gdyby´smy wylosowali bardzo du˙zo n-ele-
mentowych próbek (teoretycznie zakłada si ˛e niesko ´ncz-
nie wiele próbek losowanych z niesko ´nczonej populacji)
i obliczyli dla ka˙zdej z nich ´sredni ˛
a arytmetyczn ˛
a, czyli
´srednie próbkowe, a nast ˛epnie ´sredni ˛
a ze ´srednich, to
okazałoby si ˛e, ˙ze wielko´s´c ta jest
równa ´sredniej badanej
cechy w całej populacji
. ´
Sredni ˛
a dla populacji b ˛edziemy
dalej oznacza´c przez
µ
.
W j ˛ezyku formalnym przedstawion ˛
a własno´s´c zapisujemy:
E( ¯
X ) = µ.
Agnieszka Rossa

Prawo wielkich liczb Bernoulliego i centralne tw. graniczne
Podstawowe poj ˛ecia wnioskowania statystycznego
Własno ´sci ´srednich próbkowych – c.d.
Druga własno´s´c ´srednich próbkowych brzmi nast ˛epuj ˛
aco:
Własno ´s ´c 2.
Gdyby´smy, maj ˛
ac niesko ´nczenie wiele
n-elementowych próbek, obliczyli wariancj ˛e ´srednich
próbkowych, to okazałoby si ˛e, ˙ze jest ona
n
razy mniej-
sza ni˙z wariancja w populacji
. Wariancj ˛e w populacji
oznacza´c b ˛edziemy dalej przez
σ
2
. W zapisie formalnym
własno´s´c ta ma posta´c:
D
2
( ¯
X ) =
σ
2
n
.
Poniewa˙z w mianowniku po prawej stronie wyst ˛epuje n,
wi ˛ec wynika st ˛
ad wniosek, ˙ze zwi ˛ekszaj ˛
ac liczno´s´c n
wszystkich próbek, zmniejszamy tym samym zmienno´s´c
´srednich wyznaczonych z takich próbek. Wyja´snia to m.in.
dlaczego wraz ze wzrostem n obserwowali´smy rosn ˛
ac ˛
a
koncentracj ˛e histogramów ´srednich próbkowych wokół
´sredniej z populacji (zob. wcze´sniejsze wykresy).
Agnieszka Rossa

Prawo wielkich liczb Bernoulliego i centralne tw. graniczne
Podstawowe poj ˛ecia wnioskowania statystycznego
Własno ´sci ´srednich próbkowych – c.d.
Druga własno´s´c ´srednich próbkowych brzmi nast ˛epuj ˛
aco:
Własno ´s ´c 2.
Gdyby´smy, maj ˛
ac niesko ´nczenie wiele
n-elementowych próbek, obliczyli wariancj ˛e ´srednich
próbkowych, to okazałoby si ˛e, ˙ze jest ona
n
razy mniej-
sza ni˙z wariancja w populacji
.
Wariancj ˛e w populacji
oznacza´c b ˛edziemy dalej przez
σ
2
. W zapisie formalnym
własno´s´c ta ma posta´c:
D
2
( ¯
X ) =
σ
2
n
.
Poniewa˙z w mianowniku po prawej stronie wyst ˛epuje n,
wi ˛ec wynika st ˛
ad wniosek, ˙ze zwi ˛ekszaj ˛
ac liczno´s´c n
wszystkich próbek, zmniejszamy tym samym zmienno´s´c
´srednich wyznaczonych z takich próbek. Wyja´snia to m.in.
dlaczego wraz ze wzrostem n obserwowali´smy rosn ˛
ac ˛
a
koncentracj ˛e histogramów ´srednich próbkowych wokół
´sredniej z populacji (zob. wcze´sniejsze wykresy).
Agnieszka Rossa

Prawo wielkich liczb Bernoulliego i centralne tw. graniczne
Podstawowe poj ˛ecia wnioskowania statystycznego
Własno ´sci ´srednich próbkowych – c.d.
Druga własno´s´c ´srednich próbkowych brzmi nast ˛epuj ˛
aco:
Własno ´s ´c 2.
Gdyby´smy, maj ˛
ac niesko ´nczenie wiele
n-elementowych próbek, obliczyli wariancj ˛e ´srednich
próbkowych, to okazałoby si ˛e, ˙ze jest ona
n
razy mniej-
sza ni˙z wariancja w populacji
. Wariancj ˛e w populacji
oznacza´c b ˛edziemy dalej przez
σ
2
.
W zapisie formalnym
własno´s´c ta ma posta´c:
D
2
( ¯
X ) =
σ
2
n
.
Poniewa˙z w mianowniku po prawej stronie wyst ˛epuje n,
wi ˛ec wynika st ˛
ad wniosek, ˙ze zwi ˛ekszaj ˛
ac liczno´s´c n
wszystkich próbek, zmniejszamy tym samym zmienno´s´c
´srednich wyznaczonych z takich próbek. Wyja´snia to m.in.
dlaczego wraz ze wzrostem n obserwowali´smy rosn ˛
ac ˛
a
koncentracj ˛e histogramów ´srednich próbkowych wokół
´sredniej z populacji (zob. wcze´sniejsze wykresy).
Agnieszka Rossa

Prawo wielkich liczb Bernoulliego i centralne tw. graniczne
Podstawowe poj ˛ecia wnioskowania statystycznego
Własno ´sci ´srednich próbkowych – c.d.
Druga własno´s´c ´srednich próbkowych brzmi nast ˛epuj ˛
aco:
Własno ´s ´c 2.
Gdyby´smy, maj ˛
ac niesko ´nczenie wiele
n-elementowych próbek, obliczyli wariancj ˛e ´srednich
próbkowych, to okazałoby si ˛e, ˙ze jest ona
n
razy mniej-
sza ni˙z wariancja w populacji
. Wariancj ˛e w populacji
oznacza´c b ˛edziemy dalej przez
σ
2
. W zapisie formalnym
własno´s´c ta ma posta´c:
D
2
( ¯
X ) =
σ
2
n
.
Poniewa˙z w mianowniku po prawej stronie wyst ˛epuje n,
wi ˛ec wynika st ˛
ad wniosek, ˙ze zwi ˛ekszaj ˛
ac liczno´s´c n
wszystkich próbek, zmniejszamy tym samym zmienno´s´c
´srednich wyznaczonych z takich próbek. Wyja´snia to m.in.
dlaczego wraz ze wzrostem n obserwowali´smy rosn ˛
ac ˛
a
koncentracj ˛e histogramów ´srednich próbkowych wokół
´sredniej z populacji (zob. wcze´sniejsze wykresy).
Agnieszka Rossa

Prawo wielkich liczb Bernoulliego i centralne tw. graniczne
Podstawowe poj ˛ecia wnioskowania statystycznego
Własno ´sci ´srednich próbkowych – c.d.
Druga własno´s´c ´srednich próbkowych brzmi nast ˛epuj ˛
aco:
Własno ´s ´c 2.
Gdyby´smy, maj ˛
ac niesko ´nczenie wiele
n-elementowych próbek, obliczyli wariancj ˛e ´srednich
próbkowych, to okazałoby si ˛e, ˙ze jest ona
n
razy mniej-
sza ni˙z wariancja w populacji
. Wariancj ˛e w populacji
oznacza´c b ˛edziemy dalej przez
σ
2
. W zapisie formalnym
własno´s´c ta ma posta´c:
D
2
( ¯
X ) =
σ
2
n
.
Poniewa˙z w mianowniku po prawej stronie wyst ˛epuje n,
wi ˛ec wynika st ˛
ad wniosek, ˙ze zwi ˛ekszaj ˛
ac liczno´s´c n
wszystkich próbek, zmniejszamy tym samym zmienno´s´c
´srednich wyznaczonych z takich próbek. Wyja´snia to m.in.
dlaczego wraz ze wzrostem n obserwowali´smy rosn ˛
ac ˛
a
koncentracj ˛e histogramów ´srednich próbkowych wokół
´sredniej z populacji (zob. wcze´sniejsze wykresy).
Agnieszka Rossa

Prawo wielkich liczb Bernoulliego i centralne tw. graniczne
Podstawowe poj ˛ecia wnioskowania statystycznego
Podsumowanie rozwa˙zanych przykładów
Dotychczasowe rozwa˙zania pokazuj ˛
a, ˙ze mo˙zliwe jest
przybli˙zanie rzeczywistych warto´sci pewnych wska´zników
(parametrów) populacji na podstawie próby losowej.
Prawdopodobie ´nstwo ”trafienia” w prawdziw ˛
a warto´s´c
parametru jest tym wi ˛eksze, im wi ˛eksza jest liczno´s´c
n
próby.
Je´sli szukanym parametrem jest ´srednia okre´slonej cechy
w populacji i je´sli dysponujemy du˙z ˛
a prób ˛
a (cz ˛esto
wystarczy n ≥ 30), wówczas mo˙zemy odwoła´c si ˛e do
własno´sci rozkładu normalnego, w celu wyznaczenia
oszacowania szukanej ´sredniej.
Przybli˙zanie (estymowanie) nieznanych parametrów popu-
lacji na podstawie danych z próby losowej jest zadaniem
teorii estymacji
, szerzej–
wnioskowania statystycznego
.
Agnieszka Rossa

Prawo wielkich liczb Bernoulliego i centralne tw. graniczne
Podstawowe poj ˛ecia wnioskowania statystycznego
Podsumowanie rozwa˙zanych przykładów
Dotychczasowe rozwa˙zania pokazuj ˛
a, ˙ze mo˙zliwe jest
przybli˙zanie rzeczywistych warto´sci pewnych wska´zników
(parametrów) populacji na podstawie próby losowej.
Prawdopodobie ´nstwo ”trafienia” w prawdziw ˛
a warto´s´c
parametru jest tym wi ˛eksze, im wi ˛eksza jest liczno´s´c
n
próby.
Je´sli szukanym parametrem jest ´srednia okre´slonej cechy
w populacji i je´sli dysponujemy du˙z ˛
a prób ˛
a (cz ˛esto
wystarczy n ≥ 30), wówczas mo˙zemy odwoła´c si ˛e do
własno´sci rozkładu normalnego, w celu wyznaczenia
oszacowania szukanej ´sredniej.
Przybli˙zanie (estymowanie) nieznanych parametrów popu-
lacji na podstawie danych z próby losowej jest zadaniem
teorii estymacji
, szerzej–
wnioskowania statystycznego
.
Agnieszka Rossa

Prawo wielkich liczb Bernoulliego i centralne tw. graniczne
Podstawowe poj ˛ecia wnioskowania statystycznego
Podsumowanie rozwa˙zanych przykładów
Dotychczasowe rozwa˙zania pokazuj ˛
a, ˙ze mo˙zliwe jest
przybli˙zanie rzeczywistych warto´sci pewnych wska´zników
(parametrów) populacji na podstawie próby losowej.
Prawdopodobie ´nstwo ”trafienia” w prawdziw ˛
a warto´s´c
parametru jest tym wi ˛eksze, im wi ˛eksza jest liczno´s´c
n
próby.
Je´sli szukanym parametrem jest ´srednia okre´slonej cechy
w populacji i je´sli dysponujemy du˙z ˛
a prób ˛
a (cz ˛esto
wystarczy n ≥ 30), wówczas mo˙zemy odwoła´c si ˛e do
własno´sci rozkładu normalnego, w celu wyznaczenia
oszacowania szukanej ´sredniej.
Przybli˙zanie (estymowanie) nieznanych parametrów popu-
lacji na podstawie danych z próby losowej jest zadaniem
teorii estymacji
, szerzej–
wnioskowania statystycznego
.
Agnieszka Rossa

Prawo wielkich liczb Bernoulliego i centralne tw. graniczne
Podstawowe poj ˛ecia wnioskowania statystycznego
Podsumowanie rozwa˙zanych przykładów
Dotychczasowe rozwa˙zania pokazuj ˛
a, ˙ze mo˙zliwe jest
przybli˙zanie rzeczywistych warto´sci pewnych wska´zników
(parametrów) populacji na podstawie próby losowej.
Prawdopodobie ´nstwo ”trafienia” w prawdziw ˛
a warto´s´c
parametru jest tym wi ˛eksze, im wi ˛eksza jest liczno´s´c
n
próby.
Je´sli szukanym parametrem jest ´srednia okre´slonej cechy
w populacji i je´sli dysponujemy du˙z ˛
a prób ˛
a (cz ˛esto
wystarczy n ≥ 30), wówczas mo˙zemy odwoła´c si ˛e do
własno´sci rozkładu normalnego, w celu wyznaczenia
oszacowania szukanej ´sredniej.
Przybli˙zanie (estymowanie) nieznanych parametrów popu-
lacji na podstawie danych z próby losowej jest zadaniem
teorii estymacji
, szerzej–
wnioskowania statystycznego
.
Agnieszka Rossa

Prawo wielkich liczb Bernoulliego i centralne tw. graniczne
Podstawowe poj ˛ecia wnioskowania statystycznego
Teoretyczne podej ´scie do zagadnie ´
n wnioskowania
Przypu´s´cmy, ˙ze chcemy zbada´c np. warto´s´c ´sredni ˛
a lub
inne charakterystyki pewnej cechy
X
(zmiennej losowej)
w populacji generalnej.
W tym celu przeprowadzamy eksperyment losowy
polegaj ˛
acy na
n
-krotnym losowaniu ze zwracaniem
elementów z tej populacji (tzw.
losowanie niezale˙zne
)
oraz rejestrowaniu warto´sci badanej cechy w kolejnych
losowaniach.
Oznaczmy przez
X
i
potencjalny wynik pomiaru badanej
cechy, jaki mo˙ze pojawi´c si ˛e u i-tego elementu.
Przed wykonaniem eksperymentu wynik pomiaru
X
i
jest
zmienn ˛
a losow ˛
a, poniewa˙z nie wiemy, jaki element
zostanie wylosowany w i-tej kolejno´sci, a tym samym – jaki
b ˛edzie wynik pomiaru dla tego elementu.
Agnieszka Rossa

Prawo wielkich liczb Bernoulliego i centralne tw. graniczne
Podstawowe poj ˛ecia wnioskowania statystycznego
Teoretyczne podej ´scie do zagadnie ´
n wnioskowania
Przypu´s´cmy, ˙ze chcemy zbada´c np. warto´s´c ´sredni ˛
a lub
inne charakterystyki pewnej cechy
X
(zmiennej losowej)
w populacji generalnej.
W tym celu przeprowadzamy eksperyment losowy
polegaj ˛
acy na
n
-krotnym losowaniu ze zwracaniem
elementów z tej populacji (tzw.
losowanie niezale˙zne
)
oraz rejestrowaniu warto´sci badanej cechy w kolejnych
losowaniach.
Oznaczmy przez
X
i
potencjalny wynik pomiaru badanej
cechy, jaki mo˙ze pojawi´c si ˛e u i-tego elementu.
Przed wykonaniem eksperymentu wynik pomiaru
X
i
jest
zmienn ˛
a losow ˛
a, poniewa˙z nie wiemy, jaki element
zostanie wylosowany w i-tej kolejno´sci, a tym samym – jaki
b ˛edzie wynik pomiaru dla tego elementu.
Agnieszka Rossa

Prawo wielkich liczb Bernoulliego i centralne tw. graniczne
Podstawowe poj ˛ecia wnioskowania statystycznego
Teoretyczne podej ´scie do zagadnie ´
n wnioskowania
Przypu´s´cmy, ˙ze chcemy zbada´c np. warto´s´c ´sredni ˛
a lub
inne charakterystyki pewnej cechy
X
(zmiennej losowej)
w populacji generalnej.
W tym celu przeprowadzamy eksperyment losowy
polegaj ˛
acy na
n
-krotnym losowaniu ze zwracaniem
elementów z tej populacji (tzw.
losowanie niezale˙zne
)
oraz rejestrowaniu warto´sci badanej cechy w kolejnych
losowaniach.
Oznaczmy przez
X
i
potencjalny wynik pomiaru badanej
cechy, jaki mo˙ze pojawi´c si ˛e u i-tego elementu.
Przed wykonaniem eksperymentu wynik pomiaru
X
i
jest
zmienn ˛
a losow ˛
a, poniewa˙z nie wiemy, jaki element
zostanie wylosowany w i-tej kolejno´sci, a tym samym – jaki
b ˛edzie wynik pomiaru dla tego elementu.
Agnieszka Rossa

Prawo wielkich liczb Bernoulliego i centralne tw. graniczne
Podstawowe poj ˛ecia wnioskowania statystycznego
Teoretyczne podej ´scie do zagadnie ´
n wnioskowania
Przypu´s´cmy, ˙ze chcemy zbada´c np. warto´s´c ´sredni ˛
a lub
inne charakterystyki pewnej cechy
X
(zmiennej losowej)
w populacji generalnej.
W tym celu przeprowadzamy eksperyment losowy
polegaj ˛
acy na
n
-krotnym losowaniu ze zwracaniem
elementów z tej populacji (tzw.
losowanie niezale˙zne
)
oraz rejestrowaniu warto´sci badanej cechy w kolejnych
losowaniach.
Oznaczmy przez
X
i
potencjalny wynik pomiaru badanej
cechy, jaki mo˙ze pojawi´c si ˛e u i-tego elementu.
Przed wykonaniem eksperymentu wynik pomiaru
X
i
jest
zmienn ˛
a losow ˛
a, poniewa˙z nie wiemy, jaki element
zostanie wylosowany w i-tej kolejno´sci, a tym samym – jaki
b ˛edzie wynik pomiaru dla tego elementu.
Agnieszka Rossa

Prawo wielkich liczb Bernoulliego i centralne tw. graniczne
Podstawowe poj ˛ecia wnioskowania statystycznego
Teoretyczne podej ´scie do zagadnie ´
n wnioskowania
Po wylosowaniu i dokonaniu pomiaru uzyskujemy
konkretn ˛
a warto´s´c
x
i
, tj. pojedyczn ˛
a realizacj ˛e zmiennej
X
i
.
Poniewa˙z losowanie z populacji jest niezale˙zne, wi ˛ec
zmienne:
X
1
,
X
2
, . . . ,
X
n
s ˛
a tak˙ze niezale˙zne i maj ˛
a taki sam rozkład jak rozkład
badanej cechy X .
Przedstawiony ci ˛
ag zmiennych losowych nazywamy
n
-elementow ˛
a prób ˛
a losow ˛
a
(prost ˛
a).
Realizacj ˛
a próby losowej
jest ci ˛
ag konkretnych warto´sci
x
1
,
x
2
, . . . ,
x
n
zaobserwowanych w trakcie pomiaru badanej cechy.
Agnieszka Rossa

Prawo wielkich liczb Bernoulliego i centralne tw. graniczne
Podstawowe poj ˛ecia wnioskowania statystycznego
Teoretyczne podej ´scie do zagadnie ´
n wnioskowania
Po wylosowaniu i dokonaniu pomiaru uzyskujemy
konkretn ˛
a warto´s´c
x
i
, tj. pojedyczn ˛
a realizacj ˛e zmiennej
X
i
.
Poniewa˙z losowanie z populacji jest niezale˙zne, wi ˛ec
zmienne:
X
1
,
X
2
, . . . ,
X
n
s ˛
a tak˙ze niezale˙zne i maj ˛
a taki sam rozkład jak rozkład
badanej cechy X .
Przedstawiony ci ˛
ag zmiennych losowych nazywamy
n
-elementow ˛
a prób ˛
a losow ˛
a
(prost ˛
a).
Realizacj ˛
a próby losowej
jest ci ˛
ag konkretnych warto´sci
x
1
,
x
2
, . . . ,
x
n
zaobserwowanych w trakcie pomiaru badanej cechy.
Agnieszka Rossa

Prawo wielkich liczb Bernoulliego i centralne tw. graniczne
Podstawowe poj ˛ecia wnioskowania statystycznego
Teoretyczne podej ´scie do zagadnie ´
n wnioskowania
Po wylosowaniu i dokonaniu pomiaru uzyskujemy
konkretn ˛
a warto´s´c
x
i
, tj. pojedyczn ˛
a realizacj ˛e zmiennej
X
i
.
Poniewa˙z losowanie z populacji jest niezale˙zne, wi ˛ec
zmienne:
X
1
,
X
2
, . . . ,
X
n
s ˛
a tak˙ze niezale˙zne i maj ˛
a taki sam rozkład jak rozkład
badanej cechy X .
Przedstawiony ci ˛
ag zmiennych losowych nazywamy
n
-elementow ˛
a prób ˛
a losow ˛
a
(prost ˛
a).
Realizacj ˛
a próby losowej
jest ci ˛
ag konkretnych warto´sci
x
1
,
x
2
, . . . ,
x
n
zaobserwowanych w trakcie pomiaru badanej cechy.
Agnieszka Rossa

Prawo wielkich liczb Bernoulliego i centralne tw. graniczne
Podstawowe poj ˛ecia wnioskowania statystycznego
Teoretyczne podej ´scie do zagadnie ´
n wnioskowania
Po wylosowaniu i dokonaniu pomiaru uzyskujemy
konkretn ˛
a warto´s´c
x
i
, tj. pojedyczn ˛
a realizacj ˛e zmiennej
X
i
.
Poniewa˙z losowanie z populacji jest niezale˙zne, wi ˛ec
zmienne:
X
1
,
X
2
, . . . ,
X
n
s ˛
a tak˙ze niezale˙zne i maj ˛
a taki sam rozkład jak rozkład
badanej cechy X .
Przedstawiony ci ˛
ag zmiennych losowych nazywamy
n
-elementow ˛
a prób ˛
a losow ˛
a
(prost ˛
a).
Realizacj ˛
a próby losowej
jest ci ˛
ag konkretnych warto´sci
x
1
,
x
2
, . . . ,
x
n
zaobserwowanych w trakcie pomiaru badanej cechy.
Agnieszka Rossa

Prawo wielkich liczb Bernoulliego i centralne tw. graniczne
Podstawowe poj ˛ecia wnioskowania statystycznego
Teoretyczne podej ´scie do zagadnie ´
n wnioskowania
Niech
X
1
,
X
2
, . . . ,
X
n
b ˛edzie n-elementow ˛
a prób ˛
a losow ˛
a.
Statystyk ˛
a
nazywamy zmienn ˛
a losow ˛
a T
n
b ˛ed ˛
ac ˛
a dowoln ˛
a
funkcj ˛
a próby losowej, co zapisujemy ogólnie w postaci:
T
n
=
f (X
1
,
X
2
, . . . ,
X
n
).
Przykładami statystyk s ˛
a: ´srednia arytmetyczna z próby oraz
odchylenie standardowe z próby, zdefiniowane wzorami:
¯
X =
1
n
n
X
i=1
X
i
,
S =
v
u
u
t
1
n
n
X
i=1
(
X
i
− ¯
X )
2
.
Zauwa˙zymy, ˙ze zarówno ´srednia arytmetyczna, jak i odchy-
lenie standardowe s ˛
a tu oznaczone du˙zymi literami, dla pod-
kre´slenia, i˙z nie s ˛
a to pojedyncze liczby, ale zmienne losowe,
poniewa˙z dotycz ˛
a losowej próby.
Agnieszka Rossa

Prawo wielkich liczb Bernoulliego i centralne tw. graniczne
Podstawowe poj ˛ecia wnioskowania statystycznego
Teoretyczne podej ´scie do zagadnie ´
n wnioskowania
Niech
X
1
,
X
2
, . . . ,
X
n
b ˛edzie n-elementow ˛
a prób ˛
a losow ˛
a.
Statystyk ˛
a
nazywamy zmienn ˛
a losow ˛
a T
n
b ˛ed ˛
ac ˛
a dowoln ˛
a
funkcj ˛
a próby losowej, co zapisujemy ogólnie w postaci:
T
n
=
f (X
1
,
X
2
, . . . ,
X
n
).
Przykładami statystyk s ˛
a: ´srednia arytmetyczna z próby oraz
odchylenie standardowe z próby, zdefiniowane wzorami:
¯
X =
1
n
n
X
i=1
X
i
,
S =
v
u
u
t
1
n
n
X
i=1
(
X
i
− ¯
X )
2
.
Zauwa˙zymy, ˙ze zarówno ´srednia arytmetyczna, jak i odchy-
lenie standardowe s ˛
a tu oznaczone du˙zymi literami, dla pod-
kre´slenia, i˙z nie s ˛
a to pojedyncze liczby, ale zmienne losowe,
poniewa˙z dotycz ˛
a losowej próby.
Agnieszka Rossa

Prawo wielkich liczb Bernoulliego i centralne tw. graniczne
Podstawowe poj ˛ecia wnioskowania statystycznego
Teoretyczne podej ´scie do zagadnie ´
n wnioskowania
Niech
X
1
,
X
2
, . . . ,
X
n
b ˛edzie n-elementow ˛
a prób ˛
a losow ˛
a.
Statystyk ˛
a
nazywamy zmienn ˛
a losow ˛
a T
n
b ˛ed ˛
ac ˛
a dowoln ˛
a
funkcj ˛
a próby losowej, co zapisujemy ogólnie w postaci:
T
n
=
f (X
1
,
X
2
, . . . ,
X
n
).
Przykładami statystyk s ˛
a: ´srednia arytmetyczna z próby oraz
odchylenie standardowe z próby, zdefiniowane wzorami:
¯
X =
1
n
n
X
i=1
X
i
,
S =
v
u
u
t
1
n
n
X
i=1
(
X
i
− ¯
X )
2
.
Zauwa˙zymy, ˙ze zarówno ´srednia arytmetyczna, jak i odchy-
lenie standardowe s ˛
a tu oznaczone du˙zymi literami, dla pod-
kre´slenia, i˙z nie s ˛
a to pojedyncze liczby, ale zmienne losowe,
poniewa˙z dotycz ˛
a losowej próby.
Agnieszka Rossa

Prawo wielkich liczb Bernoulliego i centralne tw. graniczne
Podstawowe poj ˛ecia wnioskowania statystycznego
Teoretyczne podej ´scie do zagadnie ´
n wnioskowania
Niech
X
1
,
X
2
, . . . ,
X
n
b ˛edzie n-elementow ˛
a prób ˛
a losow ˛
a.
Statystyk ˛
a
nazywamy zmienn ˛
a losow ˛
a T
n
b ˛ed ˛
ac ˛
a dowoln ˛
a
funkcj ˛
a próby losowej, co zapisujemy ogólnie w postaci:
T
n
=
f (X
1
,
X
2
, . . . ,
X
n
).
Przykładami statystyk s ˛
a: ´srednia arytmetyczna z próby oraz
odchylenie standardowe z próby, zdefiniowane wzorami:
¯
X =
1
n
n
X
i=1
X
i
,
S =
v
u
u
t
1
n
n
X
i=1
(
X
i
− ¯
X )
2
.
Zauwa˙zymy, ˙ze zarówno ´srednia arytmetyczna, jak i odchy-
lenie standardowe s ˛
a tu oznaczone du˙zymi literami, dla pod-
kre´slenia, i˙z nie s ˛
a to pojedyncze liczby, ale zmienne losowe,
poniewa˙z dotycz ˛
a losowej próby.
Agnieszka Rossa

Prawo wielkich liczb Bernoulliego i centralne tw. graniczne
Podstawowe poj ˛ecia wnioskowania statystycznego
Wnioskowanie statystyczne
Wnioskowaniem statystycznym nazywamy zbiór reguł
uogólniania wyników z próby losowej na populacj ˛e
generaln ˛
a
.
W ramach wnioskowania statystycznego wyró˙zniamy:
–
estymacj ˛e,
–
weryfikacj ˛e hipotez statystycznych.
Teoria estymacji
zajmuje si ˛e metodami szacowania
(estymacji) nieznanego rozkładu lub nieznanych
parametrów rozkładu badanej cechy X w populacji
generalnej.
Teoria weryfikacji hipotez
zajmuje si ˛e metodami
testowania dowolnego przypuszczenia dotycz ˛
acego
nieznanego rozkładu lub nieznanych parametrów rozkładu
badanej cechy X w populacji generalnej.
Agnieszka Rossa

Prawo wielkich liczb Bernoulliego i centralne tw. graniczne
Podstawowe poj ˛ecia wnioskowania statystycznego
Wnioskowanie statystyczne
Wnioskowaniem statystycznym nazywamy zbiór reguł
uogólniania wyników z próby losowej na populacj ˛e
generaln ˛
a
.
W ramach wnioskowania statystycznego wyró˙zniamy:
–
estymacj ˛e,
–
weryfikacj ˛e hipotez statystycznych.
Teoria estymacji
zajmuje si ˛e metodami szacowania
(estymacji) nieznanego rozkładu lub nieznanych
parametrów rozkładu badanej cechy X w populacji
generalnej.
Teoria weryfikacji hipotez
zajmuje si ˛e metodami
testowania dowolnego przypuszczenia dotycz ˛
acego
nieznanego rozkładu lub nieznanych parametrów rozkładu
badanej cechy X w populacji generalnej.
Agnieszka Rossa

Prawo wielkich liczb Bernoulliego i centralne tw. graniczne
Podstawowe poj ˛ecia wnioskowania statystycznego
Wnioskowanie statystyczne
Wnioskowaniem statystycznym nazywamy zbiór reguł
uogólniania wyników z próby losowej na populacj ˛e
generaln ˛
a
.
W ramach wnioskowania statystycznego wyró˙zniamy:
–
estymacj ˛e,
–
weryfikacj ˛e hipotez statystycznych.
Teoria estymacji
zajmuje si ˛e metodami szacowania
(estymacji) nieznanego rozkładu lub nieznanych
parametrów rozkładu badanej cechy X w populacji
generalnej.
Teoria weryfikacji hipotez
zajmuje si ˛e metodami
testowania dowolnego przypuszczenia dotycz ˛
acego
nieznanego rozkładu lub nieznanych parametrów rozkładu
badanej cechy X w populacji generalnej.
Agnieszka Rossa

Prawo wielkich liczb Bernoulliego i centralne tw. graniczne
Podstawowe poj ˛ecia wnioskowania statystycznego
Wnioskowanie statystyczne
Wnioskowaniem statystycznym nazywamy zbiór reguł
uogólniania wyników z próby losowej na populacj ˛e
generaln ˛
a
.
W ramach wnioskowania statystycznego wyró˙zniamy:
–
estymacj ˛e,
–
weryfikacj ˛e hipotez statystycznych.
Teoria estymacji
zajmuje si ˛e metodami szacowania
(estymacji) nieznanego rozkładu lub nieznanych
parametrów rozkładu badanej cechy X w populacji
generalnej.
Teoria weryfikacji hipotez
zajmuje si ˛e metodami
testowania dowolnego przypuszczenia dotycz ˛
acego
nieznanego rozkładu lub nieznanych parametrów rozkładu
badanej cechy X w populacji generalnej.
Agnieszka Rossa

Prawo wielkich liczb Bernoulliego i centralne tw. graniczne
Podstawowe poj ˛ecia wnioskowania statystycznego
Wnioskowanie statystyczne
Wnioskowaniem statystycznym nazywamy zbiór reguł
uogólniania wyników z próby losowej na populacj ˛e
generaln ˛
a
.
W ramach wnioskowania statystycznego wyró˙zniamy:
–
estymacj ˛e,
–
weryfikacj ˛e hipotez statystycznych.
Teoria estymacji
zajmuje si ˛e metodami szacowania
(estymacji) nieznanego rozkładu lub nieznanych
parametrów rozkładu badanej cechy X w populacji
generalnej.
Teoria weryfikacji hipotez
zajmuje si ˛e metodami
testowania dowolnego przypuszczenia dotycz ˛
acego
nieznanego rozkładu lub nieznanych parametrów rozkładu
badanej cechy X w populacji generalnej.
Agnieszka Rossa

Prawo wielkich liczb Bernoulliego i centralne tw. graniczne
Podstawowe poj ˛ecia wnioskowania statystycznego
Wnioskowanie statystyczne
Wnioskowaniem statystycznym nazywamy zbiór reguł
uogólniania wyników z próby losowej na populacj ˛e
generaln ˛
a
.
W ramach wnioskowania statystycznego wyró˙zniamy:
–
estymacj ˛e,
–
weryfikacj ˛e hipotez statystycznych.
Teoria estymacji
zajmuje si ˛e metodami szacowania
(estymacji) nieznanego rozkładu lub nieznanych
parametrów rozkładu badanej cechy X w populacji
generalnej.
Teoria weryfikacji hipotez
zajmuje si ˛e metodami
testowania dowolnego przypuszczenia dotycz ˛
acego
nieznanego rozkładu lub nieznanych parametrów rozkładu
badanej cechy X w populacji generalnej.
Agnieszka Rossa

Prawo wielkich liczb Bernoulliego i centralne tw. graniczne
Podstawowe poj ˛ecia wnioskowania statystycznego
Podstawy estymacji
Rodzaje estymacji
Wyró˙zniamy:
1.
estymacj ˛e parametryczn ˛
a,
2.
estymacj ˛e nieparametryczn ˛
a.
Inny podział na:
1.
estymacj ˛e punktow ˛
a,
2.
estymacj ˛e przedziałow ˛
a.
Estymacja parametryczna
zajmuje si ˛e szacowaniem
parametrów rozkładu populacji w przypadku, gdy znamy
klas ˛e rozkładów, do której nale˙zy rozkład badanej cechy X
(np. wiemy, ˙ze jest to rozkład normalny, ale nie znamy jego
parametrów µ i σ, które estymujemy).
Je˙zeli nie znamy klasy rozkładów, do której nale˙zy rozkład
badanej zmiennej X , to estymacj ˛e nazywamy
niepara-
metryczn ˛
a
.
Agnieszka Rossa

Prawo wielkich liczb Bernoulliego i centralne tw. graniczne
Podstawowe poj ˛ecia wnioskowania statystycznego
Podstawy estymacji
Rodzaje estymacji
Wyró˙zniamy:
1.
estymacj ˛e parametryczn ˛
a,
2.
estymacj ˛e nieparametryczn ˛
a.
Inny podział na:
1.
estymacj ˛e punktow ˛
a,
2.
estymacj ˛e przedziałow ˛
a.
Estymacja parametryczna
zajmuje si ˛e szacowaniem
parametrów rozkładu populacji w przypadku, gdy znamy
klas ˛e rozkładów, do której nale˙zy rozkład badanej cechy X
(np. wiemy, ˙ze jest to rozkład normalny, ale nie znamy jego
parametrów µ i σ, które estymujemy).
Je˙zeli nie znamy klasy rozkładów, do której nale˙zy rozkład
badanej zmiennej X , to estymacj ˛e nazywamy
niepara-
metryczn ˛
a
.
Agnieszka Rossa

Prawo wielkich liczb Bernoulliego i centralne tw. graniczne
Podstawowe poj ˛ecia wnioskowania statystycznego
Podstawy estymacji
Rodzaje estymacji
Wyró˙zniamy:
1.
estymacj ˛e parametryczn ˛
a,
2.
estymacj ˛e nieparametryczn ˛
a.
Inny podział na:
1.
estymacj ˛e punktow ˛
a,
2.
estymacj ˛e przedziałow ˛
a.
Estymacja parametryczna
zajmuje si ˛e szacowaniem
parametrów rozkładu populacji w przypadku, gdy znamy
klas ˛e rozkładów, do której nale˙zy rozkład badanej cechy X
(np. wiemy, ˙ze jest to rozkład normalny, ale nie znamy jego
parametrów µ i σ, które estymujemy).
Je˙zeli nie znamy klasy rozkładów, do której nale˙zy rozkład
badanej zmiennej X , to estymacj ˛e nazywamy
niepara-
metryczn ˛
a
.
Agnieszka Rossa

Prawo wielkich liczb Bernoulliego i centralne tw. graniczne
Podstawowe poj ˛ecia wnioskowania statystycznego
Podstawy estymacji
Rodzaje estymacji
Wyró˙zniamy:
1.
estymacj ˛e parametryczn ˛
a,
2.
estymacj ˛e nieparametryczn ˛
a.
Inny podział na:
1.
estymacj ˛e punktow ˛
a,
2.
estymacj ˛e przedziałow ˛
a.
Estymacja parametryczna
zajmuje si ˛e szacowaniem
parametrów rozkładu populacji w przypadku, gdy znamy
klas ˛e rozkładów, do której nale˙zy rozkład badanej cechy X
(np. wiemy, ˙ze jest to rozkład normalny, ale nie znamy jego
parametrów µ i σ, które estymujemy).
Je˙zeli nie znamy klasy rozkładów, do której nale˙zy rozkład
badanej zmiennej X , to estymacj ˛e nazywamy
niepara-
metryczn ˛
a
.
Agnieszka Rossa

Prawo wielkich liczb Bernoulliego i centralne tw. graniczne
Podstawowe poj ˛ecia wnioskowania statystycznego
Podstawy estymacji
Estymacja punktowa
Estymacja punktowa
polega na podaniu jednej warto´sci
(wzgl ˛ednie wektora warto´sci) b ˛ed ˛
acej oszacowaniem
nieznanego parametru (wzgl ˛ednie wektora parametrów).
Ilustracj ˛
a takiego sposobu estymacji jest oszacowanie
udziału głosów na PiS (0,35 lub zamiennie 35%)
przedstawione w przykładzie wprowadzaj ˛
acym.
Okre´slenie ”estymacja punktowa” bierze si ˛e st ˛
ad, ˙ze dla
ka˙zdego parametru populacji znajdujemy jedn ˛
a liczb ˛e (na
podstawie realizacji próby), w taki sposób, aby była ona
mo˙zliwie najlepszym przybli˙zeniem nieznanego parametru.
Jest to tzw. ocena punktowa parametru.
Ocena punktowa jest wyznaczana na podstawie warto´sci
pewnej statystyki, o własno´sciach upowa˙zniaj ˛
acych nas do
szacowania za jej pomoc ˛
a danego parametru.
Statystyka taka nosi nazw ˛e
estymatora
.
Agnieszka Rossa

Prawo wielkich liczb Bernoulliego i centralne tw. graniczne
Podstawowe poj ˛ecia wnioskowania statystycznego
Podstawy estymacji
Estymacja punktowa
Estymacja punktowa
polega na podaniu jednej warto´sci
(wzgl ˛ednie wektora warto´sci) b ˛ed ˛
acej oszacowaniem
nieznanego parametru (wzgl ˛ednie wektora parametrów).
Ilustracj ˛
a takiego sposobu estymacji jest oszacowanie
udziału głosów na PiS (0,35 lub zamiennie 35%)
przedstawione w przykładzie wprowadzaj ˛
acym.
Okre´slenie ”estymacja punktowa” bierze si ˛e st ˛
ad, ˙ze dla
ka˙zdego parametru populacji znajdujemy jedn ˛
a liczb ˛e (na
podstawie realizacji próby), w taki sposób, aby była ona
mo˙zliwie najlepszym przybli˙zeniem nieznanego parametru.
Jest to tzw. ocena punktowa parametru.
Ocena punktowa jest wyznaczana na podstawie warto´sci
pewnej statystyki, o własno´sciach upowa˙zniaj ˛
acych nas do
szacowania za jej pomoc ˛
a danego parametru.
Statystyka taka nosi nazw ˛e
estymatora
.
Agnieszka Rossa

Prawo wielkich liczb Bernoulliego i centralne tw. graniczne
Podstawowe poj ˛ecia wnioskowania statystycznego
Podstawy estymacji
Estymacja punktowa
Estymacja punktowa
polega na podaniu jednej warto´sci
(wzgl ˛ednie wektora warto´sci) b ˛ed ˛
acej oszacowaniem
nieznanego parametru (wzgl ˛ednie wektora parametrów).
Ilustracj ˛
a takiego sposobu estymacji jest oszacowanie
udziału głosów na PiS (0,35 lub zamiennie 35%)
przedstawione w przykładzie wprowadzaj ˛
acym.
Okre´slenie ”estymacja punktowa” bierze si ˛e st ˛
ad, ˙ze dla
ka˙zdego parametru populacji znajdujemy jedn ˛
a liczb ˛e (na
podstawie realizacji próby), w taki sposób, aby była ona
mo˙zliwie najlepszym przybli˙zeniem nieznanego parametru.
Jest to tzw. ocena punktowa parametru.
Ocena punktowa jest wyznaczana na podstawie warto´sci
pewnej statystyki, o własno´sciach upowa˙zniaj ˛
acych nas do
szacowania za jej pomoc ˛
a danego parametru.
Statystyka taka nosi nazw ˛e
estymatora
.
Agnieszka Rossa

Prawo wielkich liczb Bernoulliego i centralne tw. graniczne
Podstawowe poj ˛ecia wnioskowania statystycznego
Podstawy estymacji
Estymacja punktowa
Estymacja punktowa
polega na podaniu jednej warto´sci
(wzgl ˛ednie wektora warto´sci) b ˛ed ˛
acej oszacowaniem
nieznanego parametru (wzgl ˛ednie wektora parametrów).
Ilustracj ˛
a takiego sposobu estymacji jest oszacowanie
udziału głosów na PiS (0,35 lub zamiennie 35%)
przedstawione w przykładzie wprowadzaj ˛
acym.
Okre´slenie ”estymacja punktowa” bierze si ˛e st ˛
ad, ˙ze dla
ka˙zdego parametru populacji znajdujemy jedn ˛
a liczb ˛e (na
podstawie realizacji próby), w taki sposób, aby była ona
mo˙zliwie najlepszym przybli˙zeniem nieznanego parametru.
Jest to tzw. ocena punktowa parametru.
Ocena punktowa jest wyznaczana na podstawie warto´sci
pewnej statystyki, o własno´sciach upowa˙zniaj ˛
acych nas do
szacowania za jej pomoc ˛
a danego parametru.
Statystyka taka nosi nazw ˛e
estymatora
.
Agnieszka Rossa

Prawo wielkich liczb Bernoulliego i centralne tw. graniczne
Podstawowe poj ˛ecia wnioskowania statystycznego
Podstawy estymacji
Estymacja punktowa
Estymacja punktowa
polega na podaniu jednej warto´sci
(wzgl ˛ednie wektora warto´sci) b ˛ed ˛
acej oszacowaniem
nieznanego parametru (wzgl ˛ednie wektora parametrów).
Ilustracj ˛
a takiego sposobu estymacji jest oszacowanie
udziału głosów na PiS (0,35 lub zamiennie 35%)
przedstawione w przykładzie wprowadzaj ˛
acym.
Okre´slenie ”estymacja punktowa” bierze si ˛e st ˛
ad, ˙ze dla
ka˙zdego parametru populacji znajdujemy jedn ˛
a liczb ˛e (na
podstawie realizacji próby), w taki sposób, aby była ona
mo˙zliwie najlepszym przybli˙zeniem nieznanego parametru.
Jest to tzw. ocena punktowa parametru.
Ocena punktowa jest wyznaczana na podstawie warto´sci
pewnej statystyki, o własno´sciach upowa˙zniaj ˛
acych nas do
szacowania za jej pomoc ˛
a danego parametru.
Statystyka taka nosi nazw ˛e
estymatora
.
Agnieszka Rossa
Prawo wielkich liczb Bernoulliego i centralne tw. graniczne
Podstawowe poj ˛ecia wnioskowania statystycznego
Podstawy estymacji
Nale˙zy zaznaczy´c, ˙ze ocena punktowana na ogół nie pokrywa
si ˛e z prawdziw ˛
a warto´sci ˛
a parametru. Na rozwa˙zanych
wcze´sniej histogramach mo˙zna było zauwa˙zy´c, ˙ze dla pewnej
cz ˛e´sci próbek warto´sci ´srednie odbiegały w mniejszym lub
wi ˛ekszy stopniu od ´sredniej w populacji (zob. wykres poni˙zej).
Copyright Giorgio Krenkel and Alex Sandri, GNU Free Documentation License, Low Resolution
Agnieszka Rossa

Prawo wielkich liczb Bernoulliego i centralne tw. graniczne
Podstawowe poj ˛ecia wnioskowania statystycznego
Podstawy estymacji
Estymacja przedziałowa
W praktyce mamy tylko jedn ˛
a prób ˛e, zatem nie mamy
pewno´sci, jak bardzo warto´s´c obliczona z dost ˛epnej próby
ró˙zni si ˛e od szukanego parametru.
Bardziej realistyczne, zamiast oceny punktowej, wydaje si ˛e
skonstruowanie przedziału, który z zadanym z góry
prawdopodobie ´nstwem, bliskim jedno´sci, pokrywałby
nieznan ˛
a warto´s´c tego parametru. Jest to zadanie
estymacji przedziałowej
.
Przedział taki nosi miano
przedziału ufno ´sci
.
Konstrukcja przedziału ufno´sci jest równoznaczna z po-
daniem jego dwóch kra ´nców. Poniewa˙z kra ´nce te s ˛
a
zale˙znego od wyników w losowej próbie, wi ˛ec cały
przedział ma tak˙ze charakter losowy.
Agnieszka Rossa

Prawo wielkich liczb Bernoulliego i centralne tw. graniczne
Podstawowe poj ˛ecia wnioskowania statystycznego
Podstawy estymacji
Estymacja przedziałowa
W praktyce mamy tylko jedn ˛
a prób ˛e, zatem nie mamy
pewno´sci, jak bardzo warto´s´c obliczona z dost ˛epnej próby
ró˙zni si ˛e od szukanego parametru.
Bardziej realistyczne, zamiast oceny punktowej, wydaje si ˛e
skonstruowanie przedziału, który z zadanym z góry
prawdopodobie ´nstwem, bliskim jedno´sci, pokrywałby
nieznan ˛
a warto´s´c tego parametru. Jest to zadanie
estymacji przedziałowej
.
Przedział taki nosi miano
przedziału ufno ´sci
.
Konstrukcja przedziału ufno´sci jest równoznaczna z po-
daniem jego dwóch kra ´nców. Poniewa˙z kra ´nce te s ˛
a
zale˙znego od wyników w losowej próbie, wi ˛ec cały
przedział ma tak˙ze charakter losowy.
Agnieszka Rossa

Prawo wielkich liczb Bernoulliego i centralne tw. graniczne
Podstawowe poj ˛ecia wnioskowania statystycznego
Podstawy estymacji
Estymacja przedziałowa
W praktyce mamy tylko jedn ˛
a prób ˛e, zatem nie mamy
pewno´sci, jak bardzo warto´s´c obliczona z dost ˛epnej próby
ró˙zni si ˛e od szukanego parametru.
Bardziej realistyczne, zamiast oceny punktowej, wydaje si ˛e
skonstruowanie przedziału, który z zadanym z góry
prawdopodobie ´nstwem, bliskim jedno´sci, pokrywałby
nieznan ˛
a warto´s´c tego parametru. Jest to zadanie
estymacji przedziałowej
.
Przedział taki nosi miano
przedziału ufno ´sci
.
Konstrukcja przedziału ufno´sci jest równoznaczna z po-
daniem jego dwóch kra ´nców. Poniewa˙z kra ´nce te s ˛
a
zale˙znego od wyników w losowej próbie, wi ˛ec cały
przedział ma tak˙ze charakter losowy.
Agnieszka Rossa

Prawo wielkich liczb Bernoulliego i centralne tw. graniczne
Podstawowe poj ˛ecia wnioskowania statystycznego
Podstawy estymacji
Estymacja przedziałowa
W praktyce mamy tylko jedn ˛
a prób ˛e, zatem nie mamy
pewno´sci, jak bardzo warto´s´c obliczona z dost ˛epnej próby
ró˙zni si ˛e od szukanego parametru.
Bardziej realistyczne, zamiast oceny punktowej, wydaje si ˛e
skonstruowanie przedziału, który z zadanym z góry
prawdopodobie ´nstwem, bliskim jedno´sci, pokrywałby
nieznan ˛
a warto´s´c tego parametru. Jest to zadanie
estymacji przedziałowej
.
Przedział taki nosi miano
przedziału ufno ´sci
.
Konstrukcja przedziału ufno´sci jest równoznaczna z po-
daniem jego dwóch kra ´nców. Poniewa˙z kra ´nce te s ˛
a
zale˙znego od wyników w losowej próbie, wi ˛ec cały
przedział ma tak˙ze charakter losowy.
Agnieszka Rossa

Prawo wielkich liczb Bernoulliego i centralne tw. graniczne
Podstawowe poj ˛ecia wnioskowania statystycznego
Podstawy estymacji
Wyprowadzenie przedziału ufno ´sci dla ´sredniej w populacji na podstawie du˙zej
próby
Do budowy
przedziału ufno ´sci dla warto ´sci ´sredniej µ w
populacji
wykorzystamy wnioski płyn ˛
ace z centralnego tw.
granicznego, w tym tak˙ze własno´sci 1 i 2 (b ˛edziemy zakła-
da´c, ˙ze dysponujemy odpowiednio du˙z ˛
a prób ˛
a).
Wyprowadzimy wzór na przedział, który z prawdopodo-
bie ´nstwem
1 − α
∈ (0, 1) zawiera´c b ˛edzie ´sredni ˛
a µ.
Liczb ˛e
1 − α
nazywamy
poziomem ufno ´sci
. Przyjmuje si ˛e
z reguły, ˙ze jest on równy 0,9 lub 0,95 (niekiedy 0,99).
Do wyznaczenia przedziału ufno´sci wystarcz ˛
a nam dane
z jednej próbki. W przypadku, gdy jej liczno´s´c jest du˙za
(cz ˛esto wystarczy n ≥ 30), wówczas przyjmujemy, ˙ze roz-
kład ´sredniej ¯
X z próbki jest zbli˙zony do rozkładu
N(µ,
σ
√
n
)
.
Agnieszka Rossa

Prawo wielkich liczb Bernoulliego i centralne tw. graniczne
Podstawowe poj ˛ecia wnioskowania statystycznego
Podstawy estymacji
Wyprowadzenie przedziału ufno ´sci dla ´sredniej w populacji na podstawie du˙zej
próby
Do budowy
przedziału ufno ´sci dla warto ´sci ´sredniej µ w
populacji
wykorzystamy wnioski płyn ˛
ace z centralnego tw.
granicznego, w tym tak˙ze własno´sci 1 i 2 (b ˛edziemy zakła-
da´c, ˙ze dysponujemy odpowiednio du˙z ˛
a prób ˛
a).
Wyprowadzimy wzór na przedział, który z prawdopodo-
bie ´nstwem
1 − α
∈ (0, 1) zawiera´c b ˛edzie ´sredni ˛
a µ.
Liczb ˛e
1 − α
nazywamy
poziomem ufno ´sci
. Przyjmuje si ˛e
z reguły, ˙ze jest on równy 0,9 lub 0,95 (niekiedy 0,99).
Do wyznaczenia przedziału ufno´sci wystarcz ˛
a nam dane
z jednej próbki. W przypadku, gdy jej liczno´s´c jest du˙za
(cz ˛esto wystarczy n ≥ 30), wówczas przyjmujemy, ˙ze roz-
kład ´sredniej ¯
X z próbki jest zbli˙zony do rozkładu
N(µ,
σ
√
n
)
.
Agnieszka Rossa

Prawo wielkich liczb Bernoulliego i centralne tw. graniczne
Podstawowe poj ˛ecia wnioskowania statystycznego
Podstawy estymacji
Wyprowadzenie przedziału ufno ´sci dla ´sredniej w populacji na podstawie du˙zej
próby
Do budowy
przedziału ufno ´sci dla warto ´sci ´sredniej µ w
populacji
wykorzystamy wnioski płyn ˛
ace z centralnego tw.
granicznego, w tym tak˙ze własno´sci 1 i 2 (b ˛edziemy zakła-
da´c, ˙ze dysponujemy odpowiednio du˙z ˛
a prób ˛
a).
Wyprowadzimy wzór na przedział, który z prawdopodo-
bie ´nstwem
1 − α
∈ (0, 1) zawiera´c b ˛edzie ´sredni ˛
a µ.
Liczb ˛e
1 − α
nazywamy
poziomem ufno ´sci
. Przyjmuje si ˛e
z reguły, ˙ze jest on równy 0,9 lub 0,95 (niekiedy 0,99).
Do wyznaczenia przedziału ufno´sci wystarcz ˛
a nam dane
z jednej próbki. W przypadku, gdy jej liczno´s´c jest du˙za
(cz ˛esto wystarczy n ≥ 30), wówczas przyjmujemy, ˙ze roz-
kład ´sredniej ¯
X z próbki jest zbli˙zony do rozkładu
N(µ,
σ
√
n
)
.
Agnieszka Rossa

Prawo wielkich liczb Bernoulliego i centralne tw. graniczne
Podstawowe poj ˛ecia wnioskowania statystycznego
Podstawy estymacji
Wyprowadzenie przedziału ufno ´sci dla ´sredniej w populacji na podstawie du˙zej
próby
Do budowy
przedziału ufno ´sci dla warto ´sci ´sredniej µ w
populacji
wykorzystamy wnioski płyn ˛
ace z centralnego tw.
granicznego, w tym tak˙ze własno´sci 1 i 2 (b ˛edziemy zakła-
da´c, ˙ze dysponujemy odpowiednio du˙z ˛
a prób ˛
a).
Wyprowadzimy wzór na przedział, który z prawdopodo-
bie ´nstwem
1 − α
∈ (0, 1) zawiera´c b ˛edzie ´sredni ˛
a µ.
Liczb ˛e
1 − α
nazywamy
poziomem ufno ´sci
. Przyjmuje si ˛e
z reguły, ˙ze jest on równy 0,9 lub 0,95 (niekiedy 0,99).
Do wyznaczenia przedziału ufno´sci wystarcz ˛
a nam dane
z jednej próbki. W przypadku, gdy jej liczno´s´c jest du˙za
(cz ˛esto wystarczy n ≥ 30), wówczas przyjmujemy, ˙ze roz-
kład ´sredniej ¯
X z próbki jest zbli˙zony do rozkładu
N(µ,
σ
√
n
)
.
Agnieszka Rossa

Prawo wielkich liczb Bernoulliego i centralne tw. graniczne
Podstawowe poj ˛ecia wnioskowania statystycznego
Podstawy estymacji
Wyprowadzenie przedziału ufno ´sci dla ´sredniej w populacji w przypadku du˙zej
próby – c.d.
Skoro ¯
X ma w przypadku du˙zej próby rozkład zbli˙zony do
rozkładu N(µ,
σ
√
n
)
, to zmienna losowa:
U =
¯
X − µ
σ
√
n
ma rozkład zbli˙zony do rozkładu N(0, 1) (o tym mniej
wi ˛ecej mówi centralne twierdzenie graniczne).
Ustalmy poziom ufno´sci 1 − α. Niech u
α
b ˛edzie kwantylem
rz ˛edu 1 −
α
2
rozkładu N(0, 1).
Wówczas dla wy˙zej zdefiniowanej zmiennej U zachodzi:
P(|U| < u
α
) =
P(−u
α
<
U < u
α
) ≈
1 − α.
Agnieszka Rossa

Prawo wielkich liczb Bernoulliego i centralne tw. graniczne
Podstawowe poj ˛ecia wnioskowania statystycznego
Podstawy estymacji
Wyprowadzenie przedziału ufno ´sci dla ´sredniej w populacji w przypadku du˙zej
próby – c.d.
Skoro ¯
X ma w przypadku du˙zej próby rozkład zbli˙zony do
rozkładu N(µ,
σ
√
n
)
, to zmienna losowa:
U =
¯
X − µ
σ
√
n
ma rozkład zbli˙zony do rozkładu N(0, 1) (o tym mniej
wi ˛ecej mówi centralne twierdzenie graniczne).
Ustalmy poziom ufno´sci 1 − α. Niech u
α
b ˛edzie kwantylem
rz ˛edu 1 −
α
2
rozkładu N(0, 1).
Wówczas dla wy˙zej zdefiniowanej zmiennej U zachodzi:
P(|U| < u
α
) =
P(−u
α
<
U < u
α
) ≈
1 − α.
Agnieszka Rossa

Prawo wielkich liczb Bernoulliego i centralne tw. graniczne
Podstawowe poj ˛ecia wnioskowania statystycznego
Podstawy estymacji
Wyprowadzenie przedziału ufno ´sci dla ´sredniej w populacji w przypadku du˙zej
próby – c.d.
Skoro ¯
X ma w przypadku du˙zej próby rozkład zbli˙zony do
rozkładu N(µ,
σ
√
n
)
, to zmienna losowa:
U =
¯
X − µ
σ
√
n
ma rozkład zbli˙zony do rozkładu N(0, 1) (o tym mniej
wi ˛ecej mówi centralne twierdzenie graniczne).
Ustalmy poziom ufno´sci 1 − α. Niech u
α
b ˛edzie kwantylem
rz ˛edu 1 −
α
2
rozkładu N(0, 1).
Wówczas dla wy˙zej zdefiniowanej zmiennej U zachodzi:
P(|U| < u
α
) =
P(−u
α
<
U < u
α
) ≈
1 − α.
Agnieszka Rossa

Prawo wielkich liczb Bernoulliego i centralne tw. graniczne
Podstawowe poj ˛ecia wnioskowania statystycznego
Podstawy estymacji
Wyprowadzenie przedziału ufno ´sci dla ´sredniej w populacji w przypadku du˙zej
próby – c.d.
Po podstawieniu w miejsce zmiennej U wyra˙zenia
¯
X −µ
σ
√
n
i po
dokonaniu kilku przekształce ´n, otrzymujemy:
P( ¯
X − u
α
σ
√
n
< µ < ¯
X + u
α
σ
√
n
) ≈
1 − α,
co oznacza, i˙z z prawdopodobie ´nstwem równym w przy-
bli˙zeniu 1 − α mo˙zemy oczekiwa´c, i´z przedział o podanych
poni˙zej kra ´ncach zawiera nieznany parametr µ:
¯
X − u
α
·
σ
√
n
,
¯
X + u
α
·
σ
√
n
Uwaga:
Je´sli nie znamy tak˙ze parametru populacji σ,
wówczas zast ˛epujemy go przybli˙zeniem z próby, tj.
statystyk ˛
a S.
Agnieszka Rossa

Prawo wielkich liczb Bernoulliego i centralne tw. graniczne
Podstawowe poj ˛ecia wnioskowania statystycznego
Podstawy estymacji
Wyprowadzenie przedziału ufno ´sci dla ´sredniej w populacji w przypadku du˙zej
próby – c.d.
Po podstawieniu w miejsce zmiennej U wyra˙zenia
¯
X −µ
σ
√
n
i po
dokonaniu kilku przekształce ´n, otrzymujemy:
P( ¯
X − u
α
σ
√
n
< µ < ¯
X + u
α
σ
√
n
) ≈
1 − α,
co oznacza, i˙z z prawdopodobie ´nstwem równym w przy-
bli˙zeniu 1 − α mo˙zemy oczekiwa´c, i´z przedział o podanych
poni˙zej kra ´ncach zawiera nieznany parametr µ:
¯
X − u
α
·
σ
√
n
,
¯
X + u
α
·
σ
√
n
Uwaga:
Je´sli nie znamy tak˙ze parametru populacji σ,
wówczas zast ˛epujemy go przybli˙zeniem z próby, tj.
statystyk ˛
a S.
Agnieszka Rossa

Prawo wielkich liczb Bernoulliego i centralne tw. graniczne
Podstawowe poj ˛ecia wnioskowania statystycznego
Przykład zastosowania przedziału ufno ´sci dla ´sredniej populacji
W ramach ilustracji, wyznaczymy przedział, który zawierał-
by rzeczywisty udział wyborców głosuj ˛
acych na PiS w wy-
borach 2007 r. (zob. przykład wprowadzaj ˛
acy).
Niech
1 − α = 0, 95
, wówczas α = 0, 05,
α
2
=
0, 025,
a st ˛
ad
1 −
α
2
=
0, 975
. Kwantyl rz ˛edu 0, 975 rozkładu
N(0, 1) jest równy
1, 96
(zob. tablice dystrybuanty N(0, 1)).
Mamy na podstawie danych z próby (dane z sonda˙zu):
n = 1018,
¯
x = 0, 35,
s ≈ 0, 48
.
Kra ´nce przedziału ufno´sci dla szukanego wska´znika to:
0, 35 − 1, 96 ·
0, 48
√
1018
;
0, 35 + 1, 96 ·
0, 48
√
1018
Otrzymujemy przedział
[
0, 32; 0, 38]
. Mo˙zemy wi ˛ec ocze-
kiwa´c z prawdopodobie ´nstwem 0, 95, ˙ze w przedziale tym
znalazł si ˛e rzeczywisty udział głosów oddanych na PiS.
Agnieszka Rossa

Prawo wielkich liczb Bernoulliego i centralne tw. graniczne
Podstawowe poj ˛ecia wnioskowania statystycznego
Przykład zastosowania przedziału ufno ´sci dla ´sredniej populacji
W ramach ilustracji, wyznaczymy przedział, który zawierał-
by rzeczywisty udział wyborców głosuj ˛
acych na PiS w wy-
borach 2007 r. (zob. przykład wprowadzaj ˛
acy).
Niech
1 − α = 0, 95
, wówczas α = 0, 05,
α
2
=
0, 025,
a st ˛
ad
1 −
α
2
=
0, 975
. Kwantyl rz ˛edu 0, 975 rozkładu
N(0, 1) jest równy
1, 96
(zob. tablice dystrybuanty N(0, 1)).
Mamy na podstawie danych z próby (dane z sonda˙zu):
n = 1018,
¯
x = 0, 35,
s ≈ 0, 48
.
Kra ´nce przedziału ufno´sci dla szukanego wska´znika to:
0, 35 − 1, 96 ·
0, 48
√
1018
;
0, 35 + 1, 96 ·
0, 48
√
1018
Otrzymujemy przedział
[
0, 32; 0, 38]
. Mo˙zemy wi ˛ec ocze-
kiwa´c z prawdopodobie ´nstwem 0, 95, ˙ze w przedziale tym
znalazł si ˛e rzeczywisty udział głosów oddanych na PiS.
Agnieszka Rossa

Prawo wielkich liczb Bernoulliego i centralne tw. graniczne
Podstawowe poj ˛ecia wnioskowania statystycznego
Przykład zastosowania przedziału ufno ´sci dla ´sredniej populacji
W ramach ilustracji, wyznaczymy przedział, który zawierał-
by rzeczywisty udział wyborców głosuj ˛
acych na PiS w wy-
borach 2007 r. (zob. przykład wprowadzaj ˛
acy).
Niech
1 − α = 0, 95
, wówczas α = 0, 05,
α
2
=
0, 025,
a st ˛
ad
1 −
α
2
=
0, 975
. Kwantyl rz ˛edu 0, 975 rozkładu
N(0, 1) jest równy
1, 96
(zob. tablice dystrybuanty N(0, 1)).
Mamy na podstawie danych z próby (dane z sonda˙zu):
n = 1018,
¯
x = 0, 35,
s ≈ 0, 48
.
Kra ´nce przedziału ufno´sci dla szukanego wska´znika to:
0, 35 − 1, 96 ·
0, 48
√
1018
;
0, 35 + 1, 96 ·
0, 48
√
1018
Otrzymujemy przedział
[
0, 32; 0, 38]
. Mo˙zemy wi ˛ec ocze-
kiwa´c z prawdopodobie ´nstwem 0, 95, ˙ze w przedziale tym
znalazł si ˛e rzeczywisty udział głosów oddanych na PiS.
Agnieszka Rossa

Prawo wielkich liczb Bernoulliego i centralne tw. graniczne
Podstawowe poj ˛ecia wnioskowania statystycznego
Przykład zastosowania przedziału ufno ´sci dla ´sredniej populacji
W ramach ilustracji, wyznaczymy przedział, który zawierał-
by rzeczywisty udział wyborców głosuj ˛
acych na PiS w wy-
borach 2007 r. (zob. przykład wprowadzaj ˛
acy).
Niech
1 − α = 0, 95
, wówczas α = 0, 05,
α
2
=
0, 025,
a st ˛
ad
1 −
α
2
=
0, 975
. Kwantyl rz ˛edu 0, 975 rozkładu
N(0, 1) jest równy
1, 96
(zob. tablice dystrybuanty N(0, 1)).
Mamy na podstawie danych z próby (dane z sonda˙zu):
n = 1018,
¯
x = 0, 35,
s ≈ 0, 48
.
Kra ´nce przedziału ufno´sci dla szukanego wska´znika to:
0, 35 − 1, 96 ·
0, 48
√
1018
;
0, 35 + 1, 96 ·
0, 48
√
1018
Otrzymujemy przedział
[
0, 32; 0, 38]
. Mo˙zemy wi ˛ec ocze-
kiwa´c z prawdopodobie ´nstwem 0, 95, ˙ze w przedziale tym
znalazł si ˛e rzeczywisty udział głosów oddanych na PiS.
Agnieszka Rossa

Prawo wielkich liczb Bernoulliego i centralne tw. graniczne
Podstawowe poj ˛ecia wnioskowania statystycznego
Przykład zastosowania przedziału ufno ´sci dla ´sredniej populacji
W ramach ilustracji, wyznaczymy przedział, który zawierał-
by rzeczywisty udział wyborców głosuj ˛
acych na PiS w wy-
borach 2007 r. (zob. przykład wprowadzaj ˛
acy).
Niech
1 − α = 0, 95
, wówczas α = 0, 05,
α
2
=
0, 025,
a st ˛
ad
1 −
α
2
=
0, 975
. Kwantyl rz ˛edu 0, 975 rozkładu
N(0, 1) jest równy
1, 96
(zob. tablice dystrybuanty N(0, 1)).
Mamy na podstawie danych z próby (dane z sonda˙zu):
n = 1018,
¯
x = 0, 35,
s ≈ 0, 48
.
Kra ´nce przedziału ufno´sci dla szukanego wska´znika to:
0, 35 − 1, 96 ·
0, 48
√
1018
;
0, 35 + 1, 96 ·
0, 48
√
1018
Otrzymujemy przedział
[
0, 32; 0, 38]
. Mo˙zemy wi ˛ec ocze-
kiwa´c z prawdopodobie ´nstwem 0, 95, ˙ze w przedziale tym
znalazł si ˛e rzeczywisty udział głosów oddanych na PiS.
Agnieszka Rossa

Prawo wielkich liczb Bernoulliego i centralne tw. graniczne
Podstawowe poj ˛ecia wnioskowania statystycznego
Przykład zastosowania przedziału ufno ´sci dla ´sredniej populacji
Komentarze do przykładu
1.
W tym przykładzie szacowanym wska´znikiem był udział
(lub zamiennie – odsetek) głosuj ˛
acych na PiS.
Uzyskali´smy 95-procentowy przedział ufno´sci
[
0, 32; 0, 38]
lub zamiennie
[
32%, 38%]
.
2.
Zgodnie z Uwag ˛
a 3, ten wska´znik mo˙zemy traktowa´c tak˙ze
jako ´sredni ˛
a w populacji składaj ˛
acej si ˛e z jedynek (np. gdy
wyborca popiera PiS) i zer (w innych przypadkach).
3.
Innymi słowy, badan ˛
a cech ˛
a w populacji była tu pewna
cecha zero-jedynkowa, a nasze zadanie polegało na
estymacji przedziałowej warto´sci ´sredniej tej cechy.
4.
Je´sli chcemy w tym zadaniu skorzysta´c z wyprowadzonego
wzoru na przedział ufno´sci, nale˙zy takie oszacowanie
oprze´c na próbie licz ˛
acej co najmniej 100 elementów.
Agnieszka Rossa

Prawo wielkich liczb Bernoulliego i centralne tw. graniczne
Podstawowe poj ˛ecia wnioskowania statystycznego
Przykład zastosowania przedziału ufno ´sci dla ´sredniej populacji
Komentarze do przykładu
1.
W tym przykładzie szacowanym wska´znikiem był udział
(lub zamiennie – odsetek) głosuj ˛
acych na PiS.
Uzyskali´smy 95-procentowy przedział ufno´sci
[
0, 32; 0, 38]
lub zamiennie
[
32%, 38%]
.
2.
Zgodnie z Uwag ˛
a 3, ten wska´znik mo˙zemy traktowa´c tak˙ze
jako ´sredni ˛
a w populacji składaj ˛
acej si ˛e z jedynek (np. gdy
wyborca popiera PiS) i zer (w innych przypadkach).
3.
Innymi słowy, badan ˛
a cech ˛
a w populacji była tu pewna
cecha zero-jedynkowa, a nasze zadanie polegało na
estymacji przedziałowej warto´sci ´sredniej tej cechy.
4.
Je´sli chcemy w tym zadaniu skorzysta´c z wyprowadzonego
wzoru na przedział ufno´sci, nale˙zy takie oszacowanie
oprze´c na próbie licz ˛
acej co najmniej 100 elementów.
Agnieszka Rossa

Prawo wielkich liczb Bernoulliego i centralne tw. graniczne
Podstawowe poj ˛ecia wnioskowania statystycznego
Przykład zastosowania przedziału ufno ´sci dla ´sredniej populacji
Komentarze do przykładu
1.
W tym przykładzie szacowanym wska´znikiem był udział
(lub zamiennie – odsetek) głosuj ˛
acych na PiS.
Uzyskali´smy 95-procentowy przedział ufno´sci
[
0, 32; 0, 38]
lub zamiennie
[
32%, 38%]
.
2.
Zgodnie z Uwag ˛
a 3, ten wska´znik mo˙zemy traktowa´c tak˙ze
jako ´sredni ˛
a w populacji składaj ˛
acej si ˛e z jedynek (np. gdy
wyborca popiera PiS) i zer (w innych przypadkach).
3.
Innymi słowy, badan ˛
a cech ˛
a w populacji była tu pewna
cecha zero-jedynkowa, a nasze zadanie polegało na
estymacji przedziałowej warto´sci ´sredniej tej cechy.
4.
Je´sli chcemy w tym zadaniu skorzysta´c z wyprowadzonego
wzoru na przedział ufno´sci, nale˙zy takie oszacowanie
oprze´c na próbie licz ˛
acej co najmniej 100 elementów.
Agnieszka Rossa

Prawo wielkich liczb Bernoulliego i centralne tw. graniczne
Podstawowe poj ˛ecia wnioskowania statystycznego
Przykład zastosowania przedziału ufno ´sci dla ´sredniej populacji
Komentarze do przykładu
1.
W tym przykładzie szacowanym wska´znikiem był udział
(lub zamiennie – odsetek) głosuj ˛
acych na PiS.
Uzyskali´smy 95-procentowy przedział ufno´sci
[
0, 32; 0, 38]
lub zamiennie
[
32%, 38%]
.
2.
Zgodnie z Uwag ˛
a 3, ten wska´znik mo˙zemy traktowa´c tak˙ze
jako ´sredni ˛
a w populacji składaj ˛
acej si ˛e z jedynek (np. gdy
wyborca popiera PiS) i zer (w innych przypadkach).
3.
Innymi słowy, badan ˛
a cech ˛
a w populacji była tu pewna
cecha zero-jedynkowa, a nasze zadanie polegało na
estymacji przedziałowej warto´sci ´sredniej tej cechy.
4.
Je´sli chcemy w tym zadaniu skorzysta´c z wyprowadzonego
wzoru na przedział ufno´sci, nale˙zy takie oszacowanie
oprze´c na próbie licz ˛
acej co najmniej 100 elementów.
Agnieszka Rossa
Document Outline
- Przyklad wprowadzajcy
- Prawo wielkich liczb Bernoulliego i centralne tw. graniczne
- Podstawowe pojcia wnioskowania statystycznego
- Podstawy estymacji
Wyszukiwarka
Podobne podstrony:
podstawy wnioskowania cz II
Biologiczne podstawy zachowań cz I Psychologia N 2012 2013
2 podstawowe pojecia cz 1id 19802 (2)
Sita angielski Kurs podstawowy książka cz 1
KONSPEKT PODSTAWY FINANSÓW CZ I, październik 08
Polityka strukturalna - podstawowe informacje cz.2, Księgozbiór, Europeistyka
Materiały do terminologii więźb?chowych podstawowe pojęcia, cz 2
Test z podstaw marketingu cz 1
BIOMEDYCZNE PODSTAWY ROZWOJU CZ즁WIEKA
Wykład podstawy zarządzania cz 3
Materiały do terminologii więźb dachowych podstawowe pojęcia, cz 2
Podstawy elektroniki cz 4
logistyka-podstawowe zagadnienia cz.5
Materiały do terminologii więźb dachowych podstawowe pojęcia, cz 1
Materiały do terminologii więźb?chowych podstawowe pojęcia, cz 1
więcej podobnych podstron