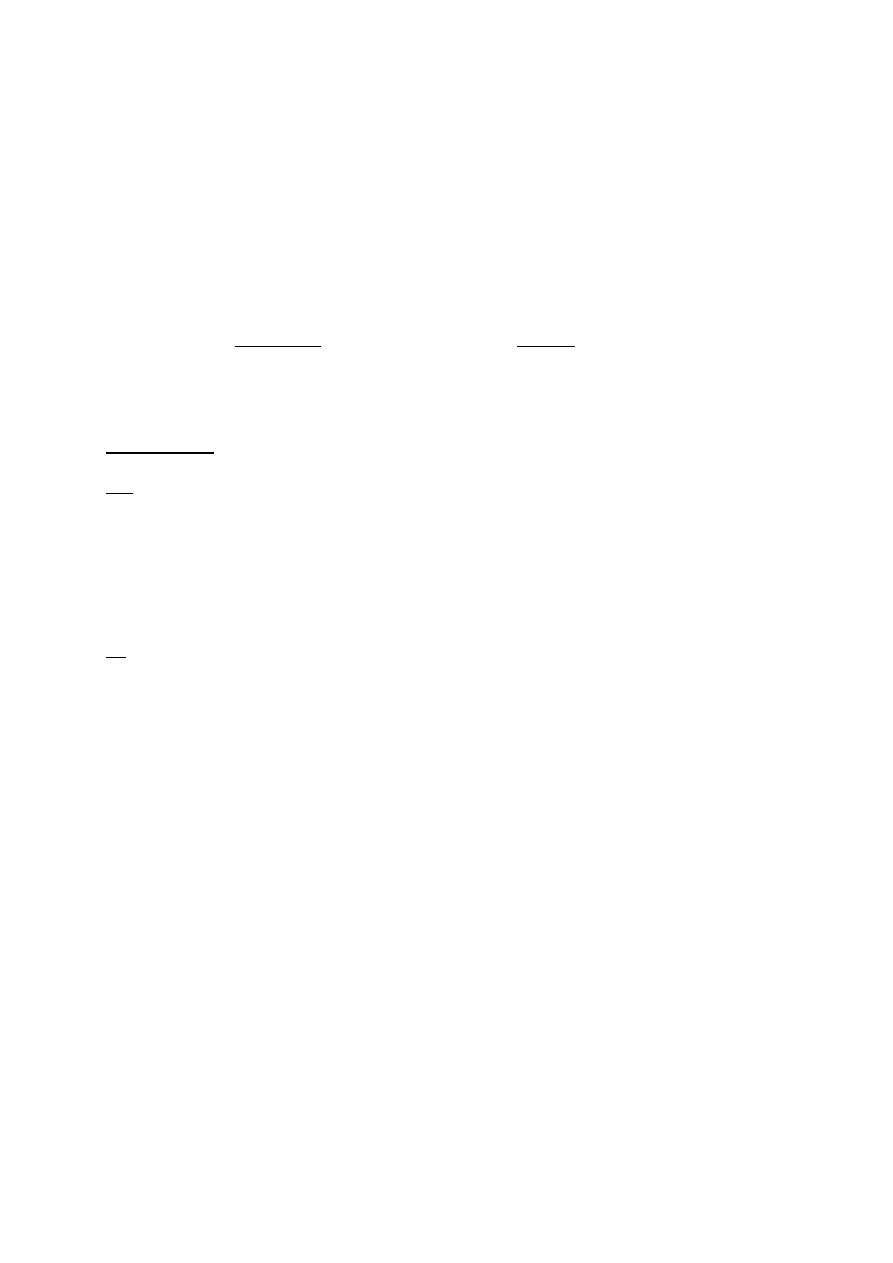
Przykład:

Rozwijamy Rozwinięcie

wyznacznik wzgl. względem 1
4 wiersza kolumny

←x3

|9 3 -4 -2 7| |9 3 -4 -2 7| |9 3 -4 -2 7| |0 3 -4 7| |3 -4 7|

|3 1 -1 0 4|

|3 1 -1 0 4| |3 1 -1 0 4| |0 1 -1 4| |1 -1 4|

|6 2 -2 -1 0|=|6 2 -2 -1 0|=3(-1)

4+4

|6 2 -2 -1 0|=3|0 2 -2 0|=3*13*(-1)

4+1

*|2 -2 0|=

|-6 -2 2 3 -8| |0 0 0 3 0| |-5 -6 0 -2 4| |13 -6 0 4|

-

3 -4 7

+

|-5 -6 0 -2 4| |-5 -6 0 -2 4|

-

1 -1 4

+

=-39(-14-32+14+24)=(-39)(-8)=312

Tw. Cauchy’ego
Dla macierzy kwadratowych A i B wymiaru n

x

n

det(A*B)=detA*detB

.

Dw.
detA*det

odwz. wieloliniowe i antysymetryczne względem

det(A*

)) oddz.. wieloliniowe i antysymetryczne względem

Dla

}

}

są równe

Df.
Macierz kwadratową A nazywamy osobliwą (nieosobliwą) jeśli detA=0 (detA 0).

Rozważamy układ równao liniowych

a

11

x

1

+a

12

x

2

+…+a

1n

x

n

=y

1

}

a

21

x

1

+a

22

x

2

+…+a

2n

x

n

=y

2

}  A

}
a

n1

x

1

+a

n2

x

2

+…+a

nn

x

n

=y

n

}

(a

11

,…,a

1n

)

A=(… …)

macierzy współczynników

(a

n1

,…,a

nn

)

(1,0,…,x

1

,…,0)

(0,1,…,x

2

,…,0)

x

j

=

(0,1,…,x

j

,…,0)(j)

(0,0,…,x

n

,…,1)

(a

11

, … ,

, … , a

1n

) (a

11

, … , y

1

, … , a

1n

)

AX

j

=

( ) = ( ) = B

j

(a

n1

, … ,

, … , a

nn

) (a

n1

, … , y

n

, … , a

nn

)

detB

j

=det(A*X

j

)=detA*detX

j

=detA*x

j

Twierdzenie Cramera
Jeżeli macierz A jest macierzą nieosobliwą, to układ równao(1) ma dokładnie jedno rozwiązane dane
wzorem:

Przykład:
Rozwiązad układ równao.
X

1

-5x

2

+x

3

=

0

2x

1

+x

2

-3x

3

=-

4

-x

1

+2x

2

+2x

3

=

6

detA =

= 18

detB

1

=

= 36

detB

2

=

= 18

detB

3

=

= 54

x

1

=detB

1

/detA=36/18=2

x

2

=18/18=1

x

3

=54/18=3

X-przestrzeo wektorowa nad K, dimX=n.
T,S:X->X liniowe
Odwzorowanie S nazywamy odwrotnym do T i piszemy S=T

-1

, jeżeli S◦T=T◦S=e

x

Niech A-reprezentacja macierzowa T

} macierze kwadratowe

B – reprezentacja macierzowa S

}

Macierz B jw. nazywamy

odwrotną

do A i piszemy B=A

-1

jeżeli S=T

-1

.

Wniosek 1:
B=A

-1

 B*A=A*B=I

Wniosek2:
(A

-1

)

-1

=A

Ponieważ (T

-1

)

-1

=T

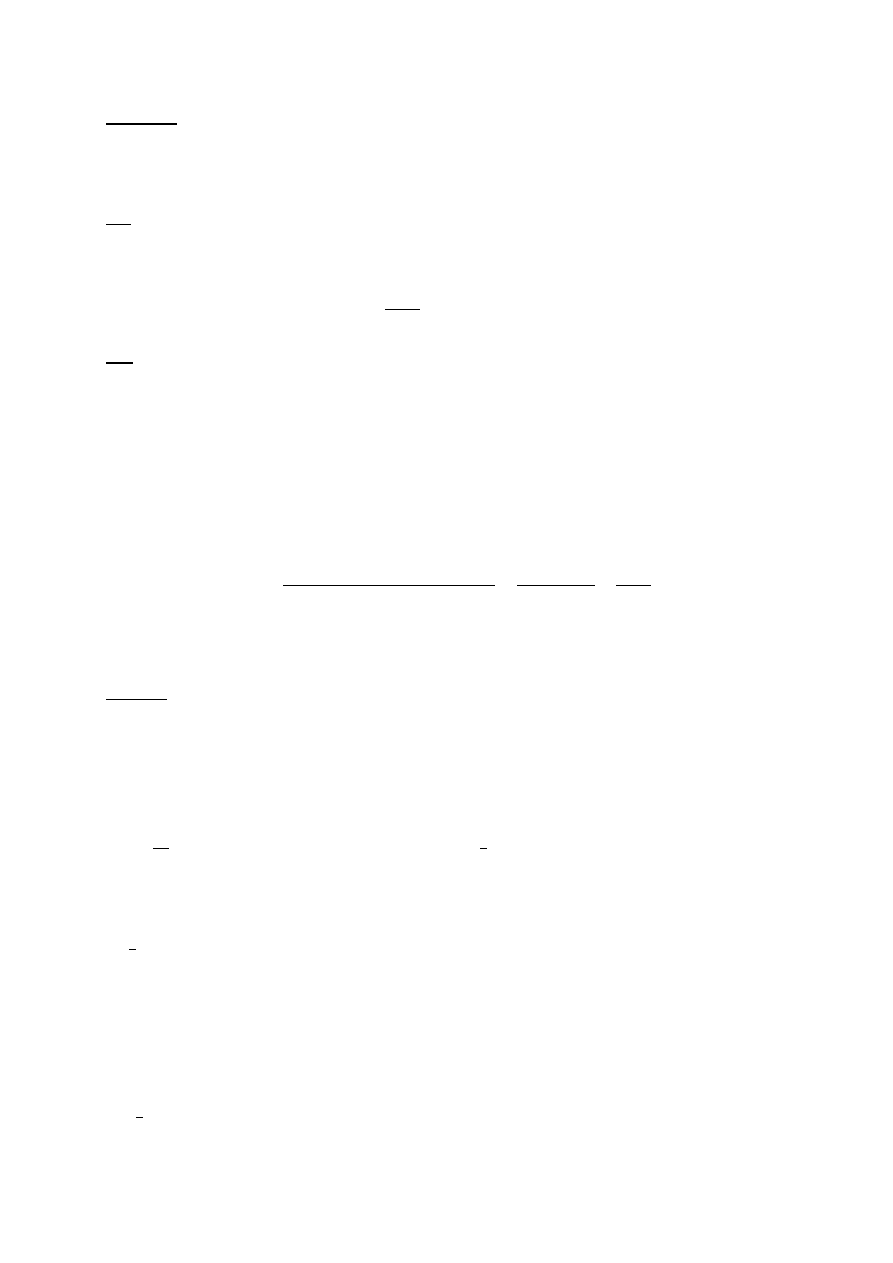
Wniosek3:
Ponieważ dla T,S : X -> X (S◦T)

-1

=T

-1

*S

-1

Zatem
(B*A)

-1

=A

-1

*B

-1

Tw.
Niech A – macierz kwadratowa wymiaru n

x

n, nieosobliwa, niech B=A

-1

(kwadratowa, wymiaru n

x

n,

nieosobliwa).
Wtedy:

Dw.
A*B=I  B=A

-1

(b

1j

) (0)

A*(… )= (…)
(b

nj

) (1)(j)

(…)
(0)

{1 dla k=j

C

k

= {0 dla k j

Przykład:

A =

detA=-3

A

-1

=B=

=

=

=

=

spr.

(

) = (