Strona 1 z 6
r
y
sin
r
x
cos
1.
Definicja modułu i argumentu liczny zespolonej. Postać trygonometryczna i wzór Moivrea. Obliczyć np.
10
i
1
.
Modułem liczby zespolonej
iy
x
Z
nazywamy liczbę rzeczywistą
2
2
df
y
x
Z
r
. Ponieważ
2
2
2
2
2
y
x
y
i
x
iy)
(x
iy
x
Z
Z
to stąd mamy
Z
Z
Z
.
Argumentem liczby zespolonej
0
iy
x
Z
nazywamy każdą liczbę rzeczywistą
spełniającą układ równań .
Postać trygonometryczna:
isin
cos
r
r
y
i
r
x
r
y
x
y
i
y
x
x
y
x
iy
x
Z
2
2
2
2
2
2
.
Twierdzenie (wzór Moivrea): Dla dowolnej liczby zespolonej danej w postaci trygonometrycznej
isin
cos
r
Z
i dowolnej liczny naturalnej
N
n
zachodzi wzór:
n
isin
n
cos
r
Z
n
n
.
2.
Definicja pierwiastka liczby zespolonej. Twierdzenie o pierwiastkowaniu liczby zespolonej. Znaleźć pierwiastki np.
3
i .
Pierwiastkiem n-tego stopnia liczby zespolonej
C
Z
nazywamy każdą liczbę zespoloną W taką, że
Z
W
n
.
Zbiór wszystkich pierwiastków n-tego stopnia liczby zespolonej Z oznaczamy przez
n
Z
.
Twierdzenie (o pierwiastkach liczby zespolonej) Każda liczba zespolona Z różna od 0 ma dokładnie n różnych pierwiastków n-tego stopnia w zbiorze liczb zespolonych C.
Gdy liczbę zespoloną Z przedstawiamy w postaci trygonometrycznej
isin
cos
r
Z
, to tymi pierwiastkami są liczby zespolone postaci
)
n
2kΠ
isin
n
2kΠ
(cos
r
W
n
k
dla
1
n
...,
2,
1,
0,
k
.
3.
Twierdzenie podstawowe algebry i własność wielomianu zespolonego i współczynnikach rzeczywistych. Znaleźć rozkład wielomianu na czynniki (przykład).
Twierdzenie (podstawowe twierdzenie algebry) Każdy wielomian zespolony
0
1
1)
(n
1)
(n
n
n
n
a
Z
a
...
Z
a
Z
a
Z
W
, dla
C
Z
, stopnia
1
n
, ma w zbiorze liczb zespol. dokładnie n miejsc zerowych.
Twierdzenie (własność wielomianu o współczynnikach rzeczywistych) Jeśli wielomian n-tego stopnia
0
1
1)
(n
1)
(n
n
n
n
a
Z
a
...
Z
a
Z
a
Z
W
, dla
C
Z
ma współczynniki rzeczywiste
R
a
,
a
,...,
a
,
a
0
1
1
n
n
oraz liczna zespolona
C
Z
0
jest miejscem zerowym tego wielomianu
0
Z
W
0
n
, to również liczba
C
Z
0
jest miejscem zerowym tego wielomianu
0
Z
W
0
n
4.
Definicja wyznacznika macierzy. Własności wyznaczników. Obliczyć wyznacznik macierzy…
Wyznacznikiem macierzy kwadratowej n-tego stopnia
ij
mxn
A
a
nazywamy liczbę
A
, określoną rekurencyjnie (rozwinięcie wyznacznika dla pierwszego wiersza).
Dla
1
n
,
11
df
11
a
a
A
; Dla
2
n
, ,
gdzie
ij
A
jest podmacierzą macierzy A,
powstałą przez skreślenie w niej i-tego wiersza i j-tej
kolumny.
Własności wyznaczników:
1) Wyznacznik macierzy zawierającej wiersze (kolumny) złożone z samych 0, jest równy 0;
2) Wyznacznik macierzy zawierającej dwa wiersze
(kolumny) proporcjonalne jest równy 0;
3) Wyznacznik macierzy trójkątnej jest równy iloczynowi elementów głównej przekątnej;
4) Zmiana dwóch wierszy (kolumn) macierzy zmienia znak wyznacznika;
5) Wspólny czynnik z wiersza (kolumny) macierzy można wynieść przed wyznacznik;
6) Wyznacznik macierzy nie ulegnie zmiany, gdy do pewnego wiersza (kolumny) macierzy dodamy inny wiersz (kolumnę) pomnożony przez liczbę.
5.
Definicja macierzy odwrotnej. Metoda wyznaczania macierzy odwrotnej. Znaleźć macierz odwrotną macierzy…
Macierzą odwrotną macierzy kwadratowej A nazywamy macierz kwadratową
1
A
taką, że
I
A
A
A
A
1
1
(macierz jednostkowa). Gdy macierz A jest nieosobliwa, co oznacza, że wyznacznik
0
A
, to jest odwracalna. Gdy macierz A jest osobliwa, co oznacza, że wyznacznik
0
A
, to nie jest odwracalna.
Procedura odwracania macierzy:
1) Obliczany wyznacznik macierzy i niech
0
A
; 2) Wyznaczamy macierz dopełnień macierzy A, taką, że
ij
j
i
d
A
1
A
;
3) Wyznaczamy macierz dołączoną macierzy A ze wzoru
T
d
D
A
A
; 4) Macierz odwrotną macierzy A wyznaczamy ze wzoru
D
1
A
A
1
A
.
1n
1n
n
1
12
12
2
1
11
11
1
1
df
nn
n2
n1
2n
22
21
1n
12
11
A
a
1
...
A
a
1
A
a
1
a
a
a
a
a
a
a
a
a
A
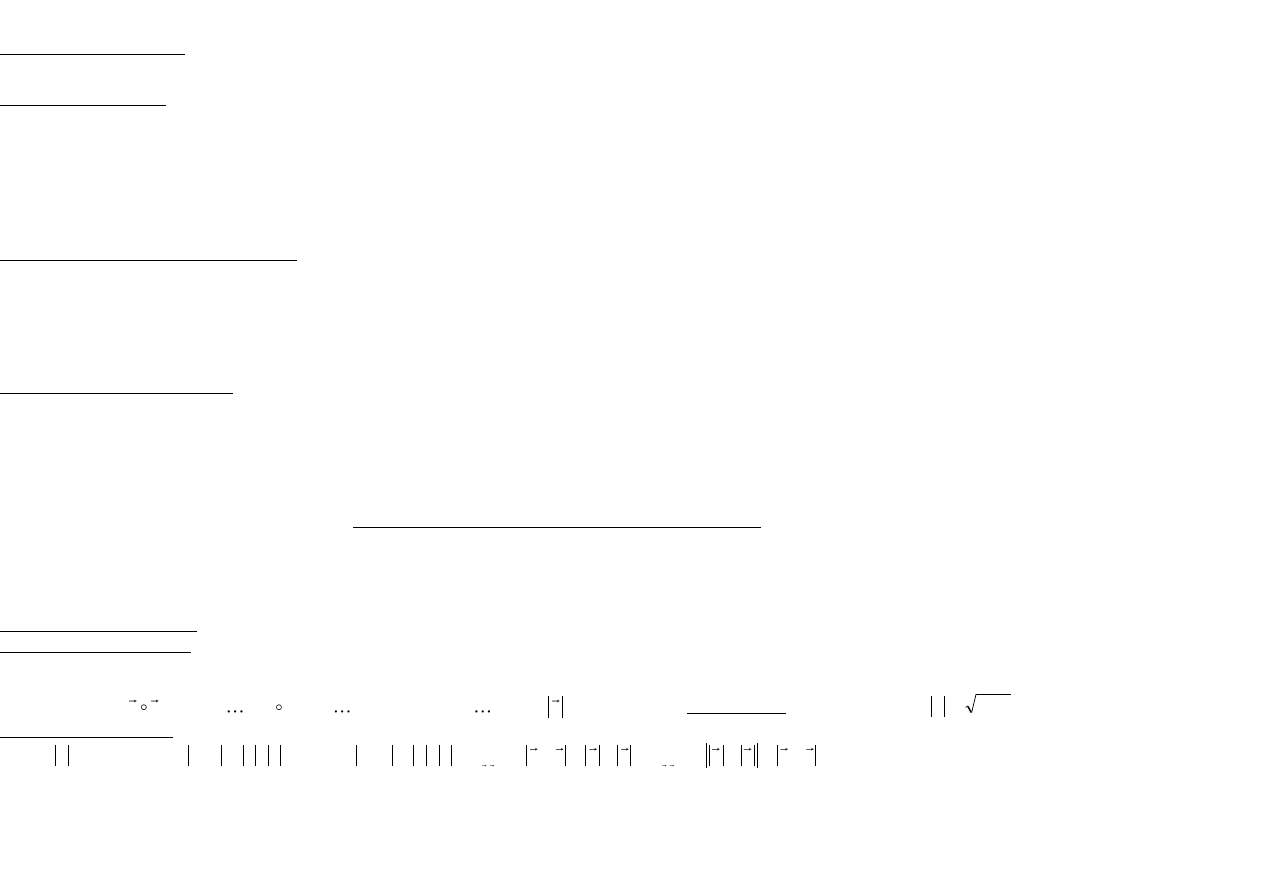
Strona 2 z 6
6.
Definicja rządu macierzy. Własności rządu macierzy. Korzystając z własności obliczyć rząd macierzy…
Rządem macierzy prostokątnej
n
m
ij
a
A
nazywamy największy stopień podmacierzy kwadratowej macierzy o
wyznaczniku różnym od 0. Rząd macierzy A będziemy oznaczać przez
A
r
. Liczba ta spełnia nierówność
n
m,
min
A
r
0
.
Własności rządu macierzy: Rząd macierzy nie ulegnie zmianie, gdy…
1) usuniemy z macierzy wiersz (kolumną) złożony z samych 0; 2) usuniemy z macierzy jeden z dwóch wierzy (kolumn) proporcjonalnych;
3) dwa wiersze (kolumny) macierzy zamienimy miejscami;4) pomnożymy wiersz (kolumnę) macierzy przez liczbę różną od 0;
5) do pierwszego wiersza (kolumny) macierzy dodamy inny wiersz (kolumnę) pomnożony przez liczbę.
Powyższe własności nazywamy przekształceniami elementarnymi dokonywanymi na wierszach (kolumnach) macierzy.
Wykonując przekształcenia elementarne na wierszach (kolumnach) macierzy każdą macierz można sprowadzić do równoważnej macierzy
bazowej, która zawiera maksymalną liczbę różnych jednostkowych wektorów kolumnowych. Liczba tych wektorów jest równa rządowi macierzy.
7.
Definicja ogólnego układu równań liniowych. Twierdzenie Kroneckera-Capelliego. Zbadać rozwiązalność układu równań liniowych…
Układem m równań liniowych o n niewiadomych nazywamy układ równań postaci:
gdzie
R
a
ij
i
R
b
i
dla
m
1,2,...,
i
;
n
1,2,...,
j
są ustalonymi liczbami rzeczywistymi.
Jeśli
0
b
i
dla
m
1,2,...,
i
to układ równań nazywamy jednorodnym, a w przeciwnym wypadku niejednorodnym.
Rozwiązaniem szczególnym układu równań liniowych
nazywamy zbiór liczb
n
3
2
z
xˆ
,...,
xˆ
,
xˆ
,
xˆ
spełniające każde
równanie układu.
Zbiór wszystkich rozwiązań szczególnych nazywamy rozwiązaniem ogólnym.
Twierdzenie (Kroneckera-Capelliego):
Układ m równań liniowych o n niewiadomych…
1) ma dokładnie jedno rozwiązanie (jest on oznaczony) wtedy i tylko wtedy, gdy
r
B
r
A
r
i
n
r
;
2) ma nieskończenie wiele rozwiązań (jest nieoznaczony) wtedy i tylko wtedy, gdy
r
B
r
A
r
i
n
r
;
3) nie ma rozwiązań (jest sprzeczny) wtedy i tylko wtedy, gdy
B
r
A
r
8.
Definicja działań na wektorach. Definicja i własności iloczynu skalarnego wektorów. Długość wektora i jego własności.
Zbiór
n
R
wektorów swobodnych, w którym są określone działania dodawania i mnożenia wektorów przez liczny rzeczywiste następująco:
n
n
2
2
1
1
df
n
2
1
n
2
1
v
u
,
,
v
u
,
v
u
v
,
,
v
,
v
u
,
,
u
,
u
v
u
n
2
1
df
n
2
1
u
α
,
,
u
α
,
u
α
u
,
,
u
,
u
α
u
α
, jest n-wymiarową przestrzenią wektorową, którą nazywamy n-wymiarową przestrzenią kartezjańską wektorową.
Iloczynem skalarnym wektorów
n
2
1
u
,
,
u
,
u
u
i
n
n
2
1
R
v
,
,
v
,
v
v
nazywamy liczbę:
n
n
2
2
1
1
df
v
u
v
u
v
u
v
u
.
Własności iloczynu skalarnego:
1)
0
u
u
n
R
u
; 2)
u
v
v
u
n
R
v
,
u
; 3)
v
u
α
v
u
α
n
R
v
,
u
R
α
; 4)
w
v
w
u
w
v
u
w
,
v
,
u
.
Łatwo zauważyć, że
2
2
2
2
1
2
n
1
2
n
1
2
n
u u
u ,u ,
,u
u ,u ,
,u
u
u
u
u
, a stąd wynika, że długość wektora
u
wyraża się wzorem
u
u
u
.
Własności długości wektora:
1)
0
u
n
R
u
; 2)
u
α
u
α
n
R
u
R
α
; 3)
v
u
v
u
n
R
v
,
u
; 4)
n
u,v, R
u
v
u
v
; 5)
n
u,v, R
u
v
u
v
;
n
1
1
n
nn
n
2n
n
1n
2
n2
2
22
2
12
1
n1
1
21
1
11
b
b
b
x
a
x
a
x
a
x
a
x
a
x
a
x
a
x
a
x
a
Strona 3 z 6
1
2
2
1
3
1
1
3
2
3
3
2
2
1
2
1
3
3
1
3
1
2
3
2
3
2
1
3
2
1
3
2
1
3
2
1
v
u
v
u
,
v
u
v
u
,
u
v
v
u
v
v
u
u
i
v
v
u
u
i
v
v
u
u
i
v
v
v
u
u
u
i
i
i
v
u
9.
Definicje wektorów równoległych, prostopadłych, kąta między wektorami i pola trójkąta. Obliczyć kąt w trójkącie…
Mówimy, że wektory
u
i
n
R
v
są równoległe, co zapisujemy
u
λ
v
v
||
u
0
λ
df
.
Gdy
0
λ
to mówimy, że wektory mają zgodne zwroty. Gdy
0
λ
to mówimy, że wektory mają zwroty przeciwne.
Mówimy, że wektory
u
i
n
R
v
są prostopadłe (ortogonalne), co zapisujemy
0
v
u
v
u
df
.
Kątem pomiędzy niezerowymi wektorami
u
i
n
R
v
nazywamy liczbę
Π
0,
v
,
u
taką, że
v
u
v
u
v
,
u
cos
.
Polem trójkąta rozpiętego na wektorach
u
i
n
R
v
nazywamy liczbę
v
,
u
sin
v
u
2
1
v
,
u
S
df
.
10.
Definicja iloczynu wektorowego wektorów, interpretacja geometryczna. Metoda obliczania i własności. Obl pole trójk o wierzch…
Iloczynem wektorowym wektorów nierównoległych
u
i
3
R
v
nazywamy wektor
3
R
v
u
, o własnościach:
1) Kierunek: Wektor
v
u
jest prostopadły do wektorów
u
i
v
; 2) Długość:
v
,
u
S
2
v
u
- dwa pola trójkąta; 3) Zwrot: Orientacja
0
v
u
,
v
,
u
.
Gdy wektory
u
i
v
są równoległe to przyjmujemy
0
v
u
.
Interpretacja geometryczna iloczynu wektorowego:(DOPISAC)
Twierdzenie (o wyznaczniku iloczynu wektorowego wektorów)
Iloczyn wektorowy wektorów
3
2
1
u
,
u
,
u
u
i
3
3
2
1
R
v
,
v
,
v
v
jest określony wzorem:
Własności iloczynu wektorowego: 1)
u
v
v
u
3
R
v
,
u
; 2)
v
u
α
v
u
α
3
R
v
,
u
R
α
; 3)
w
v
w
u
w
v
u
3
R
w
,
v
,
u
;
11.
Definicja płaszczyzny w przestrzeni R
3
. Postać parametryczna i kanoniczna płaszczyzny. Znaleźć równanie płaszczyzny…
Płaszczyzna w przestrzeni
3
R
przechodząca przez ustalony punkt
30
20
10
0
x
,
x
,
x
x
należący do przestrzeni
3
R
oraz równoległa do ustalonych
nierównoległych wektorów
3
2
1
u
,
u
,
u
u
i
3
3
2
1
R
v
,
v
,
v
v
nazywamy zbiór punktów
3
R
H
taki, że
s
v
t
u
x
x
H
x
0
dla
R
s
t,
.
Zapisując punkty i wektory we współrzędnych otrzymamy opis parametryczny płaszczyzny:
s
v
t
u
x
x
s
v
t
u
x
x
s
v
t
u
x
x
:
H
3
3
30
3
2
2
20
2
1
1
10
1
dla
R
s
t,
.
Eliminując z opisu parametrycznego płaszczyzny parametry t i s otrzymamy postać kanoniczną płaszczyzny
0
x
x
w
x
x
w
x
x
w
:
H
30
3
3
20
2
2
10
1
1
,
gdzie wektor
3
3
2
1
R
w
,
w
,
w
w
jest niezerowy i prostopadły do płaszczyzny H, a więc
w
u v
.
Strona 4 z 6
12.
Podać wzory na odległość punktu od płaszczyzny danej w postaci parametrycznej lub kanonicznej z objaśnieniami. Znaleźć odległość punktu od płaszcz
Wzór na odległość punktu
3
0
R
y
od płaszczyzny określonej parametrycznie
s
v
t
u
x
x
s
v
t
u
x
x
s
v
t
u
x
x
:
H
3
3
30
3
2
2
20
2
1
1
10
1
lub kanonicznie
0
x
x
w
x
x
w
x
x
w
:
H
30
3
3
20
2
2
10
1
1
, zawierającej punkt
H
x
,
x
,
x
x
30
20
10
0
i równoległej do nierównoległych wektorów
H
||
u
,
u
,
u
u
3
2
1
i
H
||
v
,
v
,
v
v
3
2
1
oraz prostopadłej do wektora
H
w
,
w
,
w
w
3
2
1
, jest postaci:
w
p
w
H
,
y
d
0
, gdzie:
p
- wektor o początku w punkcie
0
x
i końcu w punkcie
0
y
.
By z równania postaci parametrycznej otrzymać wektor
w
należy pomnożyć wektorowo wektory
u
i
v
. Wtedy wzór ten jest postaci: .
13.
Definicja prostej w przestrzeni R
3
. Postać parametryczna, kierunkowa i krawędziowa. Znaleźć prostą w tych postaciach…
Prostą w przestrzeni
3
R
, przechodzącą przez ustalony punkt
3
30
20
10
0
R
x
,
x
,
x
x
i równoległą do niezerowego ustalonego wektora
3
3
2
1
R
u
,
u
,
u
u
nazywamy zbiór punktów
3
R
L
, taki, że:
t
u
x
x
L
x
0
df
, dla
R
t
.
Zapisując punkty i wektory we współrzędnych, otrzymamy opis parametryczny prostej: , dla
R
t
.
Eliminując z powyższego układu równań parametr t przy założeniach, że
0
u
i
0
u
i
0
u
3
2
1
, otrzymamy postać kierunkową:
3
30
3
2
20
2
1
10
1
u
x
x
u
x
x
u
x
x
:
L
.
Dwie nierównoległe płaszczyzny wyznaczają prostą. Postać tę nazywamy postacią krawędziową prostej: .
14.
Podać wzory na odległość prostych równoległych oraz prostych skośnych. Znaleźć odległość między prostymi
2
x
1
1
x
2
2
x
:
L
3
2
1
1
i
0
1
x
x
x
0
2
x
2x
x
:
L
3
2
1
3
2
1
2
.
Wzór na odległość prostych równoległych
u
L
i
v
L
, przechodzących przez punkty
u
0
L
x
i
v
0
L
y
oraz równoległych do wektora
v
u
L
||
L
||
u
jest postaci:
, gdzie
p
- wektor o początku w punkcie
0
x
i końcu w punkcie
0
y
.
Wzór na odległość prostych skośnych
u
L i
v
L , przechodzących przez punkty
u
0
L
x
i
v
0
L
y
oraz równoległych do wektora
u
L
||
u
i
v
L
||
v
jest postaci:
v
u
p
v
u
L
,
L
d
v
u
,
gdzie
p
- wektor o początku w punkcie
0
x
i końcu w punkcie
0
y
.
15.
Podać definicję ciągu liczbowego oraz definicje ciągu monotonicznego i ograniczonego. Zbadać monotoniczność i ograniczoność ciągu…
Ciągiem liczbowym nieskończonym nazywamy funkcję przyporządkowującą każdej liczbie naturalnej
N
n
dokładnie jedną liczbę rzeczywistą
R
a
n
.
Ciąg
n
a
nazywamy: a) monotonicznie rosnącym
n
1
n
N
n
df
a
a
; b) monotonicznie niemalejącym
n
1
n
N
n
df
a
a
; c) monotonicznie malejącym
n
1
n
N
n
df
a
a
;
d) monotonicznie nierosnącym
n
1
n
N
n
df
a
a
.
Ciąg
n
a
jest: a) ograniczony z góry
M
a
n
N
n
N
M
df
; b) ograniczony z dołu
m
a
n
N
n
N
m
df
; c) ograniczony
gdy jest ograniczony z góry lub z dołu.
t
u
x
x
t
u
x
x
t
u
x
x
:
L
3
30
3
2
20
2
1
10
1
0
v
x
v
x
v
x
v
0
u
x
u
x
u
x
u
:
L
0
3
3
2
2
1
1
0
3
3
2
2
1
1
u
p
u
L
,
Y
d
L
,
L
d
u
0
v
u
v
u
p
v
u
H
,
y
d
0
Strona 5 z 6
16.
Podać definicję granicy ciągu oraz wykazać z definicji, że
2
3
1
2
lim
n
n
n
. Podać własności ciągów zbieżnych.
Granicą ciągu liczbowego
n
a
nazywamy liczbę g, co zapisujemy
ε
g
a
ε
g
ε
g
a
g
a
lim
n
n
δ
n
0
δ
0
ε
df
n
n
.
Własności ciągów zbieżnych:
1) Ciąg zbieżny ma tylko jedną granicę; 2) Ciąg zbieżny jest ograniczony;
3) Każdy ciąg częściowy (podciąg), wybrany z ciągu zbieżnego, jest zbieżny do tej samej granicy, co ciąg;
4) Gdy ciąg zawiera dwa podciągi zbieżne do różnych granic to jest rozbieżny;
5) Ciąg ograniczony z góry (z dołu) i monotonicznie rosnący (malejący) jest zbieżny do kresu górnego (dolnego).
17.
Definicja funkcji różnowartościowej, na zbiór i odwrotnej. Funkcje odwrotne do funkcji trygonometrycznych (rys).
Funkcję
Y
X
:
f
nazywamy: a) różnowartościową
2
1
2
1
X
x
,
x
df
x
f
x
f
x
x
2
1
; b) na (zbiór Y)
Y
x
f
X
x
,
x
df
2
1
; c) wzajemnie jednoznaczną
df
gdy jest różnowartościowa i jest na
Funkcją odwrotną do funkcji wzajemnie jednoznacznej
Y
X
:
f
nazywamy funkcję
X
Y
:
f
1
taką, że
y
x
f
x
y
f
df
1
.
Funkcje odwrotne do funkcji trygonometrycznych: a) Funkcja odwrotna do funkcji
1,1
2
Π
,
2
Π
:
sin
to funkcja
2
Π
,
2
Π
1,1
:
arcsin
.
x
y
sin
y
x
arcsin
df
b) Funkcja odwrotna do funkcji
cos: 0,Π
1,1
to funkcja
arccos:
1;1
0,Π
.
x
y
cos
y
x
arccos
df
c) Funkcja odwrotna do funkcji
tg:
;
R
2
2
to funkcja
2
Π
,
2
Π
R
:
arctg
.
x
y
tg
y
x
arctg
df
d) Funkcja odwrotna do funkcji
R
Π
0,
:
ctg
to funkcja
Π
0,
R
:
arcctg
.
x
y
ctg
y
x
arcctg
df
18.
Funkcje hiperboliczne i funkcje do nich odwrotne (rys). Funkcję
R
R
:
sh
określoną wzorem
x
x
df
e
e
2
1
x
sh
nazywamy sinusem hiperbolicznym. Funkcję do niej odwrotną
oznaczamy i określamy następująco:
R
R
:
arsh
.
x
y
sh
y
x
arsh
df
Funkcję
R
R
:
ch
określoną wzorem
x
x
df
e
e
2
1
x
ch
nazywamy cosinusem hiperbolicznym. Funkcja ta jest
parzysta i nie jest wzajemnie jednoznaczna, a więc nie istnieje do niej funkcja odwrotna. Natomiast do funkcji
,
1
,
0
:
ch
istnieje funkcja odwrotna, którą oznaczamy i określamy następująco:
,
0
,
1
:
arch
.
x
y
ch
y
x
arch
df
Funkcję
1,1
R
:
th
określoną wzorem
x
x
x
x
df
e
e
e
e
x
th
nazywamy tangensem hiperbolicznym. Funkcja ta jest nieparzysta, rosnąca,
ograniczona i wzajemnie jednoznaczna. Funkcję do niej odwrotną oznaczamy i określamy następująco:
R
1,1
:
arth
.
x
y
th
y
x
arth
df
Funkcję
1,1
R
0
R
:
cth
określoną
wzorem
x
x
x
x
df
e
e
e
e
x
cth
nazywamy cotangensem hiperbolicznym. Funkcja ta jest nieparzysta, przedziałami malejąca i wzajemnie jednoznaczna. Funkcję do niej odwrotną oznaczamy i określamy
następująco:
0
R
1,1
R
:
arcth
.
Y
zbiór
x
y
cth
y
x
arcth
df
Strona 6 z 6
19.
Definicja granicy funkcji w sensie Heinego. Obliczyć z definicji granicę. Def. Heinego: Mówimy, że funkcja f ma w punkcie skupienia
0
x
dziedziny D granicę równą g, co zapisujemy
g
x
f
lim
x
x
lim
x
D
x
g
x
f
lim
n
n
0
n
n
0
n
x
df
x
x
n
0
. Definicja Heinego obejmuje 9 przypadków.
20.
Definicja ciągłości funkcji. Własności funkcji ciągłych. Zbadać ciągłość funkcji (przykład). Mówimy, że funkcja f jest w punkcie skupienia
D
x
0
ciągła wtedy i tylko wtedy, gdy
0
x
x
x
f
x
f
lim
0
. Mówimy, że funkcja f jest w punkcie skupienia
D
x
0
: a) lewostronnie ciągła
df
gdy
0
x
x
x
f
x
f
lim
0
; b) prawostronnie ciągła
df
gdy
0
x
x
x
f
x
f
lim
0
.
Funkcja f jest ciągła w punkcie
D
x
0
wtedy i tylko wtedy, gdy jest ciągła lewostronnie i prawostronnie w punkcie
0
x .
Elementarne własności funkcji ciągłych:1) Suma, różnica, iloraz, iloczyn funkcji ciągłych jest funkcją ciągłą; 2) Złożenie funkcji ciągłych jest funkcją ciągłą;3) Funkcja odwrotna do funkcji ciągłej jest funkcją
ciągłą.
21.
Definicje asymptot pionowych, poziomych i ukośnych funkcji. Twierdzenie o asymptocie ukośnej.
Prostą o równaniu y=b nazywamy asymptotą poziomą funkcji f -∞ do +∞ gdy funkcja jest określona w sąsiedztwie (-∞;+∞) i
lim
( )
x
f x
b
Prostą o równaniu x=x0 nazywamy asymptotą pionową lewostronna(prawostronną) funkcji f w punkcie x0 gdy funkcja jest określona w lewostronnym (prawostronnym) sąsiedztwie punktu xo oraz
0
lim
( )
/
x
x
f x
0
(lim
( )
/
)
x
f x
Prosta o równaniu y=ax+b nazywamy asymptotą ukośną funkcji f w (-∞;+∞) gdy funkcja jest określona w sąsiedztwie
(-∞;+∞) oraz
lim [ ( ) (
)]
0
x
f x
ax b
(
lim [ ( ) (
)]
0
x
f x
ax b
)
Tw (o asymptocie ukośnej) Prosta o równaniu y=ax+b jest asymptotą ukośną funkcji f w (-∞;+∞) wtedy i tylko wtady gdy istnieją granice skończone takie że
lim
( ) /
x
a
f x
x
;
lim [ ( )
]
x
b
f x
ax