MATEMATYKA UBEZPIECZEŃ ŻYCIOWYCH

ANALIZA SKŁADKI POBIERANEJ PRZEZ NIEKTÓRE

TOWARZYSTWA UBEZPIECZEŃ.

Autor

Piotr Chrzan

SPIS TREŚCI

WSTĘP

I. POLSKIE TABLICE TRWANIA ŻYCIA

1.1.

PODSTAWOWE PARAMETRY TABLIC TRWANIA ŻYCIA

1.2.

ROZKŁAD PRAWDOPODOBIEŃSTWA DALSZEGO TRWANIA ŻYCIA

II. UBEZPIECZENIA ŻYCIOWE

2.1.

DOŻYWOTNIE UBEZPIECZENIA NA WYPADEK ŚMIERCI

2.2.

TERMINOWE UBEZPIECZENIE NA WYPADEK ŚMIERCI

2.3.

UBEZPIECZENIE NA DOŻYCIE

2.4.

UBEZPIECZENIE NA ŻYCIE I DOŻYCIE

2.5.

ODROCZONE DOŻYWOTNIE UBEZPIECZENIA NA WYPADEK ŚMIERCI

2.6.

SUMA UBEZPIECZENIA PŁATNA W MOMECIE ŚMIERCI UBEZPIE-

CZONEGO

III. RENTY ŻYCIOWE

3.1.

RENTA ŻYCIOWA DOŻYWOTNIA PŁATNA NATYCHMIAST

3.2.

RENTA ŻYCIOWA TERMINOWA PŁATNA PRZEZ N LAT

3.3.

ODROCZONA RENTA ŻYCIOWA DOŻYWOTNIA

3.4.

SKŁADKA PŁATNA ROCZNIE

IV. ANALIZA SKŁADKI POBIERANEJ PRZEZ NIEKTÓRE TOWA-

RZYSTWA UBEZPIECZEŃ NA ŻYCIE

4.1.

ANALIZA SKŁADKI DOŻYWOTNIEGO UBEZPIECZENIA NA WYPADEK

ŚMIERCI

4.2.

ANALIZA SKŁADKI TERMINOWEGO UBEZPIECZENIA NA WYPADEK

ŚMIERCI

4.3.

ANALIZA SKŁADKI UBEZPIECZENIA NA ŻYCIE I DOŻYCIE

4.4.

ZAKOŃCZENIE

LITERATURA
DODATEK A -

RENTY PEWNE

DODATEK B -

TABLICE FUNKCJI KAPITALIZACJI ZŁOŻONEJ

DODATEK C -

TABLICE LICZB KOMUTACYJNYCH

2

WSTĘP

Od trzech lat można zauważyć wśród Polaków wzrost zainteresowania ubezpiecze-

niami na życie. Obecnie na polskim rynku działa 21 firm ubezpieczeń życiowych. Firmy

te z roku na rok odnotowują znaczny wzrost dochodów z tytułu sprzedaży polis ubezpie-

czeniowych. Eksperci przewidują, że do końca 1999 roku w Polsce działać będzie ponad

50 firm ubezpieczeń na życie.

Wzrastająca liczba firm ubezpieczeniowych oraz wzrastająca liczba oferowanych

przez te firmy produktów powoduje wzrost zapotrzebowania na wiedzę, która pozwoli

indywidualnemu lub zespołowemu decydentowi wybrać w "optymalny" sposób rodzaj

ubezpieczenia oraz oferującą go firmę.

Na przeciw tym zapotrzebowaniom wychodzi niniejsze opracowanie, w którym

przedstawiono podstawowe metody wyznaczania wysokości składek ubezpieczeniowych.

W rozdziale pierwszym przedstawiono najważniejsze informacje zawarte w Pol-

skich Tablicach Trwania Życia oraz podano przykłady rozkładów prawdopodobieństwa

dalszego trwania życia.

Teoretyczne podstawy wyznaczania wysokości jednorazowych składek dla najważ-

niejszych rodzajów ubezpieczeń życiowych przedstawiono w rozdziale drugim. Rozważa-

nia teoretyczne poparto przykładami.

W rozdziale trzecim przedstawiono zasady wyznaczania wartości początkowej rent

życiowych oraz składek rocznych ubezpieczeń życiowych.

Rozdział czwarty ma charakter opracowania typu "Analiza Przypadków" (Case Stu-

dy). W rozdziale tym, na podstawie rozważań teoretycznych przedstawionych w rozdziale

drugim i trzecim, przeprowadzono analizę składek pobieranych przez towarzystwa ubez-

pieczeń: Powszechny Zakład Ubezpieczeń na Życie - PZU Życie S.A., Pierwsze Amery-

kańsko-Polskie Towarzystwo Ubezpieczeń na Życie i Reasekuracji - Amplico Life S.A.,

Towarzystwo Ubezpieczeń na Życie (Polska) - Commercial Union S.A. , Towarzystwo

Ubezpieczeń na Życie -Warta Vita S.A.

Niniejsza praca powinna zainteresować agentów i doradców ubezpieczeniowych,

którzy chcieliby zrozumieć zasady wyznaczania cen na produkty, które oferują klientom

oraz studentów akademii ekonomicznych, którzy chcieliby w przyszłości pracować w fir-

mach ubezpieczeniowych

3

I. POLSKIE TABLICE TRWANIA ŻYCIA

Pierwsze przedwojenne "Polskie Tablice Trwania Życia"

1

opracował Główny Urząd

Statystyczny na podstawie danych o liczbie zgonów zarejestrowanych w latach 1952-1953.

Od tego czasu w odstępach pięcioletnich publikowane są tablice tego typu. Ostatnie tablice

2

zostały opracowane na podstawie danych z lat 1990-1991 i opublikowane w 1993 roku.

Polskie Tablice Trwania Życia są niezbędnym narzędziem pracy demografów , socjologów

i aktuariuszy. pozwalają one na dokonywanie różnego typu analiz dotyczących umieralno-

ści i zdrowotności społeczeństwa oraz na sporządzanie prognoz demograficznych.

Wszystkie obliczenia w niniejszym opracowaniu przeprowadzono na podstawie Pol-

skich Tablic Trwania Życia 1990-1991

2

. W pierwszym rozdziale opracowania przedsta-

wiono najważniejsze informacje zawarte w tych tablicach oraz podano przykłady ilustrują-

ce rozkłady prawdopodobieństwa zmiennych losowych opisujących dalsze trwanie życia.

1

Zasępa R.,Polskie Tablice Wymieralności 1952-1953; Przegląd Statystyczny 4/1956

2

Mijakowska Jadwiga,Polskie Tablice Trwania Życia 1990-1991, GUS Warszawa 1993

4

1.1. PODSTAWOWE PARAMETRY TABLIC TRWANIA ŻYCIA

Przedmiotem

badań aktuariuszy są między innymi zmiany w czasie liczebności wy-

branych populacji losowych. Celem tych badań jest określenie liczby jednostek opuszcza-

jących daną populację. Fakt opuszczenia populacji może być interpretowany jako śmierć

danej jednostki . Jeżeli przez X oznaczymy zmienną losową wyznaczającą czas życia ele-

mentu populacji (czas bycia elementem populacji ) mierzonych w pełnych jednostkach

czasu (np. lata, półrocza, kwartały, miesiące), to gromadząc odpowiedni materiał staty-

styczny można w sposób empiryczny (statystyczny) wyznaczyć rozkład zmiennej losowej

X. Rozkład ten można wyznaczyć na wiele sposobów, w praktyce aktuarialnej preferuje

się jednak podejście, które pozwala określić rozkład prawdopodobieństwa czasu trwania

życia (element populacji) przez podanie pewnych prawdopodobieństw warunkowych.

Niech

q

ob X x

X

x

=

x

< +

≥

Pr

(

)

1

(1.1)

gdzie: X - zmienna losowa określająca czas trwania życia elementu populacji

x - wiek elementu populacji

x= 0,1,2 .... w

Prawdopodobieństwa q

x

są prawdopodobieństwami zdarzeń, że element populacji, który

dożył wieku x nie przeżyje całego kolejnego okresu (np.roku), tzn. nie osiągnie wieku x+1.

Z

prawdopodobieństw q

x

można bezpośrednio uzyskać inne ważne prawdopodobień-

stwa

p

x

= 1- q

x

(1.2)

gdzie: p

x

- prawdopodobieństwo, że element, który dożył wieku x osiągnie wiek x+1 (prze-

żyje jeszcze co najmniej jeden okres(rok)).

Prawdopodobieństwa

q

x

, p

x

pozwalają z kolei wyznaczyć prawdopodobieństwa

n x

p

ob X n X x

=

+

≥

Pr

(

)

(1.3)

(1.4)

n x

x

x

x n

x j

j

n

p

p p

p

p

=

⋅

=

+

+ −

+

=

−

∏

1

1

0

1

...

⋅

1

p

p

x

x

=

n x

p

- prawdopodobieństwo zdarzenia, że element w wieku x przeżyje jeszcze co najmniej

n okresów (lat), to znaczy dożyje wieku x+n

5

n x

n x

q

P X x n X x

p

=

< +

≥

= −

(

) 1

(1.5)

n x

x x

x x

n

x x n

j x

j

n

x j

q

p q

p q

p q

p q

=

+

+ +

=

+

−

+ −

=

−

+

∑

0

1

1

1

1

0

1

...

(1.6)

1

0

1

q

q

p

x

x

x

=

=

;

gdzie:

- prawdopodobieństwo zdarzenia, że element w wieku x nie przeżyje kolej-

nych n okresów (lat), to znaczy nie dożyje wieku x+n

n x

q

Wyżej wymienione prawdopodobieństwa pozwalają wyznaczyć rozkład bardzo waż-

nej w matematyce aktuarialnej zmiennej losowej Y

x

wyznaczającej dalszy czas trwania

życia elementu populacji w wieku x (osoby w wieku x)

Pr

(

)

ob Y

k

p q

x

k x x k

=

=

+

(1.7)

dla x =0,1,2, . . . , w oraz k=0,1,2, ... w-x

gdzie: Y

0

=X - zmienne losowa określająca czas trwania życia

x - wiek elementu populacji

k - liczba lat życia ponad wiek x

k

x

p

- prawdopodobieństwo, że osoba w wieku x przeżyje jeszcze k lat, tzn. dożyje

wieku x+k

q

x k

+

- prawdopodobieństwo, że osoba w wieku x+k nie przeżyje kolejnego roku,

tzn. nie osiągnie wieku x+k+1

w - maksymalny wiek życia osoby ubezpieczanej ( W Polsce przyjmuje się w=100)

Najważniejsze informacje o zmiennych losowych

Y

x

(X= Y

0

)

dotyczące populacji

Polaków podane są w "Polskich tablicach Trwania Życia"

3

. Tablice te należą do kategorii

tablic bieżących i odzwierciedlają poziom umieralności określonych populacji (ogółem,

mężczyźni, kobiety, miasto, wieś).

Tablice trwania życia opisują hipotetyczne populacje o liczebności początkowej

l

0

=100000 osób i podawane są w nich między innymi informacje o następujących para-

metrach:

l

x

- liczba osób dożywających wieku x (x=0,1,2, ... w=100)

3

Mijakowska J., Polskie Tablice Trwania Życia 1990-1991. Główny Urząd Statystyczny. Warszawa 1993

6

d

x

- liczba osób zmarłych w wieku x

d

x

= l

x

- l

x+1

dla x=0,1,2, ..., w-1

(1.8)

d

w

= l

w

q

x

- prawdopodobieństwo zgonu w ciągu roku osoby x -letniej

d

l

i

i

w

=

∑

=

0

0

q

d

l

x

x

x

=

dla

x=0,1,2,

...,

w

(1.9)

p

x

- prawdopodobieństwo przeżycia roku przez osobę x -letnią

p

q

l

l

x

x

x

x

= −

=

+

1

1

dla x=0,1,2, ..., w-1

(1.10)

p

w

=0

Wyżej zapisane prawdopodobieństwa pozwalają wyznaczyć (por. wzory 1.3 do 1.6)

n x

q

- prawdopodobieństwo, że osoba w wieku x nie osiągnie wieku x+n

n x

x

x

x

q

l

l

l

=

−

+ n

dla x=0,1,2 . . . w; n=0,1,2, ... w-x

(1.11)

n x

p

- prawdopodobieństwo, że osoba w wieku x osiągnie wiek x+n

n x

n x

x n

x

p

q

l

l

= −

=

+

1

dla x=0,1,2 . . . w; n=0,1,2, ... w-x

(1.12)

L

x

- średnia liczba osób dożywających w wieku x

L

l

d

x

x

x

= −

2

(1.13)

L

l

l

x

x

x

=

+

+1

2

(1.14)

T

x

- fundusz czasu jaki mają do przeżycia osoby w wieku x

T

L

l

l

x

x

i x

w

x

x

i x

w

=

=

+

=

−

= +

∑

1

1

2

∑

(1.15)

7

e

x

- przeciętne dalsze trwanie życia dożywających wieku x

e

T

l

x

x

x

=

(1.16)

s

x

- odchylenie standardowe dalszego trwania życia obliczone według wzoru

s

s

p

e

q

p

x

x

x

x

x

x

x

=

+

−

+1

2

(

)

α

2

(1.17)

gdzie:

α =

≥

1
2

5

dla x

Polskie Tablice Trwania Życia 1990-1991 zostały zbudowane na podstawie oszacowania

prawdopodobieństw zgonu q

x.

Pozostałe funkcje tablicowe

l

x

, d

x

, p

x

,L

x

, T

x

, e

x

, oraz S

x

zostały wyznaczone na podstawie wzorów (1.8) - (1.17).

W dodatku C podano fragmenty tablic zawierające informacje o parametrach populacji

Polaków ogółem oraz mężczyzn i kobiet ogółem.

1.2. ROZKŁAD PRAWDOPODOBIEŃSTWA DALSZEGO TRWANIA

ŻYCIA

Z wzorów 1.7 do 1.12 można wyprowadzić następującą zależność dla rozkładu

zmiennej losowej Y

x

- dalszego trwania życia

Pr

(

)

ob Y

k

d

l

x

x k

x

=

=

+

(1.18)

dla x=0,1,2, . ,w oraz k = 0,1,2, . . . w-x.

Korzystając z wzoru 1.13 oraz danych zamieszczonych w dodatku C wyznaczono rozkład

prawdopodobieństwa zmiennej losowej Y

x

dla mężczyzny oraz kobiety w wieku 20 i 40

lat. Wyniki obliczeń zamieszczono w tablicy 1.1.

8

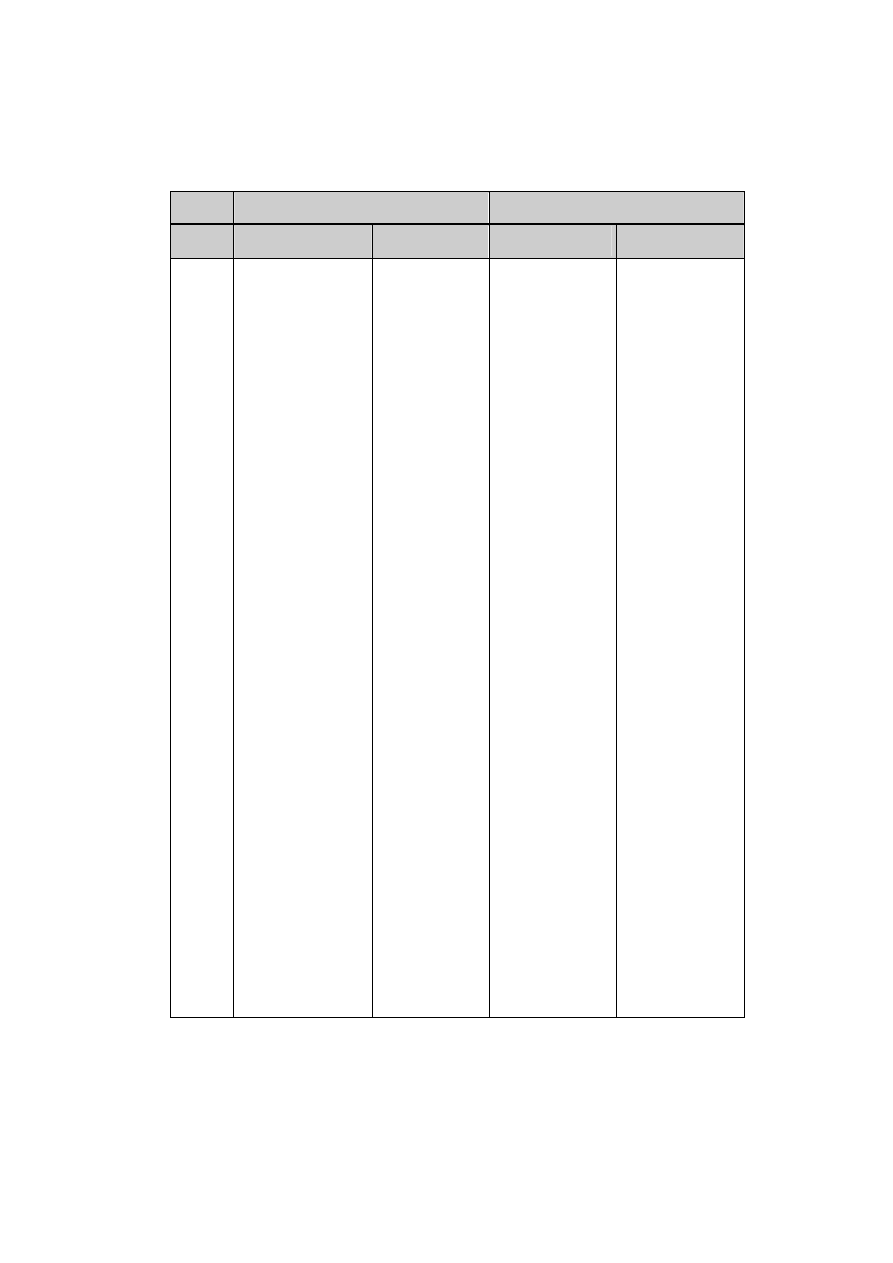
Tablica 1.1 Rozkład prawdopodobieństwa dalszego trwania życia - mężczyzna

Lata

x = 20 lat

x = 40 lat

Prob(Y

x

= k)

Prob(Y

x

≥ k) Prob(Y

x

= k)

Prob(Y

x

≥ k)

0 0,001460 1,000000 0,004951 1,000000
1 0,001635 0,998365 0,005372 0,995049
2 0,001748 0,996904 0,005848 0,989677
3 0,001790 0,995156 0,006410 0,983829
4 0,001769 0,993366 0,007026 0,977419
5 0,001738 0,991597 0,007707 0,970393
6 0,001738 0,989859 0,008388 0,962686
7 0,001769 0,988121 0,009047 0,954298
8 0,001851 0,986352 0,009674 0,945250
9 0,001985 0,984500 0,010269 0,935576

10 0,002129 0,982515 0,010896 0,925307
11 0,002294 0,980386 0,011577 0,914411
12 0,002468 0,978093 0,012323 0,902834
13 0,002664 0,975624 0,013133 0,890512
14 0,002880 0,972960 0,013998 0,877378
15 0,003127 0,970081 0,014895 0,863380
16 0,003394 0,966954 0,015836 0,848485
17 0,003692 0,963560 0,016809 0,832649
18 0,004011 0,959868 0,017857 0,815840
19 0,004351 0,955856 0,018938 0,797983
20 0,004711 0,951506 0,020051 0,779045
21 0,005112 0,946795 0,021176 0,758993
22 0,005564 0,941683 0,022170 0,737818
23 0,006099 0,936119 0,023056 0,715648
24 0,006685 0,930020 0,023867 0,692591
25 0,007333 0,923335 0,024645 0,668724
26 0,007981 0,916002 0,025445 0,644079
27 0,008609 0,908020 0,026245 0,618633
28 0,009205 0,899412 0,027034 0,592388
29 0,009771 0,890207 0,027791 0,565354
30 0,010367 0,880436 0,028483 0,537563
31 0,011015 0,870068 0,029056 0,509080
32 0,011725 0,859053 0,029499 0,480024
33 0,012496 0,847328 0,029780 0,450525
34 0,013319 0,834832 0,029910 0,420745
35 0,014173 0,821512 0,029856 0,390836
36 0,015068 0,807339 0,029629 0,360980
37 0,015993 0,792272 0,029229 0,331352
38 0,016991 0,776278 0,028634 0,302123
39 0,018020 0,759287 0,027845 0,273489
40 0,019079 0,741268 0,026786 0,245644
41 0,020149 0,722189 0,025510 0,218858
42 0,021095 0,702041 0,024040 0,193348
43 0,021938 0,680946 0,022408 0,169308
44 0,022710 0,659008 0,020657 0,146900
45 0,023450 0,636298 0,018830 0,126243

9

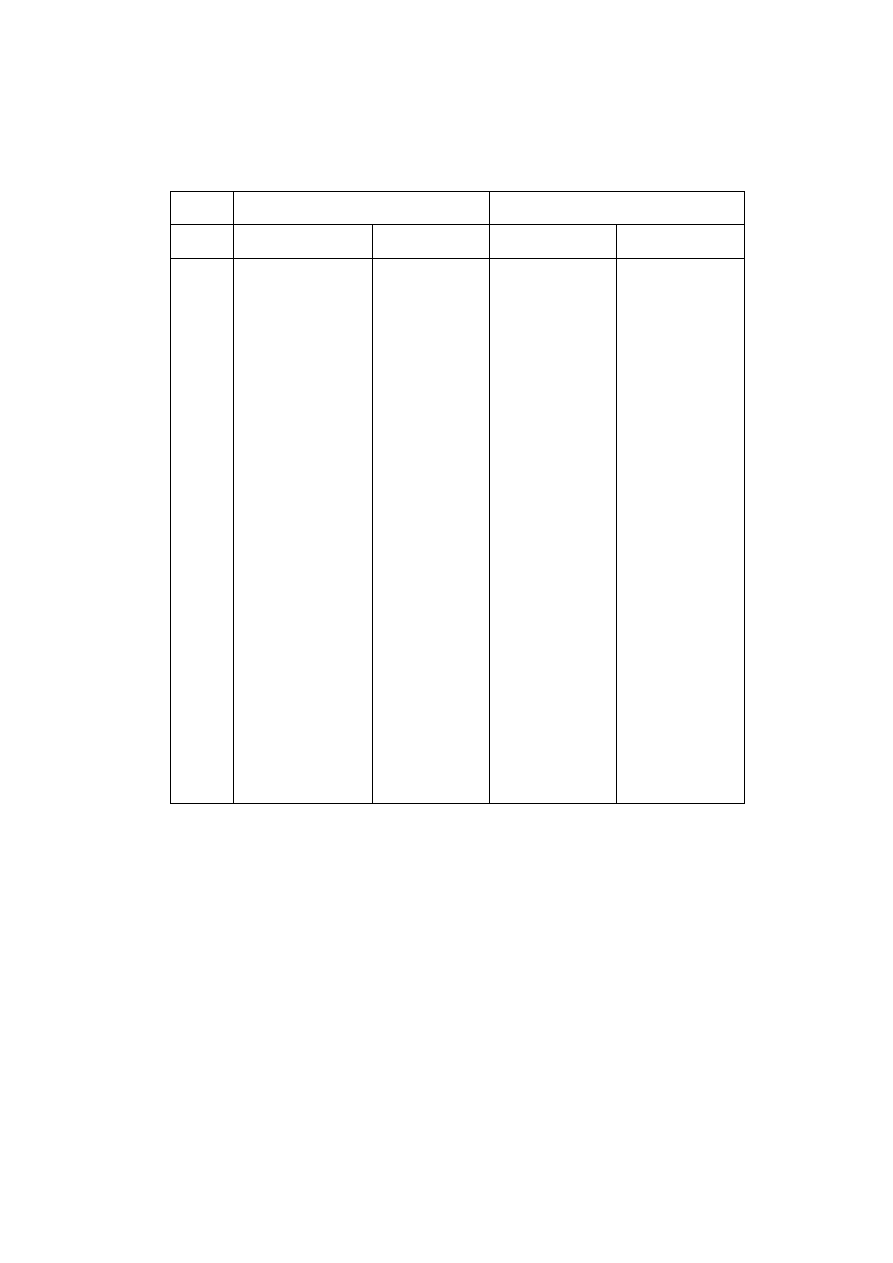
ciąg dalszy tablicy 1.1

Lata

x = 20 lat

x = 40 lat

Prob(Y

x

= k)

Prob(Y

x

≥ k) Prob(Y

x

= k)

Prob(Y

x

≥ k)

46 0,024211 0,612848 0,016971 0,107413
47 0,024972 0,588637 0,015101 0,090442
48 0,025723 0,563665 0,013274 0,075342
49 0,026443 0,537942 0,011523 0,062068
50 0,027101 0,511499 0,009869 0,050545
51 0,027646 0,484397 0,008345 0,040676
52 0,028068 0,456751 0,006961 0,032331
53 0,028335 0,428683 0,005718 0,025370
54 0,028459 0,400348 0,004637 0,019652
55 0,028407 0,371889 0,003708 0,015014
56 0,028191 0,343481 0,002919 0,011307
57 0,027811 0,315290 0,002259 0,008388
58 0,027245 0,287479 0,001719 0,006129
59 0,026494 0,260234 0,001286 0,004410
60 0,025486 0,233739 0,000951 0,003124
61 0,024273 0,208253

62 0,022874 0,183980

63 0,021321 0,161106

64 0,019655 0,139785

65 0,017917 0,120130

66 0,016148 0,102213

67 0,014368 0,086066

68 0,012630 0,071697

69 0,010964 0,059067

70 0,009390 0,048103

71 0,007940 0,038713

72 0,006624 0,030773

73 0,005441 0,024149

74 0,004412 0,018709

75 0,003528 0,014296

78 0,002777 0,010769

79 0,002150 0,007992

80 0,001635 0,005842

10

Tablica 1.2 Rozkład prawdopodobieństwa dalszego trwania życia - kobieta

Lata

x = 20 lat

x = 40 lat

Prob(Y

x

= k)

Prob(Y

x

≥ k) Prob(Y

x

= k)

Prob(Y

x

≥ k)

0 0,000377 1,000000 0,001748 1,000000
1 0,000388 0,998365 0,001935 0,995049
2 0,000388 0,999235 0,002131 0,996317
3 0,000398 0,998848 0,002338 0,994186
4 0,000398 0,998450 0,002566 0,991848
5 0,000418 0,998052 0,002814 0,989282
6 0,000428 0,997634 0,003072 0,986469
7 0,000459 0,997206 0,003310 0,983396
8 0,000489 0,996747 0,003507 0,980086
9 0,000540 0,996257 0,003683 0,976579

10 0,000591 0,995717 0,003879

0,972896

11 0,000653 0,995125 0,004128

0,969016

12 0,000724 0,994473 0,004438

0,964889

13 0,000806 0,993749 0,004821

0,960451

14 0,000897 0,992943 0,005286

0,955630

15 0,000999 0,992046 0,005814

0,950343

16 0,001112 0,991046 0,006393

0,944530

17 0,001244 0,989935 0,006993

0,938136

18 0,001387 0,988691 0,007593

0,931143

19 0,001550 0,987304 0,008224

0,923550

20 0,001723 0,985754 0,008938

0,915325

21 0,001907 0,984030 0,009745

0,906387

22 0,002101 0,982123 0,010645

0,896642

23 0,002305 0,980023 0,011638

0,885997

24 0,002529 0,977718 0,012724

0,874359

25 0,002774 0,975189 0,013925

0,861634

26 0,003029 0,972415 0,015228

0,847710

27 0,003263 0,969386 0,016614

0,832482

28 0,003457 0,966123 0,018073

0,815867

29 0,003630 0,962666 0,019604

0,797794

30 0,003824 0,959036 0,021207

0,778190

31 0,004069 0,955212 0,022873

0,756983

32 0,004375 0,951143 0,024580

0,734110

33 0,004752 0,946768 0,026318

0,709530

34 0,005211 0,942016 0,028035

0,683212

35 0,005731 0,936805 0,029690

0,655177

36 0,006302 0,931074 0,031253

0,625486

37 0,006894 0,924771 0,032660

0,594234

38 0,007485 0,917878 0,033870

0,561574

39 0,008107 0,910393 0,034853

0,527704

40 0,008811 0,902285 0,035515

0,492852

41 0,009606 0,893474 0,035867

0,457337

42 0,010493 0,883868 0,035877

0,421470

11

ciąg dalszy tablicy 1.2

Lata

x = 20 lat

x = 40 lat

Prob(Y

x

= k)

Prob(Y

x

≥ k) Prob(Y

x

= k)

Prob(Y

x

≥ k)

43 0,011472 0,873375 0,035525

0,385593

44 0,012543 0,861902 0,034822

0,350068

45 0,013726 0,849359 0,033777

0,315247

46 0,015011 0,835633 0,032401

0,281470

47 0,016378 0,820622 0,030735

0,249069

48 0,017815 0,804244 0,028821

0,218334

49 0,019325 0,786429 0,026701

0,189512

50 0,020905 0,767104 0,024425

0,162811

51 0,022547 0,746199 0,022066

0,138387

52 0,024230 0,723652 0,019676

0,116320

53 0,025943 0,699422 0,017307

0,096644

54 0,027636 0,673479 0,015021

0,079337

55 0,029267 0,645843 0,012838

0,064316

56 0,030807 0,616575 0,010821

0,051477

57 0,032194 0,585768 0,008990

0,040656

58 0,033387 0,553574 0,007345

0,031666

59 0,034356 0,520186 0,005917

0,024321

60 0,035009 0,485830 0,004686

0,018404

61 0,035356 0,450821

62 0,035366 0,415466

63 0,035019 0,380100

64 0,034326 0,345081

65 0,033296 0,310756

66 0,031939 0,277460

67 0,030297 0,245521

68 0,028411 0,215223

69 0,026320 0,186812

70 0,024077 0,160492

71 0,021752 0,136415

72 0,019396 0,114663

73 0,017061 0,095267

74 0,014807 0,078206

75 0,012655 0,063399

78 0,010667 0,050744

79 0,008862 0,040077

80 0,007240 0,031215

Na podstawie danych zawartych w tablicy 1.1 i 1.2 wykonano niżej zamieszczone rysunki,

które ilustrują wybrane rozkłady prawdopodobieństwa dalszego trwania życia.

12

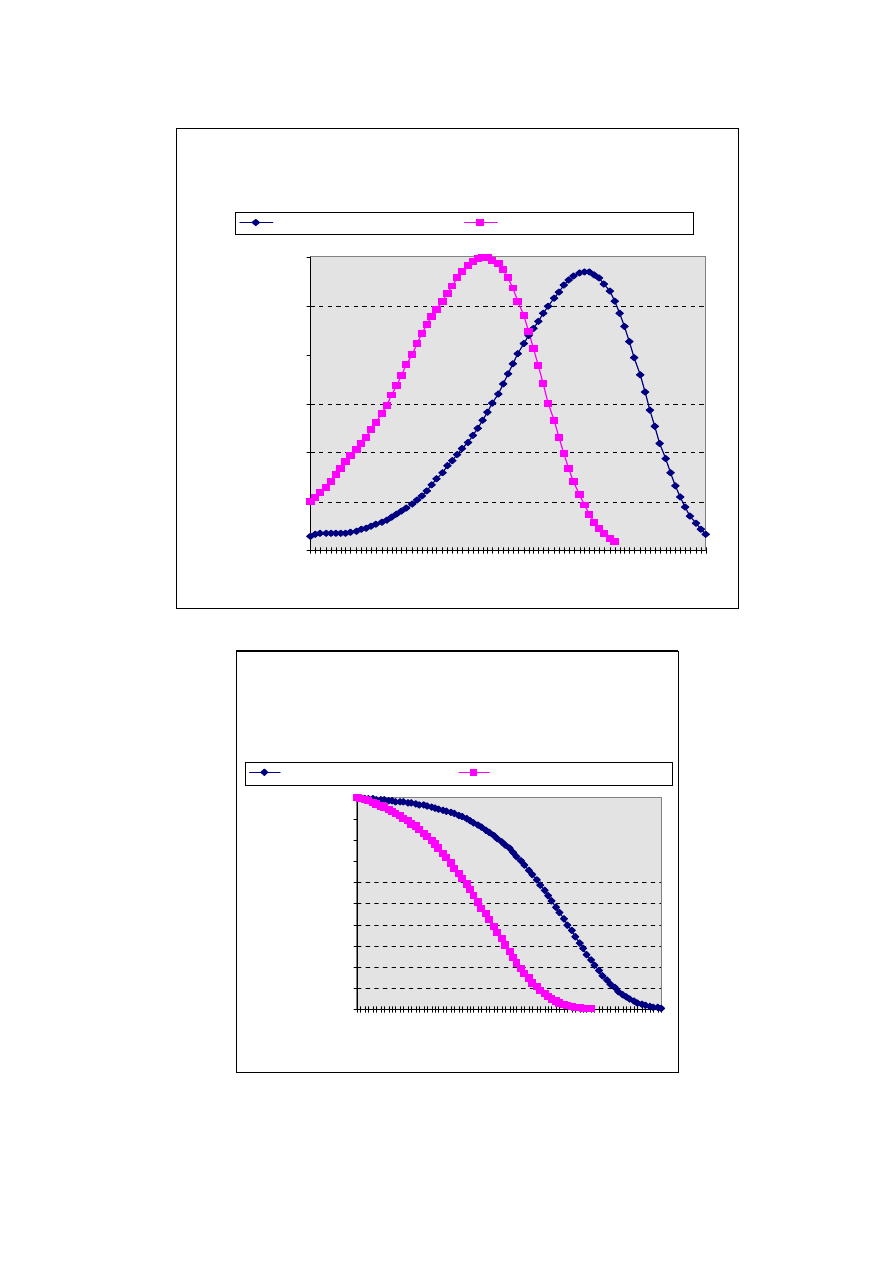
Rys.1.1. R O ZKŁ AD P R AW DO P O DO BIEŃS T W A DAL S ZEG O

T RW A NIA ŻYCIA M ĘŻCZYZN Y W W IEK U 20 i 40 L A T

( N a p o d sta w ie P T T Ż 1990-1991)

0,000000

0,005000

0,010000

0,015000

0,020000

0,025000

0,030000

0

6

12

18

24

30

36

42

48

54

60

66

72

80

DA L SZ E T RW A NIE Ż YC IA W L A T A C H

PRAWDOPODOBIE

Ń

STWO PRZE

Ż

YCIA KOLEJ

N

Y

C

k-l

a

t

PROB(Y x =k)-męz c z y z na 20 lat

PROB( Y x =k)-męż c z y z na 40 lat

Rys.1.2. PRAW DOPODOBIEŃSTW O PRZEŻYCIA
CO NAJMNIEJ k -lat. W YKRES FUNKCJI G(k)=1-

F(k)=PROB(Y

x

>=k). MĘŻCZYZNA W W IEKU 20 i

40 LAT

( Na podstaw ie PTTŻ 1990-1991)

0,000000

0,100000

0,200000

0,300000

0,400000

0,500000

0,600000

0,700000

0,800000

0,900000

1,000000

0

7

14

21

28

35

42

49

56

63

70

79

DALSZE TRWANIE ŻYCIA w latach

PRAWDOPODOBIE

Ń

STWO

PRZE

Ż

YCIA CO NAJMNIEJ k- la

t

PROB(Yx>k)-męzczyzna 20 lat

PROB( Y x>k)-mężczyzna 40 lat

13

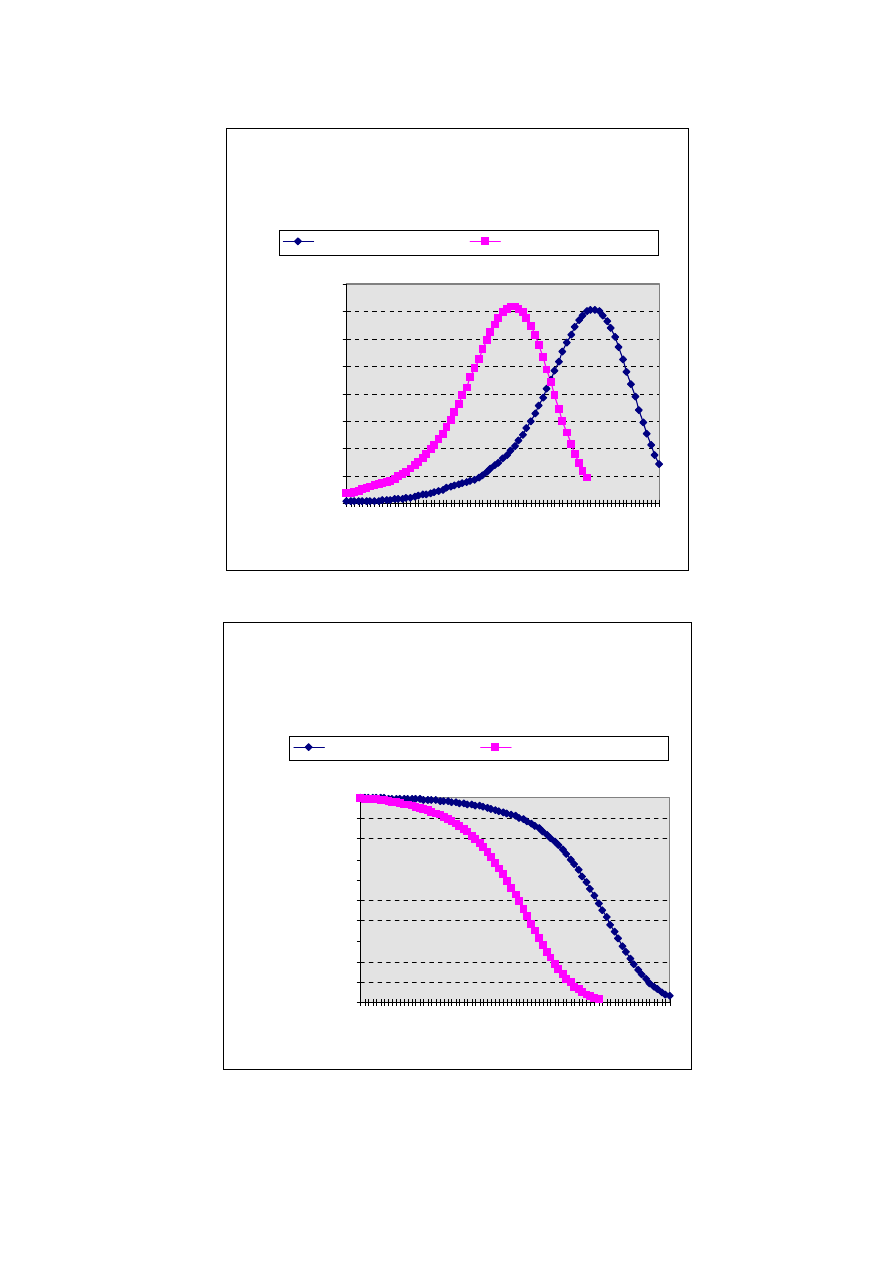
Rys.1.3. ROZKŁAD PRAWDOPODOBIEŃSTWA

DALSZEGO TRWANIA ŻYCIA KOBIETA W WIEKU

20 i 40 LAT

( Na podstawie PTTŻ 1990-1991)

0,000000

0,005000

0,010000

0,015000

0,020000

0,025000

0,030000

0,035000

0,040000

0

6

12

18

24

30

36

42

48

54

60

66

72

80

DALSZE TRWANIE ŻYCIA W LATACH

PRAWDOPODOBIE

Ń

STWO

PRZE

Ż

YCIA KOLEJNYCH k- la

PROB( Yx=k)-kobieta 20 lat

PROB( Yx=k)-kobieta 40 lat

Rys.1.4. PRAWDOPODOBIEŃSTWO PRZEŻYCIA CO

NAJMNIEJ

k-lat. WYKRES FUNKCJI G(k)=1-F(k)=PROB(Y

X

>=k). KOBIETA W WIEKU 20 i 40 LAT ( Na

podstawie PTTŻ 1990-1991)

0,000000

0,100000

0,200000

0,300000

0,400000

0,500000

0,600000

0,700000

0,800000

0,900000

1,000000

0

6

12

18

24

30

36

42

48

54

60

66

72

80

DALSZE TRWANIE ŻYCIA w latach

PRAWDOPODOBIE

Ń

STWO

PRZE

Ż

YCIA CO NAJMNIEJLEJ

k

lat

PROB( Yx>k)-kobieta 20 lat

PROB( Yx>k)-kobieta 40 lat

14

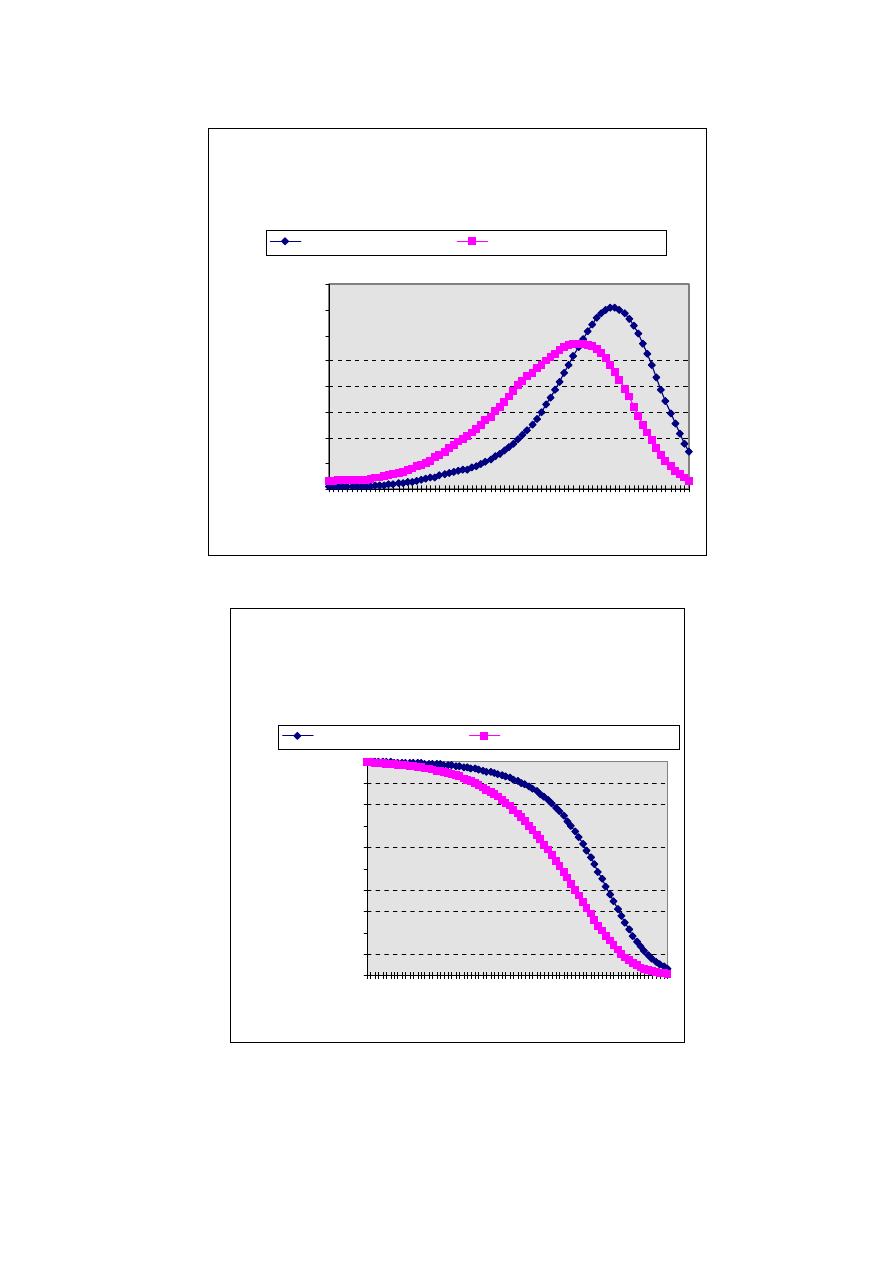
Rys.1.5. ROZKŁAD PRAWDOPODOBIEŃSTWA

DALSZEGO TRWANIA ŻYCIA. KOBIETA i MĘŻCZYZNA

W WIEKU 20 LAT

( Na podstawie PTTŻ 1990-1991)

0,000000

0,005000

0,010000

0,015000

0,020000

0,025000

0,030000

0,035000

0,040000

0

6

12

18

24

30

36

42

48

54

60

66

72

80

DALSZE TRWANIE ŻYCIA W LATACH

PRAWDOPODOBIE

Ń

STWO

PRZE

Ż

YCIA KOLEJ

N

YCH k

-la

PROB( Yx=k)-kobieta 20 lat

PROB(Yx=k)-męzczyzna 20 lat

Rys.1.6. PROWDOPODOBIEŃSTWO PRZEŻYCIA

CO NAJMNIEJ

k-lat.WYKRES FUNKCJI G(k)=1-F(k)=PROB(Y

X

>=k). KOBIETA i MĘŻCZYZNA W WIEKU 20 LAT.

( Na podstawie PTTŻ 1990-1991)

0,000000

0,100000

0,200000

0,300000

0,400000

0,500000

0,600000

0,700000

0,800000

0,900000

1,000000

0

7

14

21

28

35

42

49

56

63

70

79

DALSZE TRWANIE ŻYCIA w latach

PROWDOPODOBIE

Ń

STWO

PRZE

Ż

YCIA CO NAJ

MNIEJ

k

-

la

t

PROB( Yx>k)-kobieta 20 lat

PROB(Yx>k)-męzczyzna 20 lat

15

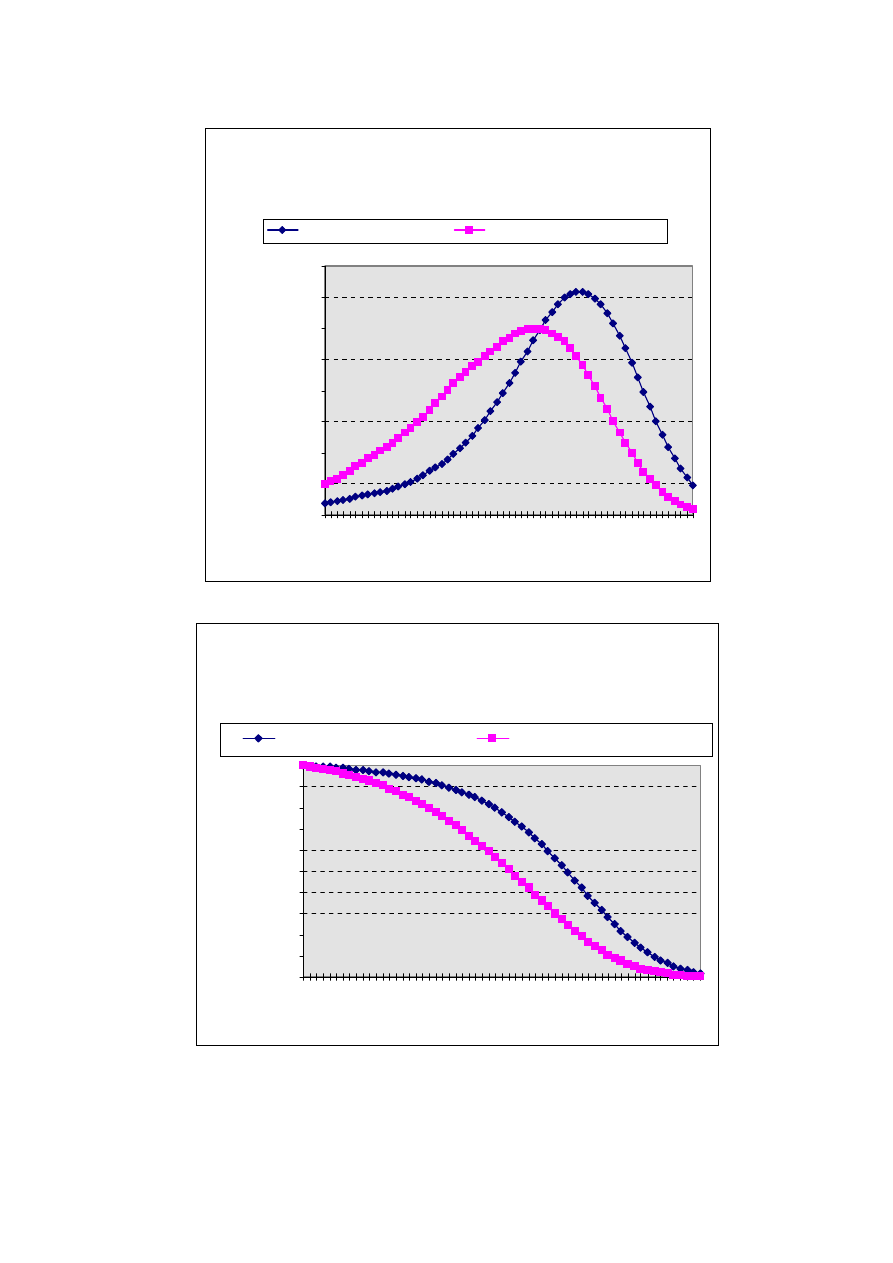
Rys.1.7. ROZKŁAD PRAWDOPODOBIEŃSTWA

DALSZEGO TRWANIA ŻYCIA. KOBIETA i MĘŻCZYZNA W

WIEKU 40 LAT( Na podstawie PTTŻ 1990-1991)

0,000000

0,005000

0,010000

0,015000

0,020000

0,025000

0,030000

0,035000

0,040000

0

4

8

12

16

20

24

28

32

36

40

44

48

52

56

60

DALSZE TRWANIE ŻYCIA W LATACH

PRAWDOPODOBIE

Ń

STWO PRZE

Ż

YC

I

KOLEJ

N

YCH k

-la

t

PROB( Yx=k)-kobieta 40 lat

PROB( Yx=k)-mężczyzna 40 lat

Rys.1.8. PRAWDOPODOBIEŃSTWO PRZEŻYCIA CO

NAJMNIEJ k-lat. WYKRES FUNKCJI

G(k)=1-F(k)=PROB(Y

X

>=k). KOBIETA i MĘŻCZYZNA W

WIEKU 40 LAT

(Na podstawie PTTŻ 1990-1991)

0,000000

0,100000

0,200000

0,300000

0,400000

0,500000

0,600000

0,700000

0,800000

0,900000

1,000000

0

4

8

12

16

20

24

28

32

36

40

44

48

52

56

60

DALSZE TRWANIE ŻYCIA w latach

PRAWDOPODOBIE

Ń

STWO

PRZE

Ż

YCIA CO NAJMNIEJ k-la

t

PROB( Yx>k)-kobieta 40 lat

PROB( Yx>k)-mężczyzna 40 lat

16

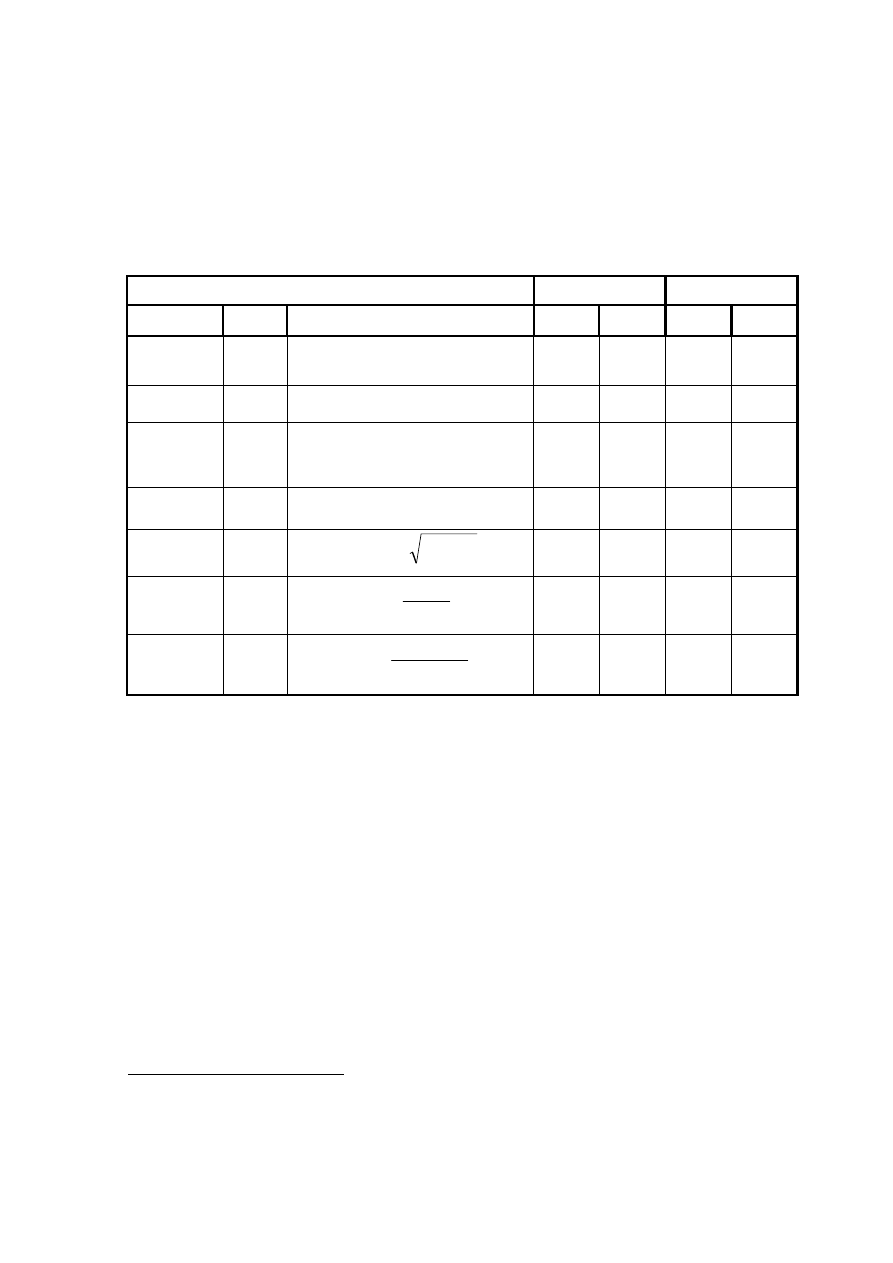
Charakterystyki liczbowe (opisowe) rozkładów dalszego trwania życia zamieszczono w

tablicy 1.3

Tablica 1.3

Charakterystyki opisowe rozkładu zmiennej losowej Y

x

- dalszego trwania życia

4

Charakterystyka Mężczyzna Kobieta

Nazwa

Symbol

Wzór

x=20 lat x=40 lat x=20 lat x=40 lat

Dminanta

d

d

ob Y

k w x

x

=

k

=

≤ ≤ −

max Pr (

)

0

54 34 62 42

Mediana

Me

Pr (

) Pr (

)

,

ob Y

M

ob Y

M

x

e

x

e

≤

=

≥

= 05

51 31 60 40

Wartość

oczekiwana

E(Y

x

)

E Y

k ob Y k

x

x

k

w x

( )

Pr (

=

)

=

=

−

∑

0

47,677

29,735

55,343

37,029

Wariancja

D Y

x

2

( )

D Y

E Y

E Y

x

x

x

2

( )

(

( ))

=

−

2

222,387 161,793 166,652 140,898

Odchylenie

standardowe

D Y

x

(

)

D Y

D Y

x

( )

( )

=

2

x

14,912 12,719

12,909 11,870

Współczynnik

zmienności

V

V

D Y

E Y

x

x

= ( )

( )

0,312 0,427 0,233

0,320

Współczynnik

asymetrii

(skośności)

A

s

A

E Y

d

D Y

s

x

x

=

−

( )

( )

-0,423 -0,335 -0,515 -0,418

Charakterystyki liczbowe zamieszczone w tablicy 1.3 obliczono na podstawie da-

nych zamieszczonych w tablicach 1.1-1.2 oraz przytoczonych wyżej wzorów. Nieznaczne

różnice liczbowe pomiędzy danymi zawartymi w tablicy 1.3 a danymi zawartymi w "Pol-

skich Tablicach Trwania Życia 1990-1991" dotyczące przeciętnego (średniego) dalszego

trwania życia (E(Y

x

), e

x

) oraz odchylenia standardowego (D(Y

x

), s

x

) wynikają z różnicy

definicji i sposobów obliczeń (por. 1.16,1.17, tablica 1.3).

Dla

ubezpieczeń na życie, gdzie ważny jest czas jaki upłynął od momentu ubezpie-

czenia do momentu wypłaty odszkodowania, istotną informację o ryzyku

5

związanym z

4

Jóźwiak J.,Podgórski J., Statystyka od podstaw, PWE Warszawa 1994

5

Ubezpieczenia w gospodarce rynkowej. Praca zbiorowa pod redakcją A. Wąsiewicza. Oficyna Wydawni-

cza Branta 1994.

17

ubezpieczeniem zawiera funkcja G(x) = (1 - F(x)) - funkcja prawdopodobieństwa dalszego

trwania życia (por. Rys.1.2, rys.1.4, Rys.1.6,Rys.1.8).

Na przykład prawdopodobieństwo przeżycia kolejnych 25 lat dla mężczyzny 20 letniego

P(Y

20

≥25) = 0,975189, a dla dla mężczyzny 40 letniego P(Y

40

≥25) = 0,861634

(por.Tab.1.1). Oznacza to, że ubezpieczenie na życie na okres 25 lat mężczyzny 20 letnie-

go jest związane z dużo mniejszym ryzykiem niż ubezpieczenie mężczyzny 40 letniego.

Prawdopodobieństwo wypłaty sumy ubezpieczenia przez firmę ubezpieczeniową w okresie

ubezpieczenia (25 lat) w pierwszym przypadku wynosi 0,024811, a w drugim 0,138366.

Różnica tych prawdopodobieństw 0,113555 jest zaznaczona na rysunkach funkcji G(x)

(por. Rys.1.2). Różnice ryzyka związanego z ubezpieczeniem kobiety bądź mężczyzny w

tym samym wieku przedstawiają rysunki 1.6 i 1.8. Dobrą miarą ryzyka związanego z ubez-

pieczeniem na życie może być również współczynnik zmienności V, którego małe warto-

ści informują o małym zróżnicowaniu faktycznie przeżytej liczby lat od momentu ubezpie-

czenia względem przeciętnej liczby lat dalszego trwania życia.

W dalszej części pracy wykażemy, że przedstawione w tablicach 1.1 i 1.2 rozkłady

prawdopodobieństwa dalszego trwania życia mają zasadniczy wpływ na wysokość jedno-

razowej składki netto ubezpieczeń życiowych.

18