Pole elektromagnetyczne

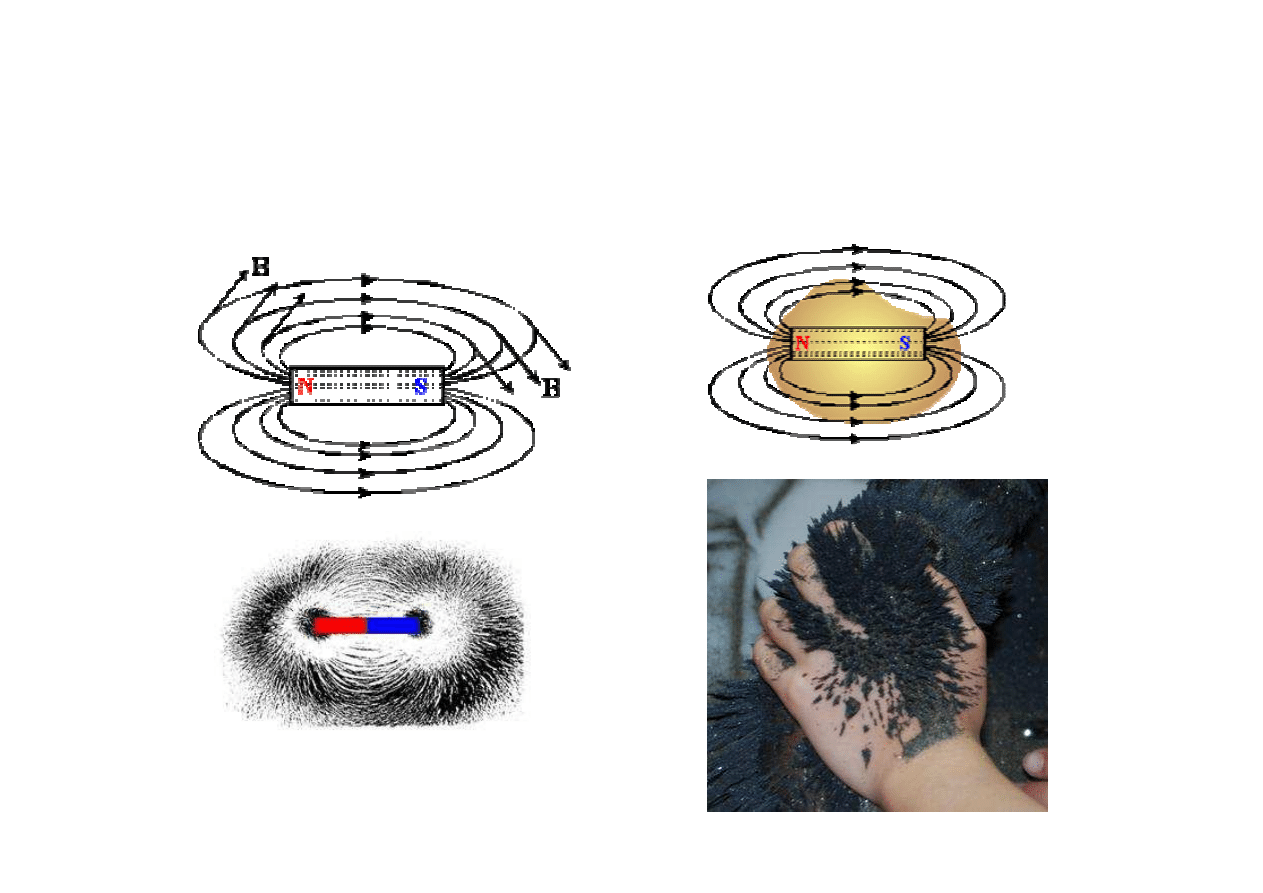
Pole magnetyczne

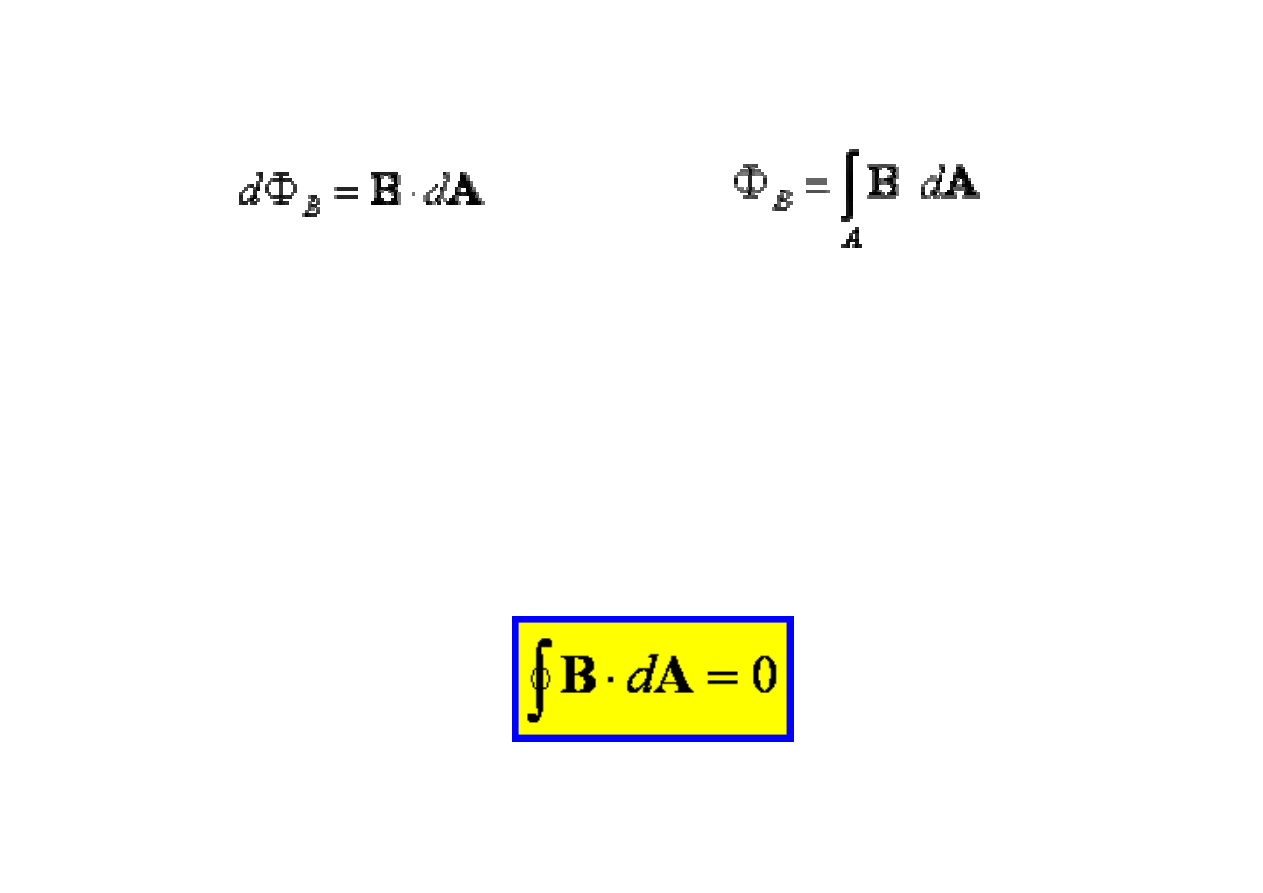
Strumie

ń

pola magnetycznego

Jednostk

ą

strumienia magnetycznego w uk

ł

adzie SI

jest 1 weber (1 Wb) = 1 N·m·A

-1

.

Zatem, pole magnetyczne B jest czasem nazywane
g

ę

sto

ś

ci

ą

strumienia i 1T = 1 Wb·m

-2

.

Prawo Gaussa:

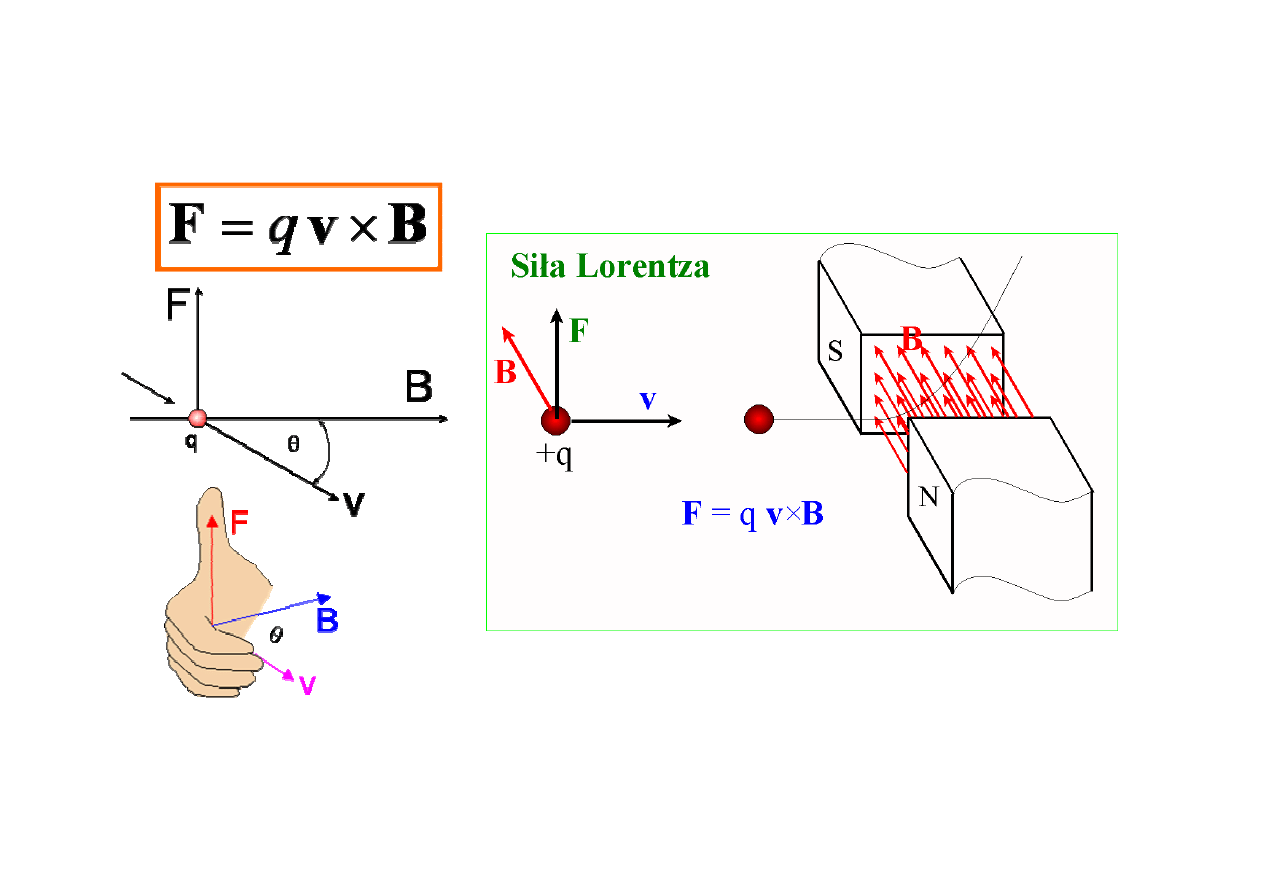
Siła Lorentza

w układzie SI jednostk

ą

B jest 1 tesla (1T).

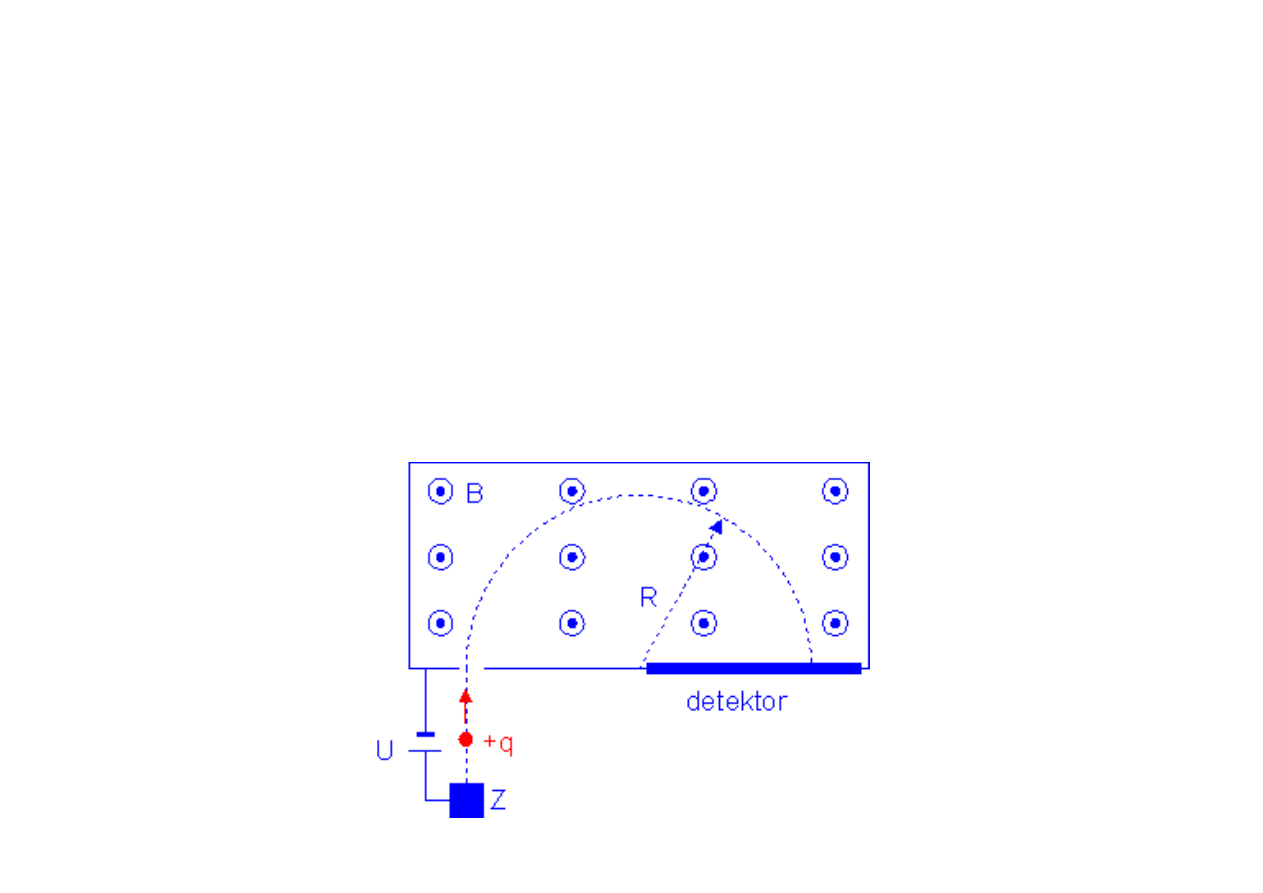
Gdy pole B obejmuje odpowiednio du

ż

y

obszar, to ładunek q poruszaj

ą

cy si

ę

prostopadle do kierunku wektora B
ustabilizuje swój ruch na torze kołowym.

(zastosowanie: spektrometria masowa)

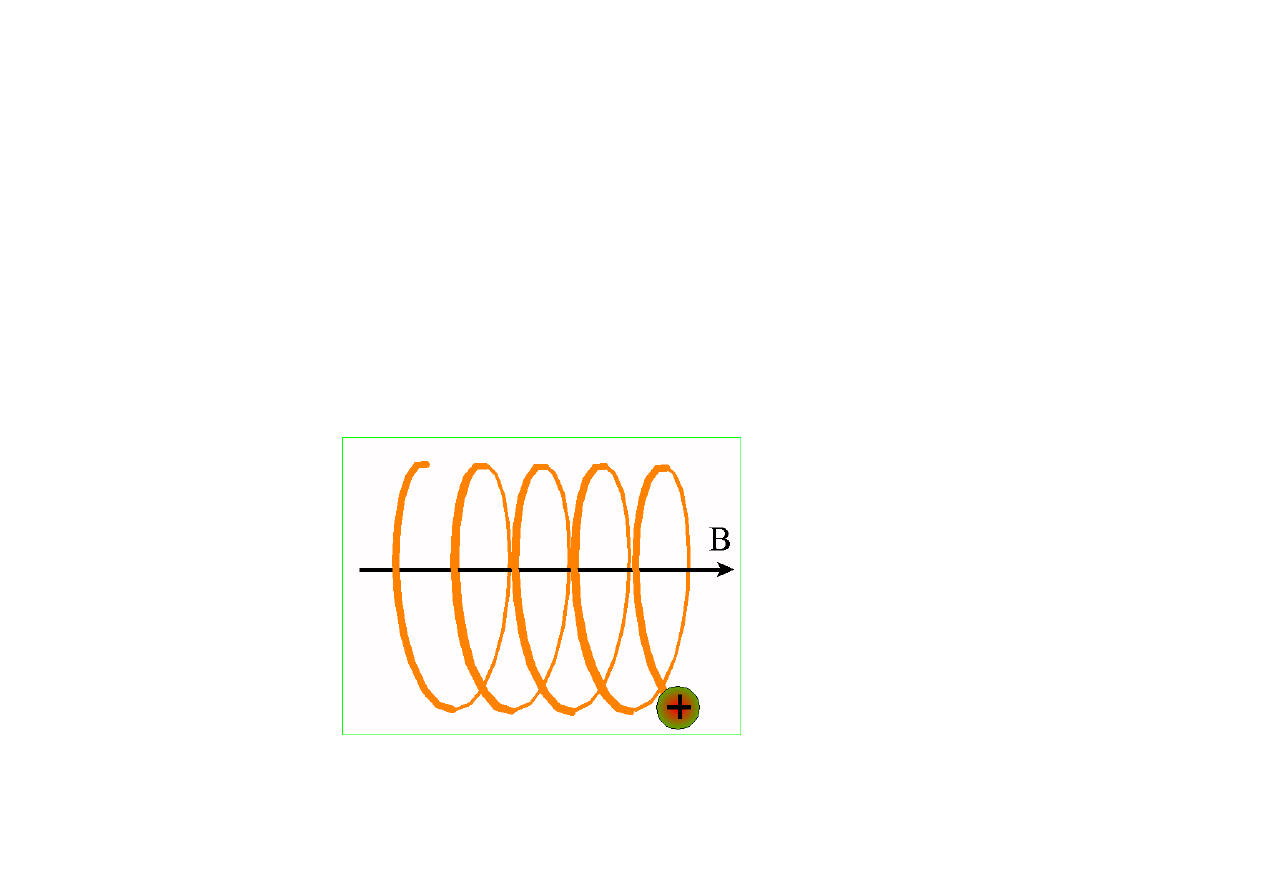
Kiedy jednak wektor v ma składow

ą

równoległ

ą

do wektora B wtedy torem

ładunku b

ę

dzie helisa:

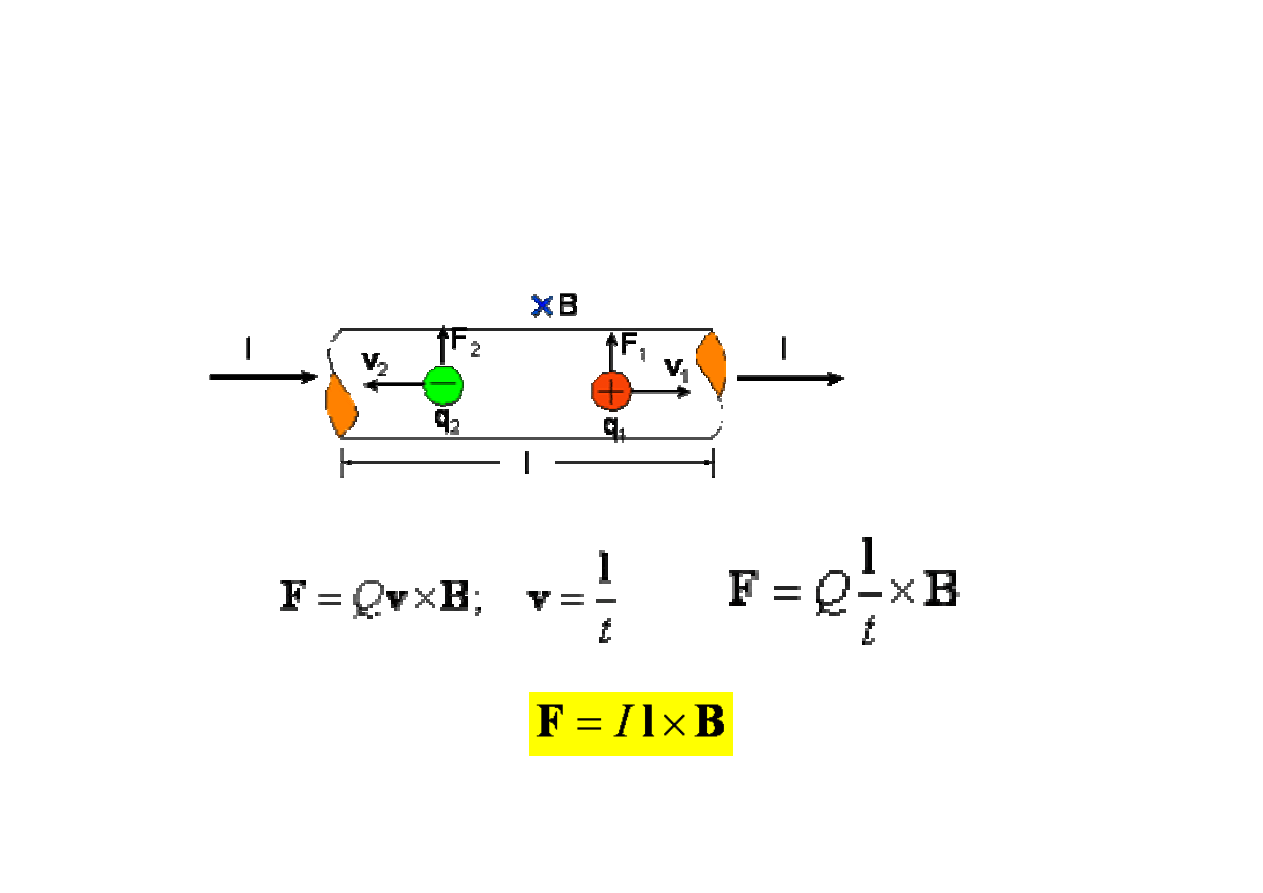
Si

ł

a dzia

ł

aj

ą

ca na przewodnik z pr

ą

dem wynika z

dzia

ł

ania si

ł

y Lorentza na poruszaj

ą

ce si

ę

no

ś

niki

ł

adunku, elektrony lub jony.

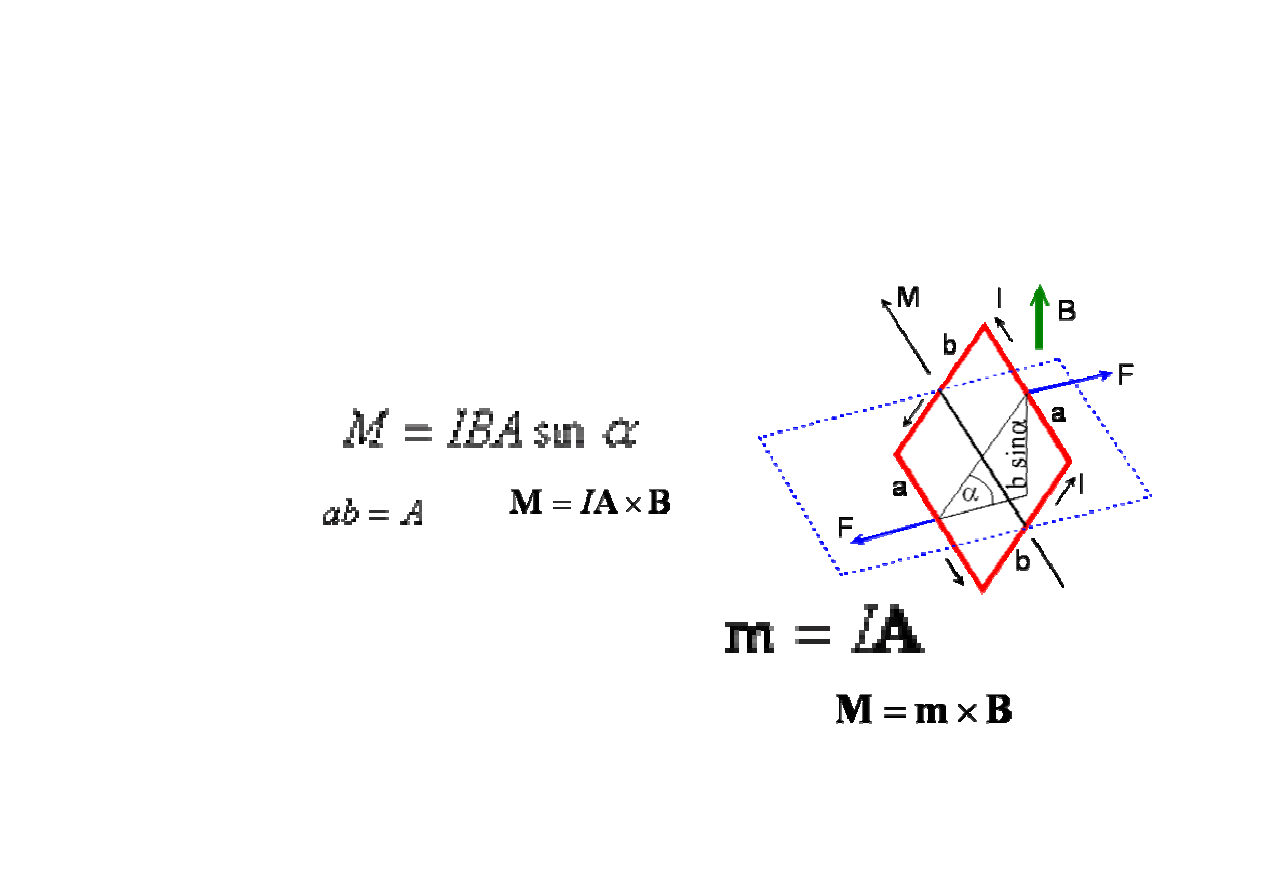
Moment si

ł

y dzia

ł

aj

ą

cy na p

ę

tl

ę

z pr

ą

dem w polu

magnetycznym (np. na zwój drutu w uzwojeniu silnika
elektrycznego). Je

ż

eli p

ę

tla mo

ż

e si

ę

obraca

ć

wokó

ł

osi

prostopad

ł

ej do pola B i przewodzi pr

ą

d I, wtedy pojawiaj

ą

si

ę

dwie niezrówa

ż

one si

ł

y F dzia

ł

aj

ą

ce na boki ramki równoleg

ł

e

do osi obrotu.

Moment tych si

ł

M wynosi

Wektor momentu magnetycznego p

ę

tli

Moment skr

ę

caj

ą

cy mo

ż

emy zapisa

ć

w postaci

Te si

ł

y, które dzia

ł

aj

ą

na elementy p

ę

tli prostopad

ł

e do osi obrotu, s

ą

przeciwnie skierowane i znosz

ą

si

ę

nawzajem.

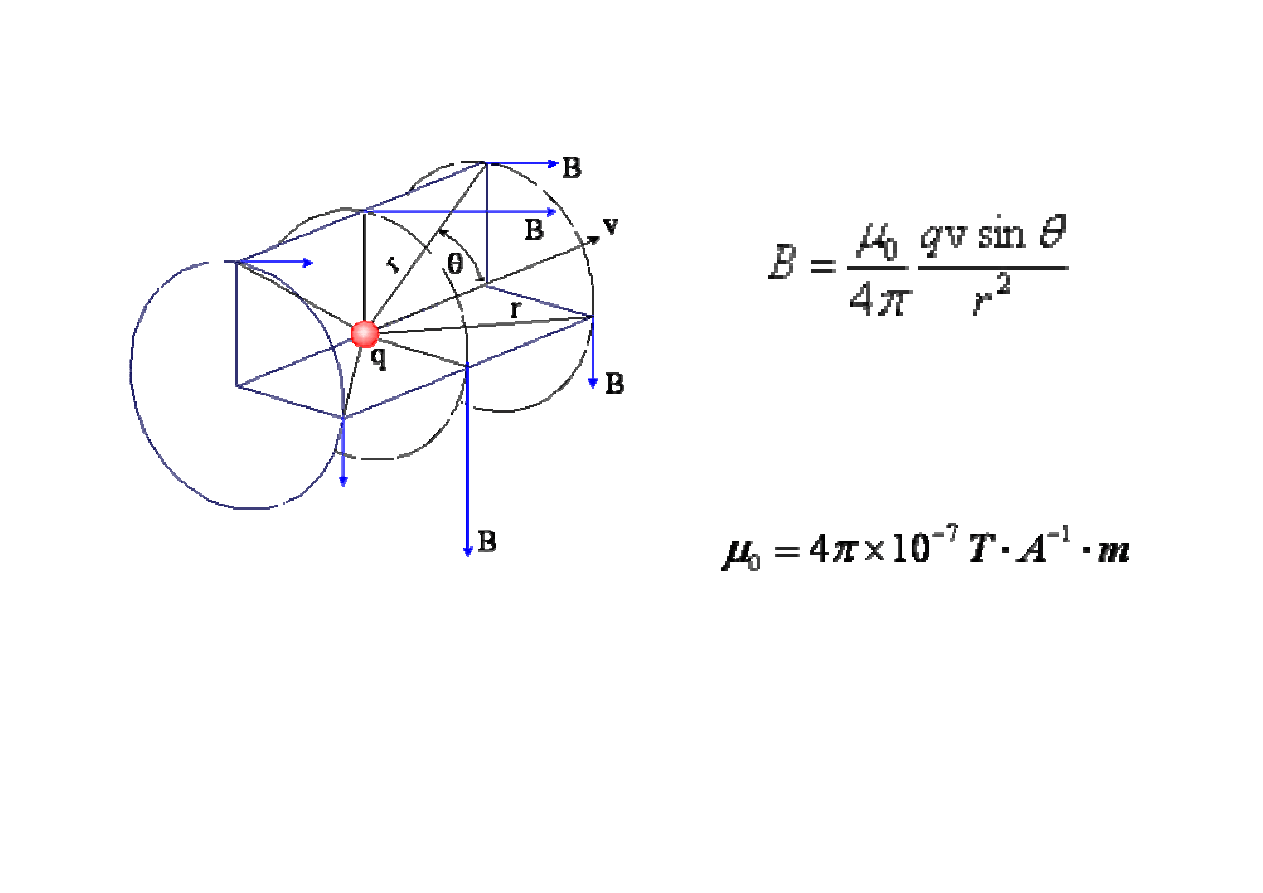
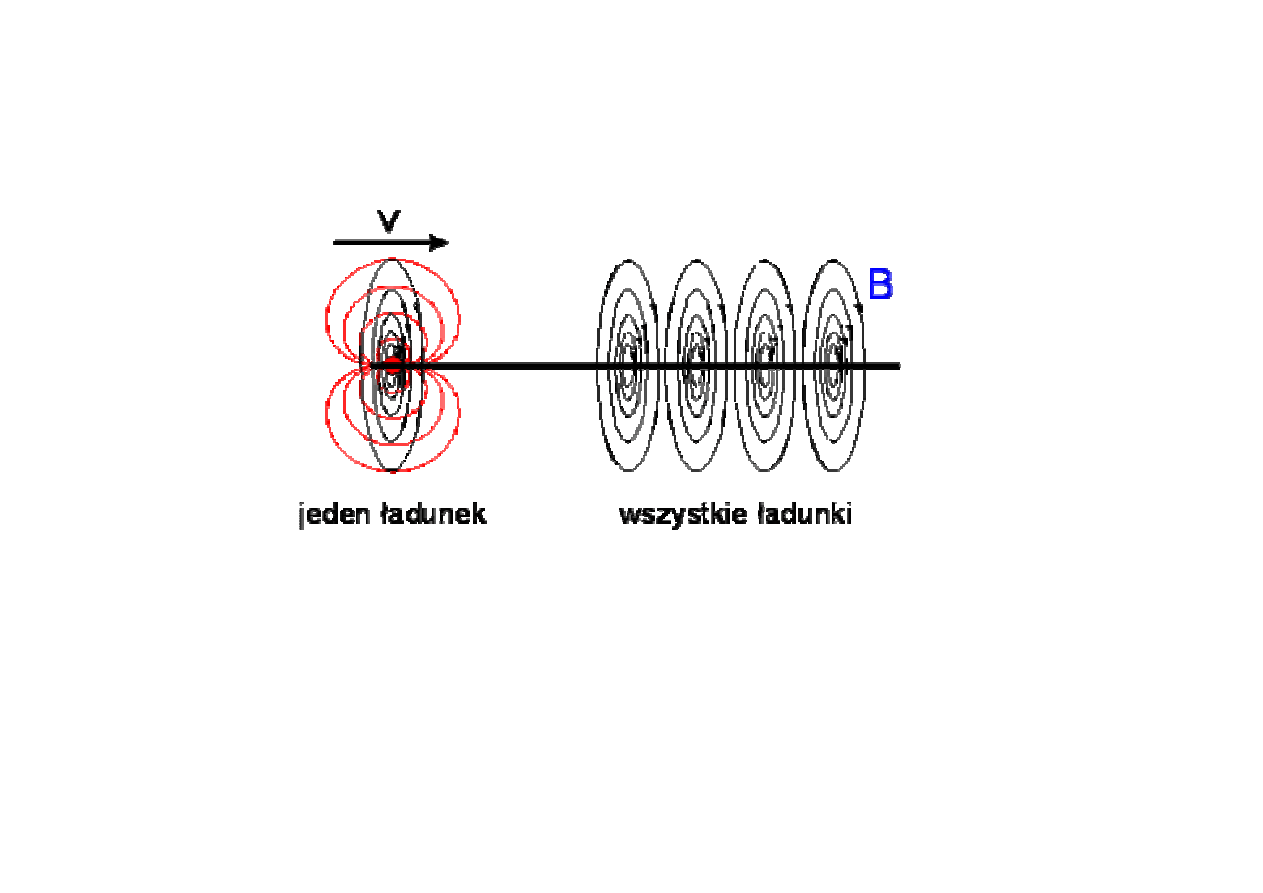
pola magnetyczne
wytwarzane przez poruszaj

ą

cy si

ę

pojedynczy ładunek punktowy

kierunek wektora B NIE le

ż

y na prostej mi

ę

dzy

ź

ródłem punktowym

a punktem pola. Jest on natomiast prostopadły do płaszczyzny
wyznaczonej przez t

ę

prost

ą

i przez wektor pr

ę

dko

ś

ci ładunku v.

Ponadto, warto

ść

pola jest proporcjonalna do sinusa k

ą

ta mi

ę

dzy tymi

dwoma kierunkami

µ

0 jest przenikalno

ś

ci

ą

magnetyczn

ą

pró

ż

ni, która

ma warto

ść

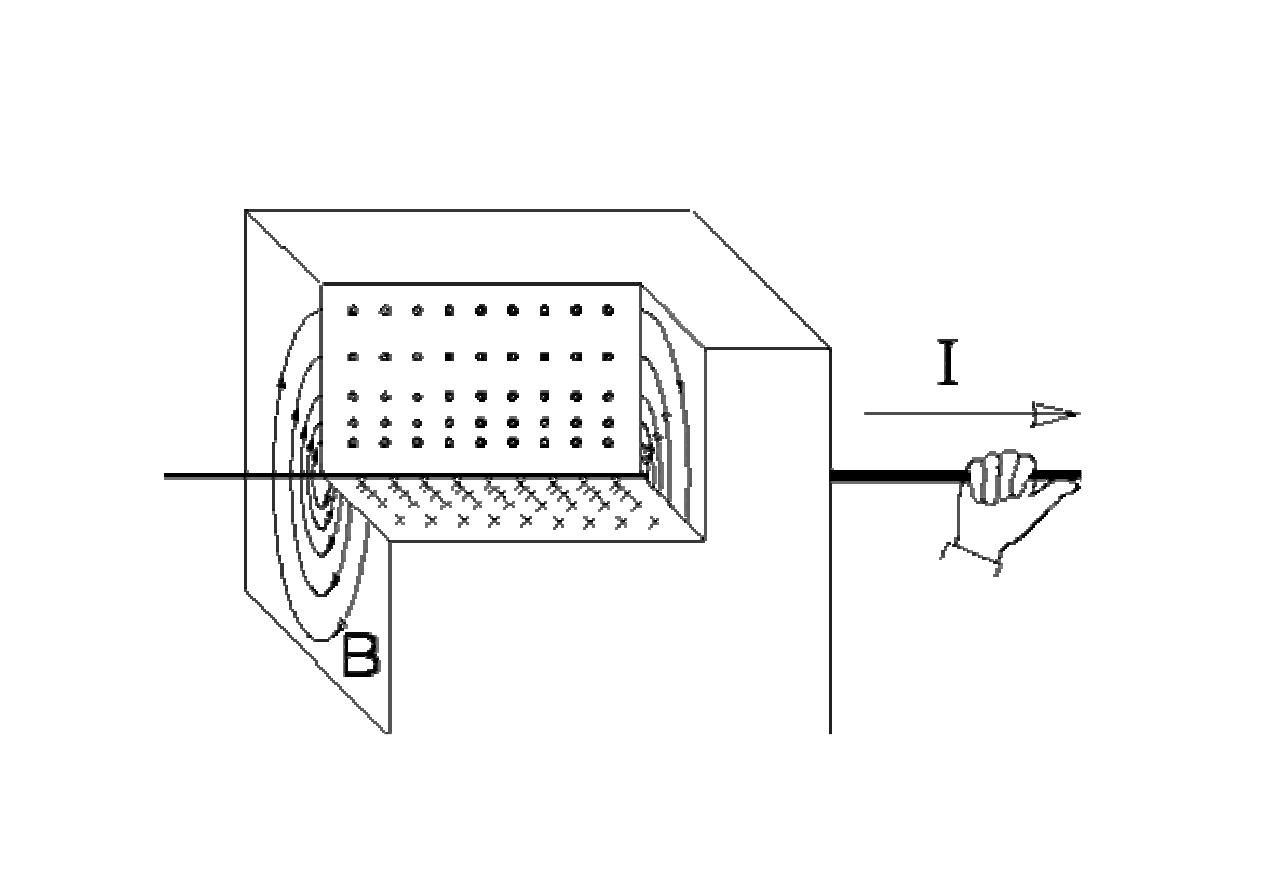
Pole B przewodnika

Kierunki pr

ą

du I oraz wektora B, jaki ten pr

ą

d wytwarza, s

ą

zgodne z reguł

ą

prawej dłoni: kciuk wskazuje kierunek pr

ą

du, a pozostałe palce pokazuj

ą

jak

pole B otacza przewodnik

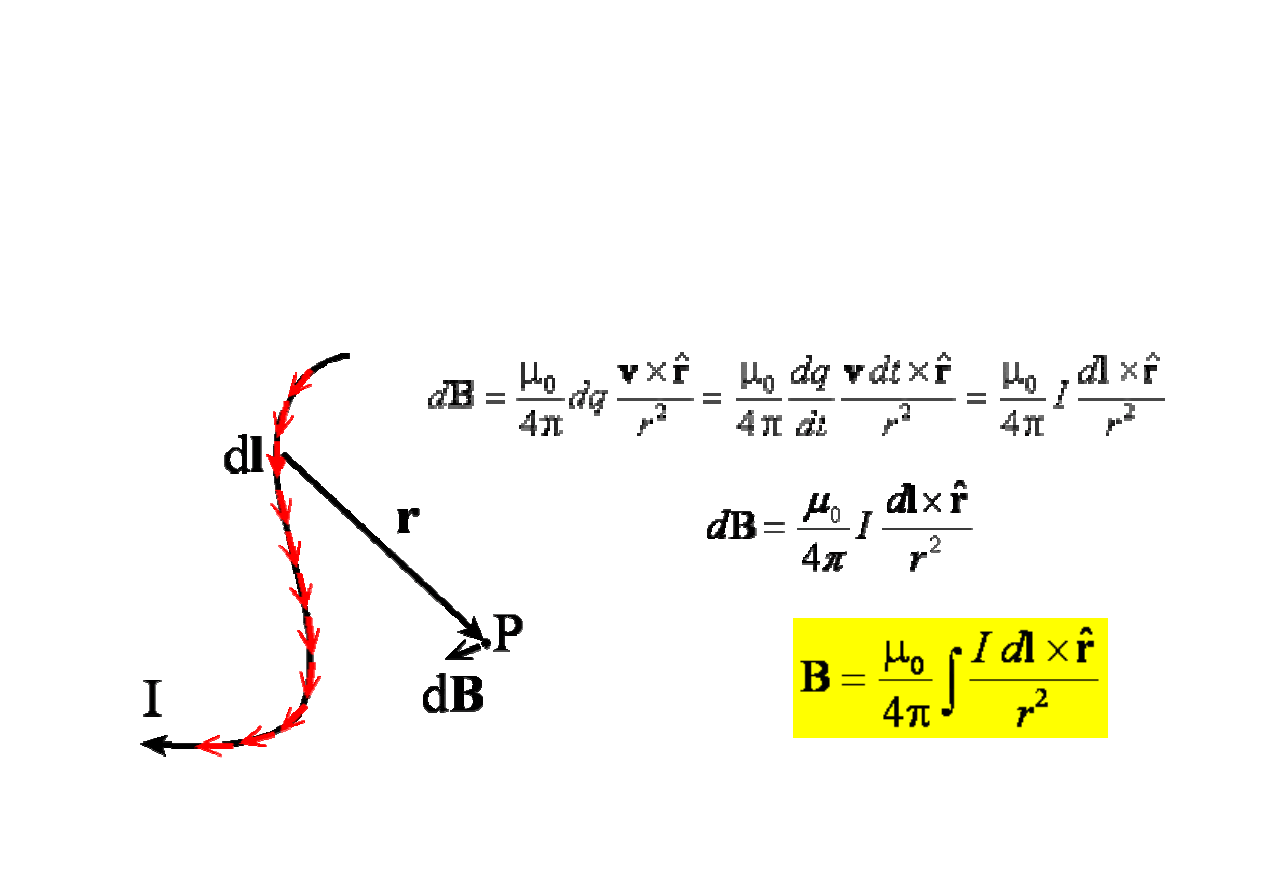
prawo Biota i Savarta

Je

ż

eli przewodnik z pr

ą

dem I podzielimy na niesko

ń

czenie

krótkie odcinki o d

ł

ugo

ś

ci dl, to w ka

ż

dym z nich b

ę

dzie

porusza

ł

si

ę ł

adunek dq i w odleg

ł

o

ś

ci r pole magnetyczne

tego odcinka pr

ą

du dB wyniesie

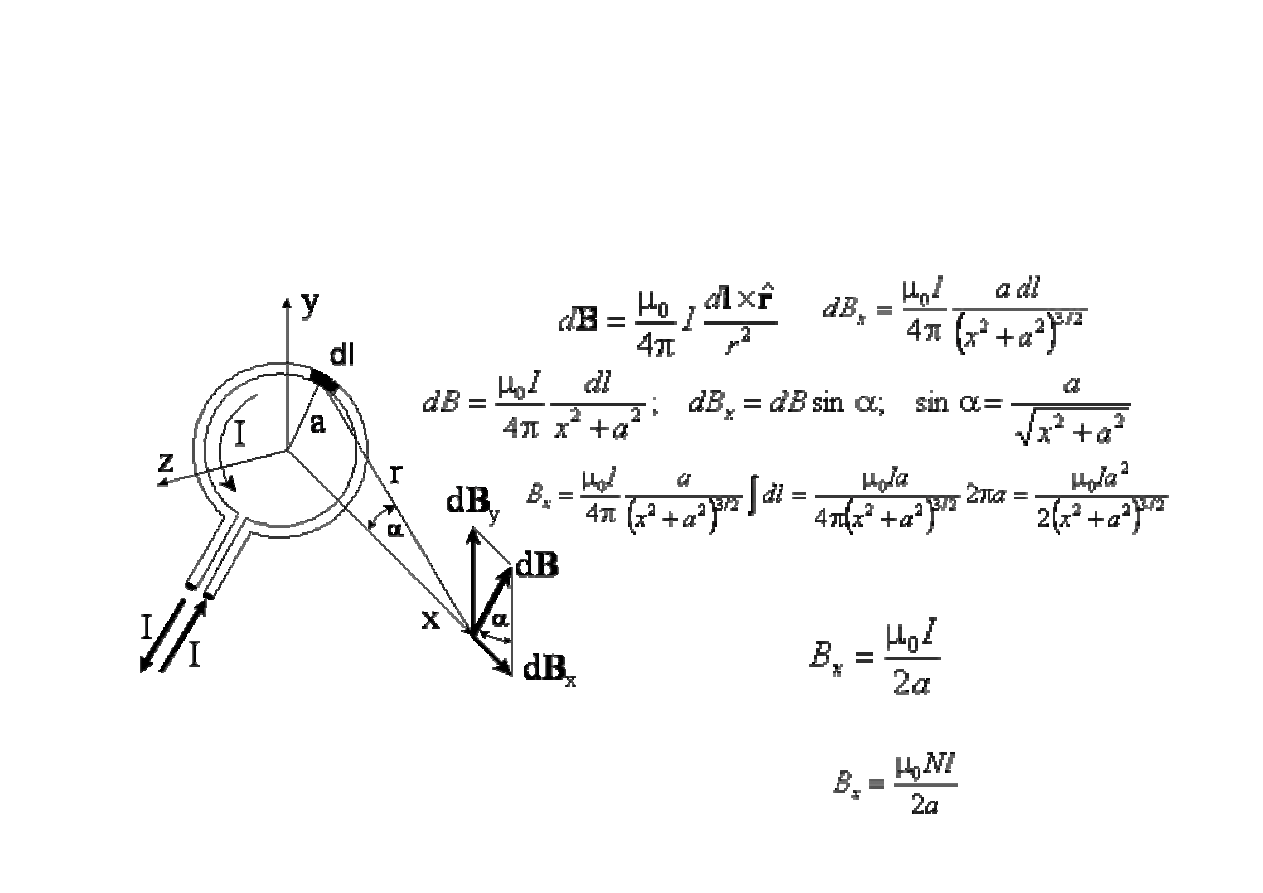
Pole magnetyczne B na osi p

ę

tli ko

ł

owej o promieniu a w

odleg

ł

o

ś

ci x od jej

ś

rodka gdy przez p

ę

tl

ę

p

ł

ynie pr

ą

d o

nat

ęż

eniu I. P

ę

tl

ę

pr

ą

dow

ą

dzielimy na niesko

ń

czenie ma

ł

e

odcinki dl. Pole dB jednego takiego odcinka znajdujemy na
podstawie prawa Biota i Savarta

W

ś

rodku p

ę

tli, gdy x maleje do zera (x = 0) pole B ma warto

ść

Dla

ś

ci

ś

le nawini

ę

tej cewki z N zwojami

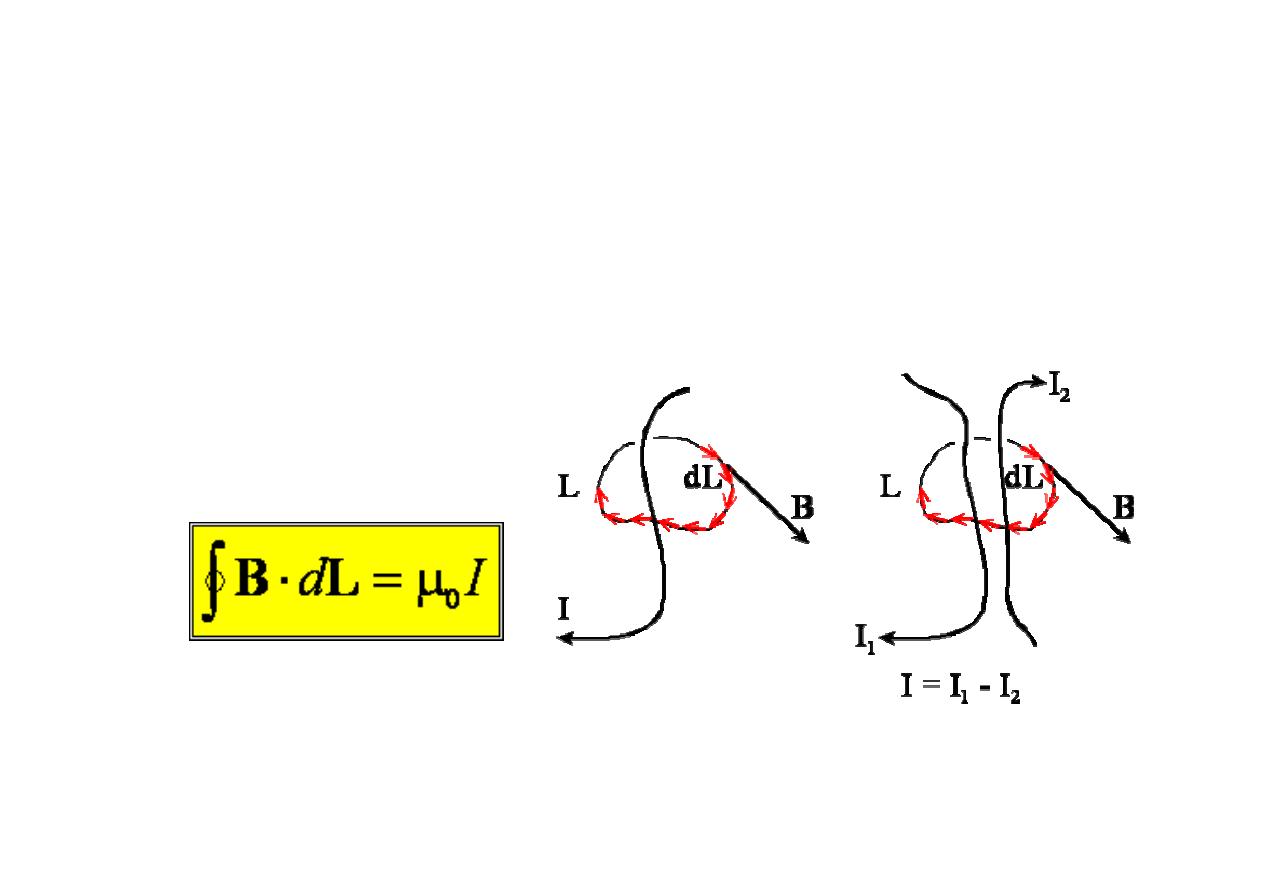
Prawo Ampera

•

okre

ś

la relacj

ę

mi

ę

dzy polem magnetycznym i pr

ą

dem

elektrycznym, który wytwarza

•

jest równaniem wi

ążą

cym cyrkulacj

ę

wektora magnetycznego B

czyli całk

ę

wzi

ę

t

ą

wzdłu

ż

zamkni

ę

tego płaskiego konturu L (na

oznaczenie elementu konturu u

ż

ywamy dL, za

ś

elementu

przewodnika dl )

cyrkulacja wektora B wzdłu

ż

zamkni

ę

tego płaskiego konturu L jest

równa iloczynowi

µ

0 i całkowitego pr

ą

du I przecinaj

ą

cego

powierzchni

ę

ograniczon

ą

tym konturem.

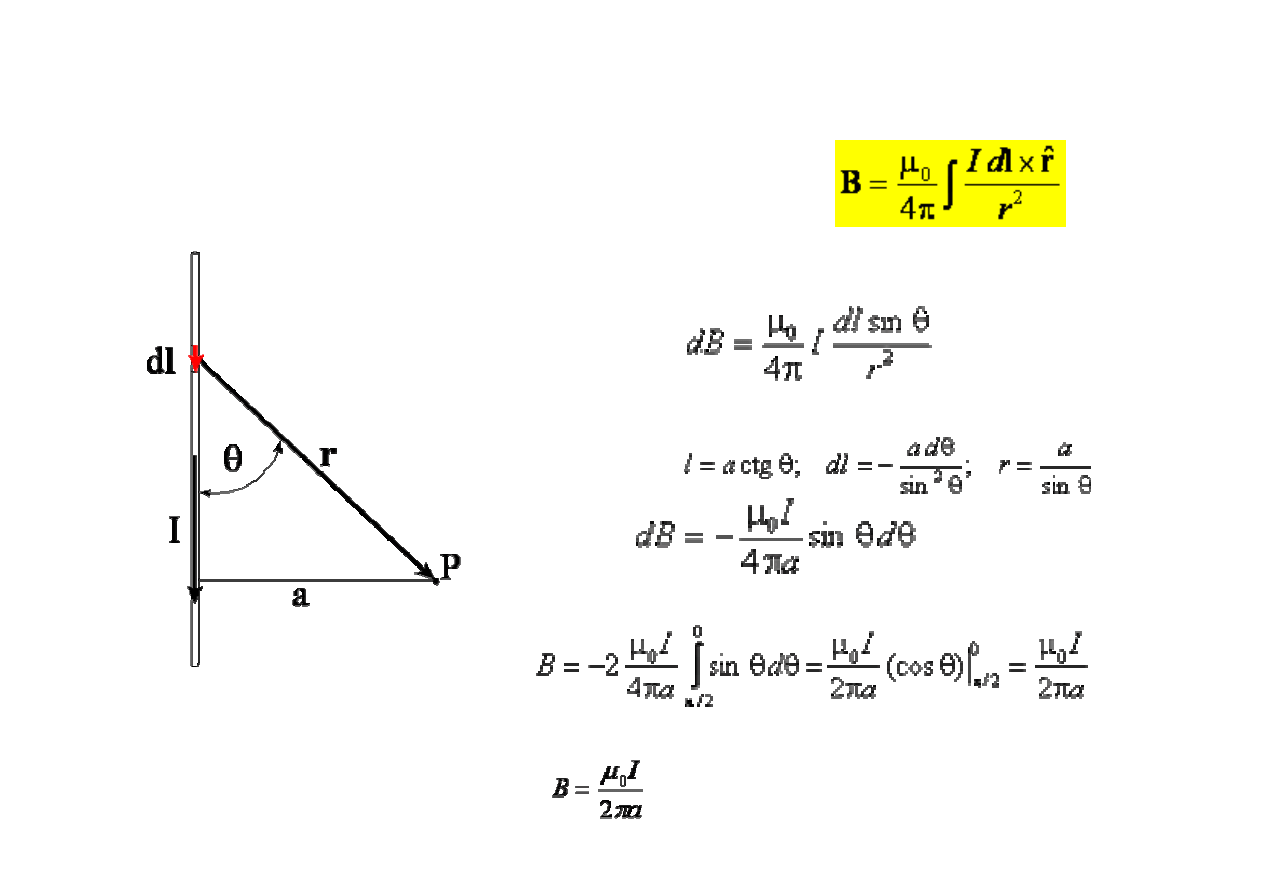
Pole magnetyczne d

ł

ugiego prostoliniowego przewodnika z pr

ą

dem -

prawo Biota i Savarta:

Pole dB odcinka z pr

ą

dem o d

ł

ugo

ś

ci dl w punkcie P (w odleg

ł

o

ś

ci a od osi przewodnika) wynosi

Aby uzale

ż

ni

ć

dB tylko od k

ą

ta

θ

zastosujemy podstawienia:

Po sca

ł

kowaniu po ca

ł

ej (niesko

ń

czonej) d

ł

ugo

ś

ci przewodnika otrzymujemy

Zatem w odleg

ł

o

ś

ci a od osi przewodnika prostoliniowego warto

ść

pola B wynosi

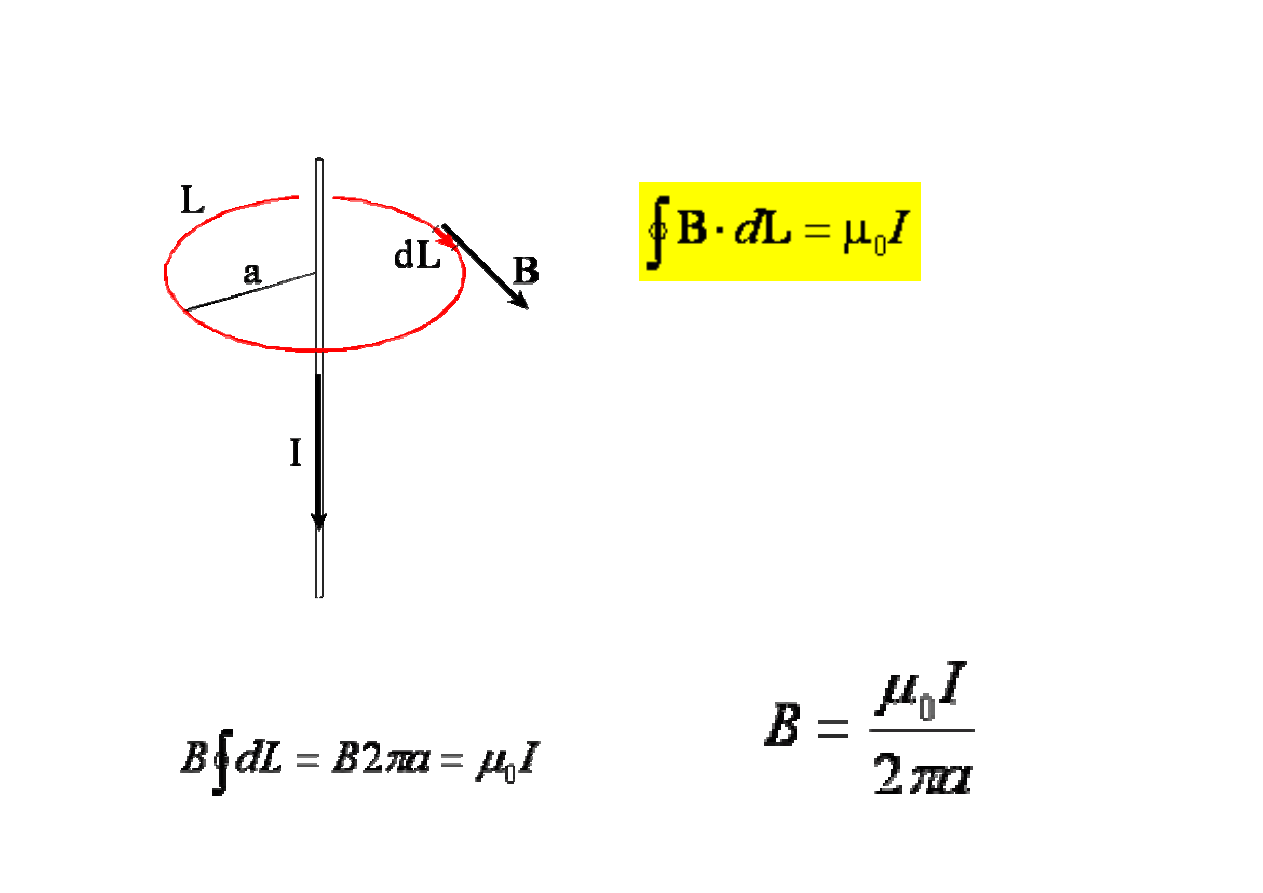
Pole magnetyczne d

ł

ugiego prostoliniowego przewodnika z pr

ą

dem

- prawo Ampere’a

Przewodnik z pr

ą

dem otaczamy p

ł

askim

konturem L o kszta

ł

cie okr

ę

gu le

żą

cym w

p

ł

aszczy

ź

nie prostopad

ł

ej do przewodnika.

Przewodnik przechodzi przez

ś

rodek okr

ę

gu.

Kontur L dzielimy na niesko

ń

czenie ma

ł

e

odcinki dL. z których ka

ż

dy jest równoleg

ł

y do

lokalnego kierunku pola B

- iloczyn skalarny pod znakiem ca

ł

ki zostaje zamieniony na zwyk

ł

y iloczyn BdL, przy czym warto

ść

B jest sta

ł

a i mo

ż

e

zosta

ć

wyniesiona przed znak ca

ł

ki. Otrzymujemy st

ą

d równanie

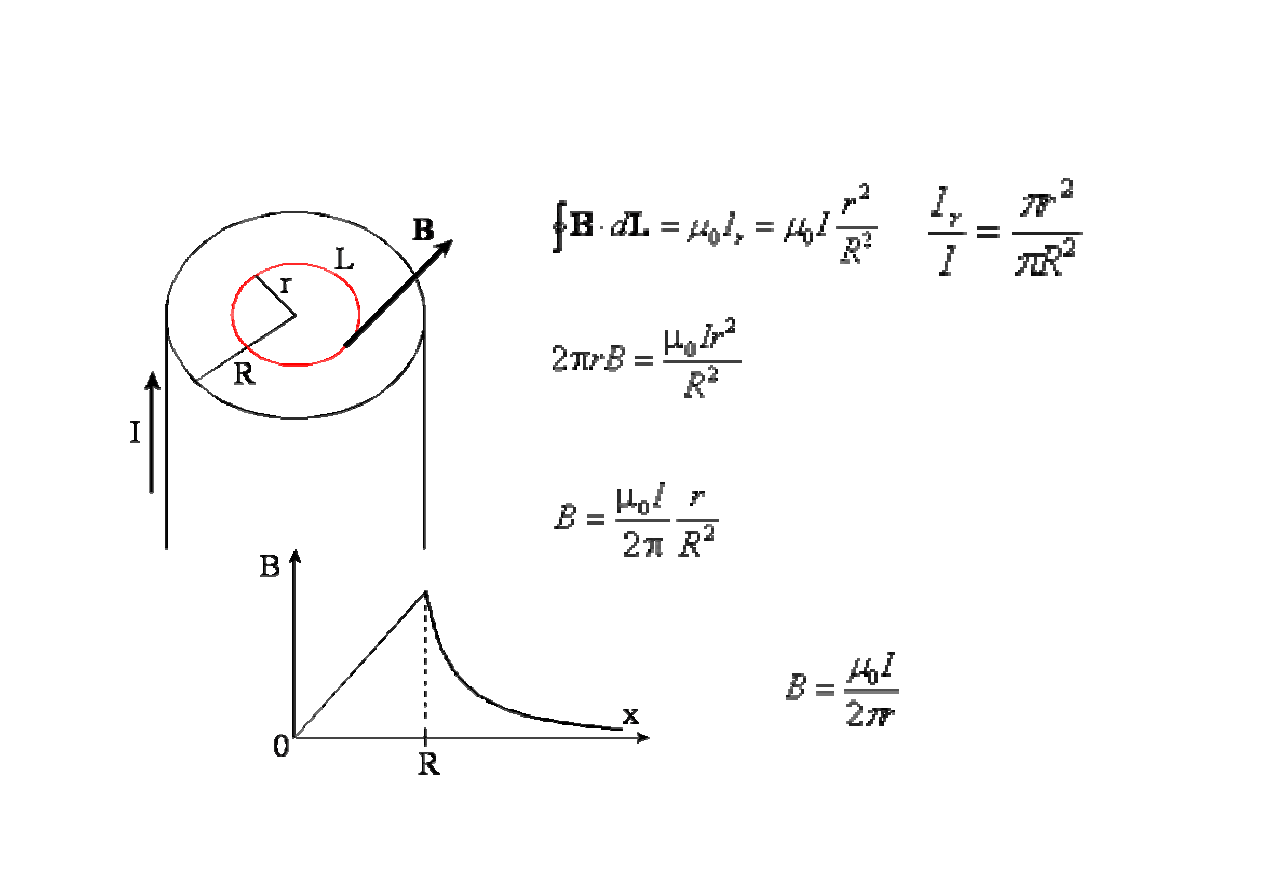
pole magnetyczne B wewn

ą

trz i na zewn

ą

trz długiego przewodnika o kształcie

walca, przez który płynie pr

ą

d o nat

ęż

eniu I.

Po sca

ł

kowaniu mamy

czyli wewn

ą

trz przewodnika pole B ro

ś

nie liniowo wraz ze wzrostem r

Na zewn

ą

trz przewodnika, gdy r > R, pole B maleje hiperbolicznie jak

wokó

ł

prostego przewodnika

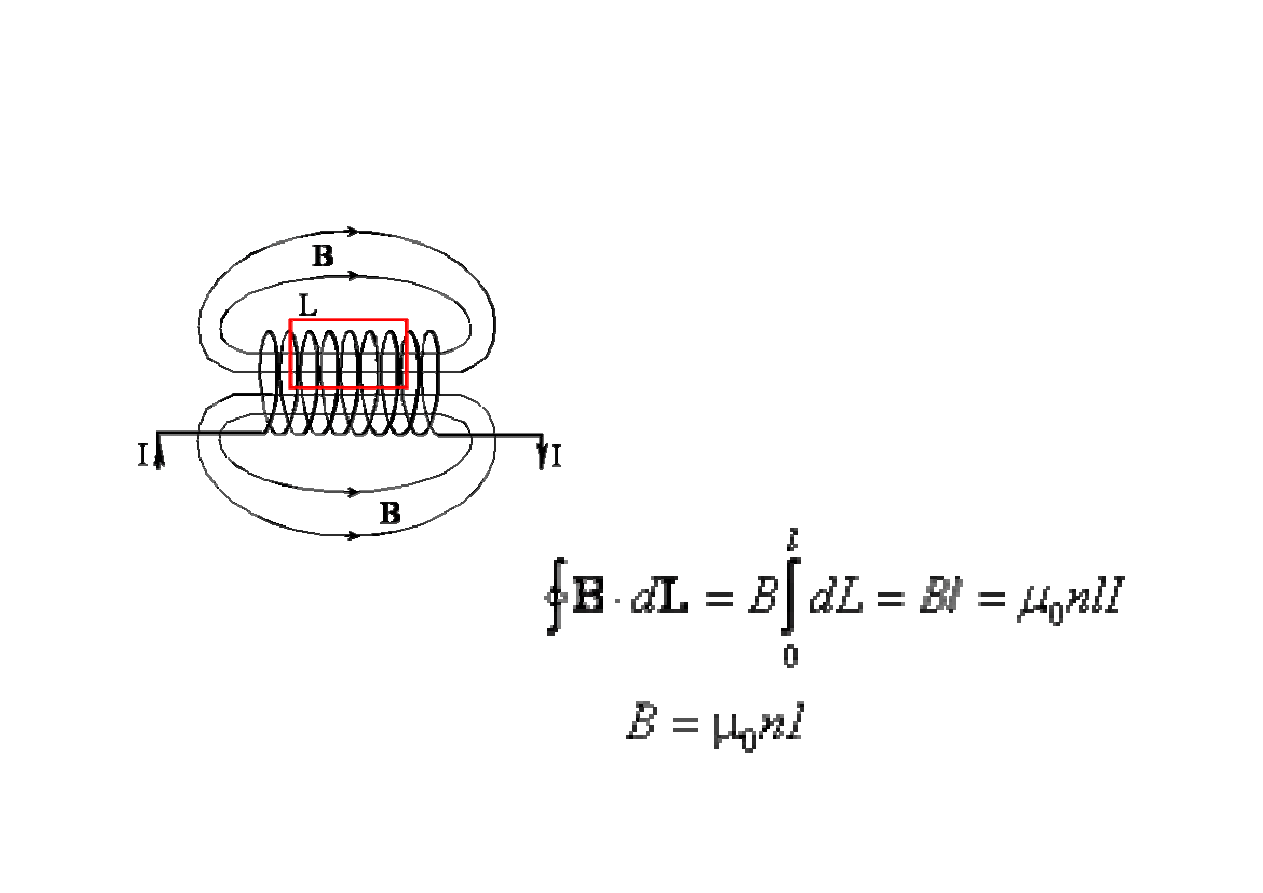
pole B na osi solenoidu zawieraj

ą

cego N zwojów, przez który płynie pr

ą

d I. .

Przyjmujemy,

ż

e warto

ść

pola B jest równa

zeru na zewn

ą

trz

ś

ciany uzwojenia. Pionowe

boki prostok

ą

ta s

ą

prostopadłe do wektora B, a

zatem iloczyn skalarny B·dL jest na tych
bokach równy zeru. W ten sposób całkowanie
w prawie Ampere’a redukuje si

ę

do zwykłej

całki wzdłu

ż

boku le

żą

cego na osi solenoidu.

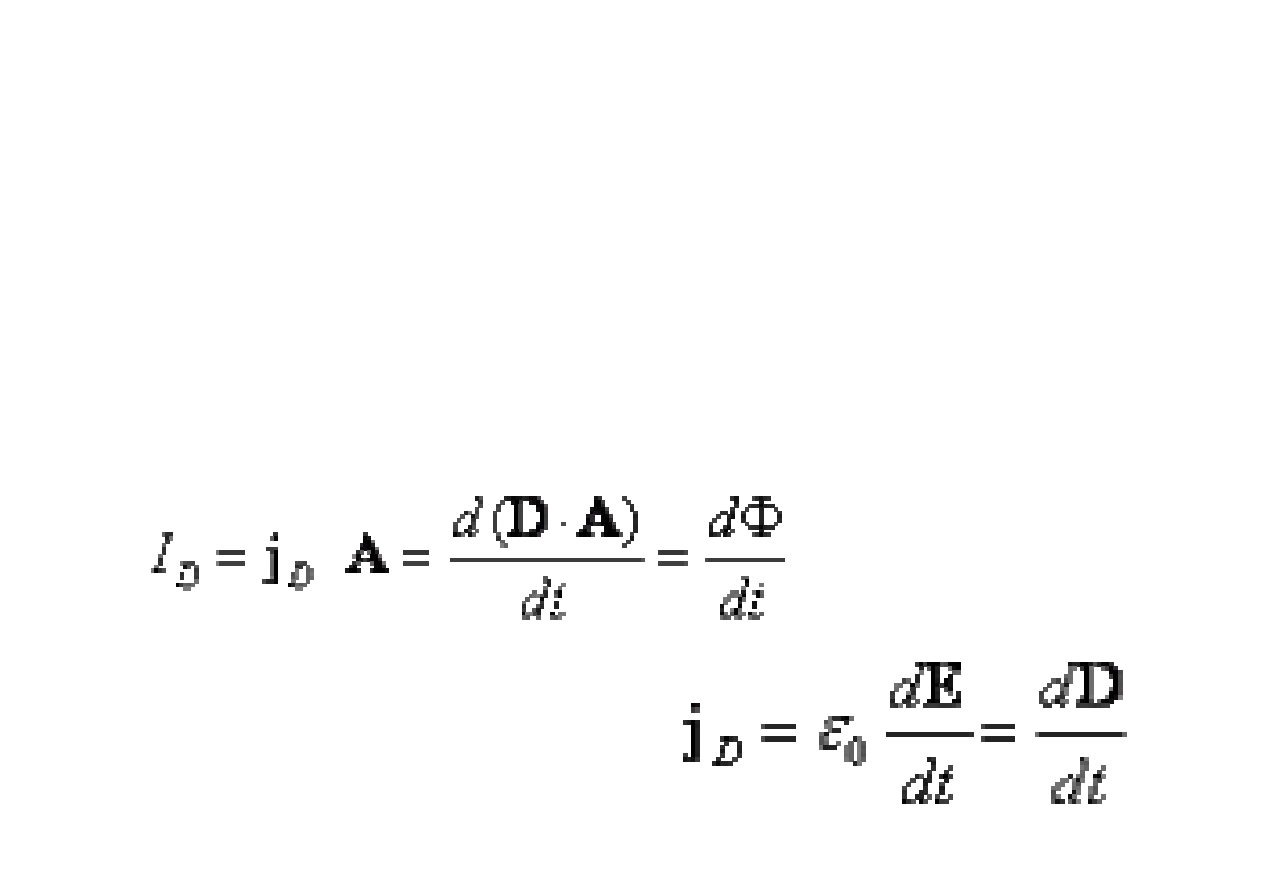
Pr

ą

d przesuni

ę

cia

Pr

ą

d przesuni

ę

cia jest tym pr

ą

dem, który jest wywołany

zmian

ą

ładunków na okładkach kondensatora, (co oznacza

przesuni

ę

cie mi

ę

dzy okładkami ładunków o tej samej

warto

ś

ci, ale o przeciwnych znakach). Je

ż

eli kondensator

ma okładki o powierzchni A to ładunek zgromadzony na
ka

ż

dej z nich ma warto

ść σ

A, gdzie

σ

jest g

ę

sto

ś

ci

ą

ładunku.

gdzie j

D

jest g

ę

sto

ś

ci

ą

pr

ą

du przesuni

ę

cia

Φ

D

jest strumieniem wektora D

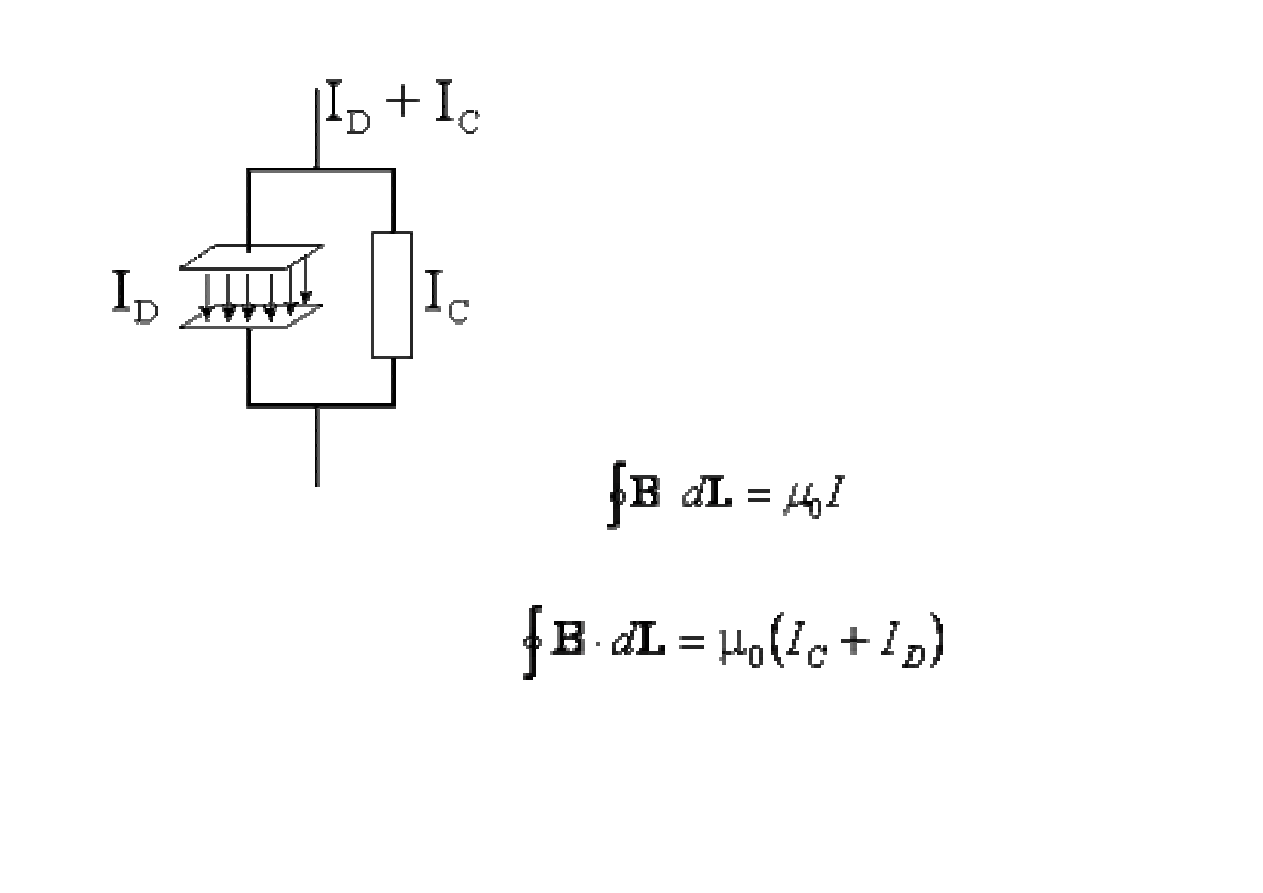
Ca

ł

kowity pr

ą

d jest teraz sum

ą

pr

ą

du przesuni

ę

cia I

D

(displacement) i

pr

ą

du przewodzenia I

C

(conduction)

Prawo Ampere’a, w postaci ogólnej

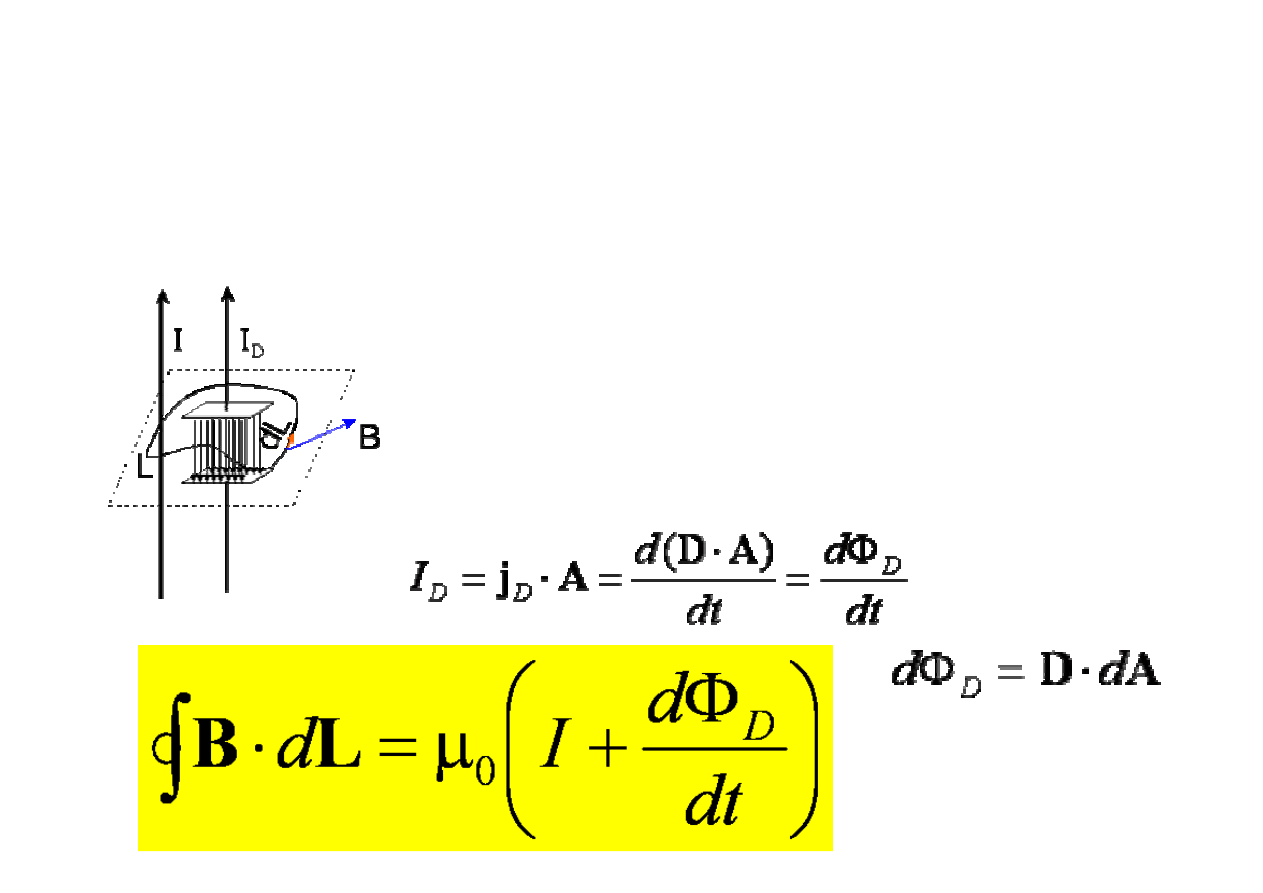
wirowe pole magnetyczne

Powstaje:
-wokół przewodnika z pr

ą

dem

- wokół linii zmieniaj

ą

cego si

ę

pola elektrycznego

Oznacza to,

ż

e pr

ą

d przesuni

ę

cia I

D

jest w prawie

Ampere’a traktowany tak, jak i zwyk

ł

y pr

ą

d

przewodzenia I

C

.

Poniewa

ż

pr

ą

d przesuni

ę

cia I

D

jest równy pr

ę

dko

ś

ci

zmian strumienia wektora przesuni

ę

cia D

cyrkulacj

ę

wektora B

wzdłu

ż

konturu

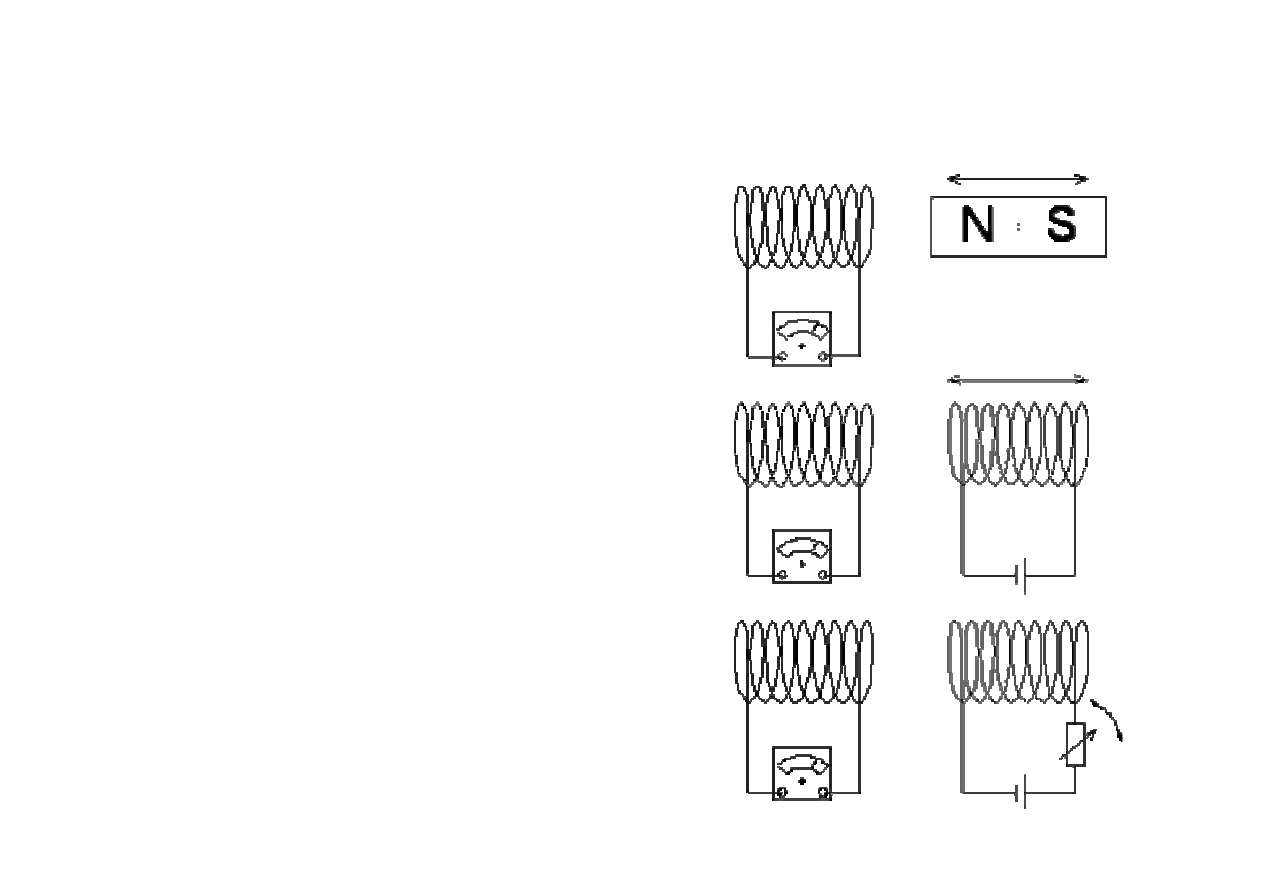
Indukcja elektromagnetyczna

zmiana pola

magnetycznego
obejmuj

ą

cego obwód

elektryczny powoduje
powstanie siły
elektromotorycznej w
tym obwodzie, co w
przypadku obwodu
zamkni

ę

tego

powoduje przepływ
pr

ą

du elektrycznego.

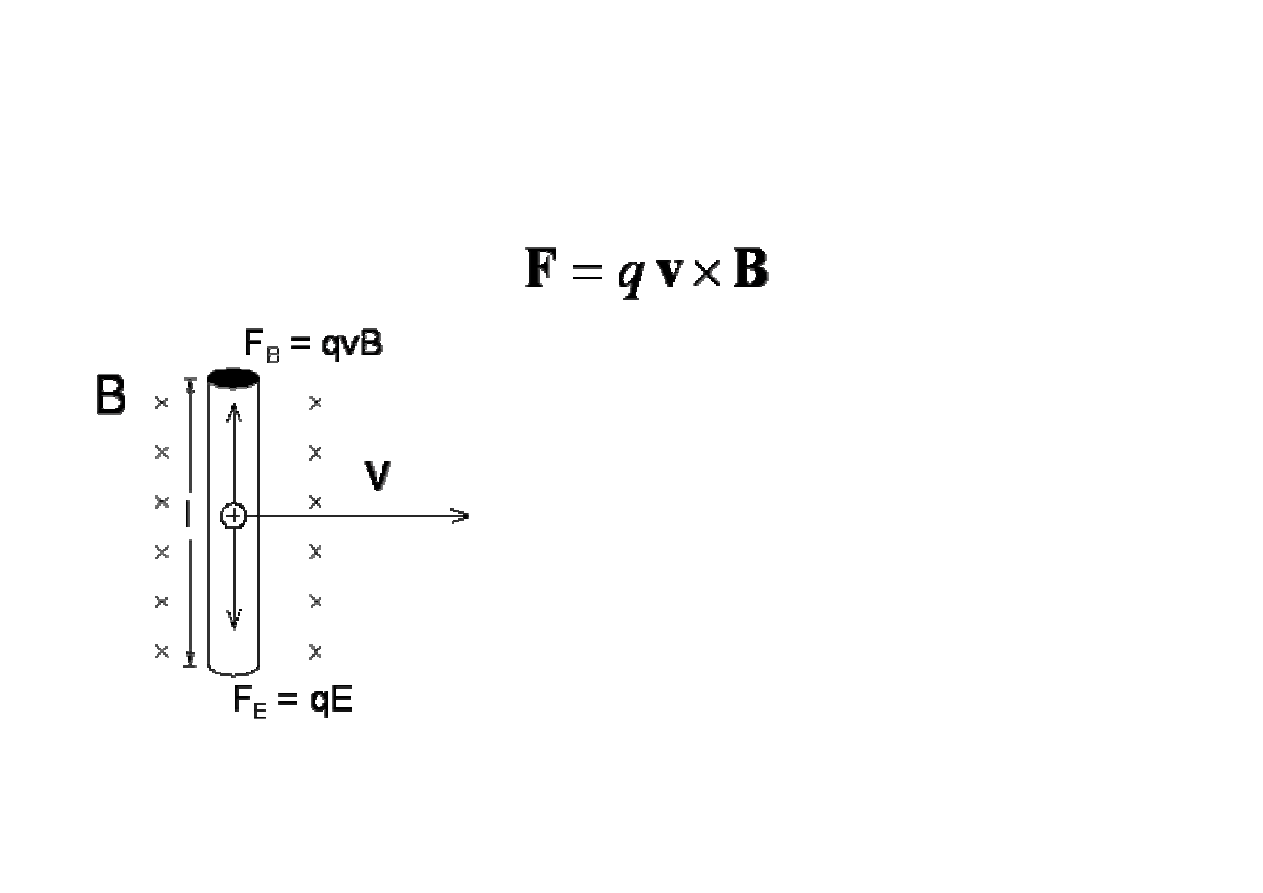
Ź

ród

ł

em zjawisk indukcyjnych jest znowu si

ł

a Lorentza F

pojawiaj

ą

ca si

ę

, gdy

ł

adunek q porusza si

ę

z pr

ę

dko

ś

ci

ą

v w

polu magnetycznym B

Gdy przewodnik przesuwamy w polu B,
to ruchome no

ś

niki

ł

adunku zostan

ą

przesuni

ę

te pod dzia

ł

aniem si

ł

y

Lorentza tak daleko a

ż

pojawi si

ę

w

przewodniku pole elektryczne E i si

ł

a

dzia

ł

aj

ą

ca na no

ś

niki F = qE zrównowa

ż

y

si

łę

Lorentza. Kiedy prostoliniowy

przewodnik o d

ł

ugo

ś

ci l porusza si

ę

z

jednostajn

ą

pr

ę

dko

ś

ci

ą

v w jednorodnym

polu magnetycznym B skierowanym
prostopadle do osi przewodnika i do
wektora pr

ę

dko

ś

ci v

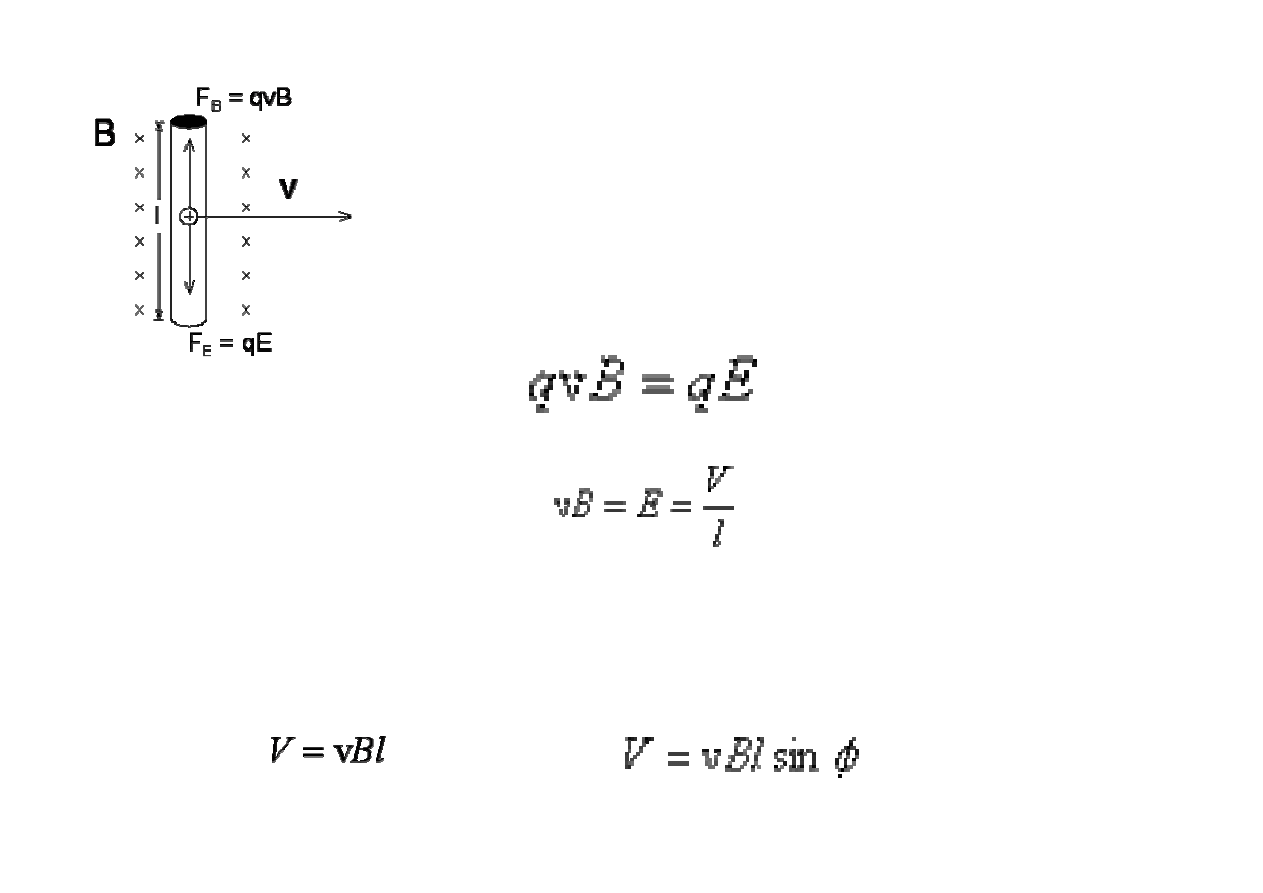
warunek równowagi mi

ę

dzy si

łą

Lorentza

a si

łą

odpychania mi

ę

dzy

ł

adunkami

zapiszemy w postaci równania

gdzie V jest ró

ż

nic

ą

potencja

ł

ów na ko

ń

cach przewodnika o d

ł

ugo

ś

ci l.

Warto

ść

tej ró

ż

nicy potencja

ł

ów wynosi zatem

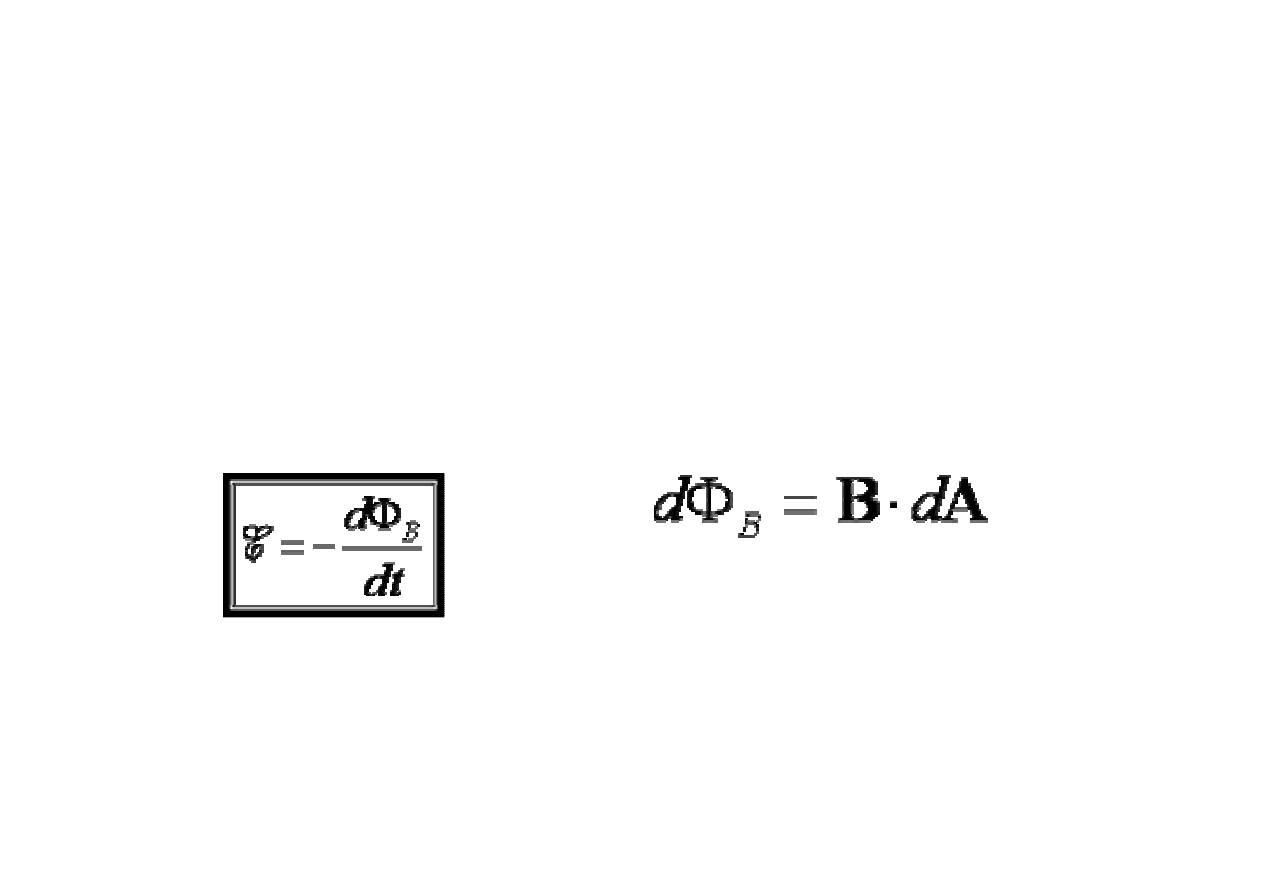
Prawo Faradaya

Michael Faraday (1791 – 1867) stwierdził,

ż

e siła elektromotoryczna E pojawia

si

ę

w przewodniku gdy otaczaj

ą

ce ten przewodnik pole magnetyczne ulega

zmianie, warto

ść

generowanej siły elektromotorycznej jest proporcjonalna do

szybko

ś

ci zmian pola magnetycznego oraz

ż

e kierunek indukowanej siły

elektromotorycznej zale

ż

y od kierunku, w którym nast

ę

puj

ą

zmiany pola

magnetycznego. Wszystkie te fakty s

ą

zawarte w jednym tylko równaniu

- zmiana warto

ś

ci wektora B;

-zmiana warto

ś

ci pola powierzchni dA;

-zmiana k

ą

ta mi

ę

dzy B i dA;

- jednoczesna zmiana B i dA;
- jednoczesna zmiana B i k

ą

ta;

- jednoczesna zmiana dA i k

ą

ta.

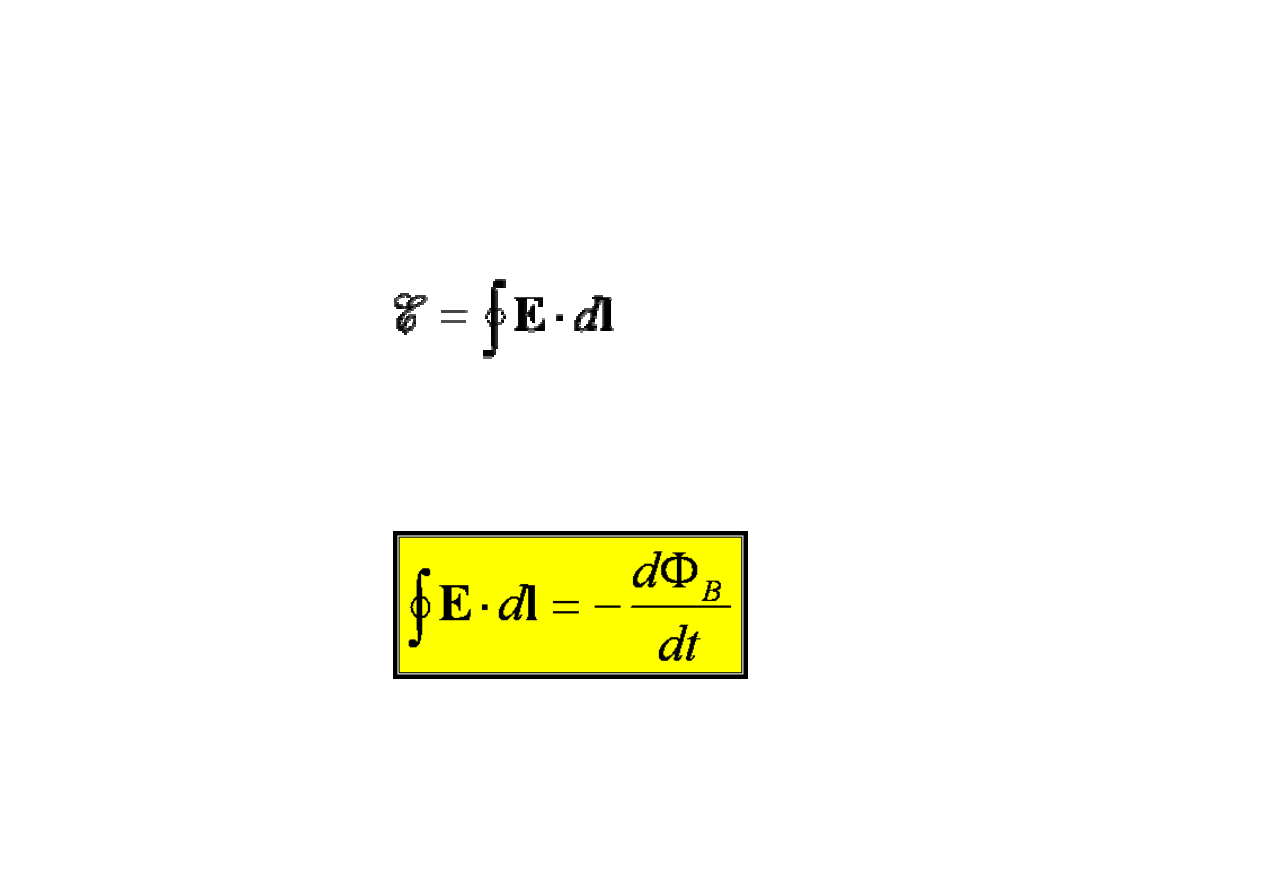
W ogólnym przypadku, nawet wtedy, gdy nie ma

ż

adnych

przewodników, si

ł

a elektromotoryczna jest równa cyrkulacji

pola elektrycznego E wzd

ł

u

ż

konturu zamkni

ę

tego

prawo Faradaya w postaci uogólnionej

Reguła Lenza

• Reguła Lenza (znak minus w prawie

Faradaya) ustala,

ż

e kierunek pr

ą

du

indukowanego w procesie indukcji
elektromagnetycznej jest taki, aby własne
pole magnetyczne tego pr

ą

du miało taki

kierunek zmian, który przeciwdziała
zmianom pola indukuj

ą

cego. aby osłabia

ć

pole narastaj

ą

ce ale wzmacnia

ć

pole

słabn

ą

ce.

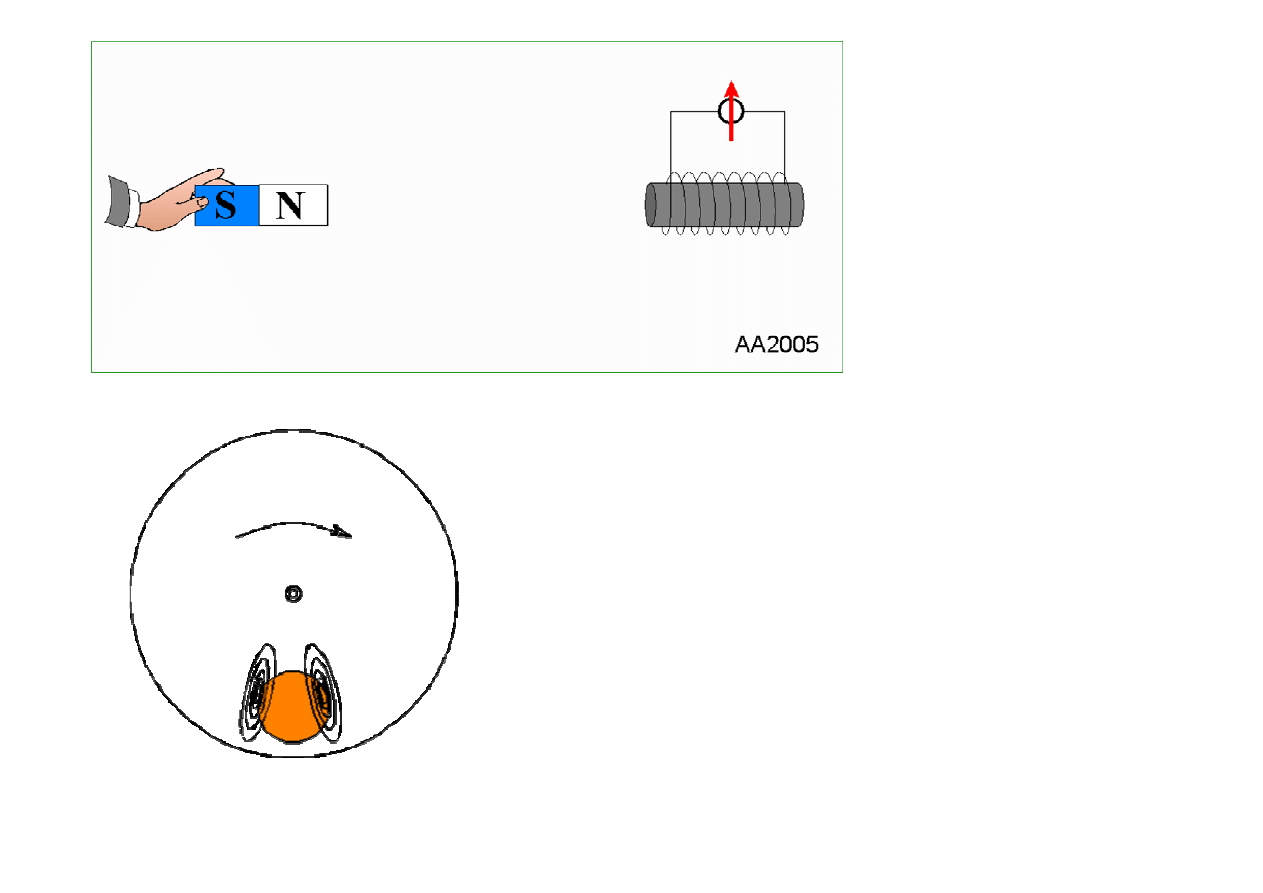
Kierunek indukowanego pr

ą

du

Pr

ą

dy wirowe

Pole magnetyczne pr

ą

dów wirowych jest tak

skierowane,

ż

e ta cz

ęść

tarczy, która

wychodzi z pola b

ę

dzie z powrotem wci

ą

gana

do pola natomiast ta cz

ęść

tarczy, która

wchodzi w obszar pola b

ę

dzie z tego pola

wypychana.

Efekt Halla

Polega on na wyst

ą

pieniu ró

ż

nicy potencjałów w

przewodniku, w którym płynie pr

ą

d elektryczny,

gdy przewodnik znajduje si

ę

w poprzecznym do

płyn

ą

cego pr

ą

du polu magnetycznym.

Napi

ę

cie to, zwane napi

ę

ciem Halla, pojawia si

ę

mi

ę

dzy płaszczyznami ograniczaj

ą

cymi

przewodnik, prostopadle do płaszczyzny
wyznaczanej przez kierunek pr

ą

du i wektor

indukcji pola magnetycznego. Jest ono
spowodowane działaniem siły Lorentza na
ładunki poruszaj

ą

ce si

ę

w polu magnetycznym.

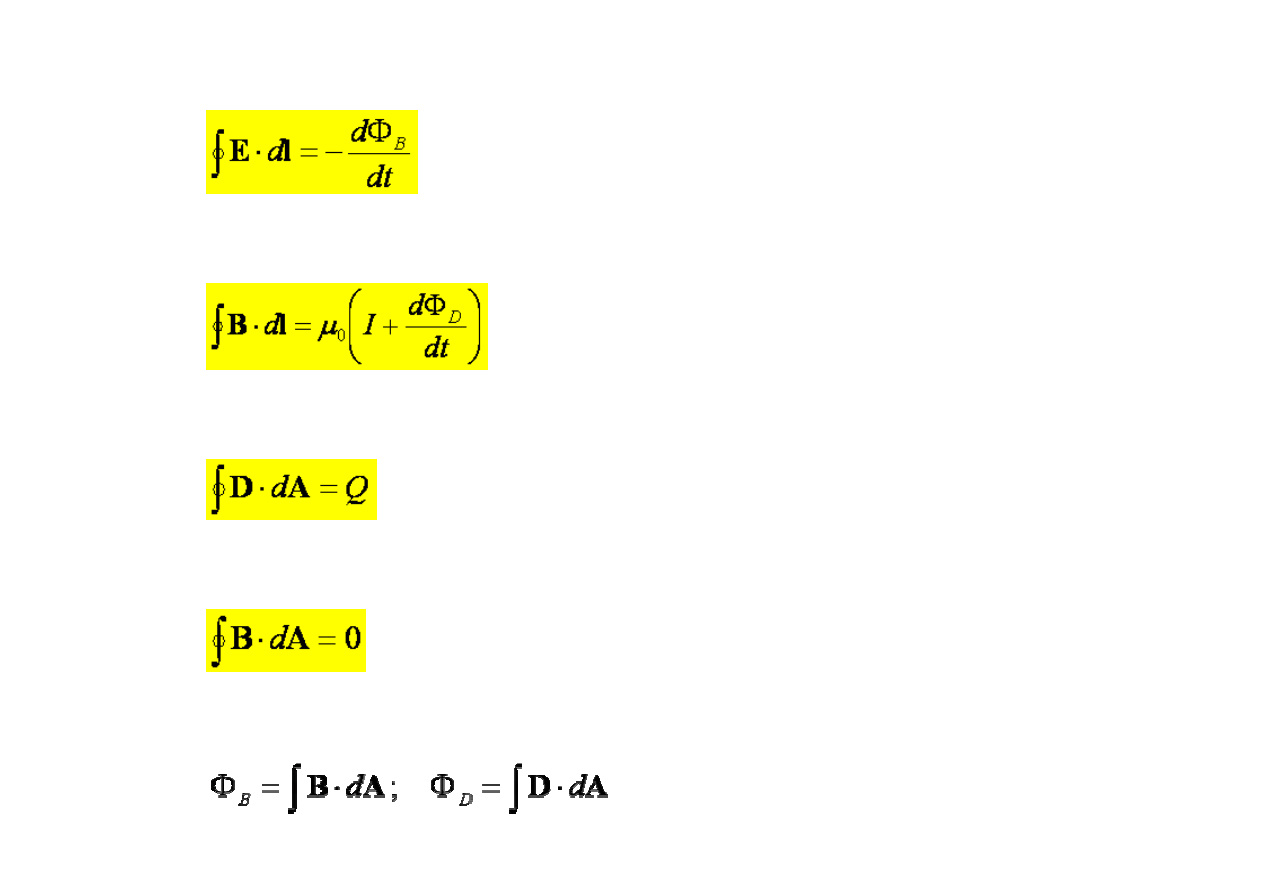
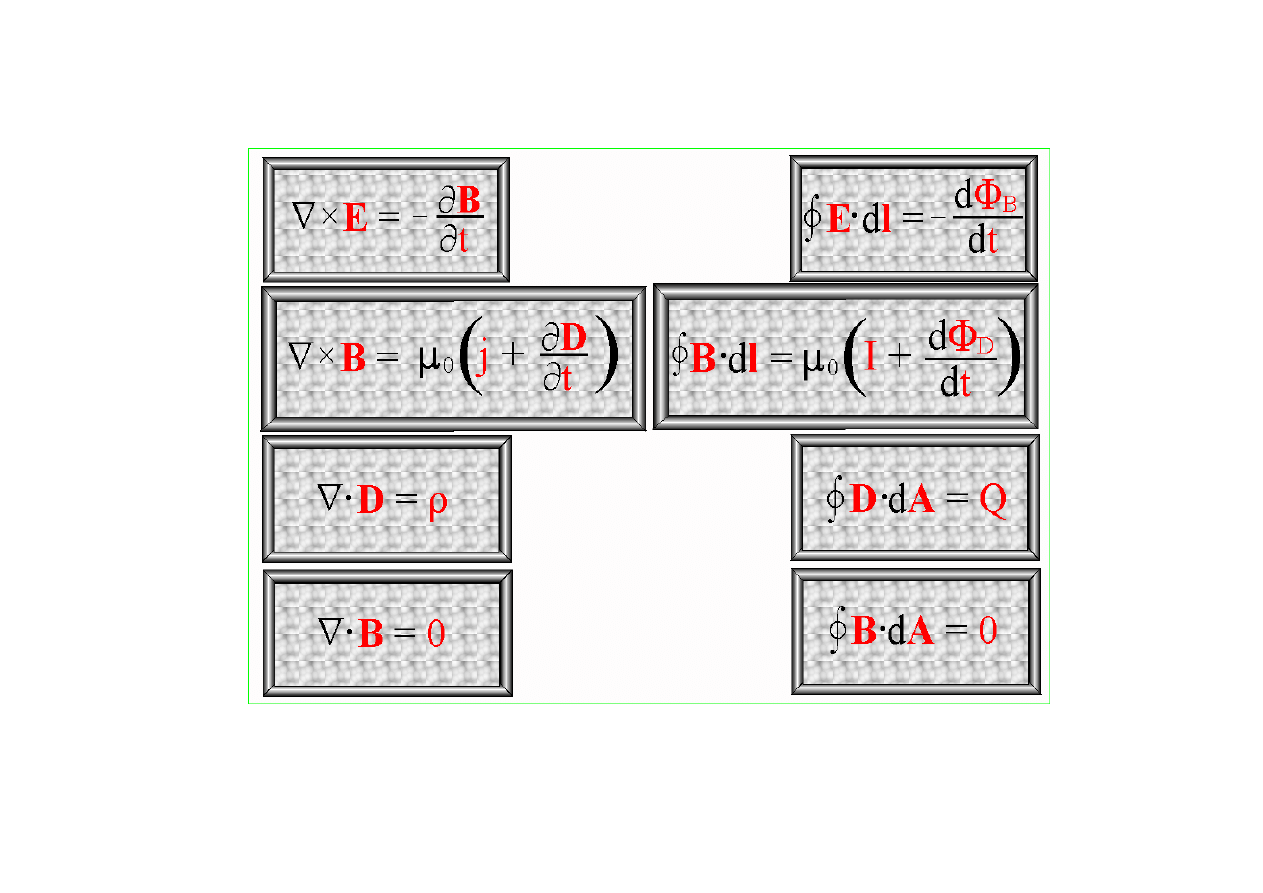
Prawo Faradaya

Uogólnione prawo Ampera

Prawo Gaussa dla pola elektrycznego

Prawo Gaussa dla pola magnetycznego