Zadanie 3: Dla belki wolnopodpartej jak na

Rys.1

(str.2), wyznaczyć

metodą Clebscha

:

• równanie odkształconej osi belki,

• równanie kątów obrotu przekrojów belki,

• sporządzić wykresy:

• odkształconej osi belki

•

kątów obrotu przekrojów belki

Metoda Clebscha

Przy określonym porządku zapisywania i całkowania równań różniczkowych

odkształconej osi belki można zredukować ilość dowolnych stałych całkowania do liczby
dwóch: C i D. Równość między sobą dowolnych stałych całkowania
(C

1

= C

2

=...= C i D

1

= D

2

= ... = D ) jest możliwa przy spełnieniu następujących

warunków:

1.

odcięte we wszystkich przedziałach powinny być liczone od jednego i tego samego

początku układu współrzędnych - skrajnego lewego (lub prawego) punktu osi belki

;

2. wszystkie składowe w wyrażeniu na moment gnący w przedziale poprzednim powinny

powtórzyć się bez zmian w wyrażeniu na moment gnący dla przedziału następnego;
warunek ten może byc spełniony, jeżeli przy zapisywaniu równania momentów
w poszczególnych przedziałach belki będziemy rozpatrywać tę część belki, która
zawiera w sobie początek układu współrzędnych;

3.

w przypadku działania obciążenia rozłożonego w sposób ciągły kończącego się
w określonym punkcie belki spełnienie warunku

(2)

wymaga doprowadzenia tego

obciążenia do końca belki z jednoczesnym dodaniem na tym odcinku równoważnego mu
obciążenia o zwrocie przeciwnym

;

4. wszystkie nowe dochodzące człony w wyrażeniu na moment gnący dla dalszych

przedziałów (odcinków belki) powinny zawierać mnożnik

(x-a)

, gdzie

a

- suma długości

wszystkich poprzednich przedziałów (odcinków);

5.

w przypadku działania w pewnym przekroju belki pary o momencie M (moment
skupiony) warunek

(4)

będzie spełniony, jeśli w wyrażeniu na M(x) wielkość M będzie

pomnożona przez

(x-a)

0

,

a

- część długości belki od początku układu współrzędnych do

punktu przyłożenia M

;

6. całkowanie równania różniczkowego powinno przebiegać bez rozwijania wyrażeń

w nawiasach.

http://www.pk.edu.pl/~iwroblew/dydaktyka

1/6

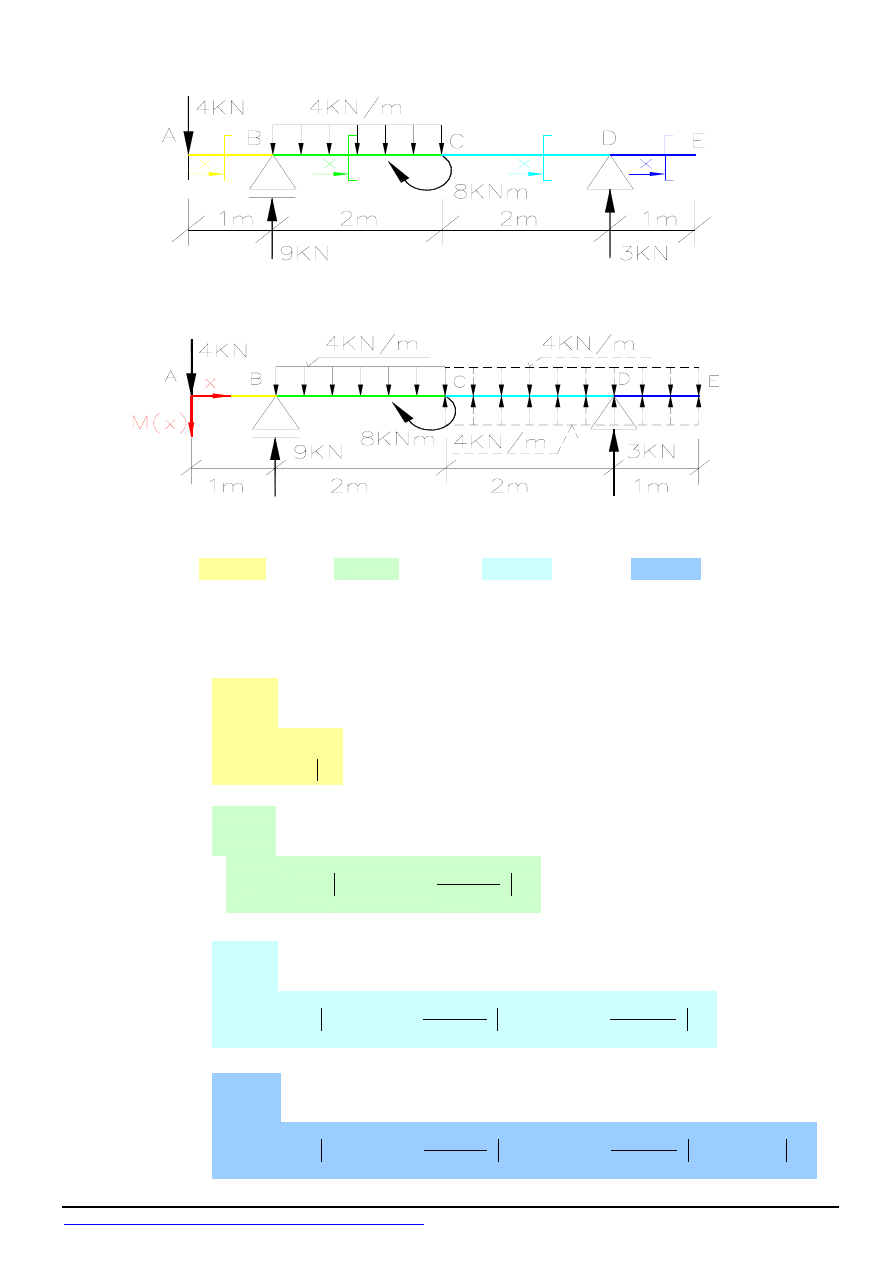
Rys.1

Rys.2

1

0

≤

≤ x

3

1

≤

≤ x

5

3

≤

≤ x

6

5

≤

≤ x

Równania momentów zginajacych w poszczególnych przedziałach osi belki -

Rys.2

wg zapisu

metodą Clebscha

:

1

0

B

A

≤

≤

−

x

[

]

AB

x

x

M

4

)

(

−

=

3

1

C

B

≤

≤

−
x













−

−

−

+

−

=

BC

AB

x

x

x

x

M

2

)

1

(

4

)

1

(

9

4

)

(

2

5

3

D

C

≤

≤

−

x













−

+

−

+

−

−

−

+

−

=

CD

BC

AB

x

x

x

x

x

x

M

2

)

3

(

4

)

3

(

8

2

)

1

(

4

)

1

(

9

4

)

(

2

0

2

6

5

E

D

≤

≤

−
x













−

+

−

+

−

+

−

−

−

+

−

=

DE

CD

BC

AB

x

x

x

x

x

x

x

M

)

5

(

3

2

)

3

(

4

)

3

(

8

2

)

1

(

4

)

1

(

9

4

)

(

2

0

2

http://www.pk.edu.pl/~iwroblew/dydaktyka

2/6

Równanie różniczkowe odkształconej osi belki:

)

(

2

2

x

M

x

d

w

d

EJ

−

=

−

=

x

d

w

d

EJ

2

2

[

x

4

−

AB

2

)

1

x

(

4

)

1

x

(

9

2

−

−

−

+

BC

2

)

3

x

(

4

)

3

x

(

8

2

0

−

+

−

+

CD

)

5

x

(

3

−

+

DE

]

1

0

≤

≤ x

3

1

≤

≤ x

5

3

≤

≤ x

6

5

≤

≤ x

Równanie kątów obrotu przekrojów belki:

2

4

2

x

C

dx

dw

EJ

+

=

AB

6

)

1

(

4

2

)

1

(

9

3

2

−

+

−

−

x

x

BC

6

)

3

(

4

)

3

(

8

3

−

−

−

−

x

x

CD

2

)

5

(

3

2

−

−

x

DE

Równanie odkształconej osi belki

6

4

3

x

Cx

D

EJw

+

+

=

AB

24

)

1

(

4

6

)

1

(

9

4

3

−

+

−

−

x

x

BC

24

)

3

(

4

2

)

3

(

8

4

2

−

−

−

−

x

x

CD

6

)

5

(

3

3

−

−

x

DE

Warunki brzegowe:

:

Dla

1

=

x

0

=

w

6

1

4

1

0

3

∗

+

∗

+

=

∗

C

D

EJ

Dla

5

=

x

0

=

w

24

)

3

5

(

4

2

)

3

5

(

8

24

)

1

5

(

4

6

)

1

5

(

9

6

5

4

5

0

4

2

4

3

3

−

−

−

−

−

+

−

−

∗

+

∗

+

=

∗

C

D

EJ

Obliczenie stałych D i C:







+

+

=

+

+

=

3333

,

11

5

0

6667

,

0

0

C

D

C

D

6667

,

2

−

=

C

0

,

2

=

D

http://www.pk.edu.pl/~iwroblew/dydaktyka

3/6

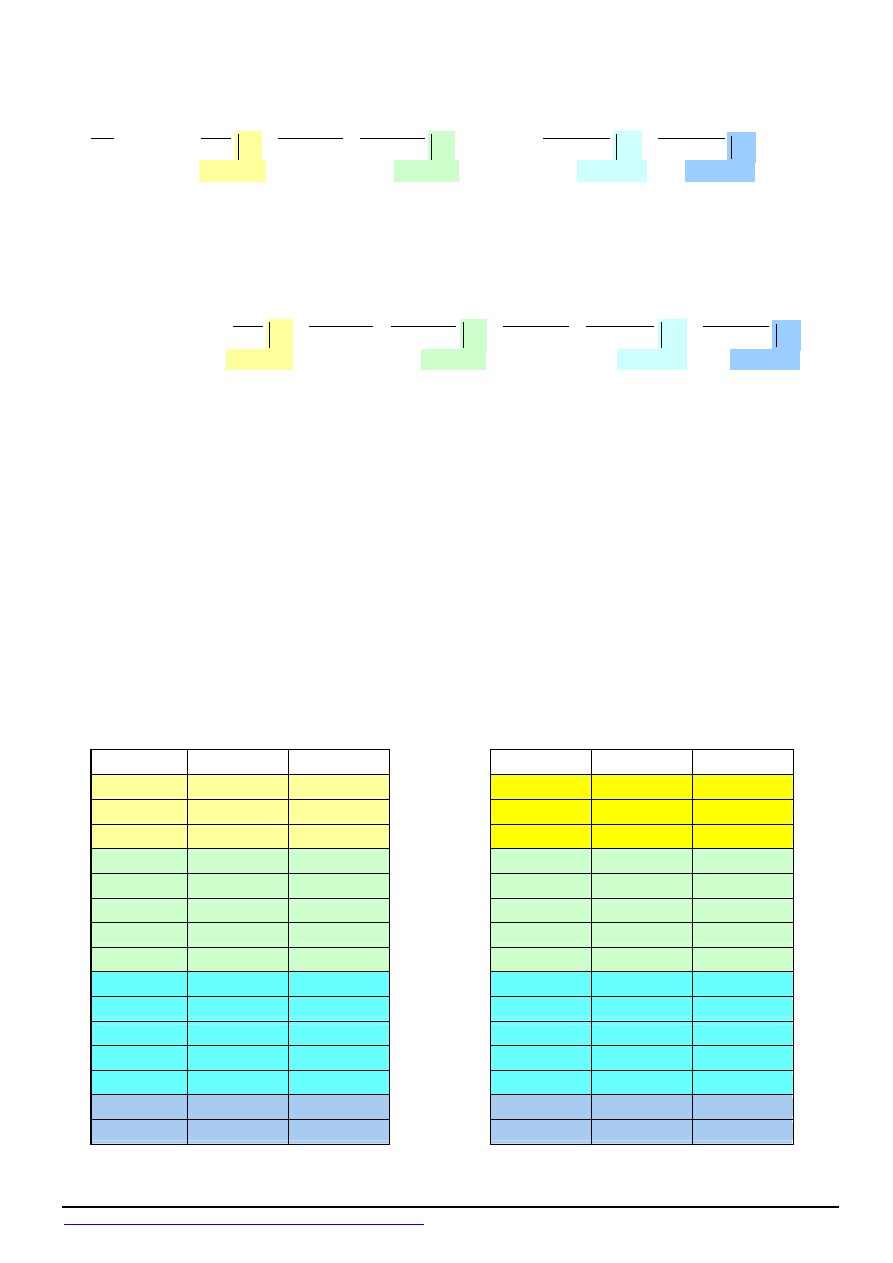
Równanie kątów obrotu przekrojów belki

2

4

667

,

2

2

x

dx

dw

EJ

+

−

=

AB

6

)

1

(

4

2

)

1

(

9

3

2

−

+

−

−

x

x

BC

6

)

3

(

4

)

3

(

8

3

−

−

−

−

x

x

CD

2

)

5

(

3

2

−

−

x

DE

1

0

≤

≤ x

3

1

≤

≤ x

5

3

≤

≤ x

6

≤

≤ x

5

Równanie odkształconej osi belki

6

4x

2,6667x

2,0

3

+

−

=

EJw

AB

24

)

1

(

4

6

)

1

(

9

4

3

−

+

−

−

x

x

BC

24

)

3

(

4

2

)

3

(

8

4

2

−

−

−

−

x

x

CD

6

)

5

(

3

3

−

−

x

DE

1

0

≤

≤ x

3

1

≤

≤ x

5

3

≤

≤ x

6

5

≤

≤ x

Obliczenie wartości w(x) -

Tabela 1

oraz w’(x) -

Tabela 2

w poszcególnych przedziałach osi belki.:

Przekrój belki – dwuteownik 100

J

y

= 171*10

−8

m

4

E = 2*10

8

KN/m

2

EJ = 342 KNm

2

Tabela 1

Tabela 2

x [m]

EJ*w(x)

w(x) [m]

x [m]

EJ*w'(x)

w'(x) rd

0

2

0,005848

0

-2,667

-0,0078

0,4

0,976

0,002854

0,4

-2,3467

-0,00686

1

0

0

1

-0,6667

-0,00195

1,19

-0,06

-0,00018

1,188

0

0

1,4

0,0043

1,26E-05

1,4

0,578

0,00169

2

0,6667

0,001949

2

1,5

0,004386

2,4

1,3403

0,003919

2,4

1,863

0,005447

3

2,6667

0,007797

3

2,667

0,007798

3,4

3,2853

0,009606

3,4

0,507

0,001482

3,609

3,3127

0,009686

3,609

0

0

4

2,8333

0,008285

4

-1,833

-0,00536

4,4

1,892

0,005532

4,4

-2,7933

-0,00817

5

0

0

5

-3,333

-0,00975

5,4

-1,3333

-0,0039

5,4

-3,3333

-0,00975

6

-3,3333

-0,00975

6

-3,3333

-0,00975

http://www.pk.edu.pl/~iwroblew/dydaktyka

4/6

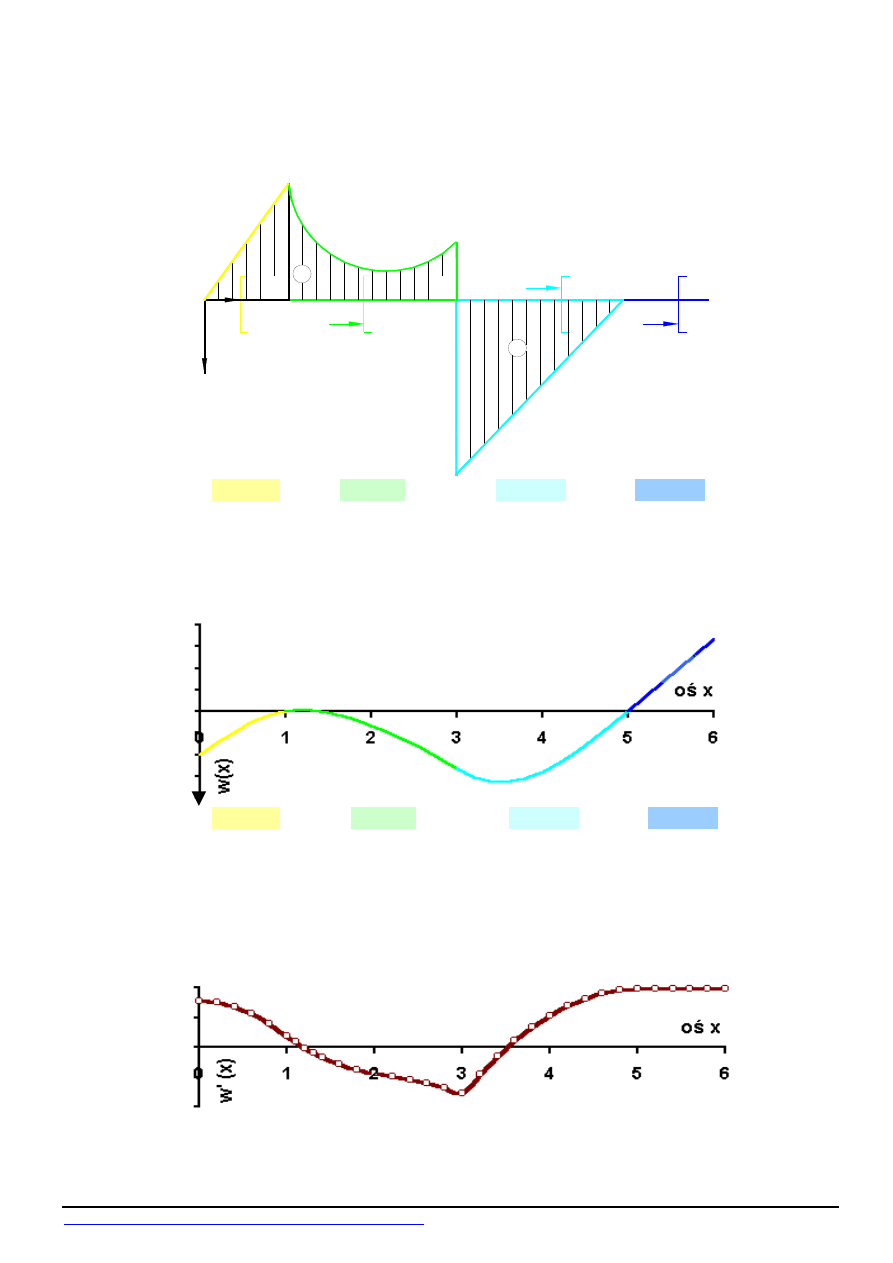
W Y K R E S Y

Wykres momentów zginających M(x)

A

C

D

E

x

x

x

x

M(x)

-4,

0

B

-2

,0

+6

,0

+

-

1

0

≤

≤ x

3

1

≤

≤ x

5

3

≤

≤ x

6

5

≤

≤ x

Wykres odkształconej osi belki w(x) [m]

1

0

≤

≤ x

3

1

≤

≤ x

5

3

≤

≤ x

6

5

≤

≤ x

Wykres kątów obrotu przekrojów belki w

′(x) [rd]

Zestawienie wykresów:

http://www.pk.edu.pl/~iwroblew/dydaktyka

5/6

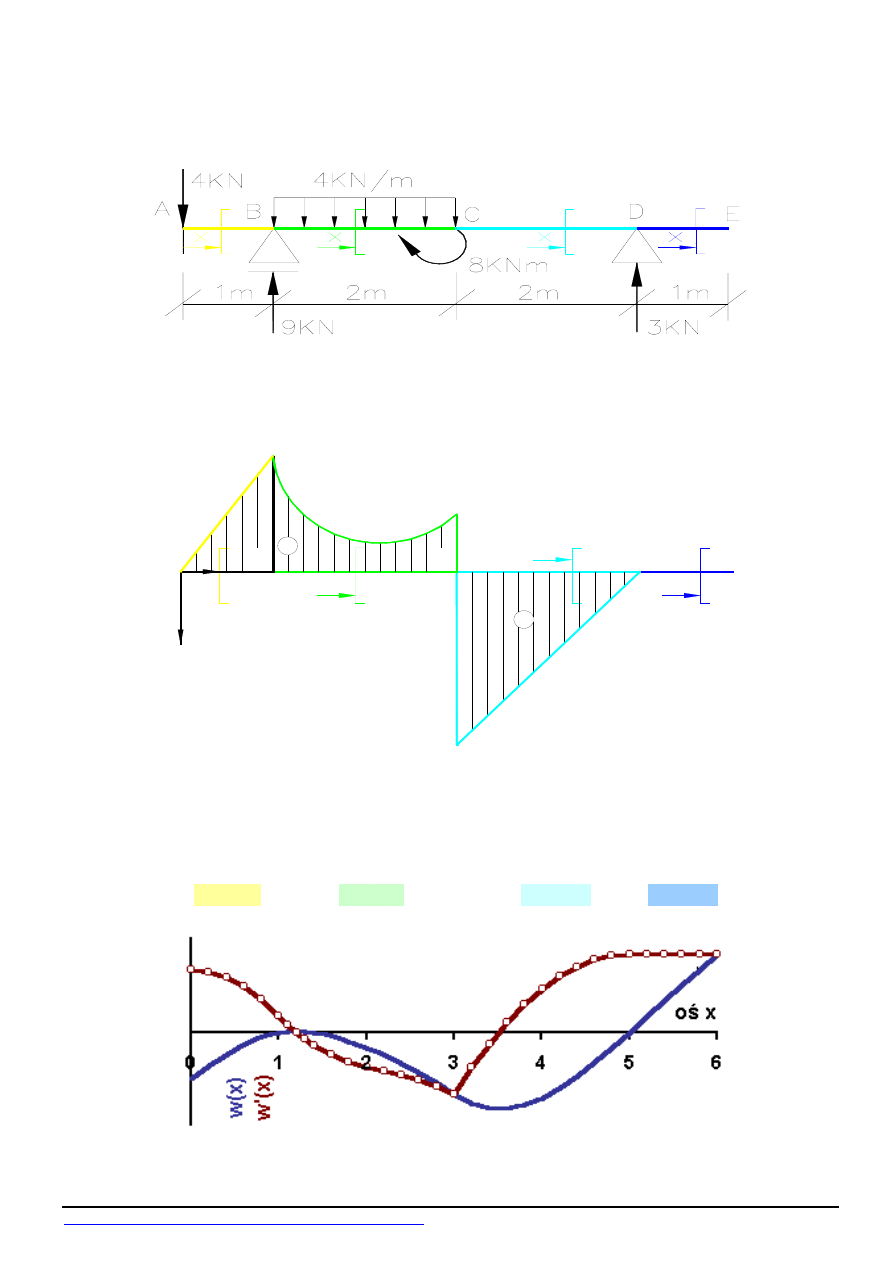
KOŃCOWE ZESTAWIENIE WYKRESÓW

1. Dana belka wolnopodparta obciążona jak na rysunku poniżej:

2. Wykres momentów zginających M(x)

A

C

D

E

x

x

x

x

M (x )

-4,

0

B

-2,

0

+6

,0

+

-

3. Wykresy:

• odkształconej osi belki w(x)

• wykres kątów obrotu przekrojów belki w′(x)

1

≤

≤ x

0

3

1

≤

≤ x

5

3

≤

≤ x

6

5

≤

≤ x

http://www.pk.edu.pl/~iwroblew/dydaktyka

6/6