Termodynamika

Równanie stanu gazu dla 1 kg masy czynnika

RT

v

p

=

⋅

gdzie: p - bezwzględne ciśnienie statyczne czynnika

T

R

p

v

⋅

=

⇒

=

ρ

ρ

1

v– objętość właściwa czynnika (dla 1 kg!!!)

R- indywidualna stała gazowa

T- bezwzględna temperatura czynnika T=(273,15 + t )[K]

Równanie stanu gazu dla całej masy czynnika

mRT

pV

V

m

v

mRT

m

v

p

=

⇒

=

⋅

⇒

=

⋅

⋅

RT

pv

RT

v

p

µ

µ

µ

=

⇒

=

⋅

/

ponieważ

m

V

v

=

⋅

µ

i

B

R

=

⋅

µ

otrzymujemy równanie

BT

V

p

m

=

⋅

µ

- masa cząsteczkowa czynnika

V

m

– objętość molowa













kmol

m

3













=

=

⇒

=

3

2

96

,

1

42

,

22

44

.

m

kg

np

V

CO

m

m

m

ρ

µ

ρ

inny wzór na gęstość w warunkach umownych:

u

u

m

u

m

u

T

R

P

stąt

T

R

p

T

R

v

p

⋅

−

⇒

⋅

=

⋅

⇒

⋅

=

⋅

ρ

ρ

,

1

stałą R liczymy ze wzoru

m

B

R

µ

=

B- 8314,3









⋅

K

kmol

J

, do obliczeń ciepła właściwego podstawiamy B=8,3143









⋅

K

kmol

kJ

W warunkach umownych

p

u

=101325 [Pa] czyli około 760[mmHg]

T

u

=273,15 [K]

Dla umownych warunków temperatury i ciśnienia V

m

dla różnych gazów przyjmuje taką samą wartość

V

m

=22,42













kmol

m

3

T

B

V

p

m

⋅

=

⋅

→

µ

⋅

=

n

m

gdzie: n- liczba kmoli cząsteczek gazu

T

R

n

V

p

m

⋅

⋅

⋅

=

⋅

µ

→

B

R

=

⋅

µ

T

B

n

V

p

m

⋅

⋅

=

⋅

Mieszaniny gazów

Równania stanu gazu przed zmieszaniem

T

R

m

V

p

1

1

1

=

⋅

i

T

R

m

V

p

2

2

2

=

⋅

Wartości które należy

pamiętać:

p

u

=101325 [Pa]

T

u

=273,15 [K]

V

m

=22,42













kmol

m

3

B- 8314,3









⋅

K

kmol

J

lub

B=8,3143









⋅

K

kmol

kJ

ps

µ

-masa cząst. powietrza

suchego = 28,87









kmol

kg

p, T

m

1

, V

1

, R

1

p, T

m

2

, V

2

, R

2

Po otwarciu zaworu

T

mR

V

p

m

=

⋅

a)

2

1

m

m

m

+

=

b)

2

1

V

V

V

+

=

c)

2

1

n

n

n

+

=

(bilans molowy)

Określanie udziałów masowych

2

2

1

1

2

1

0

,

1

g

m

m

g

m

m

m

m

m

m

=

∩

=

⇒

=

+

Udziały objętościowe

2

2

1

1

2

1

0

,

1

r

V

V

r

V

V

V

V

V

V

=

∩

=

⇒

=

+

Udziały molowe

2

2

1

1

2

1

0

,

1

z

n

n

z

n

n

n

n

n

n

=

∩

=

⇒

=

+

Przeliczanie udziałów

przeliczenie objętościowych na masowe

i

m

i

i

R

R

r

g

⋅

=

lub

m

i

i

i

r

g

µ

µ

⋅

=

przeliczenie masowych na objętościowe

m

i

i

i

R

R

g

r

⋅

=

lub

i

m

i

i

g

r

µ

µ

⋅

=

i

i

r

z

=

∑

⋅

=

i

i

m

r

µ

µ

m

m

R

B

=

µ

∑

⋅

=

i

i

m

R

g

R

m

m

B

R

µ

=

∑

⋅

=

i

i

m

r

ρ

ρ

m

i

i

V

µ

ρ

=

Cieśnienie cząstkowe

p

r

p

i

i

⋅

=

Obliczanie bilansów ciepła, mocy cieplnej układów, strumienia przekazywanego ciepła

1.)

t

c

m

Q

∆

⋅

⋅

=

lub inaczej

)

(

1

2

t

t

c

m

Q

Vm

−

⋅

⋅

=

gdzie m- masa

[ ]

kg

lub strumień masy









s

kg

czynnika, c-masowe ciepło właściwe













⋅

K

kg

kJ

2.)

t

C

V

Q

∆

⋅

⋅

=

lub inaczej

)

(

1

2

t

t

C

V

Q

Vm

−

⋅

⋅

=

gdzie V- objętość

[ ]

3

m

lub strumień obj.













s

m

3

czynnika, C-objętościowe ciepło właściwe









⋅

K

m

kJ

3

,

przy czym C musi być określone w tych samych warunkach p i T co V, najlepiej w war. umownych.

3.)

t

n

Q

c

∆

⋅

⋅

=

µ

lub inaczej

)

(

1

2

t

t

n

Q

CVm

−

⋅

⋅

=

µ

gdzie n- liczba kmoli czynnika,

c

µ

-molowe ciepło właściwe









⋅

K

kmol

kJ

,

Energia wewnętrzna molowa









kmol

kJ

U

µ









⋅

⋅

=

⇒

=

⋅

⇒









⋅

⋅

⋅

=

kmol

kJ

T

i

B

U

B

N

k

kmol

kJ

T

i

N

k

U

2

1

2

1

µ

µ

gdzie: k-stała Boltzmana, N-liczba Awogadra, i-liczba stopni swobody, T-temp. bezwzględna









⋅

=

kmol

kJ

u

U

µ

µ

gdzie u-energia wewnętrzna właściwa,

µ

-masa cząsteczkowa

T

i

B

u

⋅

⋅

=

⋅

2

1

µ

Molowe ciepło właściwe przy stałej objętości









⋅

⋅

=

K

kmol

kJ

i

B

c

v

2

1

µ

Molowe ciepło właściwe przy stałym ciśnieniu

)

2

(

2

1

+

⋅

=

⇒









⋅

+

=

i

B

c

K

kmol

kJ

c

B

c

p

v

p

µ

µ

µ

Określenie [i] dla gazów

Rodzaj gazu

liczba st. swobody

przykład gazu

gaz jednoatomowy

3

gaz 2- atomowy

5

O

2

, N

2

gaz 3-atomowy

CO

2

– 6

pozostałe 7

CO

2

H

2

0, CH

4

Obliczanie ciepła właściwego przy V= const

masowe













⋅

⋅

=

=

K

kg

kJ

i

B

c

c

v

v

µ

µ

µ

2

1

objętościowe









⋅

⋅

=

=

K

m

kJ

i

B

V

c

C

m

v

v

3

42

,

22

2

1

µ

Obliczanie ciepła właściwego przy p= const

masowe













⋅

+

⋅

=

=

K

kg

kJ

i

B

c

c

p

p

µ

µ

µ

)

2

(

2

1

objętościowe









⋅

+

⋅

=

=

K

m

kJ

i

B

V

c

C

m

p

vp

3

42

,

22

)

2

(

2

1

µ

Obliczanie ciepła właściwego mieszanin gazowych

∑













⋅

⋅

=

K

kg

kJ

c

g

c

i

i

m

∑









⋅

⋅

=

K

m

kJ

C

r

C

i

i

m

3

∑









⋅

=

3

m

kg

r

i

i

m

ρ

ρ

∑

⋅

=

i

i

m

V

g

V

∑

⋅

=

i

i

m

R

g

R

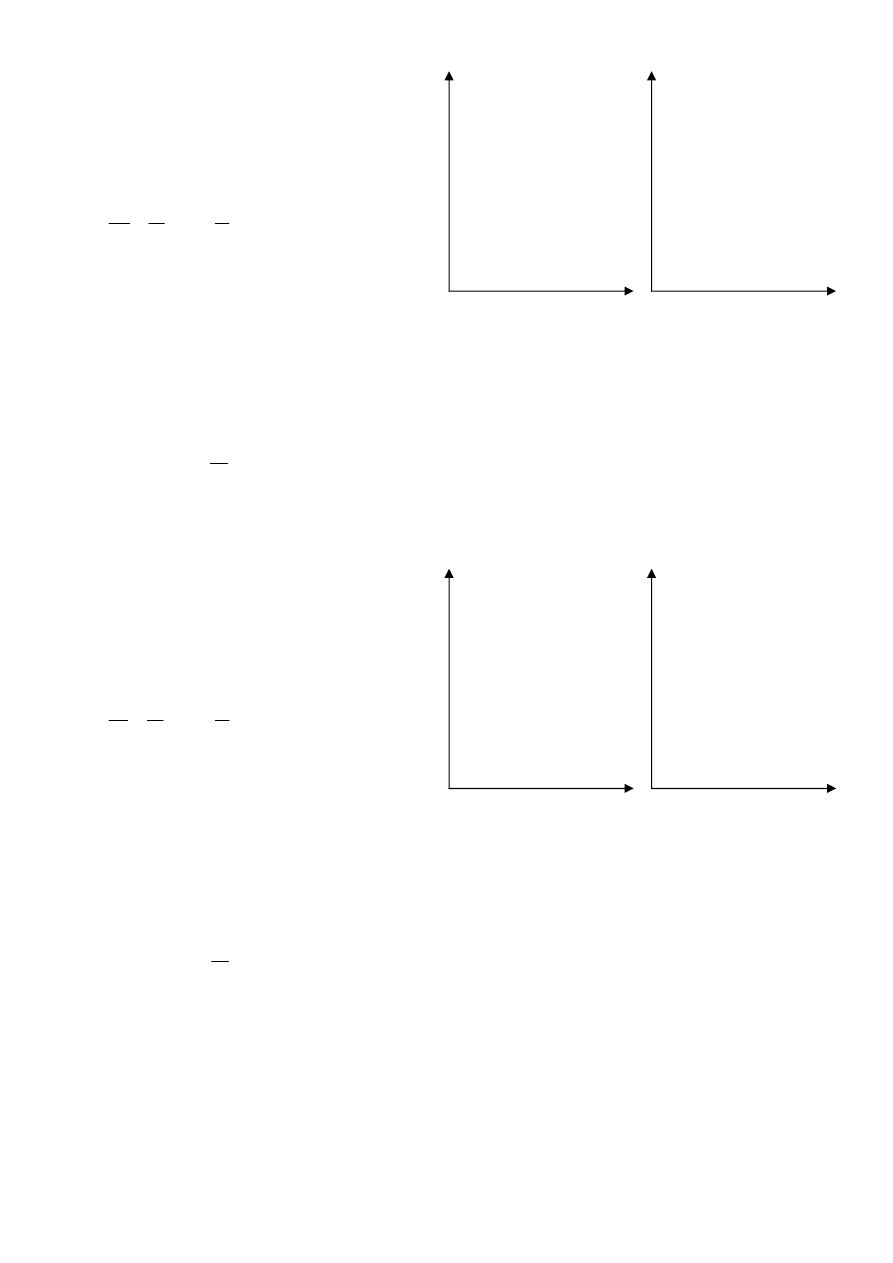
Przemiana izochoryczna

v=const

dv=0

1

1

RT

v

p

=

⋅

2

2

RT

v

p

=

⋅

1

1

2

1

T

T

p

p

=

const

T

p

=

Zmiana energii wewnętrznej

)

(

1

2

2

1

1

2

T

T

c

dT

c

u

u

v

v

−

⋅

=

⋅

=

−

∫

Zmiana entalpii właściwej

Praca rzeczywista

)

(

1

2

2

1

1

2

T

T

c

dT

c

h

h

p

p

−

⋅

=

⋅

=

−

∫

0

0

2

1

=

→

=

⇒

⋅

=

−

dv

bo

l

dv

p

dl

Zmiana entropii

Praca techniczna

1

2

1

2

ln

T

T

c

s

s

v

⋅

=

−

)

(

)

(

2

1

1

2

2

1

p

p

V

p

p

V

dl

T

−

⋅

=

−

⋅

−

=

−

Ciepło wymienione między układem a otoczeniem w czasie przemiany

1

2

2

1

u

u

q

dT

c

pdv

dT

c

dq

dl

du

dq

v

v

−

=

⇔

⋅

=

+

⋅

=

⇒

+

=

−

Przemiana izobaryczna

p=const

dp=0

1

1

RT

V

p

=

⋅

2

2

RT

V

p

=

⋅

1

1

2

1

T

T

V

V

=

const

T

V

=

Zmiana energii wewnętrznej

)

(

1

2

2

1

1

2

T

T

c

dT

c

u

u

v

v

−

⋅

=

⋅

=

−

∫

Zmiana entalpii właściwej

Praca rzeczywista

)

(

1

2

2

1

1

2

T

T

c

dT

c

h

h

p

p

−

⋅

=

⋅

=

−

∫

)

(

1

2

V

V

p

dv

p

dl

−

=

⋅

=

Zmiana entropii

Praca techniczna

1

2

1

2

ln

T

T

c

s

s

p

⋅

=

−

0

2

1

2

1

=

⇒

=

⇒

⋅

=

−

−

T

T

dl

O

dp

dp

V

dl

Ciepło wymienione między układem a otoczeniem w czasie przemiany

)

(

1

2

2

1

T

T

c

q

dh

dq

dl

dh

dq

p

T

−

=

⇔

=

⇒

+

=

−

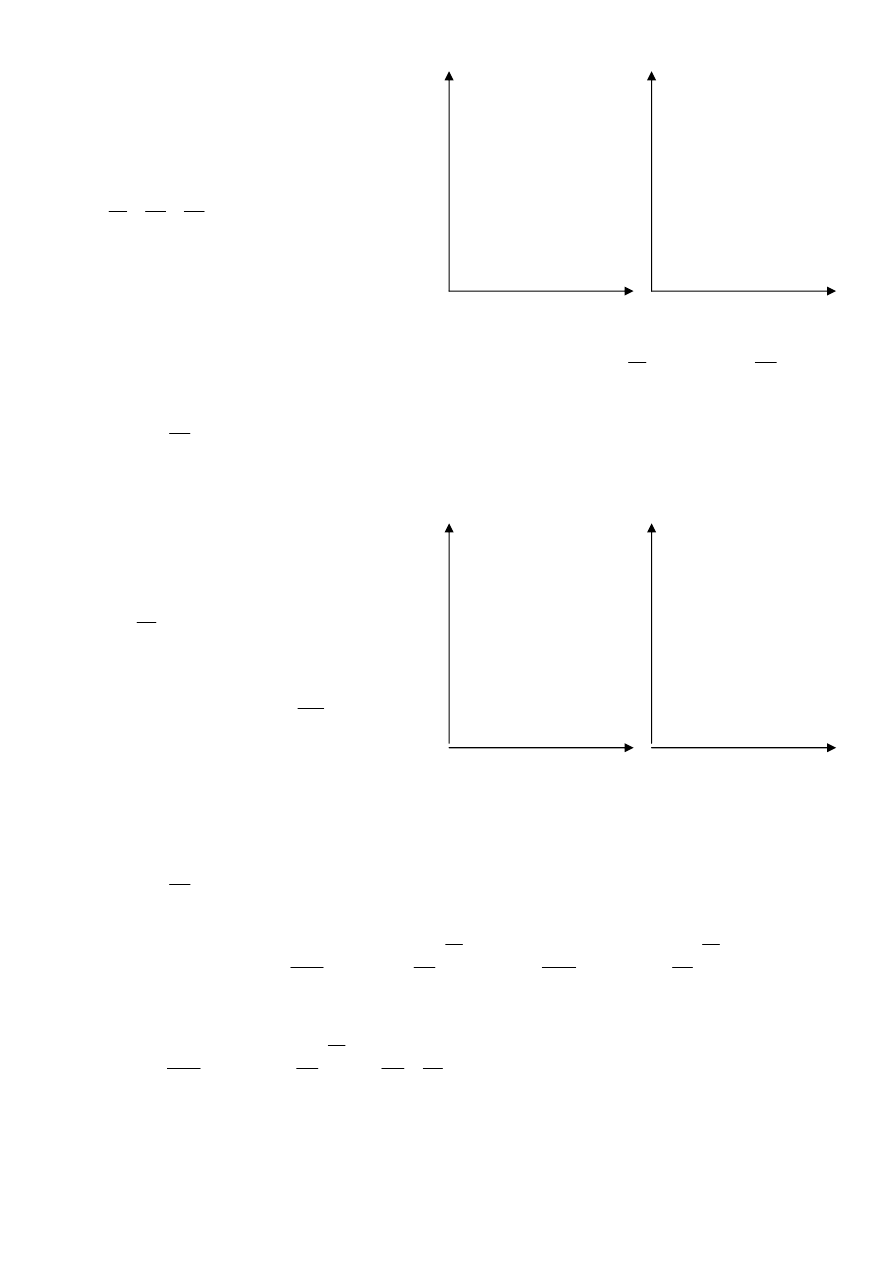
Przemiana izotermiczna
T=const

dT=0

RT

V

p

=

⋅

1

1

RT

V

p

=

⋅

2

2

2

1

2

1

2

1

ρ

ρ

=

=

p

p

V

V

const

v

p

=

⋅

Zmiana energii wewnętrznej

⇒

=

⋅

=

−

∫

0

2

1

1

2

dT

c

u

u

v

nie ma zmiany energii

Zmiana entalpii właściwej

Praca rzeczywista

⇒

=

⋅

=

−

∫

0

2

1

1

2

dT

c

h

h

p

nie ma zmiany entalpii

1

2

ln

V

V

T

R

dv

p

dl

⋅

⋅

=

⋅

=

i

2

1

ln

p

p

T

R

dl

⋅

⋅

=

Zmiana entropii

Praca techniczna

)

(

1

2

2

1

1

2

s

s

T

q

ds

T

dq

T

dq

s

s

−

⋅

=

⇒

⋅

=

⇒

=

−

−

dl

dl

T

=

−

2

1

Ciepło wymienione między układem a otoczeniem w czasie przemiany

T

dl

dl

dq

=

=

Przemiana adiabatyczna

const

V

p

k

=

⋅

v

p

c

c

k

=

k

k

V

p

V

p

2

2

1

1

⋅

=

⋅

const

pV

k

=

const

p

RT

p

k

=













⋅

const

T

p

k

k

=

⋅

−

1

Zmiana energii wewnętrznej

Zmiana entalpii właściwej

)

(

1

2

2

1

1

2

T

T

c

dT

c

u

u

v

v

−

⋅

=

⋅

=

−

∫

Zmiana entropii

Ciepło wymienione między układem a otoczeniem w czasie przemiany

0

1

2

=

=

−

T

dq

s

s

0

=

dq

Praca rzeczywista

































−

⋅

⋅

⋅

−

=

−

⋅

=

−

=

−

k

k

v

p

p

T

R

k

T

T

c

du

dl

1

1

2

1

2

1

1

1

1

)

(

lub

































−

⋅

⋅

⋅

−

=

−

k

k

p

p

V

p

k

dl

1

1

2

1

1

1

1

1

Praca Techniczna

dl

k

dl

k

c

c

dl

dl

p

p

V

p

k

k

dl

T

v

p

t

k

k

T

⋅

=

⇒

=

=

⇒

































−

⋅

⋅

⋅

−

=

−

−

−

2

1

1

1

2

1

1

2

1

1

1

Przemiana politropowa

const

V

p

n

=

⋅

v

p

c

C

c

C

n

−

−

=

n

n

V

p

V

p

2

2

1

1

⋅

=

⋅

const

pV

n

=

const

p

RT

p

n

=













⋅

const

T

p

k

k

=

⋅

−

1

n

n

p

p

T

T

1

1

2

1

2

−













=

Zmiana energii wewnętrznej

Zmiana entalpii właściwej

)

(

1

2

2

1

1

2

T

T

c

dT

c

u

u

v

v

−

⋅

=

⋅

=

−

∫

Zmiana entropii

Ciepło wymienione między układem a otoczeniem w czasie przemiany

1

2

1

2

ln

T

T

c

T

dT

c

s

s

⋅

=

⋅

=

−

0

=

dq

Praca rzeczywista

































−

⋅

⋅

⋅

−

=

−

⋅

=

−

=

−

n

n

v

p

p

T

R

n

T

T

c

du

dl

1

1

2

1

2

1

1

1

1

)

(

lub

































−

⋅

⋅

⋅

−

=

−

n

n

p

p

V

p

n

dl

1

1

2

1

1

1

1

1

Praca Techniczna

































−

⋅

⋅

⋅

−

=

−

−

n

n

T

p

p

V

p

n

n

dl

1

1

2

1

1

2

1

1

1

Moc teoretyczna dla każdej z przemian

2

1

−

⋅

=

T

t

l

m

N

gdzie m-strumień masy









s

kg

Obieg Carnota

Sprawność cieplna

q

q

q

i

0

−

=

η

q-il. ciepła dopr. ze źródła górnego
q

0

-il. ciepła odpr. z układu do źr. dolnego

T

T

T

s

s

T

s

s

T

s

s

T

q

q

q

s

s

s

s

s

s

T

s

s

T

s

s

T

q

s

s

T

q

i

0

1

2

1

2

0

1

2

0

1

4

2

3

1

2

0

4

3

0

3

4

0

0

1

2

)

(

)

(

)

(

)

(

)

(

)

(

)

(

−

=

−

⋅

−

⋅

−

−

⋅

=

−

=

=

∩

=

−

=

−

=

−

−

=

−

=

η

Procesy spalania paliw w kotłach
Każde paliwo musi być znane pod względem składu chemicznego, czyli udziałów:
c-węgla, h-wodoru pierwiastkowego, s-siarki, n-azotu (rzadko występuje),o-tlenu, w-wody związanej,
A-części niepalne.

∑ musi się równać 1kg.

−

r

i

Q

wartość opałowa, il. ciepła z 1kg masy, B - strumień paliwa doprowadzonego

















s

kg

h

kg

lub

−

p

V

strumień objętości powietrza doprowadzonego do komory spalania

( )

−

t

v

L

objętościowe teoretyczne zapotrzebowanie powietrza,

λ

λ

λ

λ- współczynnik nadmiaru powietrza

Zapotrzebowanie tlenu do spalania

Na 1 kg C przypada

3

8

12

32

=

kg O

2

Na 1 kg H

2

przypada

8

4

32

=

kg O

2

Na 1 kg S przypada 1 kg O

2

Teoretyczne zapotrzebowanie na tlen

Teoretyczne objętościowe zapotrzebowanie na tlen

( )













−

+

+

=

kgpal

kgO

o

s

h

c

O

t

m

2

8

3

8

( )

( )

( )

( )













⋅

=

⋅

=

⋅

=

kgpal

O

m

O

O

V

O

V

O

t

m

t

m

O

m

t

m

O

t

V

2

3

32

4

,

22

2

2

µ

Ponieważ źródłem tlenu jest powietrze zatem teoretyczne obj. zapotrzebowanie powietrza wynosi

( ) ( )

( )













⋅

⋅

=

=

kgpal

pow

m

O

O

L

t

m

t

v

t

v

.

32

21

,

0

4

,

22

21

,

0

3

Rzeczywistą ilość powietrza do spalania określa współczynnik nadmiaru powietrza

( )

( )

t

v

rz

v

L

L

=

λ

Określa się go ze wzorów

1.) Przy zupełnym spalaniu paliwa w spalinach nie ma CO

n

o

79

21

21

−

=

λ

przy zupełnym spalaniu skład spalin jest następujący b+o+n=100%

2.) Przy niezupełnym spalaniu – w spalinach jest CO

n

t

o

5

,

0

79

21

21

−

−

=

λ

przy czym skład spalin jest następujący b+t+o+n=100%

b - udział obj. CO

2

i SO

2

w spalinach suchych lub wartość w %

t – udział obj. CO w spalinach suchych lub wartość w %
o– udział obj. O

2

w spalinach suchych lub wartość w %

n– udział obj. azotu w spalinach suchych lub wartość w %
Przy niezupełnym spalaniu skład spalin mokrych będzie wynosił

%

100

2

=

+

+

+

+

O

H

r

n

o

t

b

O

H

r

2

-udział pary wodnej w spalinach w %

Rzeczywiste obj. zapotrzebowanie powietrza

( )

( )

t

v

rz

v

L

L

⋅

=

λ

Strumień objętości pow. doprowadzonego do komory paleniskowej

( )

( )

rz

v

t

v

p

L

B

s

pow

m

L

B

V

⋅

=













⋅

⋅

=

•

3

λ

Strumień objętości spalin

[

]

2

3

12

42

,

22

2

CO

CO

um

c

V

CO

∩

⋅

=

,

[

]

SO

um

s

V

SO

3

32

42

,

22

⋅

=

,

[

]

x

NO

NO

um

n

V

x

3

28

42

,

22

⋅

=

[

]

O

H

um

w

h

V

O

H

2

3

)

9

(

18

42

,

22

2

+

⋅

=

Spalanie przy λ=1

( )













+

+

⋅

+

⋅

+

⋅

+

⋅

=

.

.

.

.

79

,

0

)

9

(

18

42

,

22

28

42

,

22

32

42

,

22

12

42

,

22

3

pal

kg

sp

um

L

w

h

n

s

c

Vs

t

v

Spalanie przy λ>1 (nadmiar powietrza)

( )

(

) ( )













⋅

−

⋅

+

⋅

⋅

+

+

⋅

+

⋅

+

⋅

+

⋅

=

.

.

.

.

1

21

,

0

79

,

0

)

9

(

18

42

,

22

28

42

,

22

32

42

,

22

12

42

,

22

3

pal

kg

sp

um

L

L

w

h

n

s

c

Vs

t

v

t

v

λ

λ

Strumień objętości spalin wypływających z kotła













⋅

=

•

h

sp

um

V

B

V

s

sp

.

3

gdzie: B – strumień paliwa doprowadzonego do kotła

(

)

(

)

u

r

k

w

w

w

w

u

r

w

w

w

w

k

H

t

t

c

m

B

H

B

t

t

c

m

⋅

−

⋅

⋅

=

⇒

⋅

−

⋅

⋅

=

η

η

2

1

2

1

gdzie:

k

η

- sprawność kotła,

u

r

H

- wartość

opałowa w warunkach roboczych,













=

kgK

kJ

c

w

19

,

4

- średnie ciepło właściwe wody,

w

m

-ilość

podgrzewanej wody (strumień),

2

1

w

w

t

t

∩

- parametry wody podgrzewanej przez kocioł.













+

⋅

⋅

−

=

kg

kJ

w

h

r

H

H

o

r

u

r

)

9

(

gdzie: r- ciepło parowania z tablic 2500













kg

kJ

,

o

r

H

-ciepło spalania w warunkach roboczych.

Bilans cieplny kotłów opalanych paliwem stałym:

∑

+

=

.

str

u

p

Q

Q

Q

gdzie:

p

Q

-moc dostarczona z paliwem,

u

Q

-użyteczna moc cieplna,

str

Q

-ciepło strat mocy cieplnej

[ ]

kW

H

B

Q

r

u

p

⋅

=

u

Q

- dla kotłów wodnych

(

)

[ ]

kW

t

t

c

m

Q

w

w

w

w

u

2

1

−

⋅

⋅

=

⇒

u

Q

- dla kotłów parowych

(

)

[ ]

kW

t

c

i

D

Q

w

w

p

u

2

⋅

−

⋅

=

⇒

gdzie: D- strumień masy pary wypływ. z kotła,

p

i

- entalpia pary,

2

w

w

t

c

⋅

- entalpia wody przed kotłem

Sprawność cieplna kotła:

p

u

k

Q

Q

=

η

, spr. kotłów wodnych:

(

)

r

u

w

w

w

w

k

H

B

t

t

c

m

⋅

−

⋅

⋅

=

2

1

η

, spr. kotłów parowych

(

)

r

u

w

w

p

k

H

B

t

c

i

D

⋅

⋅

−

⋅

=

2

η

Obliczanie wysokości komina:

(

)

[ ]

(

)

[ ]

m

g

p

h

Pa

g

h

p

rz

s

rz
p

s

rz

s

rz
p

s

ρ

ρ

ρ

ρ

−

⋅

∆

=

⇒

−

⋅

⋅

=

∆

gdzie: h- wysokość komina (od śr. komory paleniskowej), g- przyspieszenie ziemskie 9,81 [m/s

2

]

rz

p

ρ

- gęst. powietrza w war. rzecz.,

rz

s

ρ

- gęst. spalin w war. rzecz., ∆p

s

– podciśnienie spalin [Pa]













=

=

=

3

29

,

1

42

,

22

87

,

28

m

kg

V

m

p

u

p

µ

ρ

przeliczenie na war. rzeczywiste

rz

rz

rz

u

u

u

T

p

T

p

ρ

ρ

⋅

=

⋅

ponieważ:

ρ

1

=

V

s

O

H

O

H

s

O

O

s

N

N

s

SO

So

s

CO

co

i

i

u

s

V

V

r

V

V

r

V

V

r

V

V

r

V

V

r

r

2

2

2

2

2

2

2

2

2

2

,

,

,

,

=

=

=

=

=

⇒

⋅

=

∑

ρ

ρ

m

O

H

O

H

m

CO

CO

m

O

O

m

N

N

m

SO

SO

m

CO

CO

u

s

V

r

V

r

V

r

V

r

V

r

V

r

2

2

2

2

2

2

2

2

2

2

2

2

µ

µ

µ

µ

µ

µ

ρ

⋅

+

⋅

+

⋅

+

⋅

+

⋅

+

⋅

=