Elektrotechnika elektronika miernictwo

Franciszek Gołek

([e-mail])

www.pe.ifd.uni.wroc.pl

Wykład 05 i 06

Filtry i układy RLC

Z poprzednich wykładów wiemy że:

indukcyjność i pojemność, w odróżnieniu od idealnej rezystancji, przyczyniają
się do powstawania różnicy faz między napięciem i prądem a ich impedancje
zależą od częstotliwości przebiegów elektrycznych:
X

L

= j

ω

L, X

C

= 1/j

ω

C.

Przypomnijmy nazwy:
Impedancja (oporność zespolona): Z = R + X,
R – rezystancja, X – reaktancja,
Dla szeregowo połączonych idealnych L i C - gdy pomijamy rezystancję cewki i
upływność kondensatora:
X = j(X

L

– X

C

) = j(

ω

L – 1/

ω

C), Z = R + j(X

L

– X

C

),

Admitancja (przewodność zespolona): Y = 1/Z = G + jB
G – konduktancja, B – susceptancja.
Dla równolegle połączonych idealnych L i C - gdy pomijamy rezystancję cewki i
upływność kondensatora:
B = j(B

C

– B

L

) = j(

ω

C – 1/

ω

L)



Z



=

√

(R

2

+ X

2

),



Y



=

√

(G

2

+ B

2

),

Z =



Z



e

jarctg(R/X)

, Y =



Y



e

jarctg(B/G)

Dla nie idealnych L i C, gdy znamy rezystancję
cewki R

L

i upływność kondensatora R

C

to przy ich szeregowym połączeniu z rezystorem
R Impedancję wypadkową – zawadę zapiszemy
w postaci:
Z = R + R

L

+ R

C

+ j(

ω

L – 1/

ω

C).

Natomiast przy ich równoległym połączeniu z
rezystorem o rezystancji R = 1/G
Admitancją wypadkową (zespoloną przewodność
całości) zapiszemy w postaci:
Y = 1/R + 1/R

C

+ 1(R

L

+ j

ω

L) + j

ω

C

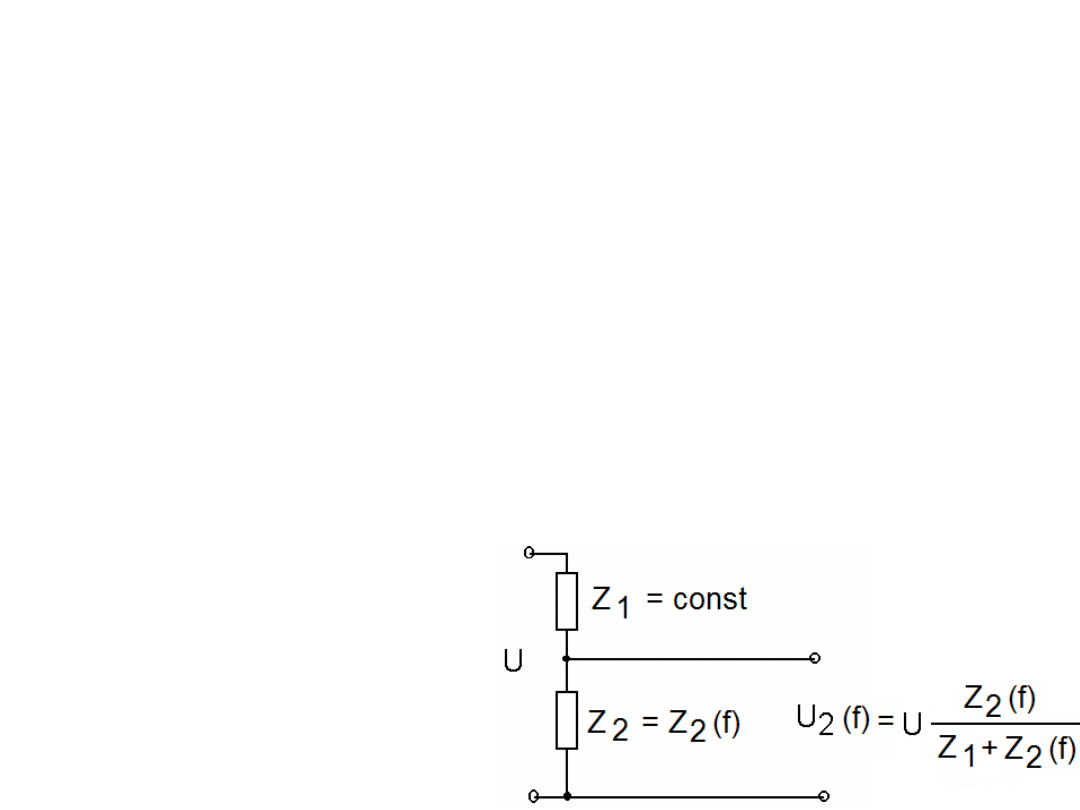
W tym wykładzie pokażemy dalsze konsekwencje
obecności pojemności i indukcyjności w obwodach
elektrycznych.
Między innymi zbadamy jaki wpływ mają one na tzw.
pasmo przenoszenia oraz kształtowanie impulsów
elektrycznych.

Najprostszy dzielnik
napięcia zawierający
impedancję zależną
od częstotliwości
sygnału.

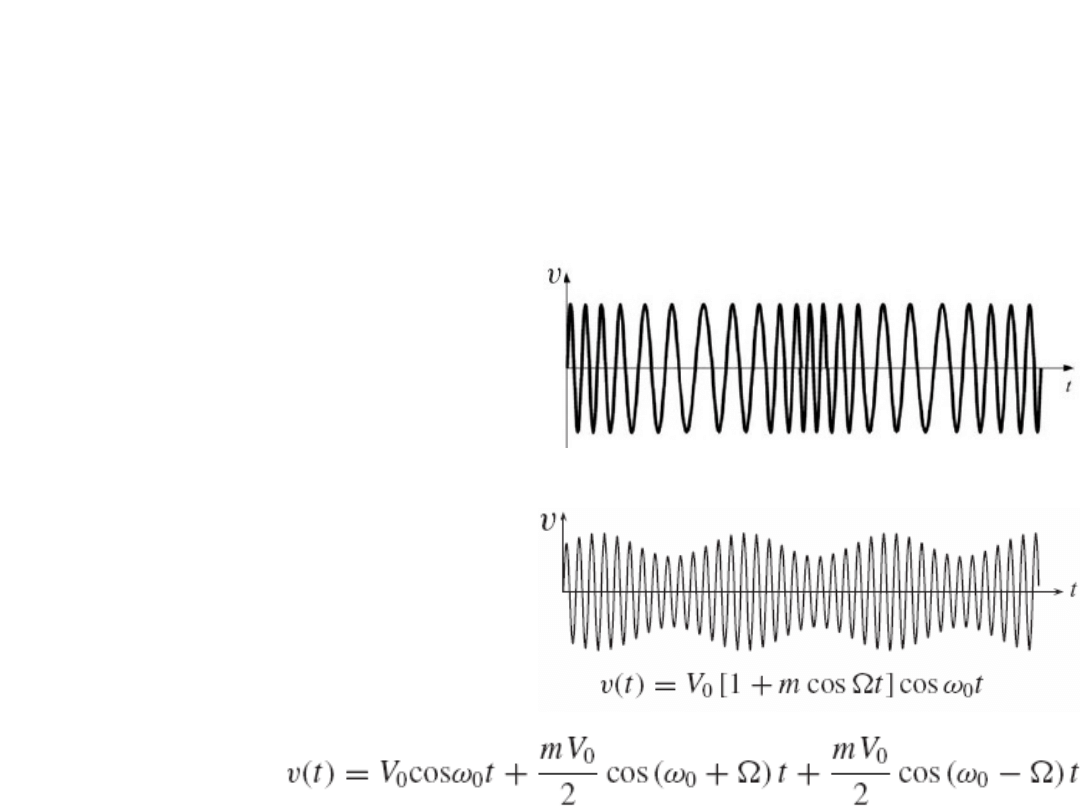
Pasmo częstotliwości

Pasmo częstotliwości jest ważną wielkością i podstawowym
pojęciem w systemach komunikacji. Pasmem częstotliwości dla
danego sygnału nazywamy zakres częstotliwości jaki obejmuje
spektrum tego sygnału.
Aby przesłać informację przy
pomocy fali nośnej
o częstotliwości

ω

o

trzeba

ją zmodulować (zdeformować)
w takt informacji.
Taka modulacja oznacza
zamianę sygnału nośnego
o jednej częstości
na sumę pewnego
spektrum sygnałów
obejmującego pewne
pasmo.

FM – modulacja częstotliwości

AM – modulacja amplitudy

Filtrem

nazywamy urządzenie, które przepuszczając

(transmitując) sygnał wejściowy może zmieniać przy tym
jego spektralny rozkład energii.
Filtry dzielimy pod względem technologii wykonania:
a) Pasywne - są nimi dzielniki napięcia (lub prądu) z

elementami pasywnymi: R, C i L).

b) Aktywne (zawierają, oprócz elementów R, C i L,

tranzystory lub wzmacniacze operacyjne).

c) Cyfrowe, w których sygnał jest zamieniany na postać

cyfrową a następnie szeregi liczb są przetwarzane,
filtrowane i ponownie zamieniane na sygnał.

d) Inne np. kwarcowe.

Filtry mają za zadanie przenosić sygnały o interesujących nas
częstotliwościach i tłumić sygnały o częstotliwościach niepożądanych. Filtry,
poprzez zmianę składowych harmonicznych, modelują impulsy elektryczne.

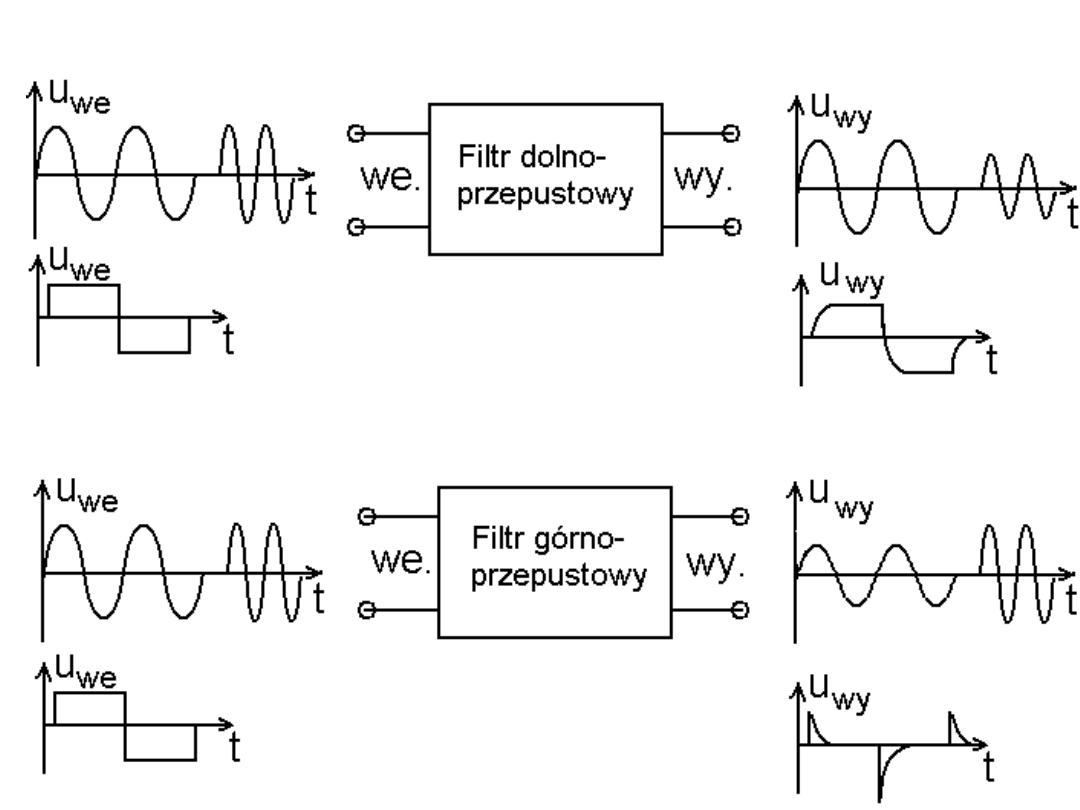
Obrazkowa ilustracja działania filtru

Pasmo przenoszenia filtra

Jest to obszar częstotliwości o najlepszym przenoszeniu sygnału
zawarty między granicami pasma. Granice pasma przenoszenia
to takie częstotliwości f

g1

, f

g2

, przy których moc sygnału spada o

50%, przy których moduł współczynnika przenoszenia sygnału k

U

=

IU

wy

/U

we

I lub k

I

= II

wy

/I

we

I jest

√

2 razy mniejszy od swej

maksymalnej wartości. W decybelach:
20log(1/

√

2) = -3 dB, czyli stosunek k(f

g

)/k

max

wyrażony w

decybelach

wynosi -3 dB. Ponieważ moc jest proporcjonalna do

kwadratu napięcia albo kwadratu natężenia prądu, P = U

2

/R = I

2

R

graniczne częstotliwości f

g

spełniają równość:

IK(f

g

)/K

max

I = k(f

g

)/k

max

=

1/

√

2

P(f

g

)/P

max

= U

2

(f

g

)/U

2

max

= I

2

(f

g

)/I

2

max

=1/2

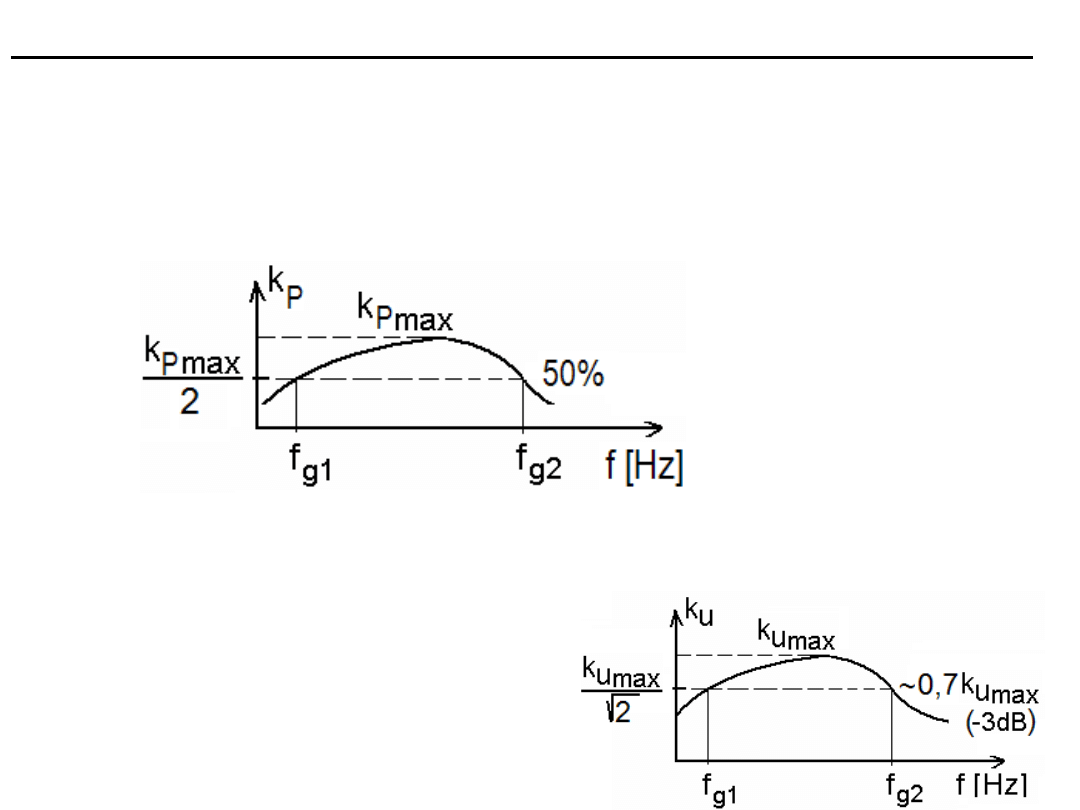
Pasmo przenoszenia dowolnego układu

W zasadzie każdy układ, przez który następuje propagacja

jakiegokolwiek sygnału ma jakieś ograniczenia dotyczące

częstotliwości propagowanego sygnału.

K

P

(f

g

) = P(f

g

)/P

max

= U

2

(f

g

)/U

2

max

= I

2

(f

g

)/I

2

max

= 1/2

IK(f

g

)/K

max

I = k(f

g

)/k

max

=

1/

√

2

Filtry pasywne –

jako dzielniki napięcia

zależne od częstotliwości. Często są to filtry RC i

stanowią bardzo ważne zastosowanie

kondensatorów. Obliczenia parametrów tych

dzielników w dziedzinie częstotliwości wymagają

stosowania uogólnionych praw Ohma i Kirchhoffa

czyli praw w zapisie zespolonym (tj. przy pomocy

liczb zespolonych i funkcji zespolonych).
Przy analizie filtrów warto też stosować

wykresy wskazowe bo mogą one stanowić

dogodną ilustrację relacji między sygnałem

wejściowym i wyjściowym danego filtra dla
wybranej częstotliwości.

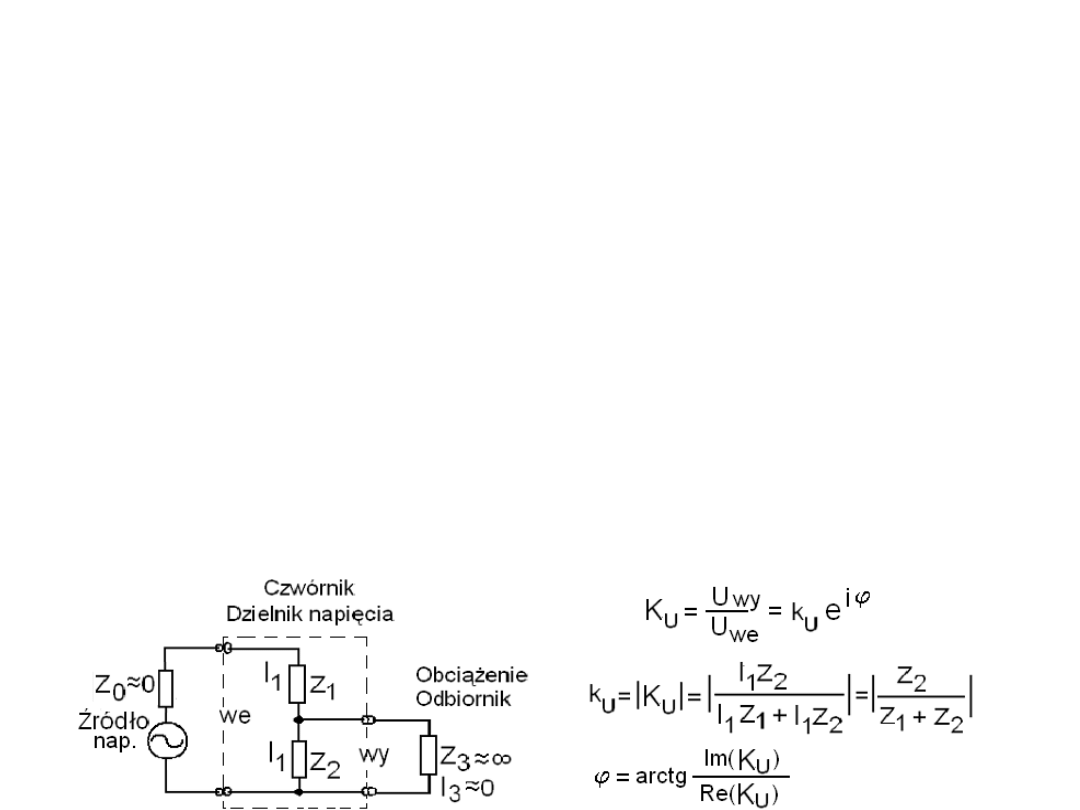
Współczynnik przenoszenia k

U

i przesunięcie fazy

ϕ

.

Rysunek przedstawia dzielnik napięcia złożony z zespolonych impedancji Z

1

i

Z

2

, zasilany przez źródło o pomijalnie małej impedancji wewnętrznej Z

0

~ 0

Ω

.

Zatem Z

0

ma pomijalny udział w podziale napięcia Thevenina. Ponadto dzielnik

jest nieobciążony, gdyż obciążenie Z

3

~

∞

.

Aby obliczyć współczynnik

przenoszenia tego dzielnika, zwanego też czwórnikiem bo ma dwa zaciski
wejściowe i dwa zaciski wyjściowe – razem cztery, stosujemy taką logikę
postępowania jak przy zwykłych opornikach ale z użyciem liczb zespolonych.
Zespolony stosunek U

wy

/U

we

= K

U

= k

U

e

i

ϕ

zawiera współczynnik przenoszenia k

U

czyli stosunek wartości skutecznych lub amplitud - modułów napięcia
wyjściowego do napięcia wejściowego IU

wy

I/IU

we

I oraz względne przesunięcie

fazy

ϕ

. Napięcie wyjściowe to spadek napięcia na

Z

2

: U

wy

= U

2

= I

1

Z

2

.

Napięcie

wejściowe to spadek na szeregowo połączonych Z

1

i Z

2

czyli U

we

= I

1

Z

1

+I

1

Z

2

.

k

U

= IU

wy

I/IU

we

I = IZ

2

I/IZ

1

+Z

2

I,

ϕ

= arctg((Im(K

U

))/(Re(K

U

))).

Filtr dolnoprzepustowy, opis w dziedzinie częstotliwości.

Opis ten mówi jak, w funkcji częstotliwości, ma się stosunek amplitud napięcia
wyjściowego do napięcia wejściowego - k

U

oraz względna różnica faz -

ϕ

sygnału wyjściowego względem wejściowego. Obie te wielkości mamy w
funkcji zespolonej przedstawiającej stosunek zespolonych wartości napięcia
wyjściowego do wejściowego. Zakładamy, że źródło sygnału ma zerową a
obciążenie nieskończoną oporność wewnętrzną.

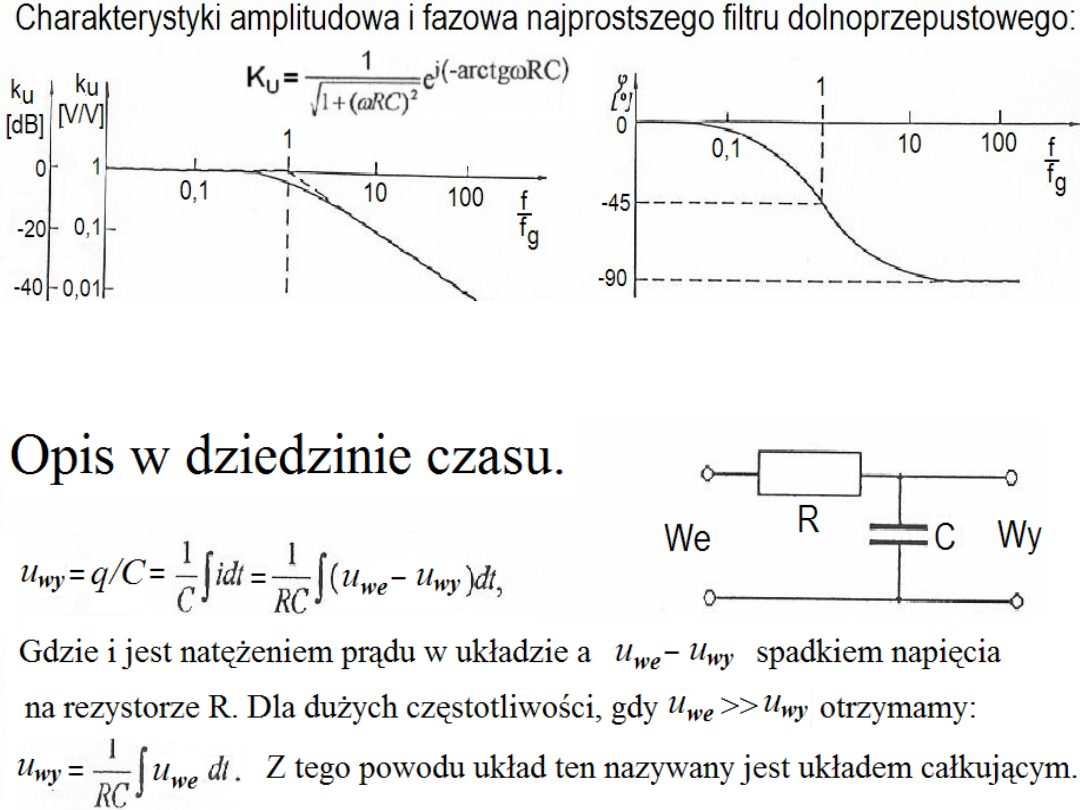
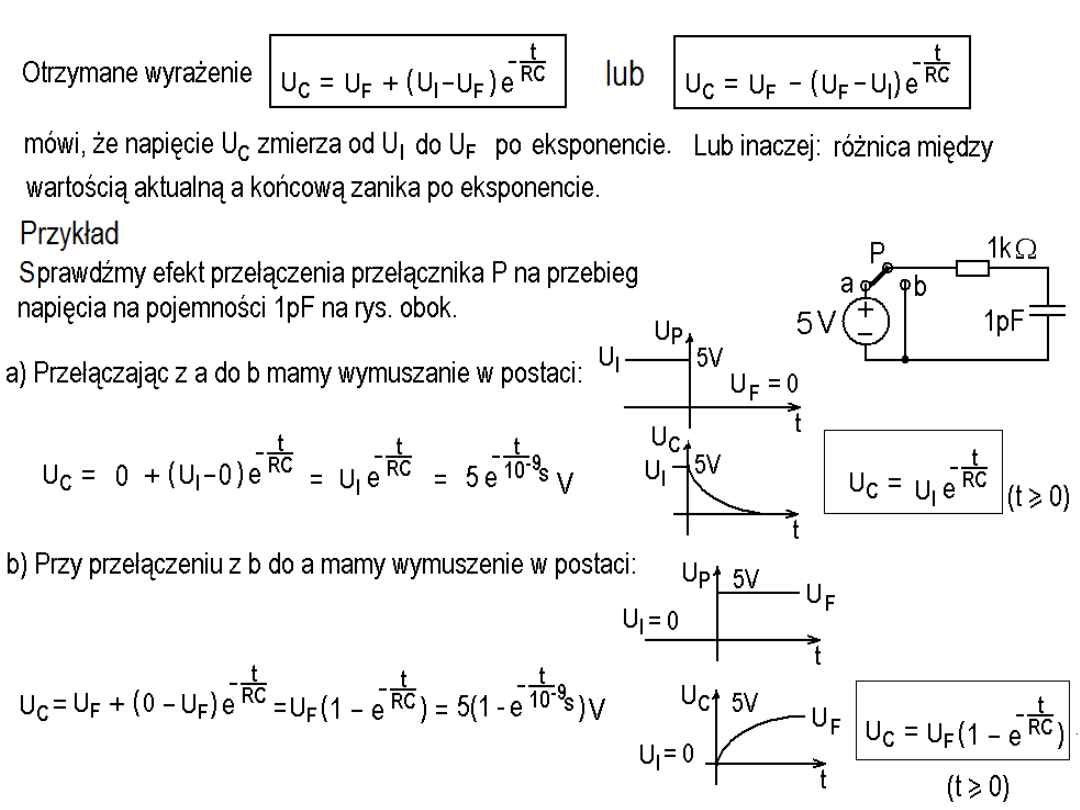
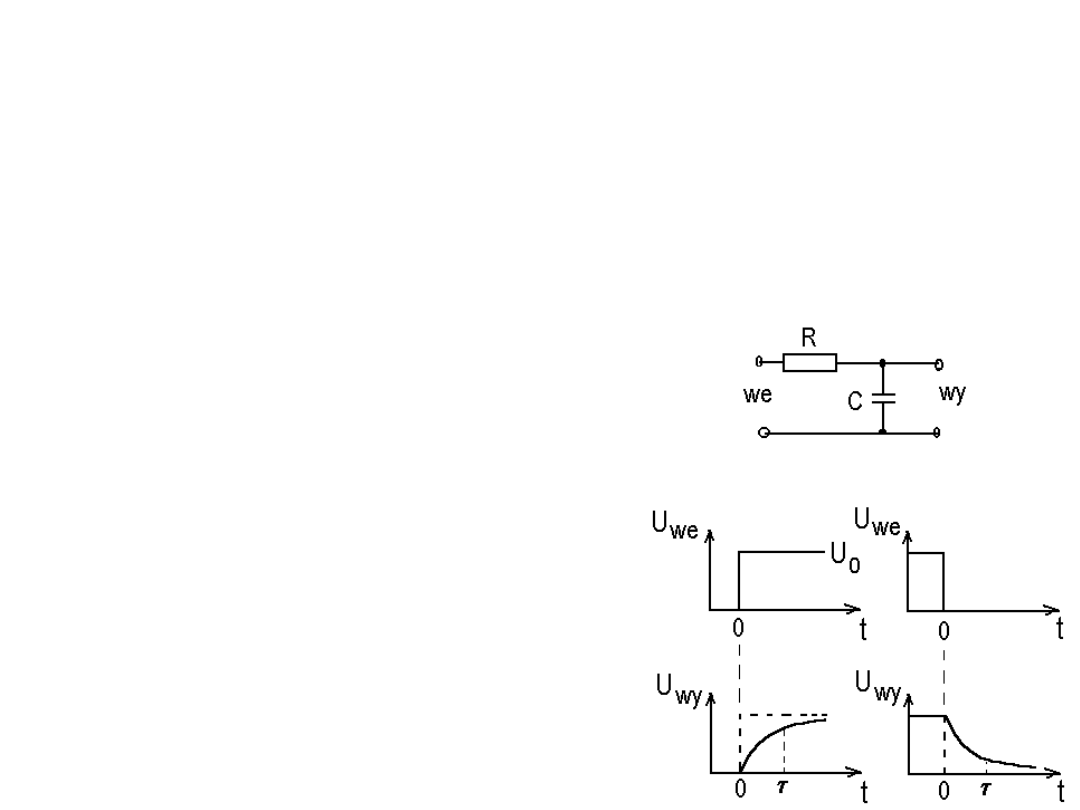
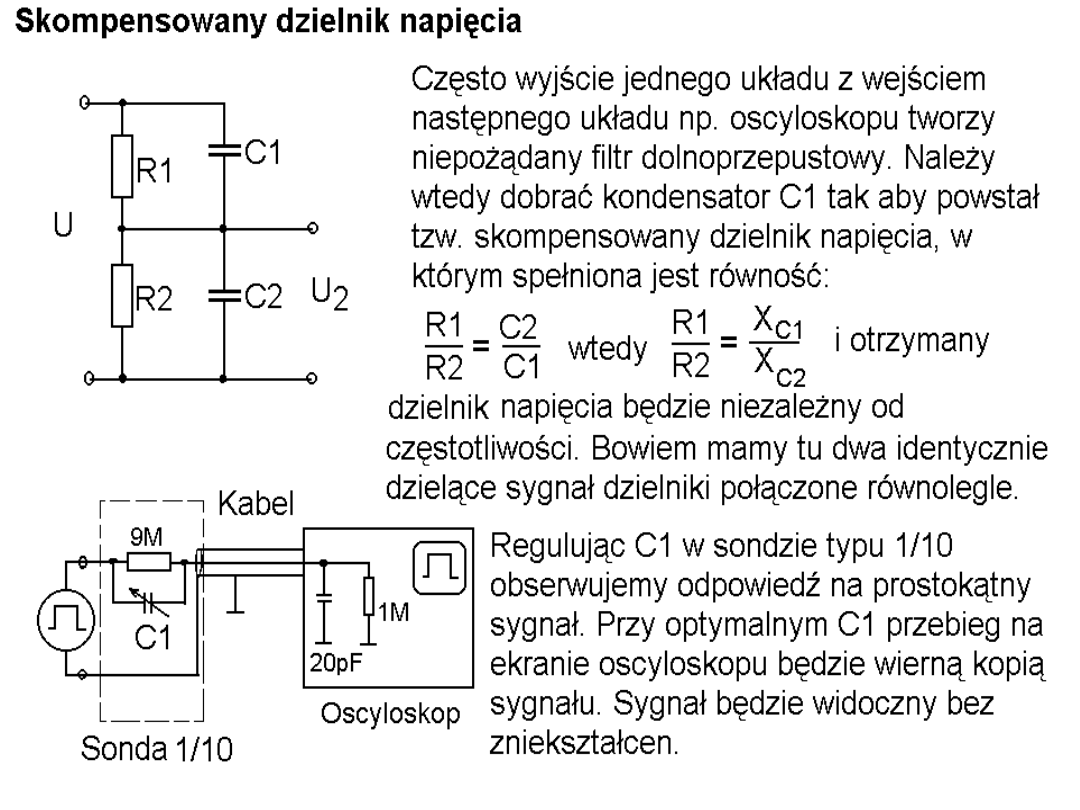
Bardzo często podczas łączenia układów elektronicznych powstają
pasożytnicze układy całkujące - filtry dolno-przepustowe (lub różniczkujące,
czyli filtry górno-przepustowe). Zwykle składają się one z rezystancji wyjściowej
jednego układu i pojemności wejściowej następnego lub pojemności
przewodów łączących. Te pasożytnicze elementy mogą przyczyniać się do
zmniejszenia górnej częstotliwości granicznej danej aparatury oraz wpływać na
kształt i czas trwania impulsów.
Przypomnijmy, co pojawia się na nieobciążonym wyjściu dolnoprzepustowego
filtru RC gdy na jego wejściu wymuszamy
skok napięcia o wartości U

0

.

Dla skoku od 0 do U

0

: u

wy

(t) = U

0

(1 - e

-t/RC

)

Dla skoku od U

0

do 0: u

wy

(t) = U

0

e

-t/RC

Iloczyn RC zwany jest stałą czasową

τ

,

określa czas, po którym u

wy

(t)

zbliża się do swej
asymptotycznej wartości na „odległość”
= 1/e wysokości skoku.

τ

= RC

Oszacujmy ile wynosi czas narastania impulsu prostokątnego

zdeformowanego filtrem dolnoprzepustowym. Czyli w jakim czasie
U

wy

(t) wzrośnie od 10% do 90% swej wartości maksymalnej?

0.9 U

0

= U

0

(1 - e

-t/RC

) -> t

90%

= -RCln0.1(U

0

≈

wartość maksymalna)

0.1 = 1 - e

-t/RC

-> t

10%

= -RCln0.9

t

r

= t

90%

- t

10%

= RC(ln0.9 - ln0.1) = RCln9

≈

2.2RC.

Pamiętając, że f

g

= 1/(2

π

RC) -> RC = 1/2

π

f

g

otrzymamy związek:

t

r

≈

2.2RC = 2.2/(2

π

f

g

). Zatem możemy napisać:

t

r

≈

1/(3f

g

).

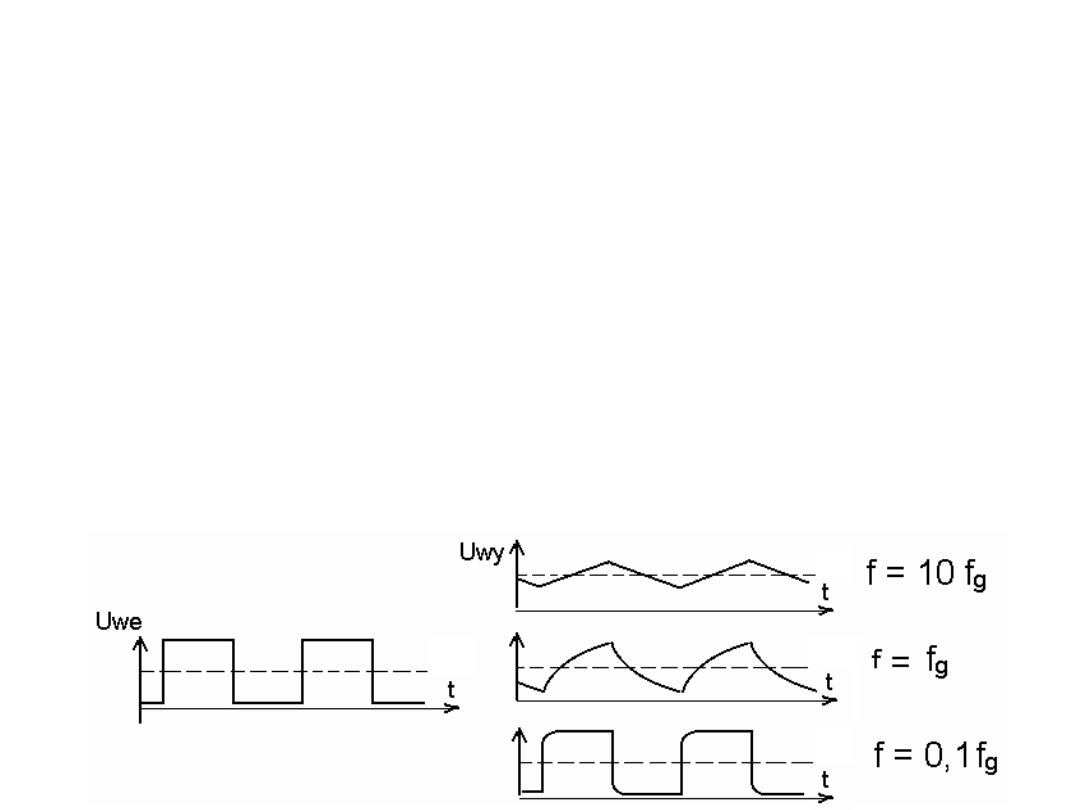
Rysunek przedstawia odpowiedź filtru dolnoprzepustowego na

ciąg impulsów prostokątnych o różnych częstotliwościach.

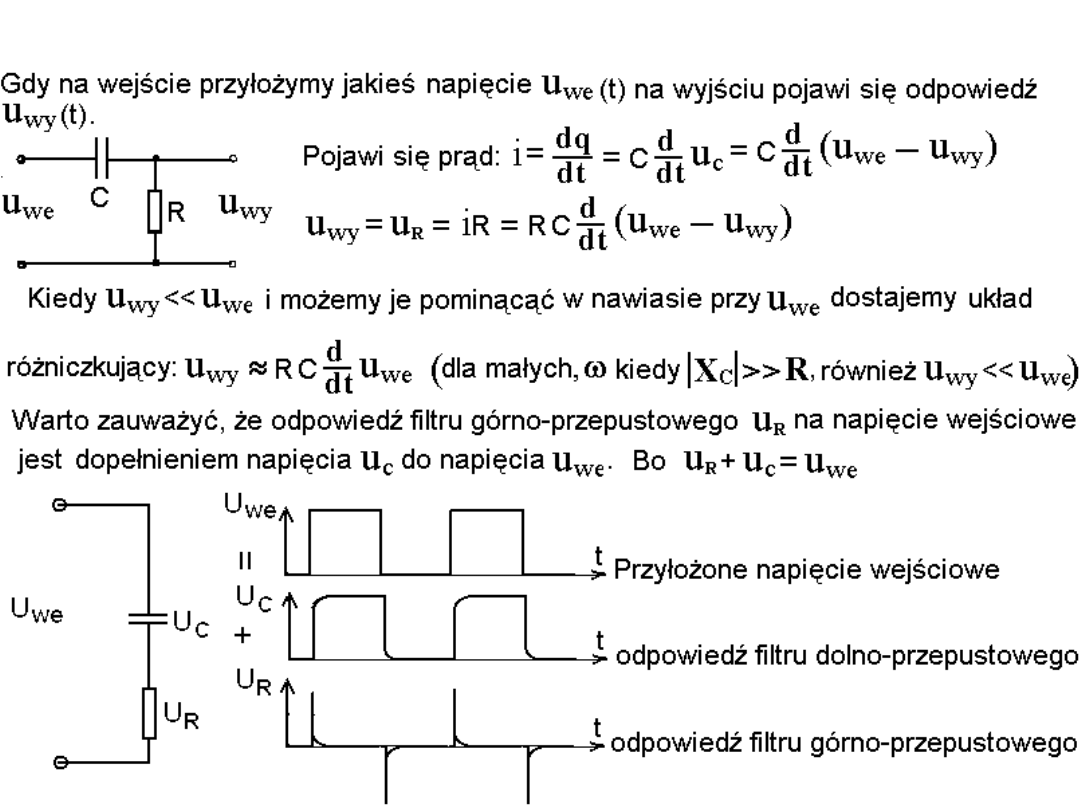
Filtr górno-przepustowy, opis w dziedzinie czasu.

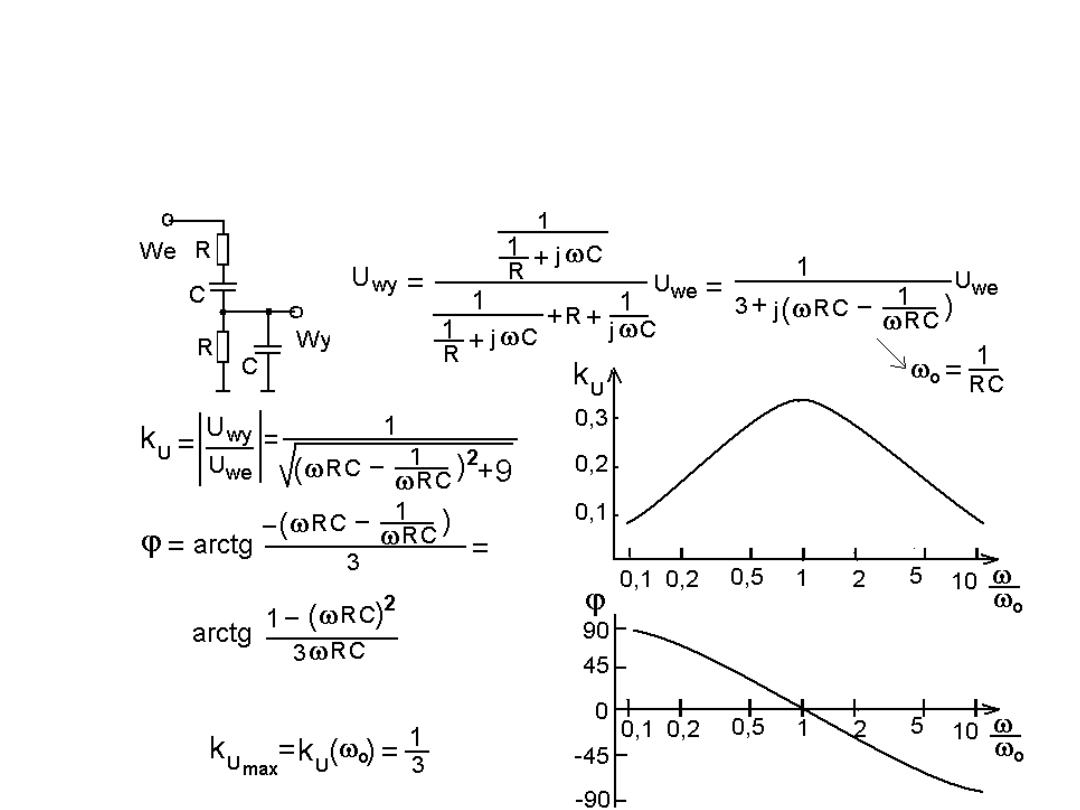
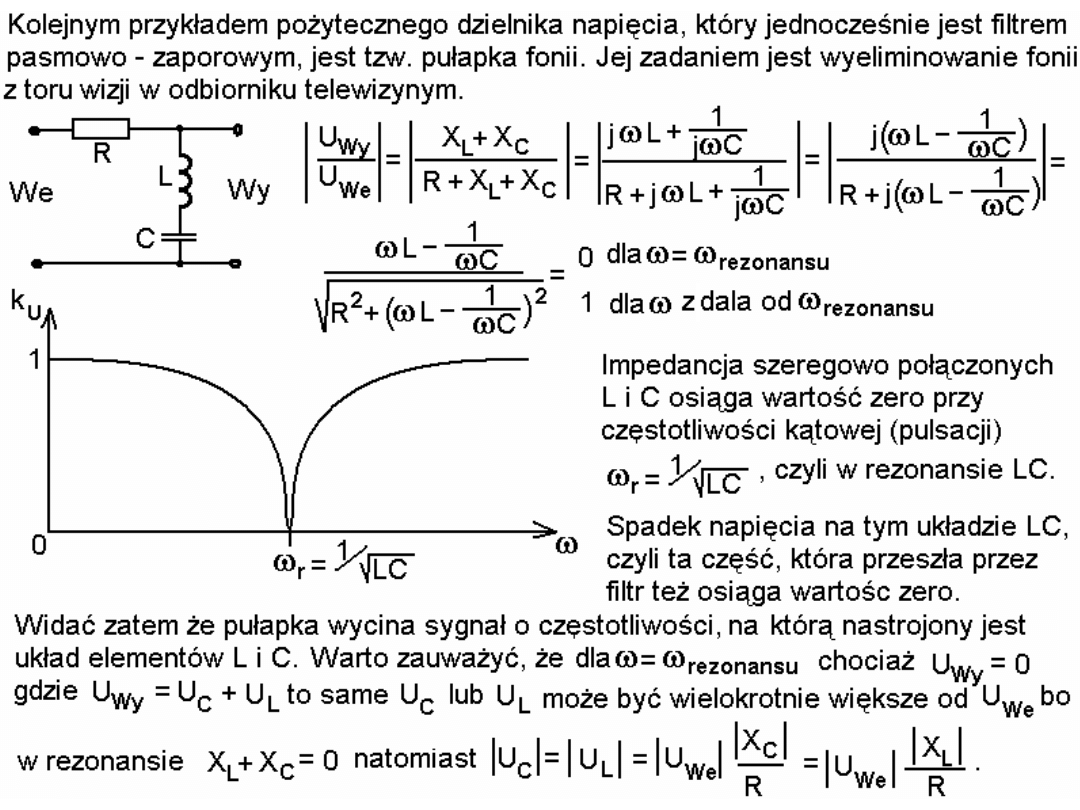
Filtr pasmowo-przepustowy

tłumi jednocześnie sygnały o

częstotliwościach niższych od f

g. dolna

oraz sygnały o częstotliwościach

wyższych od f

g. górna

. Przykładem takiego filtra może być kaskadowe połączenie

filtrów: górno i dolno przepustowego o odpowiednio dobranych
częstotliwościach granicznych. Przykład z identycznymi f

g

poniżej.

Zastosowanie filtrów

Filtry są stosowane do kształtowania charakterystyk

częstotliwościowych układów elektronicznych i do

kształtowania impulsów napięciowych. Wybierania jednych i

eliminowania innych sygnałów (zakłócających) np. tunery to

po prostu przestrajalne filtry pasmowe. W zasadzie każde

urządzenie elektroniczne zawiera filtry. Filtry górno-

przepustowe stosowane są często jako pojemnościowe

sprzężenie między układami elektronicznymi (np.

wzmacniaczami) celem zablokowania tzw. składowej stałej.

Sygnały w.cz. mogą nieoczekiwanie przeniknąć przez

pojemności wyłączników, albo zbliżonych do siebie

przewodów powodując wzajemne zakłócanie obwodów

elektronicznych.

Warto pamiętać, że filtry typu RC lub RL wykazują raczej

łagodne stromości charakterystyk. Natomiast bardziej złożone

filtry typu RLC (zawierające obwody rezonansowe o dużej

dobroci) mogą wykazywać bardzo duże stromości na brzegach

pasm!

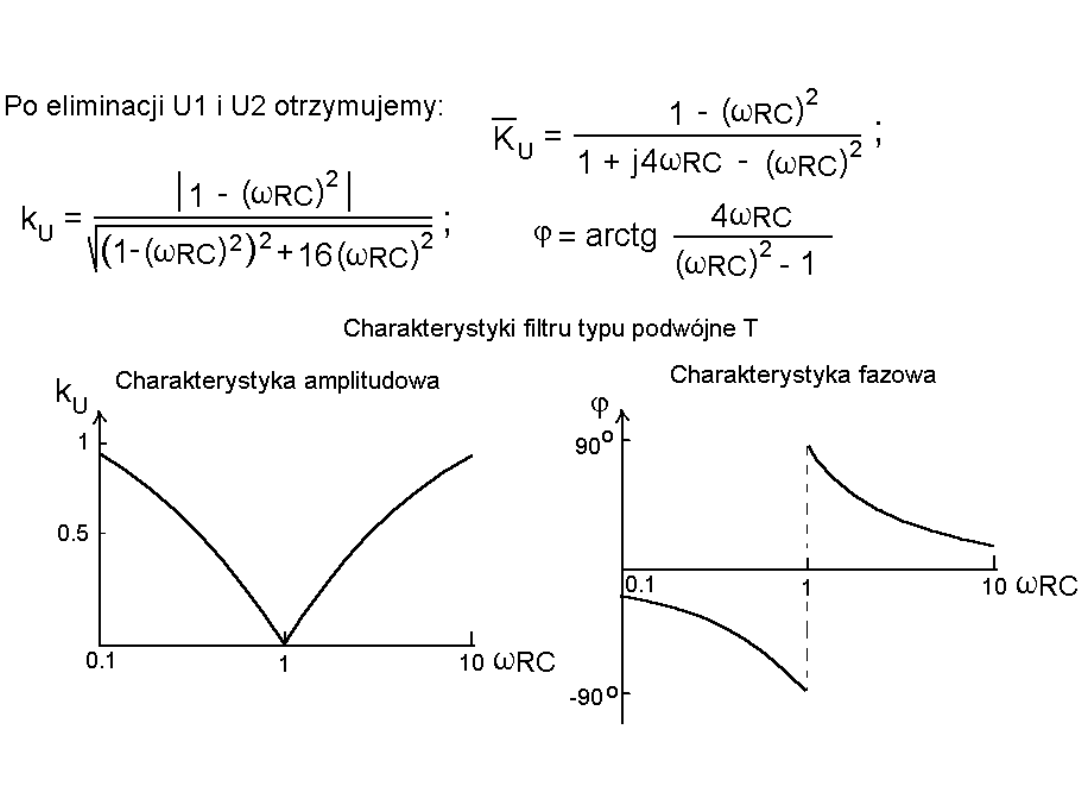
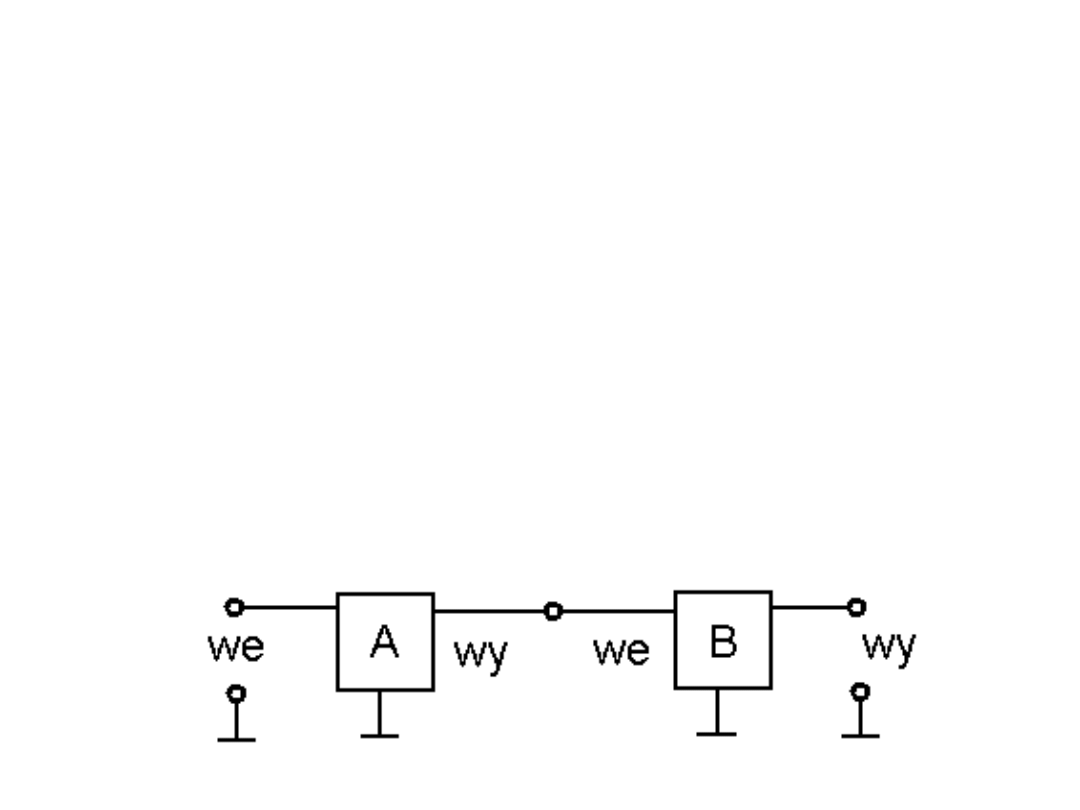
Prosta zasada łączenia układów

(np. pojedynczych filtrów w filtry wielostopniowe) mówi, że jeżeli
obwód A steruje obwodem B (B obciąża obwód A) to warto
zadbać o to aby R

wy układu A

< 0,1R

WE układu B

. Wtedy wpływ B –

układu obciążenia na A – układ sterujący będzie mało znaczący.
Układ A po obciążeniu go takim układem B działa z zaburzeniem
nie przekraczającym 10% (A wystawia na swoim wyjściu o 10%
napięcie niższe niż w przypadku braku obciążenia). W sytuacji
gdy takie 10%-we odchylenie możemy zaniedbać uzyskujemy
prosty sposób na projektowanie wielostopniowych układów. Po
prostu każdy podukład (stopień) projektujemy i obliczamy osobno
(obliczenia są proste).

Dla poprawienia efektu filtracji stosowane są bardziej
rozbudowane filtry, w tym filtry aktywne czy filtry cyfrowe.
Filtry aktywne powstają poprzez zastosowanie układów aktywnych
(tranzystorów, wzmacniaczy operacyjnych itp.) w obwodach
filtrujących RLC. Elementy aktywne (dzięki dużej impedancji
wejściowej i efektowi wzmacniania sygnału) pozwalają na
budowanie filtrów wielostopniowych o bardzo stromym przebiegu
charakterystyk na brzegach filtrowanych pasm.
Filtry cyfrowe to układy filtrujące i przetwarzające sygnały
dyskretne (cyfrowe).
Filtry cyfrowe są coraz częściej i szerzej stosowane w wielu
dziedzinach techniki bowiem każdy sygnał analogowy (prosty
jednowymiarowy jak i złożony wielowymiarowy, fotografia, film itp)
można zamieniać na sygnał cyfrowy odpowiednimi przetwornikami
analogowo-cyfrowymi.
(Skrót „DSP” oznacza: digital signal processing)

http://www.intersil.com/data/AN/an9603.pdf

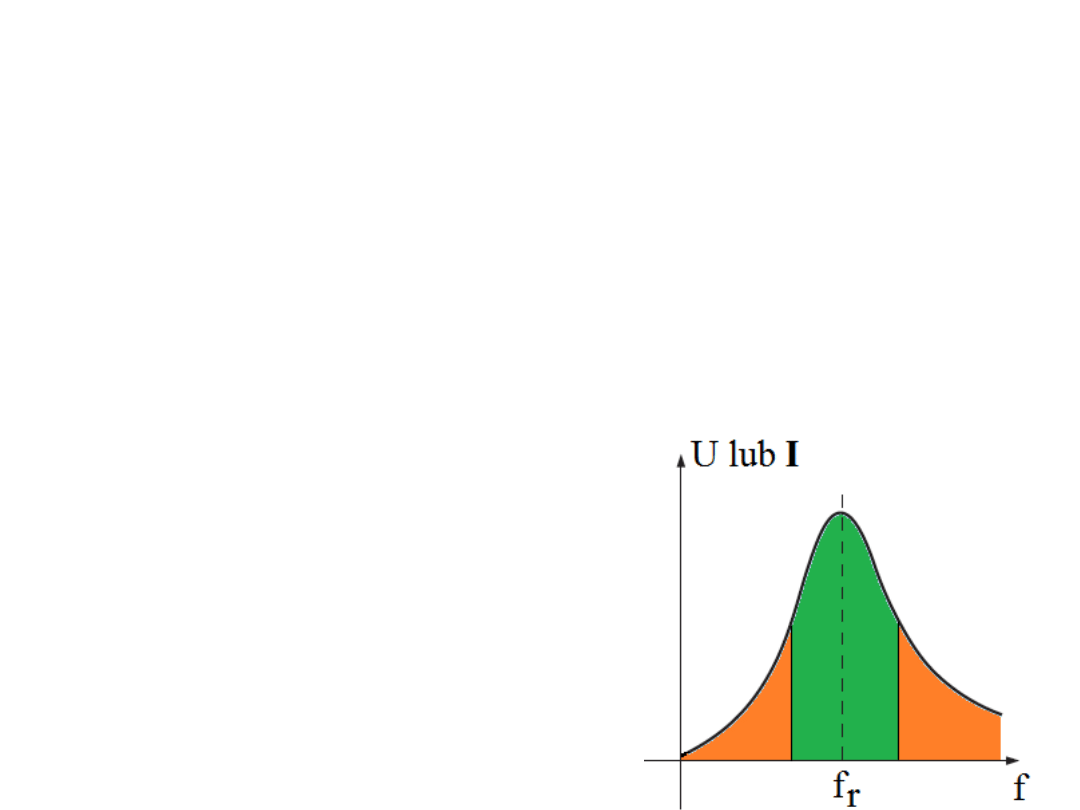
Rezonans

Obwody rezonansowe to szczególna grupa obwodów, które w
zasadzie możemy zaliczyć do filtrów. Zasługują one jednak na
odrębne potraktowanie co najmniej z dwu powodów:
1) Wykorzystywane są przy wymuszaniu oscylacji o ściśle
określonej częstotliwości fali nośnej stacji nadawczych
(emitujących fale elektromagnetyczne).
2) Jako przestrajane obwody rezonansowe wykorzystywane są w
odbiornikach radio, TV itp. do wybierania pożądanych sygnałów
(tj. pożądanych stacji nadawczych).
Przykładowa krzywa rezonansowa
pokazana jest na rys. obok.
Widać tu reakcję o dużej amplitudzie
tylko dla pewnego zakresu częstości
w otoczeniu częstotliwości
rezonansowej f

r

Dla sygnałów

o bardziej oddalonych częstościach
reakcja jest znikoma.

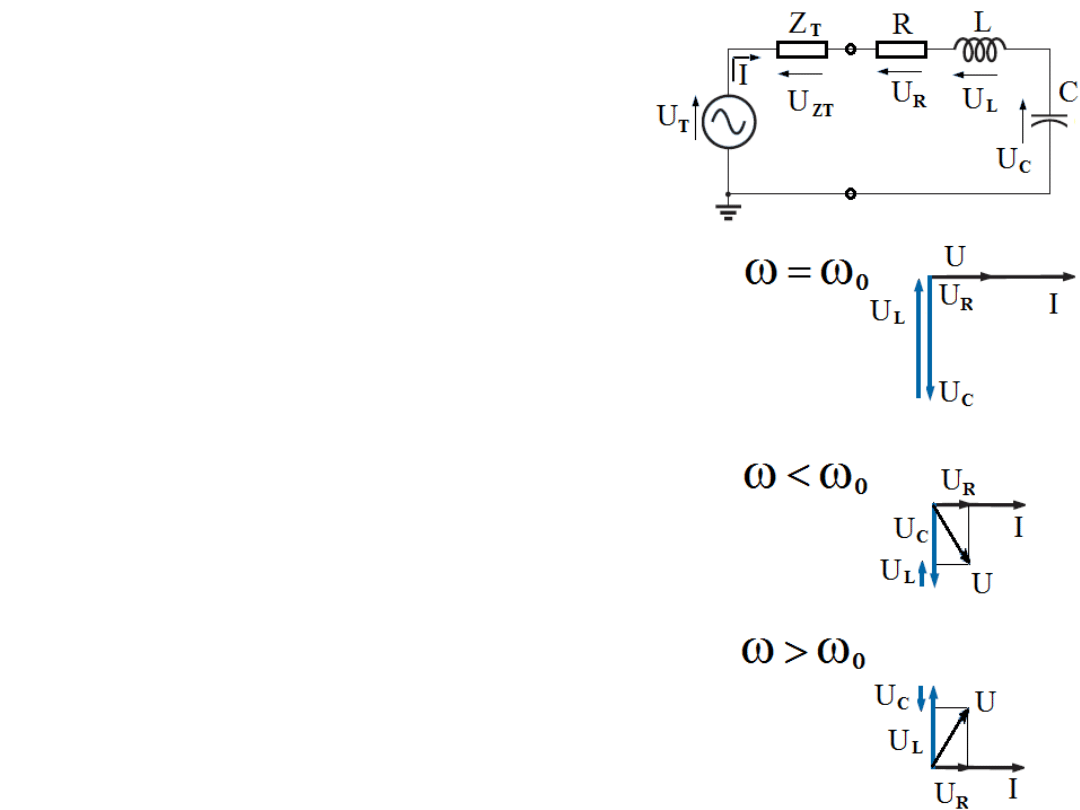
Rezonans szeregowo połączonych
elementów R, L i C.

Indukcyjność L i pojemność C są tu konieczne
natomiast rezystancja R zwykle pojawia się
jako oporność wewnętrzna źródła wymuszania i
jako rezystancja przewodu, który stanowi
uzwojenia solenoidu stanowiącego
indukcyjność L. Czasem należy uwzględnić
nawet rezystancję połączeń elementów ze
sobą.
Zawadą (impedancją) szeregowego układu
rezonansowego RLC jest
Z = R + X

L

+ X

C

= R + j(

ω

L – 1/

ω

C)

Rezonans wystąpi dla pulsacji

ω

=

ω

0

, przy

której Z = R i (

ω

0

L – 1/

ω

0

C) = 0.

Dla rezonansu zawada Z = R ma najmniejszą
wartość co skutkuje największym prądem:
I = U

T

/(Z

T

+ Z) ≈ U

T

/R – gdy Z

T

jest do

zaniedbania. Poza rezonansem, dla

ω

>

ω

0

lub

ω

=

ω

0

, moduł Z ma wartość większą co

zmniejsza prąd I a U

C

i U

L

mają różne moduły.

Czasem mówi się, że rezonans szeregowo
połączonych elementów R, L i C jest
rezonansem napięć.
Łatwo to zrozumieć gdy w rezonansie
Impedancje X

L

= X

C

>> R. Wówczas spadki

napięcia na Indukcyjności i pojemności są
wielokrotnie większe od napięcia
wymuszającego, równego spadkowi napięcia
na R.
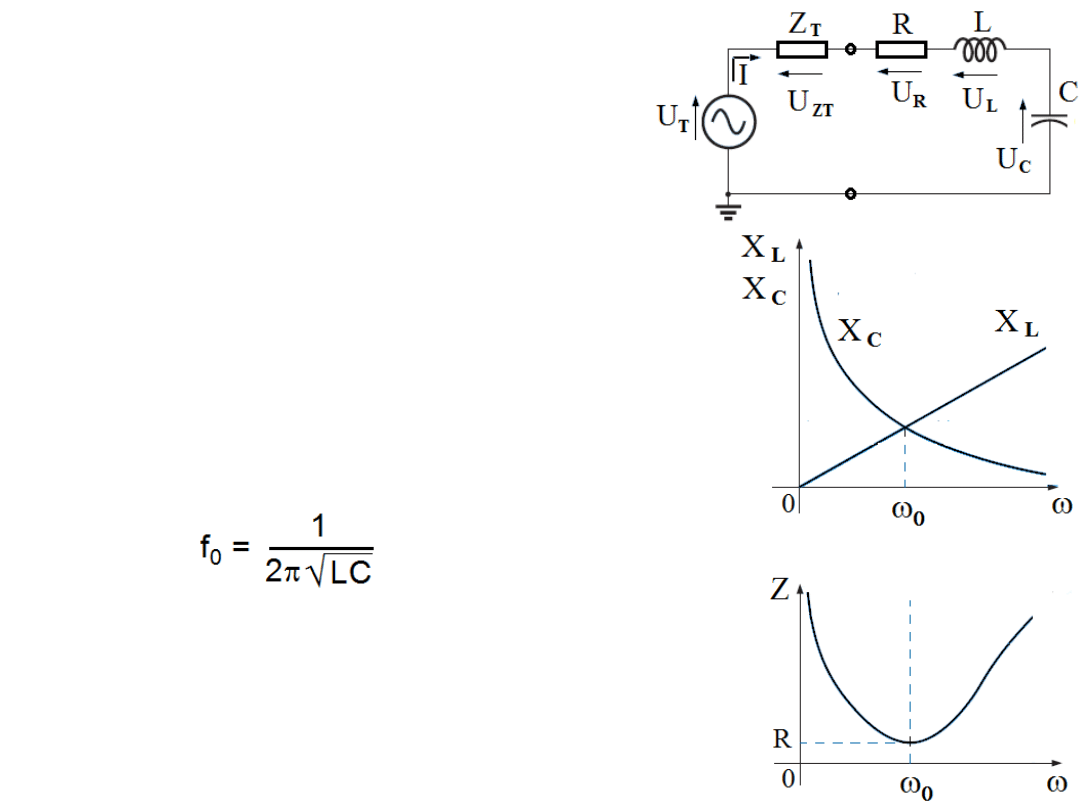
Dla zadanych wartości L i C pulsacja
rezonansowa spełnia równość:

ω

0

L = 1/

ω

0

C,

ω

0

= 1/

√

(LC) a wartość

częstotliwości rezonansowej wynosi:

Z czego wynika, że chcąc dostroić obwód
rezonansowy do częstotliwości
wybranego sygnału należy zmieniać wartość L
lub C, w praktyce zwykle zmieniamy
pojemność.

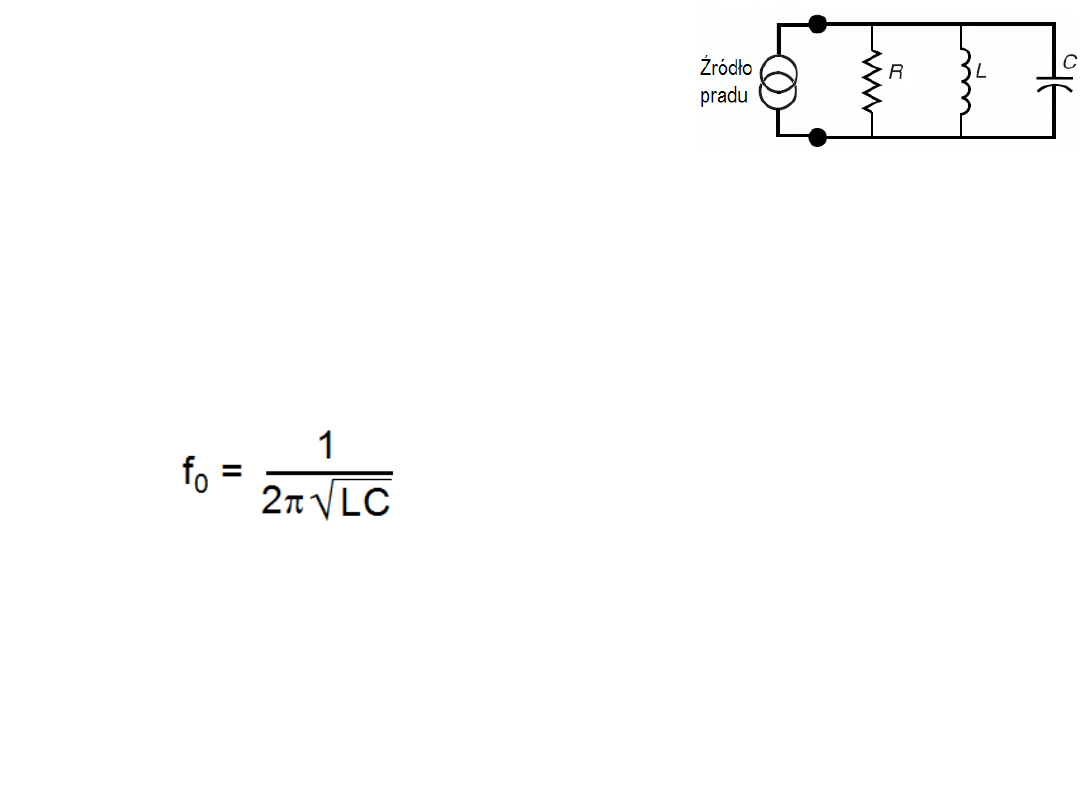
Rezonans równolegle połączonych
elementów R, L i C.
Dla zadanych wartości L i C pulsacja
rezonansowa spełnia równość
susceptancji (przewodności zespolonych)
B

L

i B

C

: 1/

ω

0

L =

ω

0

C,

ω

0

= 1/

√

(LC) a wartość częstotliwości

rezonansowej wynosi:

Mamy tu rezonans prądów, gdyż przy
małym G = 1/R (dużym R) i jednocześnie
dużych B

L

i B

C

(czyli małych

X

L

i X

C

) mamy

olbrzymi prąd w L i C wielokrotnie większy od
prądu wymuszenia, który płynie przez rezystor R.

Niestety w praktyce nie
możemy pomijać rezystancji
przewodów cewki stanowiącej
Indukcyjność i otrzymany wzór
na częstotliwość rezonansową
jest tylko przybliżeniem.

Odpowiada sytuacji idealnej
nie spotykanej w praktyce.

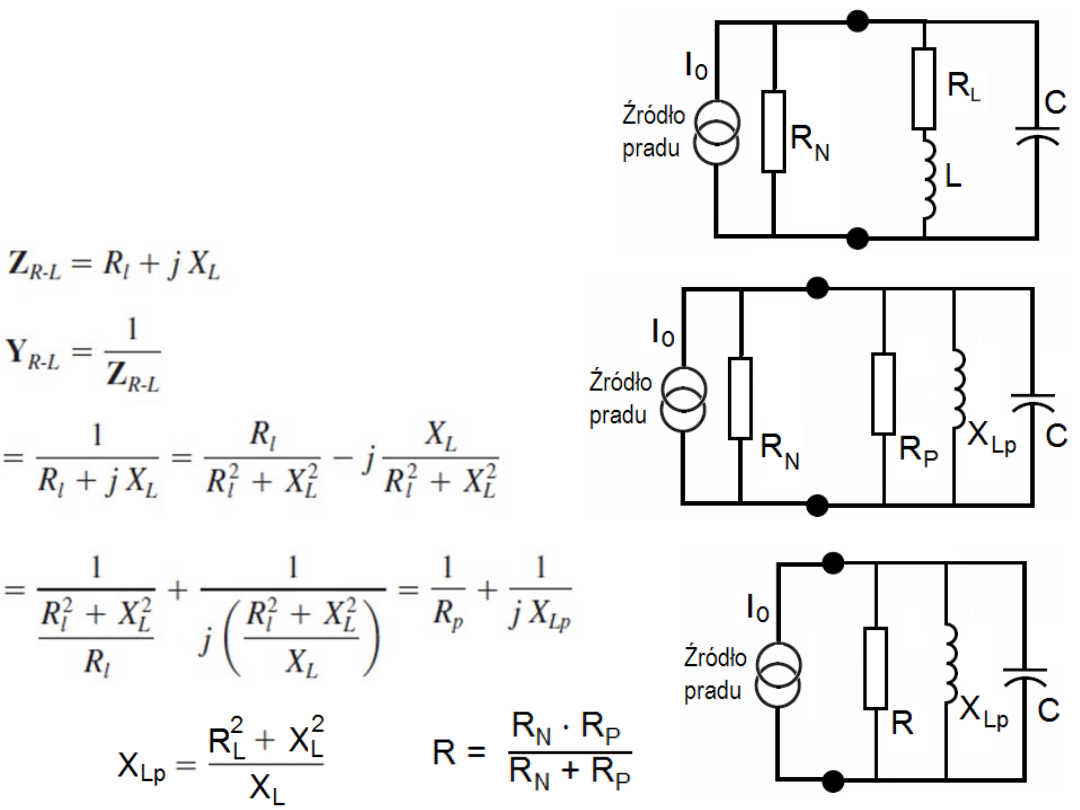
Rzeczywisty równoległy obwód
rezonansowy.
Aby wyznaczyć f

rez

szeregowy układ

L i R

L

zastąpimy równoważnym mu

obwodem równoległym:

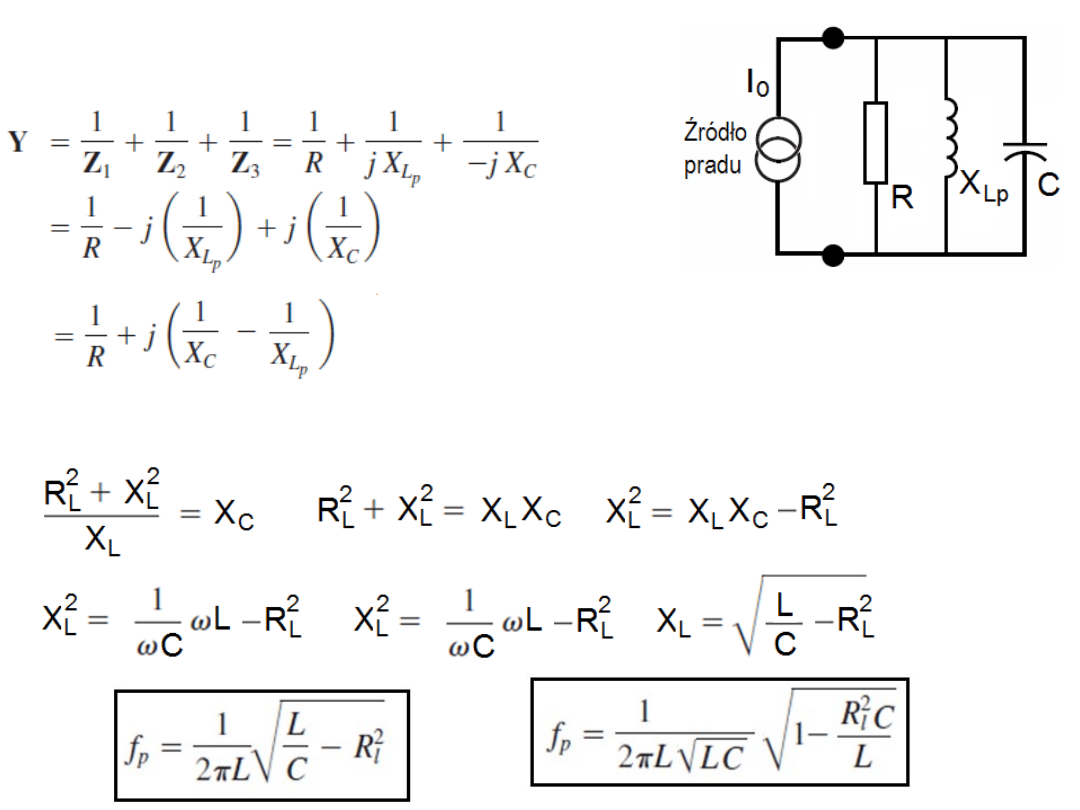
Dla tak przekształconego ale równoważnego
układu mamy:

Zerowanie się części urojonej (rezonans) oznacza: X

Lp

= X

C

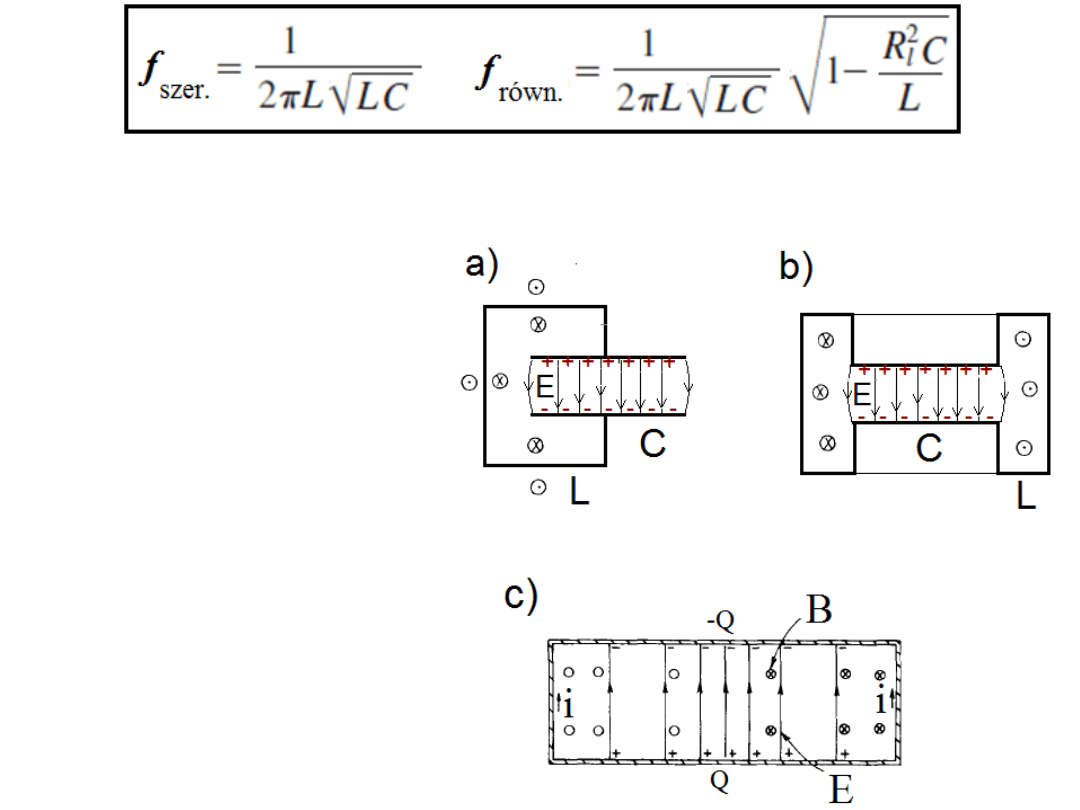
Chcąc zwiększać częstotliwość rezonansową (w obszar wielu GHz) musimy
zmniejszać L i C.

Zmniejszając L i C niemal
do granic możliwości
osiągamy tzw.

rezonatory wnękowe:

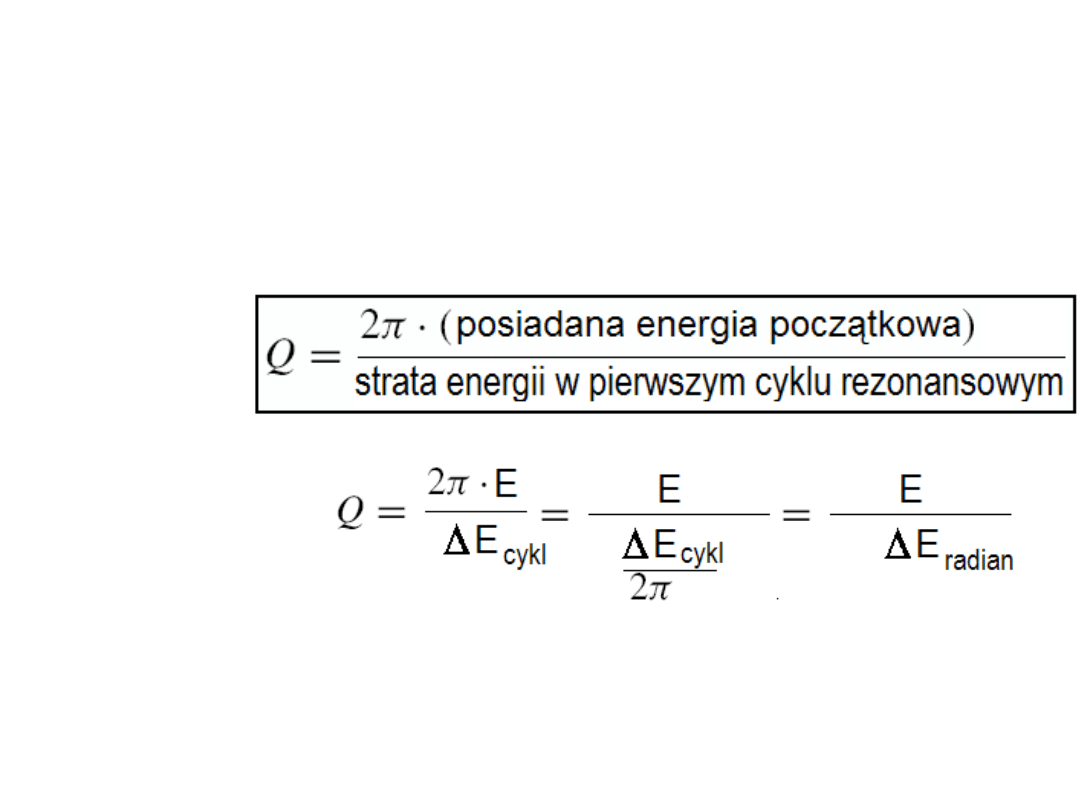
Współczynnik dobroci Q, dobroć Q,
Q factor (quality factor)

Dobroć Q dotyczy tracenia energii przez układ, który może oscylować (elektryczny lub
elektroniczny obwód rezonansowy, huśtawka, struna itp.) i wyraża się stosunkiem
posiadanej energii do względnej szybkości jej tracenia.
Dobroć układu decyduje o kształcie (ostrości) jego krzywej rezonansowej.

DEFINICJA

Po prostym
przekształceniu:

widzimy, że Q jest stosunkiem posiadanej energii do jej porcji traconej w ciągu
jednostkowej części cyklu (w rezonansie) jaką jest 1 radian!
Oczywiście dla dowolnego układu elektrycznego to część rzeczywista R jego
impedancji Z jest tym czynnikiem, który odpowiada za straty (rozpraszanie)
energii.

Współczynnik Q zależy oczywiście od budowy
elementów składowych.

Dla idealnych indukcyjności L i pojemności C przyjmujemy, że
gromadząc energię nie rozpraszają jej (dla rzeczywistych L i C
rozpraszanie energii nie jest zerowe ale może być małe a czasem
pomijalnie małe).

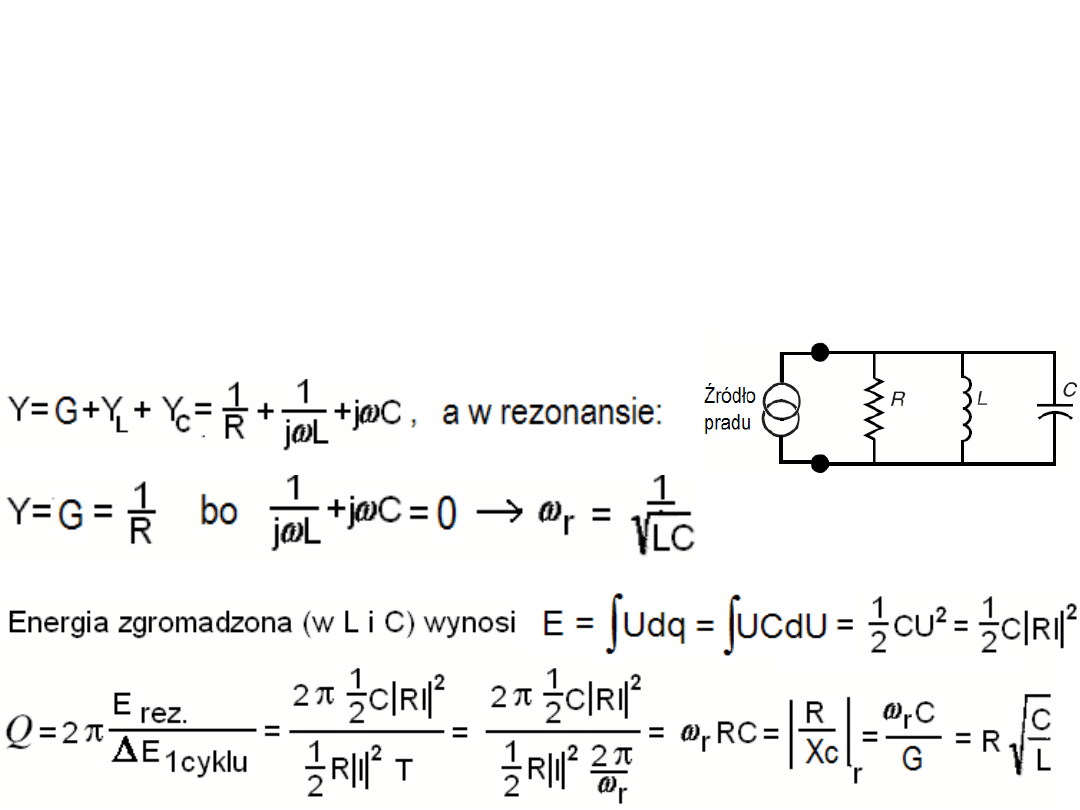
Rozważmy układ równoległy RLC, którego admitancja

(przewodność zespolona) wyraża się przez:

Zatem dla obwodu równoległego
RLC (L i C idealne) jak na rysunku
mamy Q faktor wyrażony przez:

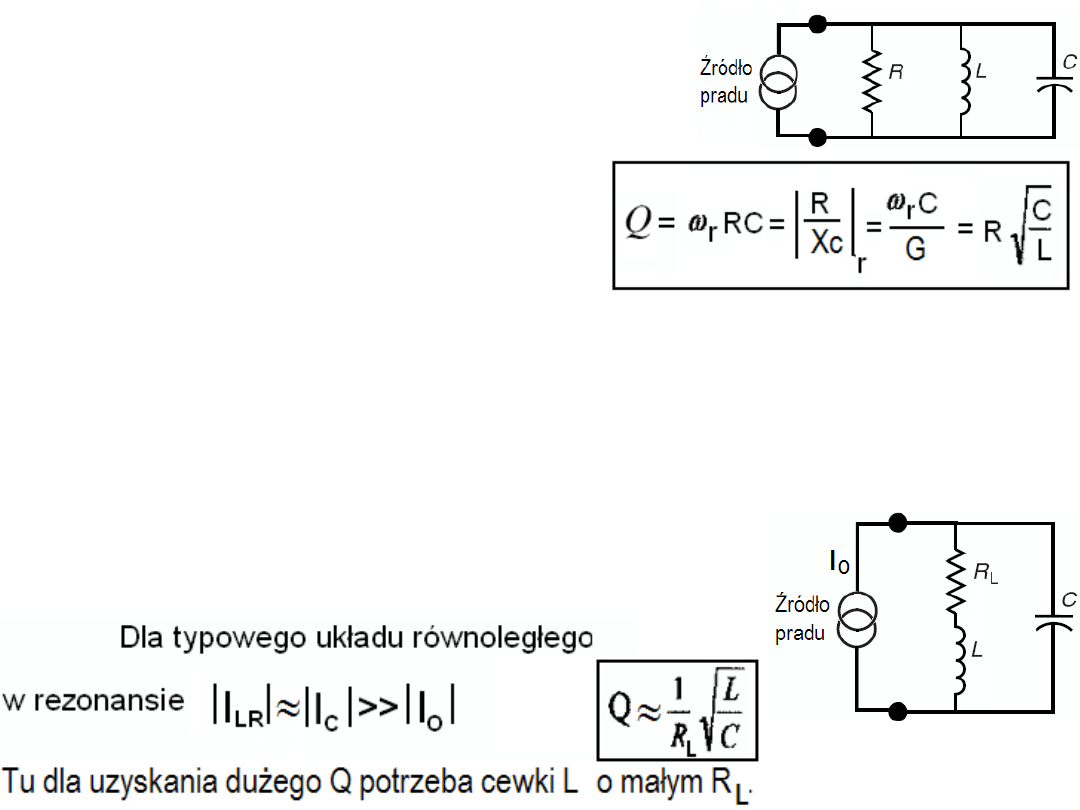
Widać, że rezystancja
równolegle włączona
do równoległego układu
LC powinna być jak największa dla największego Q (najlepiej
ten rezystor usunąć). Opornik R tak włączony osłabia dobroć
Q. W praktyce jednak należy uwzględniać przynajmniej
nieidealność L czyli niezerową oporność drutu z jakiego
wykonana jest indukcyjność.
Wtedy obowiązuje schemat jak obok:

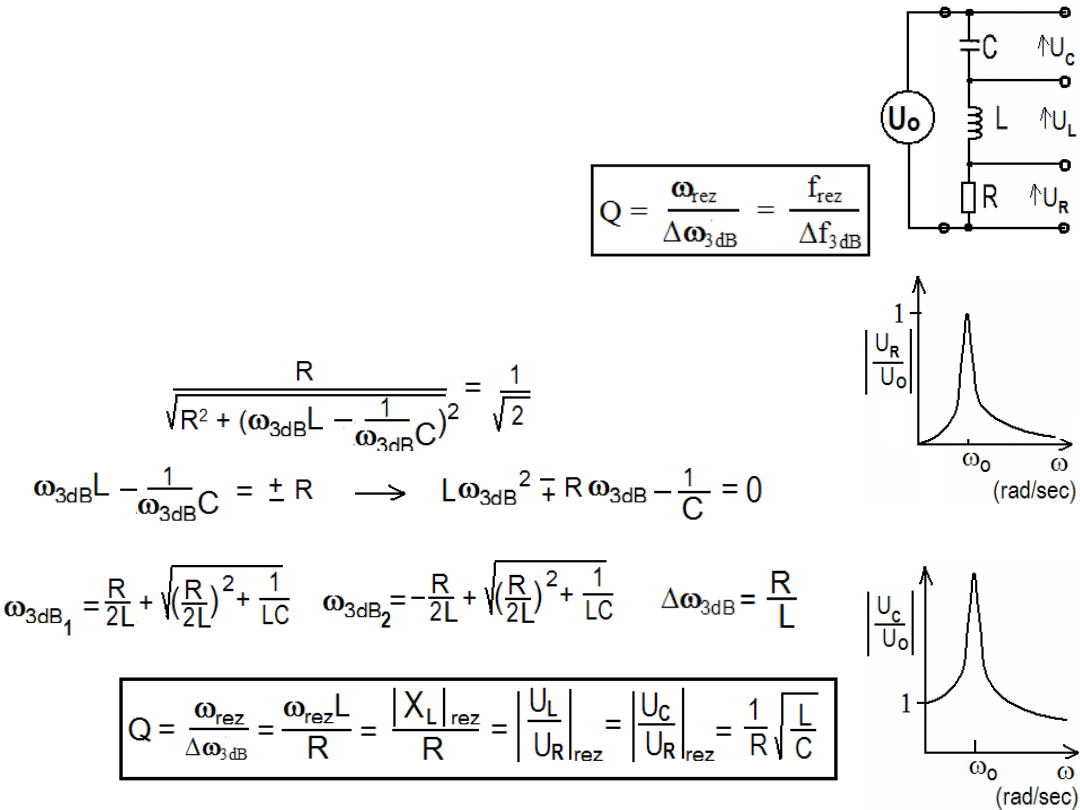
Dobroć Q

ω

r

L

∆ω

3dB

ω

jest również miarą ostrości

krzywych rezonansowych wyrażonej jako:

Dla sprawdzenia równoważności tego
wyrażenia na Q z wyrażeniem poprzez
wartości elementów filtra RLC policzmy

ω

rez

i

∆ω

3dB

.

Niech np. U

WY

= U

R

to k

u

= |U

R

/U

RLC

| i k

umax

= 1

k

u

/k

umax

=

Zatem

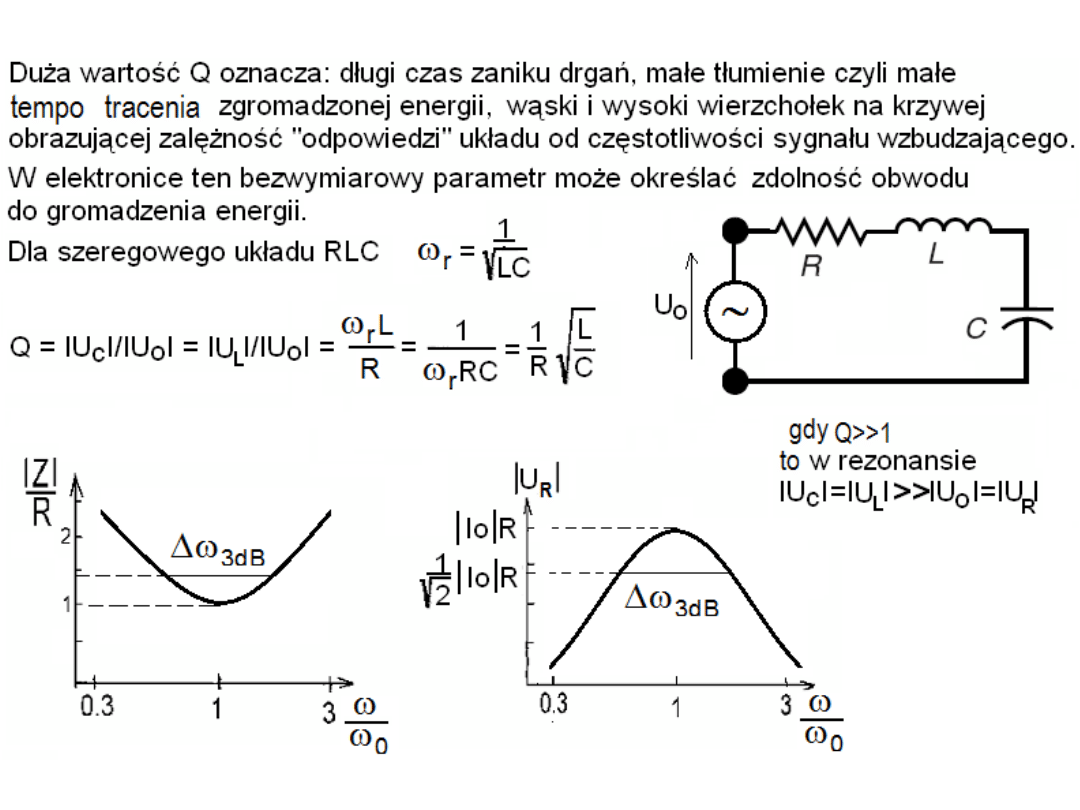
Dodajmy, że w elektronice poza dobrocią układów rezonansowych można
mówić o dobroci innych układów czy elementów.
Przykładowo straty energii w cewkach lub kondensatorach można wyrażać
przy pomocy Współczynnika dobroci Q.

Dobroć cewki zdefiniowana jest jako stosunek:

ω

L/R

Q =

ω

o

L/R albo R =

ω

o

L/Q

(gdzie L-indukcyjność cewki, R oporność cewki).

Traktując kondensator jako równoległe połączenie idealnej pojemności i
rezystancji R (reprezentującej straty dielektryczne) definiujemy dobroć
kondensatora jako stosunek prądów

Q = I

C

/I

R

= (U/X

C

)/(U/R) = R/X

C

=

ω

CR.

Wynika z tego, że układy o dużej dobroci to takie, które „marnotrawią” mało
energii na straty w rezystancjach przewodów cewki, ewentualnego rezystora R
oraz w materiale kondensatora.

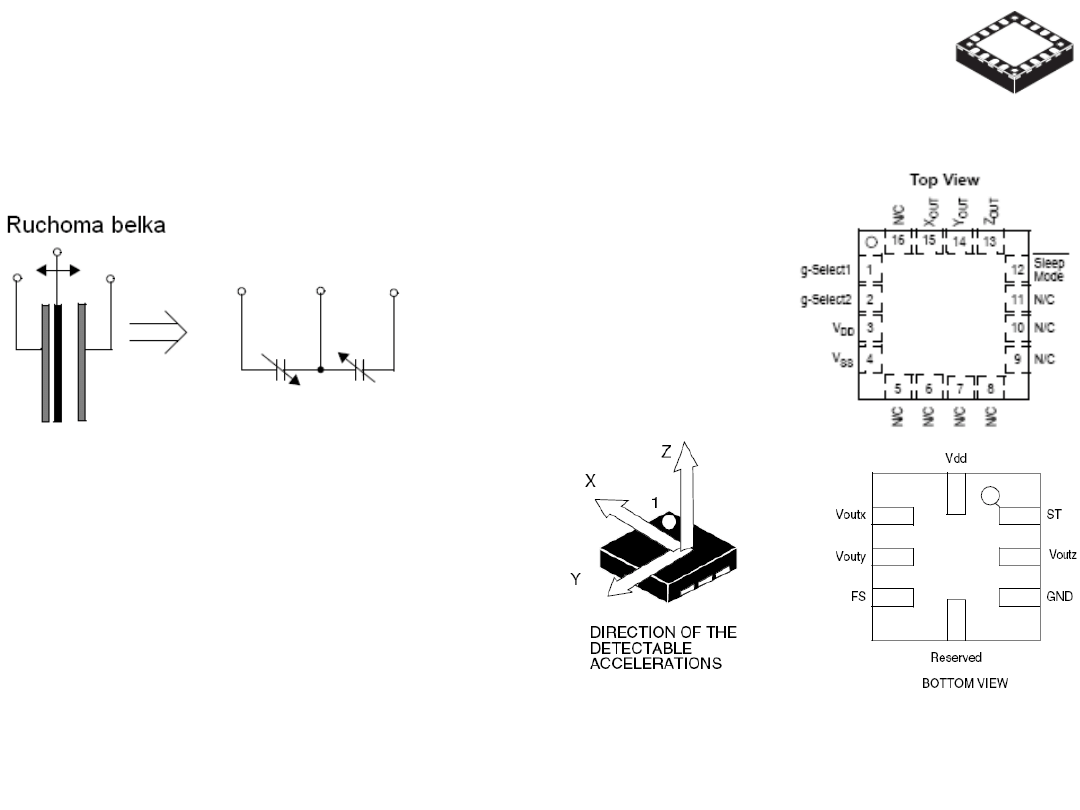
Przykładowe ekstra zastosowanie pojemności:
Trzy-osiowy akcelerometr:

MMA7260Q, MMA7261QT,

LIS3L06AL i inne.
(MEMS - MicroElectroMechanical Systems)

MMA7260Q

LIS3L06AL

Inne ekstra zastosowanie pojemności to czujniki pojemnościowe w

ekranach dotykowych.

LIS3L06AL

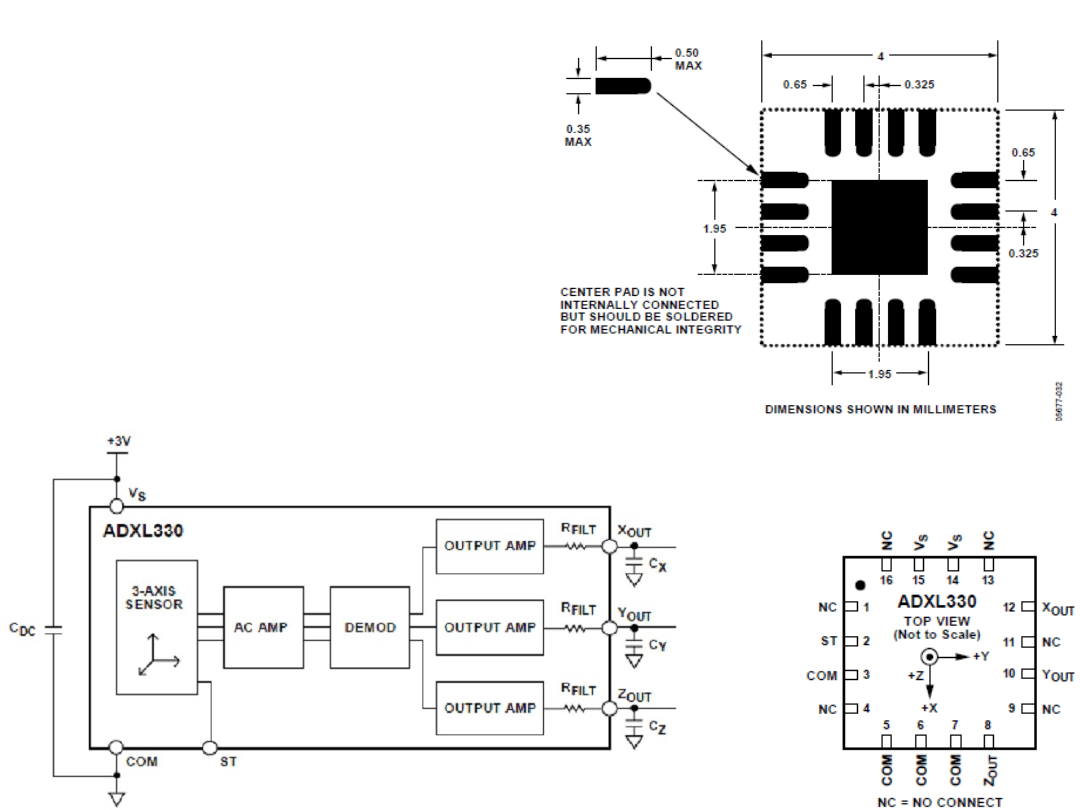
Trzy-osiowy akcelerometr
ADXL330

Czułość do 330mV/g

LIS3L06AL

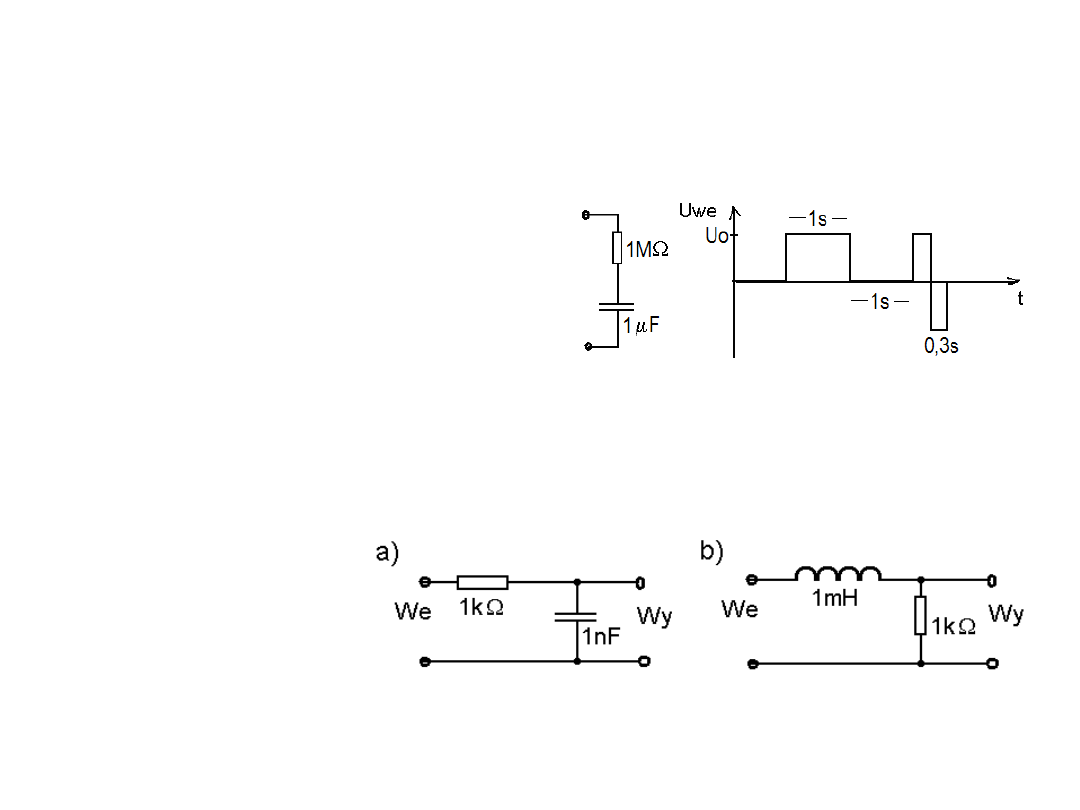
E-E-M. Lista-05

1 Narysuj wykres wskazowy dla układu równolegle połączonych L = 10mH i C
= 50µF, zasilanych z generatora napięcia sinusoidalnego o pulsacji ω = 1000
rad/s i amplitudzie 1V. Impedancja wewnętrzna generatora wynosi Rwe = 1Ω.

2 Na zaciski układu RC podano sygnał
o złożonym (prostokątnym) przebiegu.
Naszkicuj przebiegi napięć UR i UC.

3. Szeregowy obwód rezonansowy zawiera: R = 1Ω, L = 1mH, C = 1µF. Oblicz
dobroć układu i stosunki: UR/UWe, UC/UWe i UL/UWe w rezonansie (Uwe -
napięcie zasilające o częstotliwości rezonansowej).

4. Wylicz częstotliwości
graniczne i określ pasma
przenoszenia układów:

5. Zaprojektuj filtr pasmowy dla pasma 1 kHz-10kHz wykorzystując prostą
zasadę ułatwiającą obliczenia: Zwy/Zwe ≤1/10 (strona 25).