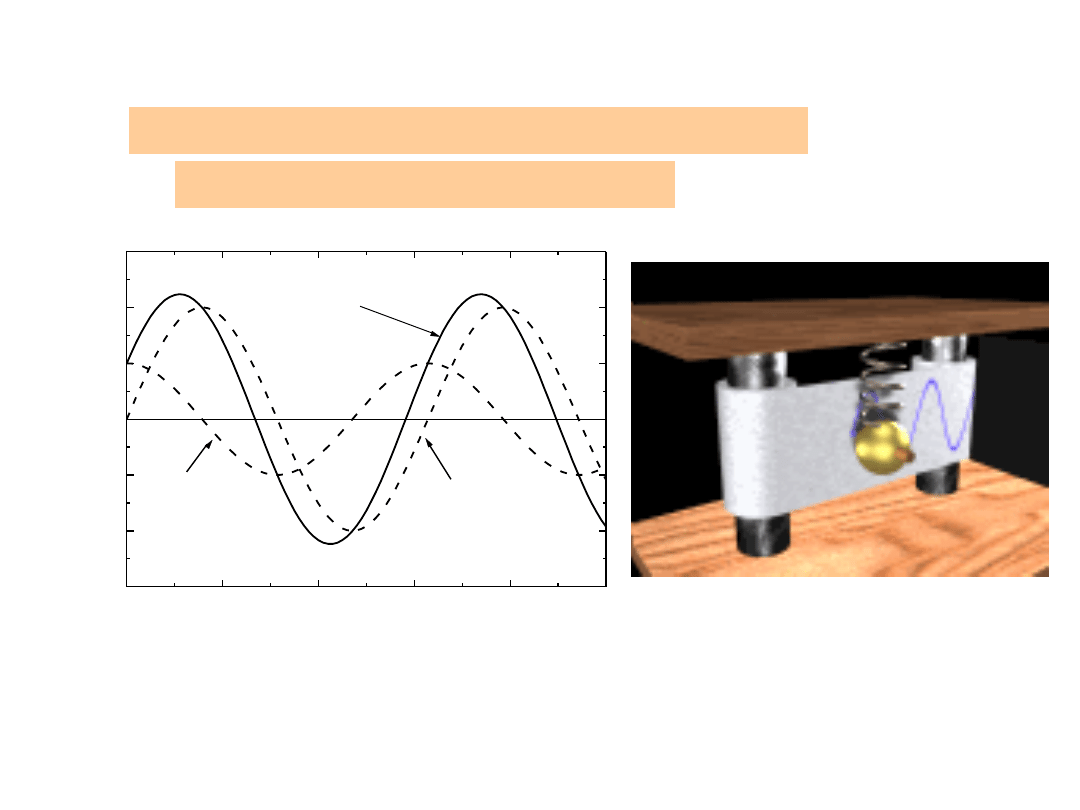
Ruch drgający

Ruch okresowy (periodyczny)

-

powtarzający się w regularnych odstępach

czasu.

Przemieszczenie cząstki

w ruchu periodycznym wyrażone za pomocą

funkcji

sinus i cosinus



drgania harmoniczne

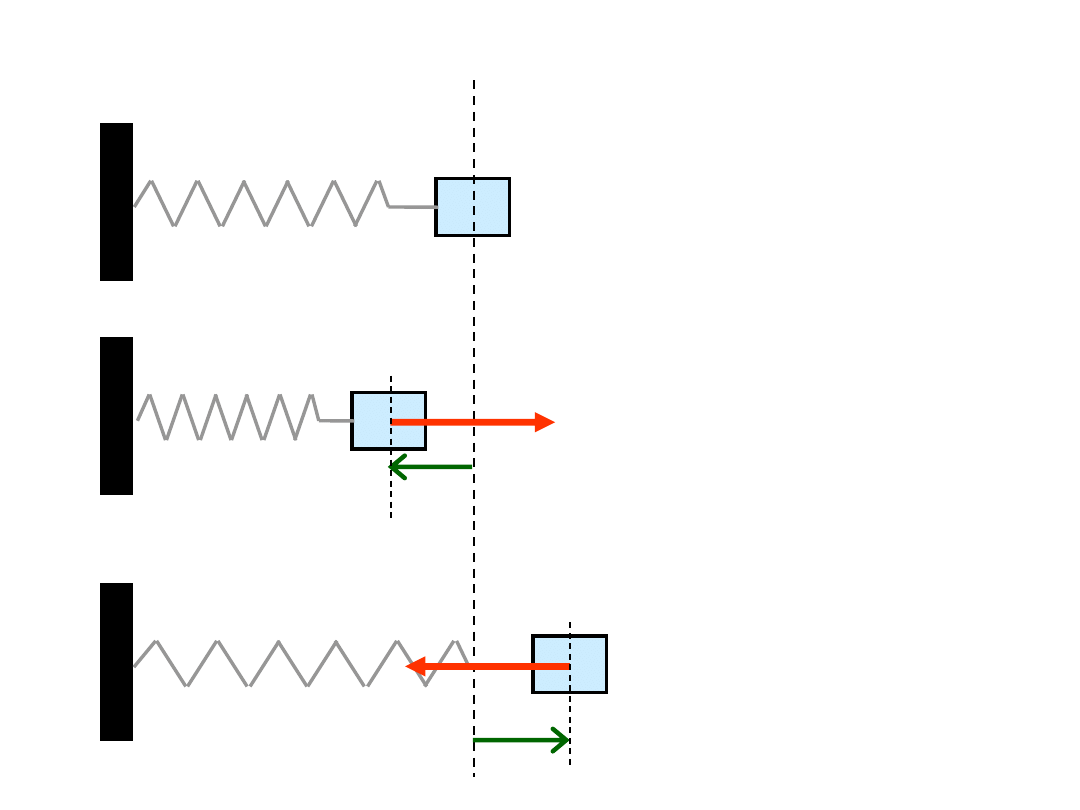
Siła harmoniczna (sprężystości)

-

proporcjonalna do przesunięcia

ciała od początku układu i skierowana ku początkowi układu

x

k

F







gdzie x -

przemieszczenie względem

położenia równowagi

F

x

http://en.wikipedia.org/wiki/Simple_harmonic_motion

Useful webpages:

http://video.answers.com/learn-about-harmonic-motion-part-3-no-calculus-99168827

http://www.electron.rmutphysics.com/physics/charud/scibook/Physics-for-Scientists-and-Engineers-
Serway-Beichner-4/13%20-%20Oscillatory%20Motion.pdf

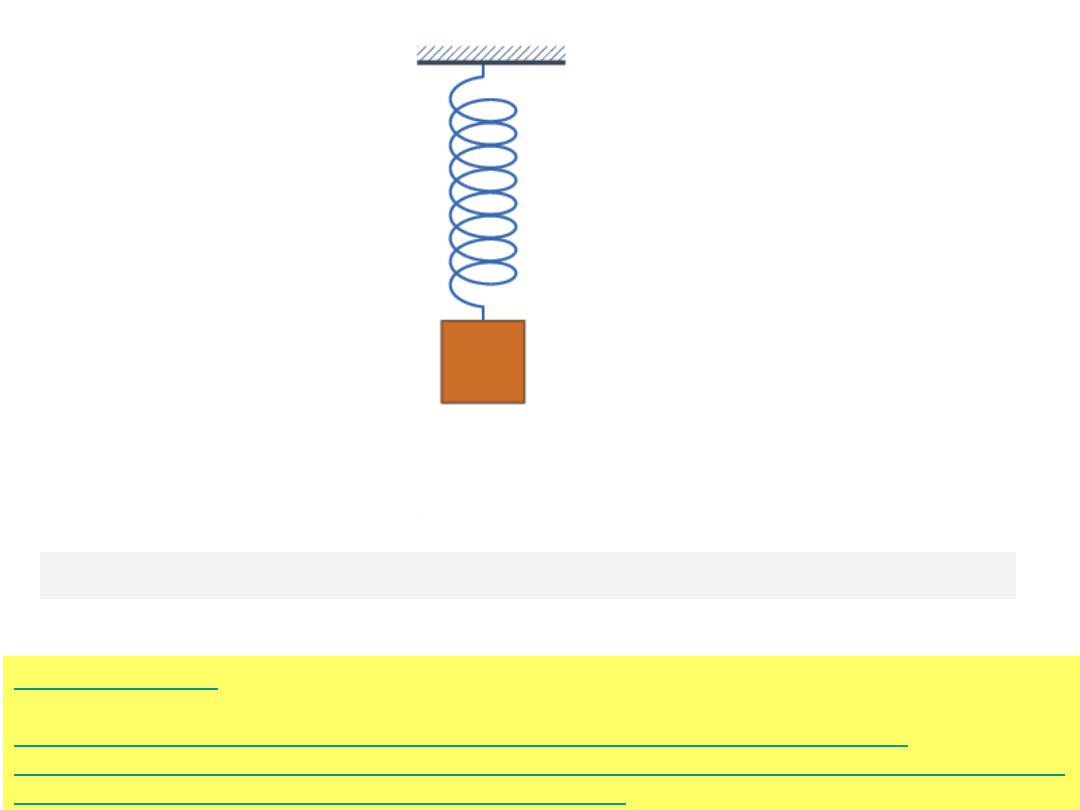
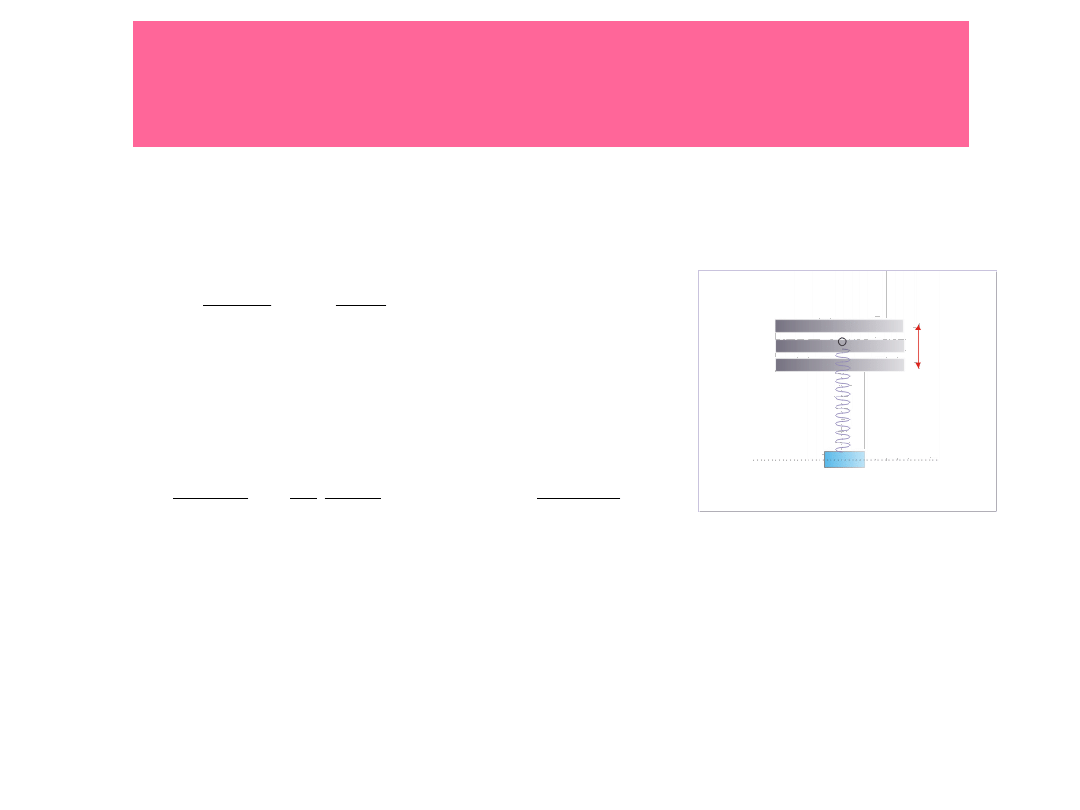
An undamped

spring-mass system

undergoes simple harmonic motion.

Drgania harmoniczne

x

k

F







położenie równowagi

F = 0

m

x = 0

x<0

F > 0

ściskanie sprężyny

F < 0

x > 0

rozciąganie sprężyny

2

2

dt

x

d

a



definicja przyspieszenia

x

m

k

dt

x

d





2

2

Stąd:

równanie różniczkowe liniowe 2. rzędu









a

m

F

II zasada dynamiki

ogólne rozwiązania (przypadek 1-wymiarowy):

)

cos(

)

sin(

)

(

0

2

0

1

t

A

t

A

t

x













m

k



0



częstość drgań (rad/s)

)

sin(

)

(

0











t

A

t

x

Stałe

A

i



trzeba wyznaczyć z warunków początkowych tzn.

x(0)

i

v(0)

A - maksymalne wychylenie (amplituda)



- faza poczatkowa

)

cos(

)

(

0











t

A

t

x

lub:

Ponieważ złożeniem funkcji okresowych jest funkcja okresowa, stąd:

A

1

cos



t + A

2

sin



t

A

2

sin



t

A

1

cos



t

Złożenie funkcji okresowych - funkcja okresowa:

A

1

cos



0

t + A

2

sin



0

t = Asin(



0

t +



)

T

f

1



częstotliwość (Hz)

0

2







T

okres (s)

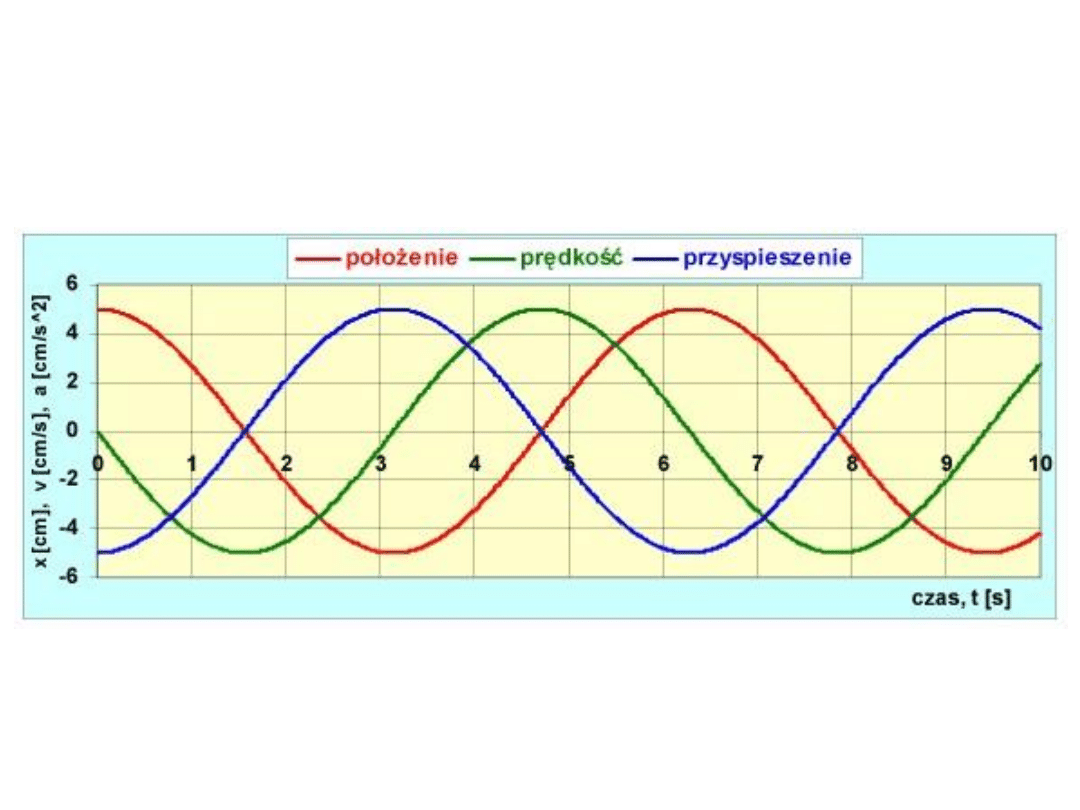
Przyspieszenie: d

2

x/dt

2

= a(t) =

– A



0

2

cos



0

t

amplituda: A



0

2

(m/s

2

)

Liczba

drgań w czasie t :

n = t/T

Po podzieleniu obu stron przez t - liczba

drgań w jednostce czasu:

T

t

n

1



Prędkość: dx/dt = v(t) = – A



0

sin



0

t amplituda: A



0

(m/s)





cos

)`

(sin







sin

)`

(cos





Położenie: x(t) = Acos



0

t

amplituda: A (m)

0





The motion of an undamped

pendulum

approximates to simple

harmonic motion if the amplitude is very small relative to that of the rod.

http://en.wikipedia.org/wiki/Simple_harmonic_motion

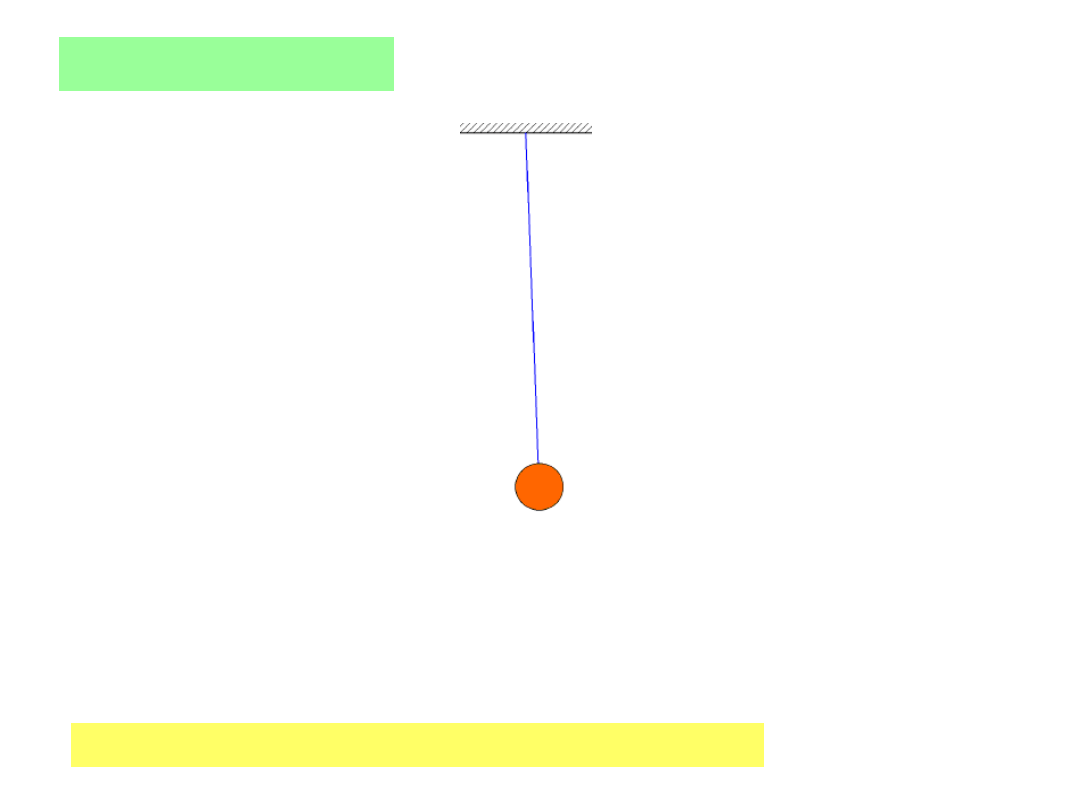
Simple pendulum

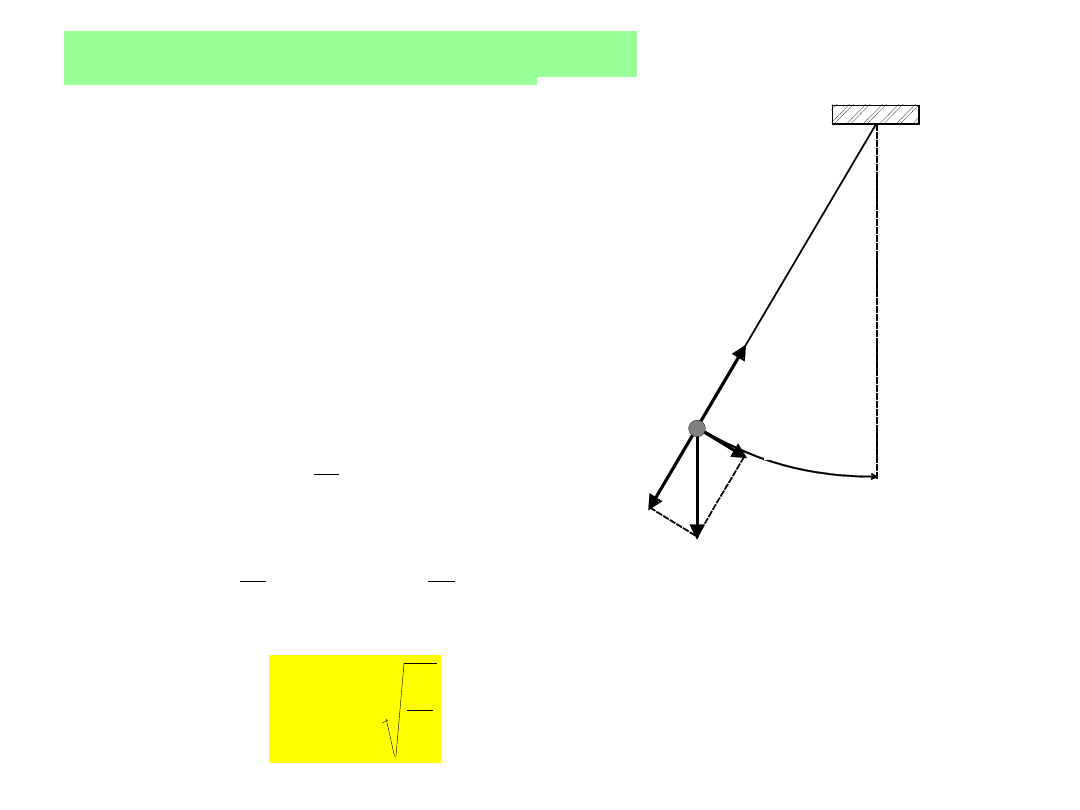
θ

sin

mg

F





dla małych kątów

θ

θ

sin



L

x

mg

F





L

g

x

L

g

a









2

0



g

L

T



2



okres małych drgań nie zależy od amplitudy
ani masy wahadła

Wahadło proste (matematyczne)



l

N

mg

mgcos



mgsin



x=l





m

x=L



L

Punkt materialny zawieszony na cienkiej,
nieważkiej i nierozciągliwej nici

T

/

2







N

Q

F











l

mg

P

S



L

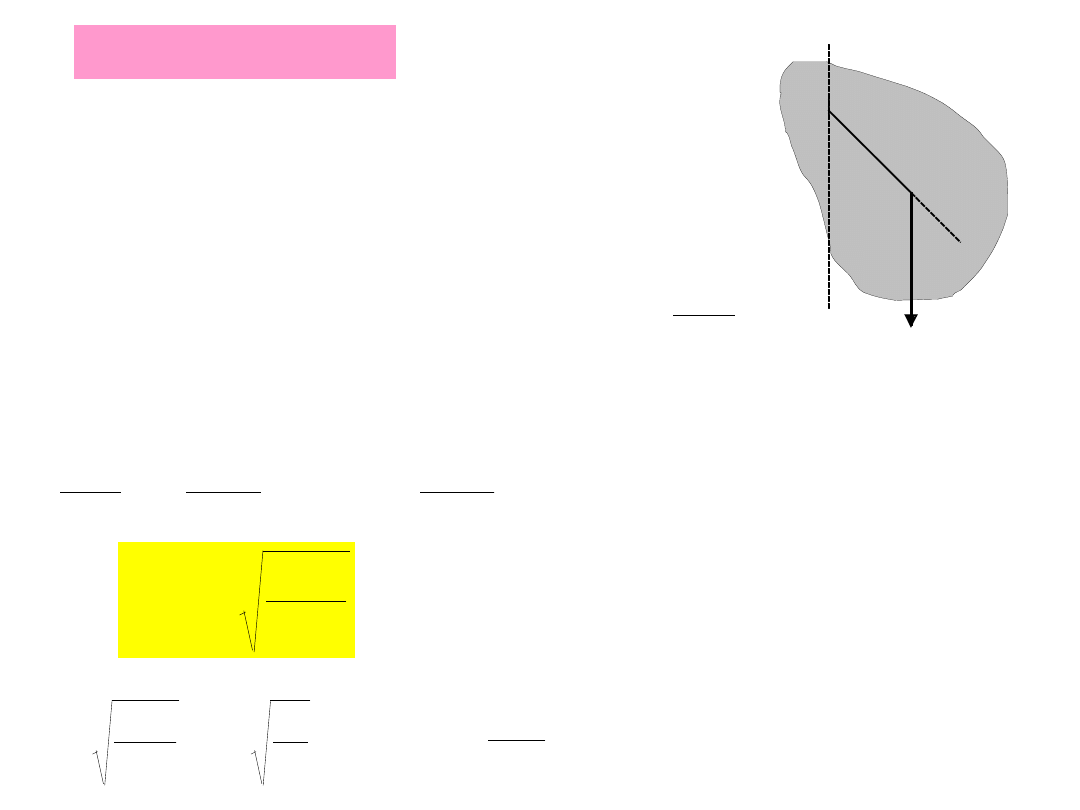
Wahadło fizyczne

Bryła sztywna zawieszona na poziomej osi
nieprzechodzącej przez środek masy

Dla małych kątów

θ

θ

sin



I

mgL

I

mgL

dt

d









2

0

2

2

θ

θ



θ

sin

mgL

M





Moment siły ciężkości:

II zasada dynamiki bryły sztywnej:

2

2

dt

d

I

I

M









mgL

l

T



2



okres drgań harmonicznych

g

L

mgL

I

z





2

2



mL

I

L

z





długość zredukowana

wahadła fizycznego

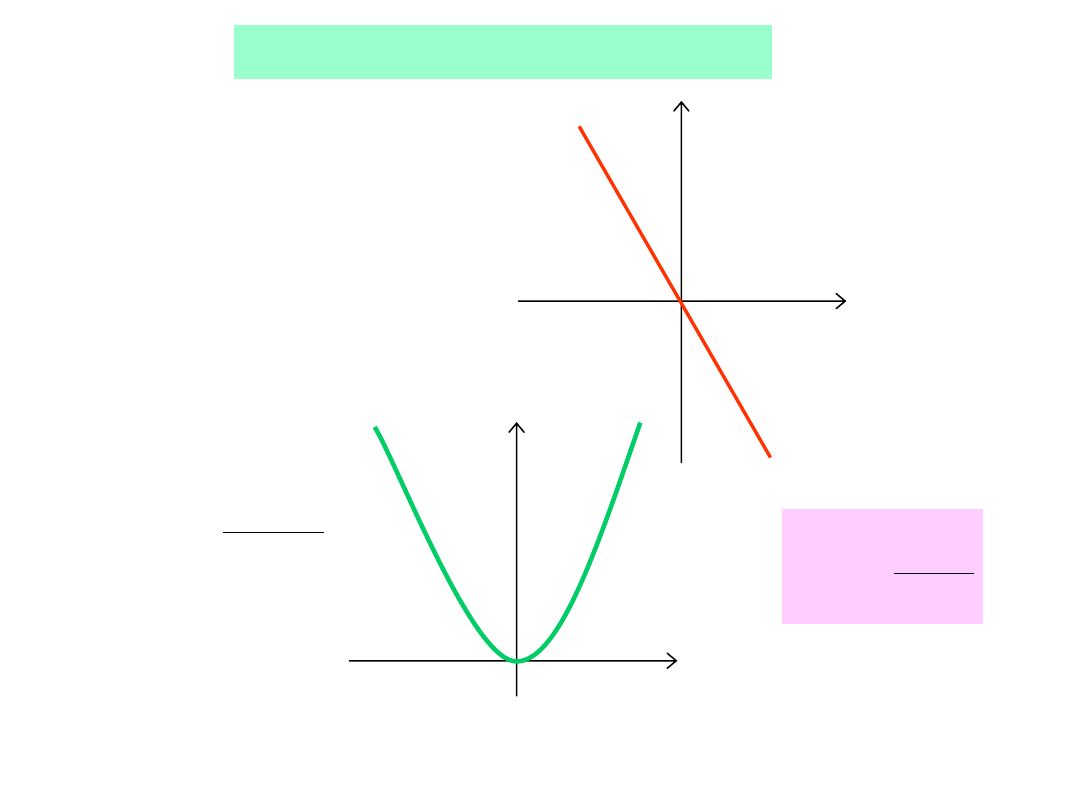
Energia drgań harmonicznych

F

x

x

k

F







E

p

x

punkt równowagi trwałej – minimum energii potencjalnej

2

2

x

k

E

p





dx

dE

F

p





Energia ruchu harmonicznego prostego

Energia potencjalna

sprężyny:

2

2

kx

E

p



Dla maksymalnie

rozciągniętej sprężyny (x = A) jej energia:

E

C

= (1/2)kA

2

E

k

= 0

2

2

2

2

1

2

1

v

2

1

kA

kx

m









2

2

2

v

x

A

m

k





Stąd:

Ponieważ

k/m =



0

2

więc:

2

2

0

v

x

A







Po zwolnieniu sprężyny (przy założeniu braku tarcia i sił oporu),
zgodnie z zasadą zachowania energii, w dowolnej chwili:

suma energii kinetycznej i potencjalnej

= (1/2)kA

2

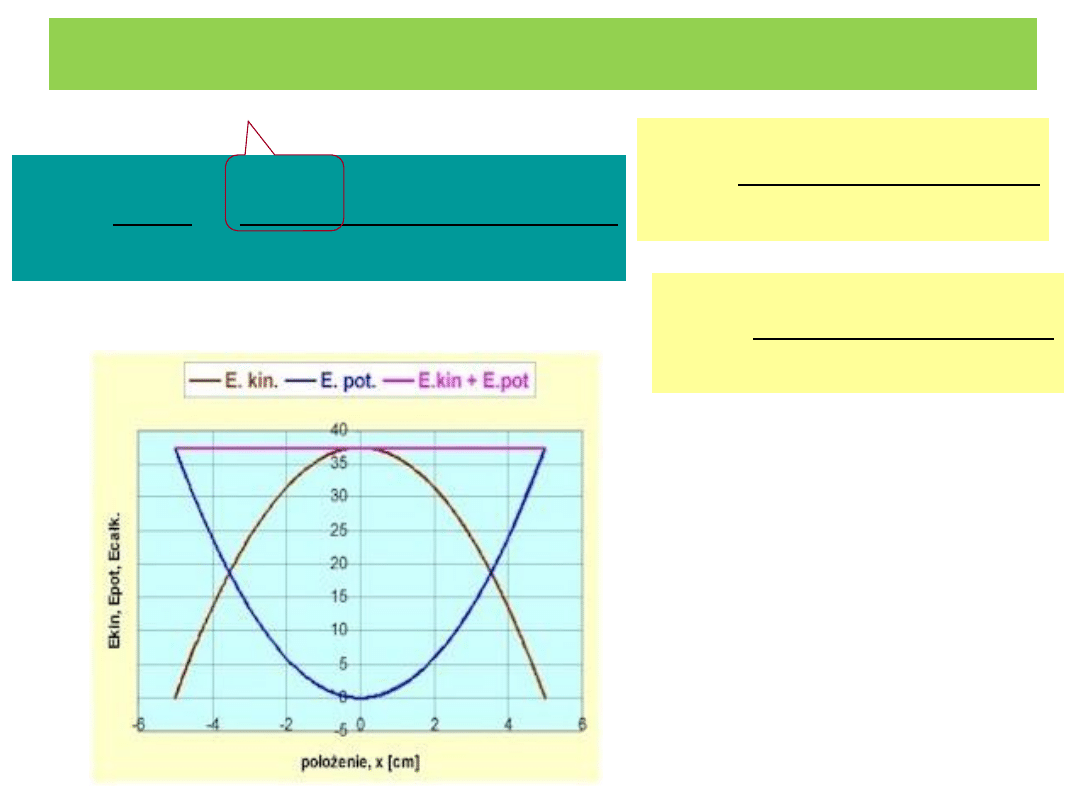
Energia kinetyczna w ruchu harmonicznym





2

sin

2

v

0

2

2

2

0

2













t

A

m

m

E

k

= k





2

sin

0

2

2









t

kA

E

k





2

cos

0

2

2









t

kA

E

p

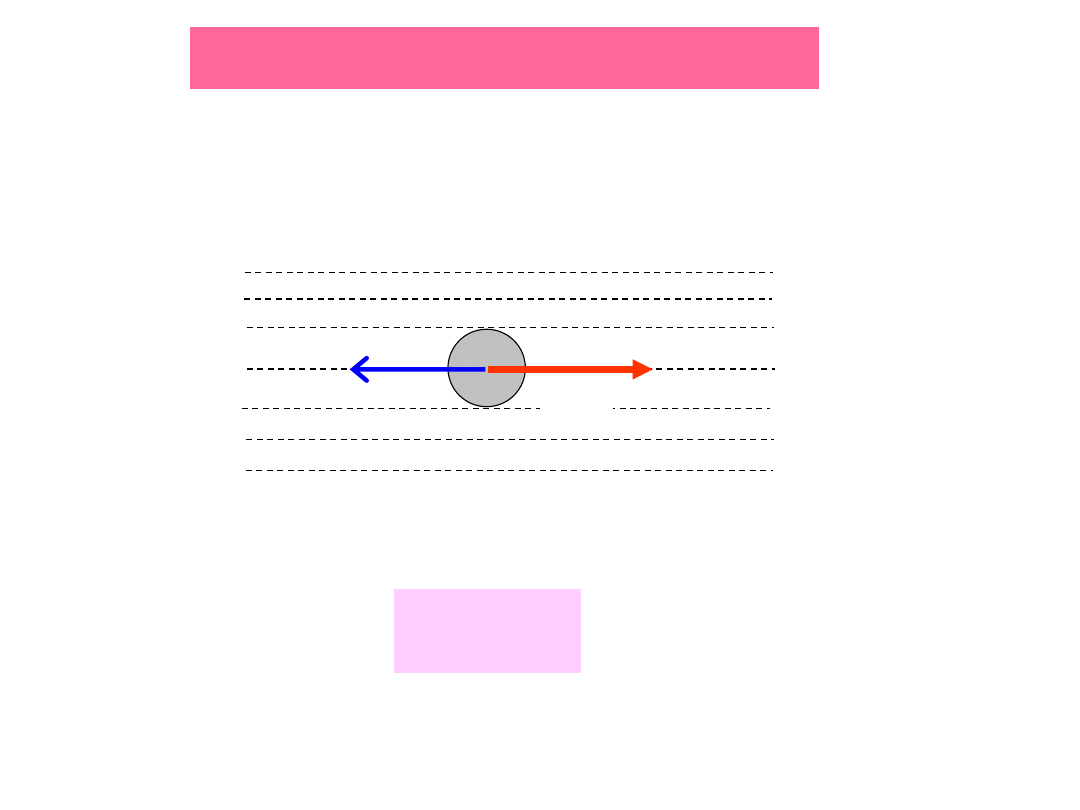
Oscylator harmoniczny tłumiony

Tłumienie oscylatora



straty energii

układu oscylatora

W przypadku

drgań mechanicznych, siłą hamującą (tłumiącą) ruch

cząstki jest

siła oporu F

op

ośrodka

.

v

F

op













v

F

op

Siła oporu lepkim płynie (cieczy lub gazie) ma zwrot przeciwny do
prędkości i jest wprost proporcjonalna do prędkości :

F

op

= -



dx/dt

Po włączeniu

siły hamującej do oscylatora

-

równanie ruchu:

t

x

kx

t

x

m

d

d

d

d

2

2









Wprowadzamy



= m/



oraz oznaczamy

częstość drgań nietłumionych



0

2

= k/m

0

d

d

1

d

d

2

0

2

2







x

t

x

t

x





Otrzymujemy:

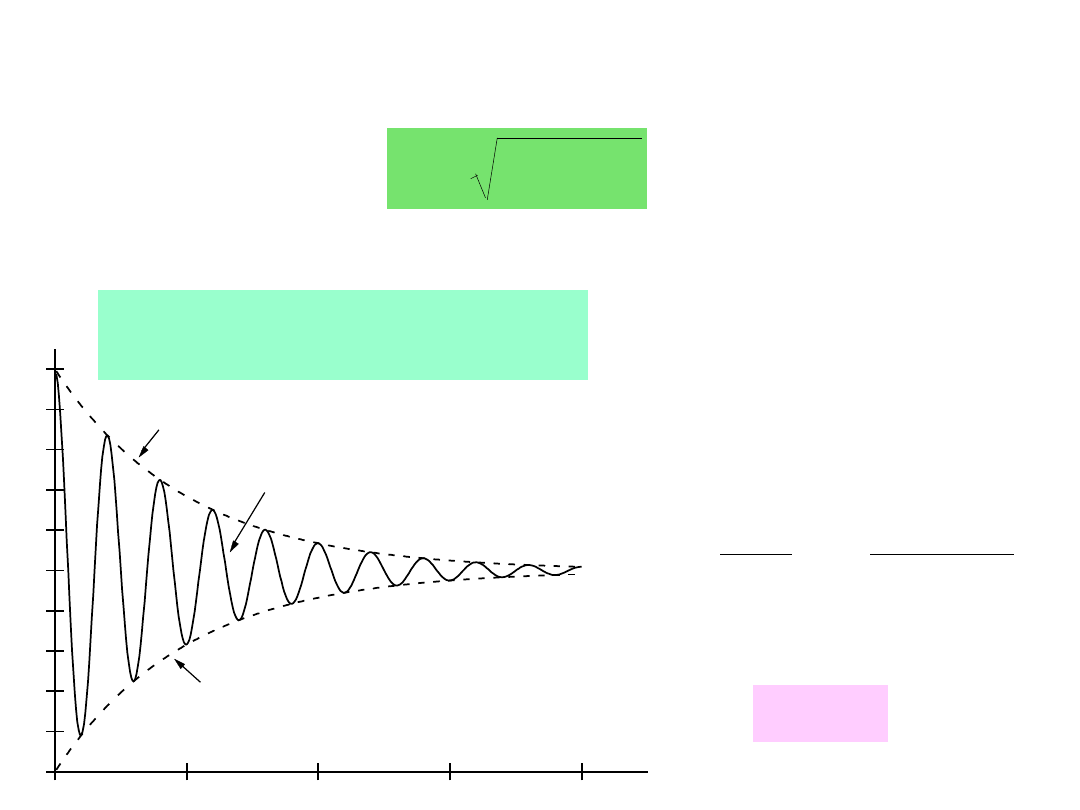
Rozwiązanie w postaci drgań okresowo zmiennych tłumionych :

t

e

A

x

t





cos





Współczynnik



= 1/(2



)

określający wielkość tłumienia nazywamy

współczynnikiem tłumienia

.

Po obliczeniu pochodnych i podstawieniu do

równania ruchu



warunek na

częstość drgań tłumionych:

2

2

0











Opór zmniejsza amplitudę i częstość drgań

Wielkość tłumienia określa:

-

współczynnik tłumienia



(lub stała czasowa



)

0

-Ae

-



t

Ae

-



t

Ae

-



t

cos



t

-A

A

t

x

Przypadek "słabego tłumienia" tj.



<



0

T







T -

okres drgań tłumionych

T

e

Ae

Ae

A

A

T

T

t

t

T

t

t





























ln

ln

ln

)

(

-

logarytmiczny dekrement

tłumienia



Przypadek

tłumienia powyżej tzw. wartości krytycznej



>



0



ruch nie

jest ruchem

drgającym, ciało wychylone z położenia równowagi powraca

do niego asymptotycznie



ruch

pełzający (aperiodyczny).



=



0



>



0

t

X

Straty mocy, współczynnik dobroci

Definicja

współczynnika dobroci

Q

:

okresie

w

stracona

ana

zmagazynow

E

E

Q

_

1

_

_

2





Dla przypadku słabo tłumionego oscylatora harmonicznego (



<<



0

)

Q





0

/2



Oscylator

Q

Ziemia dla fali sejsmicznej
Struna fortepianu lub skrzypiec
Atom wzbudzony
Jądro wzbudzone

250-400

1000

10

7

10

12

Typowe wartości Q

Drgania wymuszone oscylatora

harmonicznego

Siła zewnętrzna

F(t)

przyłożona do oscylatora - podtrzymuje gasnące

drgania



równanie ruchu:

)

(

d

d

d

d

2

2

t

F

kx

t

x

t

x

m









Po podstawieniu



= m/



oraz



0

2

= k/m:

m

t

F

x

t

x

t

x

)

(

d

d

1

d

d

2

0

2

2











gdzie:



0

-

częstość własna

układu, tj. częstość drgań swobodnych, gdy nie

działa siła zewnętrzna i nie ma tarcia ani innych sił oporu,



-

stała czasowa

związana ze

współczynnikiem tłumienia





= 1/(2



)

Gdy

układ jest

zasilany

częstością



różną od



0

,

wówczas

drgania

będą odbywały się z częstością siły zewnętrznej, a nie z

częstością własną

.

Siłę

F

w tym przypadku nazywamy

siłą wymuszającą

.

t

m

t

F

m

t

F







sin

sin

)

(

0

0





Założenie:

gdzie



0

= F

0

/m

Rozwiązanie postaci:

x=Asin(



t +



)

gdzie:

A

- amplituda



-

przesunięcie fazowe

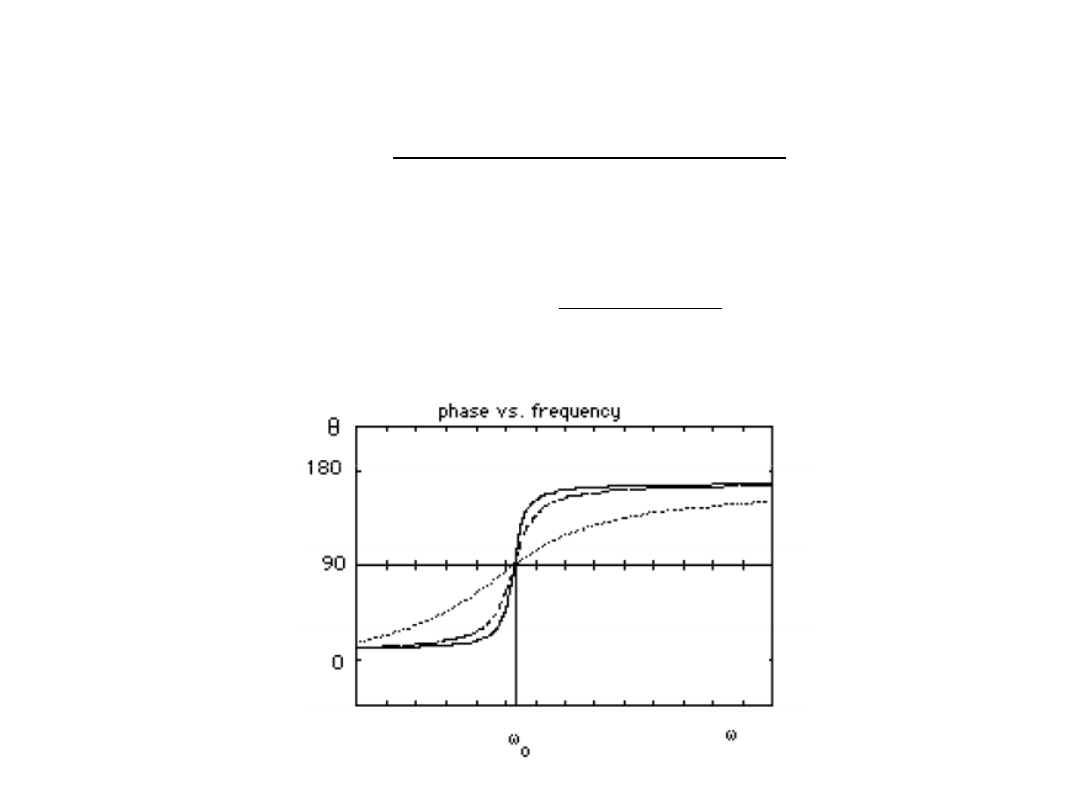
Przesunięcie fazowe



mówi nam, o jaki kąt maksimum przemieszczenia

wyprzedza maksimum siły

(o ile przesunięte są wykresy x(t) i F(t)).

Np.

Siła osiąga swoje maksimum, gdy przemieszczenie jest równe zeru (i rośnie w

kierunku dodatnim). Oznacza to,

że x opóźnia się względem siły o



/2.

2

/

1

2

2

2

2

2

0

0

]

4

)

[(

















A

Amplituda:

Rozwiązanie

2

2

0

2













tg

Przesunięcie
fazowe:

http://www.physics.rutgers.edu/~jackph/2005s/PS02.pdf

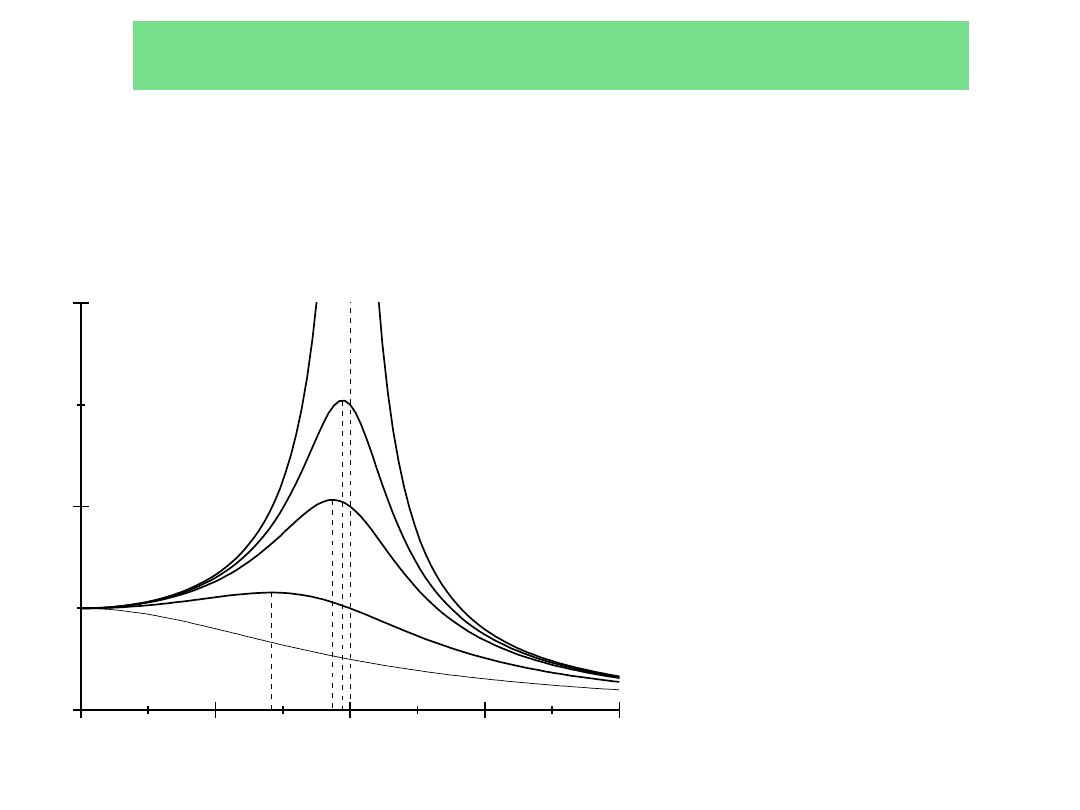
REZONANS

Zjawisko rezonansu

występuje, gdy siła wymuszająca ma odpowiednią

częstotliwość



gwa

łtowny wzrost

amplitudy

drgań nawet przy

niewielkiej

wartości siły wymuszającej.





A





4



3



2



1



0

= 0

Częstość rezonansową



r

i

amplitudę rezonansową

A

r

możemy obliczyć z warunku na
maksimum amplitudy

drgań.

2

2

0

0

2













A

Funkcja

A(



) osiąga maksimum

dla

częstości rezonansowej

:

2

2

0

2











r

Im mniejsze

tłumienie



(dłuższy czas



), tym

większa amplituda A.

Moc pochłaniana przez oscylator zasilany siłą wymuszającą F zależy od
prędkości

P = Fv

Jeżeli tłumienie jest słabe (



<<



0

), to maksymalna amplituda

odpowiada częstości drgań własnych



r

=



0

.

Wówczas - przesunięci fazowe pomiędzy siłą a wychyleniem



=



/2.



s

iła nie jest zgodna w fazie z wychyleniem.

Graficzne przedstawienie drgania harmonicznego

Ruch rzutu

końca wektora

r

na

oś OY, przy czym wektor

r

wiruje

dookoła

środka O ze stałą prędkością kątową



D

ługość rzutu wektora: r

y

= Asin(



t+



0

)

A

- promie

ń koła



0

-

k

ąt, jaki tworzy wektor

r

z

osią OX w chwili t=o

X

Y

O



0

r

y

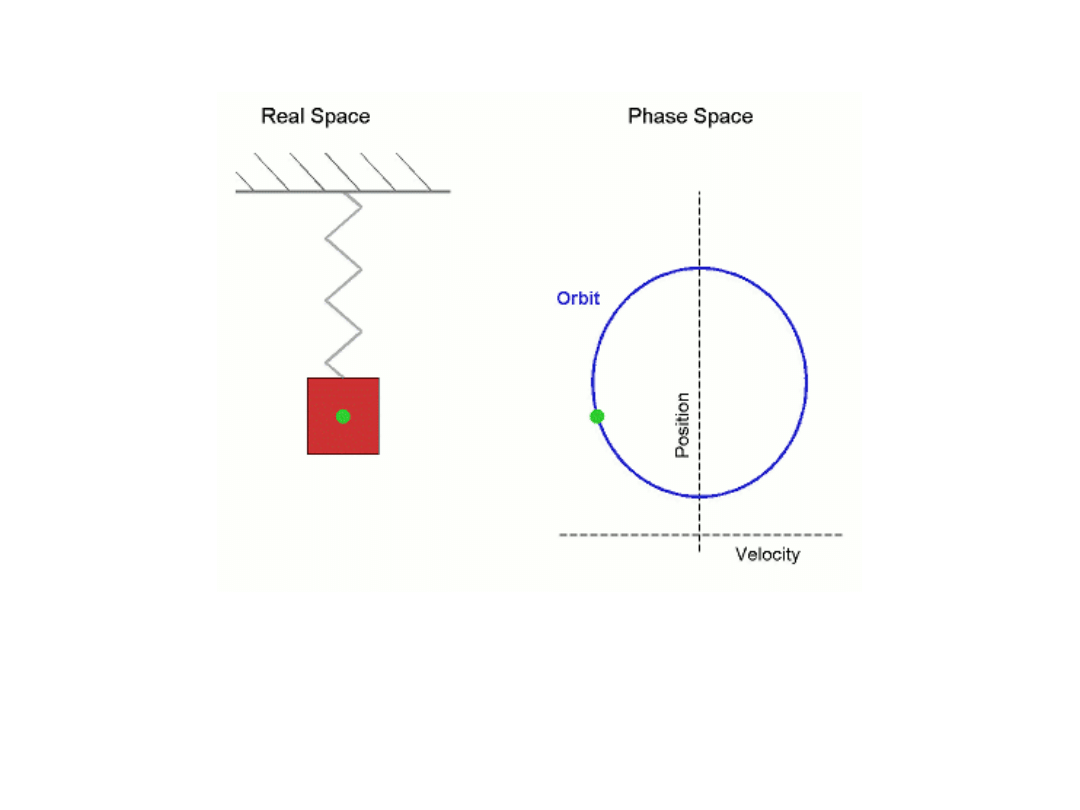
Simple harmonic motion shown both in real space and phase space.

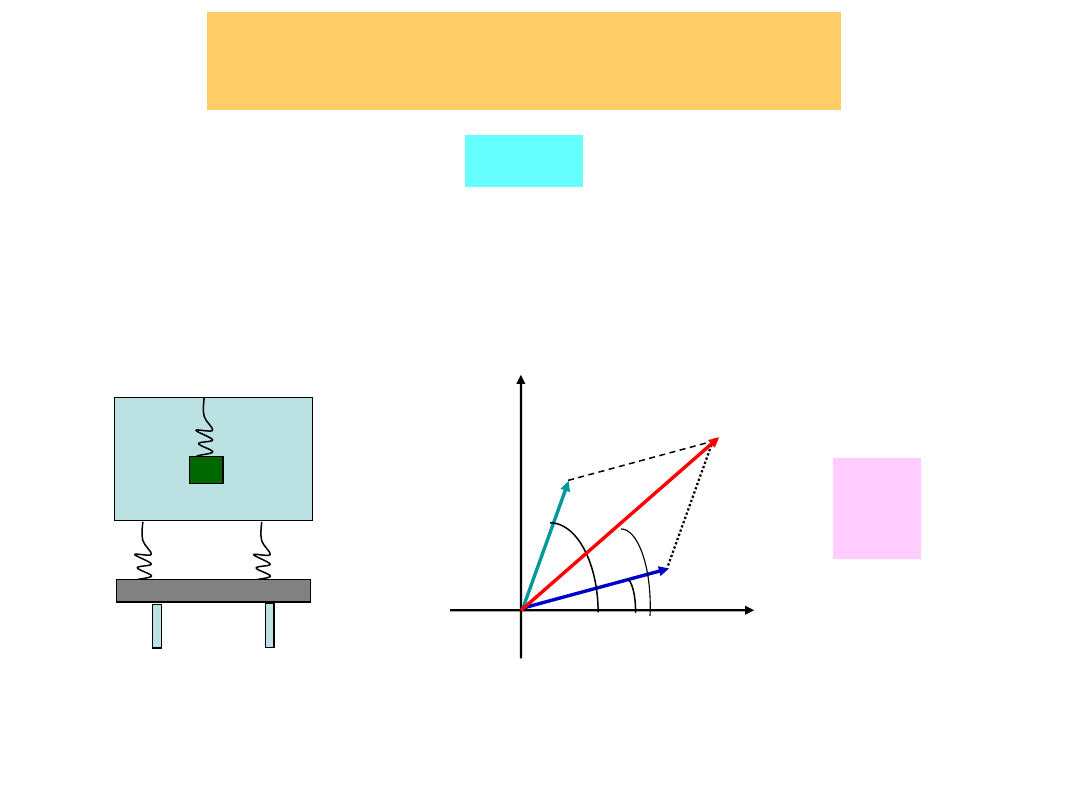
Składanie drgań w jednym kierunku

(drgania równoległe)

)

sin(

)

(

)

sin(

)

(

2

2

1

1

t

A

t

x

t

A

t

x









2

1







2

1

x

x

x





drganie wypadkowe

X

Y

O



1

A

1



2

A

2

A



A=?



=?

k

1

k

2

k

2

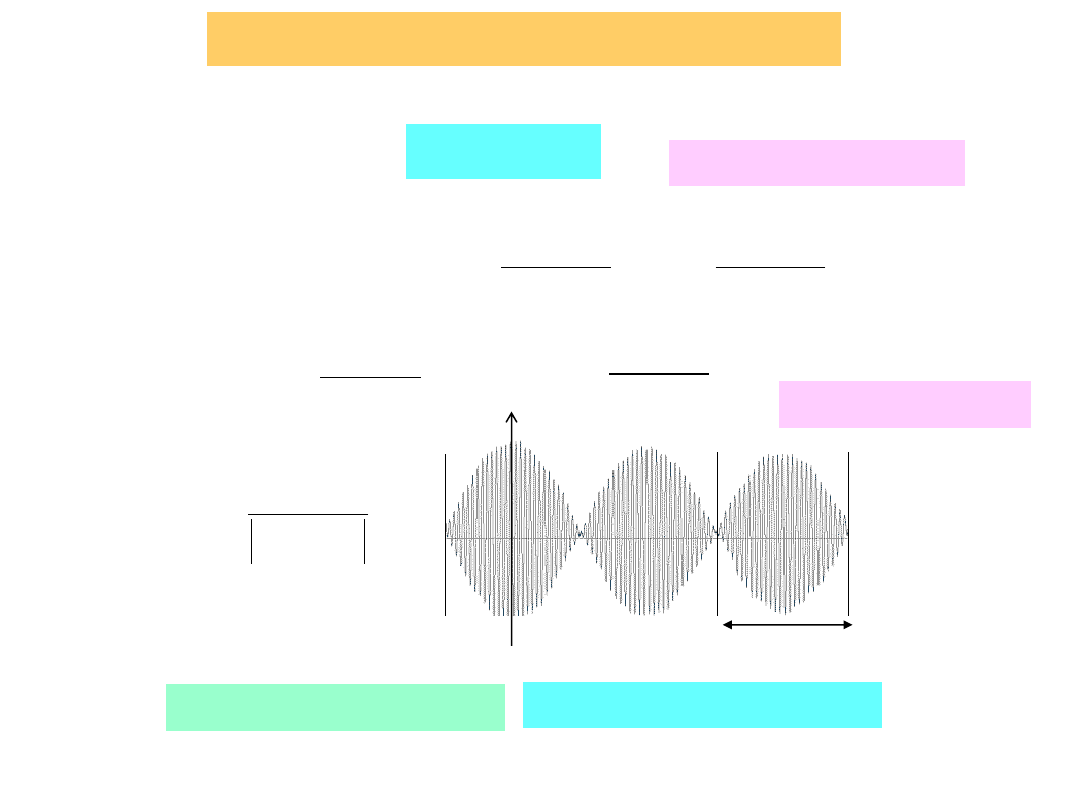
Składanie drgań w jednym kierunku



































t

t

A

t

x

t

x

x

2

cos

2

sin

2

)

(

)

(

2

1

2

1

2

1









)

sin(

)

(

)

sin(

)

(

2

2

1

1

t

A

t

x

t

A

t

x









A

A

A





2

1

2

1

x

x

x





drganie wypadkowe

Gdy



1

i



2

niewiele się różnią 

dudnienia

2

1

2











d

T

T

d

Modulacja amplitudowa

Zmienna amplituda C

Oznaczenia:

2

2

1











t

A

C

2

cos

2

2

1









t

C

x



sin



ruch periodyczny





y

/

x

)

sin(

)

(

)

sin(

)

(













t

A

t

y

t

A

t

x

y

y

x

x

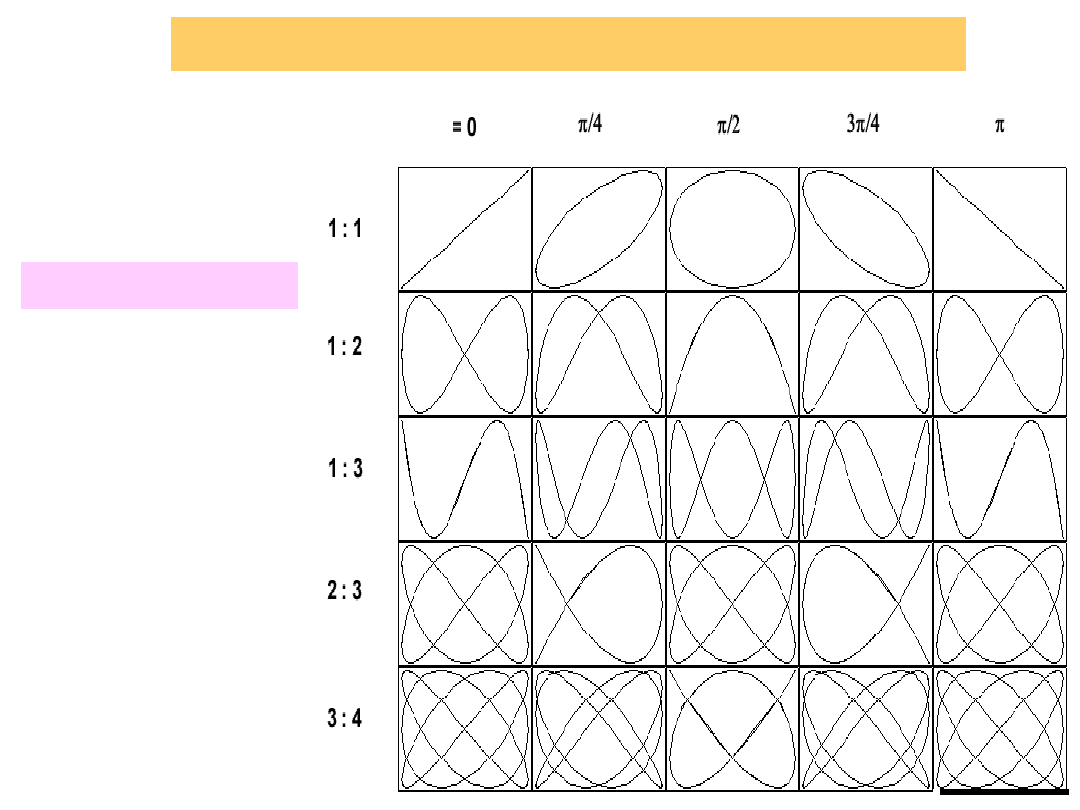
Krzywe Lissajous

Składanie drgań w kierunkach prostopadłych

Szczególne przypadki

)

sin(

)

(

)

sin(

)

(

t

A

t

y

t

A

t

x

y

x









odcinek linii prostej

x

A

A

y

x

y







x

=



y

=



,



=0



x

=



y

=



,



=



/2

)

cos(

)

2

sin(

)

(

)

sin(

)

(

t

A

t

A

t

y

t

A

t

x

y

y

x

















1

2

2

2

2







x

y

A

x

A

y

elipsa