Relacje równoważności, funkcje

Kolejnym ważnym rodzajem relacji są tak zwane relacje równoważności. Związana z nimi zasada
abstrakcji jest ważną metodą tworzenia nowych pojęć w matematyce. Najpierw wprowadzimy pojęcie
partycji (podziału) zbioru

.

Partycją (podziałem) zbioru

nazywamy każdą rodzinę niepustych, parami rozłącznych podzbiorów

zbioru

, pokrywających w sumie cały zbiór

. Innymi słowy, zbiór

nazywamy partycją

zbioru

, gdy:

(a) każdy zbiór

jest niepusty, tzn.

,

(b) różne zbiory

są rozłączne, tzn.

oraz

(c) każdy element

należy do jakiegoś

, tzn.

.

Z każdą partycją

zbioru

wiążemy pewną relację

na zbiorze

określoną następująco:

Zwróćmy uwagę, że relacja

jest zwrotna, symetryczna i przechodnia.

Przykład 0. Niech

. Podział zbioru

na zbiory

i

to przykład partycji

. Partycja ta ma trzy elementy. W szczególności,

oraz

, jednak

. W tym przykładzie możemy łatwo wypisać

wszystkie elementy relacji

:

Jako ćwiczenie pozostawiamy czytelnikowi sprawdzenie, ile jest różnych partycji zbioru

w tym

przykładzie. Szczególną partycją jest partycja zbioru

składająca się z jednego zbioru, mianowicie

samego zbioru

.

Przykład 1. Niech

. Dla

niech

. Zatem

jest partycją płaszczyzny

na proste równoległe do osi

. Relacja

na zbiorze

odpowiadająca tej partycji ma tu proste określenie: dla

mamy

Przykład 2. Załóżmy, że

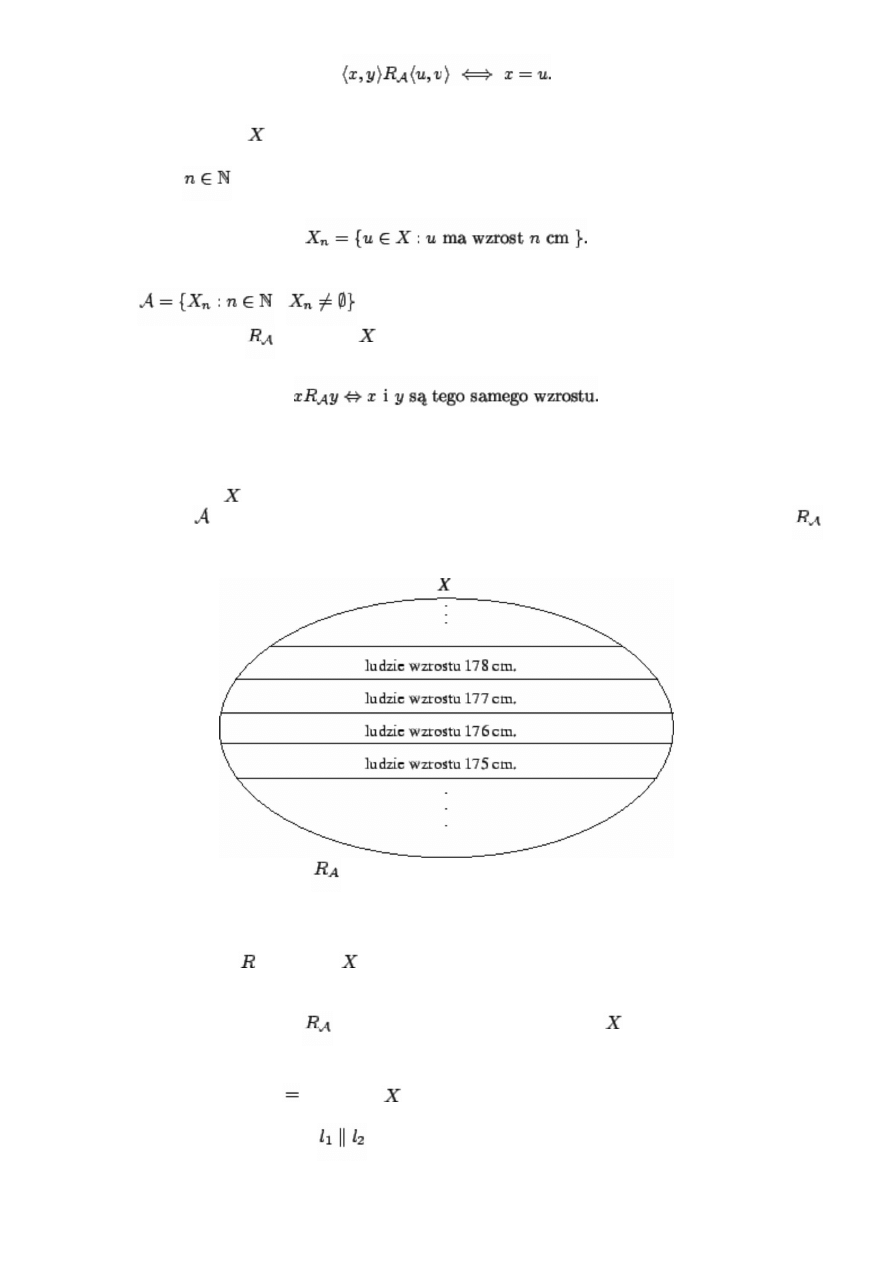
oznacza zbiór ludzi. Możemy próbować klasyfikować ludzi według pewnej

cechy, na przykład według wzrostu wyrażonego w centymetrach (w zaokrągleniu do najbliższej liczby
calkowitej). Dla

niech

Wówczas

i

jest partycją zbioru ludzi składającą się ze zbiorów ludzi tego

samego wzrostu. Relację

na zbiorze

możemy tu określić następująco:

Relacja ta, jak łatwo sprawdzić, jest zwrotna, symetryczna i przechodnia.

Z drugiej strony zbiór

rozpada się tu na rozłączne podzbiory złożone z ludzi tego samego wzrostu:

elementy partycji

. W każdym z takich podzbiorów każde dwie osoby są względem siebie w relacji

,

osoby z różnych grup nie są względem siebie w relacji.

Okazuje się, że ta własność relacji

jest wspólna dla wszystkich relacji, które są zwrotne, symetryczne i

przechodnie. Wracając do naszego przykładu, osoby w tej samej grupie z punktu widzenia rozważanej
cechy (wzrost) są od siebie nieodróżnialne, inaczej mówiąc: równoważne. To uzasadnia poniższą definicję.

Definicja 9..1 Relacja

na zbiorze

nazywa się relacją równoważności, gdy jest zwrotna,

symetryczna i przechodnia.

Widzimy więc, że każda z relacji

wyznaczonych przez partycje zbioru

jest relacją równoważności.

Podamy teraz kilka dalszych przykładów relacji równoważności.

Przykład 3. Relacja równości

na zbiorze

.

Przykład 4. Relacja równoległości

na zbiorze prostych na płaszczyźnie.

Przykład 5. Relacja

na zbiorze liczb całkowitych.

Przykład 6. Relacja ``

i mają tych samych rodziców'' na zbiorze ludzi.

Przykład 7. Niech

. Relacja

na

określona przez

Zwróćmy uwagę, że gdy jest wektorem jednotkowym na osi

, relacja

pokrywa się z relacją

z

przykładu 1.

Relacje równoważności często oznaczamy symbolami podobnymi do

, takimi jak na przykład

.

Załóżmy teraz, że

jest relacją równoważności na zbiorze

. Elementy

takie, że

nazywamy równoważnymi (w sensie relacji

). Na mocy symetryczności znaczy to również, że

.

Dla dowolnego

definiujemy zbiór

innymi słowy,

to zbiór wszystkich elementów zbioru

równoważnych (w szczególności

). Zbiór ten nazywamy klasą abstrakcji (lub klasą równoważności) elementu (względem relacji

).

Zbiory

dla

nazywamy klasami abstrakcji (lub równoważności) relacji

.

Klasy abstrakcji relacji

na zbiorze

to po prostu zbiory-elementy partycji

. Okazuje się, że klasy

abstrakcji dowolnej relacji równoważności tworzą partycję.

Uwaga 9..2 Załóżmy, że

jest relacją równoważności na zbiorze

. Wtedy

jest

partycją zbioru

(zwaną podziałem zbioru

na klasy abstrakcji relacji

). Ponadto,

.

Dowód. 1. Zbiory z

są niepuste i pokrywają

, bo dla

mamy

, czyli

.

2. Jeśli

, to

. By tego dowieść najpierw pokażemy, że

. W tym celu załóżmy,

że

, tzn.

. Wtedy z

i przechodniości dostajemy

, czyli

. Podobnie

pokazujemy, że

.

3. Jeśli

(tzn.

), to

. Tu prowadzimy dowód nie wprost. Przypuśćmy, że

pewne

. Wtedy (na mocy definicji klasy abstrakcji i symetryczności

):

i

,

więc z przechodniości

, sprzeczność.

Stąd dostajemy, że różne zbiory należące do

są parami rozłączne, tzn. jeśli

, to

. Istotnie, rozumujemy tu nie wprost. Przypuśćmy, że

. Na mocy 3. i

prawa transpozycji dostajemy stąd

, czyli (na mocy 2.)

.

Wniosek 9..3 Dla

,

.

Wniosek 9..4 Jeśli relacje równoważności

i

na zbiorze

mają te same klasy abstrakcji, to

.

Zasada abstrakcji. W przykładzie 2. podział zbioru ludzi na klasy abstrakcji odbywał się według znanej
cechy: wzrostu. Załóżmy, że

jest relacją równoważności na zbiorze

. Możemy traktować klasę

abstrakcji elementu

jako nowy obiekt, swoistą cechę elementu wspólną dla wszystkich

elementów w tej samej klasie abstrakcji (w przykładzie 0. tą cechą był wzrost). Zasada abstrakcji polega
własnie na definiowaniu w ten sposób nowych pojęć, nowych własności różnych obiektów.

W ten sposób definiuje się na przykład kierunek prostej na płaszczyźnie: jest to klasa abstrakcji prostej
względem relacji równoległości prostych z przykładu 4, czyli wspólna cecha klasy prostych równoległych.
Opis klas abstrakcji relacji z pozostałych przykładów pozostawiamy jako ćwiczenie.

Rodzina klas abstrakcji wyznacza relację równoważności, podobnie jak tabelka wartości logicznych
wyznacza spójnik logiczny. W rachunku zdań określaliśmy wręcz nowe abstrakcyjne spójniki logiczne
zadając dowolnie ich tabelki wartości. Teraz sytuacja jest podobna: wychodząc od dowolnego podziału
zbioru

na zbiory rozłączne i niepuste dostajemy relację równoważności

, której klasami abstrakcji

są dokładnie te zbiory.

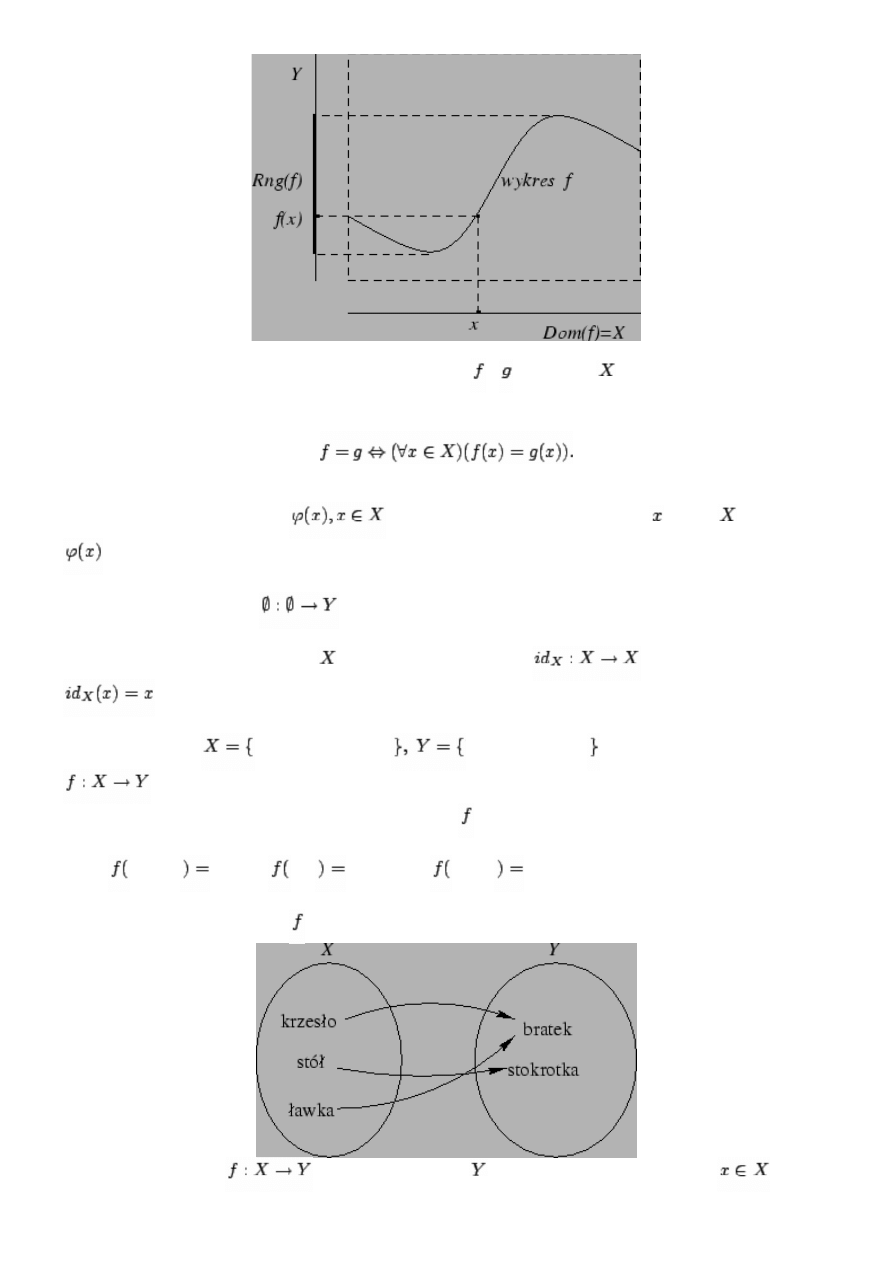
Funkcje. Jeśli każdemu elementowi zbioru

przypisany jest jeden element zbioru

(niekoniecznie

ten sam dla różnych elementów ), to mówimy, że na zbiorze

określona jest funkcja (inaczej:

przekształcenie lub odwzorowanie) przekształcająca zbiór

w zbiór

, zaś jest wartością tej funkcji

dla argumentu . Oznaczając taką funkcję przez , piszemy wtedy

Funkcje oznaczamy często literami

.

Innymi słowy, funkcja

jest to dowolna relacja między elementami zbioru

a elementami

zbioru

, której dziedzina to cały zbiór

, taka że dla każdego

istnieje dokładnie jeden

taki, że

. Z tego względu, gdy zbiory

i

są skończone, możemy przedstawić funkcję w

postaci diagramu. Strzałka od do oznacza, że

.

Definicja 9..5 Załóżmy, że

.

(1) Zbiór

nazywamy dziedziną funkcji . Dziedzinę funkcji oznaczamy też przez

.

(2) Zbiór

nazywamy obrazem lub zbiorem wartości funkcji .

(3) Zbiór

nazywamy wykresem funkcji .

Uwaga 9..6 Wprost z definicji wynika, że dwie funkcje i na zbiorze

są równe dokładnie wtedy,

gdy mają te same wartości dla wszystkich argumentów. Formalnie:

Przykład 0. Funkcja zdaniowa

, to funkcja przypisująca elementom zbioru

zdania

.

Przykład 1. Funkcja pusta

, dziedziną i obrazem tej funkcji jest również zbiór pusty.

Przykład 2. Dla dowolnego zbioru

funkcja identycznościowa

dana jest wzorem

. Funkcja stała to funkcja, która dla wszystkich argumentów przyjmuje tę samą stałą wartość.

Przykład 3. Niech

krzesło, stół, ławka

bratek, stokrotka . By określić funkcję

wystarczy wypisać jej wartości dla wszystkich argumentów. Zamiast tego można też

narysować jej diagram. Przykładowo możemy określić przez zdefiniowanie:

krzesło

bratek,

stół

stokrotka i

ławka

bratek.

Diagram tak określonej funkcji wygląda następująco:

Jest 8 różnych funkcji

. Istotnie, skoro zbiór

ma dwa elementy, dla każdego

wartość

możemy wybrać na dwa sposoby. Zbiór

ma trzy elementy, razem więc funkcję można

określić na

sposobów.

Przykład 4. Funkcje

i

określone wzorami

nazywamy rzutami na pierwszą i drugą oś odpowiednio.

Z każdą funkcją

związana jest pewna relacja

na zbiorze

określona wzorem

Łatwo sprawdzić, że

jest relacją równoważności. W przypadku, gdy

, klasy

abstrakcji relacji

to zbiory par

o tej samej pierwszej współrzędnej.

Definicja 9..7 Niech

.

(1) jest różnowartościowa (inaczej: 1-1, wzajemnie jednoznaczna, jest injekcją), gdy dla różnych

argumentów ma różne wartości, tzn.

Przez transpozycję warunek ten możemy równoważnie zapisać w postaci

Piszemy wówczas

.

(2) jest ``na'' (inaczej: jest surjekcją), gdy cały zbiór

jest zbiorem wartości . Symbolicznie:

Piszemy wówczas

.

(3) jest bijekcją, gdy jest 1-1 i ``na'', tzn. jest zarówno injekcją, jak i surjekcją. Piszemy wówczas

.

Czytelnik powinien stwierdzić, jak przy pomocy diagramu funkcji

(gdy zbiory

są

skończone) rozpoznać, czy funkcja jest bijekcją, injekcją czy surjekcją.

Uwaga 9..8 Jeśli

jest różnowartościowa, to

jest bijekcją.

Dowód. Z założenia, , traktowana jak funkcja przekształcająca zbiór

w

, jest

. Z

określenia zbioru

mamy, że jest również ``na''.

Przykład 1.

dana jest wzorem

. Wówczas jest

``na'', jednak nie jest 1-1, bo np.

.

Przykład 2.

określona jest wzorem

Zatem

Przy ustalonym , dla

wartości funkcji przebiegają więc okrąg o środku

i promieniu

. jest więc ``na'', ale nie jest 1-1.

Definicja 9..9 Załóżmy, że

jest bijekcją. Wtedy każdemu

przypisane jest jedyne

takie, że

. W ten sposób określona jest funkcja

, która spełnia dla

wszystkich

zdanie

Funkcję

nazywamy funkcją odwrotną do .

Uwaga 9..10

jest również bijekcją oraz jest funkcją odwrotną do

(tzn.

).

Dowód. (1)

jest 1-1: niech

. Wybierzmy

takie, że

Znaczy to, że

i

. Zatem jeśli

, to

, więc w tym

przypadku

(na mocy

).

(2)

jest ``na''. Niech

oraz

. Widzimy, że

i

. Dlatego

, czyli

.

(3) jest odwrotna do

, gdyż mamy

.

Przykład.

dana jest wzorem

. Zatem jest to bijekcja. Wzór na funkcję

odwrotną znajdujemy następująco. Mamy następujący ciąg równoważnych funkcji zdaniowych
zmiennych

:

Dlatego funkcja

dana jest wzorem

, czy też równoważnie (po zamianie zmiennej

w ostatnim wzorze na równie dobrą zmienną )

.

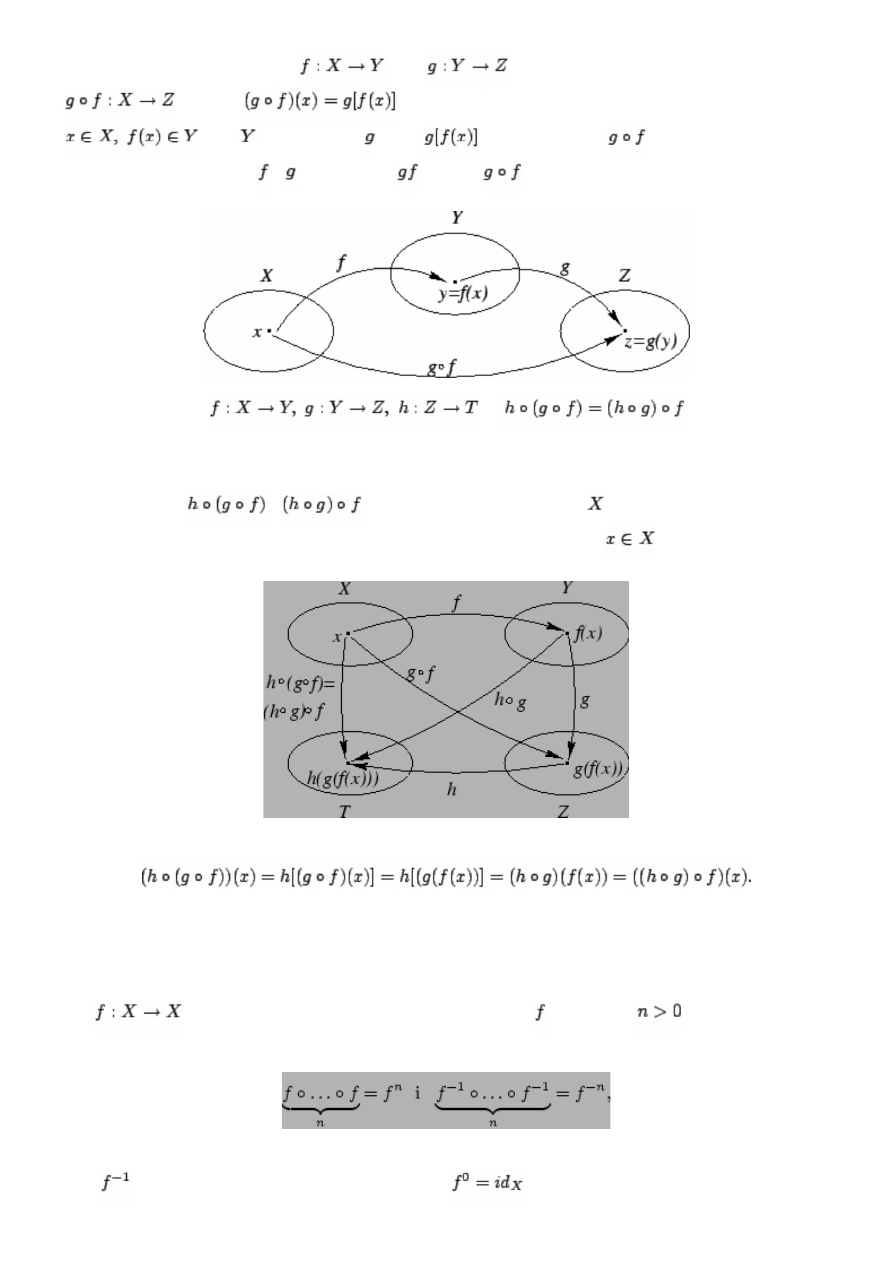
Składanie funkcji. Załóżmy, że

oraz

. Wtedy definiujemy funkcję

wzorem

. Prawa strona tego wzoru ma sens, bo dla

oraz

jest dziedziną , więc

istnieje. Funkcję

nazywamy złożeniem

(lub superpozycją) funkcji i . Piszemy też

zamiast

.

Uwaga 9..11 Jeśli

to

.

Uwaga ta mówi o łączności składania funkcji. Z tego względu w wielokrotnych złożeniach funkcji wolno
opuszczać nawiasy.
Dowód. Funkcje

i

mają wspólną dziedzinę: zbiór

. Są one równe dokładnie

wtedy, gdy mają te same wartości dla wszystkich argumentów. Niech więc

będzie dowolnym

argumentem.

Z definicji złożenia funkcji dostajemy

Dla

możemy wykonywać wielokrotną superpozycję z sobą. Dla

przyjmujemy

oznaczenia:

o ile

w drugim wzorze istnieje. Przyjmujemy też

.

Obcinanie (ograniczanie) i rozszerzanie funkcji.

Załóżmy, że

,

oraz

.

(1) Definiujemy funkcję

. Dla argumentów

wartości

są te same, co

wartości , tzn.

. Funkcję tę nazywamy obcięciem (ograniczeniem) funkcji do zbioru

.

(2) Funkcję

nazywamy rozszerzeniem funkcji

dla każdego

mamy

(innymi słowy, gdy jest obcięciem funkcji

do

).

Załóżmy teraz, że

. Wartość funkcji dla

zapisujemy w postaci

. Funkcję nazywamy wtedy -argumentową, zaś elementy

nazywamy argumentami funkcji .