1
Gliwice, 12.11.2005
OBWIEDNIA MOMENTÓW ZGINAJĄCYCH
BELKA WOLNOPODPARTA ZE WSPORNIKAMI
________________________________________________________________________________
TEMAT:
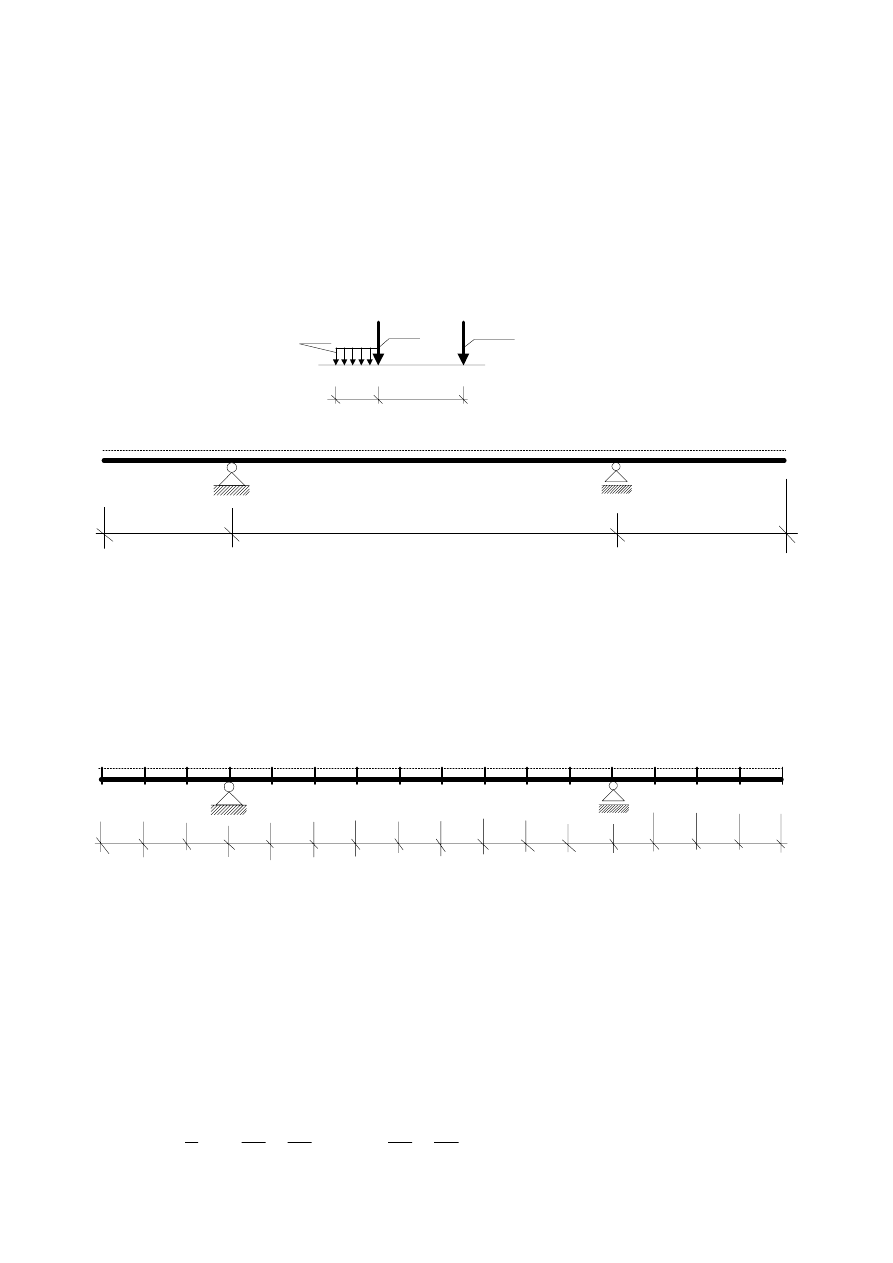
Grupa obciążeń (rys.1) porusza się po konstrukcji (w przedziale oznaczonym linią
przerywaną). Ciężar własny ustroju g=10 kN/m (g=
γ⋅A, gdzie: γ - ciężar objętościowy
materiału, A – pole przekroju poprzecznego pręta).
Wyznaczamy obwiednię momentu zginającego w belce –rys.2.
2,0
1,0
60 kN
60 kN
20 kN/m
Rys.1
3,0
9,0
4,0
Rys.2
________________________________________________________________________________
ROZWIĄZANIE:
Ustalamy położenia przekrojów, dobranych dostatecznie gęsto, aby zapewnić
niezbędną dokładność obliczeń (rys.3).
1
0
2
3
4
5
6
16
15
13
11
7
14
12
10
9
8
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
Rys.3.
Dla kolejnych przekrojów sporządzamy linie wpływu analizowanej wielkości
wewnętrznej (w naszym przypadku momentu zginającego). Następnie wykorzystując linie
wpływu znajdujemy wartości ekstremalne (maksimum i minimum w sensie liczbowym) tej
wielkości, pochodzące od danej grupy obciążeń.
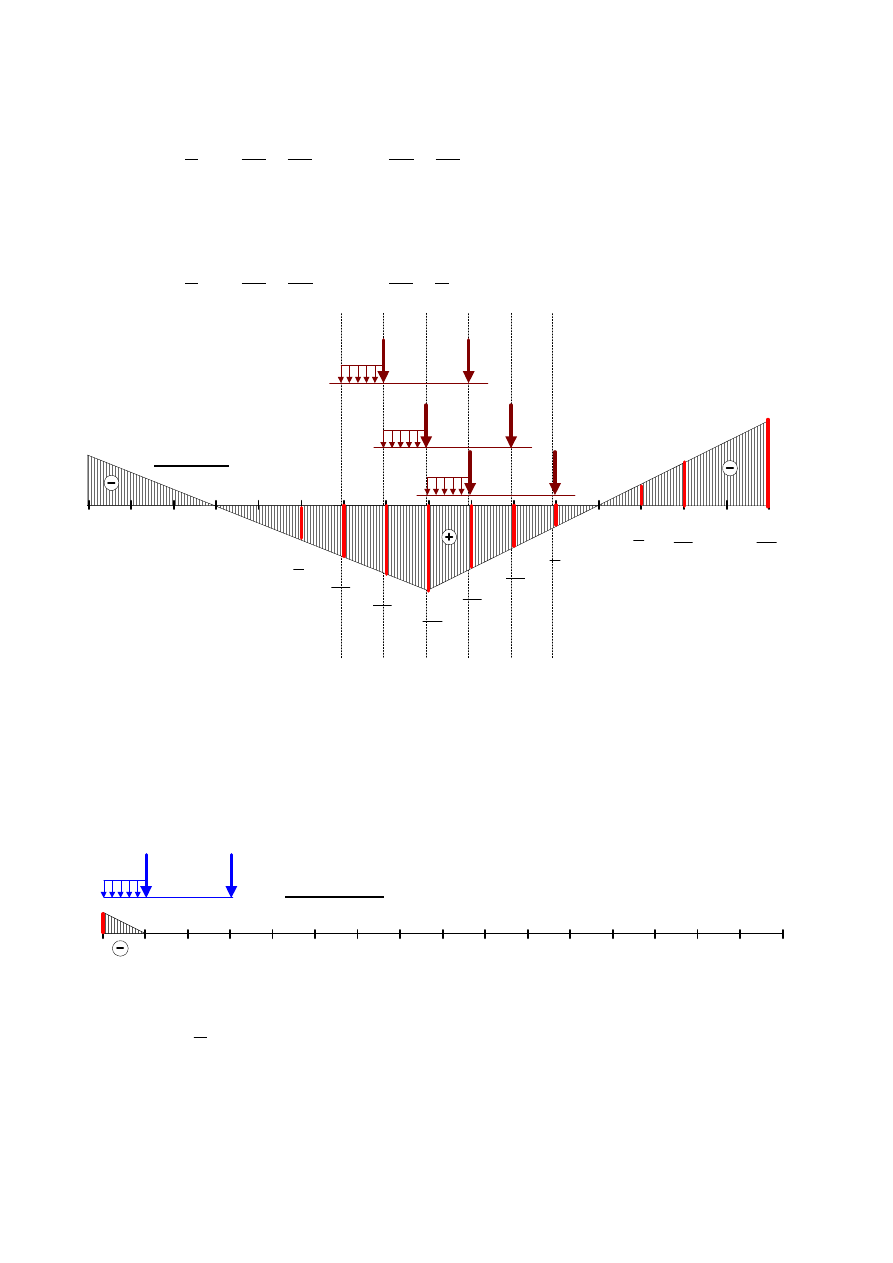
Wielkości ekstremalne wyznaczamy tu metodą prób, co pokazano przykładowo na
rys.4, poszukując maksymalnego momentu zginającego w przekroju 8 belki z rys.3.
Rozpatrzono trzy ustawienia grupy obciążeń nad linią wpływu momentu w przekroju 8 (M
8
).
- Dla ustawienia pierwszego
U1
mamy:
m
kN
237,78
9
15
9
16
60
9
16
9
12
1
2
1
20
M
max
8
⋅
+
=
⎟
⎠
⎞
⎜
⎝
⎛
+
⋅
+
⎟
⎠
⎞
⎜
⎝
⎛
+
⋅
⋅
⋅
=
,
2
- Dla ustawienia drugiego
U2
:
m
kN
240,00
9
10
9
20
60
9
20
9
16
1
2
1
20
M
max
8
⋅
+
=
⎟
⎠
⎞
⎜
⎝
⎛
+
⋅
+
⎟
⎠
⎞
⎜
⎝
⎛
+
⋅
⋅
⋅
=
,
- Dla ustawienia trzeciego
U3
:
m
kN
172,22
9
5
9
15
60
9
15
9
20
1
2
1
20
M
max
8
⋅
+
=
⎟
⎠
⎞
⎜
⎝
⎛
+
⋅
+
⎟
⎠
⎞
⎜
⎝
⎛
+
⋅
⋅
⋅
=
,
9
16
9
5
9
10
9
20
9
10
9
20
60
60
20
9
15
9
5
9
12
9
8
60
60
20
(U_1)
(U_2)
(U_3)
Lw M_8
60
60
20
Rys.4.
Najbardziej niekorzystnym ustawieniem jest ustawienie U2, a wartość maksymalna momentu
zginającego wynosi: M=240,00 kN
⋅m
________________________________________________________________________________
Rozpatrzymy teraz kolejne przekroje belki.
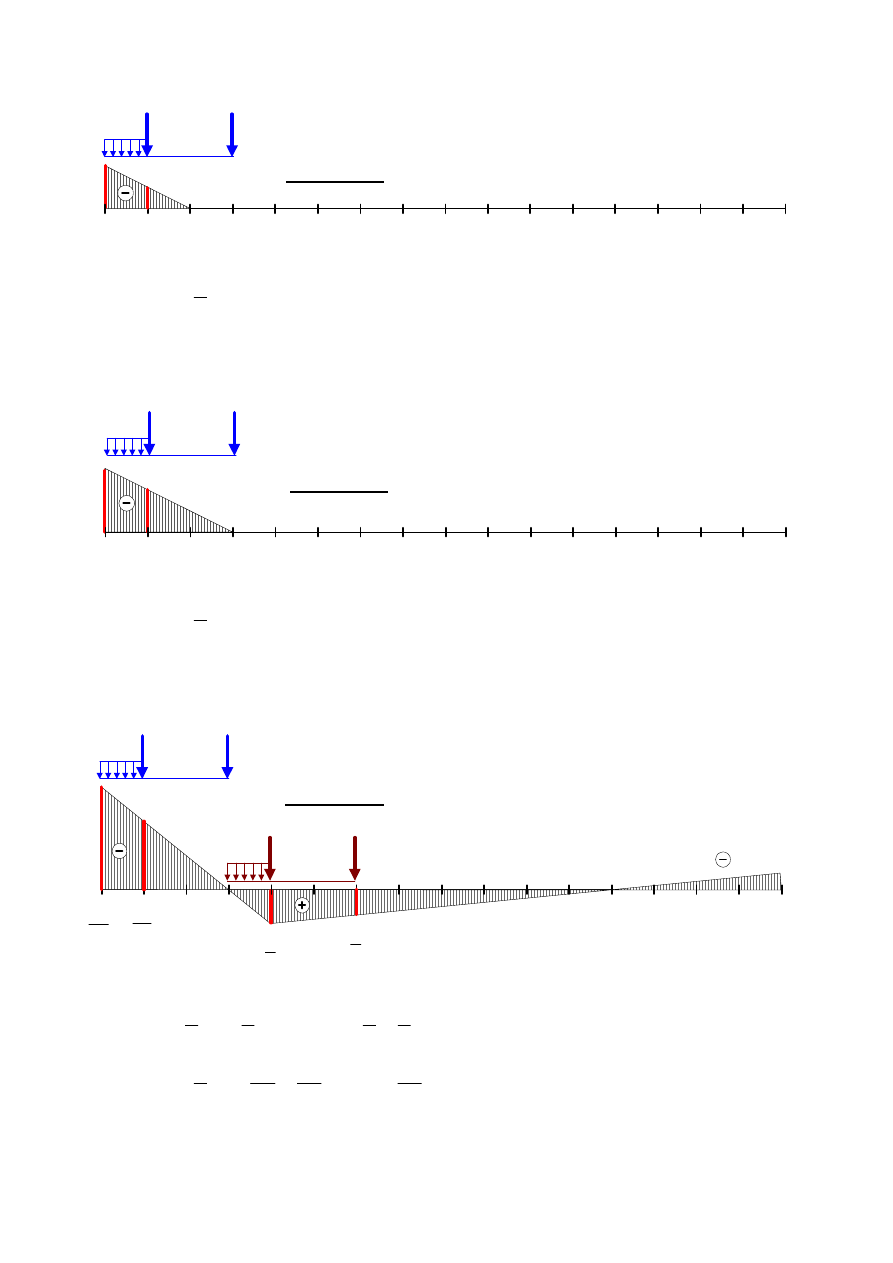
PRZEKRÓJ 1
1
Lw M - 1
60
60
20
Rys.5.
0
M
max
1
=
m
kN
10,00
-
1
2
1
20
M
min
1
⋅
−
=
⋅
⋅
−
=
________________________________________________________________________________
3
PRZEKRÓJ 2
2
1
Lw M - 2
60
60
20
Rys.6.
0
M
max
2
=
(
)
m
kN
90,00
-
1
60
1
2
1
2
1
20
M
min
2
⋅
−
=
⋅
−
+
⋅
⋅
⋅
−
=
________________________________________________________________________________
PRZEKRÓJ 3
3
2
Lw M - 3
60
60
20
Rys.7.
0
M
max
3
=
(
)
(
)
m
kN
230,00
-
1
2
60
3
2
1
2
1
20
M
min
3
⋅
−
=
+
⋅
−
+
⋅
⋅
⋅
−
=
________________________________________________________________________________
PRZEKRÓJ 4
9
6
9
8
9
16
9
24
Lw M - 4
60
60
20
60
60
20
Rys.8.
m
kN
102,22
9
6
9
8
60
0
9
8
1
2
1
20
M
max
4
⋅
+
=
⎟
⎠
⎞
⎜
⎝
⎛ +
⋅
+
⎟
⎠
⎞
⎜
⎝
⎛ +
⋅
⋅
⋅
=
,
m
kN
151,11
0
9
16
60
9
16
9
24
1
2
1
20
M
min
4
⋅
−
=
⎟
⎠
⎞
⎜
⎝
⎛
+
⋅
−
⎟
⎠
⎞
⎜
⎝
⎛
+
⋅
⋅
⋅
−
=
________________________________________________________________________________
4
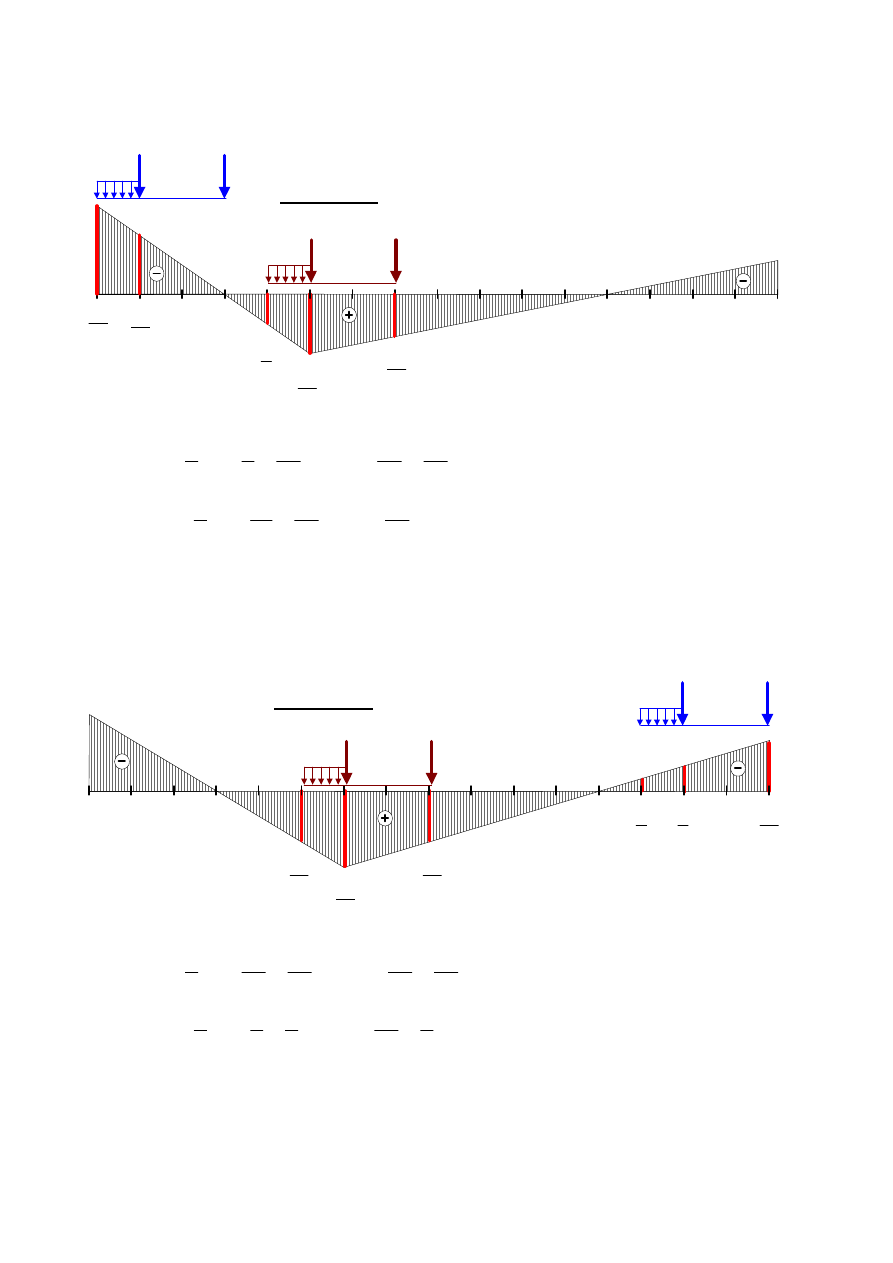
PRZEKRÓJ 5
9
21
9
14
9
10
9
7
9
14
Lw M - 5
60
60
20
60
60
20
Rys.9.
m
kN
183,33
9
10
9
14
60
9
14
9
7
1
2
1
20
M
max
5
⋅
+
=
⎟
⎠
⎞
⎜
⎝
⎛
+
⋅
+
⎟
⎠
⎞
⎜
⎝
⎛ +
⋅
⋅
⋅
=
,
m
kN
132,22
9
14
60
9
14
9
21
1
2
1
20
M
min
5
⋅
−
=
⋅
−
⎟
⎠
⎞
⎜
⎝
⎛
+
⋅
⋅
⋅
−
=
________________________________________________________________________________
PRZEKRÓJ 6
9
3
9
6
9
12
9
12
9
12
9
18
Lw M - 6
60
60
20
60
60
20
Rys.10.
m
kN
233,33
9
12
9
18
60
9
18
9
12
1
2
1
20
M
max
6
⋅
+
=
⎟
⎠
⎞
⎜
⎝
⎛
+
⋅
+
⎟
⎠
⎞
⎜
⎝
⎛
+
⋅
⋅
⋅
=
,
m
kN
130,00
9
6
9
12
60
9
6
9
3
1
2
1
20
M
min
6
⋅
−
=
⎟
⎠
⎞
⎜
⎝
⎛
+
⋅
−
⎟
⎠
⎞
⎜
⎝
⎛ +
⋅
⋅
⋅
−
=
________________________________________________________________________________
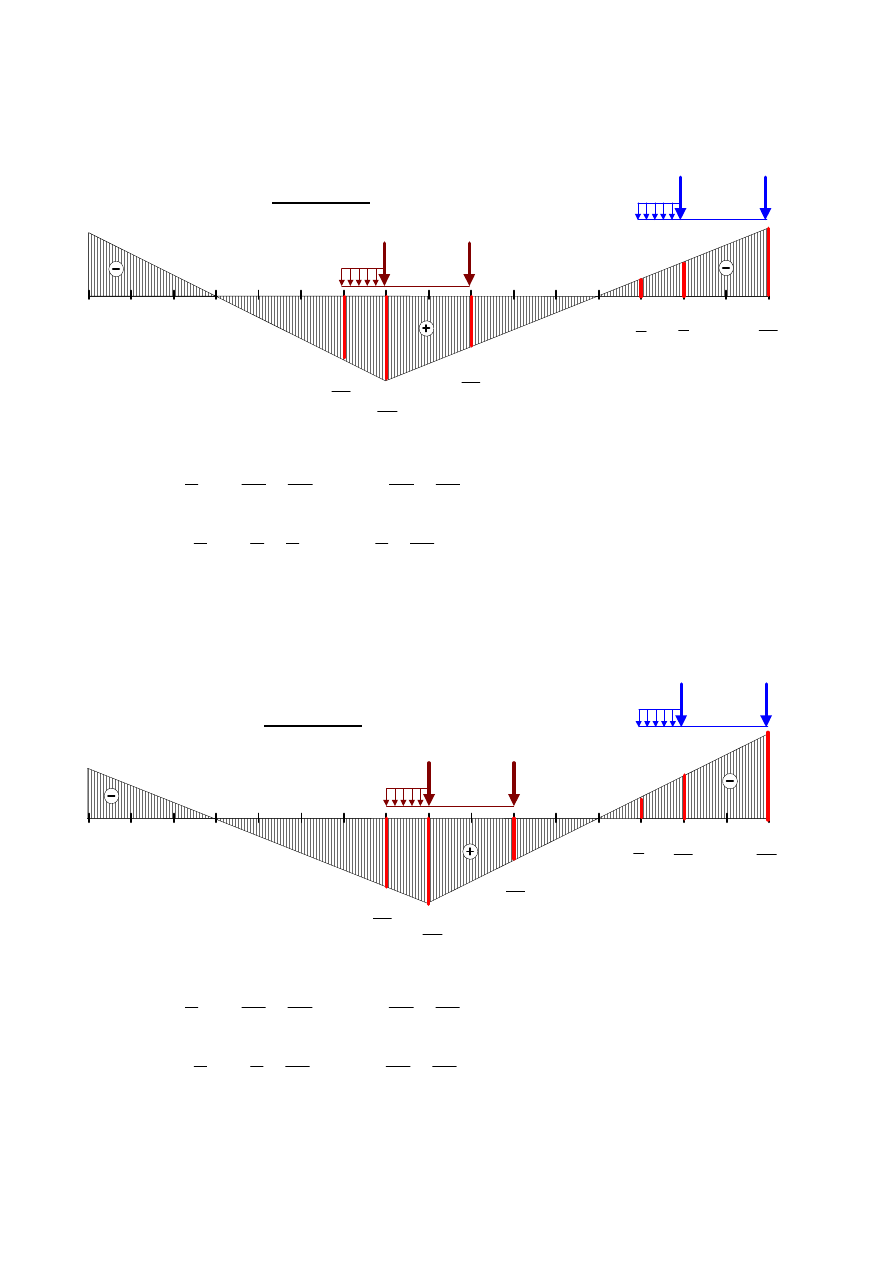
5
PRZEKRÓJ 7
9
8
9
16
9
20
9
4
9
12
9
15
Lw M - 7
60
60
20
60
60
20
Rys.11.
m
kN
252,22
9
12
9
20
60
9
20
9
15
1
2
1
20
M
max
7
⋅
+
=
⎟
⎠
⎞
⎜
⎝
⎛
+
⋅
+
⎟
⎠
⎞
⎜
⎝
⎛
+
⋅
⋅
⋅
=
,
m
kN
173,33
9
16
9
8
60
9
8
9
4
1
2
1
20
M
min
7
⋅
−
=
⎟
⎠
⎞
⎜
⎝
⎛ +
⋅
−
⎟
⎠
⎞
⎜
⎝
⎛ +
⋅
⋅
⋅
−
=
________________________________________________________________________________
PRZEKRÓJ 8
9
16
9
5
9
10
9
20
9
10
9
20
Lw M - 8
60
60
20
60
60
20
Rys.12.
m
kN
240,00
9
10
9
20
60
9
20
9
16
1
2
1
20
M
max
8
⋅
+
=
⎟
⎠
⎞
⎜
⎝
⎛
+
⋅
+
⎟
⎠
⎞
⎜
⎝
⎛
+
⋅
⋅
⋅
=
,
m
kN
216,67
9
10
9
20
60
9
10
9
5
1
2
1
20
M
min
8
⋅
−
=
⎟
⎠
⎞
⎜
⎝
⎛
+
⋅
−
⎟
⎠
⎞
⎜
⎝
⎛ +
⋅
⋅
⋅
−
=
________________________________________________________________________________
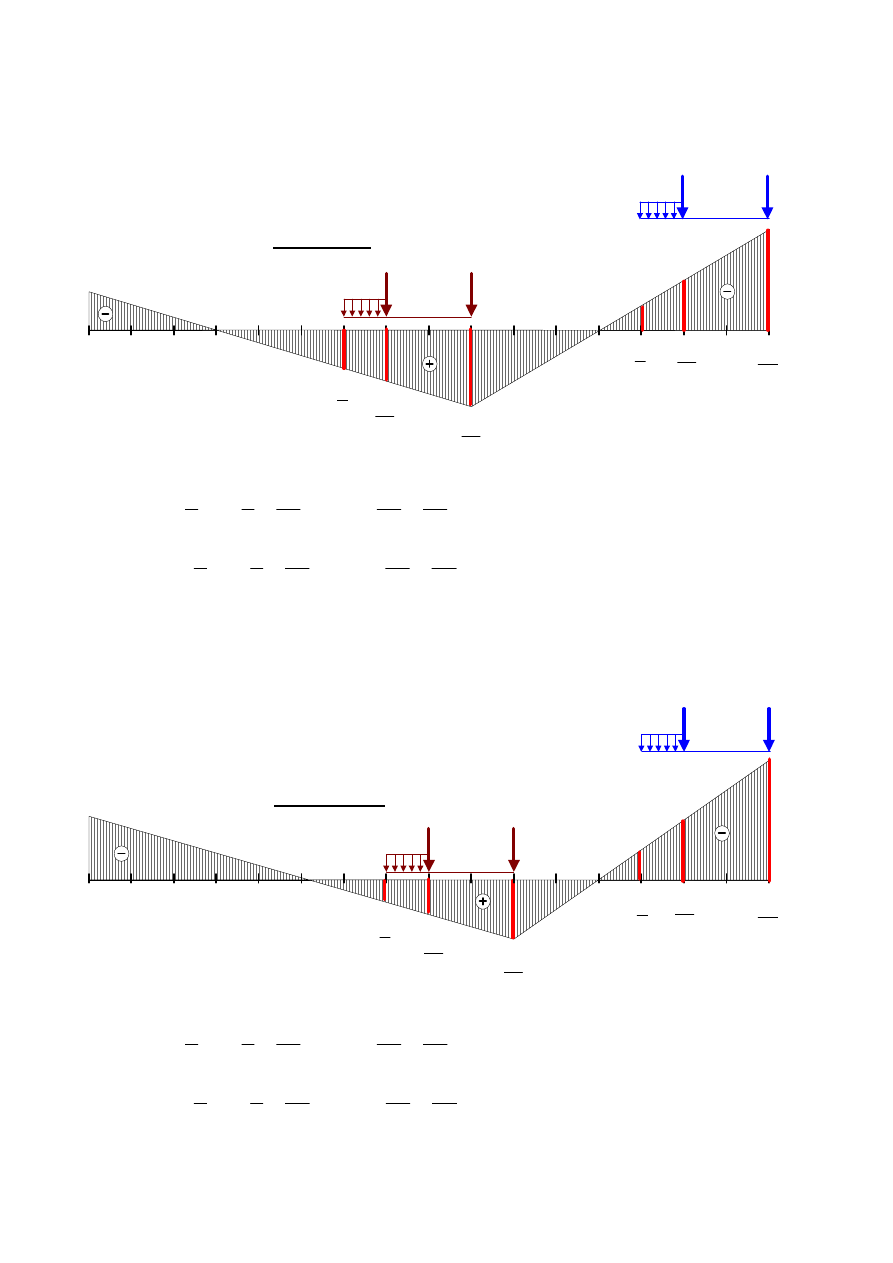
6
PRZEKRÓJ 9
9
6
9
9
9
12
9
24
9
12
9
18
Lw M - 9
60
60
20
60
60
20
Rys.13.
m
kN
223,33
9
18
9
12
60
9
12
9
9
1
2
1
20
M
max
9
⋅
+
=
⎟
⎠
⎞
⎜
⎝
⎛
+
⋅
+
⎟
⎠
⎞
⎜
⎝
⎛ +
⋅
⋅
⋅
=
,
m
kN
260,00
9
24
9
12
60
9
12
9
6
1
2
1
20
M
min
9
⋅
−
=
⎟
⎠
⎞
⎜
⎝
⎛
+
⋅
−
⎟
⎠
⎞
⎜
⎝
⎛ +
⋅
⋅
⋅
−
=
________________________________________________________________________________
PRZEKRÓJ 10
9
7
9
14
9
28
9
8
9
10
9
14
Lw M - 10
60
60
20
60
60
20
Rys.14.
m
kN
180,00
9
14
9
10
60
9
10
9
8
1
2
1
20
M
max
10
⋅
+
=
⎟
⎠
⎞
⎜
⎝
⎛
+
⋅
+
⎟
⎠
⎞
⎜
⎝
⎛ +
⋅
⋅
⋅
=
,
m
kN
303,33
9
28
9
14
60
9
14
9
7
1
2
1
20
M
min
10
⋅
−
=
⎟
⎠
⎞
⎜
⎝
⎛
+
⋅
−
⎟
⎠
⎞
⎜
⎝
⎛ +
⋅
⋅
⋅
−
=
________________________________________________________________________________
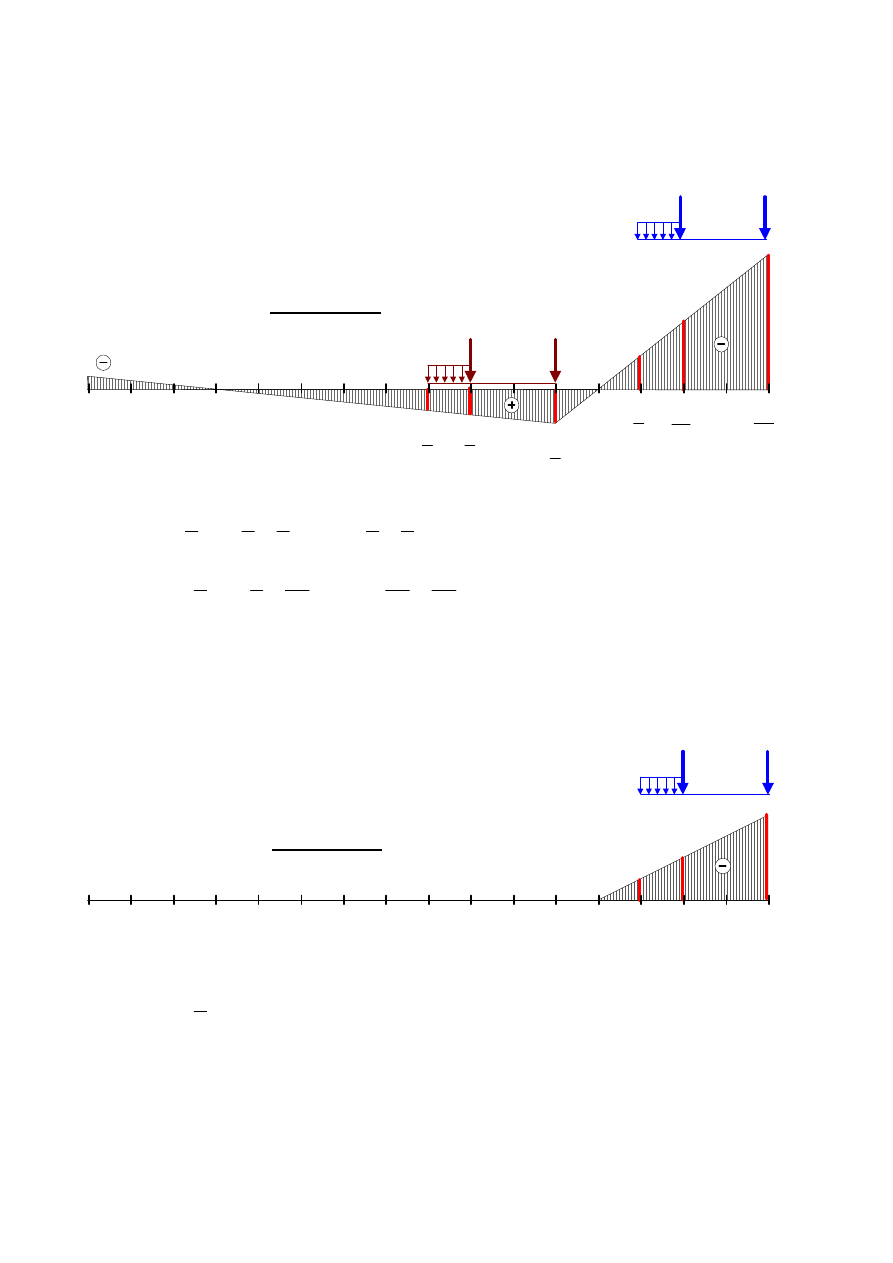
7
PRZEKRÓJ 11
9
8
9
6
9
5
9
8
9
16
9
32
Lw M - 11
60
60
20
60
60
20
Rys.15.
m
kN
105,56
9
8
9
6
60
9
6
9
5
1
2
1
20
M
max
11
⋅
+
=
⎟
⎠
⎞
⎜
⎝
⎛ +
⋅
+
⎟
⎠
⎞
⎜
⎝
⎛ +
⋅
⋅
⋅
=
,
m
kN
346,67
9
32
9
16
60
9
16
9
8
1
2
1
20
M
min
11
⋅
−
=
⎟
⎠
⎞
⎜
⎝
⎛
+
⋅
−
⎟
⎠
⎞
⎜
⎝
⎛ +
⋅
⋅
⋅
−
=
________________________________________________________________________________
PRZEKRÓJ 12
Lw M - 12
2
4
1
60
60
20
Rys.16.
0
M
max
12
=
(
)
(
)
m
kN
390,00
-
2
4
60
2
1
1
2
1
20
M
min
12
⋅
−
=
+
⋅
−
+
⋅
⋅
⋅
−
=
________________________________________________________________________________
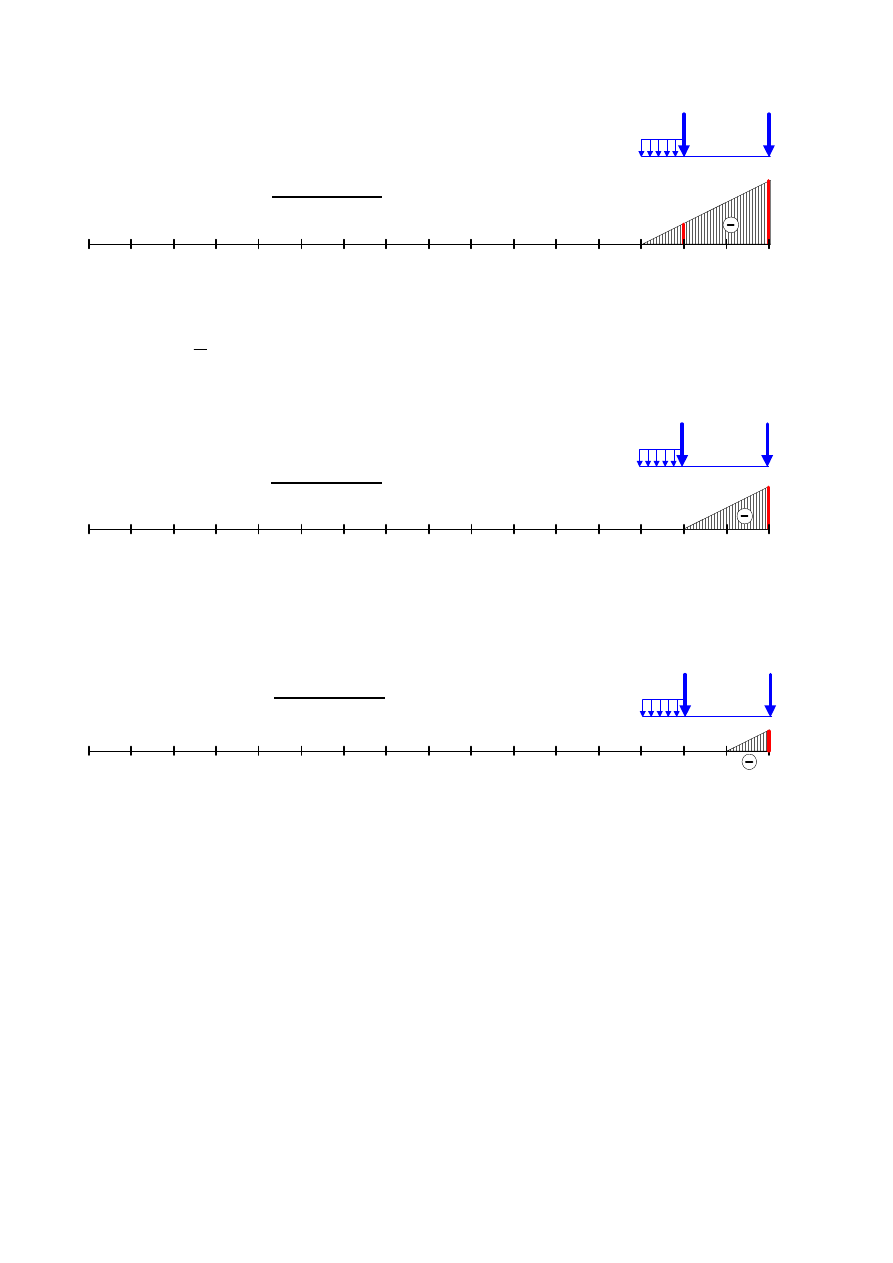
8
PRZEKRÓJ 13
Lw M - 13
1
3
60
60
20
Rys.17.
0
M
max
13
=
(
)
m
kN
250,00
-
1
3
60
1
2
1
20
M
min
13
⋅
−
=
+
⋅
−
⋅
⋅
−
=
________________________________________________________________________________
PRZEKRÓJ 14
2
60
60
20
Lw M - 14
Rys.18.
0
M
max
14
=
m
kN
120,00
-
60
M
min
14
⋅
−
=
⋅
−
=
2
________________________________________________________________________________
PRZEKRÓJ 15
1
60
60
20
Lw M - 15
Rys.19.
0
M
max
15
=
m
kN
60,00
-
60
M
min
15
⋅
−
=
⋅
−
=
1
________________________________________________________________________________
________________________________________________________________________________
Obliczamy teraz wartości momentów zginających w kolejnych przekrojach belki,
pochodzące od ciężaru własnego konstrukcji – rys.20 i tablica 1.
Następnie sumujemy wartości momentów zginających od ciężaru własnego z
wartościami ekstremalnymi momentów od obciążenia ruchomego (otrzymanymi na podstawie
linii wpływu) - tablica 1 oraz rys.21.
9
1
0
2
4
16
15
13
11
14
10
9
45,00
80,00
M
q
3
12
5
6
7
8
Rys.20.
Tablica 1
Przekrój
M
q
M
max
M
min
M
max
+q M
min
+q
0 0 0 0 0 0
1 -5,00 0
-10,00
-5,00
-15,00
2 -20,00 0 -90,00
-20,00
-110,00
3 -45,00 0
-230,00
-45,00
-275,00
4 -8,89
+102,22 -151,11
+93,33
-160,00
5 +17,22
+183,33 -132,22 +200,55
-115,00
6 +33,33
+233,33 -130,00 +266,66
-96,67
7 +39,44
+252,22 -173,33 +291,66
-133,89
8 +35,56
+240,00 -216,67 +275,56
-181,11
9 +21,67
+223,33 -260,00 +245,00
-238,33
10 -2,22
+180,00 -303,00 +177,78
-305,22
11 -36,11
+105,56 -346,67
+69,45
-382,78
12 -80,00 0 -390,00
-80,00
-470,00-
13 -45,00 0 -250,00
-45,00
295,00
14 -20,00 0 -120,00
-20,00
-140,00
15 -5,00 0 -60,00
-5,00
-65,00
16 0 0 0 0 0
obwiednia M
w belce wolnopodpartej
-400
-300
-200
-100
0
100
200
300
400
500
600
0
1
2
3
4
5
6
7
8
9
10 11 12 13 14 15 16
M [kN.m]
Mmax+q
Mmin+q
Rys.21.
Document Outline
Wyszukiwarka
Podobne podstrony:
obwiednia-belki, Studia Inż, III semestr inż, Mechanika Budowli
04 18 belki i ramy zadanie 18id Nieznany (2)
belki A0
AS Projektowanie swobodnie podpartej belki zespolonejczęste
PT Technologia obróbki kształtowej i obwiedniowej kół zębatych
04 05 belki i ramy zadanie 05id 4920
04 16 belki i ramy zadanie 16id 4940
belki proste zadania z rozwiaza Nieznany (2)
Belki rozwiązania
10 RÓW OSI UG BELKI
04 08 belki i ramy zadanie 08id 4924
Belki Układ1
obwiednia momentów zginających
Mathcad Projekt belki kablobetonowej
LABORATORIUM 4 badanie belki zelbetowej
Badanie odksztalcen belki zginanej metoda tensometrii oporowej
Belki proste Siły wewnętrzne 3
Instukcja BHP-frezarka obwiedniowa, BHP
więcej podobnych podstron