Część 1

8. ANALIZA KINEMATYCZNA I STATYCZNA USTROJÓW PRĘTOWYCH

1

8.



8. ANALIZA KINEMATYCZNA I STATYCZNA USTROJÓW PRĘTOWYCH

8.1. Analiza kinematyczna płaskiego układu tarcz sztywnych. Układy statycznie wyznaczalne

Rozważania należy rozpocząć od wyjaśnienia pojęcia stopni swobody. Liczbą stopni swobody danego

układu nazywamy liczbę niezależnych parametrów niezbędnych do jednoznacznego określenia możliwości jego
ruchu w przestrzeni. Swobodna tarcza na płaszczyźnie ma trzy stopnie swobody.

Aby   układ   był   geometrycznie   niezmienny,   musi   on   zostać   unieruchomiony.   Jeżeli   do   układu

wprowadziliśmy tyle więzów ile ma stopni swobody, to po tym zabiegu liczba stopni swobody 

s tego układu

będzie równa zeru:

s

=3t−r

(8.1)

gdzie:

t to liczba tarcz w układzie,

r to liczba więzów (liczba stopni swobody odebranych przez więzy).

Jednak  o  geometrycznej  niezmienności  nie  decyduje  wyłącznie  liczba   więzów.  Istotny  jest   również

sposób połączenia układu (bryły) z podłożem.

Wyjaśnijmy to na przykładach:

•

Układ trójprzegubowy składa się z dwóch tarcz i trzech przegubów. W zależności od położenia przegubów
układ jest niezmienny (rys. 8.1) lub zmienny (rys. 8.2).

Rys. 8.1. Układ trójprzegubowy 

geometrycznie niezmienny

Rys. 8.2. Układ trójprzegubowy chwilowo geometrycznie 

zmienny

s=0

Układ jest geometrycznie niezmienny.

s=0

Układ jest chwilowo geometrycznie zmienny, ponieważ

trzy przeguby leżą na jednej prostej.

•

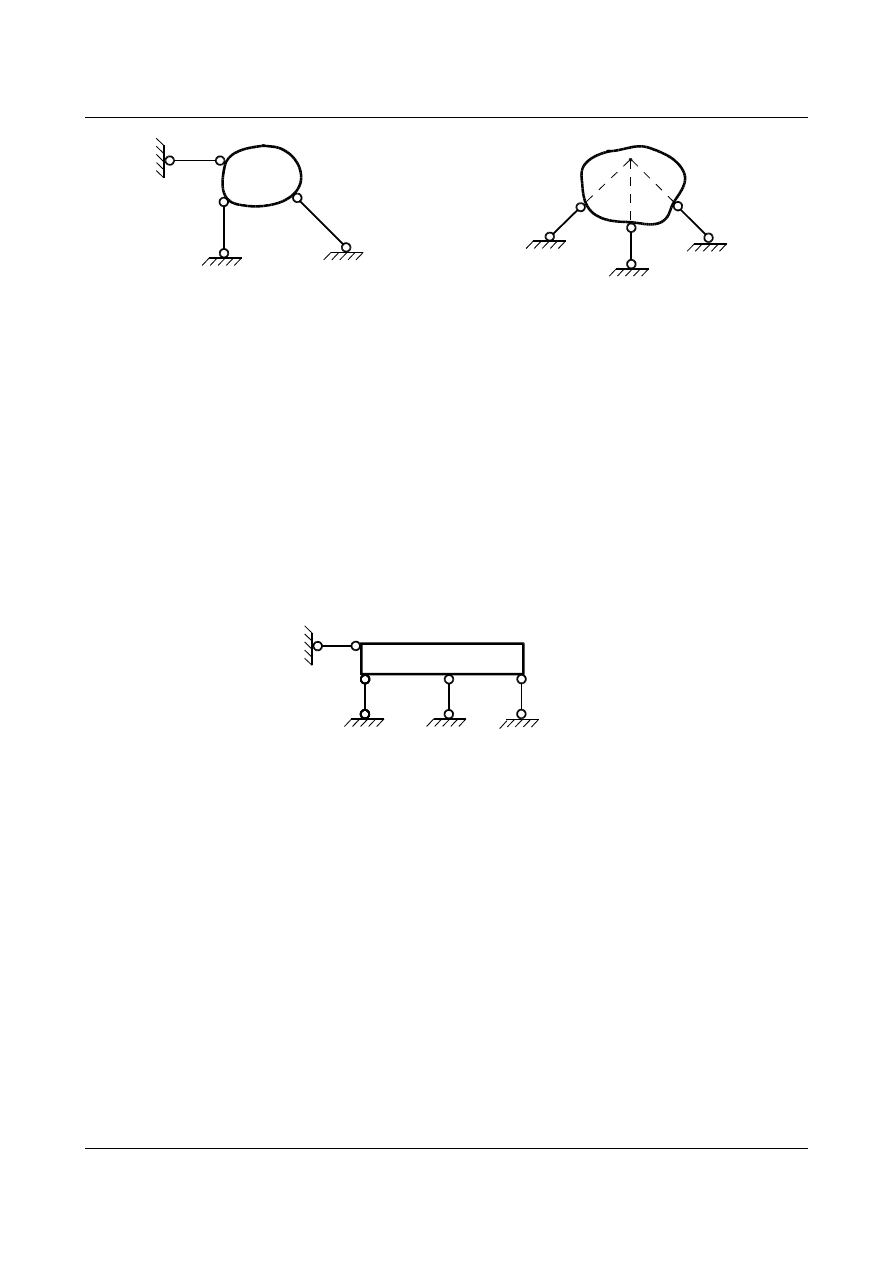
Tarcza  połączona z  podłożem  za  pomocą trzech prętów jest  układem  geometrycznie niezmiennym pod
warunkiem, że kierunki więzy nie przecinają się w jednym punkcie (rys. 8.3).

Dobra D., Jambrożek S., Komosa M., Mikołajczak E., Przybylska P., Sysak A., Wdowska A.

AlmaMater

Część 1

8. ANALIZA KINEMATYCZNA I STATYCZNA USTROJÓW PRĘTOWYCH

2

Rys. 8.3. Układ geometrycznie niezmienny

Rys. 8.4. Układ geometrycznie zmienny

s=0

Układ jest geometrycznie niezmienny.

s=0

Układ jest geometrycznie zmienny, ponieważ trzy pręty

przecinają się w jednym punkcie, tzn. istnieje biegun

chwilowego obrotu.

8.2. Układy statycznie niewyznaczalne

Aby  zapisać   warunki  równowagi  dowolnego  układu  sił  na   płaszczyźnie  mamy  do  dyspozycji  trzy

równania równowagi. Jeżeli liczba więzów jest większa od liczby równań równowagi, to taki układ określa się
jako statycznie niewyznaczalny.

Rys. 8.5. Przykład układu statycznie niewyznaczalnego

Stopnień statycznej niewyznaczalności 

SSN, jest to liczba więzów jaką należałoby odrzucić, aby układ

stał   się   statycznie   wyznaczalny.   Więzy   można   odrzucić   tylko  w   taki   sposób,   aby   powstały   układ   był
geometrycznie niezmienny.

8.3. Określanie stopnia statycznej niewyznaczalności

8.3.1. Metoda I

Stopień  statycznej  niewyznaczalności  SSN  dla  układów  składających  się  z kilku  tarcz   połączonych

więzami można określić ze wzoru:

n

=SSN =r p

1 

2  p

2 

3  p

3 

−2  w

2 

3  w

3



(8.2)

Dobra D., Jambrożek S., Komosa M., Mikołajczak E., Przybylska P., Sysak A., Wdowska A.

AlmaMater

Część 1

8. ANALIZA KINEMATYCZNA I STATYCZNA USTROJÓW PRĘTOWYCH

3

gdzie:

r - liczba reakcji (liczba więzów, prętów podporowych),

p

1

- liczba prętów zakończonych obustronnie przegubami (przesuwnymi i nie przesuwnymi),

p

2

- liczba prętów zakończonych z jednej strony przegubem, a z drugiej strony sprężyście zamocowanym

(wewnętrznie lub zewnętrznie utwierdzonym),

p

3

- liczba prętów obustronnie sprężyście zamocowanych (utwierdzonych zewnętrznie lub wewnętrznie),

w

2

- liczba   węzłów   przegubowych   (węzeł   to   element   konstrukcji,   w   którym   spotykają   się   pręty),   z

wyłączeniem przegubów  wewnętrznych, tzw. dołączonych, czyli  nie  obejmujących wszystkich prętów
zbiegających się w tym węźle,

w

3

- liczba węzłów, w których zbiegają się sprężyście zamocowane pręty.

W 

p

1

 i 

p

2

 uwzględniamy również pręty, które łączą się z więzami podporowymi, także przesuwnymi. Do 

w

2

 i

w

3

 wlicza się również więzy podporowe, przeguby, podpory przesuwne.

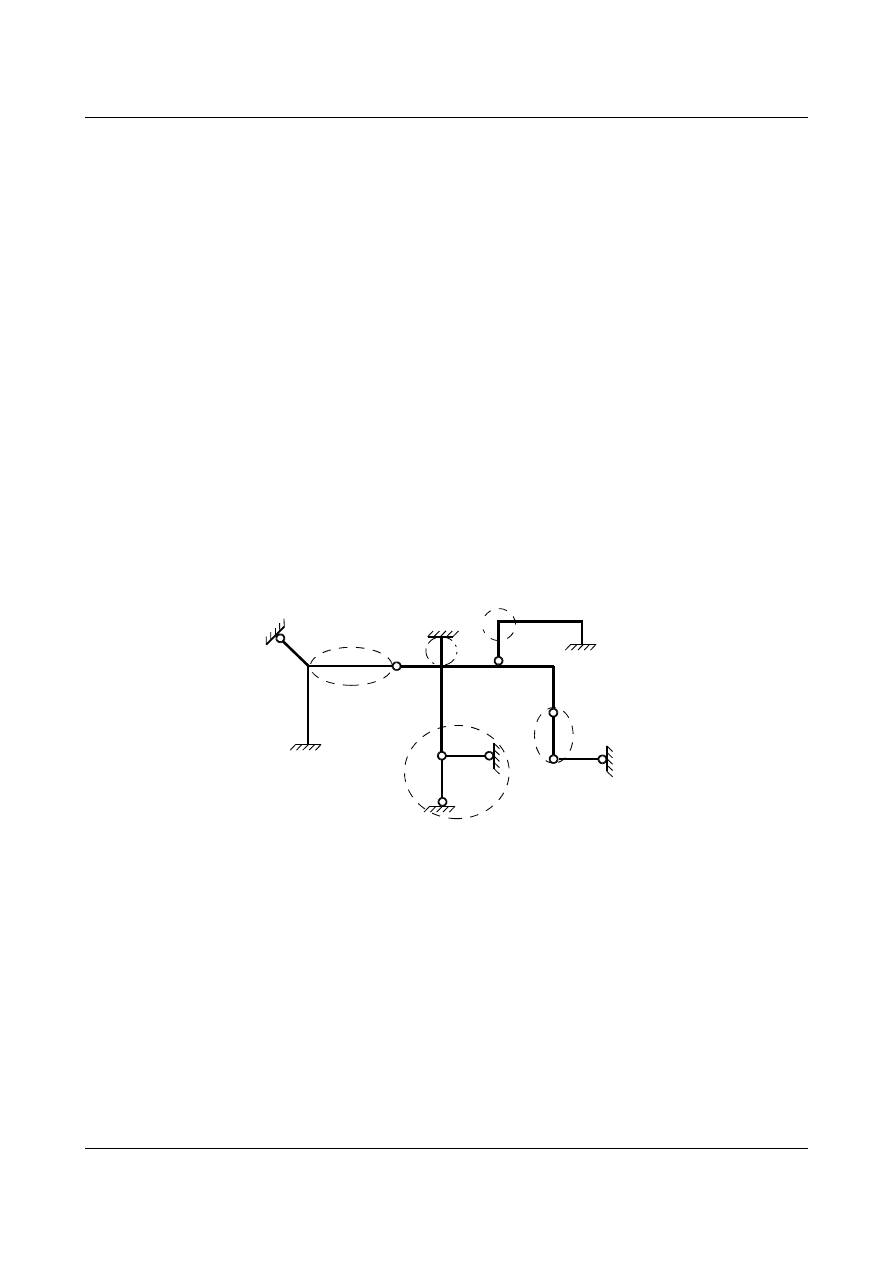
Przykład 1

Na rys 8.6 zaznaczono przypadki prętów typu 

p

1

, 

p

2

, 

p

3

 oraz przypadki węzłów typu  

w

2

 i 

w

3 

.

Rys. 8.6. Układ statycznie niewyznaczalny z różnymi rodzajami węzłów i prętów

p

2

p

3

p

1

w

2

w

3

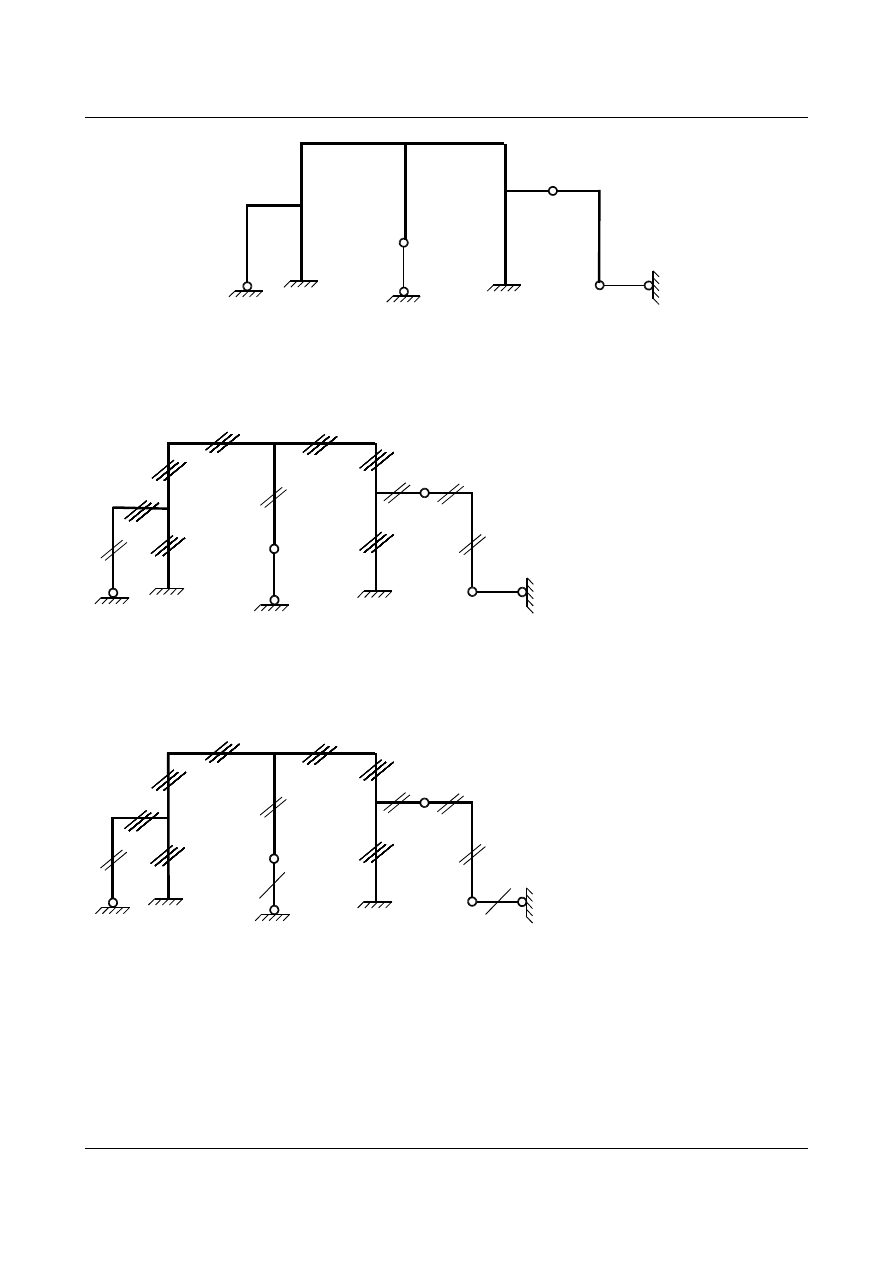
Zadanie 1

Określ stopień statycznej niewyznaczalności ramy podanej na schemacie.

Dobra D., Jambrożek S., Komosa M., Mikołajczak E., Przybylska P., Sysak A., Wdowska A.

AlmaMater

Część 1

8. ANALIZA KINEMATYCZNA I STATYCZNA USTROJÓW PRĘTOWYCH

4

Zaznaczono  pręty  typu  

p

2

  dwoma  kreskami,   pręty  typu  

p

3

  trzema   kreskami.  Liczbę  reakcji  w  podporze

podajemy w nawiasie. Liczymy węzły i wyznaczamy 

SSN:

(2)

(1)

(1)

(3)

(3)

r = 10

p

1

= 0

p

2

= 5

p

3

= 7

w

2

= 4

w

3

= 9

SSN=10+2·5+3·7–(2·4+3·9)=6

Podpory przesuwne można zaliczyć do prętów typu 

p

1

. Wynik jest ten sam.

(2)

(2)

(2)

(3)

(3)

r = 12

p

1

= 2

p

2

= 5

p

3

= 7

w

2

= 6

w

3

= 9

SSN=12+2·5+3·7–(2·6+3·9)=6

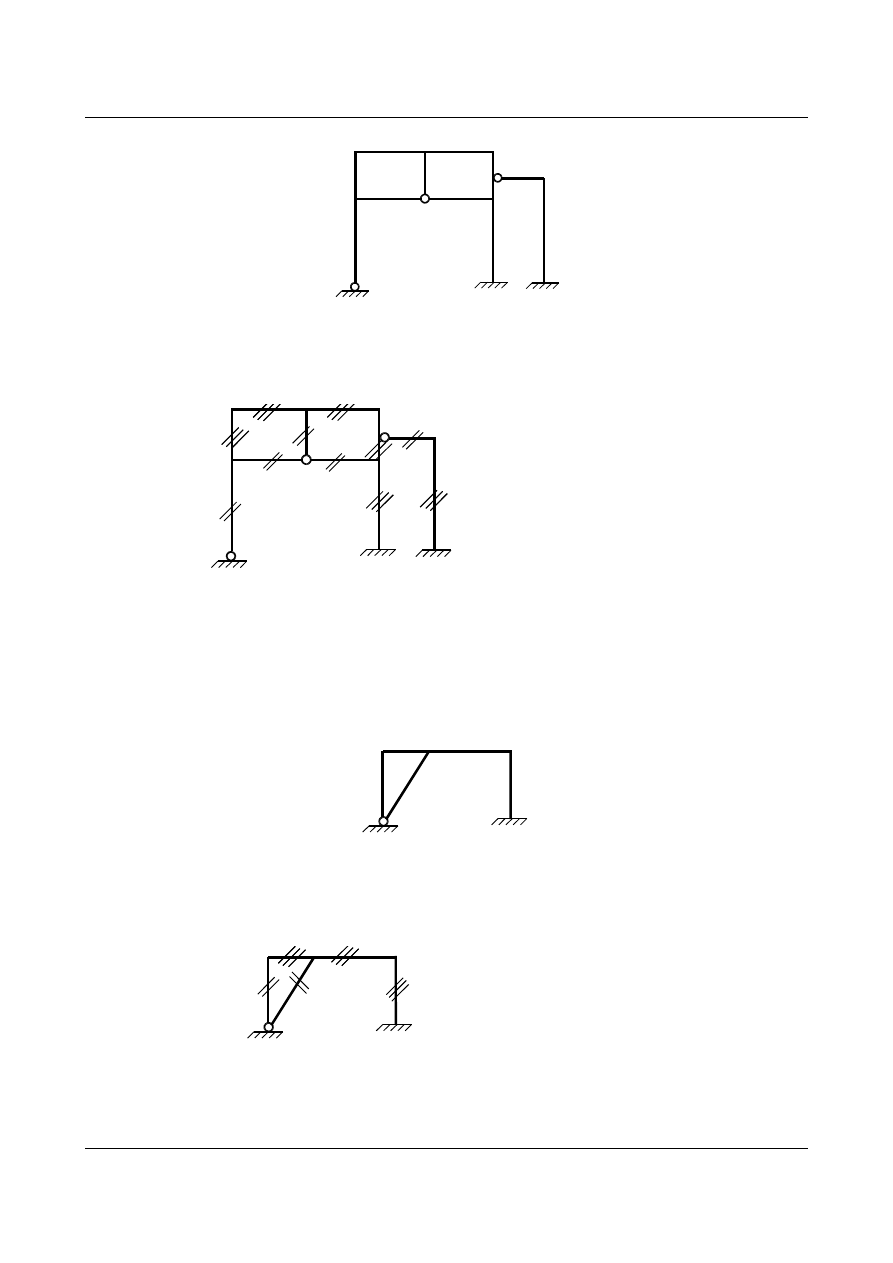
Zadanie 2 

Określić stopień statycznej niewyznaczalności dla poniższego układu.

Dobra D., Jambrożek S., Komosa M., Mikołajczak E., Przybylska P., Sysak A., Wdowska A.

AlmaMater

Część 1

8. ANALIZA KINEMATYCZNA I STATYCZNA USTROJÓW PRĘTOWYCH

5

Podobnie jak poprzednio oznaczamy pręty i reakcje.

(2)

(3)

(3)

r = 8

p

1

= 0

p

2

= 5

p

3

= 6

w

2

= 2

w

3

= 8

SSN=8+2·5+3·6–(2·2 + 3·8)=8

Zadanie 3 

Określić stopień statycznej niewyznaczalności dla poniższego układu.

Zaznaczono typy prętów.

(3)

(2)

r = 5

p

1

= 0

p

2

= 2

p

3

= 3

w

2

= 1

w

3

= 4

SSN=5+2·2+3·3–(2·1+3·4)=4

Dobra D., Jambrożek S., Komosa M., Mikołajczak E., Przybylska P., Sysak A., Wdowska A.

AlmaMater

Część 1

8. ANALIZA KINEMATYCZNA I STATYCZNA USTROJÓW PRĘTOWYCH

6

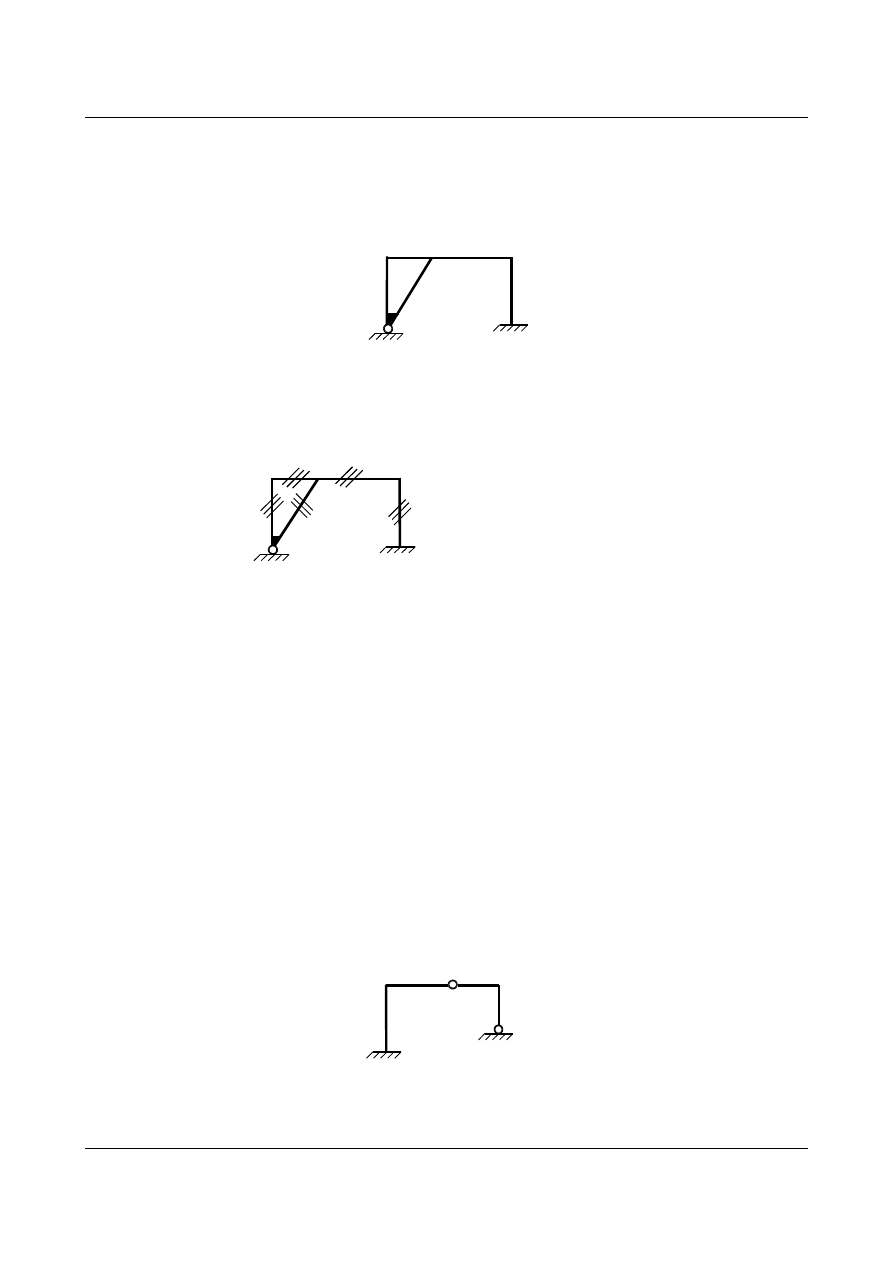
Zadanie 4 

Określić stopień statycznej niewyznaczalności dla poniższego układu.

W ramie występują tylko pręty sprężyście zamocowane.

(2)

(3)

r = 5

p

1

= 0

p

2

= 0

p

3

= 5

w

2

= 0

w

3

= 5

SSN=5+3·5–(2·0+3·5)=5

8.3.2. Metoda II

Do ramy w miejsce przegubów wprowadzamy dodatkowe więzy utwierdzające przekroje stykające się z

przegubem,   zamieniając   w   ten   sposób   podpory   na   utwierdzenia,   a   połączenia   prętów   na   sprężyście
zamocowane (wewnętrznie utwierdzone). Określamy liczbę wprowadzonych dodatkowo więzów 

d. Następnie

wyznaczamy   stopnień   statycznej   niewyznaczalności   nowego   układu  

N,  odrzucając   myślowo   wszystkie

utwierdzenia z wyjątkiem jednego (w przypadku ram zamkniętych musimy “otworzyć” obieg). 

Stopień statycznej niewyznaczalności układu wyjściowego 

n jest różnicą:

n

=SSN =N −d

(8.3)

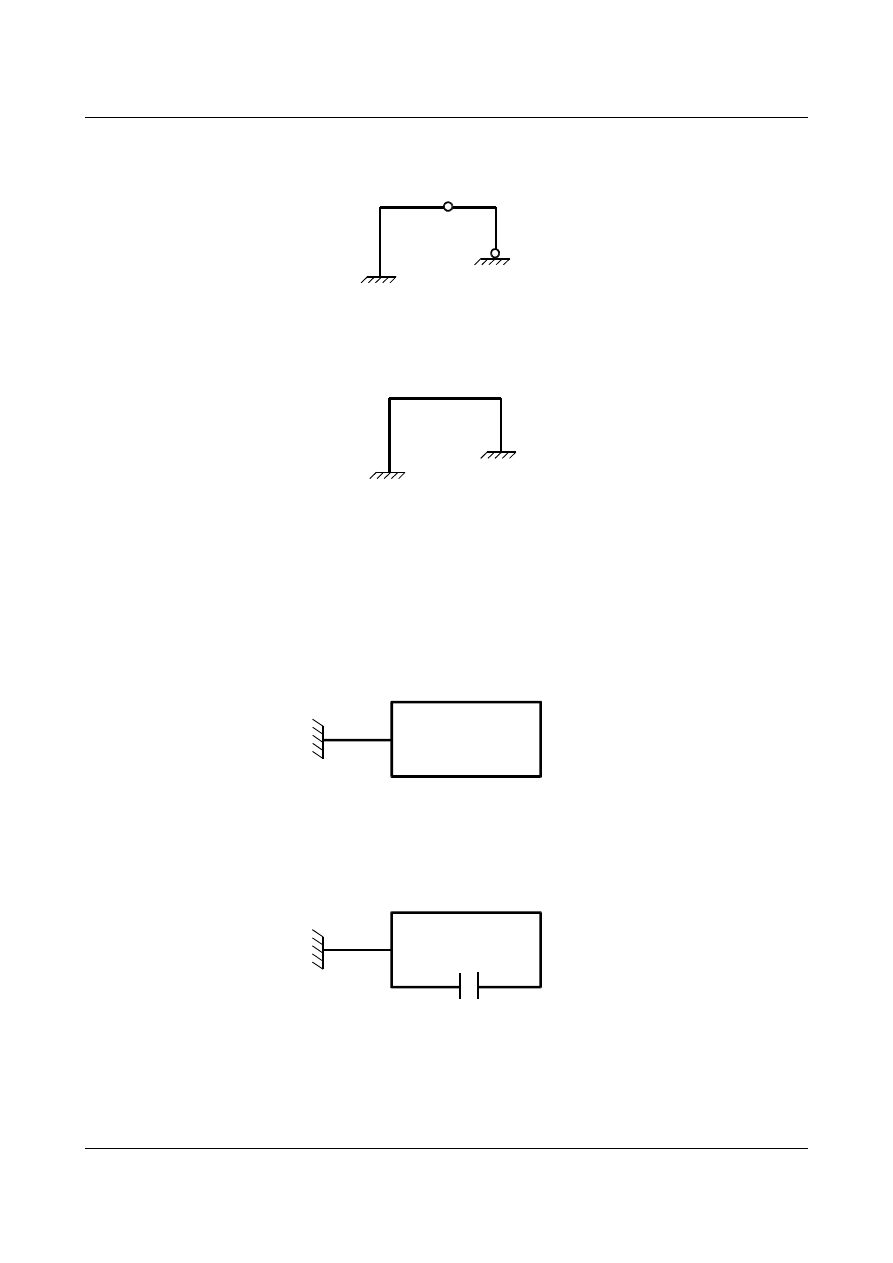
Przykład 2

W ramie o podanym schemacie należy wprowadzić dwa więzy (

d = 2), aby utwierdzić pręty. 

Dobra D., Jambrożek S., Komosa M., Mikołajczak E., Przybylska P., Sysak A., Wdowska A.

AlmaMater

Część 1

8. ANALIZA KINEMATYCZNA I STATYCZNA USTROJÓW PRĘTOWYCH

7

(+1)

(+1)

d=2

Nowy układ jest trzykrotnie statycznie niewyznaczalny (

N = 3). 

N=3

Wobec tego wyjściowy układ jest 1-krotnie statycznie niewyznaczalny.

 SSN = 3 – 2 = 1

Przykład 3

Pręty w ramie o podanym schemacie tworzą obieg “zamknięty”. 

Aby uzyskać układ statycznie wyznaczalny należy przeciąć obieg (każde przecięcie daje 3 stopnie statycznej
niewyznaczalności 

SSN = 3.

Jeżeli   w   przegubie   wewnętrznym  zbiegają   się   więcej   niż   dwa   pręty,   to   taki   przegub   nazywamy

wielokrotnym. Liczbę sił w przegubie (niezależnych) określa wzór:

Dobra D., Jambrożek S., Komosa M., Mikołajczak E., Przybylska P., Sysak A., Wdowska A.

AlmaMater

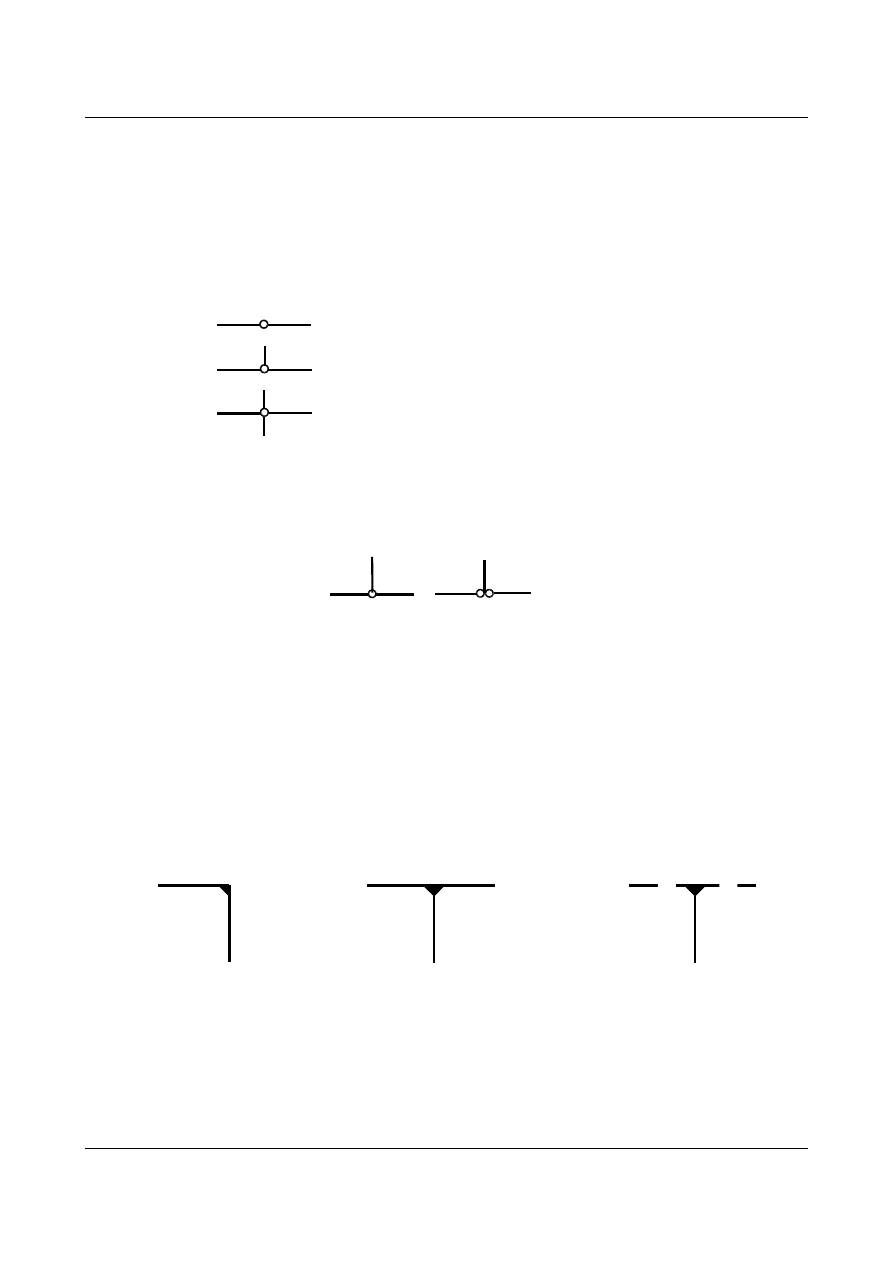
Część 1

8. ANALIZA KINEMATYCZNA I STATYCZNA USTROJÓW PRĘTOWYCH

8

S

k

=2 ⋅k −1

(8.4)

gdzie:

k  - liczba prętów w przegubie.

W przegubie, w którym zbiegają się 2, 3, 4 pręty liczba niezależnych sił wynosi odpowiednio 2, 4 i 6.

S

2 

=2 ⋅2−1=2 

S

3 

=2 ⋅3−1=4 

S

4 

=2 ⋅4−1=6 

Jeżeli  w  przegubie  spotykają   się  trzy   pręty,   to  możemy  zastąpić   ten  węzeł  w  taki   sposób  jak  na

poniższym rysunku.

=

Wobec tego, aby usztywnić ten węzeł należy wprowadzić dwa więzy (

d = 2).

W   przypadku   prętów   sprężyście   zamocowanych   liczbę   sił   niezależnych   można   określić   według

zależności:

S

k

=3 ⋅k−1

(8.4)

Dla przykładu:

3 siły wewnętrzne

=

6 sił wewnętrznych

(3)

(3)

Zadanie 5

Określić stopień statycznej niewyznaczalności dla poniższego układu.

Dobra D., Jambrożek S., Komosa M., Mikołajczak E., Przybylska P., Sysak A., Wdowska A.

AlmaMater

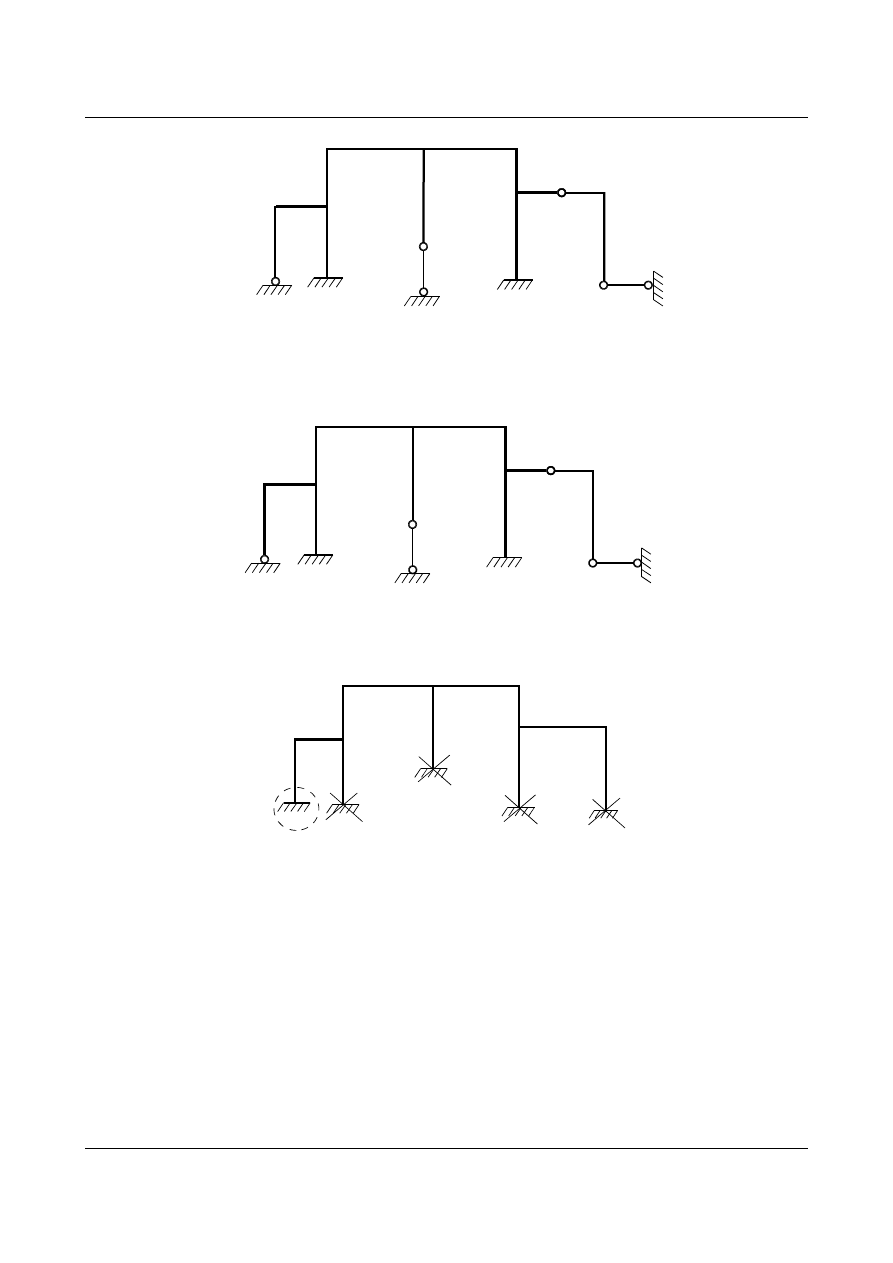
Część 1

8. ANALIZA KINEMATYCZNA I STATYCZNA USTROJÓW PRĘTOWYCH

9

Wprowadzamy dodatkowe więzy aby usztywnić połączenia (

d = 6). W nawiasach podano dodatkowe więzy w

poszczególnych węzłach.

(+2)

(+1)

(+2)

(+1)

(+2)

(+1)

Odrzucamy sztywne podpory pozostawiając jedną (

N = 4·3 = 12)

Ostatecznie SSN wynosi 

n = SSN = 12 - 6 = 6

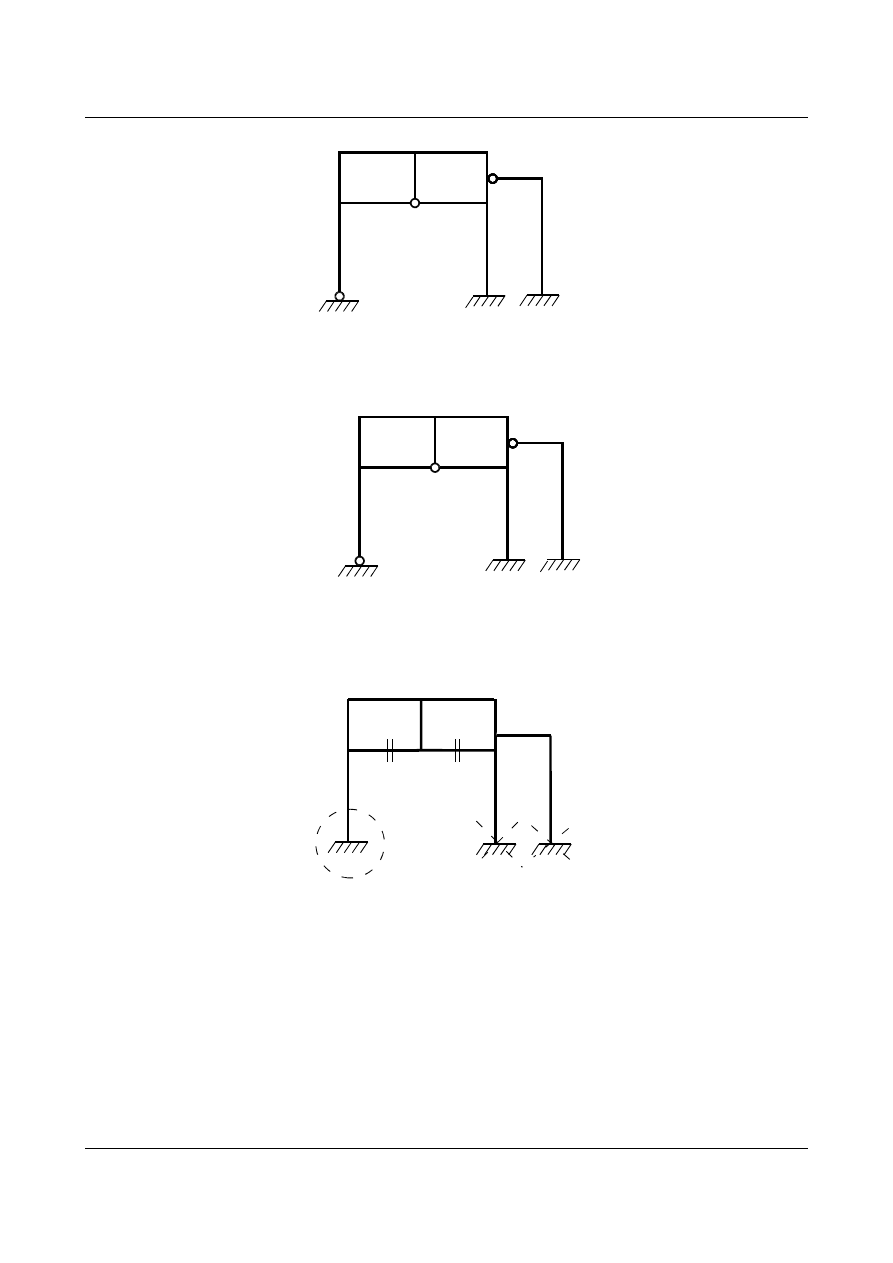
Zadanie 6

Określić stopień statycznej niewyznaczalności dla poniższego układu.

Dobra D., Jambrożek S., Komosa M., Mikołajczak E., Przybylska P., Sysak A., Wdowska A.

AlmaMater

Część 1

8. ANALIZA KINEMATYCZNA I STATYCZNA USTROJÓW PRĘTOWYCH

10

Wprowadzamy dodatkowe więzy (

d = 4).

(+1)

(+1)

(+2)

Następnie, aby otrzymać układ statycznie wyznaczalny odrzucamy dwie podpory i przecinamy ramę w dwóch
miejscach. (

N = 2·3 + 2·3 = 12)

Stopień statycznej niewyznaczalności SSN wynosi 

n = SSN = 12 - 4 = 8

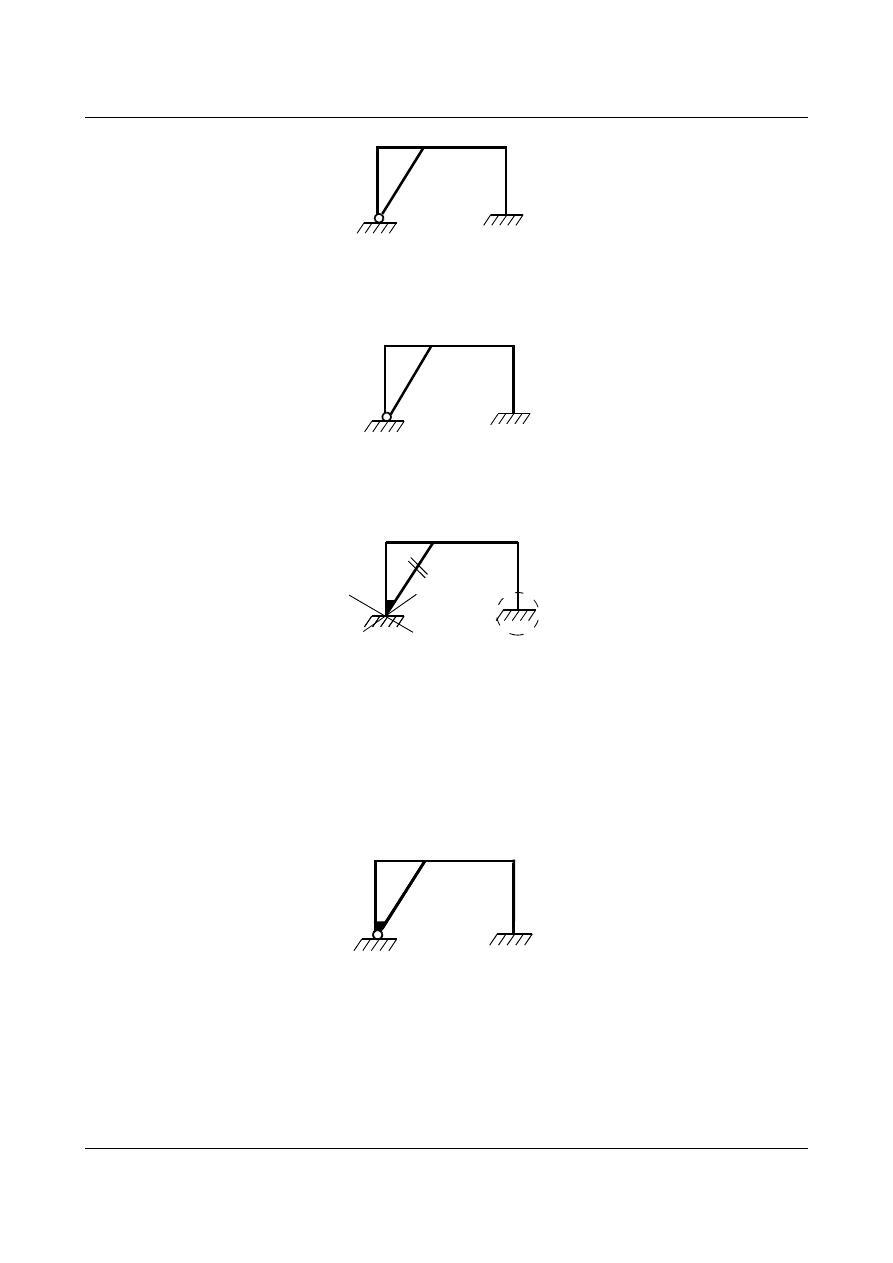
Zadanie 7

Określić stopień statycznej niewyznaczalności dla poniższego układu.

Dobra D., Jambrożek S., Komosa M., Mikołajczak E., Przybylska P., Sysak A., Wdowska A.

AlmaMater

Część 1

8. ANALIZA KINEMATYCZNA I STATYCZNA USTROJÓW PRĘTOWYCH

11

Aby usztywnić każdy z prętów należy wprowadzić dwa więzy (

d = 2), po jednym dla każdego pręta.

(+2)

Dalej likwidujemy jedną podporę i przecinamy ramę (

N = 3 +3 = 6)

Ostatecznie 

SSN = 6 – 2 = 4

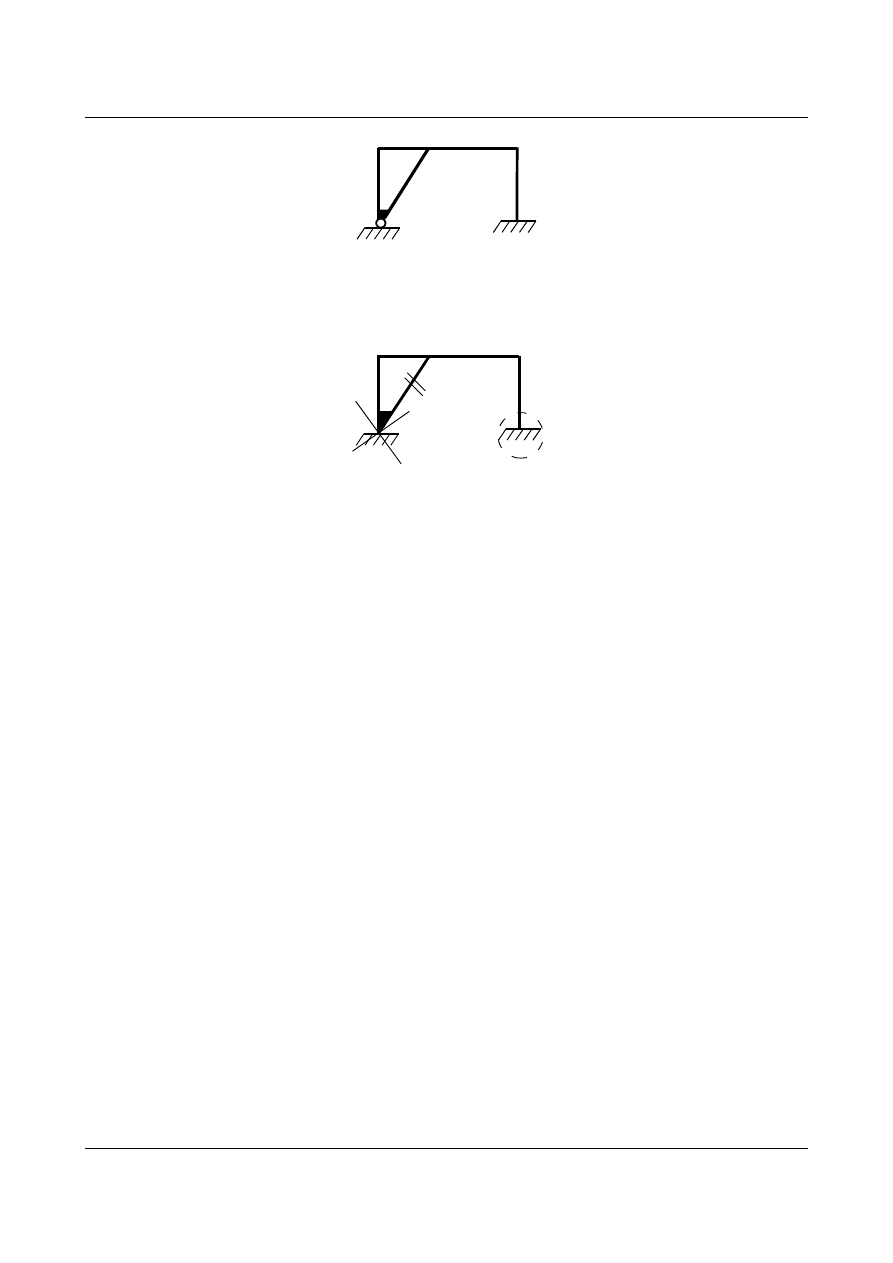
Zadanie 8 

Określić stopień statycznej niewyznaczalności dla poniższego układu.

Pręty są ze sobą sztywno połączone, wystarczy jeden dodatkowy więz podporowy (

d = 1)

Dobra D., Jambrożek S., Komosa M., Mikołajczak E., Przybylska P., Sysak A., Wdowska A.

AlmaMater

Część 1

8. ANALIZA KINEMATYCZNA I STATYCZNA USTROJÓW PRĘTOWYCH

12

(+1)

Dalej odrzucamy podporę i “otwieramy” obieg (

N = 3 + 3 = 6)

SSN = 6 – 1 = 5

8.3.3. Metoda III

Ramę  zamieniamy  poprzez  myślowe  “cięcia”  (przecięcia prętów  na  kawałki)  na  pojedyncze  tarcze.

Poprzez   tarczę   rozumiemy  pojedynczy  pręt   lub   grupę   prętów   połączonych  ze   sobą,   o   trzech   stopniach
swobody. Stopnień statycznej niewyznaczalności określamy ze wzoru:

n

=SSN =c−3⋅t

(8.5)

gdzie:

c - liczba cięć, równa się liczbie odebranych więzów,

t - to liczba pojedynczych prętów lub grup prętów.

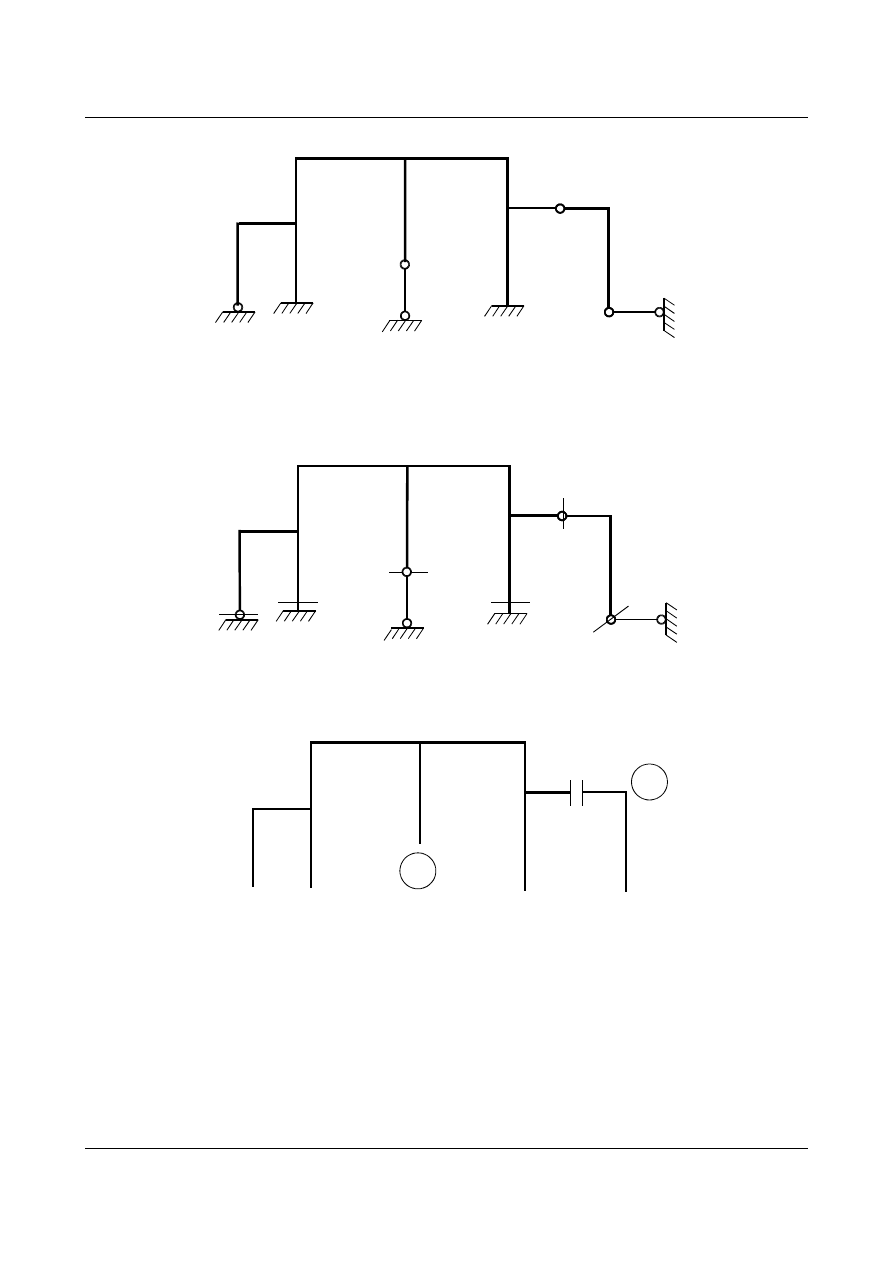
Zadanie 9

Określić stopień statycznej niewyznaczalności dla poniższego układu.

Dobra D., Jambrożek S., Komosa M., Mikołajczak E., Przybylska P., Sysak A., Wdowska A.

AlmaMater

Część 1

8. ANALIZA KINEMATYCZNA I STATYCZNA USTROJÓW PRĘTOWYCH

13

Przecinając   pręt   sztywny  likwidujemy  trzy   więzy,  przecinając   przegub   dwa   więzy,   a   odcinając   podporę
przegubowo przesuwną jeden więz. W nawiasach podano liczbę “przecinanych” więzów.

(2)

(3)

(1)

(3)

(1)

(2)

Po tym zabiegu powstają dwie swobodne tarcze (

t = 2). 

I

II

Tak więc 

n = SSN = 12 – 3·2 = 6

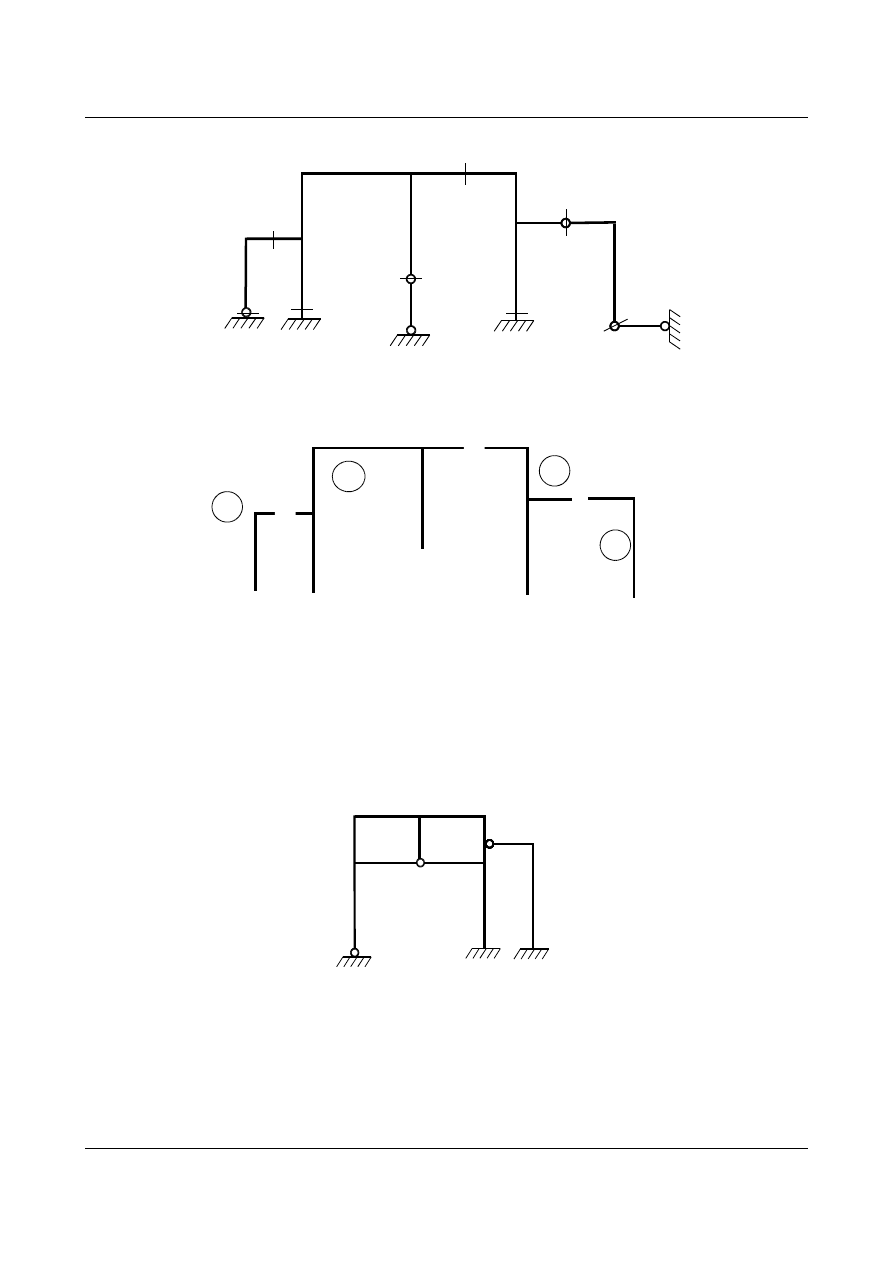
Innym sposobem rozwiązania tego zadania jest podział układu na cztery tarcze (

t = 4)

Dobra D., Jambrożek S., Komosa M., Mikołajczak E., Przybylska P., Sysak A., Wdowska A.

AlmaMater

Część 1

8. ANALIZA KINEMATYCZNA I STATYCZNA USTROJÓW PRĘTOWYCH

14

(1)

(2)

(1)

(3)

(3)

(2)

(3)

(3)

Liczba niezbędnych cięć wyniosła 18 (

c = 18)

I

IV

III

II

Ostatecznie 

n = SSN = 18 – 3·4 =6

Zadanie 10

Określić stopień statycznej niewyznaczalności dla poniższego układu.

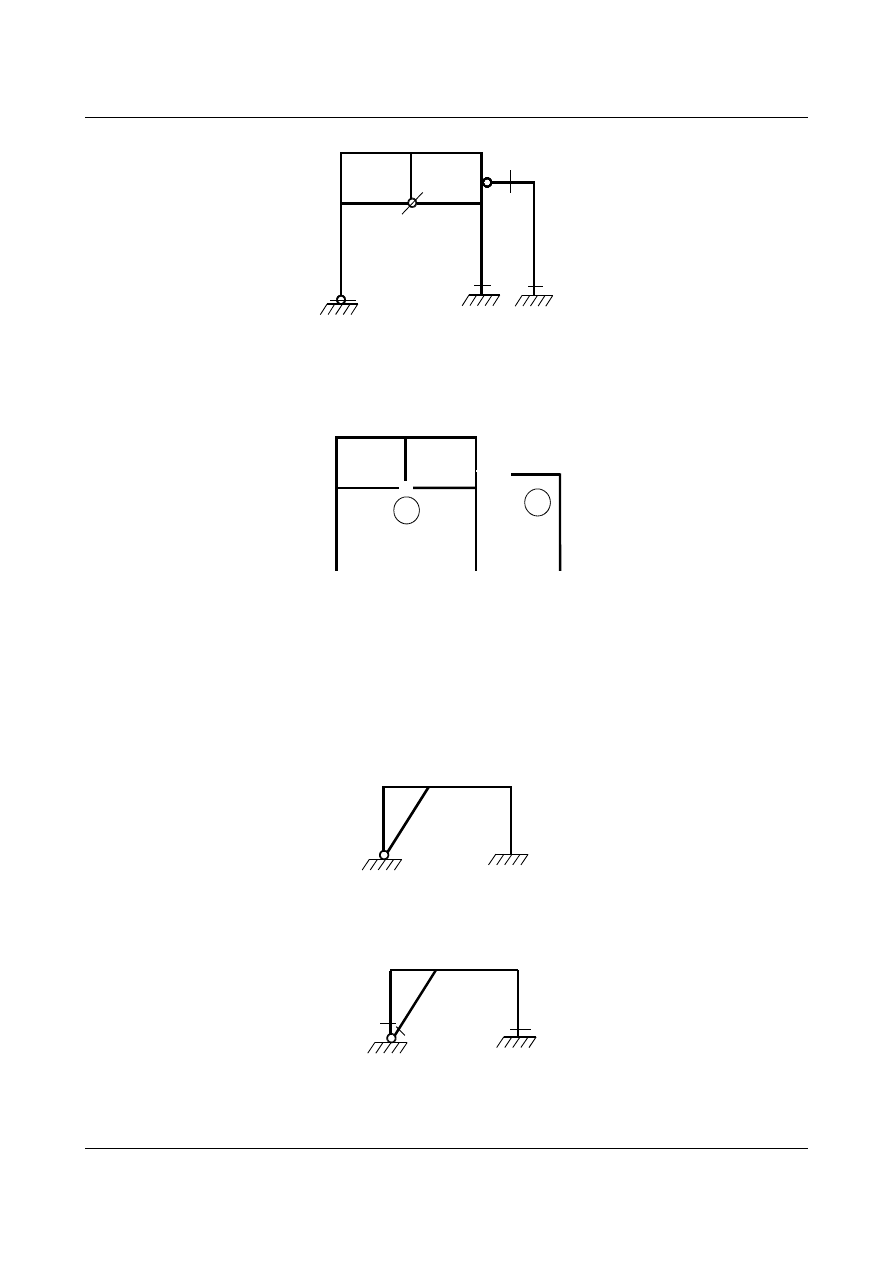
W podobny sposób jak w poprzednim zadaniu tniemy ramę na pojedyncze tarcze. W przegubie wielokrotnym
odłączamy wszystkie pręty od siebie (likwidujemy wszystkie więzy).

Dobra D., Jambrożek S., Komosa M., Mikołajczak E., Przybylska P., Sysak A., Wdowska A.

AlmaMater

Część 1

8. ANALIZA KINEMATYCZNA I STATYCZNA USTROJÓW PRĘTOWYCH

15

(2)

(3)

(4)

(3)

(2)

Liczba niezbędnych cięć wyniosła 14 (

c = 14), a liczba uzyskanych poprzez te cięcia tarcz jest równa 2

(

t = 2)

II

I

Ostatecznie 

n = SSN = 14 – 3·2 =8

Zadanie 11

Określić stopień statycznej niewyznaczalności dla poniższego układu.

Tniemy ramę tak, aby uzyskać jedną tarczę.

(3)

(2)

(2)

Wykonaliśmy 7 cięć więzów (

c = 7), przez co otrzymaliśmy 1 tarczę (t = 1).

Dobra D., Jambrożek S., Komosa M., Mikołajczak E., Przybylska P., Sysak A., Wdowska A.

AlmaMater

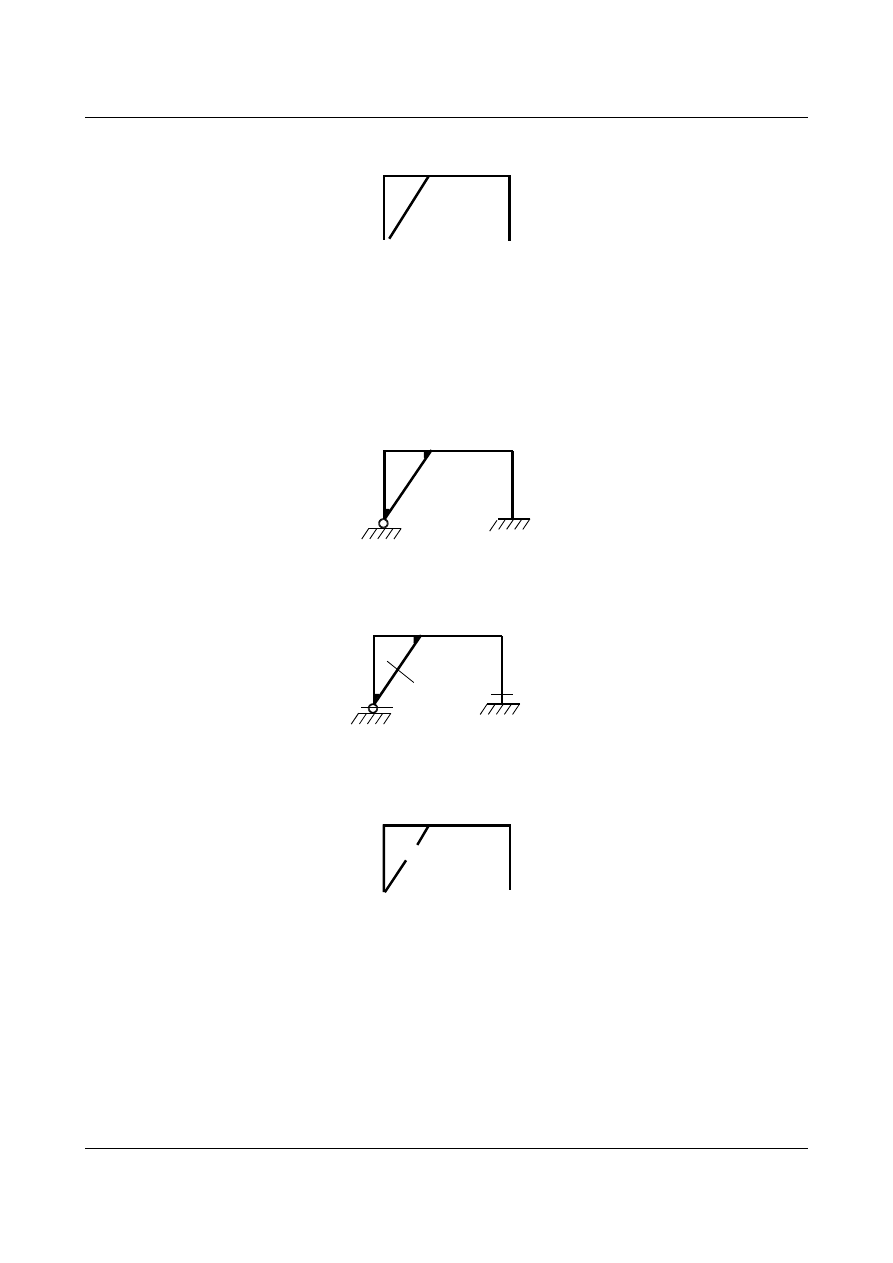
Część 1

8. ANALIZA KINEMATYCZNA I STATYCZNA USTROJÓW PRĘTOWYCH

16

A zatem 

n = SSN = 7 – 3·1 = 4

Zadanie 12

Określić stopień statycznej niewyznaczalności dla poniższego układu.

Tniemy ramę w trzech miejscach.

(2)

(3)

(3)

Wykonaliśmy 8 cięć więzów (

c = 8), przez co otrzymaliśmy 1 tarczę (t = 1).

Ostatecznie 

n = SSN = 8 – 3·1 = 5

Dobra D., Jambrożek S., Komosa M., Mikołajczak E., Przybylska P., Sysak A., Wdowska A.

AlmaMater