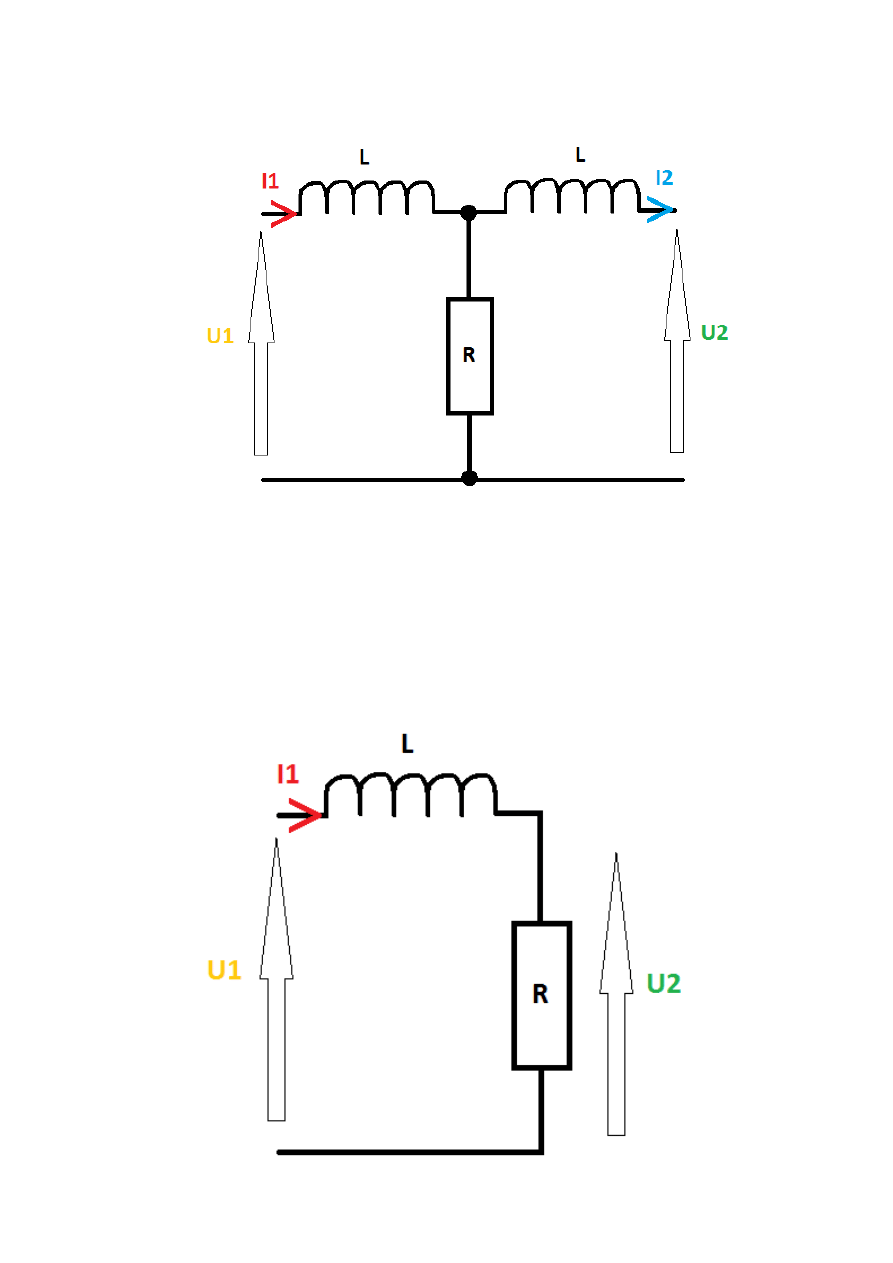
Czwórnik Typu „T” (macierz łańcuchowa):

U1 = A*U2 + B*I2
I1 = C*U2 + B*I2


Założenie I2=0:

U1 = A*U2 => A = U1/U2
I1 = C*U2 => C = I1/U2

Rysunek:

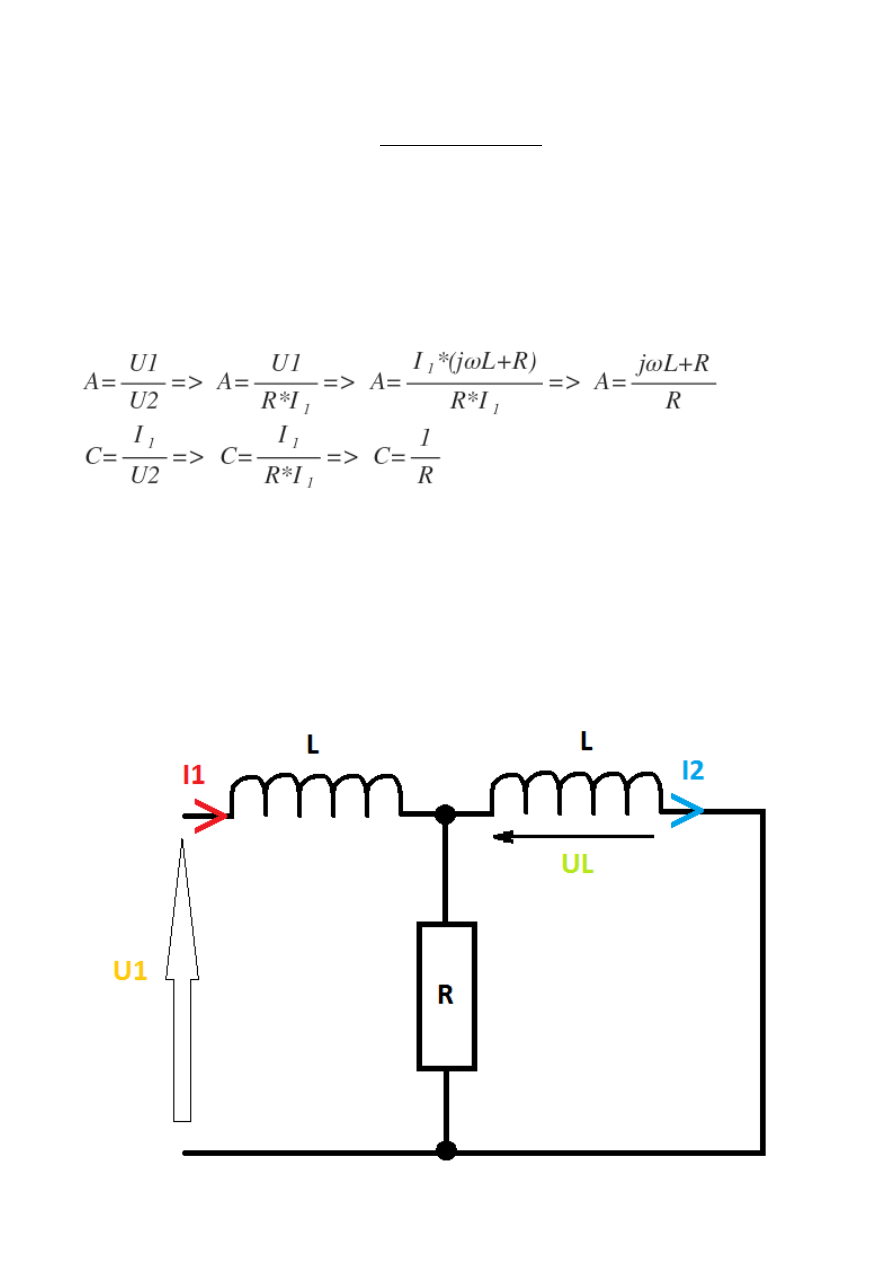
„Po usunięciu prądu I2 gałąź, na której była cewka nie istnieje tak, więc cewka ta jest po prostu
nieaktywna i w ten sposób powstaje nam szeregowe połączenie.”

Przy połączeniu szeregowym prąd się nie zmienia, lecz napięcie na
poszczególnych odbiornikach!!!

Więc:

Można zauważyć, że łatwiej się zmienia U1 niż kąbinować z I1 ponieważ U1 jest to suma wszystkich
rezystancji w układzie narysowanym po pozbyciu się prądu razy prąd I1 analogicznie jest z U2.

- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -

Założenie U2=0:

U1 = B*I2 => B = U1/I2
I1 = D*I2 => D = I1/I2

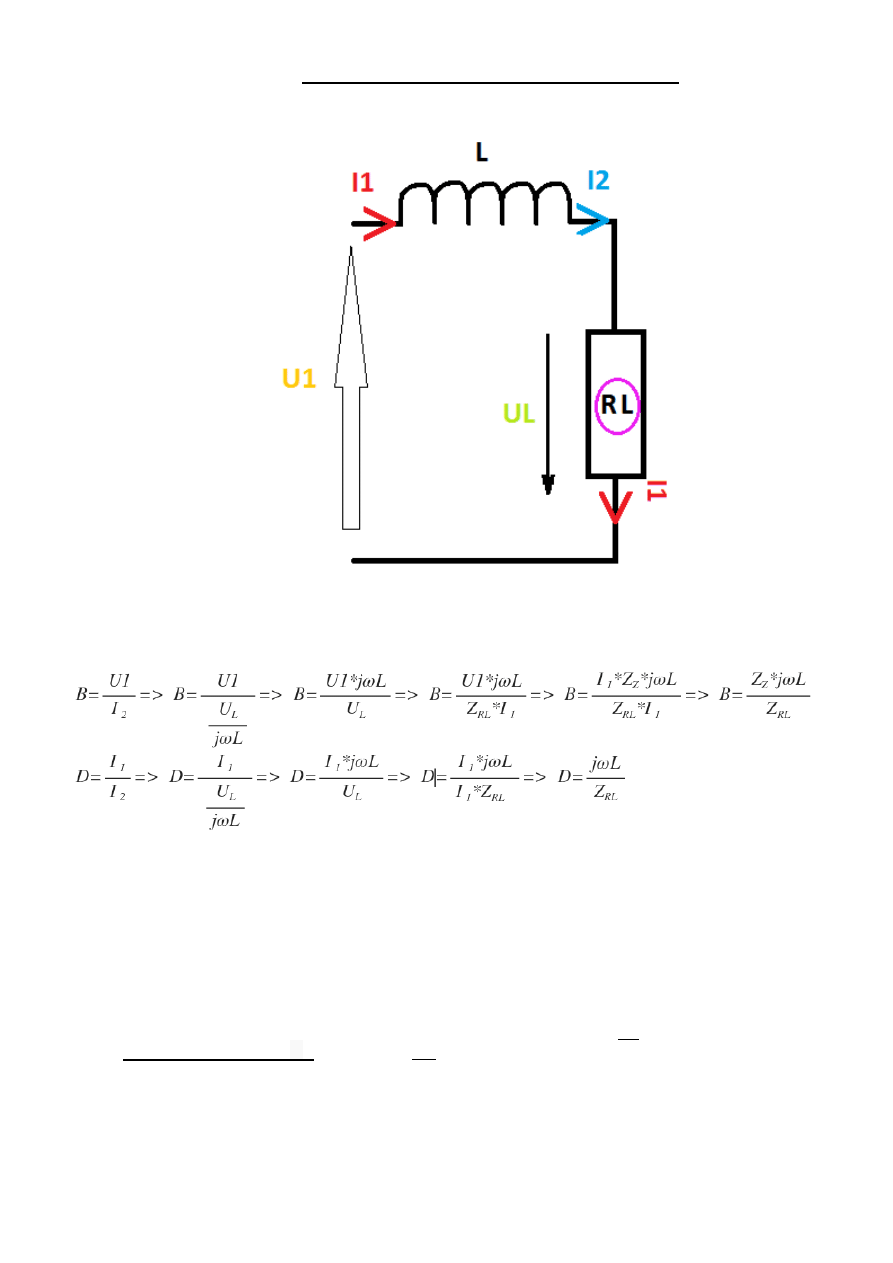
„Rysunek na dole przedstawia RL, czyli cewkę z rezystorem połączoną równolegle. Robi się to po to
by uprościć sobie liczenie i w tym momencie mamy połączenie szeregowe z L i RL.”

Więc:

Z

RL

to jest impedancja połączenia równoległego cewki i rezystora

Z

Z

to jest impedancja połączenia szeregowego cewki i impedancji Z

RL

( czyli suma całej rezystancji

obwodu).

U

L

jest to napięcie na L i RL gdzie te napięcie jest takie samo na każdym z tych elementów,

ponieważ mamy połączenie równoległe.

Gdy połączyliśmy rezystor i cewkę w jedno (RL) wtedy prąd I2 przeszedł przed cewkę. Skutkuję to
tym, że prąd I2 można przedstawić jako stosunek napięcia na tej gałęzi (U

L

)

przez rezystancję

gałęzi ( w tym wypadku samo jϖL). Natomiast U

L

można przedstawić też jako iloczyn I1 z Z

RL

ponieważ napięcie na RL jest takie jak na cewce połączonej wcześniej z rezystancją.