
Notacja wektorowo-macierzowa równań ruchu,
linearyzacja nieliniowych równań ruchu
Literatura:
1. Bodo Heimann, Wilfried Gerth, Karl Popp (przekład Marek Gawrysiak).: Mechatronika. Komponenty, metody, przykłady. Wydawnictwo Naukowe PWN,
Warszawa, 2001.
2. Henryk Achtelik, Józef Grzelak.: Ćwiczenia laboratoryjne z modelowania i symulacji układów mechanicznych w programie MATLAB-SIMULINK. Skrypt
uczelniany, Politechnika Opolska, Opole, 2004.
Równania ruchu w notacji wektorowo-macierzowej można zapisać w postaci
)
(
)
,
(
)
(
)
,
(
)
(
t
nap
R
Q
q
q
Q
q
g
q
q
c
q
q
M
,
(1)
gdzie:
q
- współrzędne uogólnione,
)
(q
M
- macierz masowa,
)
,
(
q
q
c
- siły Eulera i
Coriolisa,
)
(q
g
- siły zachowawcze,
)
,
(
q
q
Q
R
- siły dyssypatywne,
)
(t
nap
Q
- siły
nastawcze.

W postaci wektorowo-macierzowej możemy zapisać je jako
nap
Q
Kq
q
D
q
M
,
(2)
gdzie: M - macierz masowa, D - macierz tłumienia, K - macierz sztywności,
nap
Q
- wektor sił uogólnionych, q
- wektor położeń uogólnionych, q - wektor
prędkości uogólnionych,
q
- wektor przyspieszeń uogólnionych.
Przykład 1
Równania ruchu
)
(
)
(
0
)
(
1
2
2
2
2
2
1
2
1
1
1
1
t
F
q
q
k
q
m
q
q
k
q
k
q
m
zapisać w postaci wektorowo-macierzowej.

Rozwiązanie:
Przedstawiony układ równań jest układem równań liniowych. Na początek
przepiszemy równania w postaci
)
(
0
)
(
2
2
1
2
2
2
2
2
1
2
1
1
1
t
F
q
k
q
k
q
m
q
k
q
k
k
q
m
.
Postać wektorowo-macierzowa
nap
Q
Kq
q
D
q
M
jest następująca
)
(
0
0
0
0
0
0
0
2
1
2
2
2
2
1
2
1
2
1
2
1
t
F
q
q
k
k
k
k
k
q
q
q
q
m
m
,
gdzie:
M
2
1
0
0
m
m
,
D
0
0
0
0
,
K
2
2
2
2
1
k
k
k
k
k
,
q
2
1
q
q
,
q
2
1
q
q
,
1
q
2
1
q
q
,
nap
Q
)
(
0
t
F
.

Przykład 2
Równania ruchu
0
)
(
)
(
)
(
)
(
)
(
1
2
1
2
2
2
2
1
2
1
1
1
q
q
k
q
q
c
q
m
t
F
q
q
k
q
q
c
q
m
zapisać w postaci wektorowo-macierzowej.
Rozwiązanie:
Przedstawiony układ równań jest układem równań liniowych. Na początek
przepiszemy równania w postaci
0
)
(
2
1
2
1
2
2
2
1
2
1
1
1
kq
kq
q
c
q
c
q
m
t
F
kq
kq
q
c
q
c
q
m
.

Postać wektorowo-macierzowa
nap
Q
Kq
q
D
q
M
jest następująca
0
)
(
0
0
2
1
2
1
2
1
2
1
t
F
q
q
k
k
k
k
q
q
c
c
c
c
q
q
m
m
,
gdzie:
M
2
1
0
0
m
m
,
D
c
c
c
c
,
K
k
k
k
k
,
q
2
1
q
q
,
q
2
1
q
q
,
1
q
2
1
q
q
,
nap
Q
0
)
(t
F
.

Przykład 3
Równania ruchu
)
(
)
(
)
(
)
(
)
(
)
(
2
1
2
2
1
2
2
2
2
1
2
2
1
2
1
2
2
1
2
1
1
1
t
P
x
x
k
x
x
c
x
m
t
P
x
k
x
k
k
x
c
x
c
c
x
m
zapisać w postaci wektorowo-macierzowej.
Rozwiązanie:
Przedstawiony układ równań jest układem równań liniowych. Na początek
przepiszemy równania w postaci
)
(
)
(
)
(
)
(
2
2
2
1
2
2
2
1
2
2
2
1
2
2
1
2
1
2
2
1
2
1
1
1
t
P
x
k
x
k
x
c
x
c
x
m
t
P
x
k
x
k
k
x
c
x
c
c
x
m
.

Postać wektorowo-macierzowa
nap
Q
Kx
x
D
x
M
jest następująca
)
(
)
(
0
0
2
1
2
1
2
2
2
2
1
2
1
2
2
2
2
1
2
1
2
1
t
P
t
P
x
x
k
k
k
k
k
x
x
c
c
c
c
c
x
x
m
m
,
gdzie:
M
2
1
0
0
m
m
,
D
2
2
2
2
1
c
c
c
c
c
,
K
2
2
2
2
1
k
k
k
k
k
,
x
2
1
x
x
,
x
2
1
x
x
,
x
2
1
x
x
,
nap
Q
0
)
(t
F
.

LINEARYZACJA NIELINIOWYCH RÓWNAŃ RUCHU
Przyjmijmy, że
)
(
)
(
t
t
s
q
q
q
i
)
(
)
(
)
(
t
t
t
nap
nap_s
nap
Q
Q
Q
. Jeśli układ
nieliniowych
różniczkowych
równań
ruchu
zapiszemy
w
postaci
)
(
)
,
,
(
t
nap
Q
q
q
q
f
, wówczas linearyzacji można dokonać poprzez rozwinięcie
w szereg Taylora funkcji
)
,
,
(
q
q
q
f
i przerwanie rozwinięcia po pierwszym
(liniowym) wyrazie
)
(
)
(
)
,
,
(
)
,
,
(
t
t
s
s
s
s
s
s
s
s
s
nap
nap_s
Q
Q
q
q
f
q
q
f
q
q
f
q
q
q
f
q
q
q
q
q
q
f
(3)
Równanie równowagi ma postać
)
(
)
,
,
(
t
s
s
s
nap_s
Q
q
q
q
f
(4)
Odejmując równanie (4) od równania (3) otrzymujemy równanie dynamiczne
wokół położenia równowagi

)
(t
s
s
s
nap
Q
q
q
f
q
q
f
q
q
f
.
(5)
Inną możliwością jest zapisanie równań ruchu w postaci
)
(
)
,
(
)
(
t
nap
Q
q
q
h
q
q
M
.
(6)
Obliczając kolejno
)
(q
M
,
s
x
h
D
i
s
x
h
K
,
równania ruchu w postaci macierzowej można zapisać jako
)
(t
K
nap
Q
q
q
D
q
M
.
(7)
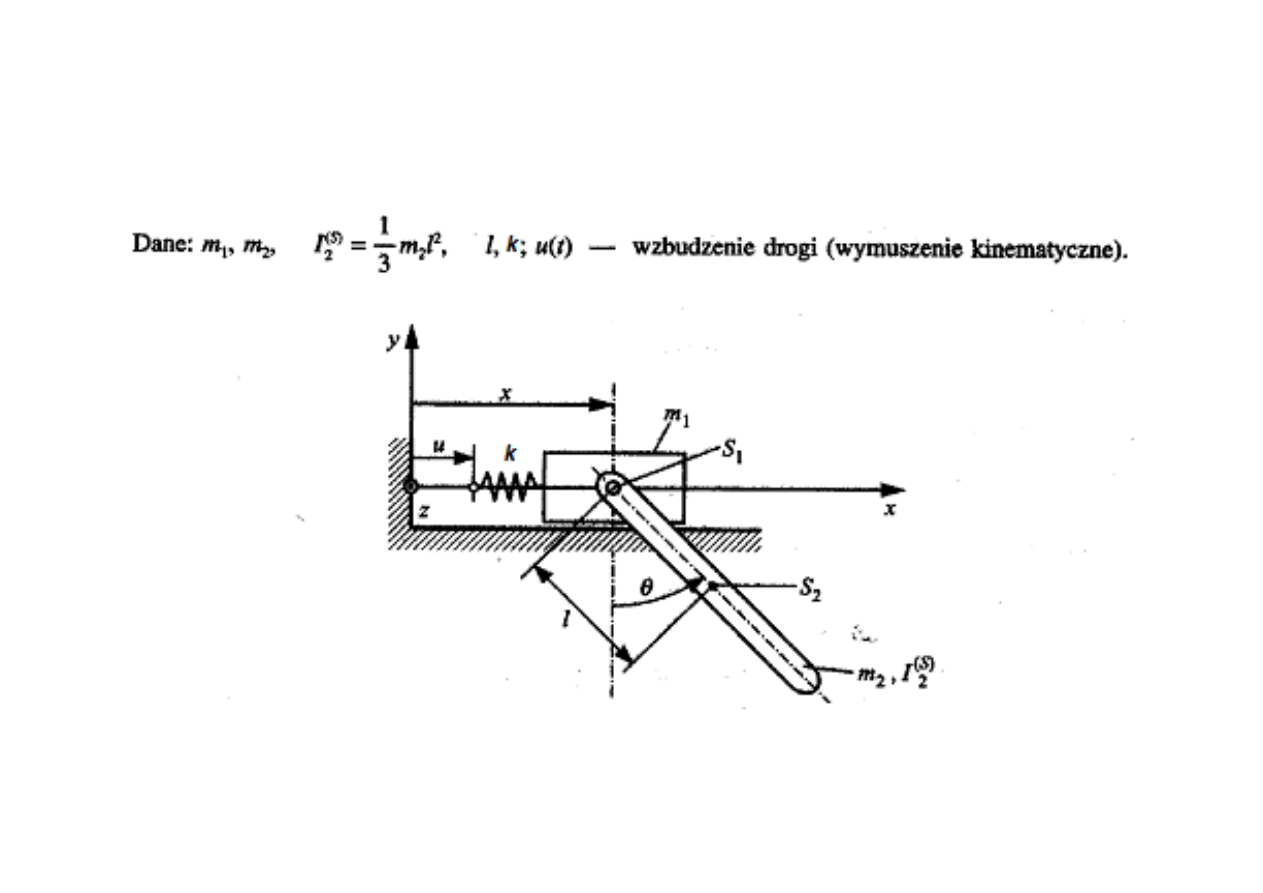
Przykład
Dla układu z rysunku określić statyczne położenie równowagi i zlinearyzowane
równania ruchu w okolicy tego punktu równowagi.

Rozwiązanie:
Równania ruchu mają postać
0
sin
cos
)
(
sin
cos
)
(
2
2
2
2
)
(
2
2
2
2
2
1
gl
m
x
l
m
l
m
I
ku
kx
l
m
l
m
x
m
m
S
.
Załóżmy, że:
)
(
)
(
t
u
u
t
u
s
,
)
(
)
(
t
x
x
t
x
s
,
)
(
)
(
t
t
s
, gdzie
s
u ,
s
x ,
s
= const.
Wstawiając do równań ruchu i przyjmując dla stanu równowagi prędkości i
przyspieszenia współrzędnych uogólnionych równe zeru otrzymujemy dla
statycznego położenia równowagi
0
sin
2
s
s
s
gl
m
ku
kx
.

Statyczne położenie równowagi ma postać
równowagi
polozenie
e
niestabiln
równowagi
polozenie
stabilne
0
s
s
s
u
x
.
Teraz linearyzacja:
sin
cos
)
(
sin
cos
)
(
)
,
,
(
)
,
,
(
)
,
,
(
2
2
2
2
)
(
2
2
2
2
2
1
2
1
gl
m
x
l
m
l
m
I
kx
l
m
l
m
x
m
m
f
f
S
q
q
q
q
q
q
q
q
q
f
Funkcje
)
,
,
(
1
q
q
q
f
i
)
,
,
(
2
q
q
q
f
rozwijamy w szereg Taylora i przerywamy po
pierwszym (liniowym) wyrazie
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
s
s
s
s
s
s
s
s
s
f
f
f
f
f
1
1
1
1
1
)
,
,
(
)
,
,
(
,
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
s
s
s
s
s
s
s
s
s
f
f
f
f
f
2
2
2
2
2
)
,
,
(
)
,
,
(
.

Dla rozważanego przypadku otrzymujemy
x
k
l
m
l
m
l
m
x
m
m
kx
f
s
s
s
s
s
s
s
s
s
cos
sin
2
cos
)
,
,
(
2
2
2
2
2
1
1
q
q
q
q
q
q
s
s
S
s
s
s
s
gl
m
x
l
m
l
m
I
gl
m
f
cos
cos
)
(
sin
)
,
,
(
2
2
2
2
)
(
2
2
2
q
q
q
q
q
q
.
Zatem zlinearyzowane równania ruchu (łącznie z równaniem statycznym) wokół
położenia równowagi
s
s
x
,
mają postać
0
cos
cos
)
(
sin
cos
)
(
2
2
2
2
)
(
2
2
2
2
1
s
s
S
s
s
s
s
gl
m
x
l
m
l
m
I
gl
m
u
k
ku
x
k
l
m
x
m
m
kx
.

Odejmując równanie statyczne otrzymujemy zlinearyzowane równanie
dynamiczne
0
cos
cos
)
(
cos
)
(
2
2
2
2
)
(
2
2
2
1
s
s
S
s
gl
m
x
l
m
l
m
I
u
k
x
k
l
m
x
m
m
.
Otrzymane równania ruchu są liniowe, ponieważ wszystkie współrzędne
uogólnione występujące w tym równaniu są w pierwszej potędze. Równania są
poprawne w okolicy punktu równowagi
s
s
x
,
a współczynniki równania zależą
od tego położenia równowagi.
Interesujące są dwa przypadki:
a)
0
s
- stabilne wahadło. Wtedy równania ruchu upraszczają się do postaci:
0
)
(
)
(
2
2
2
)
(
2
2
2
2
1
gl
m
l
m
I
x
l
m
u
k
x
k
l
m
x
m
m
S
,

co można zapisać w postaci macierzowej
0
0
0
2
2
2
)
(
2
2
2
2
1
u
k
x
gl
m
k
x
l
m
I
l
m
l
m
m
m
S
.
b)
s
- niestabilne wahadło. Wtedy równania ruchu upraszczają się do
postaci:
0
)
(
)
(
2
2
2
)
(
2
2
2
2
1
gl
m
l
m
I
x
l
m
u
k
x
k
l
m
x
m
m
S
,
co można zapisać w postaci macierzowej
0
0
0
2
2
2
)
(
2
2
2
2
1
u
k
x
gl
m
k
x
l
m
I
l
m
l
m
m
m
S
.

II sposób:
W rozważanym przypadku otrzymujemy z ogólnych nieliniowych równań ruchu
sin
cos
sin
)
,
(
)
,
(
)
,
(
2
2
2
2
2
1
gl
m
x
l
m
kx
l
m
h
h
q
q
q
q
q
q
h
,
)
(
cos
cos
2
2
)
(
2
2
2
2
1
l
m
I
l
m
l
m
m
m
S
s
s
M
,
0
0
sin
2
0
2
2
2
1
1
l
m
h
x
h
h
x
h
D
,
cos
sin
0
cos
2
2
2
2
2
2
1
1
gl
m
x
l
m
l
m
k
h
x
h
h
x
h
K
.

W postaci macierzowej
)
(t
K
nap
Q
q
q
D
q
M
otrzymujemy
0
cos
sin
0
cos
0
0
sin
2
0
cos
cos
2
2
2
2
2
2
2
)
(
2
2
2
2
1
u
k
x
gl
m
x
l
m
l
m
k
x
l
m
x
l
m
I
l
m
l
m
m
m
S
s
s
Tutaj też rozważymy te same dwa szczególne przypadki:
a)
0
s
- stabilne wahadło. Wtedy równania ruchu upraszczają się do postaci:
0
0
0
2
2
2
)
(
2
2
2
2
1
u
k
x
gl
m
k
x
l
m
I
l
m
l
m
m
m
S
.
b)
s
- niestabilne wahadło. Wtedy równania ruchu upraszczają się do
postaci:
0
0
0
2
2
2
)
(
2
2
2
2
1
u
k
x
gl
m
k
x
l
m
I
l
m
l
m
m
m
S
.
Wyszukiwarka
Podobne podstrony:
Abolicja podatkowa id 50334 Nieznany (2)
4 LIDER MENEDZER id 37733 Nieznany (2)
katechezy MB id 233498 Nieznany
metro sciaga id 296943 Nieznany
perf id 354744 Nieznany
interbase id 92028 Nieznany
Mbaku id 289860 Nieznany
Probiotyki antybiotyki id 66316 Nieznany
miedziowanie cz 2 id 113259 Nieznany
LTC1729 id 273494 Nieznany
D11B7AOver0400 id 130434 Nieznany
analiza ryzyka bio id 61320 Nieznany
pedagogika ogolna id 353595 Nieznany
Misc3 id 302777 Nieznany
cw med 5 id 122239 Nieznany
D20031152Lj id 130579 Nieznany
mechanika 3 id 290735 Nieznany
więcej podobnych podstron