dr Agnieszka Bobrowska

1

Ekonomia matematyczna II

Wykład 3

Modele wzrostu gospodarczego

3.1. Model Harroda-Domara

1

Model Harroda-Domara to jeden z klasycznych modeli wzrostu. Jego idea polega na okre

ś

leniu

ś

cie

ż

ki czasowej dla zmiennych (wyst

ę

puj

ą

cych w tym modelu), jaka musi wyst

ą

pi

ć

, aby gospodarka

mogła si

ę

znale

źć

w stanie równowagi.

Zanim go przedstawimy, omówimy najpierw zale

ż

no

ść

jaka wyst

ę

puje mi

ę

dzy inwestycjami

a tworzeniem kapitału. Najogólniej rzecz bior

ą

c, tworzenie kapitału polega na powi

ę

kszaniu danego

zasobu funduszy. O ile proces tworzenia kapitału potraktujemy jako ci

ą

gły w czasie, o tyle zasoby

kapitału

K

mo

ż

emy uzna

ć

jako funkcj

ę

czasu

t

:

)

(t

K

K

=

.

Pochodna

dt

dK

okre

ś

la wówczas stop

ę

tworzenia kapitału, która w momencie

t

jest równa stopie

strumienia inwestycji netto

I

w chwili t, co opisuje to

ż

samo

ść

:

)

(t

I

dt

dK

≡

.

Jednocze

ś

nie mo

ż

emy powiedzie

ć

,

ż

e

)

(t

K

jest całk

ą

pierwotn

ą

inwestycji netto

)

(t

I

, co pokazuje

nast

ę

puj

ą

ce równanie:

∫

∫

∫

=

=

=

dK

dt

dt

dK

dt

t

I

t

K

)

(

)

(

.

Nale

ż

y napomnie

ć

, i

ż

w niektórych modelach wzrostu oprócz inwestycji netto

I

mog

ą

wyst

ę

powa

ć

inwestycje brutto, oznaczane symbolem

g

I

. Zale

ż

no

ść

mi

ę

dzy inwestycjami netto i brutto mo

ż

na

wyrazi

ć

równaniem:

K

I

I

g

δ

+

=

,

gdzie:

δ

- stopa deprecjacji kapitału,

K

δ

- stopa reinwestycji kapitału.

1

Charakterystyk

ę

modelu przygotowano na podstawie A.C. Chiang: Podstawy ekonomii matematycznej, PWE,

Warszawa 1994, s. 464 i dalsze oraz R.G.D. Allen: Teoria makroekonomiczna, PWN, Warszawa 1975, rozdział
11, M. Garbicz, E. Golachowski, Elementarne modele makroekonomiczne, Szkoła Główna Handlowa, Warszawa
1996, rozdział 9

dr Agnieszka Bobrowska

2

Ekonomia matematyczna II

W modelu wzrostu Harroda-Domara zakłada si

ę

,

ż

e ka

ż

da zmiana rocznej stopy strumienia

inwestycji

)

(t

I

(

dt

dK

≡

) wpływa na ukształtowanie si

ę

zagregowanego popytu (efekt popytowy),

a tak

ż

e na zdolno

ś

ci produkcyjne gospodarki. Efekt popytowy jest natychmiastowy i powstaje za

po

ś

rednictwem procesu mno

ż

nikowego. Mno

ż

nik wynosi

const

s

k

=

=

1

, gdzie s oznacza dan

ą

kra

ń

cow

ą

skłonno

ść

do oszcz

ę

dzania. Wpływ zmiany stopy strumienia inwestycji

)

(t

I

na stop

ę

strumienia dochodów

)

(t

Y

mo

ż

na zapisa

ć

za pomoc

ą

równo

ś

ci:

s

dt

dI

dt

dY

1

=

,

któr

ą

to równo

ść

interpretujemy nast

ę

puj

ą

co:

wzrost (spadek) stopy strumienia inwestycji

)

(t

I

powoduje wzrost (spadek) stopy strumienia

dochodów

)

(t

Y

o dan

ą













s

1

cz

ęść

przyrostu

)

(t

I

.

O

)

(t

I

zakłada si

ę

ponadto,

ż

e jest jedynym strumieniem wydatków wpływaj

ą

cym na stop

ę

strumienia dochodu

)

(t

Y

.

Je

ż

eli chodzi o wpływ zmiany rocznej stopy strumienia inwestycji

)

(t

I

na zdolno

ś

ci produkcyjne,

to mierzy si

ę

go przy pomocy zmiany stopy potencjalnej produkcji. Produkcja potencjalna to produkcja

jak

ą

gospodarka jest w stanie wytworzy

ć

, czyli produkcja przy optymalnym wykorzystaniu mocy

produkcyjnych oraz czynników produkcji: zasobów kapitału, siły roboczej oraz ziemi.

W modelu Harroda-Domara zakłada si

ę

,

ż

e stosunek mo

ż

liwo

ś

ci produkcyjnych

κ

do kapitału

K

jest stały i wynosi

ρ

:

ρ

κ

≡

K

.

Stała proporcja wydajno

ś

ci i kapitału oznacza,

ż

e gdy dany jest zasób kapitału

)

(t

K

, to

gospodarka jest w stanie osi

ą

gn

ąć

w skali roku produkcj

ę

(dochód) na poziomie

K

ρ

.

Przekształcaj

ą

c wyj

ś

ciow

ą

to

ż

samo

ść

ρ

κ

≡

K

, mamy bowiem:

K

ρ

κ

≡

(funkcja produkcji).

dr Agnieszka Bobrowska

3

Ekonomia matematyczna II

Ró

ż

niczkuj

ą

c obie strony powy

ż

szej równo

ś

ci po

t

otrzymujemy:

dt

dK

dt

d

ρ

κ

=

.

Poniewa

ż

jednak

)

(t

I

dt

dK

≡

, wi

ę

c:

)

(t

I

dt

dK

dt

d

ρ

ρ

κ

=

=

.

W omawianym modelu stan równowagi jest zdefiniowany jako sytuacja, w której zagregowany

popyt równa si

ę

potencjalnej rocznej produkcji, czyli gdy mo

ż

liwo

ś

ci produkcyjne s

ą

w pełni

wykorzystywane. Warunek równowagi zapisujemy zatem w postaci:

κ

=

Y

.

Je

ż

eli zało

ż

ymy,

ż

e w chwili pocz

ą

tkowej gospodarka znajduje si

ę

w stanie równowagi, wówczas

warunek równowagi doprowadza nas do kolejnego wniosku o zrównowa

ż

eniu odpowiednich zmian

mo

ż

liwo

ś

ci produkcyjnych i zagregowanego popytu:

dt

d

dt

dY

κ

=

.

W tym momencie nale

ż

y zada

ć

sobie pytanie o rodzaj

ś

cie

ż

ki czasowej dla inwestycji

)

(t

I

.

Interesuje nas bowiem taka posta

ć

ś

cie

ż

ki, która spełniałaby warunek równowagi w ka

ż

dym

momencie. Aby j

ą

znale

źć

podstawiamy do ostatniej równo

ś

ci za

dt

dY

, wyra

ż

enie

s

dt

dI 1

, a za

dt

d

κ

,

wyrażeni I

ρ

, sk

ą

d otrzymujemy równanie ró

ż

niczkowe pierwszego rz

ę

du jednorodne postaci:

I

s

dt

dI

ρ

=

1

, czyli

s

dt

dI

I

ρ

=

1

.

Całkuj

ą

c wzgl

ę

dem

t

obie strony ostatniego równania otrzymujemy:

c

st

I

+

=

ρ

ln

,

+

∈

R

c

.

Wykorzystuj

ą

c własno

ść

liczby

e

:

a

e

a

ln

=

, otrzymujemy:

st

c

st

I

Ae

I

e

e

ρ

ρ

=

⇒

=

+

)

(

ln

, gdzie

c

e

A

≡

.

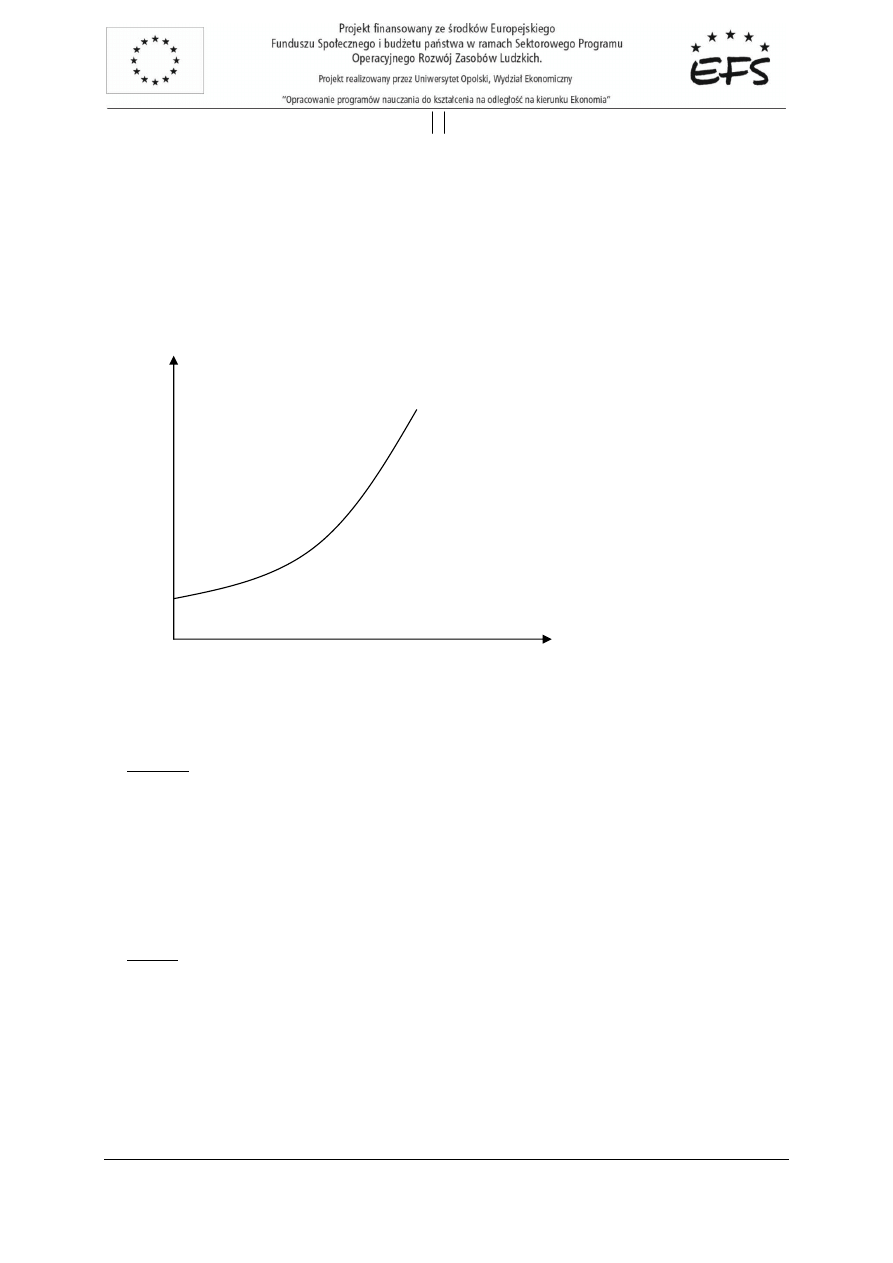
dr Agnieszka Bobrowska

4

Ekonomia matematyczna II

Je

ż

eli przyjmiemy,

ż

e inwestycje s

ą

dodatnie (

I

I

=

) oraz

ż

e

A

Ae

I

=

=

0

)

0

(

, wówczas

ś

cie

ż

ka

inwestycji przyjmuje posta

ć

:

st

e

I

t

I

ρ

)

0

(

)

(

=

,

gdzie:

)

0

(

I

- pocz

ą

tkowa stopa inwestycji.

Wykres szukanej

ś

cie

ż

ki czasowej dla inwestycji

)

(t

I

przedstawia rysunek 3.1.

Rys. 3.1.

Ś

cie

ż

ka czasowa inwestycji

I

danych wzorem

st

e

I

t

I

ρ

)

0

(

)

(

=

.

Wniosek:

1. Aby w gospodarce utrzymany został stan równowagi pomi

ę

dzy produkcj

ą

potencjalna

a zagregowanym popytem, stopa strumienia inwestycji musi mie

ć

wzrost wykładniczy o stopie

równej

s

ρ

, gdzie

ρ

oznacza proporcj

ę

mo

ż

liwo

ś

ci produkcyjnych i kapitału, a

s

to kra

ń

cowa

skłonno

ść

do oszcz

ę

dzania.

2. Ponadto im wi

ę

ksze b

ę

d

ą

warto

ś

ci

ρ

i

s

, tym wi

ę

ksza b

ę

dzie wymagana stopa wzrostu.

Uwaga:

Rzeczywista stopa wzrostu inwestycji mo

ż

e si

ę

ró

ż

ni

ć

od wymaganej.

t

)

(t

I

0

st

e

I

t

I

ρ

)

0

(

)

(

=

)

0

(

I

dr Agnieszka Bobrowska

5

Ekonomia matematyczna II

Załó

ż

my zatem,

ż

e prawdziwa stopa wzrostu inwestycji wynosi

s

r

ρ

≠

. Oznaczmy przez

u

współczynnik stopnia wykorzystania mocy wytwórczych okre

ś

lony w nast

ę

puj

ą

cy sposób:

)

(

)

(

lim

t

t

Y

u

t

κ

∞

→

=

.

Poka

ż

emy,

ż

e

s

r

u

ρ

=

, przy czym:

•

s

r

u

ρ

=

⇔

=

1

oznacza pełne wykorzystanie mocy produkcyjnych,

•

s

r

u

ρ

>

⇔

>

1

oznacza niedobór zdolno

ś

ci produkcyjnych,

•

s

r

u

ρ

<

⇔

<

1

oznacza nadwy

ż

k

ę

zdolno

ś

ci produkcyjnych.

Poniewa

ż

zało

ż

yli

ś

my,

ż

e prawdziwa stopa wzrostu inwestycji wynosi

r

, to:

rt

e

I

t

I

)

0

(

)

(

=

.

Ró

ż

niczkuj

ą

c obustronnie to równanie wzgl

ę

dem

t

otrzymujemy:

rt

e

rI

dt

dI

)

0

(

=

.

Na mocy warunków z modelu Harroda-Domara i dwóch powy

ż

szych równa

ń

mamy:

rt

e

I

s

dt

dI

dt

dY

)

0

(

s

r

1

=

=

oraz

rt

e

I

t

I

dt

d

)

0

(

)

(

ρ

ρ

κ

=

=

.

St

ą

d stosunek pochodnej

dt

dY

do

pochodnej

dt

d

κ

,

okre

ś

laj

ą

cy

wielko

ś

ci

wzgl

ę

dne

efektu

popytowego zmiany inwestycji

)

(t

I

i efektu zmiany

)

(t

I

dla mo

ż

liwo

ś

ci produkcyjnych, w ka

ż

dej

chwili

t

, przy stopie wzrostu inwestycji równej

r

wynosi:

s

r

dt

d

dt

dY

ρ

κ

=

.

dr Agnieszka Bobrowska

6

Ekonomia matematyczna II

Pokazali

ś

my zatem,

ż

e współczynnik

s

r

u

ρ

=

, co wi

ę

cej, wykazali

ś

my,

ż

e równo

ść

ta zachodzi nie

tylko dla

∞

→

t

, ale obowi

ą

zuje w ka

ż

dym momencie

t

.

Je

ż

eli wymagana stopa inwestycji

s

ρ

jest mniejsza od stopy

r

, wówczas efekt dochodowy

dt

dY

b

ę

dzie przewy

ż

szał efekt dla mo

ż

liwo

ś

ci produkcyjnych

dt

d

κ

, co przyczyni si

ę

do powstania

niedoborów mo

ż

liwo

ś

ci produkcyjnych.

W przypadku, gdy wymagana stopa inwestycji

s

ρ

jest wi

ę

ksza od stopy rzeczywistej

r

, wtedy

efekt dla mo

ż

liwo

ś

ci produkcyjnych

dt

d

κ

b

ę

dzie przewy

ż

szał efekt dochodowy

dt

dY

, co oznacza,

ż

e

popyt zagregowany oka

ż

e si

ę

niewystarczaj

ą

cy, a co za tym idzie moce produkcyjne nie zostan

ą

w pełni wykorzystane.

Otrzymane wyniki wydaj

ą

si

ę

do

ść

paradoksalne. We

ź

my dla przykładu przedsi

ę

biorc

ę

, któremu

pozwalamy dostosowa

ć

stop

ę

wzrostu inwestycji

r

do mo

ż

liwo

ś

ci produkcyjnych.

W przypadku, gdy

r

s

<

ρ

, czyli gdy ma miejsce niedobór mo

ż

liwo

ś

ci produkcyjnych, przedsi

ę

biorca

ten zapewne podj

ą

łby decyzj

ę

o dodatkowych inwestycjach, co spowodowałby najmniej w tym

momencie potrzebny wzrost

r

, a w konsekwencji jeszcze wi

ę

kszy niedobór mo

ż

liwo

ś

ci

produkcyjnych.

Jedynym rozs

ą

dnym rozwi

ą

zaniem problemu niedoborów lub nadwy

ż

ek mocy produkcyjnych, jest

pokierowanie strumienia inwestycji wzdłu

ż

ś

cie

ż

ki równowagi ze stop

ą

wzrostu

s

r

ρ

=

. Jakakolwiek

rozbie

ż

no

ść

mi

ę

dzy stanem faktycznym zmian w przebiegu strumienia inwestycji a stanem

oczekiwanym uniemo

ż

liwi spełnienie postulatu pełnego wykorzystania zdolno

ś

ci produkcyjnych,

zawartej w modelu Harroda-Domara.

Nieco bardziej elastyczne wyniki daje model Solowa, o którym jest mowa w kolejnym podrozdziale.

3.2. Neoklasyczny model Solowa

2

Model wzrostu Solowa, który przedstawimy w tym podrozdziale, ró

ż

ni si

ę

od omówionego ju

ż

modelu Harroda-Domara przede wszystkim zało

ż

eniami o funkcji produkcji.

W modelu Harroda-Domara produkcja była funkcj

ą

jedynie kapitału, natomiast w modelu Solowa

produkcja jest funkcj

ą

zarówno kapitału, jak i nakładów pracy, które mog

ą

by

ć

poł

ą

czone w zmiennych

proporcjach.

Wprowad

ź

my zatem nast

ę

puj

ą

ce oznaczenia:

Q

- wielko

ść

produkcji w gospodarce,

2

Charakterystyk

ę

modelu przygotowano na podstawie A.C. Chiang: Podstawy ekonomii matematycznej, PWE,

Warszawa 1994, s. 495 i dalsze, D. Romer: Makroekonomia dla zaawansowanych, PWN, Warszawa 2000,
rozdział 1, M. Garbicz, E. Golachowski, Elementarne modele makroekonomiczne, Szkoła Główna Handlowa,
Warszawa 1996, rozdział 9

dr Agnieszka Bobrowska

7

Ekonomia matematyczna II

K

- nakłady kapitału,

L

- nakłady pracy.

Przy tych oznaczeniach funkcja produkcji w modelu Solowa ma nast

ę

puj

ą

c

ą

posta

ć

:

)

,

(

L

K

f

Q

=

.

Przyjmuje si

ę

,

ż

e kapitał

K

i zasoby siły roboczej

L

s

ą

funkcjami czasu, natomiast funkcja

produkcji

Q

jest stała w czasie.

O funkcji

f

zakłada si

ę

ponadto,

ż

e jest liniowo jednorodna, co oznacza stałe przychody skali.

Ponadto przyjmuje si

ę

,

ż

e pochodne cz

ą

stkowe

L

f

K

f

∂

∂

∂

∂

,

s

ą

dodatnie (dodatnie produkty kra

ń

cowe),

natomiast pochodne cz

ą

stkowe

2

2

2

2

,

L

f

K

f

∂

∂

∂

∂

s

ą

ujemne (malej

ą

ce przychody dla ka

ż

dego czynnika).

Ze wzgl

ę

du na liniow

ą

jednorodno

ść

funkcji

f

, funkcj

ę

produkcji mo

ż

na zapisa

ć

w postaci:

)

(

1

,

k

L

L

K

Lf

Q

ϕ

=













=

, gdzie

L

K

k

≡

,

gdzie:

ϕ

- funkcja jednoargumentowa,

k

- techniczne uzbrojenie pracy, inaczej koszt stanowiska pracy.

Nale

ż

y podkre

ś

li

ć

,

ż

e je

ż

eli funkcja produkcji

)

,

(

L

K

f

Q

=

jest liniowo jednorodna, wówczas

kra

ń

cowe produkty kapitału i pracy:

K

Q

MPP

K

∂

∂

≡

i

L

Q

MPP

L

∂

∂

≡

mo

ż

na wyrazi

ć

jako funkcje

samego

k

:

)

(

'

'

1

'

k

L

K

L

L

K

L

K

L

K

L

K

L

K

L

K

Q

MPP

K

ϕ

ϕ

ϕ

ϕ

ϕ

=













=

⋅













=

∂













∂

=

∂













∂

=

∂

∂

≡

)

(

'

)

(

'

'

2

k

k

k

L

K

L

K

L

K

L

K

L

K

L

L

K

L

L

K

L

L

L

K

L

L

Q

MPP

L

ϕ

ϕ

ϕ

ϕ

ϕ

ϕ

ϕ

ϕ

−

=













−













+













=

=













−

⋅













+













=

∂













∂

=

∂













∂

=

∂

∂

≡

dr Agnieszka Bobrowska

8

Ekonomia matematyczna II

Z zało

ż

e

ń

o pochodnych cz

ą

stkowych po

K

z funkcji produkcji

)

,

(

L

K

f

Q

=

i z tego,

ż

e:

k

K

Q

∂

∂

=

∂

∂

ϕ

oraz

2

2

2

2

1

k

L

K

Q

∂

∂

⋅

=

∂

∂

ϕ

.

mamy:

0

,

0

2

2

<

∂

∂

>

∂

∂

k

k

ϕ

ϕ

.

Zatem funkcja

ϕ

jest rosn

ą

c

ą

funkcj

ą

k

, ale tempo wzrostu jest malej

ą

ce.

W modelu Solowa zakłada si

ę

,

ż

e w gospodarce inwestowana jest stała cz

ęść

Q

, a wielko

ść

siły

roboczej ro

ś

nie wykładniczo, co zapisujemy w postaci warunków:

(I)

sQ

dt

dK

I

=

=

,

gdzie:

s

- stała okre

ś

laj

ą

ca kra

ń

cow

ą

skłonno

ść

do oszcz

ę

dzania

(II)

(

)

0

;

>

=

λ

λ

L

dt

dL

,

gdzie:

λ

- stopa wzrostu siły roboczej (stała).

Warunki (I) i (II) wraz z funkcj

ą

produkcji wyra

ż

on

ą

przy u

ż

yciu funkcji

ϕ

stanowi

ą

całkowity model

Solowa, czyli:

(

)



















>

=

∈

=

=

=

0

,

)

1

;

0

(

,

),

(

λ

λ

ϕ

L

dt

dL

s

sQ

dt

dK

L

K

k

k

L

Q

Podstawiaj

ą

c pierwsze równanie do drugiego otrzymujemy:

)

(k

sL

dt

dK

ϕ

=

.

dr Agnieszka Bobrowska

9

Ekonomia matematyczna II

Poniewa

ż

dana jest to

ż

samo

ść

kL

K

≡

, st

ą

d po jej zró

ż

niczkowaniu i podstawieniu do powy

ż

szej

równo

ś

ci mamy:

)

(k

sL

dt

dL

k

L

dt

dk

ϕ

=

+

.

Z trzeciego równania wiemy natomiast,

ż

e

L

dt

dL

λ

=

. Zatem ostatecznie otrzymujemy:

)

(k

sL

L

k

L

dt

dk

ϕ

λ

=

+

.

Po wyeliminowaniu wspólnego dla wszystkich elementów tego równania zmiennej

L

i odpowiednim

przekształceniu otrzymujemy równanie ró

ż

niczkowe wzgl

ę

dem

k

z dwoma parametrami

λ

,

s

:

k

k

s

dt

dk

λ

ϕ

−

=

)

(

,

b

ę

d

ą

ce podstawowym równaniem modelu Solowa.

Ze wzgl

ę

du na ogóln

ą

posta

ć

funkcji

ϕ

wyst

ę

puj

ą

cej w tym równaniu, niemo

ż

liwe jest otrzymanie

konkretnego rozwi

ą

zania i tym samym niemo

ż

liwa staje si

ę

jego analiza ilo

ś

ciowa. Mo

ż

emy jednak

dokona

ć

graficznej analizy jako

ś

ciowej równania ró

ż

niczkowego poprzez sporz

ą

dzenie wykresu linii

fazowej z

k

na osi rz

ę

dnych i z pochodn

ą

k

na osi odci

ę

tych.

Praw

ą

stron

ę

rozwa

ż

anego równania ró

ż

niczkowego mo

ż

emy potraktowa

ć

jako dwie oddzielne

funkcje

k

i narysowa

ć

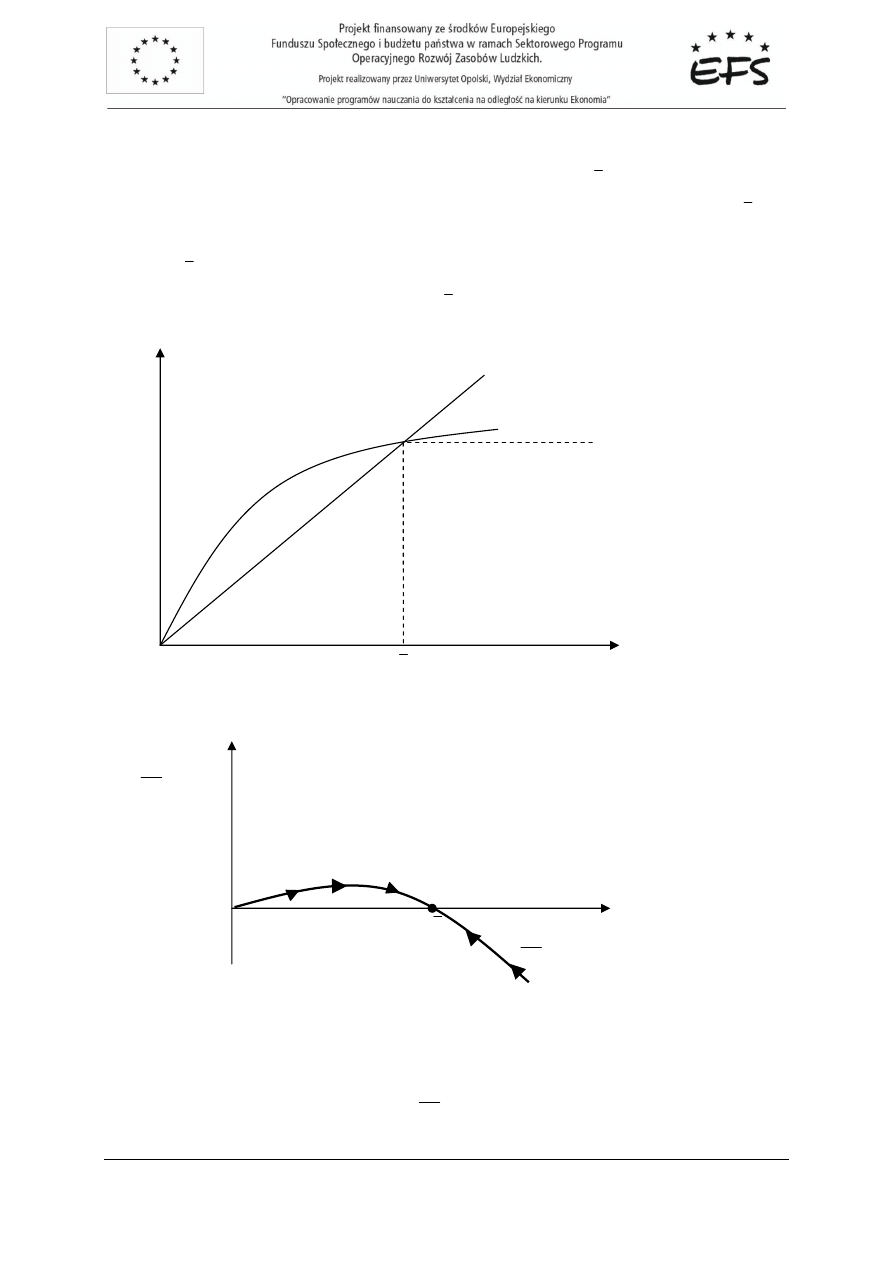
ich wykresy (rysunek 3.2.):

k

k

h

h

k

s

k

h

h

λ

ϕ

=

=

=

=

)

(

)

(

)

(

2

2

1

1

.

Wykres pierwszej funkcji ma posta

ć

krzywej rosn

ą

cej w coraz wolniejszym stopniu, co wynika

z zało

ż

e

ń

o pochodnych z funkcji

ϕ

(pami

ę

tamy przy tym,

ż

e

s

jest pewn

ą

stał

ą

). Natomiast

wykresem drugiej funkcji jest prosta przechodz

ą

ca przez pocz

ą

tek układu współrz

ę

dnych i nachyleniu

równym

λ

. Przyjmuje si

ę

,

ż

e wykresy obu funkcji przecinaj

ą

si

ę

w pewnym dodatnim punkcie, czyli

ż

e

istnieje zbiór warto

ś

ci

k

, dla których krzywa

)

(k

s

ϕ

przebiega powy

ż

ej prostej

k

λ

. Punkt przeci

ę

cia

krzywych oznaczony został na rysunku 3.2. symbolem

k

.

Dodatkowo mo

ż

na zało

ż

y

ć

,

ż

e aby efekt produkcyjny był dodatni konieczne s

ą

nakłady kapitału.

Wówczas wykres pierwszej funkcji rozpoczyna si

ę

w pocz

ą

tku układu współrz

ę

dnych. Maj

ą

c wykresy

funkcji

1

h

oraz

2

h

mo

ż

na przyst

ą

pi

ć

do sporz

ą

dzenia wykresu szukanej linii fazowej, które sprowadza

si

ę

do wyznaczenia warto

ś

ci

dt

dk

dla ka

ż

dej warto

ś

ci

k

i zaznaczenia ich na wykresie. Warto

ś

ci

dt

dk

dr Agnieszka Bobrowska

10

Ekonomia matematyczna II

otrzymujemy odejmuj

ą

c od warto

ś

ci

)

(k

s

ϕ

warto

ść

k

λ

. Szukan

ą

lini

ę

fazow

ą

przedstawia rysunek

3.3.

Zauwa

ż

my,

ż

e w punkcie, w którym proporcja kapitału i pracy wynosi

k

, czyli w punkcie przeci

ę

cia

si

ę

dwóch krzywych na rysunku 3.2., linia fazowa przecina o

ś

rz

ę

dnych, co oznacza,

ż

e

k

jest

mi

ę

dzyokresowym poło

ż

eniem równowagi dla proporcji kapitału i pracy. Nachylenie linii fazowej

w punkcie

k

jest ujemne. Wynika st

ą

d,

ż

e dla ka

ż

dej warto

ś

ci pocz

ą

tkowej

k

dynamiczny ruch

w modelu musi prowadzi do poło

ż

enia równowagi

k

, co oznacza,

ż

e jest ono stabilne.

Rys.3.2. Wykresy funkcji

1

h

i

2

h

.

.

Rys.3.3. Linii fazowa równania ró

ż

niczkowego

k

k

s

dt

dk

λ

ϕ

−

=

)

(

.

k

0

k

k

k

s

dt

dk

λ

ϕ

−

=

)

(

k

0

k

k

λ

)

(k

s

ϕ

2

1

, h

h

dt

dk

dr Agnieszka Bobrowska

11

Ekonomia matematyczna II

Wnioski:

1. Gospodarka w pewnym momencie osi

ą

gnie stan równowagi (tj. kiedy proporcja kapitału i pracy

jest stała). Aby ten stan si

ę

utrzymał, kapitał i praca musz

ą

wzrasta

ć

w tym samym stopniu, tzn.

ze stop

ą

wzrostu równ

ą

λ

(stop

ą

wzrostu siły roboczej).

2. Inwestycje netto musz

ą

rosn

ąć

z t

ą

sam

ą

stop

ą

wzrostu co kapitał, czyli ze stop

ą

λ

.

3. Produkcja

Q

wzrasta z t

ą

sam

ą

stop

ą

wzrostu co praca, o ile proporcja kapitału i pracy jest

stała (wynika to z postaci funkcji produkcji:

)

(k

L

Q

ϕ

=

).

Uwaga:

Zaprezentowana graficzna analiza jako

ś

ciowa dotyczy przypadku funkcji produkcji stałej w czasie.

(zało

ż

enie braku mo

ż

liwo

ś

ci rozwoju technologicznego).

Chc

ą

c uwzgl

ę

dni

ć

post

ę

p technologiczny, nale

ż

y odpowiednio zmodyfikowa

ć

funkcj

ę

produkcji np.

poprzez wprowadzenie funkcji zmian technologicznych

T

jako rosn

ą

cej funkcji czasu. Wówczas

funkcja produkcji mo

ż

e zosta

ć

zapisana w postaci:













>

=

0

),

,

(

)

(

dt

dT

L

K

f

t

T

Q

.

Uwzgl

ę

dnienie post

ę

pu technologicznego jest bardzo wa

ż

ne i oznacza,

ż

e dla tych samych

wielko

ś

ci

L

K ,

, wielko

ść

produkcji w chwili

t

t

>

'

b

ę

dzie wi

ę

ksza ni

ż

w chwili

t

. Poza tym na skutek

rozwoju technologii nast

ę

puje wzrost wyposa

ż

enia kapitałowego przypadaj

ą

cego na jednego

pracownika (uzbrojenia technicznego pracy), co z kolei powoduje wzrost wydajno

ś

ci pracy.

Analiza jako

ś

ciowa modelu Solowa pozwala na wyci

ą

gniecie jedynie ogólnych wniosków

dotycz

ą

cych warunków istnienia wzrostu zrównowa

ż

onego. Przyj

ę

cie w modelu okre

ś

lonej funkcji

produkcji pozwala znale

źć

konkretne rozwi

ą

zanie ilo

ś

ciowe i przeprowadzi

ć

szczegółow

ą

analiz

ę

ilo

ś

ciow

ą

.

Przyjmijmy,

ż

e funkcja produkcji jest liniowo jednorodn

ą

funkcj

ą

produkcji Cobba-Douglasa postaci:

α

α

α

α

Lk

L

K

L

L

K

Q

=













=

=

−

1

.

Sytuacj

ę

, w której produkcja

Q

, kapitał

K

, siła robocza

L

oraz inwestycje netto

I

maj

ą

identyczn

ą

stop

ę

wzrostu równ

ą

(danej) stopie wzrostu siły roboczej

λ

nazywamy

stanem

wzrostu zrównowa

ż

onego

.

dr Agnieszka Bobrowska

12

Ekonomia matematyczna II

W modelu Solowa z funkcj

ą

produkcji Cobba-Douglasa, funkcja

ϕ

przyjmuje posta

ć

α

ϕ

k

k

=

)

(

.

Wynika st

ą

d nast

ę

puj

ą

ca posta

ć

podstawowego równania modelu Solowa:

k

sk

dt

dk

λ

α

−

=

.

Po przekształceniu otrzymujemy równanie Bernoulliego wzgl

ę

dem zmiennej

k

:

α

λ

sk

k

dt

dk

=

+

.

Stosujemy zatem nast

ę

puj

ą

ce podstawienie:

α

−

=

1

k

z

.

Ró

ż

niczkuj

ą

c je obustronnie po

t

otrzymujemy:

dt

dk

k

dt

dz

α

α

−

−

=

)

1

(

.

St

ą

d:

dt

dz

k

dt

dk

α

α

−

=

1

.

Podstawiaj

ą

c ostatni uzyskany wynik do wyj

ś

ciowego równania Bernoulliego, a nast

ę

pnie

przemna

ż

aj

ą

c to równanie obustronnie przez

α

α

k

−

1

, otrzymujemy równanie ró

ż

niczkowe liniowe

niejednorodne o stałych współczynnikach

λ

α

)

1

(

−

i

s

)

1

(

α

−

o postaci:

s

z

dt

dz

)

1

(

)

1

(

α

λ

α

−

=

−

+

.

Rozwi

ą

zaniem powy

ż

szego równania jest funkcja

z

postaci:

λ

λ

λ

α

s

e

s

z

t

z

t

+









−

=

−

−

)

1

(

)

0

(

)

(

.

Wracaj

ą

c do podstawienia

α

−

=

1

k

z

otrzymujemy ostateczn

ą

posta

ć

rozwi

ą

zania równania

Bernoulliego, okre

ś

laj

ą

cego

ś

cie

ż

k

ę

czasowa dla

k

, a mianowicie:

λ

λ

λ

α

α

α

s

e

s

k

k

t

+









−

=

−

−

−

−

)

1

(

1

1

)

0

(

,

gdzie:

dr Agnieszka Bobrowska

13

Ekonomia matematyczna II

)

0

(

k

- pocz

ą

tkowa warto

ść

Chc

ą

c zbada

ć

stabilno

ść

tego rozwi

ą

zania liczymy granic

ę

z

k

, przy

∞

→

t

. Poniewa

ż

λ

α

s

k

t

=

−

∞

→

1

lim

, wi

ę

c

∞

<

=

−

∞

→

α

λ

1

lim

s

k

t

. Pokazali

ś

my zatem,

ż

e rozwi

ą

zanie jest dynamicznie

stabilne. Zatem proporcja kapitału i pracy dla stanu wzrostu zrównowa

ż

onego w modelu Solowa

z liniowo jednorodn

ą

funkcj

ą

Cobba-Douglasa wynosi

α

λ

−

1

s

. Proporcja kapitału i pracy w stanie

równowagi jest proporcjonalna do skłonno

ś

ci do oszcz

ę

dzania

s

i odwrotnie proporcjonalna do stopy

wzrostu siły roboczej

λ

.

Podsumowanie:
1. Model Harroda-Domara jest klasycznym modelem wzrostu, przedstawiaj

ą

cym

ś

cie

ż

ki czasowe

zmian kapitału i inwestycji przy zało

ż

eniu pełnego zatrudnienia w gospodarce, jakie musz

ą

wyst

ą

pi

ć

, aby gospodarka mogła si

ę

znale

źć

w stanie równowagi.

2. Wyj

ś

ciowym zało

ż

eniem w modelu Harroda-Domara jest stała relacja produkcji do kapitału przy

pełnym wykorzystaniu mocy produkcyjnych.

3. Z analizy modelu wynika,

ż

e rozwój gospodarczy odbywa si

ę

w sposób zrównowa

ż

ony tylko

wtedy, gdy faktyczna stopa wzrostu inwestycji jest równa wymaganej (wynikaj

ą

cej z modelu).

4. Model Solowa charakteryzuj

ą

mniej ostre zało

ż

enia ni

ż

model Harroda-Domara.

5. W modelu tym produkcja jest funkcj

ą

zarówno kapitału, jak i nakładów pracy, które mog

ą

by

ć

poł

ą

czone w zmiennych proporcjach, kiedy w modelu Harroda-Domara produkcja była funkcj

ą

jedynie kapitału.

6. W modelu Solowa mo

ż

na przyj

ąć

rozmaite postaci funkcji produkcji, np. rozwa

ż

an

ą

w wykładzie

funkcj

ę

Cobba-Douglasa.

7. Wyznaczona w modelu Solowa

ś

cie

ż

ka czasowa technicznego uzbrojenia pracy jest

dynamicznie stabilna.

dr Agnieszka Bobrowska

14

Ekonomia matematyczna II

Pytania kontrolne:

1. Przytocz podstawowe zało

ż

enia modelu Harroda-Domara.

2. Jaka zale

ż

no

ść

wyst

ę

puje w modelu Harroda-Domara pomi

ę

dzy inwestycjami netto a kapitałem

w chwili

t

?

3. Dlaczego, je

ż

eli w gospodarce faktyczna stopa wzrostu inwestycji ró

ż

ni si

ę

od wymaganej, to

gospodarka nie osi

ą

ga równowagi stabilnej?

4. Podaj podstawowe zało

ż

enia modelu Solowa.

5. Jak definiowane jest w modelu Solowa z funkcj

ą

produkcji Cobba-Douglasa techniczne

uzbrojenie pracy?

6. Jak rozumie si

ę

dynamiczn

ą

stabilno

ść

stanu równowagi?