MODELE WZROSTU GOSPODARCZEGO

1. Ogólne spojrzenie na różne teorie wzrostu gospodarczego

2. Model wzrostu gospodarczego R. Harroda

3. Model wzrostu gospodarczego E. Domara

4. Model wzrostu gospodarczego R. Solowa

Wszystkie teorie wzrostu gospodarczego starają się ustalić najważniejsze czynniki określające tempo wzrostu dochodu narodowego.

Modele wywodzące się z nurtu ekonomii keynesowskiej wyjaśniają wzrost dochodu narodowego na podstawie dwoistego charakteru nakładów in­westycyjnych, które: z jednej strony przyczyniają się do rozbudowy istniejących zdolności produkcyjnych, z drugiej zaś wpływają na wzrost popytu i tym sa­mym na stopień wykorzystania rozbudowanych zdolności produkcyjnych. For­mułuje się przy tym różnego rodzaju warunki, po spełnieniu których rosnący potencjał produkcji może być w pełni wykorzystywany i wzrost gospodarczy nabiera charakteru zrównoważonego. Gdy gospodarka rynkowa nie spełnia tych warunków, wówczas wzrost gospodarczy jest niestabilny przy zmieniającym się stopniu wykorzystania rosnącego potencjału produkcyjnego i niepełnym oraz zmiennym stanie zatrudnienia.

Modele wywodzące się z nurtu ekonomii neoklasycznej obejmują anali­zą wzrost dochodu narodowego nie od strony popytowo-podażowej, lecz wy­łącznie od strony podażowej. Dla ekonomii neoklasycznej nie istnieje problem niedostatecznego efektywnego popytu jako źródła niestabilności wzrostu. Czynnikami decydującymi o wzroście produkcji są przede wszystkim: podaż za­sobu kapitału, podaż pracy. Na podstawie tych dwóch czynników produkcji buduje się różnego rodzaju funkcje produkcji dla długiego okresu, które umoż­liwiają w warunkach pełnego zatrud­nienia siły roboczej analizę współzależności między: technicznym uzbrojeniem pracy, wy­dajnością pracy, kapitałochłonnością produkcji. Wywodzą się one bądź bezpośrednio z funkcji produkcji typu Cobba-Douglasa, bądź też stanowią jej istotną modyfikację.

Atrakcyjność tych postaci funkcji produkcji wynika stąd, iż: opierają się one na neoklasycznej teorii produkcyjności czynników wytwórczych, stanowią dobrą podstawę do budowania różnych modeli wzrostu gospo­darczego, są wykorzystywane w badaniach empirycznych na szczeblu mikro-, i makroekonomicznym. Stwarzają one w ten sposób metodologiczne podstawy do empirycznego potwierdzenia słuszności teorii produkcyjności czynników wytwórczych.

Modele wzrostu wywodzące się zarówno z nurtu keynesowskiego, jak i z wieloczynnikowej funkcji produkcji opierają się na analizie agregatowej, która nie uwzględnia ważnych aspektów współzależności między strukturą gos­podarki narodowej a dynamiką wzrostu gospodarczego.

Istnieje duża grupa modeli wzrostu gospodarcze­go, w których: struktura ekonomiczna jest jednym z głównych wyznaczni­ków ścieżki wzrostu, dynamicznie pojmowane proporcje rozwojowe - zmien­ną decyzyjną. Struktura produkcji wynika z przyjętego układu preferencji spo­łecznych wyznaczających - niezależnie od technologii - docelowy wzorzec konsumpcji i produkcji. Gospodarce zmierzającej do zmiany struktury w dłuż­szym czasie opłaca się tak kształtować proporcje produkcji, aby zapewnić najwyższą stopę wzrostu gospodarczego. Strukturalna analiza wzrostu jest o wiele bardziej złożona i wymaga bar­dziej skomplikowanego aparatu matematycznego niż jakikolwiek model agregatowy.

2. Model wzrostu gospodarczego R. Harroda

Ekonomista angielski, Roy Harrod, wykorzystał keynesowską interpretację współzależności między inwestycjami a oszczędnościami i przekształcił w proste równanie tempa wzrostu dochodu narodowego.

W tym celu obie strony równości I = Os podzielił przez dochód narodowy Y, do tej nowej równość wprowadził niezwykle ważną relację między wydatkami inwestycyjnymi I a przyrostem dochodu narodowego ΔY. Relacja ta została nazwana przyrostową kapitałochłonnością produkcji i uznana za najważniejszy wkład R. Harroda do teorii ekonomii.

W zapisie formalnym można to ująć w następujące równania:

lub

stąd

gdzie:

- tempo wzrostu dochodu narodowego,

- udział oszczędności w dochodzie narodowym, który wyraża przeciętną i krańcową skłonność do oszczędzania,

- krańcowy współczynnik kapitałochłonności produkcji mierzony wielkością nakładu inwestycyjnego na jednostkę przyrostu dochodu narodowego.

Równanie wzrostu Harrod zapisał w następującej postaci: Załóżmy, że stopa skłonności do oszczędzania wynosi = 0,15, zaś współczynnik kapitałochłonności k = 3, wówczas tempo wzrostu dochodu narodowego będzie się równać Gf= 0,05, czyli 5% rocznie.

Analiza mecha­nizmu wzrostu

Ta stopa wzrostu jest dopiero punktem wyjścia do analizy samego mecha­nizmu wzrostu i sama w sobie jeszcze niczego nie wyjaśnia.

Harrod sformułował faktyczną stopę wzrostu Gf, naturalną stopę wzrostu, oznaczoną Gn gwarantowaną stopę wzrostu, oznaczoną Gw.

Naturalna stopa wzrostu gospodarczego Gn jest określona przez dwa podstawowe czynniki: stopę przyrostu naturalnego, która w długim okresie de­cyduje o stopie podaży siły roboczej β, oraz postęp techniczny, który decyduje o stopie wzrostu wydajności pracy λ . Stąd: Gn = β + λ Gn jest zatem miarą potencjalnych możliwości wzrostu danej gospodarki narodowej, określonych przez naturalne czynniki związane z przyrostem natu­ralnym ludności oraz możliwym postępem technicznym.

Gwarantowana stopa wzrostu gospodarczego Gw, wyraża wzrost docho­du narodowego przy pełnym wykorzystaniu istniejących zdolności produkcyj­nych gospodarki narodowej. Jest to ścieżka zrównoważonego wzrostu. Jeśli zo­stanie osiągnięta, wówczas wywoła wśród przedsiębiorców i chęć dalszego utrzymania się na tej ścieżce wzrostu, gdyż popyt na ich produkty będzie wystarczający, aby zapewnić pełne wykorzystanie zdolności produkcyjnych ich przedsiębiorstw.

Harrod założył, że: pełne wykorzystanie zdolności produkcyj­nych gospodarki narodowej nie musi być równoznaczne z pełnym zatrudnie­niem siły roboczej, jeśli w przeszłości aparat wytwórczy rozwijał się w tempie niewystarczającym do wchłonięcia wszystkich potencjalnych rezerw siły robo­czej. Stąd możliwe są rozbieżności między Gw oraz Gn.

Rozpatrzmy trzy podstawowe przypadki: przypadek pierwszy, gdy wszystkie stopy wzrostu są sobie równe, przypadek drugi, gdy faktyczna stopa wzrostu odchyla się w dół od stopy gwarantowanej, przypadek trzeci, gdy faktyczna stopa wzrostu odchyla się w górę od stopy gwarantowanej.

Przypadek pierwszy, gdy: Gw=Gf=Gn,

Równość trzech stóp wzrostu wyraża stan równowagi dynamicznej. Fak­tyczna stopa wzrostu Gf kształtuje się na poziomie zapewniającym: pełne wykorzystanie rosnących zdolności produkcyjnych, ale także pełne za­trudnienie rosnących zasobów siły roboczej. Interpretując równość tych trzech stóp wzrostu w kategoriach ekonomii keynesowskiej, można inaczej powie­dzieć, że społeczeństwo tyle oszczędza ze swojego dochodu, zaś przedsiębiorcy tyle inwestują, ile jest niezbędne do stworzenia agregatowego popytu, określającego pełne wykorzystanie istniejących możliwości produkcyjnych i pełne zatrudnienie siły roboczej. I = S Oszczędności są stałą częścią dochodu narodowego, zaś inwestycje zależą od stopy wzrostu dochodu narodowego. Jak długo inwestuje się tyle ile się oszczędza z rosnącego dochodu narodowego przy pełnym wykorzystaniu istniejących czynników produkcji, gospodarka znajduje się na wąskiej ścieżce równowagi.

Jest to jednak równowaga niestabilna, gdyż jakiekolwiek odchyle­nie faktycznej stopy wzrostu od stopy gwarantowanej uruchamia mechanizmy pogłębiające zaistniały stan nierównowagi, a nie mechanizmy przywracające równowagę.

Owa niestabilność wynika z uzależnienia decyzji inwestycyjnych przedsiębiorców od faktycznej stopy wzrostu dochodu narodowego, która w gospodarce rynkowej nigdy nie rośnie równomiernie, lecz podlega różnym i nieregularnym wahaniom.

Wraz z tym wahają się także wydatki inwestycyjne i inne składniki agregatowego popytu. Rozpatrzmy przypadek drugi, gdy: Gw < Gf < Gn. Odchylenie faktycznej stopy wzrostu poniżej gwarantowanej stopy wzro­stu uruchamia mechanizm depresyjny. Gwarantowana stopa wzrostu jest wy­rażona równaniem: gdzie kw oznacza wymagany współczynnik kapitałowy, tj. niezbędną sumę inwestycji do przyrostu dochodu narodowego, który zapewni pełne wykorzysta­nie rosnących zdolności produkcyjnych. Skoro Gw > Cf tzn. że: Ponieważ s = s, to nierówność będzie spełniona, jeśli k > kw. Oznacza to, że faktyczny współczynnik kapitałochłonności k jest większy od wymagane­go kw, gdyż zaczynają gromadzić się nie sprzedane zapasy towarów. Obniżana stopa wzrostu dochodu narodowego powoduje zmniejszenie wydatków inwes­tycyjnych w stosunku do nagromadzonych oszczędności. Zmniejszy się efek­tywny popyt i nie sprzedane zapasy towarów jeszcze bardziej pogłębiają spadek inwestycji. Pojawiają się i coraz bardziej rosną nie wykorzystane zdol­ności produkcyjne, a wraz z tym zwiększa się bezrobocie. Faktyczna stopa wzrostu Gf staje się więc coraz mniejsza w stosunku do naturalnej stopy wzrostu Gn.

Inwestycje dzielą się na dwie kategorie, tj. na inwestycje indukowane, czyli zależne od wzrostu dochodu narodowego, inwestycje autonomiczne, niezależne od poziomu dochodu narodowego, związane z długofalowym postę­pem technicznym w gospodarce narodowej.

Wraz ze spadkiem stopy wzrostu dochodu narodowego kurczą się jedynie inwestycje indukowane. Dolną granicą spadku dochodu narodowego są więc inwestycje autonomiczne oraz autono­miczny poziom wydatków konsumpcyjnych, które są niezależne od wytwarza­nego dochodu narodowego. Harrod nie wyjaśnił w swoim modelu wzrostu dy­namicznego, jakie czynniki i jakie mechanizmy są w stanie odwrócić spadkową tendencję dochodu narodowego i inwestycji oraz zapewnić gospodarce rynko­wej ponowne wejście w fazę wzrostu gospodarczego.

Rozpatrzmy wobec tego przypadek trzeci, w którym: Gw < Gf ≤ Gn. Z nierówności tych wynika, że Gw < Gn. Oznacza to, że ścieżka wzrostu przy pełnym wykorzystaniu zdolności produkcyjnych leży poniżej ścieżki wzrostu wyznaczonej przez potencjalne rezerwy siły roboczej oraz postęp tech­niczny. Istnienie tych rezerw umożliwia podniesienie faktycznej stopy wzro­stu Gf powyżej dotychczasowej ścieżki wzrostu przy pełnym wykorzystaniu istniejących zdolności produkcyjnych Gw. W tym przypadku uzyskujemy nie­równość typu: czyli kw>k. Faktyczny współczynnik kapitałowy k staje się mniejszy od współczynni­ka wymaganego kw, gdyż występuje zjawisko zmniejszania się stanu zapasów w gospodarce narodowej w stosunku do wymaganych ich wielkości (zalicza­nych w teorii keynesowskiej także do inwestycji). Wyższa stopa wzrostu do­chodu narodowego pobudzi zwiększone wydatki inwestycyjne ponad zwięk­szone oszczędności, co będzie prowadziło do wzrostu globalnego popytu i wzrostu zatrudnienia. Tej fazie wzrostu będzie towarzyszył inflacyjny wzrost cen. Górną granicą wzrostu gospodarczego jest Gn, gdyż faktyczne tempo wzrostu dochodu naro­dowego nie może przewyższać możliwości określonych przez podaż siły robo­czej oraz przez postęp techniczny.

Od stosunku Gf do Gw zależy odpowiedź na pytanie, czy gospodarka rynkowa będzie się rozwijała: w kierunku pełnego zatrudnienia siły roboczej, w kierunku stagnacji przy rosnącym bezrobociu i zmniejszającym się stopniu wykorzystania istnie­jących zdolności produkcyjnych,

R. Harrod w swoim modelu ograniczył się do analizy sił pogłębiających zaistniałe stany odchylenia Gf od Gw, natomiast nie uzasadnił długofalowego trendu wzrostu gospodarczego. postęp techniczny określił jedynie jako poten­cjalny wzrost gospodarczy, reprezentowany przez Gn, który nie wywierał żadne­go wpływu na faktyczną stopę wzrostu Gf.

3. Model wzrostu gospodarczego E. Domara

E. Domar uwzględnił dwa aspekty nakładów inwestycyjnych: popytowy, podażowy.

ASPEKT POPYTOWY - jest związany z wydatkami inwestycyjnymi, które tworzą rynek zbytu na dobra inwestycyjne. Te wydatki po pewnym okresie zwiększają zdolności produkcyjne gospodarki i tym samym tworzą możliwości zwiększenia podaży produkcji.

Stawia on wówczas pytania: jak powinny rosnąć inwestycje i dochód narodowy, aby rosnące zdolności produkcyjne dzięki tym inwestycjom mogły być nadal w pełni wykorzystane?

Przyjmuje założenie: skłonność do oszczę­dzania jest stała, gospodarka narodowa w punkcie wyjściowym funkcjonuje w warunkach pełnego zatrudnienia i pełnego wykorzystania zdolności produkcyjnych, nie uwzględnia on ani salda handlu zagranicznego, ani wydatków rządo­wych,

Proces tworzenia nowych zdolności produkcyjnych w wyniku działalności inwestycyjnej wyraża on równaniem: ΔYz = I * δ gdzie: ΔY - przyrost zdolności produkcyjnych, δ- potencjalna produkcyjność inwestycji mierzona stosunkiem potencjalne­go przyrostu dochodu narodowego ΔYp do poniesionych nakładów inwe­stycyjnych I.

Wymagany popyt, który decyduje o wykorzystaniu rosnących zdolności produkcyjnych, wyrażony jest równaniem: gdzie: ΔYp - potencjalny przyrost dochodu narodowego, ΔI - przyrost wydatków inwestycyjnych, - odwrotność krańcowej skłonności do oszczędzania, która z założenia jest sta­ła i określa wielkość mnożnika inwestycyjnego mi.

Z teorii Keynesa wynika, że wzrost inwestycji ΔI tylko za pośrednictwem mnożnika inwestycyjnego mi, wpływa na wzrost dochodu narodowego ΔY. Jeśli inwestycje będą stałe, czyli nie będzie przyrostu wydatków inwestycyjnych, wówczas nie będzie także przyrostu dochodu narodowego. Pojawiają się wtedy nie wykorzystane zdolności produkcyjne oraz bezrobocie.

Warunkiem wzrostu gospodarczego przy pełnym wykorzystaniu zdolności produkcyjnych i pełnym zatrudnieniu siły roboczej jest spełnienie równości: I * δ= ΔY

To sprowadza się do równania ΔYz = ΔYp, tzn., że dochód rośnie w takich roz­miarach, w jakich rosną zdolności produkcyjne gospodarki narodowej.

Powyższe równanie można również zapisać w postaci: ΔY/I = δ*α

W modelu Domara zakłada się: stałe tem­po wzrostu nakładów inwestycyjnych, które równa się stałemu tempu wzrostu dochodu narodowego. przy jednakowym tempie wzrostu nakładów inwesty­cyjnych roczne przyrosty inwestycji ΔI muszą być coraz wyższe, współczynnik skłonności do oszczędzania jest stały, stała jest także potencjalna produk­cyjność inwestycji.

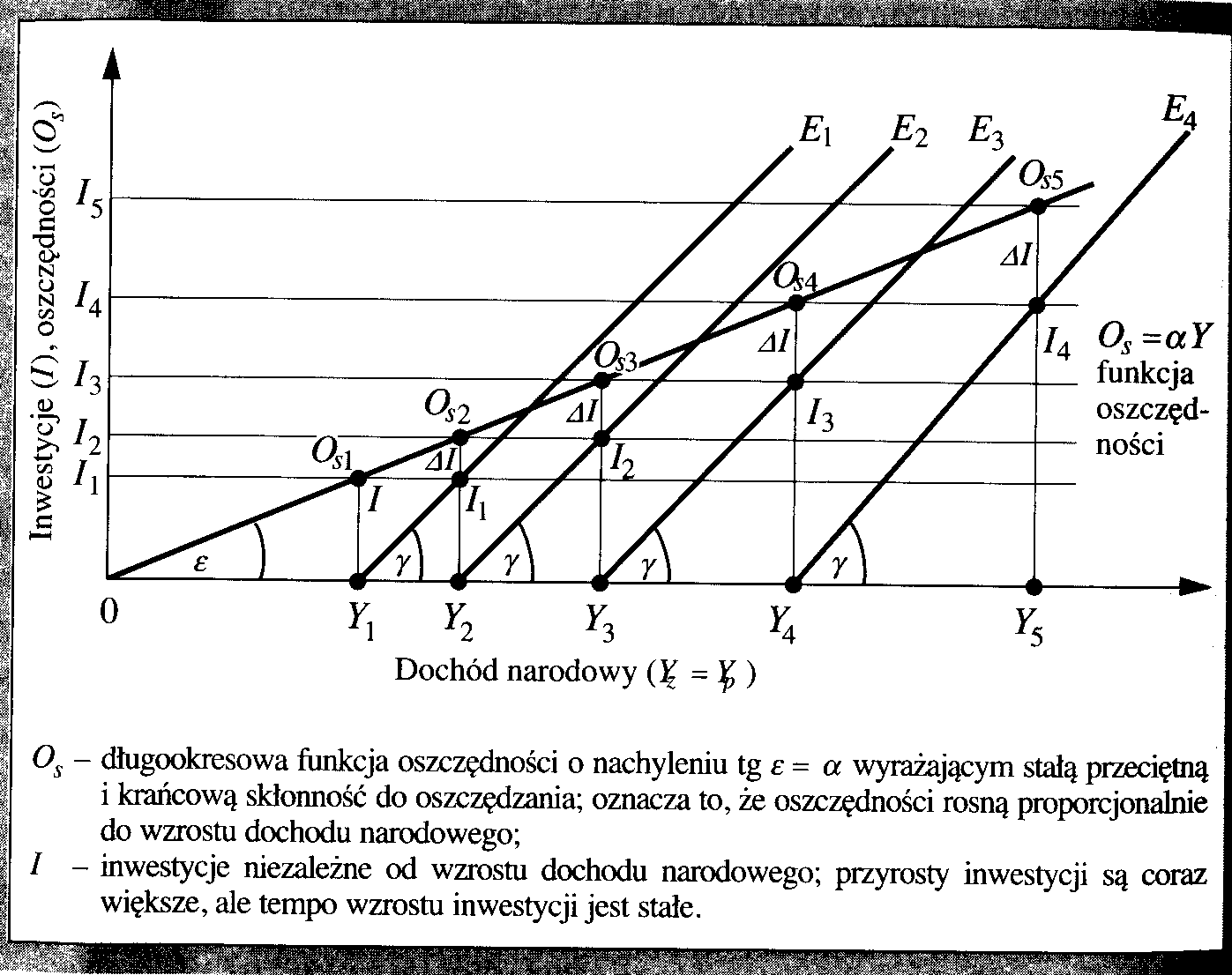
Kąt nachylenia linii E^1, E^2, E^3, do osi Y wyraża stosunek nakładów in­westycyjnych do przyrostu dochodu narodowego. Stosunek ten jest miarą krań­cowego współczynnika kapitałochłonności produkcji k, a jego odwrotność jest potencjalną produkcyjnością inwestycji, Przy dochodzie narodowym Y1 gospodarka znajduje się w stanie równowa­gi przy pełnym zatrudnieniu i pełnym wykorzystaniu zdolności produkcyj­nych. Wówczas I = 0S1.

Te rozmiary inwestycji powiększają zdolności produkcyjne gospodarki narodowej, które będą wykorzy­stane pod warunkiem, że nastąpi przyrost wydatków inwestycyjnych ΔI (reprezentowanych odcinkiem I1 0S2.) Wówczas nakłady inwestycyjne w rozmiarach I2 zrównają się z oszczędnościami 0S2.

TEN MECHANIZM SIĘ POWTARZA!

Schemat ilustrujący wpływ inwestycji na wzrost zdolności produkcyjnych i wzrost dochodu narodowego w granicach potencjalnych możliwości

W ten sposób działa w modelu Domara mechanizm wzrostu inwestycji, dochodu narodowego oraz oszczędności przy stałych parametrach Wa­runki przyjęte w punkcie wyjściowym, dotyczące pełnego wykorzystania zdol­ności produkcyjnych oraz pełnego zatrudnienia siły roboczej, zostają spełnio­ne. Rosnące proporcjonalnie do dochodu narodowego oszczędności będą wchłonięte przez odpowiadające im inwestycje i gospodarka przez cały czas rozwija się w stanie równowagi ogólnej.

Na tej podstawie Domar wyciąga ważny wniosek praktyczny

Gos­podarka rynkowa musi ciągle zwiększać inwestycje, jeśli ma rosnąć dochód narodowy. Wraz z tym będzie rosło zatrudnienie i tylko w ten spo­sób można uniknąć bezrobocia. Ten warunek nie jest jednak spełniony, gdyż inwestycje w prywatnej gospodarce nie mogą rosnąć w nieskończoność. Dla­tego w rzeczywistym świecie mamy do czynienia zarówno z niepełnym wykorzystaniem zdolności produkcyjnych, jak i niepełnym zatrudnieniem siły roboczej. Wydatki na inwestycje prywatne powinny być wspierane i uzupełniane wydatkami rządowymi finansowanymi z budżetu państwa.

4. Model wzrostu gospodarczego R. Solowa

Zmierzenie wkładu poszczególnych przyczyn we wzrost gospodarczy wymaga dokładniejszego wyjaśnienia sposobu, w jaki dochodzi do zwiększenia się produkcji. Umożliwia to np. bardzo popularny w drugiej połowie XX w. model wzrostu Roberta Solowa.

Do opisu wzrostu gospodarczego służy Solowowi tzw. makroekonomiczna funkcja produkcji: Makroekonomiczna funkcja produkcji opisuje związek ilości zużywanych czyn­ników produkcji z wielkością produkcji. Q = F(L, C, T). Opisuje ona związek ilości zużywanych: pracy, L, kapitału, C, i stanu technologii, T, z wielkością produkcji, Q. (Dla uproszczenia dalej przyjmiemy, że dostępna ilość ziemi w gospodarce jest stała).

Dzieląc makroekonomiczną funkcję produkcji stronami przez wielkość nakładu pracy, L, możemy jej nadać następującą formę: y = A • f(k) gdzie: y - wielkość produkcji przypadająca na 1 zatrudnionego (y = Q/L), A - stała, której zmiany ilustrują wzrost produkcyjności pracy spowodowany zmianami technologii, k - ilość kapitału rzeczowego przypadająca na 1 zatrudnionego, czyli jego uzbrojenie techniczne (k = C/L).

Solow zakłada, że wzrost ilości kapitału przypadającej na 1 zatrudnionego powoduje coraz wol­niejszy przyrost przypadającej na tego zatrudnionego porcji produkcji, (prawo malejącej wydajności krańcowej)

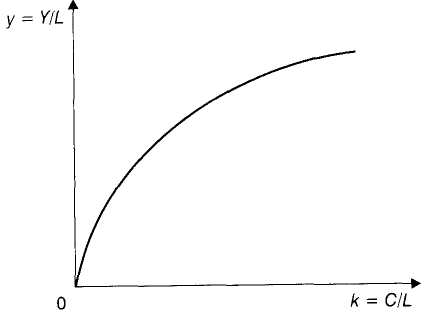
Na rysunku widzimy wykres makroekonomicznej funkcji produkcji określonej wzorem:

y = A • k^α,

α - opisuje wpływ wzrostu nakładu kapitału przypadającego na 1 zatrud­nionego na produkcyjność pracy.

Makroekonomiczna funkcja produkcji

Według Solowa wzrostowi gospodarczemu towarzyszą malejące przychody. Zwiększanie ilości kapitału przypadającej na 1 zatrudnionego powoduje coraz mniejsze przyrosty wielkości produkcji przypadającej na 1 zatrudnionego. Wykres ten jest „gasnący": zwiększaniu technicznego uzbrojenia pra­cy towarzyszy coraz wolniejszy wzrost produkcyjności pracy, co odzwierciedla właśnie działanie pra­wa malejących przychodów.

Solow oszacował makroekonomiczną funkcję produkcji dla Stanów Zjednoczonych. Z jego obli­czeń wynika reguła 1/3. zgodnie z którą zwiększenie nakładu kapitału, k, o 1% powoduje wzrost stopy wzrostu PKB, y, o 1/3 punktu procentowego. Solow posługiwał się k i y nie w ujęciu „na 1 zatrudnionego", lecz w ujęciu „na godzinę pracy".

Ustalenia te są ważne praktycznie, ponieważ pozwalają cenić siłę z jaką działają poszczególne przyczyny wzrostu. Przyjmijmy np. że ilość kapitału na godzinę pracy rośnie w Stanach Zjednoczonych w tempie 6% rocznie, a realny PKB na godzinę pracy przyrasta o 5% na rok. Reguła 1/3 mówi wówczas, że w Stanach Zjednoczonych wzrost ilości kapitału odpowiada za 2 p.p. stopy wzrostu PKB. co oznacza, iż uzasadnieniem reszty (jest to tzw. reszta Solowa), czyli 5-2 p.p. stopy wzrostu, jest zmiana technologiczna.

MECHANIZM WZROSTU GOSPODARCZEGO

Solow wykazuje, że gospodarka samoczynnie osiąga stan wzrostu zrównoważonego (ang. steady stete). Wzrost zrównoważony - to sytuacja, w której produkcja, Y, ilość pracy, L, i ka­pitału, C, zwiększają się w tempie równym tempu wzrostu liczby ludności. Zauważmy, że jeśli wzrost jest zrównoważony, to produkcyjność pracy, y = Y/L, i techniczne uzbrojenie pracy, k = C/L, są stałe.

W zrozumieniu poglądów Solowa pomoże rysunek.

• Na osi poziomej mierzymy tech­niczne uzbrojenie pracy, k = C/L.

• Na osi pionowej umieszczono aż cztery zmienne uzależnione od po­ziomu technicznego uzbrojenia pracy, k:

1. produkcyjność pracy, y = Y/L;

2. oszczędności przypadające na 1 zatrudnionego, s • y, gdzie s stanowi parametr opisujący skłonność mieszkańców do oszczędzania;

3. rzeczywiste inwestycje przypadające na 1 zatrudnionego, ΔC/L,

4. oraz inwestycje przypadające na 1 zatrudnionego zapewniające wzrost zrównoważony (ΔC/L)_E

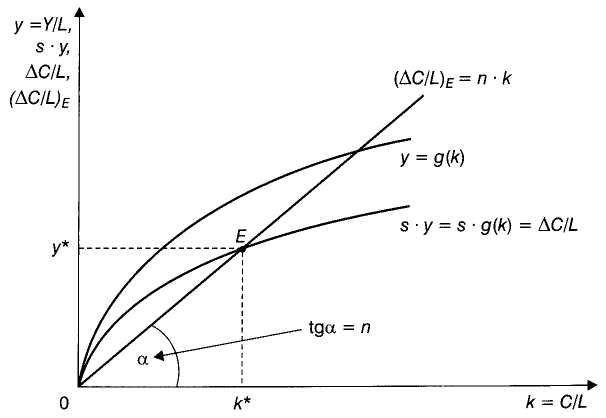
Gospodarka samoczynnie osiąga stan wzrostu zrównoważonego

Gospodarka samoczynnie wchodzi na ścieżkę wzrostu zrównoważonego. Jedno z dwojga: k<k* → s • y> n • k →k↑; lub k >k* → s • y < n • k → k↓.

Oczywiście produkcyjność pracy, y = Y/L, zależy od technicznego uzbrojenia pracy, k = C/L, w sposób opisany makroekonomiczną funkcją produkcji (na rysunku: y = g(k)).

Oszczędności przypadające na 1 zatrudnionego, s • y, są stałą częścią wartości produkcji przypadającej na 1 zatrudnionego, y = Y/L, wyznaczoną przez parametr s. Rzeczywista wielkość inwestycji przypadająca na 1 zatrudnio­nego, ΔC/L, jest równa oszczędnościom przypadającym na 1 zatrudnionego, s • y. (Jesteśmy w gospo­darce bez państwa i handlu zagranicznego, więc inwestycje równają się oszczędnościom).

Wreszcie, na mocy definicji, wzrost jest zrównoważony tylko wtedy, gdy tempo wzrostu ilości kapitału, ΔC/C jest równe tempu wzrostu ilości pracy, ΔL/L: ΔC/C = ΔL/L; wielkości te zrównują się na poziomie w; znaczonym przez tempo wzrostu liczby ludności.

Zapewniający trwanie wzrostu zrównoważonego poziom inwestycji przypadających na 1 zatrudnionego (ΔC/L)E równa się iloczynowi tempa wzrostu zatrudnienia, n, i technicznego uzbrojeń pracy, k: (ΔC/L)E = n • k. Przecież jeśli: ΔC/L = AΔL/L -C/L = n • k, to: ΔC/C = ΔL/L Wynika stąd, że związek wielkości inwestycji przypadającej na 1 zatrudnionego, która zapewni wzrost zrównoważony (ΔC/L)E, i poziomu technicznego uzbrojenia pracy, k, ma charakter liniowy (tempo wzrostu zatrudnienia, n, jest stałe).

Zakładane przez Solowa malejące przychody z kapitału sprawiają, że w miarę zwiększania się technicznego uzbrojenia pracy, k, produkcyjność pracy, y, wzrasta najpierw szybko, a potem coraz wolniej. W takiej sytuacji zwykle istnieje tylko jeden poziom technicznego uzbrojenia pracy, k, przy którym rzeczywisty poziom inwestycji przypadających na 1 zatrudnionego, ΔC/L = s • y = s • g(k), osiąga wysokość zapewniającą wzrost zrównoważony (ΔC/L)E. Na rysunku chodzi o poziom technicznego uzbrojenia pracy, k*, który odpowiada punktowi E.

Jak się okazuje, gospodarka automatycznie osiąga wzrost zrównoważony.

Powiedzmy, że rzeczywisty poziom technicznego uzbrojenia pracy, k, jest niższy od tego poziomu, przy którym wzrost jest zrównoważony, k*. Odpowiadające rzeczywistemu poziomowi technicznego uzbrojenia pracy rzeczywiste oszczędności i rzeczywiste inwestycje przypadające na 1 zatrudnionego przewyższają wtedy poziom inwestycji zapewniający zrównoważenie wzrostu (ΔC/L > n • k). Przecież za sprawą prawa malejących przychodów dla względnie niskich poziomów technicznego uzbrojenia pracy, produkcja na 1 zatrudnionego, a zatem również rzeczywiste oszczędności i rzeczywiste inwestycje przypadające na 1 zatrudnionego wzrastają bardzo szybko. Sprawia to, że dochodzi do wzrostu technicznego uzbrojenia pracy, k. Przecież inwestycje są większe od tych, które zapewniają stałość k.

W ujęciu symbolicznym: k < k* → s • y > n • k → k↑

Odwrotnie, kiedy rzeczywiste uzbrojenie pracy, k, przewyższa poziom, przy którym wzrost jest zrównoważony, k*, rzeczywiste oszczędności i rzeczywiste inwestycje przypadające na 1 zatrudnionego są mniejsze od inwestycji zapewniających wzrost zrównoważony (ΔC/L <n • k). Sprawia to, że dochodzi do spadku technicznego uzbrojenia pracy, k (inwestycje są mniejsze od tych, które zapewniają stałość k) Zapis symboliczny wygląda tym razem następująco: k > k* → s • y < n • k → k↓.

Przecież.

Czy zwiększenie oszczędności i technicznego uzbrojenia pracy zapewni trwałe przyśpieszenie tempa wzrostu? Zdaniem Solowa odpowiedź na to pytanie brzmi „nie".

Sytuację taką widzimy na rysunku. Wzrost skłonności do oszczędzania z i do s przesunął tu w górę wykres funkcji oszczędności z położenia s • y do położenia s' • y. Wraz z oszczędnościami zwiększyły się również inwestycje przypadające na 1 zatrudnionego. Wzrost zrównoważony trwa teraz w punkcie £,, a nie w punkcie E, jak do tej pory, przy wyższym poziomie technicznego uzbrojenia pracy, £,, a nie kQ. (Pamiętamy, że u Solowa gospodarka automatycznie osiąga wzrost zrównoważony). Nadal jednak mamy do czynienia ze wzrostem w tempie równym tempu wzrostu liczby ludności co oznacza, że nie doszło do trwałego przyśpieszenia wzrostu gospodarczego.

Próba przyśpieszenia wzrostu metodą zwiększania oszczędności i technicznego uzbrojenia pracy osta­tecznie kończy się powrotem do wzrostu z szybkością wyznaczoną tempem powiększania się liczby lud­ności.

Rysunek

Zwiększenie oszczędności i technicznego uzbrojenia pracy zapewnia jedynie przejściowe

przyśpieszenie wzrostu

A co dzieje się w trakcie okresu, w którym techniczne uzbrojenie pracy zwiększa się z poziomu k₀ do poziomu k₁, a nie po jego zakończeniu? Otóż zwiększanie się ilości kapitału, którą dysponuje prze­ciętny pracownik, powoduje wtedy dodatkowe przyrosty wielkości produkcji ponad te, które są spo­wodowane zwiększaniem się liczby pracujących. Oznacza to przyśpieszenie wzrostu gospodarczego. Efekt ten zanika dopiero po powrocie przez gospodarkę na ścieżkę wzrostu zrównoważonego w punk­cie Ex.

Opłacalność takiej operacji przyśpieszenia tempa wzrostu gospodarczego jest sprawą otwartą. Jej ocena wymaga porównania odpowiednich korzyści i strat. Korzyścią jest chwilowe przyśpieszenie wzrostu, które sprawia, że dalszy wzrost zrównoważony odbywa się od względnie wyższego poziomu PKB i daje stosunkowo większe przyrosty produkcji. Kosztem jest przejściowe zmniejszenie tempa wzrostu konsumpcji, stanowiące nieuchronną cenę zwiększenia oszczędności i inwestycji.

Zob. E. Domar, Szkice z teorii wzrostu gospodarczego. Warszawa 1962.

10

---