4W15

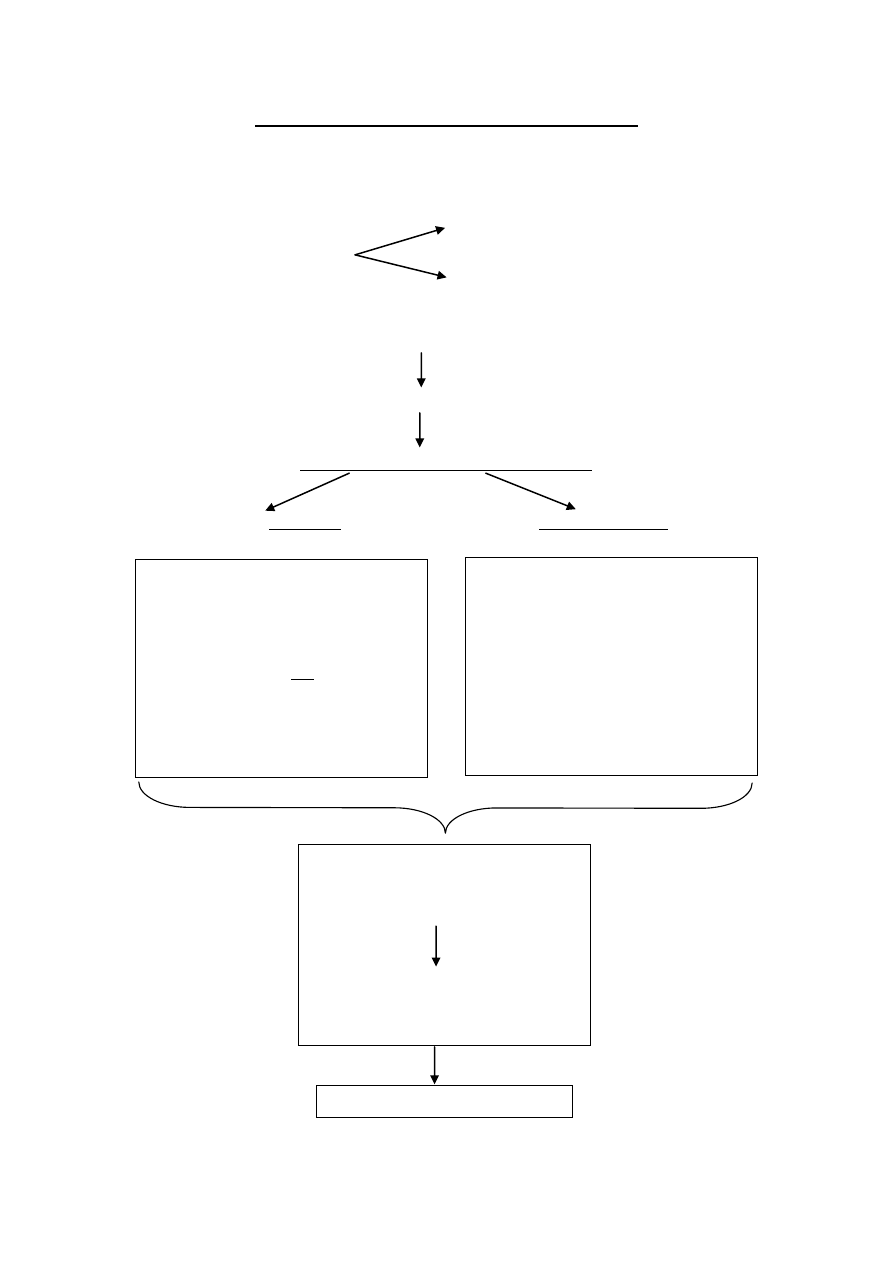
Skutki skończonej długości słowa binarnego

Precyzja -

odległość pomiędzy kolejnymi reprezentowanymi wartościami liczbowymi.

Zakres dynamiki -

różnica pomiędzy największą i najmniejszą wartością reprezentowaną.

nieskończona precyzja

Rzeczywiste sy

gnały analogowe

nieskończony zakres dynamiki

Konwersja analogowo-cyfrowa

Sygnał cyfrowy

Skończona długość słowa binarnego

określona precyzja

określony zakres dynamiki

Skończona liczba wzorców

bitowych, czyli skończona liczba

wartości, które reprezentuje

słowo binarne.

Ograniczona różnica pomiędzy

największą i najmniejszą

reprezentowaną wartością.

Ograniczona

rozdzielczość

reprezentacji.

błąd kwantyzacji

n

E

q

2

1



szum kwantyzacji

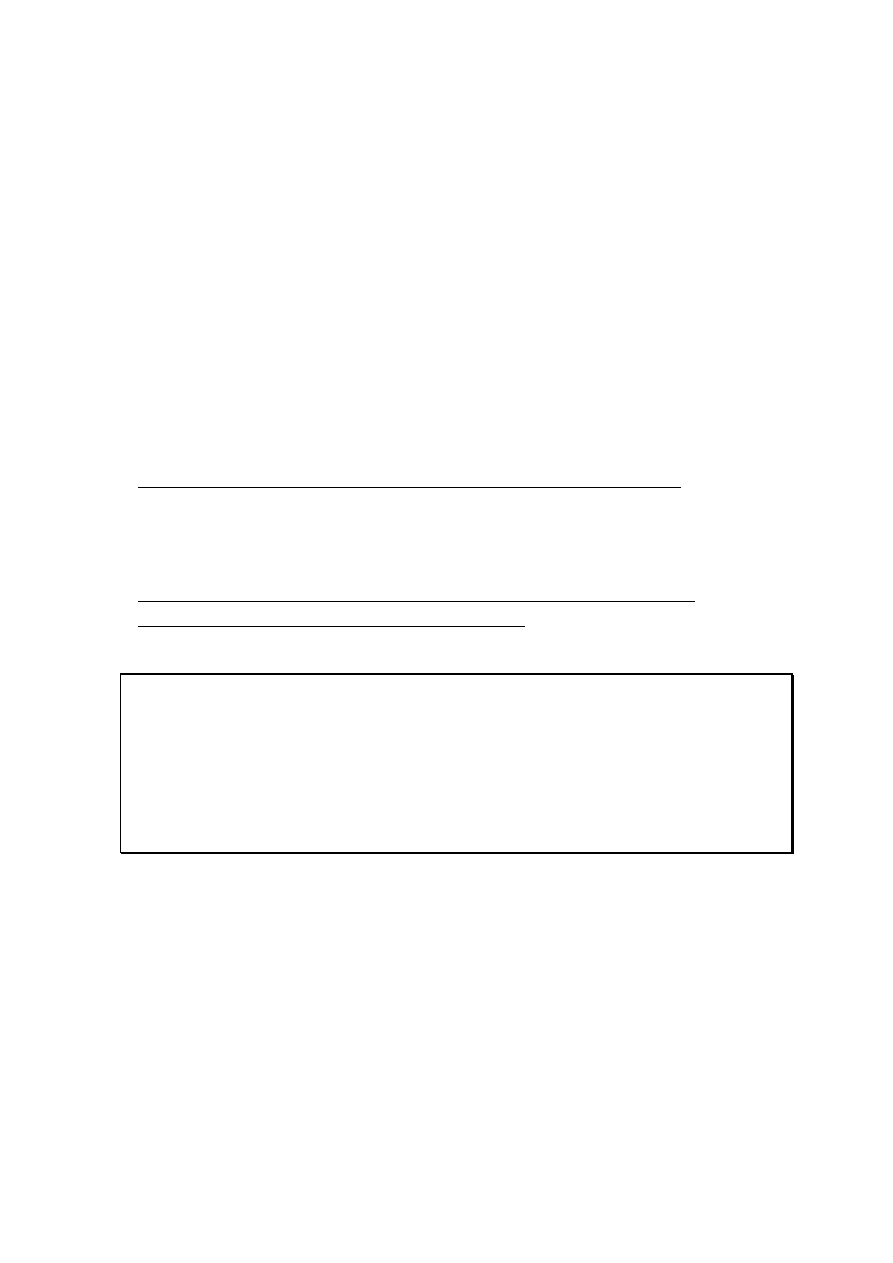
Procesor DSP

Zakres dynamiki procesora

Precyzja reprezentacji

Szum kwantyzacyjny

obliczeń arytmetycznych

Rezultaty przetwarzania

4W16

Ograniczona precyzja reprezentacji liczb i zakres dynamiki procesora dają efekty
w postaci:

 błędów kwantyzacji powstałych podczas operacji arytmetycznych.

Błąd zaokrąglenia występuje za każdym razem kiedy wprowadzana lub
generowana liczba po obliczeniach matematycznych wymaga zaokrąglenia do
najbliższej wartości, która może być reprezentowana przez dany format.
Wówczas musi być zaokrąglona, w górę lub w dół, o maksimum połowę
odstępu między liczbami (połowę kroku kwantyzacji).
Błąd obcięcia powstaje w wyniku odrzucania (obcinania) mniej znaczących
bitów rezultatu operacji arytmetycznej, leżących poza
n-bitowym słowem binarnym reprezentacji.

Występowanie błędów kwantyzacji w operacjach arytmetycznych powoduje
dodawanie szumu do sygnału – szumu kwantyzacji.
Im większa precyzja zapisu tym skutki tych błędów są mniejsze.

 możliwości przepełnienia. Kiedy rezultat operacji arytmetycznej jest większy

niż największa dodatnia lub ujemna wartość reprezentowana przez format
pojawia się przepełnienie i utrata poprawnego rezultatu.

Im większy zakres dynamiki procesora tym większa odporność na
przepełnienie i większy stosunek sygnał szum.

Zakres dynamiki procesora powinien być na tyle duży względem zakresu
dynamiki sygnału wejściowego, żeby szum generowany przez operacje
arytmetyczne, w wyniku błędów kwantyzacyjnych spowodowanych
skończoną precyzją reprezentacji, leżał poniżej poziomu szumu wejściowego
sygnału cyfrowego.
Zakres dynamiki procesora nie powinien ograniczać dynamiki sygnału.

4W17

Zakres dynamiki reprezentacji stało- i zmiennoprzecinkowej
Zakres dynamiki można wyrazić w decybelach, korzystając z wyrażenia

















slowa

wartość

a

najmniejsz

slowa

wartość

największa

10

log

20

dB

dynamiki

zakres

Dla reprezentacji stałoprzecinkowej otrzymamy

n

n







02

,

6

)

2

(

log

20

10

dB

dynamiki

zakres

Zakres dynamiki dla 16-bitowego stałoprzecinkowego słowa binarnego

dB

96

16

02

,

6





Dla reprezentacji zmiennoprzecinkowej otrzymamy

ne

2

02

,

6





dB

dynamiki

zakres

Dla standardu IEE 754 zakres dynamiki jest równy

dB

1536

256

02

,

6

2

02

,

6

8









Zakres dynamiki reprezentacji zmiennoprzecinkowej jest wielokrotnie większy od
reprezentacji stałoprzecinkowej.

Stałoprzecinkowe reprezentacje binarne:

16-bitowe



zakres reprezentowanych wartości 2

16

32-bitowe



zakres reprezentowanych wartości 2

32

Zmiennoprzecinkowa reprezentacja binarna:

32-bitowa



zakres reprezentowanych wartości 4,6



10

76

Skutki skończonej długości słowa binarnego procesora zależą od
stosowanego formatu reprezentacji, który decyduje o zakresie dynamiki i
precyzji liczb.

n - ilość bitów słowa binarnego

ne - ilość bitów wykładnika

4W18

Precyzja reprezentacji
Stałoprzecinkowe reprezentacje binarne:

 formatu Q0 (liczb całkowitych) odstęp pomiędzy liczbami jest zawsze równy

dokładnie 2

0

= 1 (zmiana na pozycji najmłodszego bitu).

 formatu Q15 odstęp pomiędzy liczbami jest również stały i wynosi 2

-16

.

Dla największych wartości reprezentowanych przez format: +0,999 i –1,000
odległość między liczbami stanowi 2

-16

części liczby. Dla liczb bliskich zeru

zbliża się do wartości liczby.

Efekt!:

Błąd zaokrąglenia, w przypadku zapisu stałoprzecinkowego zmienia się w dużych
granicach i przy małych liczbach przyjmuje duże wartości – granicznie 50% (połowa
odstępu między liczbami).

Zmiennoprzecinkowe reprezentacje binarne:

 odstęp zależy od wartości liczby. Duże liczby mają większe odstępy między nimi,

małe liczby mniejsze odstępy.

 zachowana jest relacja, że odstęp do następnej liczby reprezentowanej przez zapis

stanowi od 2

-24

do 2

-23

części liczby.

Jeśli mamy liczbę zmiennoprzecinkową reprezentującą wartość

M



2

e

To zmiana bitu na najmłodszej pozycji daje nową wartość liczby

(M + 2

-23

)



2

e

Odległość między liczbami jest więc równa

(M + 2

-23

)



2

e

- M



2

e

= 2

-23



2

e

czyli jest zależna do wartości liczby.
Odstęp między liczbami względem reprezentowanej wartości wynosi

M

M

e

e

23

2

2

2









-23

2

Ponieważ mantysa liczby M przyjmuje wartości od 1 do prawie 2, to odstęp stanowi
odpowiednio

od

6

23

23

10

12

,

0

2

1

2













do

6

24

23

10

06

,

0

2

2

2















części liczby.

Precyzja reprezentacji zmiennoprzecinkowej jest wielokrotnie większa od
reprezentacji stałoprzecinkowej.

4W19

Zalety reprezentacji zmiennoprzecinkowej

 Reprezentacja zmiennoprzecinkowa pojedynczej precyzji daje więcej bitów

zapisu niż analogiczna reprezentacja stałoprzecinkowa.

 Wynikiem tego jest mniejsza waga najmłodszego bitu i mniejsze wartości

względne odstępów między liczbami.

 Jeśli występuje zaokrąglenie, to dla reprezentacji stałopozycyjnej wartość błędu

zaokrąglenia wynosi

16

2

2

1







i jest stałe niezależnie od wartości liczby. Jest to przyczyną dużych błędów dla
małych wartości liczb.

 Dla reprezentacji zmiennopozycyjnej wartość błędu zaokrąglenia jest równa

e

2

2

2

1

23









i jest zmienna, mała dla małych liczb, większa dla dużych liczb.

 Wnoszony względny błąd zaokrąglenia w przypadku reprezentacji

zmiennoprzecinkowej jest dużo mniejszy a jego wartość zmienia się w
niewielkim zakresie.

 W przypadku występowania błędów odcięcia efekt jest analogiczny – mniejsza

wartość względna odciętych bitów.

 W rezultacie końcowym reprezentacja zmiennoprzecinkowa dzięki wyższej

precyzji daje efektywnie mniejsze szumy obliczeń arytmetycznych.

 Większy zakres dynamiki reprezentacji zmiennoprzecinkowej daje większą

odporność na przepełnienia i pozwala na przetwarzanie sygnałów wejściowych o
większej dynamice, przy zachowaniu wysokiego stosunku sygnału do szumu.

4W20

Aspekty reprezentacji binarnych liczb w różnych formatach

Format Q0:

 nie wymaga skalowania liczb dla przedstawienia ich w postaci binarnej
 dokładność reprezentacji liczby w rejestrach sprzętowych jest 100%
 operacji dodawania, odejmowania i mnożenia bez błędów kwantyzacji
 dzielenie liczb całkowitych może dać liczbę rzeczywistą – wnoszony błąd
 największym problemem jest przepełnienie
 można zastosować arytmetykę podwójnej precyzji, ale to wymaga zabiegów

programowych i zmniejsza szybkość przetwarzania.

Format Q15:

 wymaga skalowania liczb do zakresu (–1: +1)
 liczby przedstawiane są w postaci ułamka binarnego, co wymaga skalowania do

formatu Q15

 dokładność reprezentacji zależy od tego, czy liczba dziesiętna może być

przedstawiona w postaci ułamka o podstawie 2 a nie 10 – wówczas nie ma błędu
zaokrąglenia.

 jeśli spełniona jest równość podczas skalowania do formatu Q15

ułamek dziesiętny



2

15

= liczba całkowita Q15

to reprezentacja liczby jest w pełni dokładna.
Inaczej występuje błąd zaokrąglenia.

 stosowanie formatu Q15, eliminuje problem przepełnienia w operacjach

mnożenia, nie daje natomiast tego efektu dla operacji dodawania

 ciągłe wykonywanie procesu skalowania danych wejściowych i wyjściowych

operacji arytmetycznych wprowadza dodatkowe błędy kwantyzacyjne, które
zwiększają szum generowany w sygnale.

Format IEE745:

 mantysa ma postać ułamka binarnego z ukrytym bitem 1 na pozycji części

całkowitej liczby

 jeśli część ułamkowa mantysy (M-1) da się przedstawić w postaci ułamka

binarnego, to mamy reprezentację w pełni dokładną. W innym przypadku
powstaje błąd zaokrąglenia

4W21

 dla standardu IEE745, możemy zapisać równanie, którego spełnienie gwarantuje

bezbłędną reprezentację liczby



















23

e

2

1

2

dziesięzie

liczba

liczba całkowita IEE745

 skalowanie do formatu IEE745 oraz podczas operacji arytmetycznych daje

mniejsze szumy kwantyzacyjne.

 zmiennoprzecinkowa reprezentacja binarna odwzorowuje dokładnie liczby

całkowite w przedziale ±16,8 miliona (±224). Powyżej tej wartości odstępy
pomiędzy liczbami (krok kwantyzacji) jest większy od 1 i niektóre liczby
całkowite mogą być gubione.

 pozwala to na dodawanie, odejmowanie i mnożenie liczb całkowitych w

przedziale ±16,8 miliona bez błędu zaokrąglenia

 praktycznie nie ma problemu przepełnienia

Ułamek dziesiętny będzie miał dokładną reprezentację binarną kiedy jego wartość da
się zapisać jako skończoną sumę ułamków binarnych

n

n

k

k

2

1

...

8

1

4

1

2

1

2

1

1





















Na przykład liczba dziesiętna 0,125 ma dokładną stałoprzecinkową reprezentację
binarną w formacie Q15

0.001000000000000 = 0,125

natomiast liczba 0,1 wypada pomiędzy dwoma liczbami

0.000110011001100 = 0,0999755

0.000110011001101 = 0,1000061

Analogicznie liczba dziesiętna 1,125 ma dokładną zmiennoprzecinkową
reprezentację binarną

1.00100000000000000000000



2

0

= 1,125

Natomiast liczba dziesiętna 1,1 wypada pomiędzy dwoma liczbami

1.00011001100110011001100



2

0

= 1,0999999046

1.00011001100110011001101



2

0

= 1,1000000238

4W22

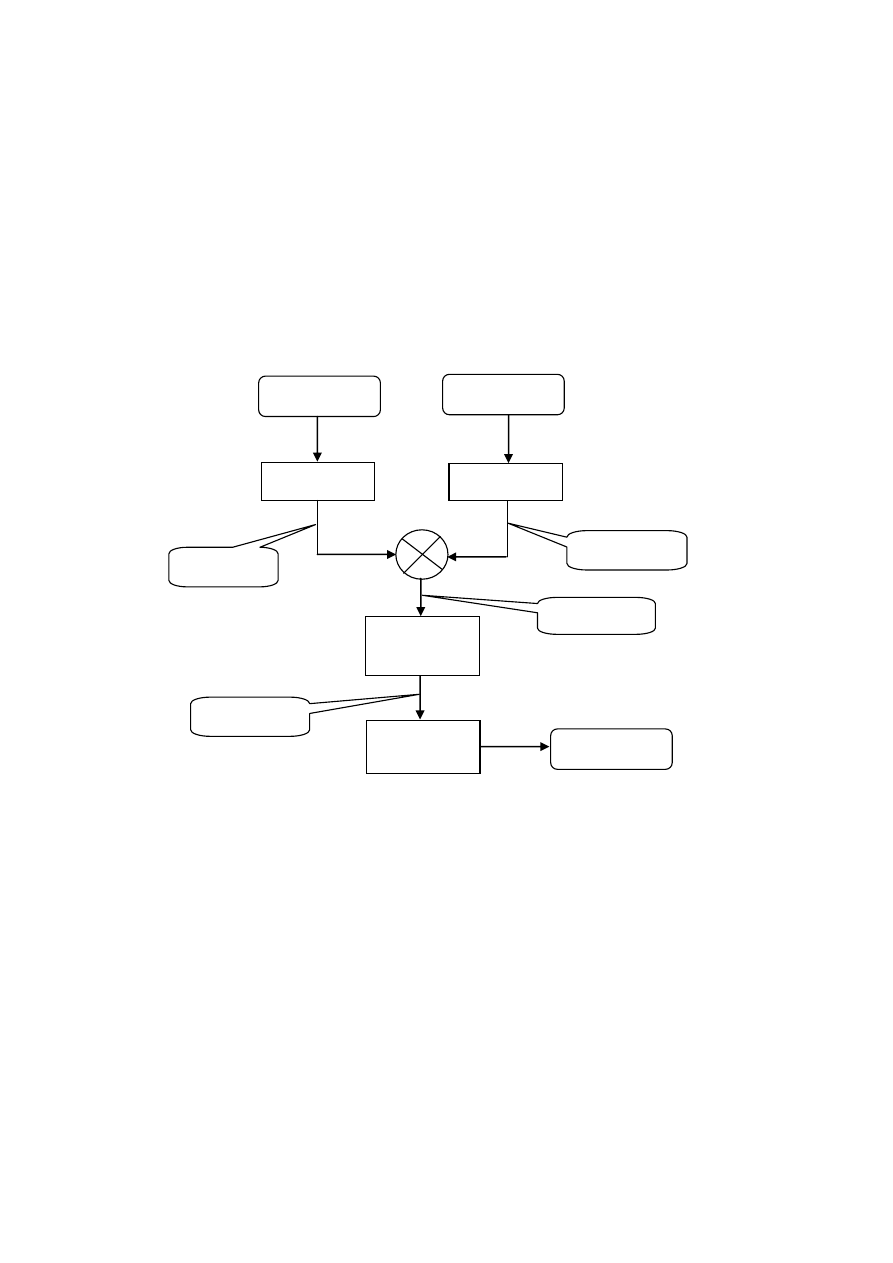
Przykład operacji na formacie Q15 oraz IEE745.

Mnożenie dziesiętne

0,46



0,625 = 0,2875

Spodziewamy się wynikowego operandu o wartości dziesiętnej 0,2875.
Taką wartość uzyskamy jeśli operacja mnożenia nie wniesie żadnego błędu.

Format Q15

Algorytm realizacji operacji

Skalowanie wykonujemy według wzoru

liczba całkowita Q15



q = ułamek dziesiętny

liczba całkowita Q15 = ułamek dziesiętny



1/q

Współczynnik skalowania wartości bitów

q = 2

-15

Skalujemy ułamek 0,625 do formatu Q15

liczba całkowita Q15 = 0,625



2

15

= 0,625



32768 = 20480

20480 = 2

14

+ 2

12

skalowanie

Operand A

Operand B

skalowanie

skalowanie

powrotne

skalowanie

powrotne

Operand W

format Q15

format Q15

format Q30

format Q15

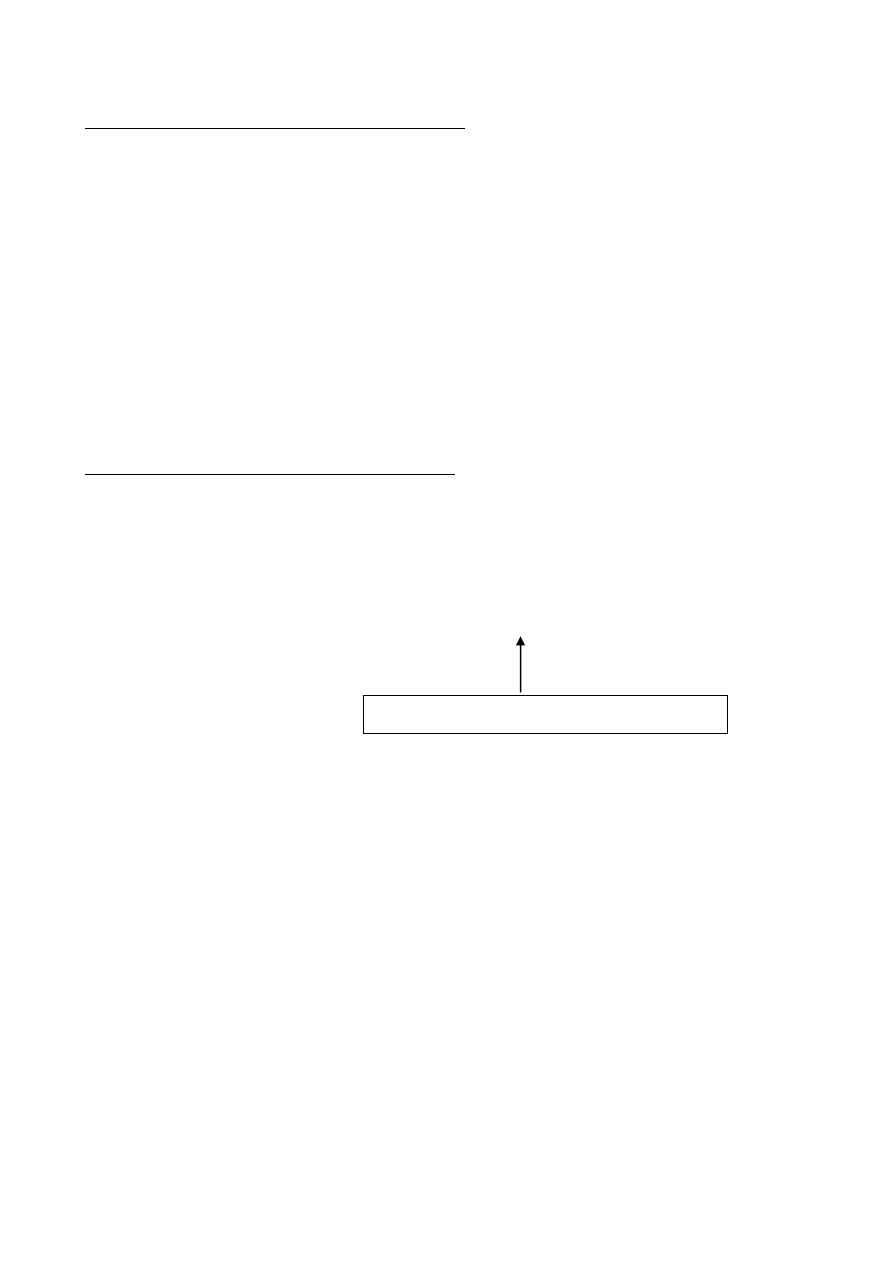
4W23

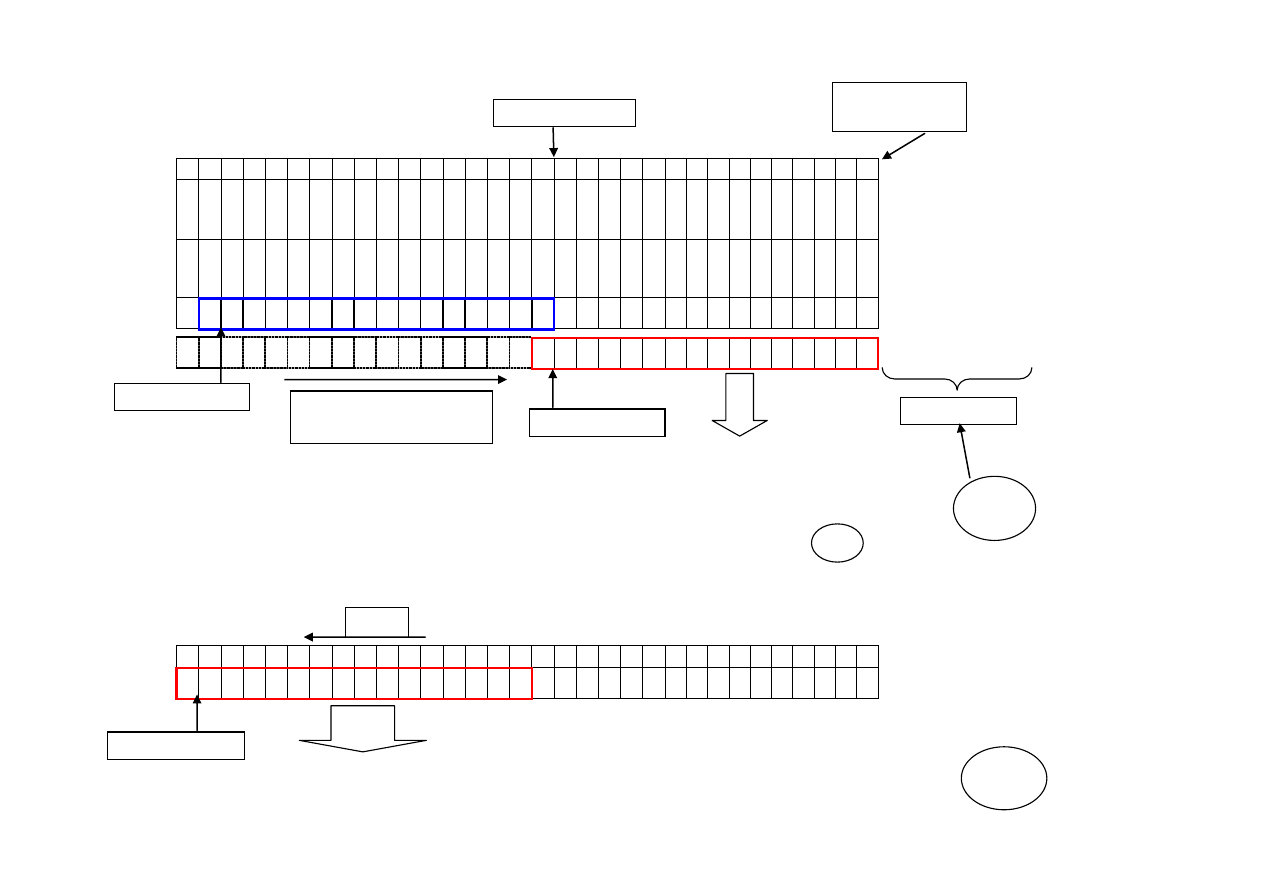
Reprezentacja ułamka 0,625 w formacie Q15

(15)(14)(13)(12)(11)(10)(9)(8)(7)(6)(5)(4)(3)(2)(1)(0)

0 1 0 1 0 0 0 0 0 0 0 0 0 0 0 0 = q



20480 = 2

-15



20480 = 0,625 d

Skalujemy ułamek 0,46 do formatu Q15

liczba całkowita Q15 = 0,46



2

15

= 0,46



32768 = 15073,28

Musimy stosować zaokrąglenie do najbliższej liczby całkowitej 15073.

Wprowadzany jest do operacji błąd zaokrąglenia.

15073 = 2

13

+ 2

12

+ 2

11

+ 2

9

+ 2

7

+ 2

6

+ 2

5

+ 2

0

=

= 8192 + 4096 + 2048 + 512 + 128 + 64 + 32 + 1

Reprezentacja ułamka 0,46 w formacie Q15

(15)(14)(13)(12)(11)(10)(9)(8)(7)(6)(5)(4)(3)(2)(1)(0)

0 0 1 1 1 0 1 0 1 1 1 0 0 0 0 1 b = q



15073 = 0,4599914

Mnożenie binarne ułamków w formacie Q15

15073



20480 = 308695040

Mnożenie dwóch liczb skalowanych powoduje mnożenie współczynnika skalującego.

Aby zapisać i sprawdzić rezultat mnożenia w formacie Q15 musimy wykonać
podwójne skalowanie powrotne.

32-bitowa liczba binarna w formacie Q30

4W24

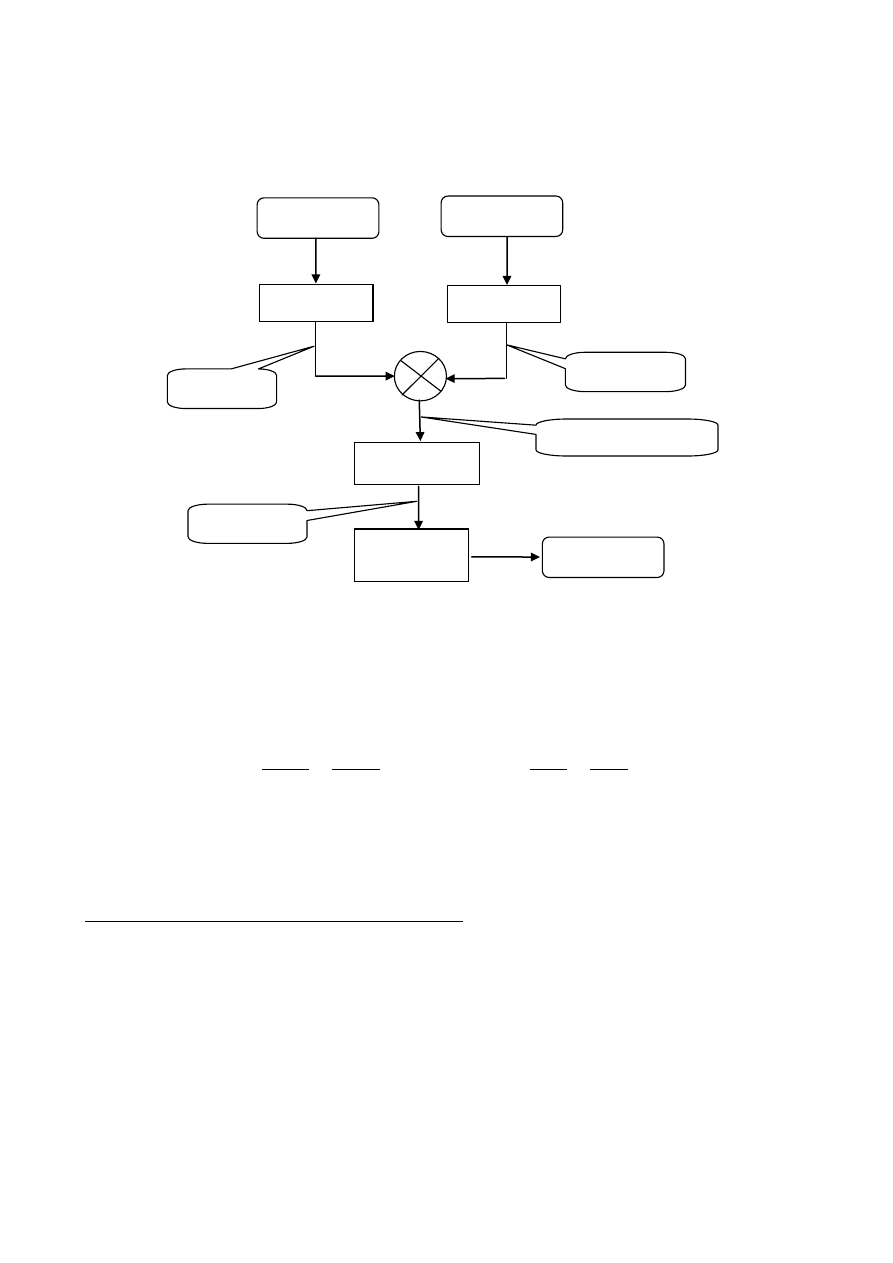
31 30 29 28 27 26 25 24 23 22 21 20 19 18 17 16 15 14 13 12 11 10 9 8 7 6 5 4 3 2 1 0

0 0 1 1 1 0 1 0 1 1 1 0 0 0 0 1



0 1 0 1 0 0 0 0 0 0 0 0 0 0 0 0

0 0 1 1 1 0 1 0 1 1 1 0 0 0 0 1
0 0 1 1 1 0 1 0 1 1 1 0 0 0 0 1

0 0 0 1 0 0 1 0 0 1 1 0 0 1 1 0 0 1 0 1 0 0 0 0 0 0 0 0 0 0 0 0

0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0

0 0 1 0 0 1 0 0 1 1 0 0 1 1 0 0 1 0 1 0 0 0

2

28

+ 2

25

+ 2

22

+ 2

21

+ 2

18

+ 2

17

+ 2

14

+ 2

12

= 308695040

2

-15



(2

28

+ 2

25

+ 2

22

+ 2

21

+ 2

18

+ 2

17

+ 2

14

+ 2

12

) = 2

13

+ 2

10

+ 2

7

+ 2

6

+ 2

3

+ 2

2

+ 2

-1

+ 2

-3

2

-15



308695040= 308695040/32768 =

9420

, 625

2

-15



9420= 9420/32768 = 0,2874755859375

31 30 29 28 27 26 25 24 23 22 21 20 19 18 17 16 15 14 13 12 11 10 9 8 7 6 5 4 3 2 1 0

0 0 1 0 0 1 0 0 1 1 0 0 1 1 0 0

1 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0

2

1



(2

28

+ 2

25

+ 2

22

+ 2

21

+ 2

18

+ 2

17

+ 2

14

+ 2

12

) = 2

29

+ 2

26

+ 2

23

+ 2

22

+ 2

19

+ 2

18

+ 2

15

+ 2

13

numer pozycji

wagowej

punkt binarny

punkt binarny

przesunięcie o 15 bitów



2

-15

punkt binarny

bity obcięte



2

1

punkt binarny



2

-16

0,46 d

0,625 d

4W25

Format IEE745

Algorytm realizacji operacji

Celem przedstawienia ułamków w formacie IEE745 musimy najpierw zapisać je w
postaci wykładniczej

M



2

e

Mantysa M musi być liczbą z przedziału od 1 do 2, stąd

25

,

1

5

,

0

625

,

0

2

625

0

1

1









,

M

84

,

1

25

,

0

46

,

0

2

46

0

2

2









,

M

Mnożenie ułamków dziesiętnych 0,46 i 0,625 w postaci wykładniczej

1,25



2

-1



1,84



2

-2

= 2,30



2

-3

= 1,15



2

-2

= 0,2875

Konwersja ułamka 0,625 do formatu IEE745
Wykonujemy skalowanie części ułamkowej mantysy M

1

0,25



2

23

= 2097152 = 2

21

Uwzględniając, że wykładnik jest w notacji przesunięcia binarnego otrzymamy

0,625 = + 1,25



2

-1

= + 1,25



2

(126-127)

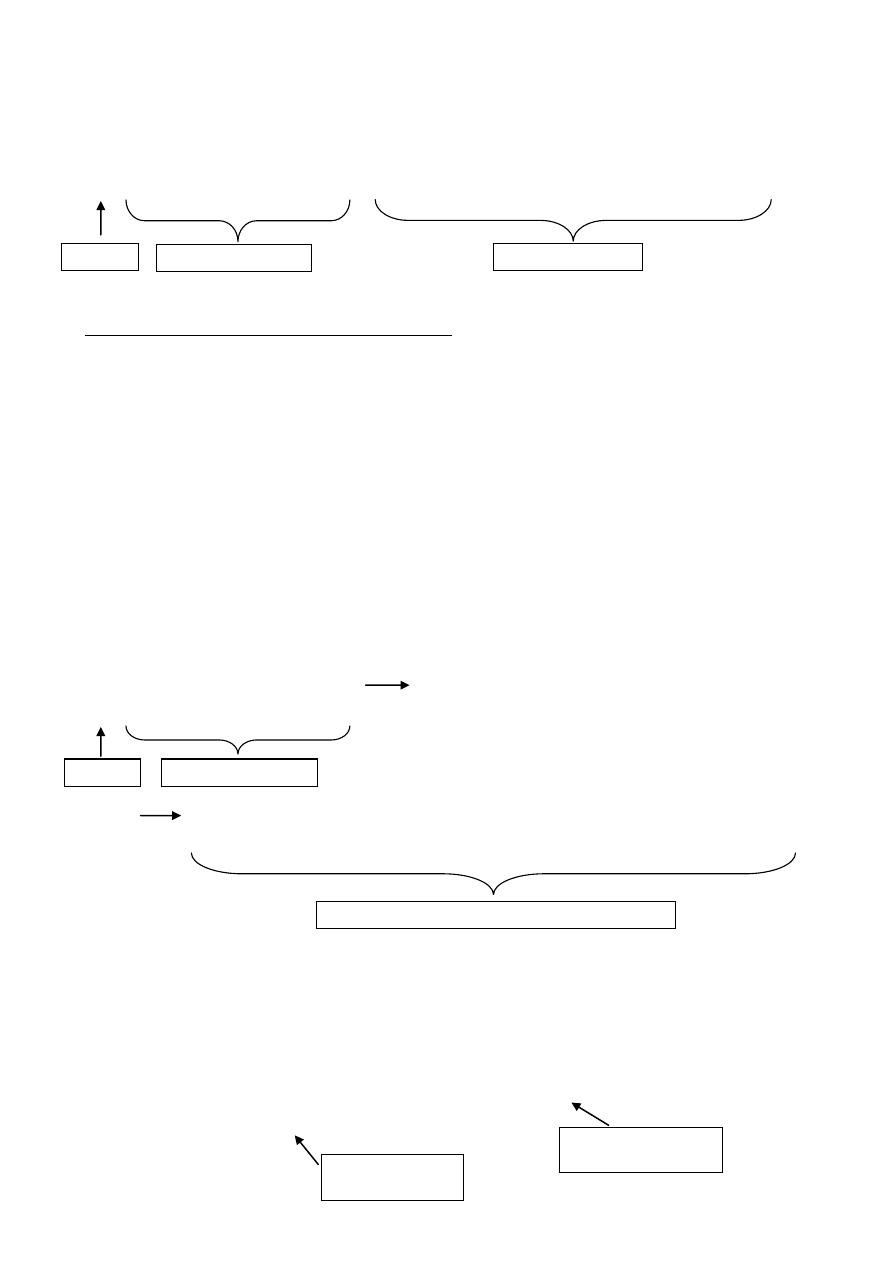
konwersja

Operand A

Operand B

konwersja

normalizacja

konwersja

powrotna

Operand W

format IEE

format IEE

rezultat przejściowy

format IEE

4W26

Reprezentacja ułamka 0,625 w formacie zmiennoprzecinkowym IEE745

(31) (30)(29)(28)(27)(26)(25)(24)(23) (22)(21)(20)(19) .........................................(4)(3)(2)(1)(0)

0 0 1 1 1 1 1 1 0 0 1 0 0 .....................................0 0 0 0 0

Konwersja ułamka 0,46 do formatu IEE745
Wykonujemy skalowanie części ułamkowej mantysy M

2

0,84



2

23

= 7046430,72

Musimy stosować zaokrąglenie do najbliższej liczby całkowitej 7046431 - powstaje
błąd zaokrąglenia.

7046431 = 2

22

+ 2

21

+ 2

19

+ 2

17

+ 2

16

+ 2

15

+ 2

10

+ 2

8

+ 2

4

+ 2

3

+ 2

2

+ 2

1

+ 2

0

7046431



2

-23

= 0,84000003337860107421875

Ostatecznie ułamek dziesiętny 0,46 będzie miał reprezentację wykładniczą postaci

+ 1,84000003337860107421875



2

-2

= + 1,84000003337860107421875



2

(125-127)

Reprezentacja ułamka 0,46 w formacie zmiennoprzecinkowym IEE745

(31) (30)(29)(28)(27)(26)(25)(24)(23)

0 0 1 1 1 1 1 0 1

(22)(21)(20)(19)(18)(17)(16)(15)(14)(13)(12)(11)(10)(9)(8)(7)(6)(5)(4)(3)(2)(1)(0)

1 1 0 1 0 1 1 1 0 0 0 0 1 0 1 0 0 0 1 1 1 1 1

Mnożenie liczb zmiennoprzecinkowych w formacie IEE745

1,25



2

126



1,84000003337860107421875



2

125

=

= 2,3000000417232513427734375



2

251

Wynik wymaga normalizacji i skalowania

(-1 + 127) + (-2 + 127) = 251 = (-3 + 254) = -3 + 254

-127

=

(-3 + 127)

-3 + 254

+ (2 + 127)

= 256 +

(-3 + 127

znak (+)

wykładnik E

1

= 126

mantysa M

1

= 1,25

wykładnik E

2

= 125

znak (+)

mantysa M

2

= 1,84000003337860107421875

Nie można wykonać

odejmowania

Przeniesienie

pomijane

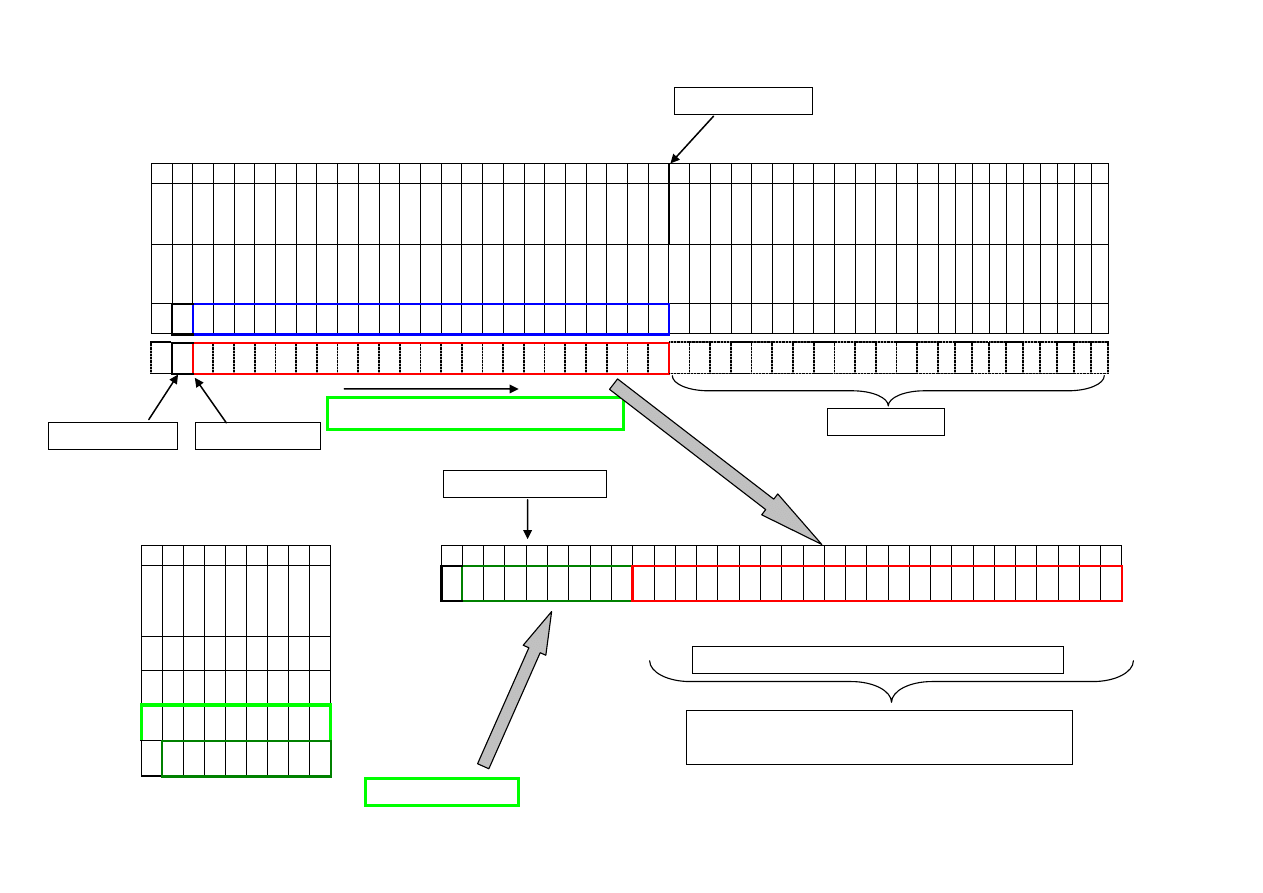
4W27

47 46 45 44 43 42 41 40 39 38 37 36 35 34 33 32 31 30 29 28 27 26 25 24 23 22 21 20 19 18 17 16 15 14 13 12 11 10 9 8 7 6 5 4 3 2 1 0

1 1 1 0 1 0 1 1 1 0 0 0 0 1 0 1 0 0 0 1 1 1 1 1

0,46



1 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0

0,625

1 1 1 0 1 0 1 1 1 0 0 0 0 1 0 1 0 0 0 1 1 1 1 1

1 1 1 0 1 0 1 1 1 0 0 0 0 1 0 1 0 0 0 1 1 1 1 1

1 0 0 1 0 0 1 1 0 0 1 1 0 0 1 1 0 0 1 1 0 0 1 1 0 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0

1 0 0 1 0 0 1 1 0 0 1 1 0 0 1 1 0 0 1 1 0 0 1 1 0 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0

punkt binarny

MNOŻENIE MANTYS

przesunięcie w prawo o 1 bit (



2

-1

)

bity obcięte

ukryta jedynka

punkt binarny

Wykładnik E = 125

(



2

-23

)

SUMOWANIE

WYKŁADNIKÓW

7 6 5 4 3 2 1 0

31 30 29 28 27 26 25 24 23 22 21 20 19 18 17 16 15 14 13 12 11 10 9 8 7 6 5 4 3 2 1 0

+ 0 1 1 1 1 1 1 0

126

0 0 1 1 1 1 1 0 1 0 0 1 0 0 1 1 0 0 1 1 0 0 1 1 0 0 1 1 0 0 1 1

+ 0 1 1 1 1 1 0 1

125

= 1 1 1 1 1 0 1 1

251

- 1 0 0 0 0 0 0 1

-127 (+129)

+ 1

1 0 1 1 1 1 1 0 1

Mantysa M = 1,14999997615814208984375

NORMALIZACJA

1,14999997615814208984375



2

(125-127)

=

= 0,2874999940395355224609375

4W28

Normalizacja

2

-1



2,3000000417232513427734375



2

(124-127) + 1

=

= 1,15000002086162567138671875



2

-2

Na skutek błędu obcięcia uzyskamy liczbę zmiennoprzecinkową postaci

1,14999997615814208984375



2

-2

która reprezentuje ułamek dziesiętny

0,2874999940395355224609375

Zestawienie operandów i błędu wynikowego operacji w obu formatach

Wielkość

Format Q15

Format IEE745

0,625

20480



0,625

1,25



2

(126-127)

= 0,625

0,46

15073



0,4599914

1,84000003337860107421875



2

(125-127)

=

= 0,4600000083446502685546875

0,46



0,625

= 0,2875

9420



0,2874755859375 1,14999997615814208984375



2

(125-127)

=

= 0,2874999940395355224609375



2,44140625



10

-5

5,9604644775390625



10

-8



[%]

0,0085

2,0732050356657608695652



10

-6

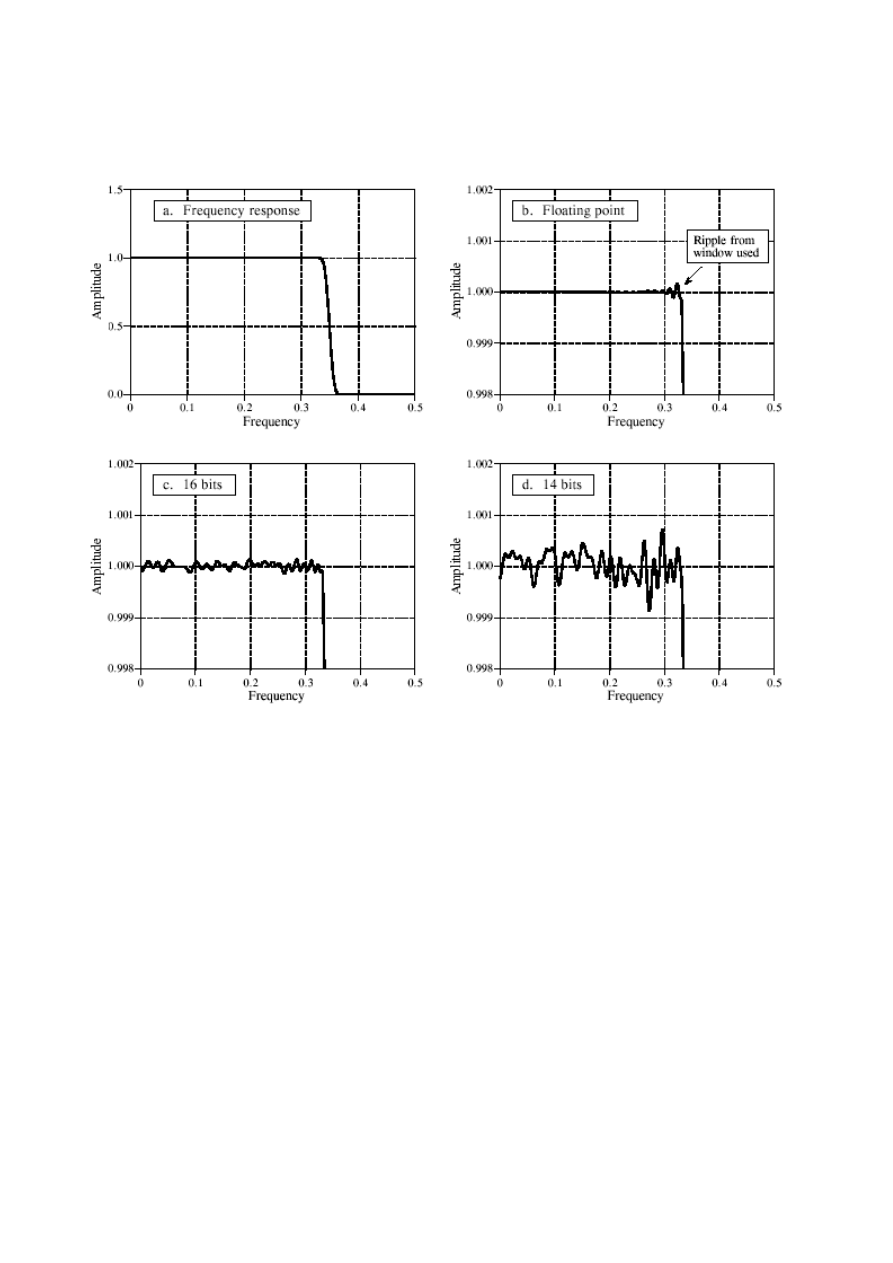
4W29

Przykłady obserwacji skutków błędów kwantyzacji

Charakterystyka częstotliwościowa filtru dolnoprzepustowego o skończonej

odpowiedzi impulsowej (SOI)

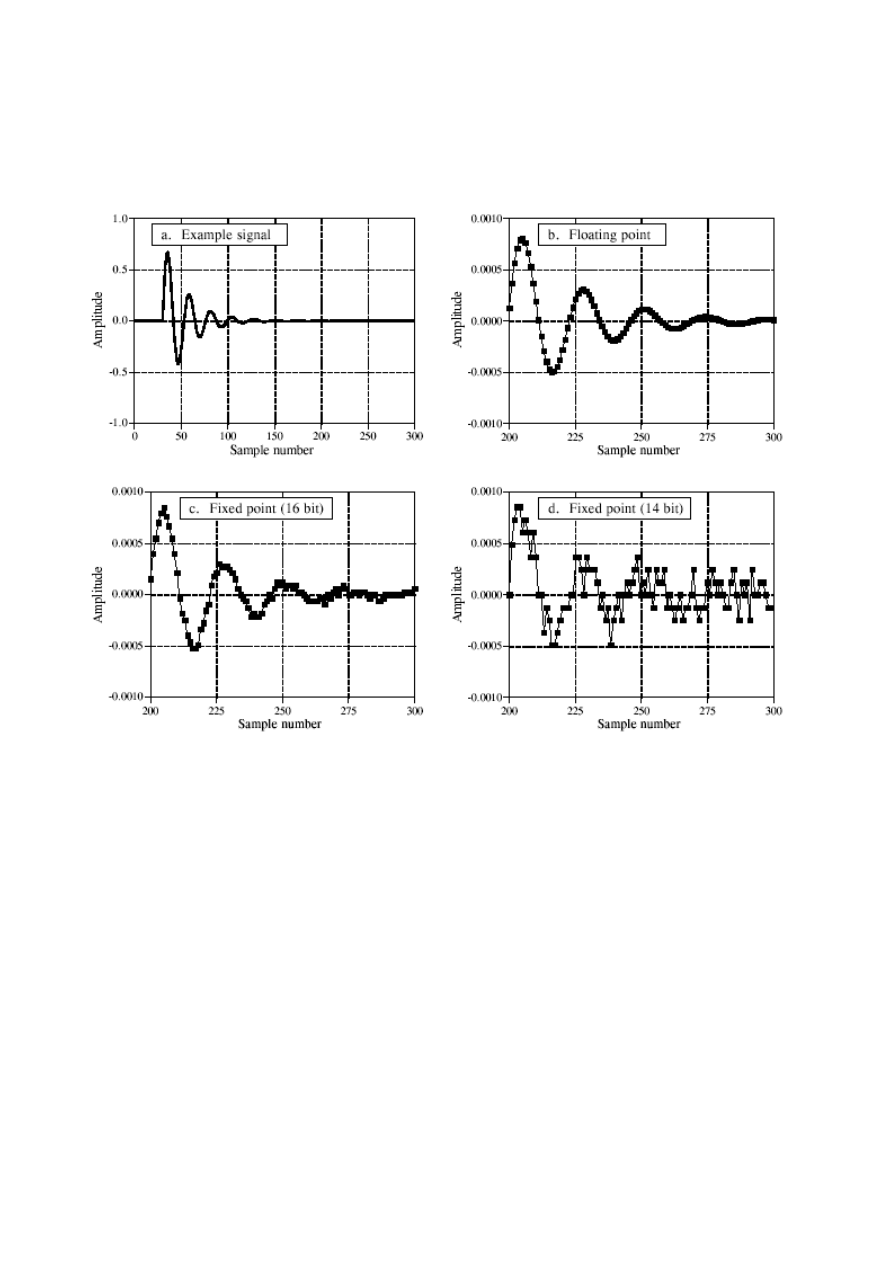
4W30

Różnice wynikające z zastosowania reprezentacji stało- lub zmiennoprzecinkowej,

na przykładzie sygnału w dziedzinie czasu.