Obliczenia statyczno-wytrzymało

ś

ciowe.

Obliczenie stropu grzybkowego metod

ą

współczynników tabelarycznych.

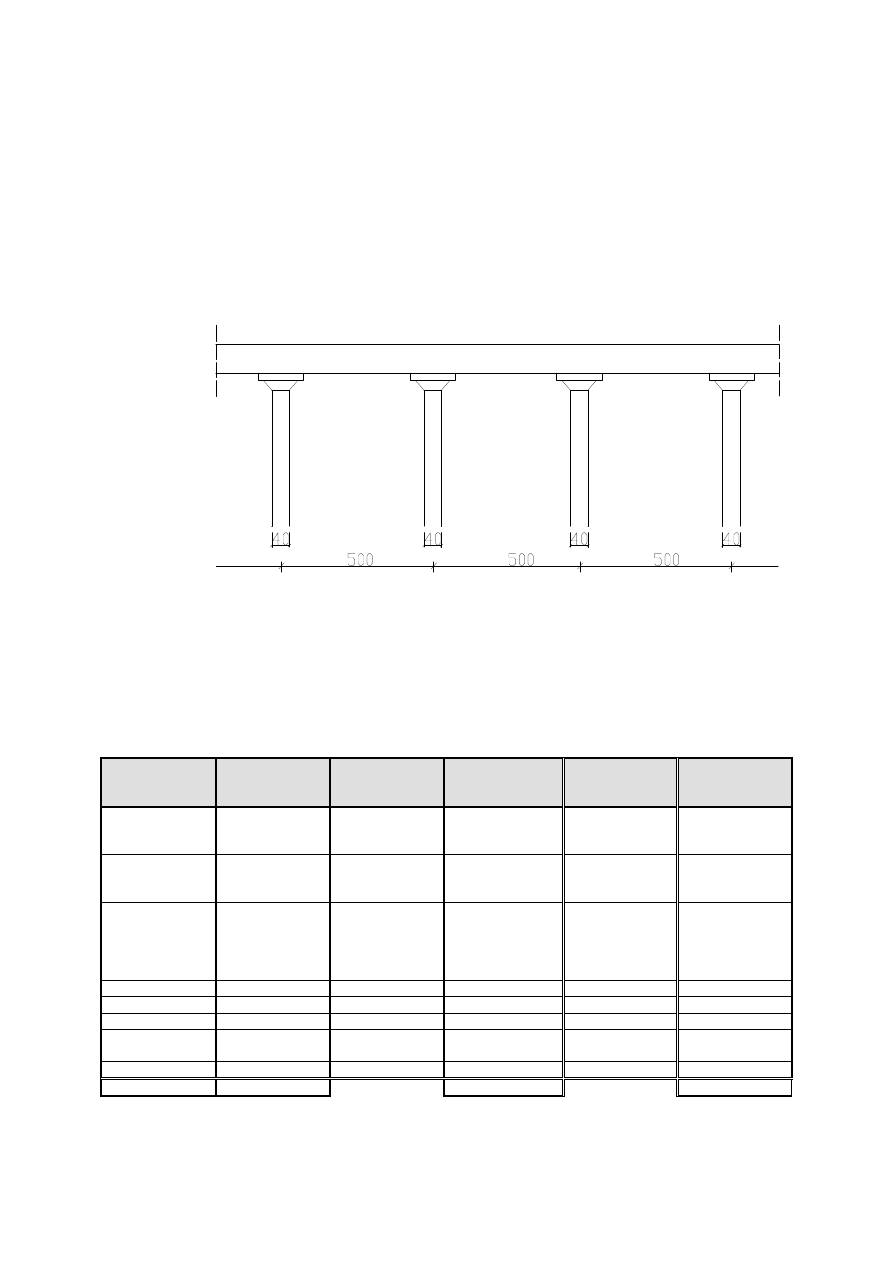
1.

Przekrój poprzeczny.

2.

Zestawienie obci

ąż

e

ń

.

2.1

Obci

ąż

enia stałe stropu przej

ś

cia.

Rodzaj warstwy

Grubo

ść

[m]

Ci

ęż

ar

γ

[kN/m

2

]

Obci

ąż

enia

charakterystyczne

[kN/m

2

]

γ

f

Obci

ąż

enia

obliczeniowe

[kN/m

2

]

Beton asfaltowy

(warstwa

ś

cieralna)

0,04

23

0,92

1,5

1,38

Beton asfaltowy

(warstwa
wi

ążą

ca)

0,04

23

0,92

1,5

1,38

Masa mineralno-

bitumiczna o

zawarto

ś

ci

kruszywa

łamanego >25%

0,06

23

1,38

1,5

2,07

Piasek gruby

0,20

13

3,80

1,5

5,70

Beton ochronny

0,10

23

2,30

1,5

3,45

Izolacja

0,03

11

0,33

1,2

0,39

Warstwa

wyrównawcza

0,33

23

7,59

1,3

9,87

Płyta stropowa

0,20

25

5

1,2

6,00

Σ

1,00

q

k

=22,24

q

o

=30,24

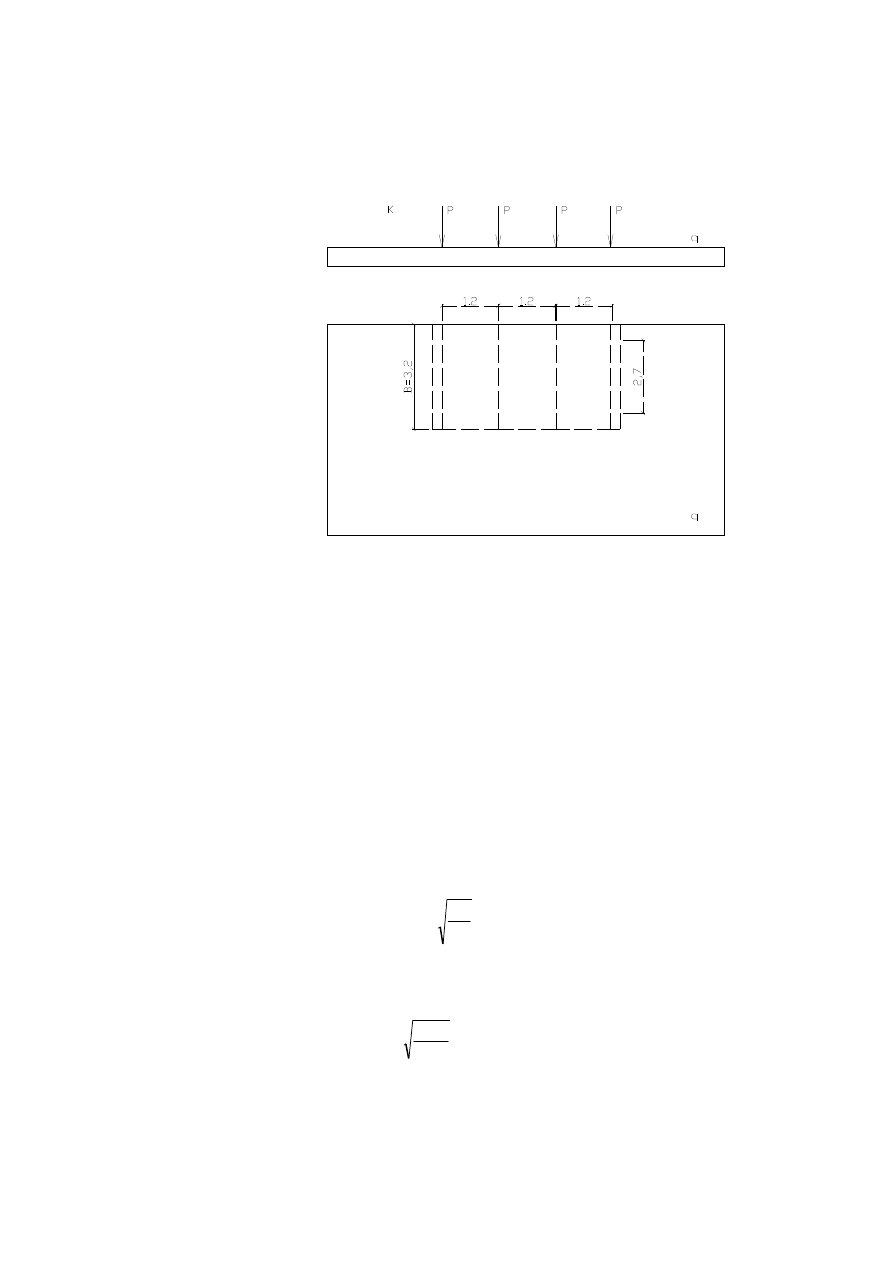
2.2

Obci

ąż

enie zmienne stropu przej

ś

cia od taboru samochodowego.

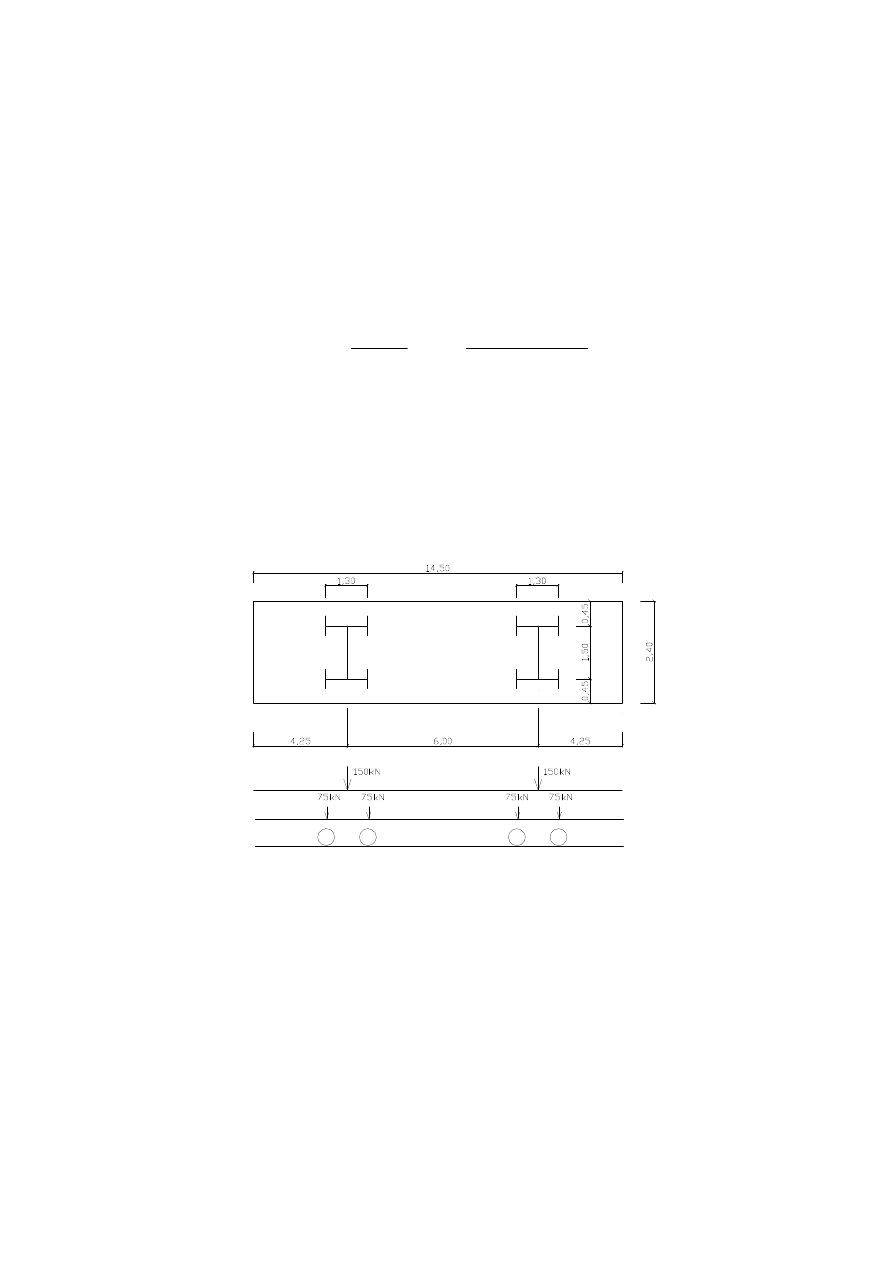
Schemat obci

ąż

enia od taboru samochodowego.

Przyj

ę

to klas

ę

obci

ąż

enia A.

K=800 kN
Nacisk na o

ś

200 kN

q=4 kN/m

2

2.2.1

Obliczenie współczynnika dynamicznego.

φ

=1.35-0.005*l<1.325

φ

=1.35-0.005*45.4=1.123<1.325

Przyj

ę

to

φ

=1.123

φ

(n)

=1+((1-h)(

φ

-1))/0.5=1+((1-0.8)( 1.123-1))/0.5=1.05

2.2.2

Obliczenie wysoko

ś

ci h

1

umieszczenia siły P.

h

1

= h

1

I

+ h

1

II

h

1

I

=h

h

h

3

g

h

h

E

E

−

⋅

Edometryczny moduł nawierzchni drogowej E

h

=1000 Mpa

Edometryczny moduł gruntu E

g

=23 Mpa

h

1

I

=

m

76

0

3

0

23

1000

3

0

3

,

,

,

=

−

⋅

h

1

II

=0,26m

h

1

=0,76+0,26=1,02m

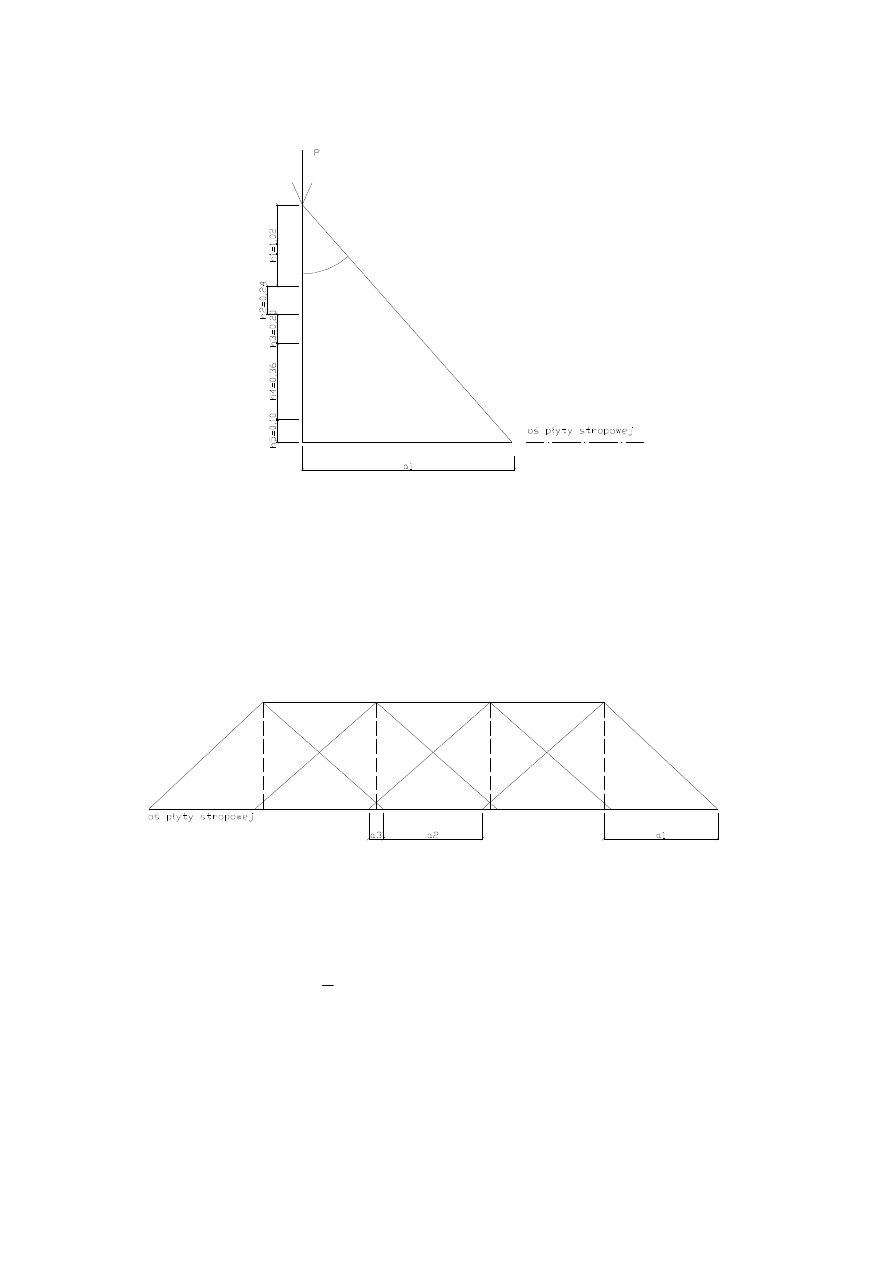
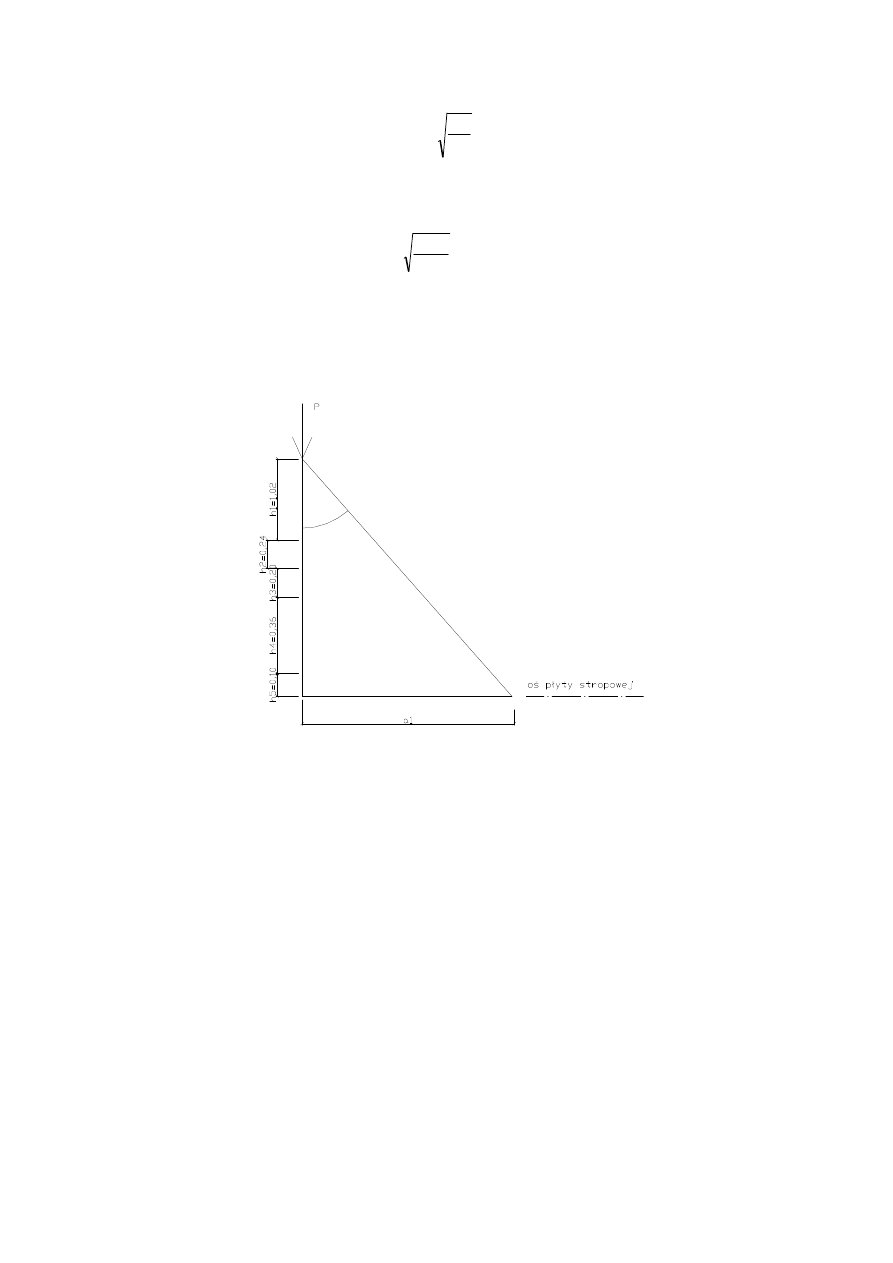
2.2.3

Obliczenie zasi

ę

gu działania siły P na gł

ę

boko

ś

ci

Σ

h.

β=35°

Σ

h=h

1

+h

2

+h

3

+h

4

+h

5

=1,02+0,24+0,20+0,36+0,10=1,92m

a

1

=

Σ

h*tg35

0

=1,34m

2.2.4

Ustalenie najniekorzystniejszego poło

ż

enia pojazdu w stosunku do konstrukcji przej

ś

cia.

a

1

=1,34=1,2+

m

28

0

2

2

1

34

1

2

2

1

a

a

a

2

1

1

3

3

,

)

,

,

(

)

,

(

=

⋅

−

=

⋅

−

=

⇒

⋅

a

2

+a

3

=1,2

m

92

0

28

0

2

1

a

2

1

a

3

2

,

,

,

,

=

−

=

−

=

⇒

2.2.5

Obliczenie obci

ąż

e

ń

zmiennych stropu tunelu.

a)

obci

ąż

enie zmienne charakterystyczne.

-

od jednej siły skupionej.

kPa

62

18

34

1

14

3

100

05

1

a

P

P

2

2

1

n

p

1

,

,

,

,

)

(

=

⋅

⋅

=

⋅

⋅

=

π

ϕ

-

od dwóch sił skupionych.

kPa

24

37

62

18

2

P

2

P

p

1

p

2

,

,

=

⋅

=

⋅

=

-

od trzech sił skupionych.

kPa

86

55

62

18

3

P

3

P

p

1

p

3

,

,

=

⋅

=

⋅

=

b)

obci

ąż

enie zmienne obliczeniowe.

-

od jednej siły skupionej.

kPa

93

27

62

18

5

1

P

P

p

1

f

o

p

1

,

,

,

=

+

=

⋅

=

γ

-

od dwóch sił skupionych.

kPa

86

55

93

27

2

P

2

P

o

p

1

o

p

2

,

,

=

⋅

=

⋅

=

-

od trzech sił skupionych.

kPa

79

83

93

27

3

P

2

P

o

p

1

o

p

3

,

,

=

⋅

=

⋅

=

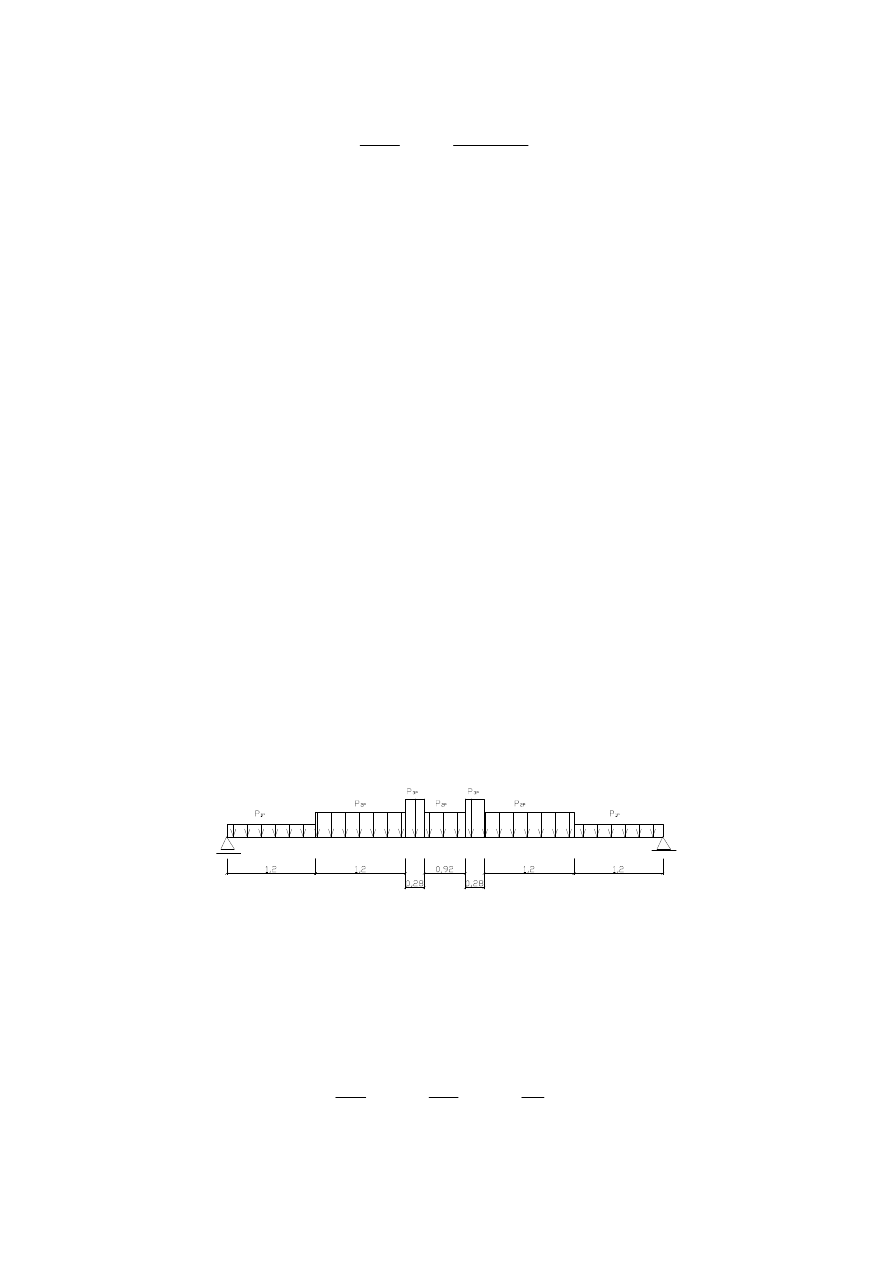
Schemat obci

ąż

enia płyty stropowej.

Do oblicze

ń

przyj

ę

to obci

ąż

enie równomiernie rozło

ż

one o stałej warto

ś

ci p od siły skupionej

oraz obci

ąż

enie równomiernie rozło

ż

one q na całej długo

ś

ci płyty stropowej.

p=

kN

99

46

8

6

4

2

93

27

8

6

14

3

86

55

8

6

92

0

79

83

,

,

,

,

,

,

,

,

,

,

=

⋅

+

⋅

+

⋅

kPa

51

kPa

99

55

4

99

46

q

p

P

≅

=

+

=

+

=

,

,

2.2.6

Obliczenie obci

ąż

e

ń

zmiennych w płaszczy

ź

nie dna przej

ś

cia.

h

d

=

Σ

h+h

t

=1,92+3,38=5,3m

Zasi

ę

g działania siły P na gł

ę

boko

ś

ci h

d

.

a

1

I

=

m

71

3

35

tg

h

o

d

,

=

⋅

Obci

ąż

enie zmienne charakterystyczne od jednej siły skupionej.

kPa

43

2

71

3

14

3

100

05

1

a

100

P

2

2

I

1

n

p

1

,

,

,

,

)

(

)

(

=

⋅

⋅

⋅

=

⋅

⋅

=

π

ϕ

Na gł

ę

boko

ś

ci h

d

nakładaj

ą

si

ę

obci

ąż

enia od wszystkich o

ś

miu kół pojazdu.

- charakterystyczne:

kPa

44

19

43

2

8

P

8

P

p

1

p

8

,

,

=

⋅

=

⋅

=

- obliczeniowe:

kPa

16

29

44

19

5

1

P

P

p

8

f

o

p

8

,

,

,

=

⋅

=

⋅

=

γ

2.3

Obci

ąż

enie zmienne stropu przej

ś

cia od taboru tramwajowego.

2.3.1

Obliczenie współczynnika dynamicznego.

φ

=1,35-0,005*l>1,1

φ

=1,35-0,005*35,4=1,173>1,1

Przyj

ę

to

φ

=1,173

φ

(n)

=1+((1-h)(

φ

-1))/0.5=1+((1-0.8)( 1.173-1))/0.5=1.07

2.3.2

Obliczenie wysoko

ś

ci h

1

umieszczenia siły P.

h

1

= h

1

I

+ h

1

II

h

1

I

=h

h

h

3

g

h

h

E

E

−

⋅

Edometryczny moduł nawierzchni drogowej E

h

=1000 Mpa

Edometryczny moduł gruntu E

g

=23 Mpa

h

1

I

=

m

76

0

3

0

23

1000

3

0

3

,

,

,

=

−

⋅

h

1

II

=0,26m

h

1

=0,76+0,26=1,02m

2.3.3

2.3.3

Obliczenie zasi

ę

gu działania siły P na gł

ę

boko

ś

ci

Σ

h.

β=35°

Σ

h=h

1

+h

2

+h

3

+h

4

+h

5

=1,02+0,24+0,20+0,36+0,10=1,92m

a

1

=

Σ

h*tg35

0

=1,34m

2.3.4

Ustalenie najniekorzystniejszego poło

ż

enia pojazdu w stosunku do konstrukcji przej

ś

cia.

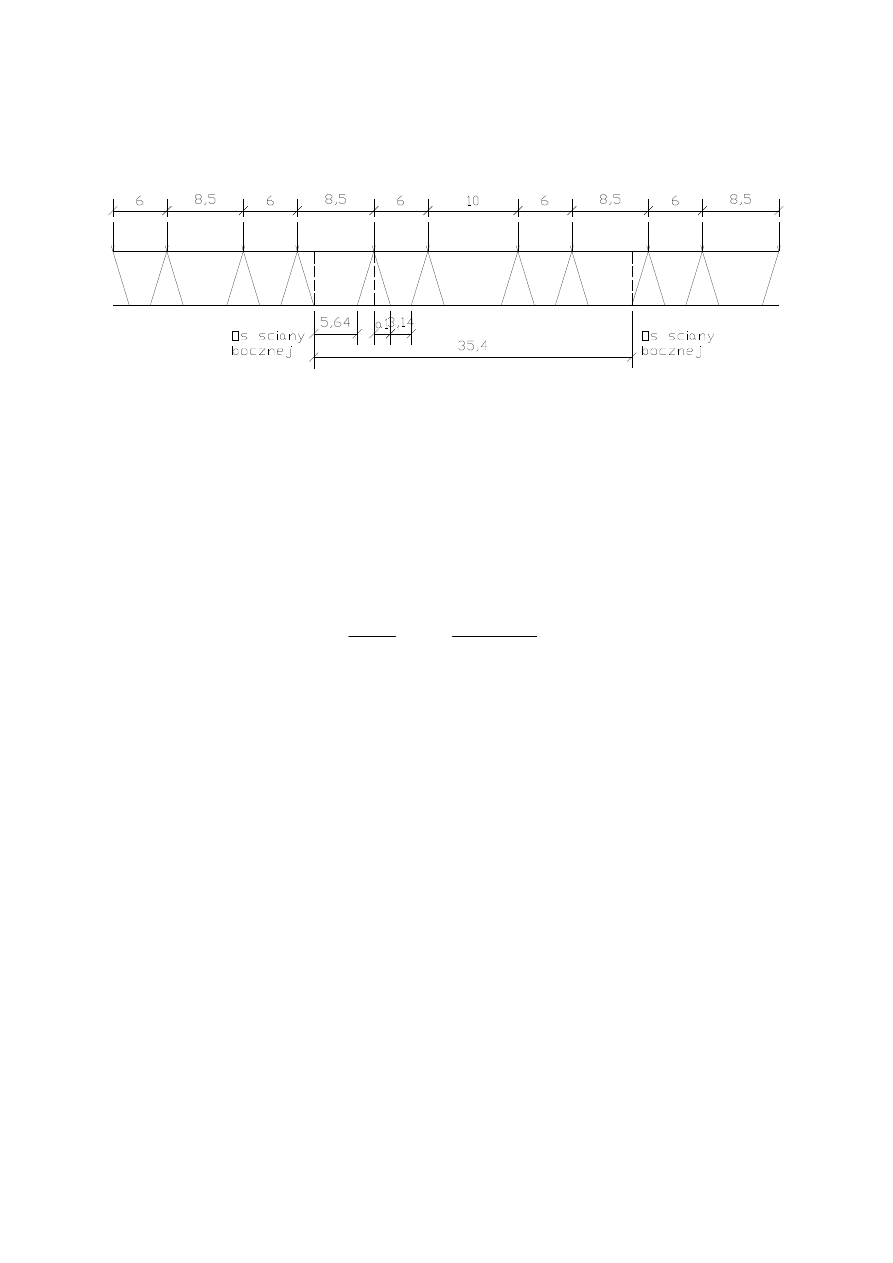
2.3.5

Obliczenie obci

ąż

e

ń

zmiennych:

a) obci

ąż

enie zmienne charakterystyczne:

-od siły skupionej:

kPa

45

28

34

1

14

3

150

07

1

a

P

P

2

2

1

h

p

1

,

)

,

(

,

.

)

(

)

(

=

⋅

⋅

=

⋅

=

π

ϕ

b) obci

ąż

enie zmienne obliczeniowe:

-od siły skupionej:

kPa

68

42

45

28

5

1

P

P

p

1

h

0

p

1

,

,

,

)

(

=

⋅

=

⋅

=

ϕ

Schemat obci

ąż

enia płyty stropowej:

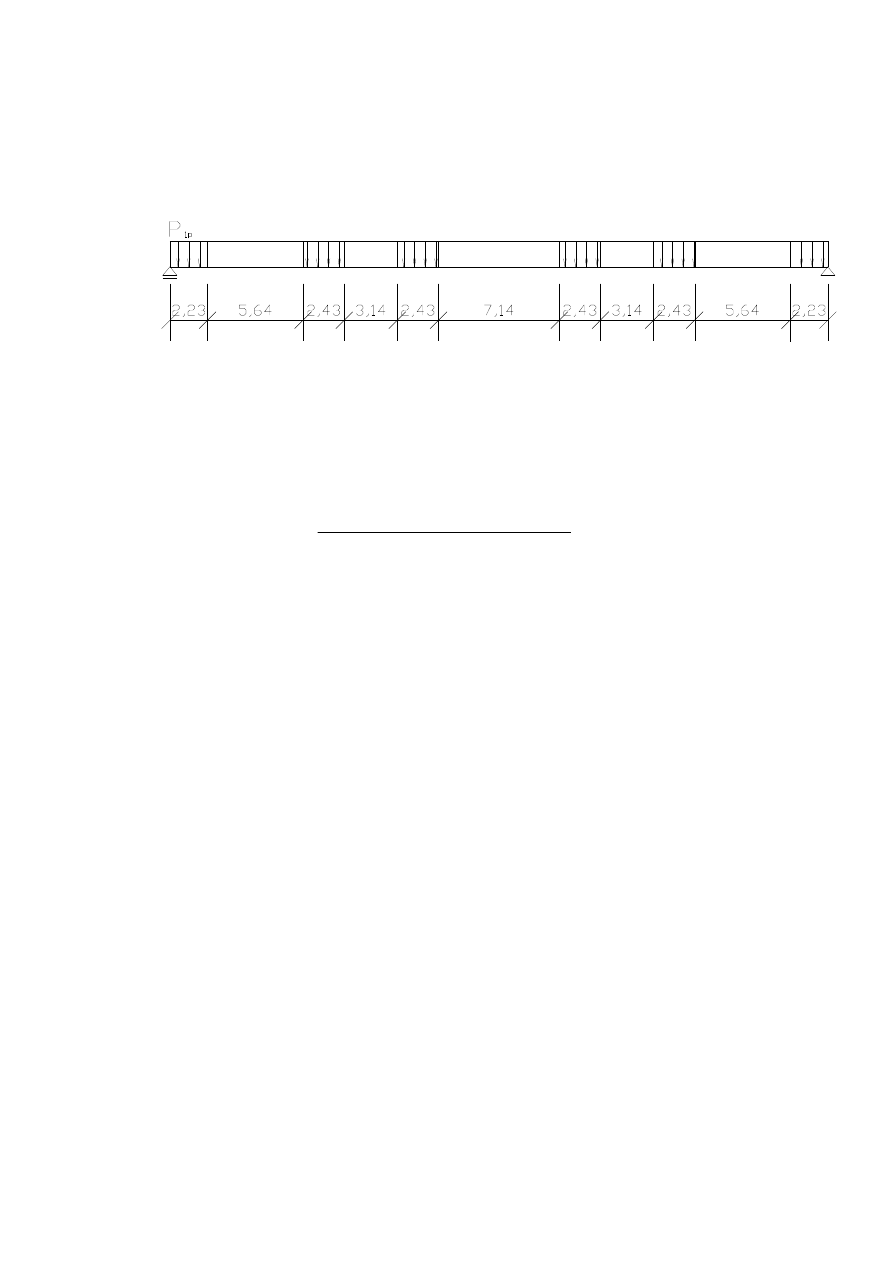
Do oblicze

ń

przyj

ę

to obci

ąż

enie równomiernie rozło

ż

one o stałej warto

ś

ci p jako warto

ść

ś

redni

ą

z obci

ąż

enia p

1p

o

na całej długo

ś

ci płyty stropowej.

kPa

10

17

40

35

23

2

43

2

43

2

43

2

43

2

23

2

68

42

P

,

,

,

,

,

,

,

,

,

=

+

+

+

+

+

⋅

=

2.3.6

Suma obci

ąż

e

ń

od taboru tramwajowego i samochodowego:

P=51 kN/m

2

+17,10 kN/m

2

=68,10 kN/m

2

2.

Obliczenie płyty stropowej:

Obliczenia przeprowadzono metod

ą

współczynników tabelarycznych. Metoda ta zakłada,

ż

e

ró

ż

nica odległo

ś

ci mi

ę

dzy poszczególnymi prz

ę

słami nie przekracza 20%.

Do oblicze

ń

przyj

ę

to:

-

rozpi

ę

to

ść

obliczeniow

ą

prz

ę

seł skrajnych i

ś

rodkowych l=5,00m

-

beton B30 o f

cfd

=1,20 MPa i f

cd

=16,7 MPa

-

stal klasy AII o f

yd

=310 MPa

-

grubo

ść

płyty stropowej t

i

=20 cm

-

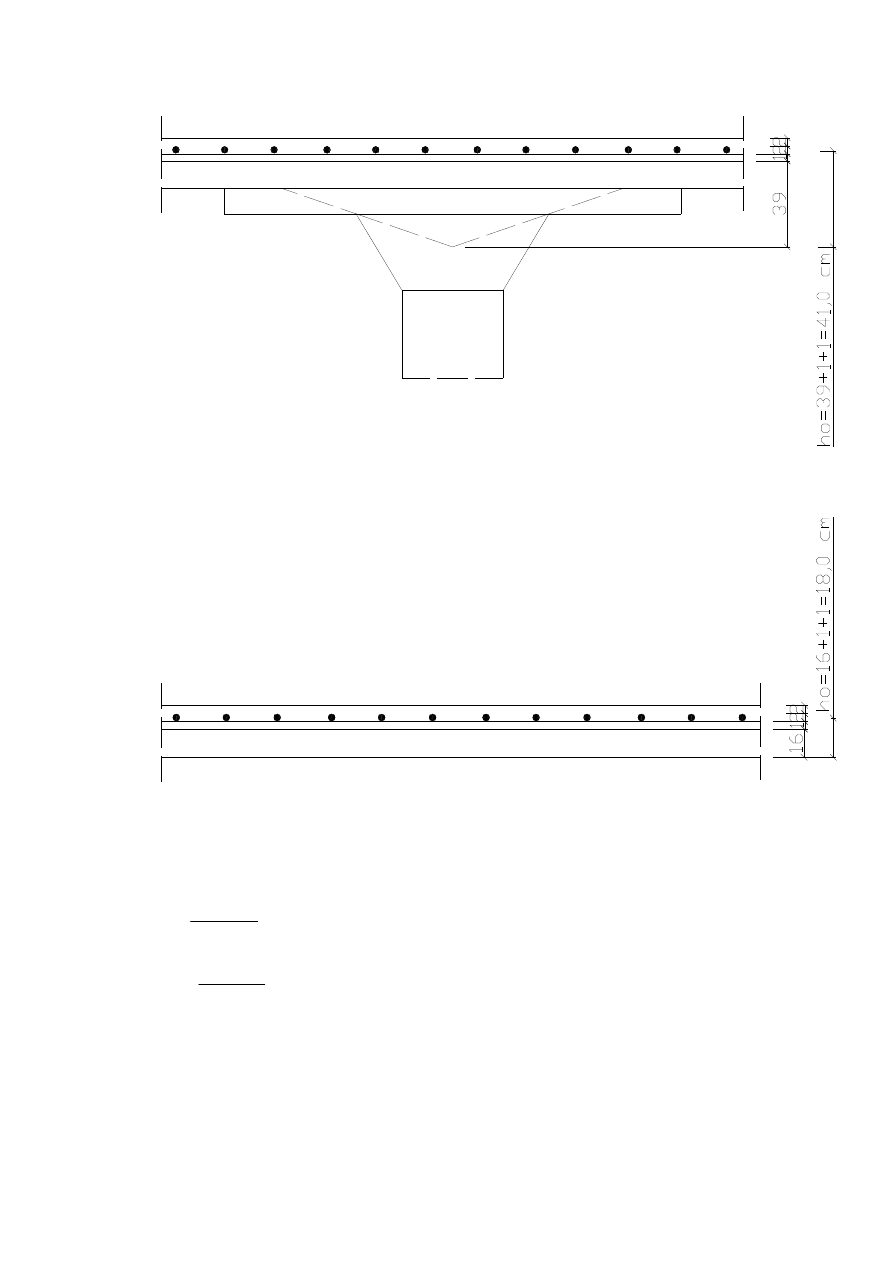
głowic

ę

słupa wg rysunku:

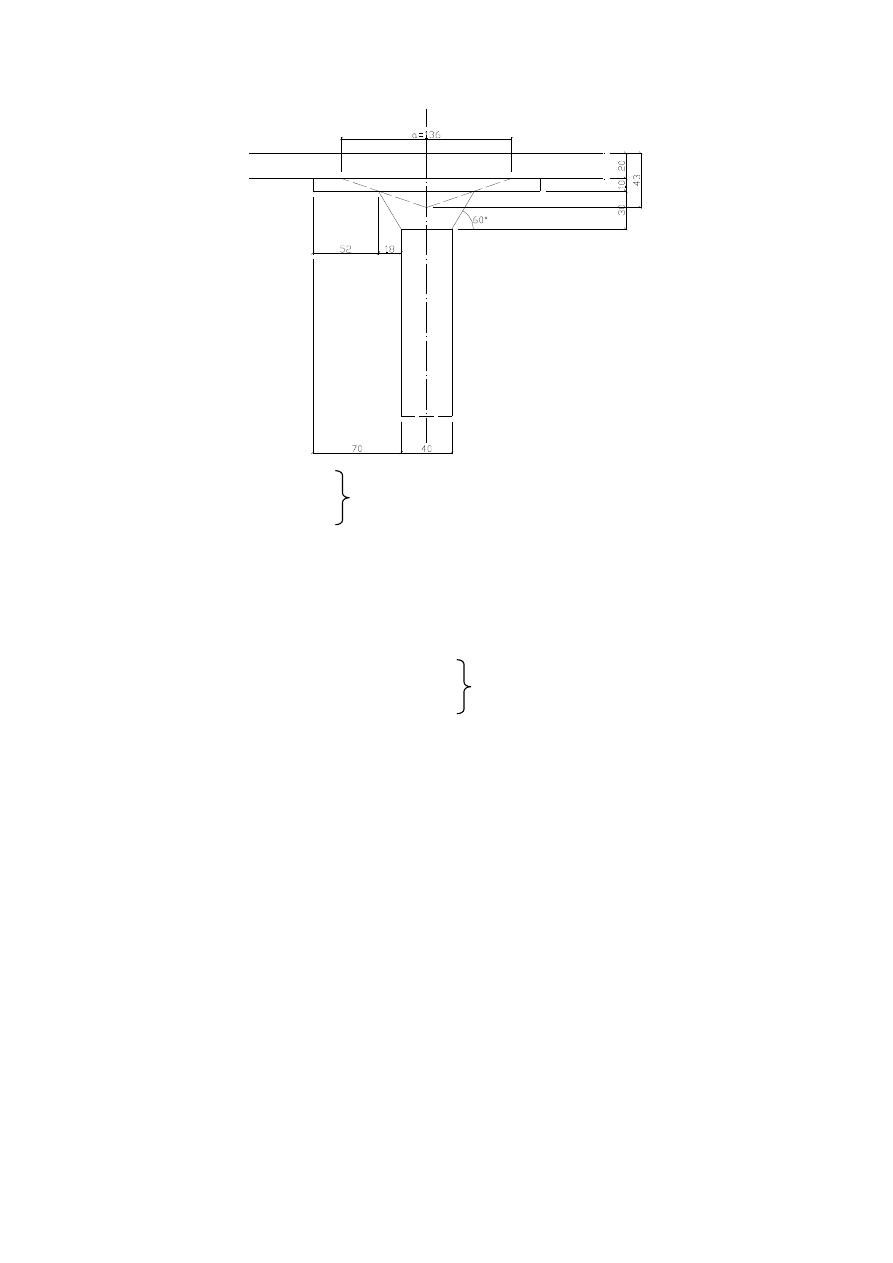
a=0.40+2*0.18+2*0.30=1.36 m

zakres ukrytego skosu

h=0.20+0.68/3=0.43 m

-

szeroko

ść

współpracuj

ą

ca b

f

I

b

f

I

=a+12*f

I

=1.36+12*0.20=3.76 > l/2=5.00/2=2.50 m

st

ą

d szeroko

ść

pasma głowicowego I=2.50 m

α

=

936

0

00

5

36

1

5

0

0

1

l

a

5

0

0

1

2

2

,

)

,

/

,

(

,

,

)

/

(

,

,

=

⋅

−

=

⋅

−

wg tab 10.46 [1]

β

=

926

0

00

5

36

1

0

1

l

a

0

1

2

2

,

)

,

/

,

(

,

)

/

(

,

=

−

=

−

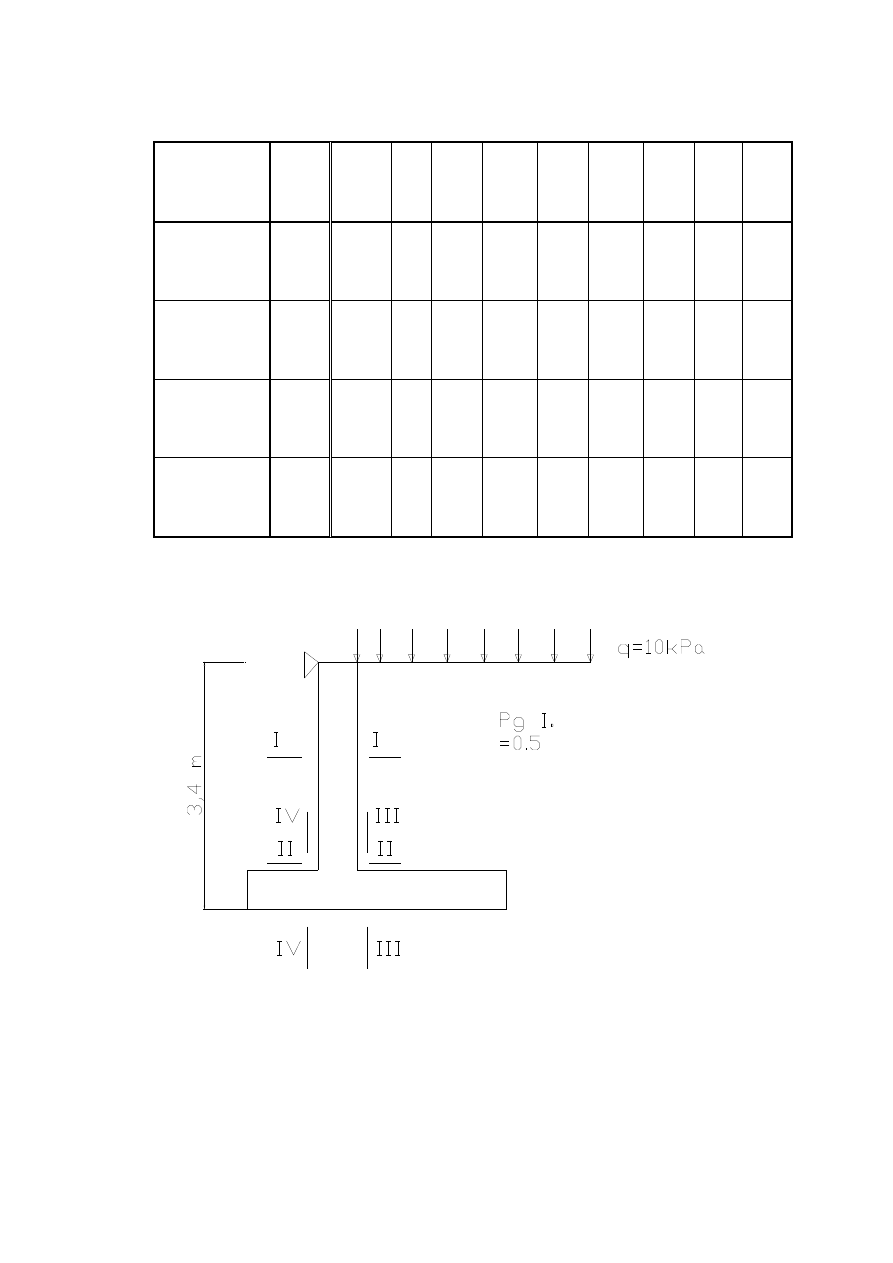
3.1

Obliczenie momentów (wg tab 10.46 [1] ):

a)

momenty prz

ę

słowe:

-

pasma głowicowe I-I :

przekroje skrajne 1-1

kNm

68

222

00

5

963

0

10

68

101

0

24

30

078

0

l

p

101

0

g

078

0

M

2

2

1

I

,

,

*

,

*

)

,

*

,

,

*

,

(

)

,

,

(

=

+

=

⋅

⋅

+

=

α

przekroje po

ś

rednie 2-2 i 3-3

kNm

14

151

00

5

923

0

10

68

075

0

24

30

047

0

l

p

075

0

g

047

0

M

2

2

3

2

I

,

,

*

,

*

)

,

*

,

,

*

,

(

)

,

,

(

,

=

+

=

⋅

⋅

+

=

β

przekroje po

ś

rednie 4-4

kNm

50

165

00

5

926

0

10

68

077

0

24

30

063

0

l

p

077

0

g

063

0

M

2

2

4

I

,

,

*

,

*

)

,

*

,

,

*

,

(

)

,

,

(

=

+

=

⋅

⋅

+

=

β

-

pasma mi

ę

dzygłowicowe II-II :

przekroje 1-1

kNm

17

206

00

5

963

0

10

68

096

0

24

30

067

0

l

p

096

0

g

067

0

M

2

2

1

II

,

,

*

,

*

)

,

*

,

,

*

,

(

)

,

,

(

=

+

=

⋅

⋅

+

=

α

przekroje po

ś

rednie 2-2 i 3-3

kNm

02

138

00

5

926

0

10

68

076

0

24

30

026

0

l

p

076

0

g

026

0

M

2

2

3

2

II

,

,

*

,

*

)

,

*

,

,

*

,

(

)

,

,

(

,

=

+

=

⋅

⋅

+

=

β

przekroje po

ś

rednie 4-4

kNm

02

135

00

5

926

0

10

68

063

0

24

30

051

0

l

p

063

0

g

051

0

M

2

2

4

II

,

,

*

,

*

)

,

*

,

,

*

,

(

)

,

,

(

=

+

=

⋅

⋅

+

=

β

-

pasma pozagłowicowe III-III

(liczymy na ¾ momentów powstaj

ą

cych w pasmach II )

przekroje 1-1

kNm

63

154

17

206

75

0

M

1

III

,

,

*

,

=

=

przekroje po

ś

rednie 2-2 i 3-3

kNm

52

103

02

138

75

0

M

3

2

III

,

,

*

,

,

=

=

przekroje po

ś

rednie 4-4

kNm

27

101

02

135

75

0

M

4

III

,

,

*

,

=

=

-

półpasma podporowe IV

(liczymy na ½ momentów powstaj

ą

cych w pa

ś

mie I )

przekroje 1-1

kNm

19

111

38

222

5

0

M

1

IV

,

,

*

,

=

=

przekroje 2-2 i 3-3

kNm

57

75

14

151

5

0

M

3

2

IV

,

,

*

,

,

=

=

przekroje 4-4

kNm

75

82

50

165

5

0

M

4

IV

,

,

*

,

=

=

b)

momenty podporowe (odczytano z tab 10.46 [1] dla a/l=1,36/5,00=0,272=0,3 )

-

pasma głowicowe I-I

przekroje 5-5 i 7-7

kNm

44

270

00

5

10

68

114

0

24

30

101

0

l

p

114

0

g

0101

M

2

2

7

5

I

,

,

*

)

,

*

,

,

*

,

(

)

,

(

,

−

=

+

−

=

⋅

+

−

=

przekroje po

ś

rednie 6-6

kNm

85

221

00

5

10

68

101

0

24

30

066

0

l

p

101

0

g

066

0

M

2

2

6

I

,

,

*

)

,

*

,

,

*

,

(

)

,

,

(

−

=

+

−

=

⋅

+

−

=

pasma mi

ę

dzygłowicowe II-II

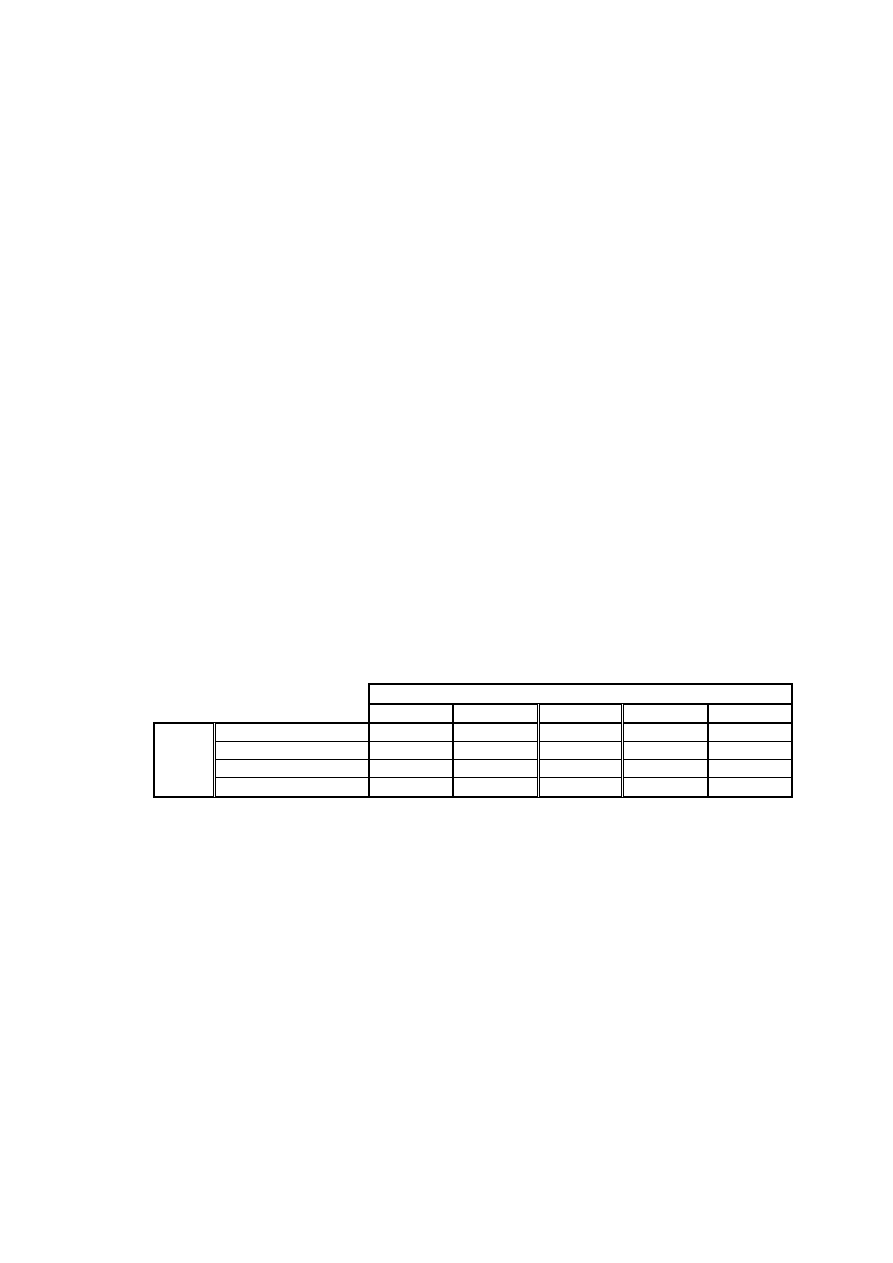
przekroje 5-5 i 7-7

kNm

02

90

00

5

926

0

10

68

042

0

24

30

034

0

l

p

042

0

g

034

0

M

2

2

7

5

II

,

,

*

,

*

)

,

*

,

,

*

,

(

)

,

,

(

,

−

=

+

−

=

⋅

⋅

+

−

=

β

przekroje 6-6

kNm

00

62

00

5

926

0

10

68

034

0

24

30

012

0

l

p

034

0

g

012

0

M

2

2

6

II

,

,

*

,

*

)

,

*

,

,

*

,

(

)

,

,

(

−

=

+

−

=

⋅

⋅

+

−

=

β

-

pasma pozagłowicowe III-III

przekroje 5-5 i 7-7

kNm

52

67

02

90

75

0

M

7

5

III

,

)

,

(

*

,

,

−

=

−

=

przekroje 6-6

kNm

50

46

00

62

75

0

M

6

III

,

)

,

(

*

,

−

=

−

=

-

półpasma podporowe IV-IV

przekroje 5-5 i 7-7

kNm

22

135

44

270

5

0

M

7

5

IV

,

)

,

(

*

,

,

−

=

−

=

przekroje 6-6

kNm

93

110

85

221

5

0

M

6

IV

,

)

,

(

*

,

−

=

−

=

Tabelaryczne zestawienie momentów w kNm :

Przekroje

1-1

2-2,3-3

4-4

5-5,7-7

6-6

Pasma

Głowicowe I-I

222,38

151,14

165,50

-270,50

-221,85

Mi

ę

dzygłowicowe II-II

206,17

138,02

135,02

-90,02

-62,00

Pozagłowicowe III-III

154,63

103,52

101,27

-67,52

-46,50

Podporowe IV-IV

111,19

75,57

82,75

-135,22

-110,93

3.2

Przekroje przez płyt

ę

Przyj

ę

to zbrojenie pr

ę

tami

Φ

20

a)

w kierunku 1

-

w prz

ęś

le, pasma I, II, III, IV oraz przekroje 1, 2, 3, 4

-

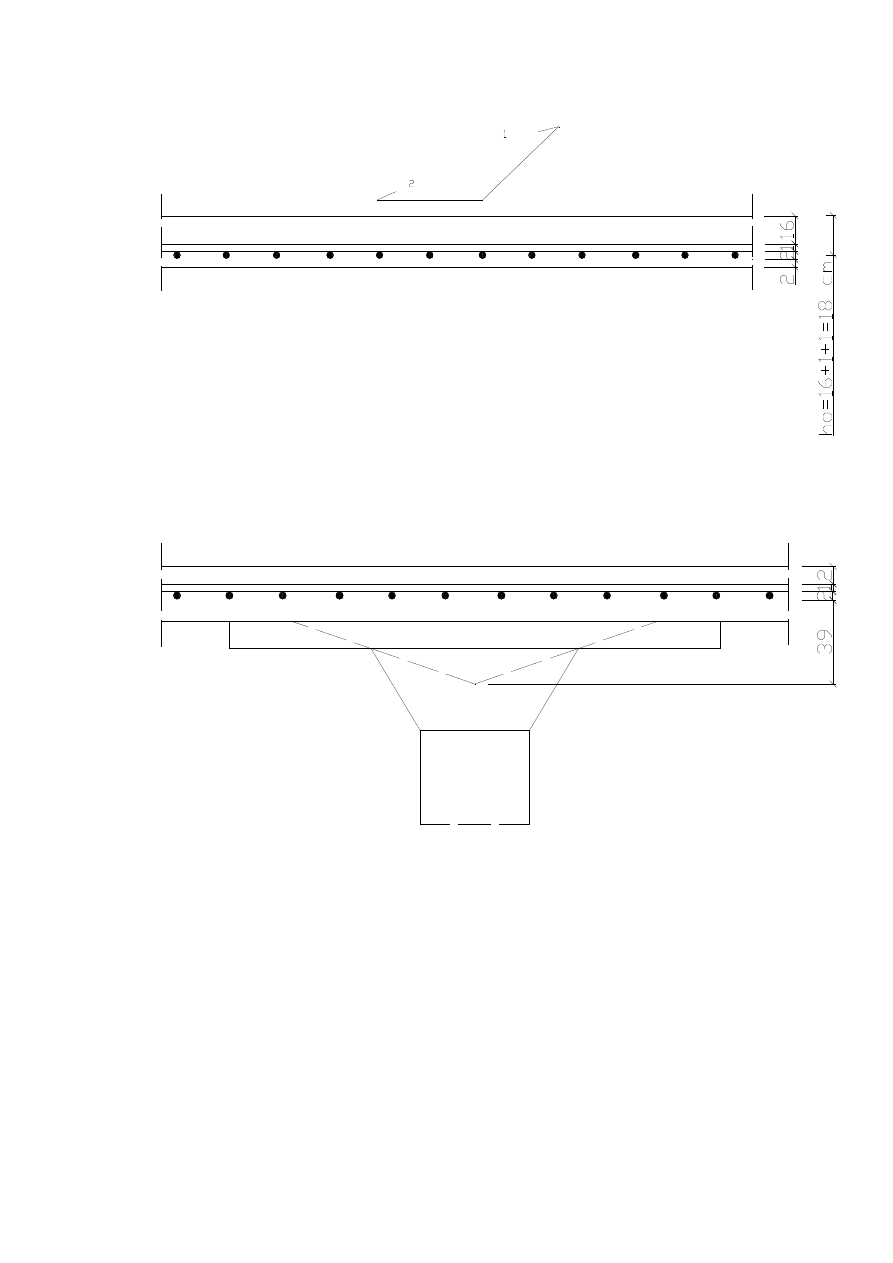
nad podpor

ą

, pasmo I, przekroje 5, 6, 7, 8

(h

o

obliczone z zało

ż

enia ukrytego skosu)

-

pasma II, III i IV, przekroje 5, 6, 7, 8

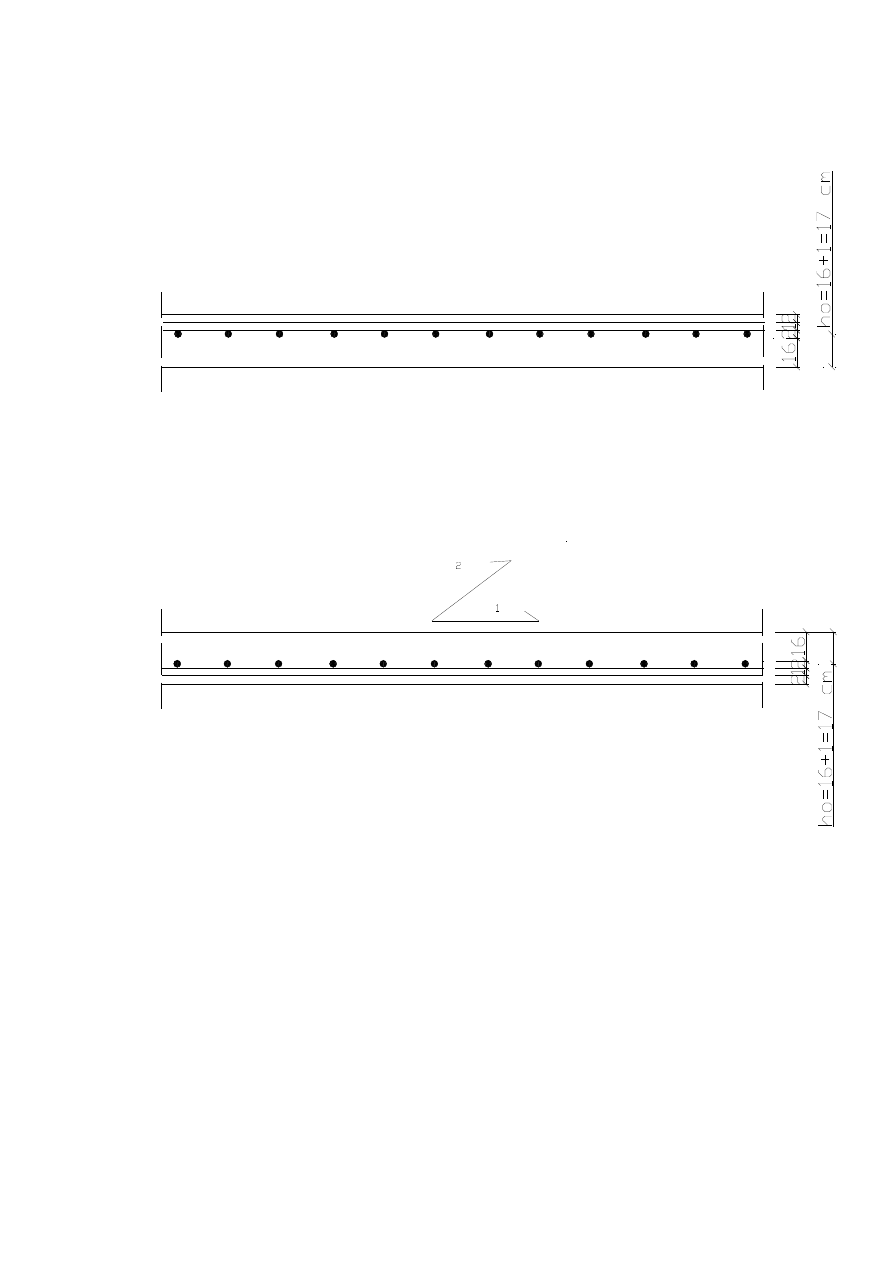
b)

w kierunku 2

w prz

ęś

le, pasma II, III, IV oraz I, przekroje 1, 2, 3, 4

-

nad podpor

ą

, pasma I, przekroje 5, 6, 7, 8

-

pasma II, III, IV , przekroje 5, 7, 6

Obliczenia przeprowadzono na 1,0mb szeroko

ś

ci stropu. Wyniki przedstawiono w

tabeli poni

ż

ej.

cd

2

o

f

h

b

M

A

⋅

⋅

=

->

ξ

( tab 10.7 [1] )

o

yd

s

h

f

M

A

⋅

⋅

=

ξ

Ze wzgl

ę

dów konstrukcyjnych (unikni

ę

cia pomyłek, jednoznaczno

ś

ci wykonania) ilo

ść

zbrojenia w obu kierunkach przyj

ę

to jednakow

ą

. Obliczenia przeprowadzono dobieraj

ą

c

niewykorzystane h

o

(mniejsze) dla poszczególnych przekrojów.

Literatura:

[1] – Grabiec Kalikst – „Konstrukcje betonowe – przykłady oblicze

ń

”

Zestawienie zbrojenia dla poszczególnych przekrojów w pasmach.

Pasmo

Przekrój Moment

[kNm]

b

[m]

h

o

[m]

A

ξ

A

s

[m

2

]

A

s

[cm

2

]

Φ

20

[szt.

na

1mb]

Φ

20

[szt.

dla

całej

pow.]

Głowice I-I o
szeroko

ś

ci 2,5m

1-1

2-2,3-3

4-4

5-5,7-7

6-6

222,38
151,14
165,50

-270,44
-221,85

1,0
1,0
1,0
1,0
1,0

0,180
0,180
0,180
0,400
0,400

0,4110
0,2793
0,3059
0,1012
0,0830

0,713
0,832
0,812
0,947
0,952

0,0056
0,0033
0,0001
0,0023
0,0019

55,89
32,56

1,18

23,03
18,79

18
11

1
8
6

45
25
28
23
20

Mi

ę

dzygłowicowe

II-II o szeroko

ś

ci

2,5m

1-1

2-2,3-3

4-4

5-5,7-7

6-6

206,17
138,02
135,02

-90,02
-62,00

1,0
1,0
1,0
1,0
1,0

0,180
0,180
0,180
0,170
0,170

0,3810
0,2551
0,2495
0,1865
0,1285

0,744
0,850
0,854
0,897
0,932

0,0049
0,0029
0,0028
0,0019
0,0013

49,66
29,10
28,33
19,04
12,62

16
10
10

7
5

33
23
23

8
8

Pozagłowicowe
III-III o
szeroko

ś

ci 2,5m

1-1

2-2,3-3

4-4

5-5,7-7

6-6

154,63
103,52
101,27

-67,52
-46,50

1,0
1,0
1,0
1,0
1,0

0,180
0,180
0,180
0,170
0,170

0,2858
0,1913
0,1872
0,1399
0,0963

0,828
0,893
0,896
0,925
0,959

0,0033
0,0021
0,0020
0,0014
0,0009

33,47
20,77
20,25
13,85

9,20

11

7
7
5
3

25
18
18

5
5

Półpasmo
podporowe o
szeroko

ś

ci 1,25m

1-1

2-2,3-3

4-4

5-5,7-7

6-6

111,19

75,57
82,75

-135,22
-110,93

1,0
1,0
1,0
1,0
1,0

0,180
0,180
0,180
0,170
0,170

0,2055
0,1397
0,1529
0,2802
0,2298

0,884
0,925
0,916
0,831
0,867

0,0023
0,0015
0,0016
0,0031
0,0024

22,54
14,64
16,19
16,38
12,78

8
7
7
7
5

9
7
7
7
5

4.

Obliczenia

ś

ciany oporowej

4.1

Parametry geotechniczne

a)

grunt wyst

ę

puj

ą

cy w poziomie posadowienia płyty fundamentowej

-

piaski gruboziarniste I

D

=0,5

-

k

ą

t tarcia wewn

ę

trznego

Φ

u

(n)

=33

o

,

Φ

u

(r)

=(1+-0,1)33

o

={30-36

o

}

-

spójno

ść

C

u

(r)

=0

-

Ci

ęż

ar obj

ę

to

ś

ciowy

γ

β

(n)

=17,0 kN/m3,

γ

β

(r)

=(1+-0,1)*17,0={15,3-18,7}kN/m3

-

Współczynnik no

ś

no

ś

ci N

D

=18,4, N

B

=7,53

b)

parametry dla zasypki jak wy

ż

ej

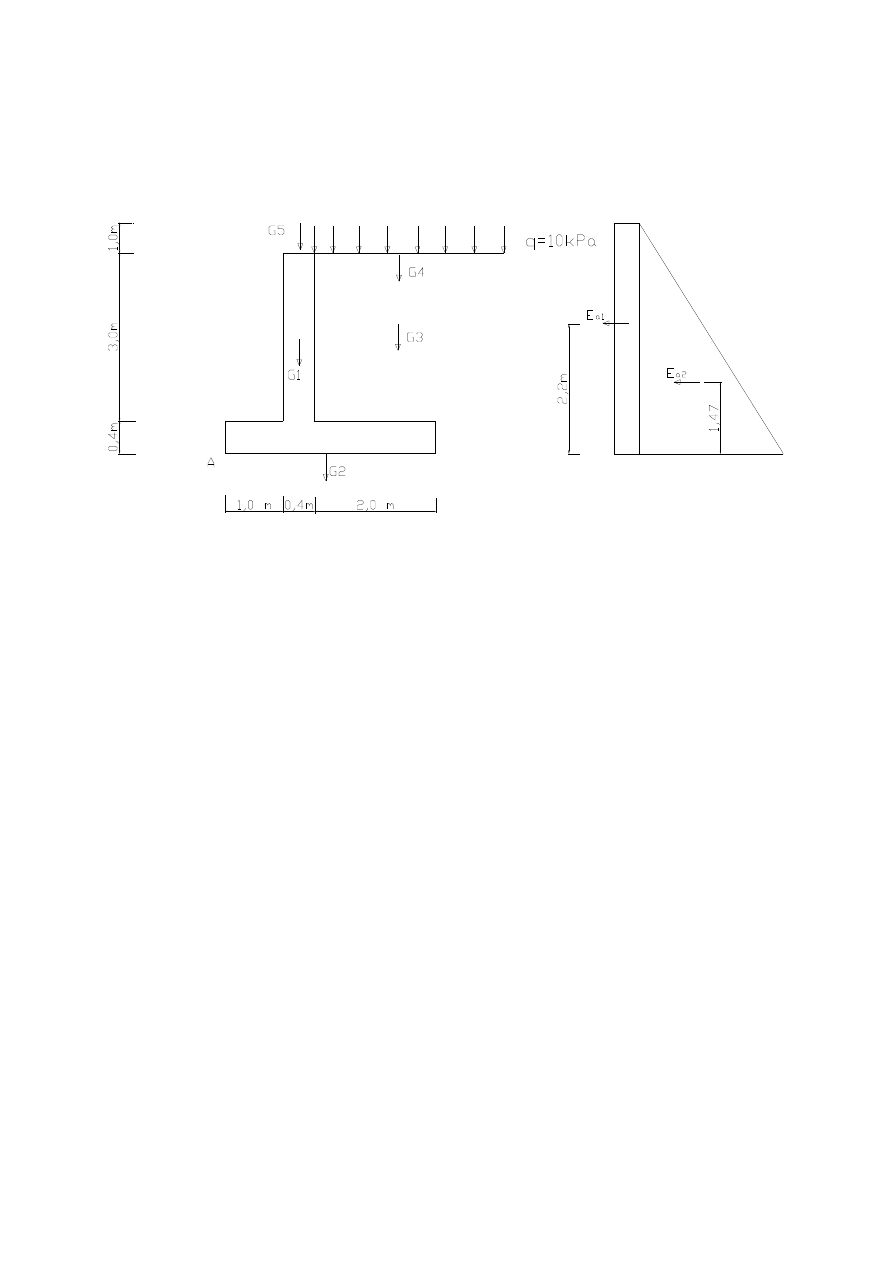
4.2

Obci

ąż

enia działaj

ą

ce na

ś

cian

ę

oporow

ą

-

warto

ść

obliczeniowa naziomu

q

r

=g

r

=(1+-0,2)*10={8,0-12,0} kPa

-

współczynnik parcia granicznego, czynnego dla gładkiej

ś

ciany

Ka=tg

2

(45

o

-

Φ

(n)

/2)=0,307

-

jednostkowe parcie graniczne gruntu

e

a

=

γ

(n)

(z+h

z

)K

a

, gdzie h

z

-wysoko

ść

zast

ę

pcza h

z

=q

(n)

/

γ

(n)

czyli

e

a

=(17*z+10)*0,307

dla z=0

e

a

=3,07 kN/m2

dla z=4,4 e

a

=26,03 kN/m2

-

wypadkowa parcia granicznego gruntu

E

a1

(n)

=4,4*3,07=13,51 kN/m

E

a2

(n)

=0,5*4,4*22,96=50,51 kN/m

-

przyjmuj

ą

c wymiary

ś

ciany oporowej jak na rysunku składowe pionowe obci

ąż

enia wynosz

ą

G

1

(n)

=0,4*3,0*1,0*25,0=30,0kN/m

G

1

=(1+-0,1)*30,0={27-33} kN/m

G

2

(n)

=0,4*3,4*1,0*25,0=34,0kN/m

G

2

=(1+-0,1)*34,0={30,6-37,4} kN/m

G

3

(n)

=2,0*3,0*1,0*17,0=102,0kN/m

G

3

=(1+-0,2)*102,0={81,6-122,4} kN/m

G

4

(n)

=2,0*10,0*1,0=20,0kN/m

G

4

=(1+-0,2)*20,0={16,0-24,0} kN/m

G

5

(n)

=((30,24+68,10)*5,0/2=244,50kN/m

G

5

=(1+-0,2)*244,50={195,6-293,4} kN/m

Σ

G

i

(n)

=430,50 kN/m

350,80

Σ

G

i

=

kN/m

510,20

4.3

Sprawdzenie stanów granicznych gruntów

a)

wypieranie gruntu spod płyty fundamentowej

Nr<m*Q

fnb

Nr<

Σ

G

i

=510,20 kN/m m=0,9

)]

)

,

(

)

,

(

)

*

,

[(

)

(

min

)

(

)

(

B

r

B

B

D

r

D

D

L

r

u

L

fnb

i

B

g

N

L

B

25

0

1

i

D

g

N

L

B

5

1

1

i

c

N

L

B

3

0

1

L

B

Q

⋅

⋅

⋅

⋅

⋅

−

+

⋅

⋅

⋅

⋅

⋅

+

+

⋅

⋅

⋅

+

⋅

=

ρ

ρ

L=1,0 m
B=B-2e

B

, e

B

=

Σ

Mo/

Σ

G

i

B/L=0
D

min

=0

b)

wypadkowa siły parcia

)

(

)

(

*

*

n

2

f

1

f

r

Ea

Ea

γ

γ

=

γ

f1

=1,2

γ

f2

=1,0

Ea1

(r)

=1,2*1,0*13,51=16,21 kN/m

Ea2

(r)

=1,2*1,0*50,51=60,61 kN/m

M

o

(n)

=33*0,5+16,21*2,2+60,61*1,47-122,4*0,7-24*0,7+293,4*0,5=185,48 kNm

E

B

=185,48/510,20=0,33 m

B=3,4-2*0,33=2,74 m

16

0

20

510

61

60

21

16

G

E

tg

i

a

B

,

,

,

,

=

+

=

Σ

Σ

=

δ

5

0

i

30

0

28

0

5774

0

16

0

tg

tg

B

,

,

,

,

,

=

⇒

≈

=

=

φ

δ

Q

fnb

=3,4*1,0*(7,50*17,0*2,74*0,5)=593,90 kN/m

M*Q

fnb

=0,9*593,90=534,50 kN/m > 510,20 kN/m

Warunek obliczeniowy I stanu granicznego spełniony.

c)

obliczeniowe obci

ąż

enia jednostkowe podło

ż

a

∑

∑

±

=

W

Mo

B

0

1

G

q

i

r

/

*

,

/

gdzie W=3,4

2

*1,0

0

1

4

3

48

185

4

3

0

1

20

510

q

2

r

,

*

,

,

,

*

,

,

±

=

q

rmax

=166,10

q

rmin

=134,01

0

4

24

1

01

134

10

166

q

q

r

r

,

,

,

,

min

max

<

=

=

4.4

Przesuni

ę

cie w poziomie posadowienia fundamentu i w podło

ż

u

a)

przesuni

ę

cie w poziomie posadowienia

Q

f

(r)

=

Σ

E

a

(r)

=16,21+60,61=76,82 kN

Q

ft

=

Σ

G

i

*

µ

=350,80*0,5=175,4 kN

Q

f

(r)

*m

f

=175,4*0,95=166,63>76,82

b)

przesuni

ę

cie w podło

ż

u

Q

f

(r)

=76,82 kN

Q

ft

=

Σ

G

i

*tg

Φ

u

(r)

=350,8*tg30=202,53 kN

Q

ft

*m

f

=0,95*202,53=192,41 kN>76,82 kN

W obu przypadkach warunek obliczeniowy I stanu granicznego jest spełniony.

4.5

Sprawdzenie stateczno

ś

ci na obrót wzgl

ę

dem przedniej kraw

ę

dzi podstawy (pkt a))

Moment obracaj

ą

cy

ś

cian

ę

oporow

ą

Mo

(r)

=16,21*2,2+60,61*1,47=213,66 kNm

Moment utrzymuj

ą

cy

ś

cian

ę

oporow

ą

Mu

(r)

=27*1,2+30,6*1,7+195,60*1,2+(81,6+16)*2,4=553,38 kN

Mu

(r)

*mo=553,38*0,8=442,70>Mo

(r)

=213,66 kNm

Warunek spełniony

4.6

Sprawdzenie stanów granicznych konstrukcji

A)

warto

ść

obliczeniowa jednostkowego parcia gruntu

e

ar

=

γ

f1

*

γ

f2

*e

i

dla z=0

e

ar

=1,2*1,1*10,0*0,307=4,05

dla z=1

e

ar

=1,2*1,1*(17*1,0+10)*0,307=10,49

dla z=3

e

ar

=1,2*1,1*(17*3,0+10)*0,307=27,42

dla z=4,4 e

ar

=1,2*1,1*(17*4,4+10)*0,307=34,36

c)

płyta pionowa – obliczeniowe momenty zginaj

ą

ce w przekroju I-I, II-II

M

1I

=4,05*4,0*2,0+0,5*20,67*4*1/3*4,0=87,52 kNm

M

1II

=4,05*2,0*0,5*2,0+0,5*12,36*2*1/3*2,0=16,34 kNm

Do wykonania

ś

ciany oporowej przyj

ę

to beton klasy B30

d)

powierzchnia zbrojenia na 1m długo

ś

ci

ś

ciany oporowej wynosi

-

w przekroju I-I

h=0,4 m ho=h-0,05=0,35 m b=1 m

805

0

06

0

12

35

0

0

1

088

0

f

h

b

M

A

2

cd

2

o

I

1

,

,

*

,

*

,

,

=

⇒

=

=

⋅

⋅

=

ζ

2

2

yd

o

I

1

cm

29

22

m

002229

0

35

0

210

805

0

088

0

f

h

M

Fa

,

,

,

*

*

,

,

=

=

=

⋅

⋅

=

ζ

przyj

ę

to 12

Φ

16 o fa=24,14

-

w przekroju II-II

h=0,4 m ho=h-0,05=0,35 m b=1 m

995

0

011

0

12

35

0

0

1

016

0

f

h

b

M

A

2

cd

2

o

II

1

,

,

*

,

*

,

,

=

⇒

=

=

⋅

⋅

=

ζ

2

2

yd

o

II

1

cm

39

6

m

000639

0

35

0

210

995

0

016

0

f

h

M

Fa

,

,

,

*

*

,

,

=

=

=

⋅

⋅

=

ζ

przyj

ę

to 4

Φ

16 o fa=8,04

a)

płyta pozioma

-

warto

ść

obliczeniowa wypadkowych sił parcia

γ

f1

=1,2

γ

f2

=1,1

E

a1

(r)

=4,05*4,4=17,82 kN

E

a2

(r)

=0,5*30,31*4,4=66,68 kN

Σ

M

o

(r)

=33,0*0,5+17,82*2,2+66,68*1,47-122,4*0,7-24*0,7+293,4*0,5=197,94 kNm

-

obci

ąż

enie jednostkowe obliczeniowe podło

ż

a

q

r

=510,20/1,0*3,4+-(197,94*5,20)/(1,0*3,4

2

)=150,05+-89,04

q

rmax

=239,09 kN/m

2

q

rmin

=61,02 kN/m

2

q

rmax

/ q

rmin

=3,92<4,0

-

w przekroju III-III

Obci

ąż

enie obliczeniowe działaj

ą

ce od góry (ci

ęż

ar płyty fundamentowej, ci

ęż

ar gruntu i

obci

ąż

enie naziomu

G

III

=1,1*0,4*25+1,2*4,0*17,0=92,60 kN/m

2

-

warto

ść

obliczeniowa momentu zginaj

ą

cego w przekroju III-III

M

1III

=

kNm

2

5

2

0

2

2

20

133

60

92

02

61

60

92

d

2

q

q

2

2

III

III

1

III

1

III

,

,

*

)

,

,

(

)

,

,

(

*

)

(

)

(

min

=

−

+

−

=

−

+

−

σ

σ

-

powierzchnia zbrojenia na 1m długo

ś

ci płyty fundamentowej

h=0,4 m ho=h-0,05=0,35 m b=1 m

0

1

0035

0

12

35

0

0

1

0052

0

f

h

b

M

A

2

cd

2

o

II

1

,

,

*

,

*

,

,

=

⇒

=

=

⋅

⋅

=

ζ

2

2

yd

o

II

1

cm

32

9

m

000932

0

35

0

210

0

1

0052

0

f

h

M

Fa

,

,

,

*

*

,

,

=

=

=

⋅

⋅

=

ζ

przyj

ę

to 5

Φ

16 o fa=10,05cm

2

-

w przekroju IV-IV

Moment zginaj

ą

cy w przekroju IV-IV od odporu gruntu działaj

ą

cego na wspornik o długo

ś

ci 1m

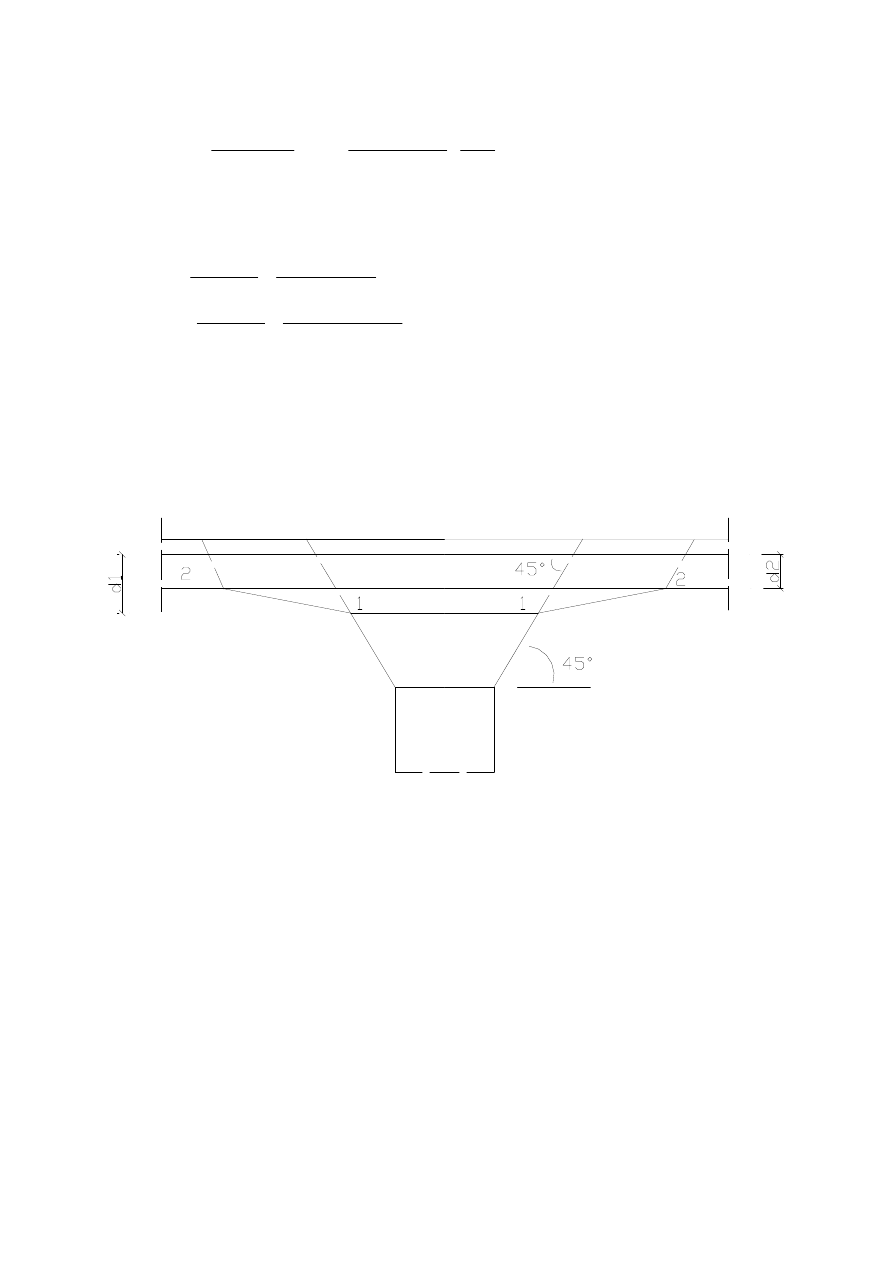
07

93

2

0

1

2

2

133

09

239

d

2

q

q

M

2

2

IV

rIV

r

IV

1

,

,

,

*

,

,

*

max

=

+

=

+

=

-

powierzchnia zbrojenia na 1m długo

ś

ci płyty fundamentowej

h=0,4 m ho=h-0,05=0,35 m b=1 m

980

0

044

0

12

35

0

0

1

093

0

f

h

b

M

A

2

cd

2

o

IV

1

,

,

*

,

*

,

,

=

⇒

=

=

⋅

⋅

=

ζ

2

2

yd

o

IV

1

cm

09

15

m

001509

0

35

0

210

980

0

093

0

f

h

M

Fa

,

,

,

*

*

,

,

=

=

=

⋅

⋅

=

ζ

przyj

ę

to 8

Φ

16 o Fa=16,08cm

2

Zbrojenie płyty pokazano na rysunku

5.

Sprawdzenie stropu grzybkowego na przebicie

W przypadku głowic w stropach grzybkowych no

ś

no

ść

na przebicie nale

ż

y sprawdzi

ć

w

przekrojach 1 i 2

5.1 Przekrój 1

N

sd

=(g+p)*A<N

rd

=f

ctd

*d

1

A=1,12 m beton B30 o f

ctd

=1,20Mpa

N

sd

=(30,24+68,10)*1,12<1200*0,43=N

rd

110,14 kN<516 kN -> warunek spełniony

5.2 Przekrój 2

N

sd

=(g+p)*A<N

rd

=f

ctd

*d

2

A=1,42 m beton B30 o f

ctd

=1,20Mpa

N

sd

=(30,24+68,10)*1,42<1200*0,19=N

rd

139 kN<228 kN -> warunek spełniony

Przebicie nie nast

ą

pi.