[e-mail]

hasło: 2011wmimb

Wydz. In

ż

ynierii

Ś

rodowiska

Politechniki Warszawskiej

1

WYTRZYMAŁO

ŚĆ

MATERIAŁÓW I MECHANIKA BUDOWLI

Wykład 4

Wi

ę

zy nieidealne, tarcie

1. Tarcie po

ś

lizgowe - definicja, podział, prawa tarcia, modele tarcia

2. Tarcie toczne - definicja, podział, prawa tarcia

3. Analiza stanu równowagi granicznej układów z tarciem

Opracowanie : dr in

ż

. Szymon Imiełowski

prof. Zbigniew Kowalewski

W przypadku gdy wi

ę

zy nie s

ą

powierzchniami idealnie gładkimi (wi

ę

zy nieidealne), z wi

ę

zami

stowarzyszona jest składowa styczna siły reakcji - siła tarcia.

Podstawowe przypadki tarcia

- tarcie po

ś

lizgowe

- tarcie toczne
- tarcie ci

ę

giem o kr

ąż

ek

2

1

F

F

≠

Wi

ę

zy nieidealne, tarcie

2

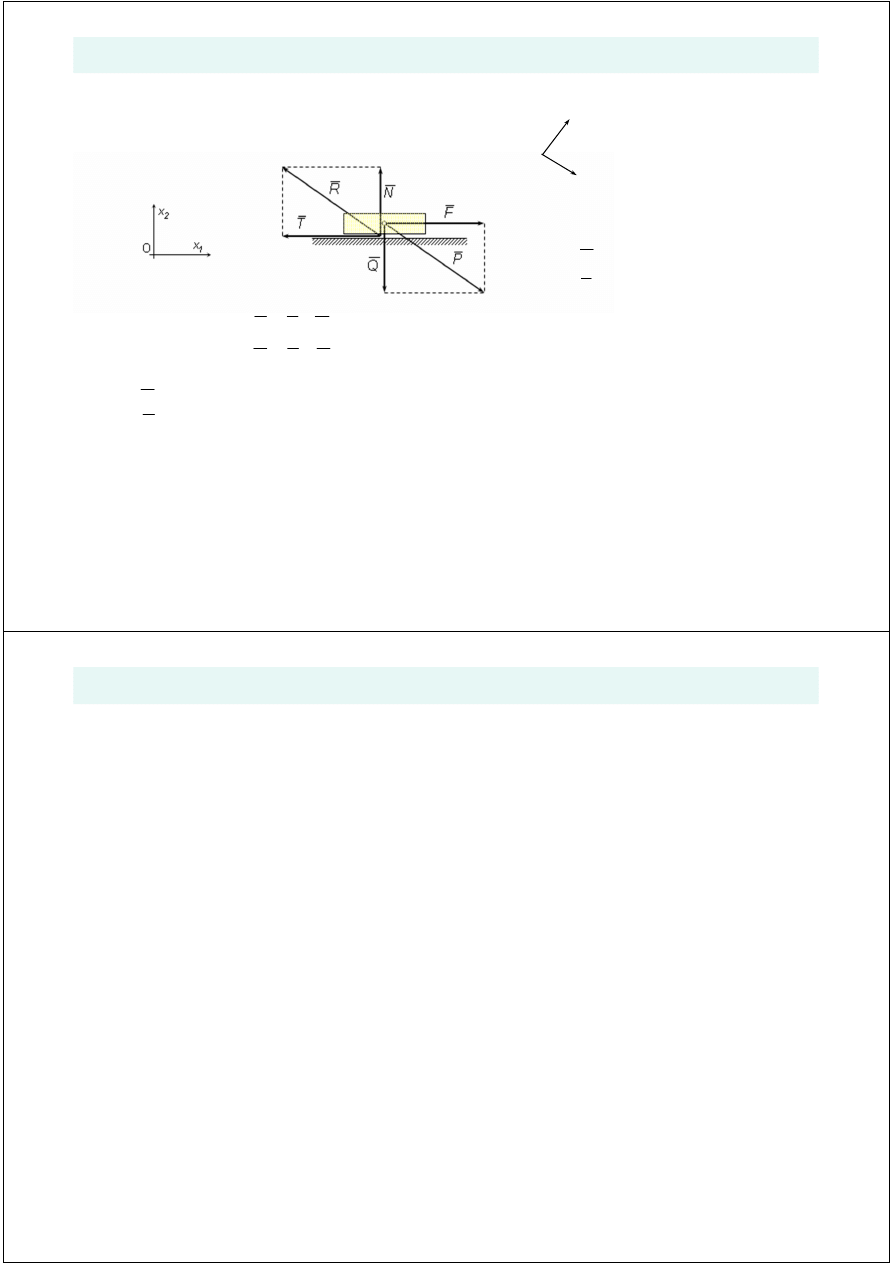
- składowa normalna siły nacisku równa sile reakcji w przypadku wi

ę

zów idealnych

- siła tarcia po

ś

lizgowego, jest opisana wektorem stycznym do powierzchni wi

ę

zów

- wypadkowa sił czynnych

- wypadkowa sił reakcji

Q

F

P

+

=

N

T

R

+

=

- ci

ęż

ar

- siła zewn

ę

trzna

Q

F

N

T









=

=

−

=

=

=

−

=

∑

∑

(*)

,

0

,

0

1

2

F

T

T

F

X

Q

N

Q

N

X

2

ε

1

ε

∑

=

−

=

0

1

R

P

ε

Tarcie Po

ś

lizgowe

3

•

Tarcie suche:

wyst

ę

puje w przypadku, gdy powierzchnie tr

ą

ce stykaj

ą

si

ę

ze sob

ą

bez po

ś

rednictwa

rozdzielaj

ą

cej jej warstwy smarów

•

Tarcie płynne:

wyst

ę

puje w przypadku, gdy pomi

ę

dzy stykaj

ą

cymi si

ę

ciałami znajduje si

ę

warstwa smaru

(ciecz)

•

Tarcie półpłynne:

jest przypadkiem po

ś

rednim mi

ę

dzy wy

ż

ej wymienionymi typami tarcia po

ś

lizgowego

Typy tarcia po

ś

lizgowego

4

Podział tarcia po

ś

lizgowego ze wzgl

ę

du na mo

ż

liwo

ść

ruchu ciał

1. Tarcie statyczne

– ciało pozostaje w spoczynku

●

siła tarcia statycznego równowa

ż

y składow

ą

styczn

ą

obci

ąż

enia,

przeciwdziała mo

ż

liwemu ruchowi ciała;

●

jej zwrot jest przeciwny do zwrotu wektora mo

ż

liwego przesuni

ę

cia;

●

jej warto

ść

i warto

ść

graniczna zale

żą

od aktualnej warto

ś

ci obci

ąż

enia i rodzaju podło

ż

a

f

S

- jest wyznaczanym do

ś

wiadczalnie

współczynnikiem tarcia statycznego

2. Tarcie kinetyczne

– ciało porusza si

ę

●

siła tarcia przyjmuje stała warto

ść

równ

ą

f

k

- jest wyznaczalnym do

ś

wiadczalnie

współczynnikiem tarcia kinetycznego

●

zwrot wektora siły tarcia kinetycznego jest przeciwnym do zwrotu wektora pr

ę

dko

ś

ci

Analiza zachowania ciała przy wzrastaj

ą

cej warto

ś

ci siły zewn

ę

trznej F

T

N

k

f

gr

T

T

=

=

N

f

T

T

s

gr

=

≤

<

0

Zało

ż

enie:

Warto

ś

ci współczynników tarcia f

s

i f

k

zale

żą

tylko od rodzaju powierzchni tn

ą

cych

,

nie zale

żą

od:

warto

ś

ci siły nacisku

N

;

wielko

ś

ci powierzchni tr

ą

cych;

pr

ę

dko

ś

ci po

ś

lizgu;

F

R

Q

T

P

N

v

5

1. Wi

ę

zy punktowe

a) Siła tarcia statycznego

równanie jest równie

ż

warunkiem stanu równowagi (spoczynku) ciała

b) Siła tarcia kinetycznego wyst

ę

puje podczas ruchu ciała

gdzie: f

S

, f

K

– współczynniki tarcia statycznego i kinetycznego, N – siła nacisku

2. Wi

ę

zy ci

ą

głe (powierzchniowe lub liniowe)

- Siły tarcia s

ą

siłami ci

ą

głymi o intensywno

ś

ci t.

- Prawa tarcia maj

ą

posta

ć

:

tarcie statyczne
tarcie kinetyczne

gdzie:

n

– intesywno

ść

(g

ę

sto

ść

) sił nacisku [ N / m ]

t

- intesywno

ść

(g

ę

sto

ść

) sił tarcia [ N / m ]

N

s

f

gr

T

T

=

≤

≤

0

N

k

f

gr

T

T

=

=

n

s

f

gr

t

t

=

≤

≤

0

n

k

f

gr

t

t

=

=

Prawa tarcia

- okre

ś

laj

ą

warto

ść

siły tarcia statycznego i kinetycznego

6

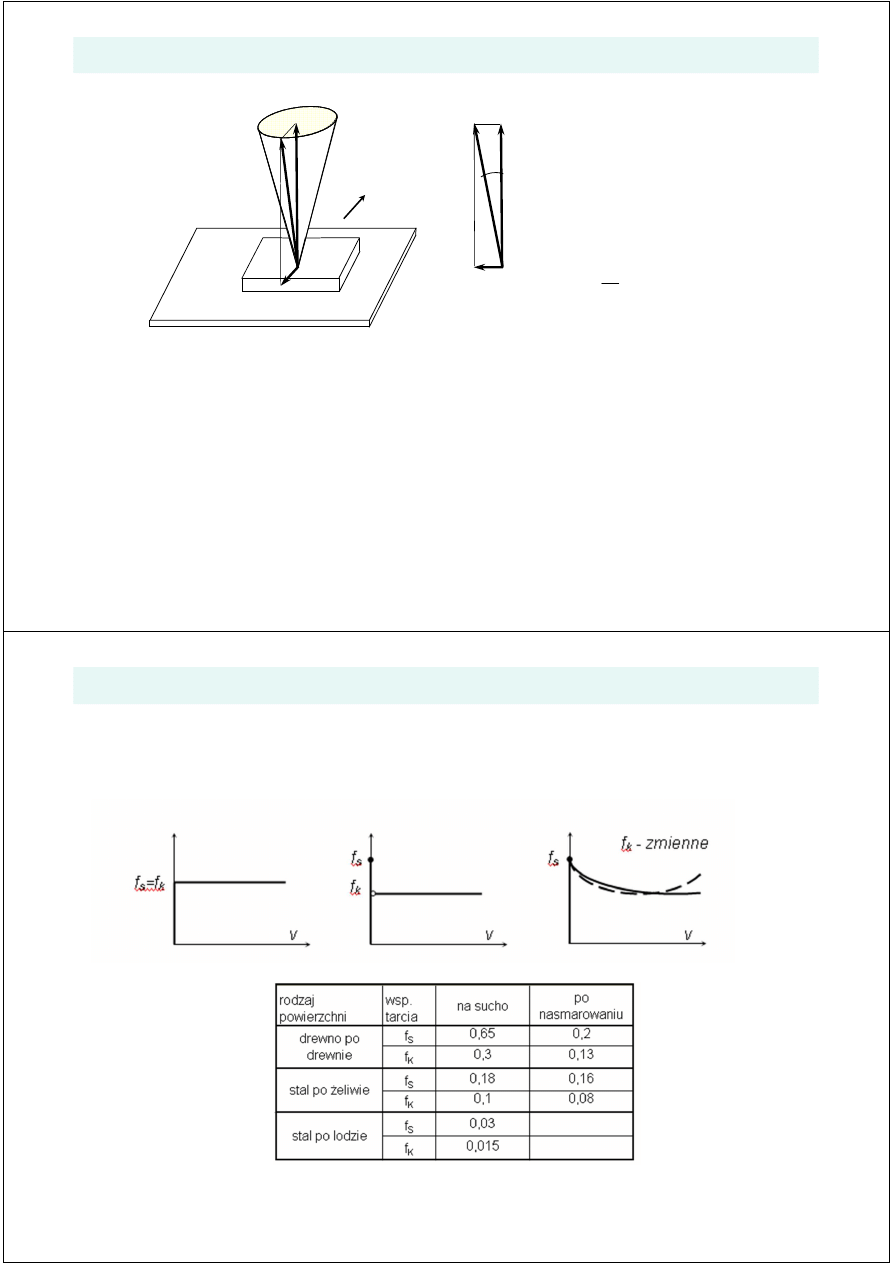
α

tg

f

fN

T

N

T

α

tg

=

⇒









=

=

- Miejscem geometrycznym poło

ż

e

ń

reakcji R w granicznym poło

ż

eniu równowagi jest pole powierzchni

bocznej sto

ż

ka zwanego sto

ż

kiem tarcia,

- W przypadku gdy reakcja R znajduje si

ę

wewn

ą

trz sto

ż

ka tarcia mamy zachowany stan równowagi,

- Gdy natomiast reakcja R le

ż

y na powierzchni bocznej sto

ż

ka tarcia otrzymujemy graniczny przypadek

równowagi.

T

N

R

α

T

N

π

v

R

Przypadek rozwini

ę

tej siły tarcia

7

N i T s

ą

składowymi siły R,

wypadkowej siły tarcia

1. Stała warto

ść

współczynnika tarcia - w przypadku, gdy ciała s

ą

nieruchome (tarcie statyczne)

oraz w ruchu przypadek a) i b)

2. Współczynnik tarcia zmienia si

ę

i zale

ż

y od pr

ę

dko

ś

ci wzgl

ę

dnego przemieszczenia si

ę

ciał,

gdy ciała przesuwaj

ą

si

ę

wzgl

ę

dem siebie (tarcie kinetyczne) – przypadek c)

Modele tarcia po

ś

lizgowego

8

c)

b)

a)

•

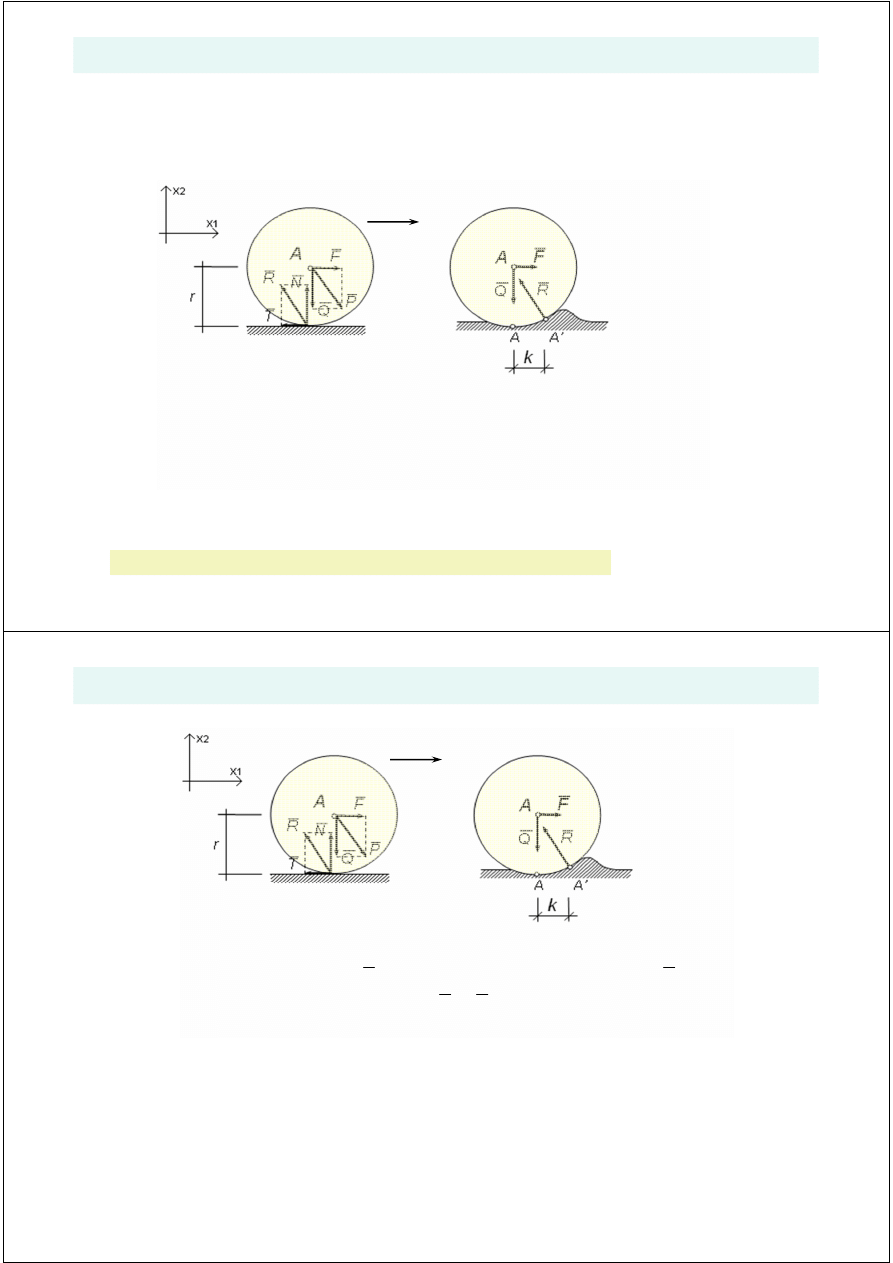
przy modelu idealnie sztywnego podlo

ż

a nie jest spełnione równanie równowagi:

•

dlatego w analizie uwzgl

ę

dnia si

ę

odkształcalno

ść

podło

ż

a poprzez przesuni

ę

cie wektora

siły reakcji o odcinek „k”

•

długo

ść

odcinka k [m] jest nazywana współczynnikiem tarcia tocznego

Siła tarcia tocznego

T

wyst

ę

puje podczas toczenia bryły po powierzchni (bryle)

•

Wektor siły jest równoległy do wektora pr

ę

dko

ś

ci, zwrot przeciwny

•

T

powoduje odchylenie od kierunku prostopadłego wektora reakcji

0

0

0

1

2

≠

=

=

−

=

=

−

=

∑

∑

∑

Tr

M

T

F

X

Q

N

X

A

v

Tarcie toczne

9

–

siły tarcia tocznego – analiza styczna (spoczynek)

•

zwi

ę

kszenie obci

ąż

enia powoduje zwi

ę

kszenie warto

ś

ci siły tarcia

•

koło pozostaje w spoczynku dopóki

•

mimo

ś

ród przyło

ż

enia siły AA’ wzrasta, a

ż

osi

ą

gnie wielko

ść

graniczn

ą

k

[m]

–

siły tarcia tocznego – analiza kinematyczna (toczenie)

•

warto

ść

siły tarcia

T

i współczynnika tarcia

k

s

ą

stałe

F

T

GR

T

T

<

v

Tarcie toczne

10

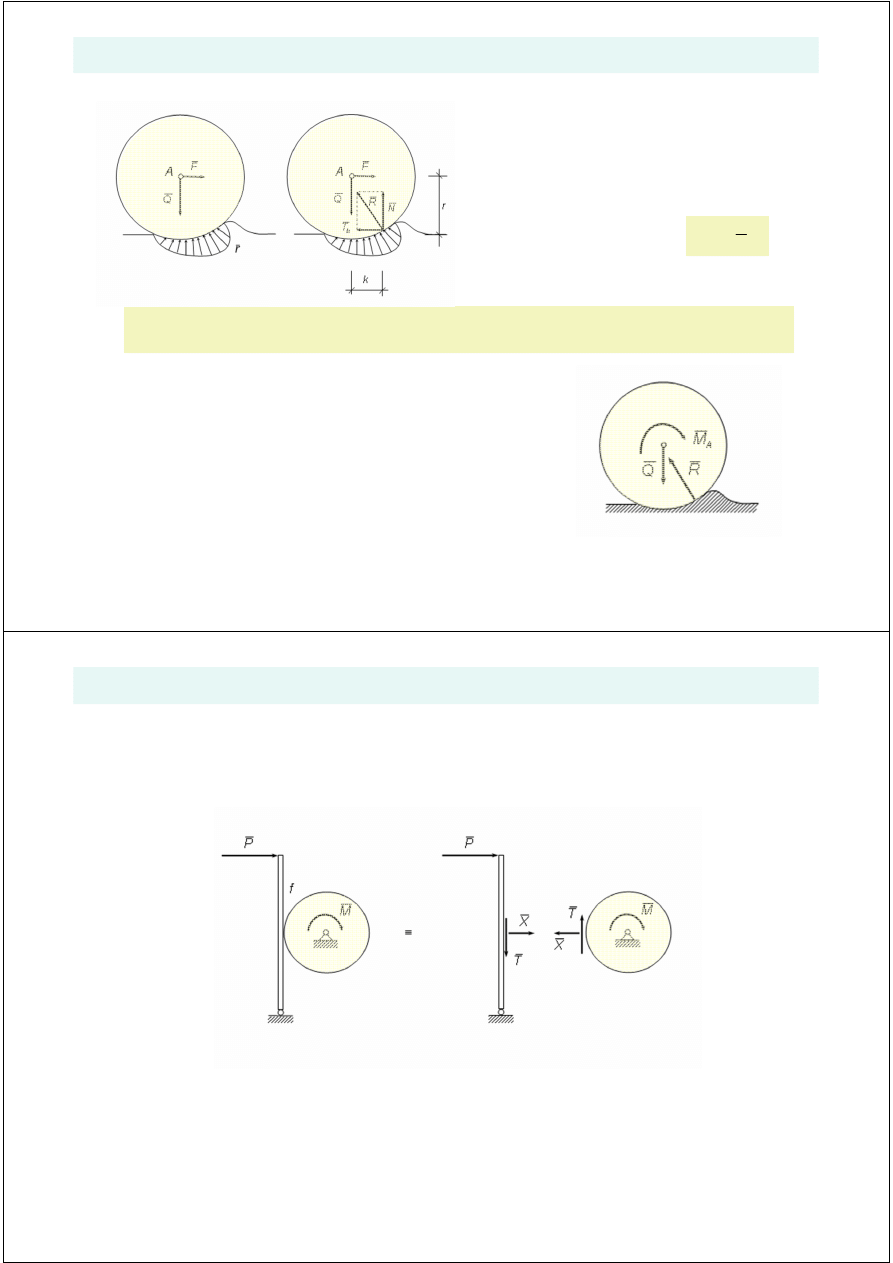
r

k

N

T

Nk

r

T

M

Q

N

X

T

F

X

k

k

A

k

=

=

−

=

=

−

=

=

−

=

∑

∑

∑

,

0

0

,

0

2

1

Opór toczenia jest wprost proporcjonalny do współczynnika tarcia k oraz odwrotnie proporcjonalny

do promienia koła r .

Uwaga: Analogicznie rozwa

ż

ania mo

ż

na prowadzi

ć

w przypadku

obci

ąż

enia momentem skupionym

(momentem nap

ę

dowym M) zaczepionym w

ś

rodku koła

Tarcie toczne

11

Uwaga 1.

Siła tarcia po

ś

lizgowego jako składowa reakcji wewn

ę

trznej

Przypadki szczególne tarcia

Mo

ż

liwo

ść

ruchu kr

ąż

ka powoduje,

ż

e w miejscu kontaktu powstaje

składowa styczna reakcji wewn

ę

trznej – siła tarcia

12

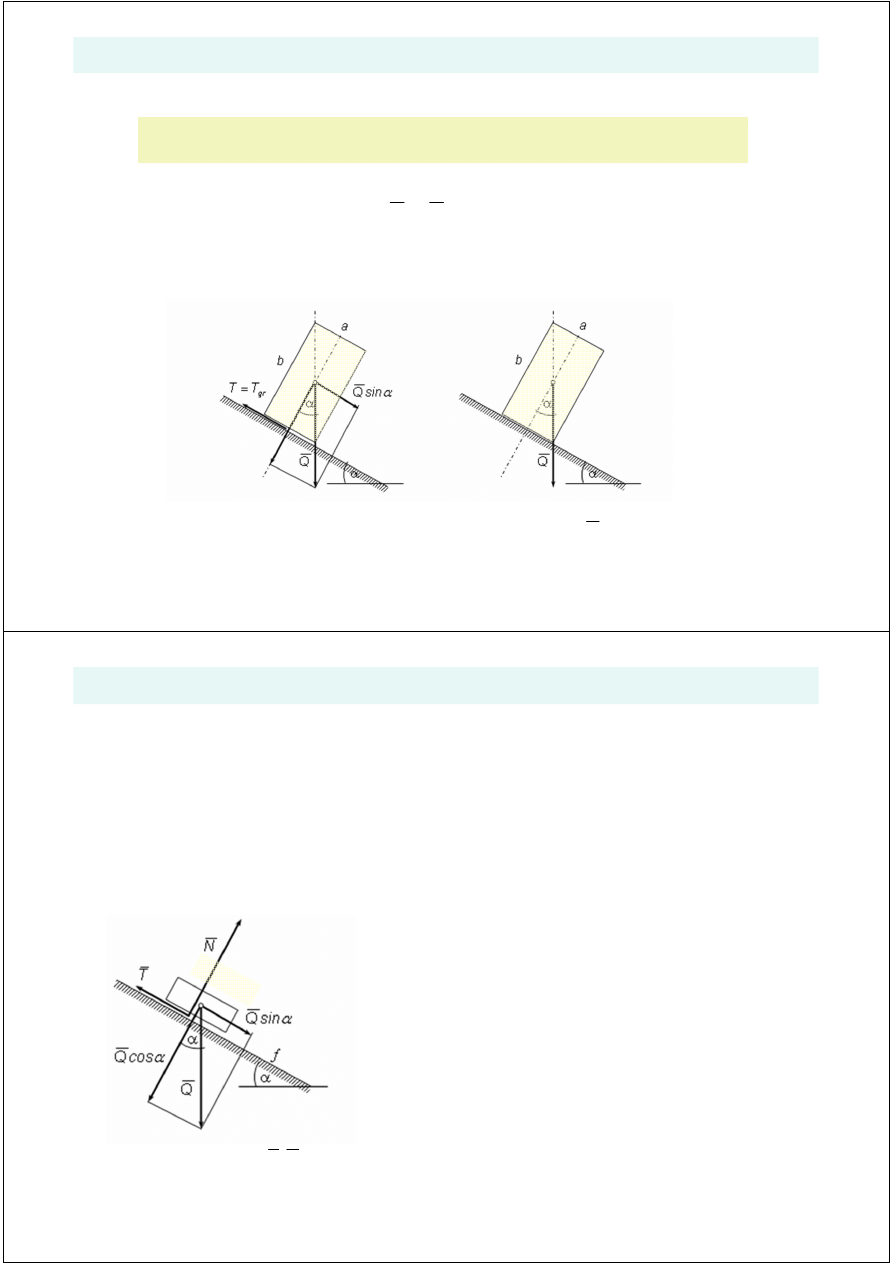
Stan równowagi granicznej rozumiemy jako stan przej

ś

cia z poło

ż

enia równowagi do stanu

ruchu mo

ż

e by

ć

osi

ą

gni

ę

ty wskutek:

-

osi

ą

gni

ę

cie przez siły tarcia warto

ś

ci granicznej

(warunek statyczny)

-

utrat

ę

stateczno

ś

ci

(warunek geometryczny)

gdy pion wyprowadzimy ze

ś

rodka ci

ęż

ko

ś

ci bryły sztywnej wychodzi poza pole

powierzchni podstawy

N

f

T

α

Q

s

gr

=

=

sin

b

a

α

tg

=

Uwaga 2.

gr

T

T

≤

Przypadki szczególne tarcia

13

2 niewiadome statyczne: - ?

Uwaga 3.

W zadaniach statystyki, w których uwzgl

ę

dniono siły tarcia, stan równowagi jest mo

ż

liwy gdy

siły tarcia T

≤

T

gr

- układ jest stacjonarny (nie ma mo

ż

liwo

ś

ci ruchu) . Jest to mo

ż

liwe gdy

a) obci

ąż

enie Q nie przekracza warto

ś

ci granicznej

Q

min

< Q < Q

max

b) nachylenie równi pochyłej

α

nie przekracza warto

ś

ci granicznej

α

min

<

α

<

α

max

(w ogólnym przypadku

α

jest parametrem geometrycznym opisuj

ą

cym poło

ż

enie układu)

Etap 1.

Poło

ż

enie równowagi gdy T = Qsin

α

< T

gr

→

2 r.r.

S

N

= LNS – LRR = 2 – 2 = 0 .

Etap 2.

Stan graniczny dla Q = Q

gr

oraz T = Qsin

α

= T

gr

. Nale

ż

y

uwzgl

ę

dni

ć

dodatkowe równanie, prawo tarcia (PT). Gdy T > T

gr

ci

ęż

arek zsuwa si

ę

po równi (układ geometrycznie zmienny)

2 r.r. + prawo tarcia

S

N

= LNS – (LRR+PT) = 2 – (2+1) = -1 .

N

T

,

Przypadki szczególne tarcia

Aby rozwi

ą

za

ć

zadanie do niewiadomych statycznych nale

ż

y

doda

ć

1 parametr geometryczny (LNG) k

ą

t

α

wtedy :

S

N

= (LNS+LNG) – (LRR+PT) = (2+1) - 3 = 0 .

Ad a)

obci

ąż

enie Q wzrasta od zera ale nie przekracza warto

ś

ci granicznej 0 < Q < Q

max

14

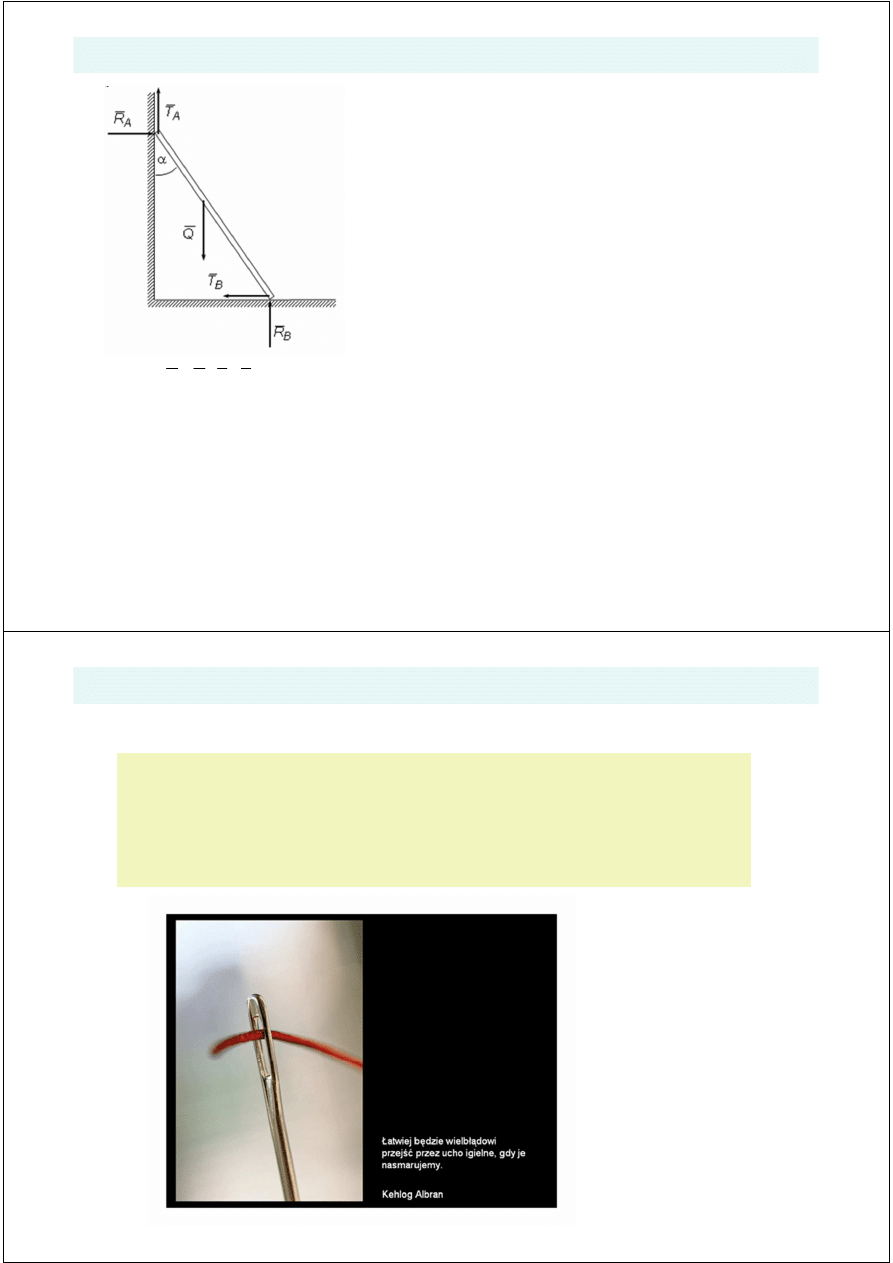
Siły tarcia wyst

ę

puj

ą

w punktach A i B : T

A

i T

B .

Etap 1.

Poło

ż

enie równowagi gdy obydwie siły tarcia

T < T

gr

→

3 r.r (płaski dowolny uklad sił),

S

N

= LNS – LRR = 4 – 3 = 1 ,

układ jednokrotnie statycznie niewyznaczalny.

Etap 2.

Jedna z sił tarcia osi

ą

gnie warto

ść

graniczn

ą

T

A

= T

gr

lub T

A

= T

gr

. Nale

ż

y uwzgl

ę

dni

ć

jedno dodatkowe równanie,

prawo tarcia (PT), wtedy układ jest statycznie wyznaczalny

S

N

= LNS – (LRR+PT) = 4 – (3+1) = 0 .

Przypadki szczególne tarcia

4 niewiadome statyczne:

- ?

B

A

B

A

T

T

R

R

,

,

,

Ad b)

k

ą

t

αααα

wzrasta ale nie przekracza warto

ś

ci granicznej O

≤

αααα

≤

αααα

gr

Etap 3.

Obydwie siły tarcia osi

ą

gn

ą

warto

ść

graniczn

ą

dla

α

=

α

gr

. Nale

ż

y uwzgl

ę

dni

ć

dwa

dodatkowe równania prawa tarcia. Dla

α

>

α

gr

pr

ę

t zsuwa si

ę

(układ geometrycznie zmienny)

3 r.r + 2 prawa tarcia S

N

= LNS – (LRR+PT) = 4 - ( 3 + 2) = -1 .

Aby rozwi

ą

za

ć

zadanie do niewiadomych nale

ż

y doda

ć

1 parametr geometryczny k

ą

t

α

wtedy :

S

N

= (LNS+LNG) – (LRR+PT) = (4+1) - (3+2) = 0 .

15

Wniosek :

Przy okre

ś

laniu stopnia statycznej niewyznaczalno

ś

ci równanie prawa tarcia mo

ż

e

by

ć

uwzgl

ę

dnione jako dodatkowe równanie równowagi w przypadku

- zada

ń

statyki przy okre

ś

laniu stanu granicznego równowagi

- zada

ń

dynamiki przy uwzgl

ę

dnieniu rozwini

ę

tej siły tarcia kinetycznego

Przypadki szczególne tarcia

16