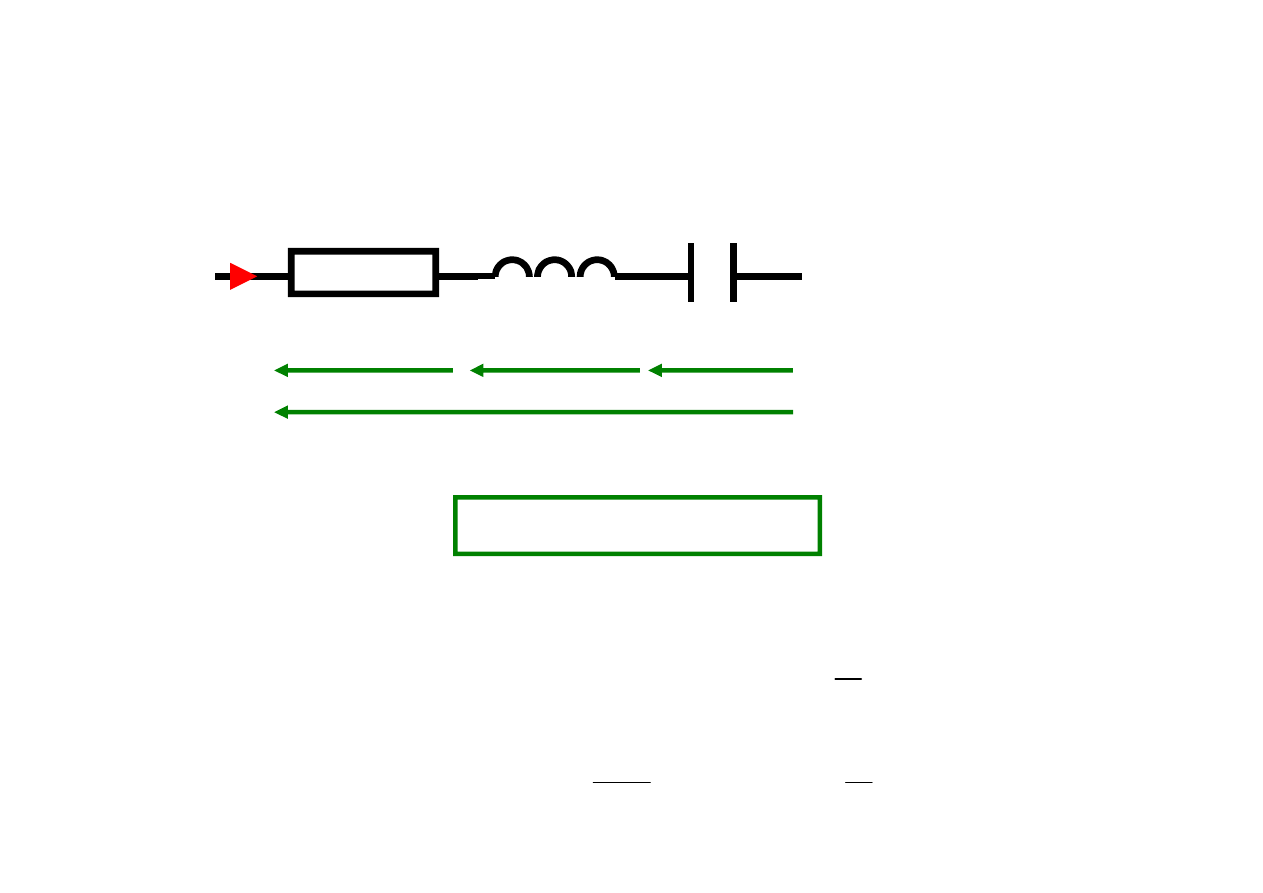
Połączenie R L C

R

L

C

u

R

u

L

u

C

u

i

)

sin(

)

(

i

m

t

I

t

i

ϕ

ω

+

=

Przyjmijmy, że

(

)













−

+

=













+

+

=

+

=

2

sin

1

2

sin

sin

π

ϕ

ω

ω

π

ϕ

ω

ω

ϕ

ω

i

m

C

i

m

L

i

m

R

t

C

I

u

t

L

I

u

t

R

I

u

(

)

ϕ

ϕ

ω

ω

ω

+

+













−

+

=

=

+

+

=

i

m

C

L

R

t

C

L

R

I

u

u

u

u

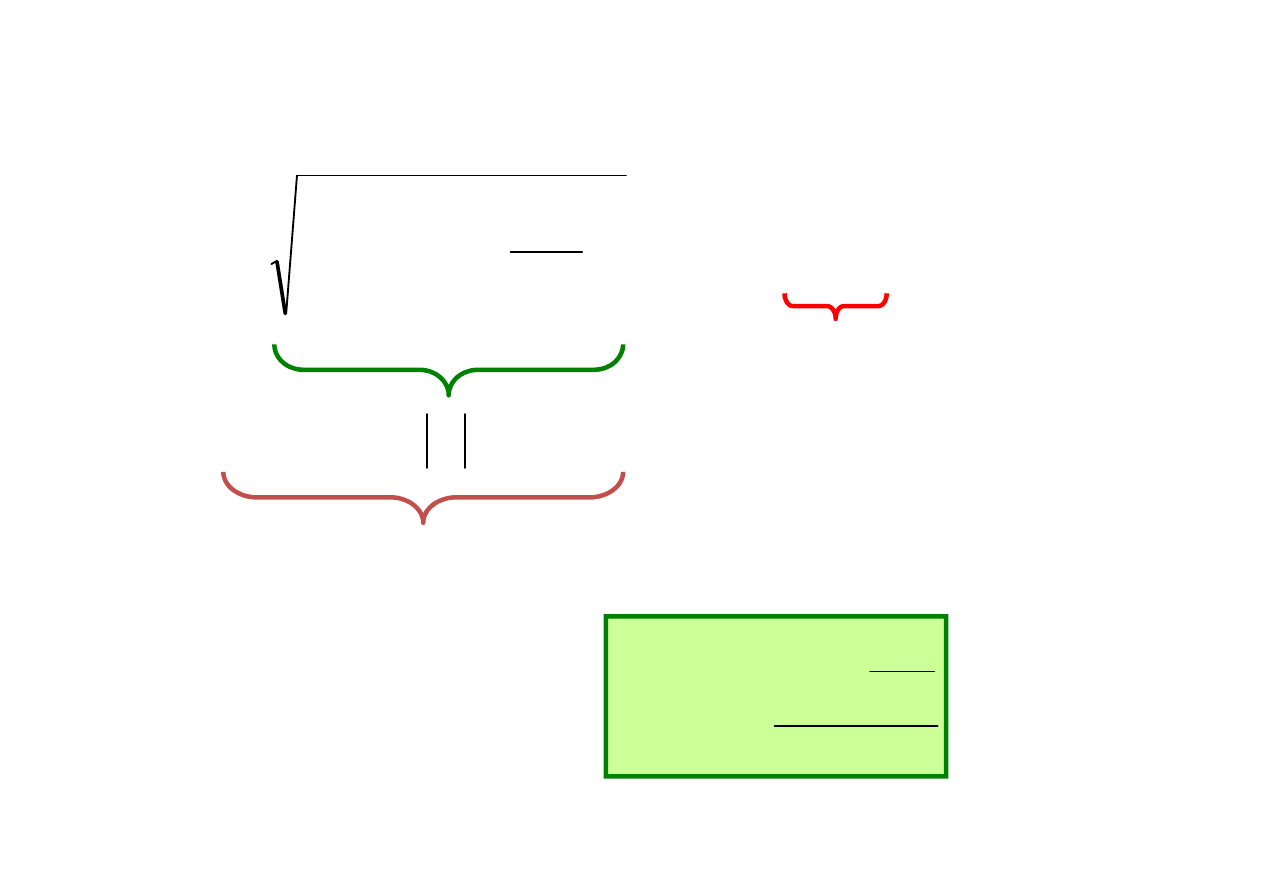
sin

1

2

2

Z

u

ϕ

Z

U

m

R

C

L

tg

arc

ω

ω

ϕ

1

−

=

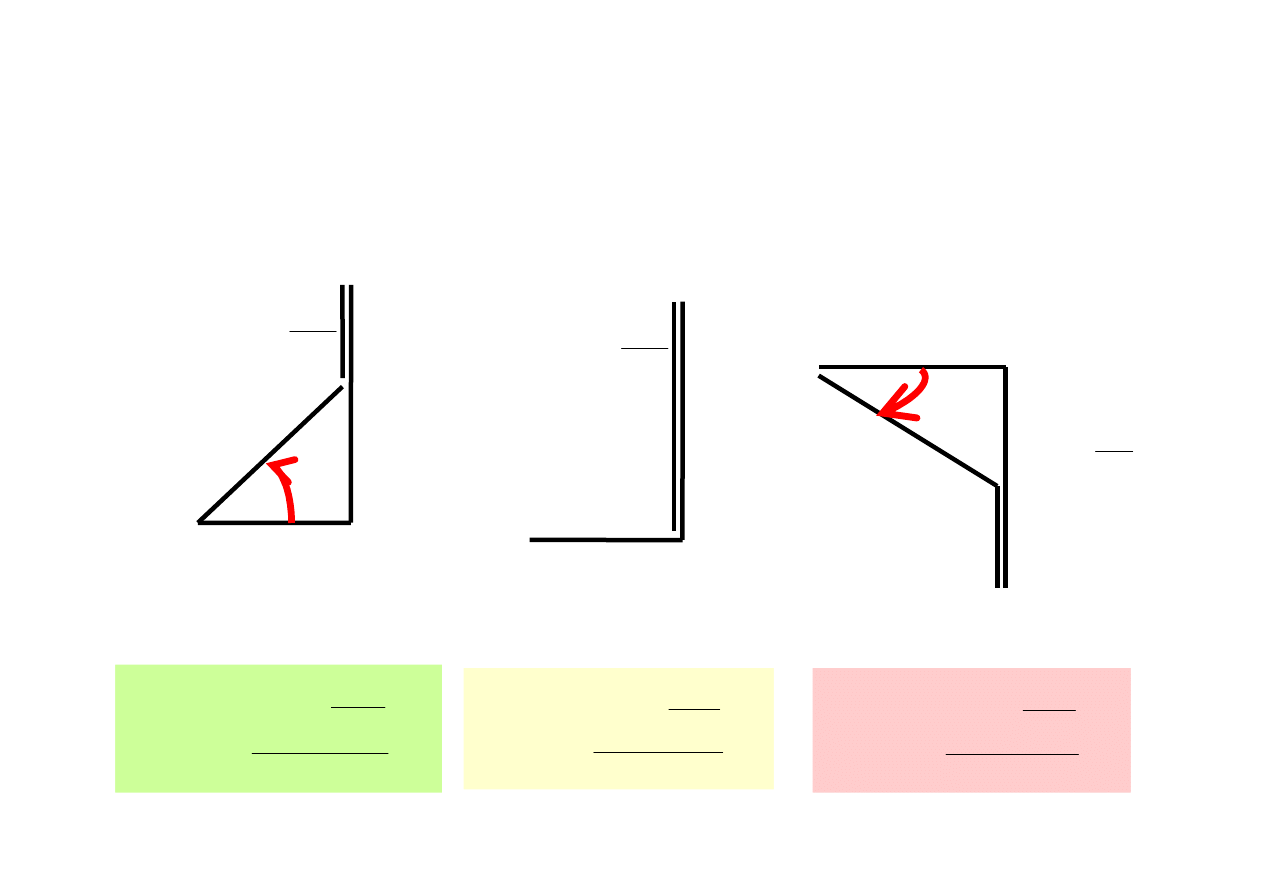
Takiemu połączeniu odpowiada trójkąt impedancji:

C

X

C

ω

1

−

=

L

X

L

ω

=

C

X

C

ω

1

−

=

L

X

ω

=

R

X

1

−

=

0

1

>

−

=

R

C

L

tg

arc

ω

ω

ϕ

0

1

=

−

=

R

C

L

tg

arc

ω

ω

ϕ

0

1

<

−

=

R

C

L

tg

arc

ω

ω

ϕ

R

L

X

L

ω

=

R

L

X

L

ω

=

C

X

C

ω

1

−

=

L

X

L

ω

=

0

>

X

0

1

>

−

C

L

ω

ω

C

L

ω

ω

1

>

C

L

U

U

>

L

U

C

U

I

RI

U

R

=

C

U

U

ϕ

0

>

ϕ

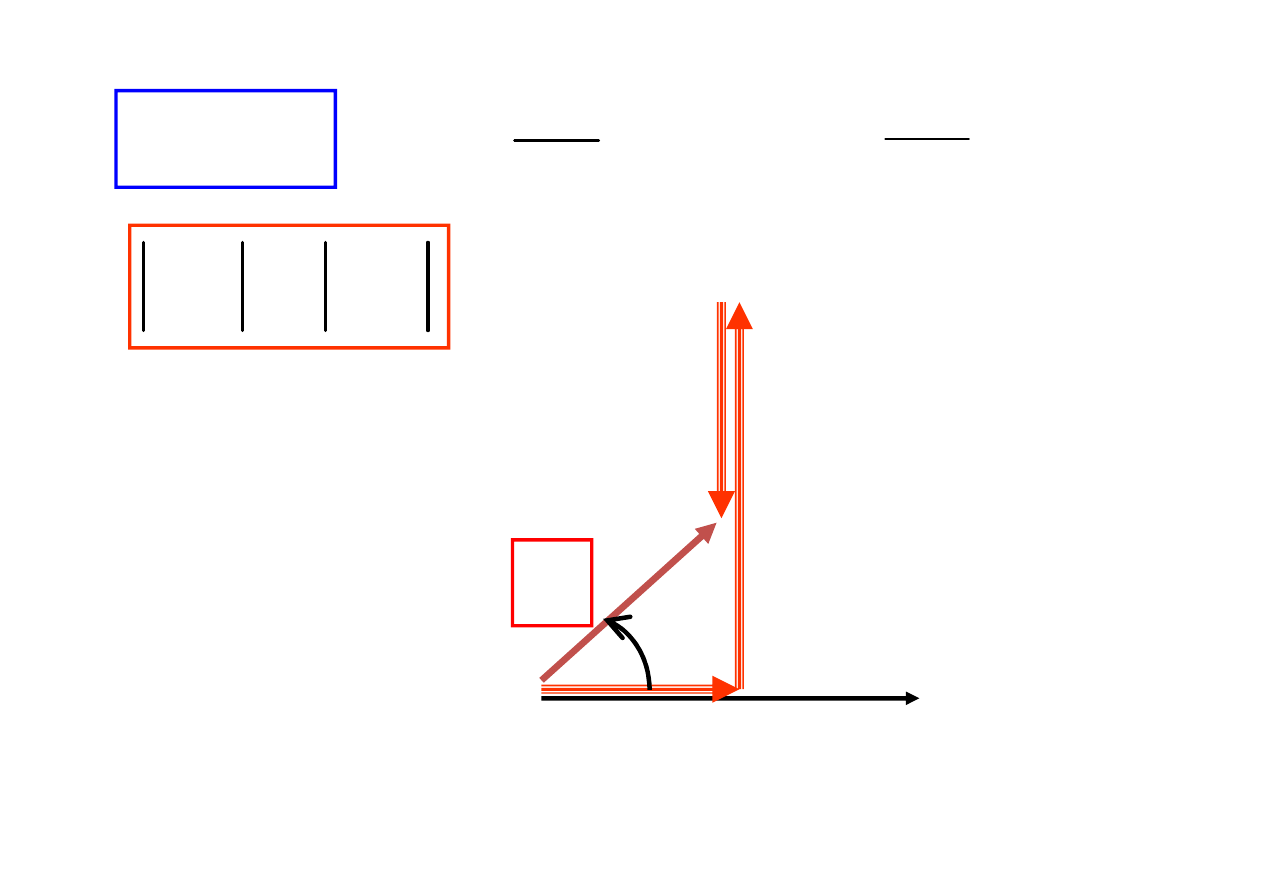
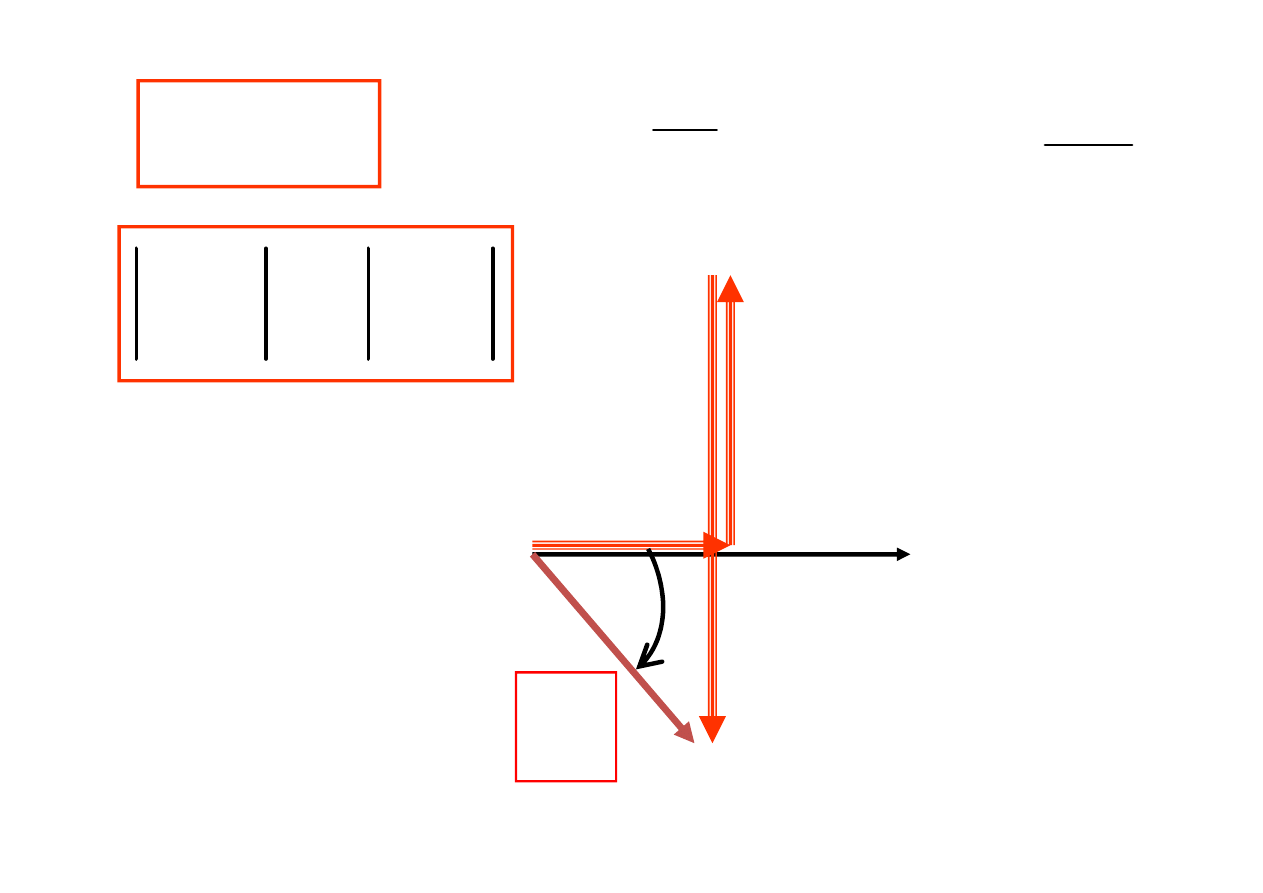
OBWÓD O CHARAKTERZE INDUKCYJNYM

OBWÓD O CHARAKTERZE INDUKCYJNYM

0

<

X

0

1

<

−

C

L

ω

ω

C

L

ω

ω

1

<

L

C

U

U

<

RI

U

=

L

U

I

RI

U

R

=

C

U

U

ϕ

0

<

ϕ

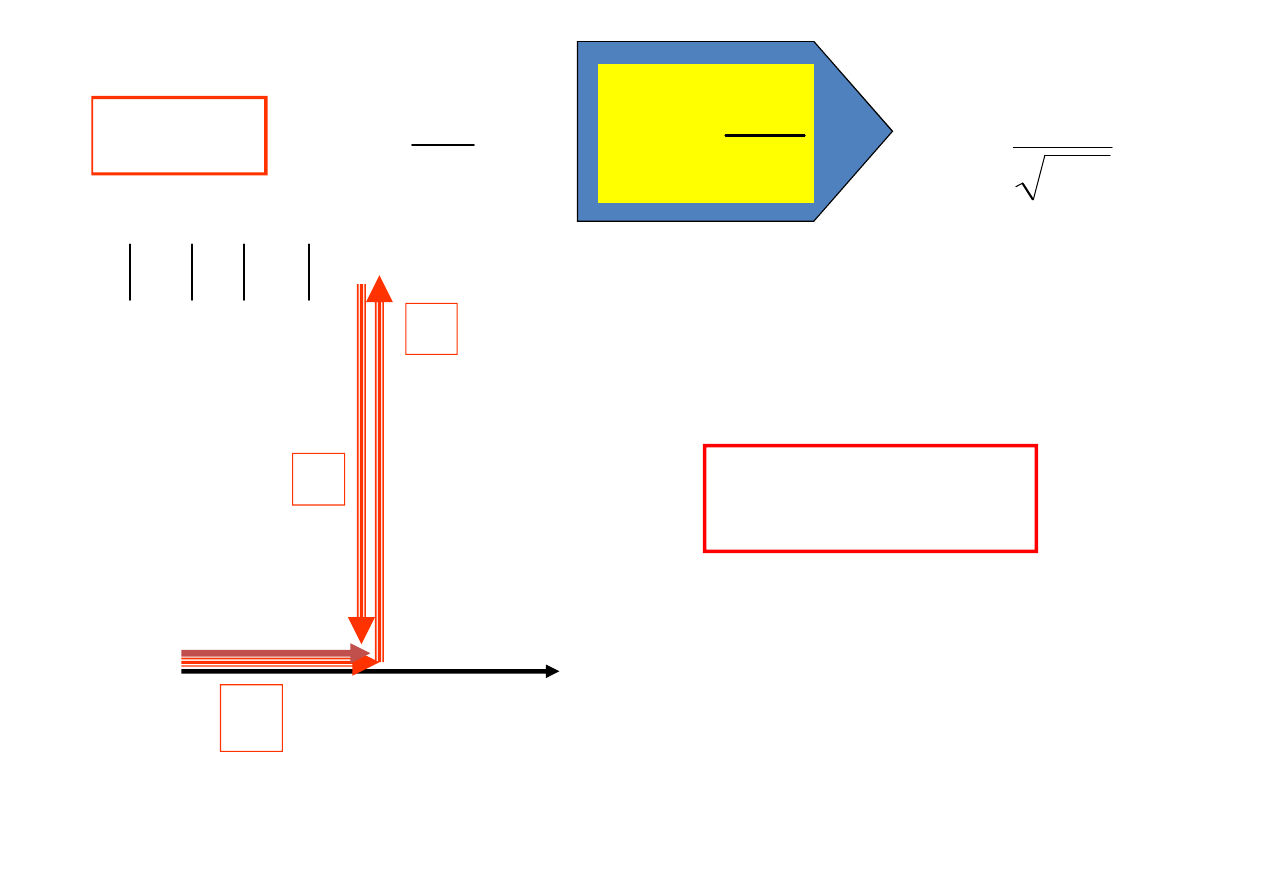
OBWÓD O CHARAKTERZE POJEMNOŚCIOWYM

OBWÓD O CHARAKTERZE POJEMNOŚCIOWYM

0

=

X

0

1

=

−

C

L

ω

ω

C

L

ω

ω

1

=

C

L

U

U

=

L

U

LC

1

r

=

ω

=

ω

I

U

C

U

R

U

=

0

=

ϕ

OBWÓD O CHARAKTERZE REZYSTANCYJNYM

OBWÓD O CHARAKTERZE REZYSTANCYJNYM

0

)

(

=

r

X

ω