POLITECHNIKA ŚLĄSKA
INSTYTUT DRÓG I MOSTÓW
ZAKŁAD GEODEZJI
OBLICZANIE POWIERZCHNI
POLITECHNIKA ŚLĄSKA
INSTYTUT DRÓG I MOSTÓW
ZAKŁAD GEODEZJI
OBLICZANIE POWIERZCHNI
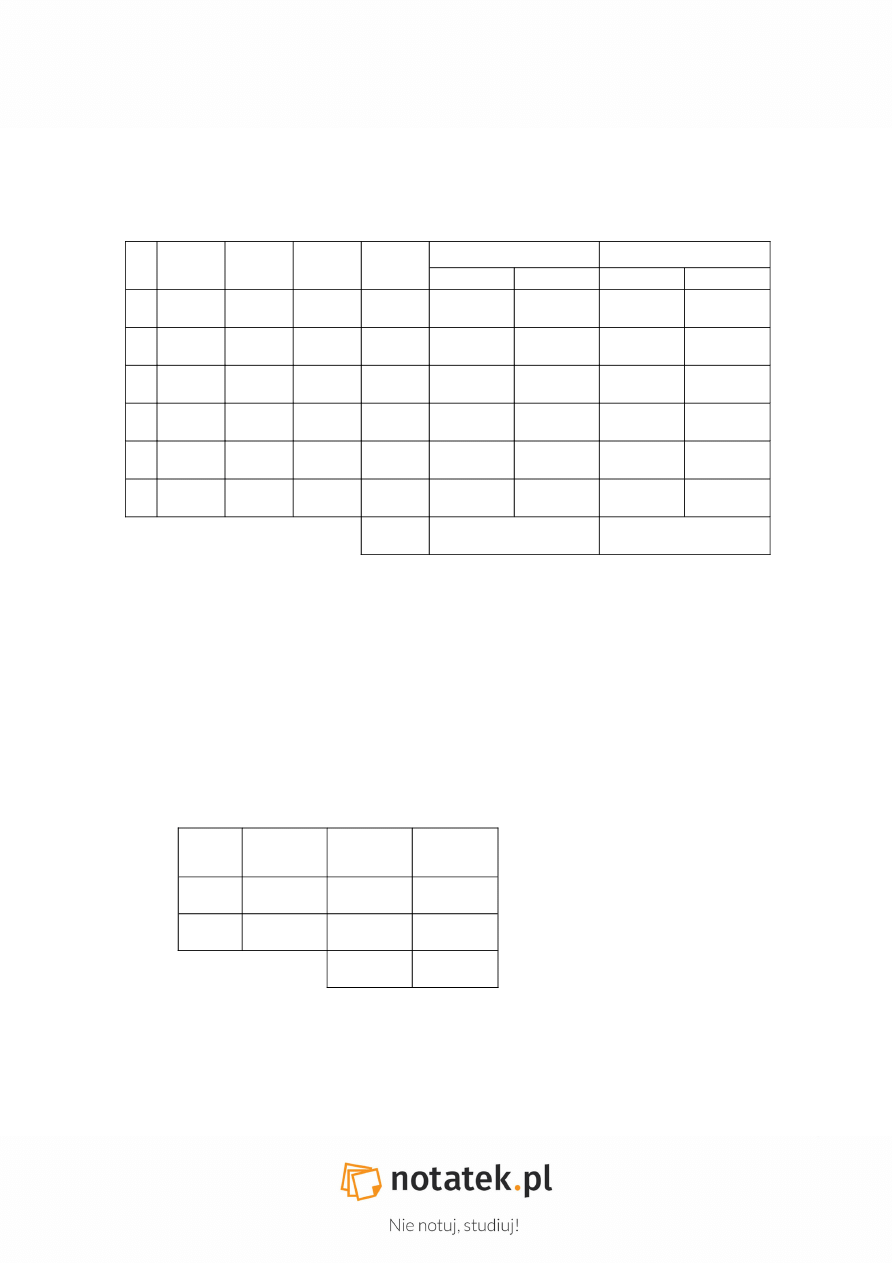
Obliczanie powierzchni z miar rzeczywistych
(na podstawie wzoru Gaussa)
L
Y
X
Y
n+1
-Y
n-1
X
n+1
-X
n-1
X
n
(Y
n+1
-Y
n-1
)
- Y
n
(X
n+1
-X
n-1
)
+
-
+
-
833 16841,01 13652,08
-
-
-
-
-
-
1
16900,00 13700,00
158,99
-52,08
2178163,00
-
880152,00
-
2
17000,00 13600,00
-33,57
-125,62
-
456552,00
2135540,00
-
847 16866,43 13574,38
-158,99
52,08
-
2158190,68
-
878403,67
833 16841,01 13652,08
33,57
125,62
458300,33
-
-
2115567,68
1
16900,00 13700,00
-
-
-
-
-
-
Σ
21 720,65
21 720,65
∑
−
+
−
=
n
i
i
i
Y
Y
X
P
1
1
1
)
(
2
∑
−
+
−
−
=
n
i
i
i
X
X
Y
P
1
1
1
)
(
2
P
1
= 10 860,36 m
2
Obliczanie pola powierzchni z planu
a). metodą geometryczną – podział na trójkąty
Trójkąt
Podstawa
„P”
Wysokość
„w”
P x w
1
128,10
124,20 15 910,02
2
128,10
44,90
5 751,69
Σ
21 661,71
P
2
= ½ [P x w] = 10 830,86 m
2
b). metodą mechaniczną (za pomocą planimetru )
Wyznaczenie stałej C
1
Nastawienie ramienia wodzącego = 10,00
2
L
Odczyt
Różnica
odczytów
„n”
01
1000
1000
02
1995
995
03
2992
997
04
3990
998
05
4986
996
06
5981
995
07
6978
997
08
7972
994
09
8966
994
10
9957
991
11
10952
995
12
11943
991
[n]
11943
Średnie n
995
w skali 1 : 1
2
2
1
05
,
10
995
10000
m
m
n
P
C
śr
p
=
=
=
Obliczenie powierzchni
L
Odczyt
n
01
1078
1078
02
2160
1082
03
3239
1079
04
4317
1078
[n]
4317
Średnie n
1079,25
P
3
= C
1
x n
śr
= 10 846,46 m
2
L
Wyniki
obliczeń
Różnice
∆
P
P
1
10 860,33
29,47
P
2
10 830,86
15,60
P
3
10 846,46
13,87
P
1
10 860,33
Dozwolona różnica oblicz. powierzchni
∆
P
przy skali 1 : 1000 wynosi 31,70 m
2
.
0,001 x P + 0,2 x P
1/2
http://notatek.pl/geodezja-kartowanie-mapy-oblicza
nie-powierzchni-terenu-na-mapie?notatka