1. Co to jest geodezja? Jakie elementy najcz
ęś
ciej podlegaj
ą
pomiarowi?
Geodezja – nauka zajmuj
ą
ca si
ę
ustalaniem wielko
ś
ci i kształtu Ziemi oraz okre
ś
laniem poło
ż
enia punktów
na jej powierzchni. Wynikiem prac i pomiarów terenowych w geodezji s
ą
mapy oraz inne dokumenty o
charakterze prawnym (np. podczas rozgraniczania nieruchomo
ś
ci).
Współczesna geodezja dzieli si
ę
na:
•
Geodezj
ę
wy
ż
sz
ą
– nauk
ę
o pomiarach wykonywanych na wielkich obszarach, o powierzchni ponad
50 km
2
, uwzgl
ę
dniaj
ą
cych kulisto
ść
Ziemi,
•
geodezj
ę
szczegółow
ą
(miernictwo)– nauk
ę
o pomiarach wykonywanych na powierzchniach małych,
do 50 km
2
, bez uwzgl
ę
dniania kulisto
ś
ci Ziemi.
Elementy podlegaj
ą
ce pomiarowi:
a) pomiar linii w terenie
b) tyczenie linii prostych
c) tyczenie linii prostopadłych
d) wyznaczanie punktów
e) pomiar k
ą
tów oraz długo
ś
ci w poligonach
f) pomiary wysoko
ś
ciowe (liniowe i k
ą
towe)
2. Jak dzielimy pomiary geodezyjne ze wzgl
ę
du na rodzaj ich wykonywania?
Pomiary sytuacyjne (pomiary poziome) – okre
ś
laj
ą
wzajemne poło
ż
enie wzgl
ę
dem siebie ró
ż
nych obiektów
szczegółowych znajduj
ą
cych si
ę
Pomiary wysoko
ś
ciowe maj
ą
na celu okre
ś
lenie tzw. Rze
ź
by terenu, który podlega pomiarowi, a wi
ę
c
okre
ś
lenie wzajemnego wysoko
ś
ciowego poło
ż
enia punktów i obiektów le
żą
cych na danym obszarze, czyli
okre
ś
lenie ukształtowania powierzchni ziemi w granicach mierzonego obiektu.
3. Jak dzielimy pomiary ze wzgl
ę
du na cel ich wykonywania
1.
pomiary osnów geodezyjnych, oraz pomiary podstawowych
2.
pomiary szczegółowe sytuacyjne i wysoko
ś
ciowe,
3.
pomiary realizacyjne i obsługa inwestycji,
4.
prace geodezyjne zwi
ą
zane z ewidencj
ą
gruntów,
5.
inne prace geodezyjne.
4. Jak dzielimy pomiary ze wzgl
ę
du na sposób ich wykonywania
1.
pomiary bezpo
ś
rednie
2.
pomiary po
ś
rednie
5. Na czym polega ró
ż
nica pomi
ę
dzy pomiarami bezpo
ś
rednimi i po
ś
rednimi. Podaj przykłady.
Pomiary bezpo
ś
rednie – polega na bezpo
ś
rednim porównaniu mierzonego elementu z jednostk
ą
miary.
Np. mierzenie ta
ś
m
ą
odcinka, domiar prostopadły ruletk
ą
, mierzenie k
ą
ta teodolitem, oznaczenie azymutu
odcinka, itp.
Pomiary po
ś
rednie – jest to wyznaczenie wielko
ś
ci danego elementu mierzonego polegaj
ą
ce na jego
rachunkowym obliczeniu, na podstawie bezpo
ś
redniego pomiaru pewnych elementów pomocniczych
zwi
ą
zanych w okre
ś
lony sposób z mierzonym elementem.
Np. obliczenie k
ą
ta w trójk
ą
cie, znaj
ą
c pozostałe dwa k
ą
ty tego trójk
ą
ta, obliczenie długo
ś
ci odcinka metod
ą
wci
ę
cia k
ą
towego, lub liniowego, itp.
6. W zale
ż
no
ś
ci od wielko
ś
ci mierzonego obszaru matematyczn
ą
powierzchni
ą
odniesienia mo
ż
e by
ć
elipsoida obrotowa, kula lub płaszczyzna. Geodezja ni
ż
sza zajmuje si
ę
pomiarami na niewielkich obszarach.
Na jakim obszarze mo
ż
emy nie uwzgl
ę
dnia
ć
wpływu kulisto
ś
ci
a.
przy pomiarach sytuacyjnych
b.
przy pomiarach wysoko
ś
ciowych
Uzasadnij odpowiedz, podaj wzory i rysunki.
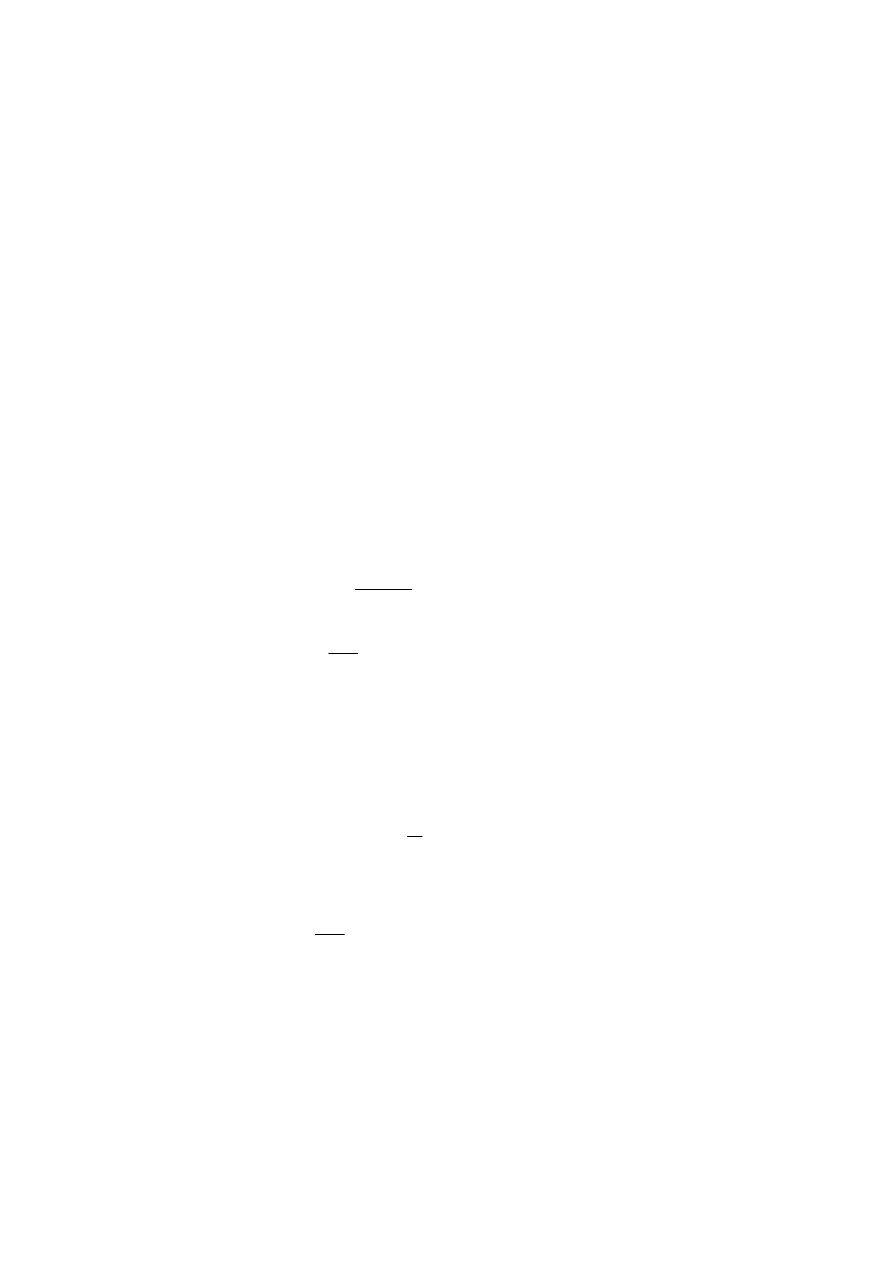
7. Co decyduje o jednolito
ś
ci prac geodezyjnych
1) jednolity system miar,
2) jednolity system odniesienia i odwzorowania wyników pomiarów,
3) znormalizowana tre
ść
, dokładno
ść
i forma opracowa
ń
typowych.
8. Pomiary długo
ś
ci linii mo
ż
emy wykona
ć
:
a.
ta
ś
m
ą
stalow
ą
o długo
ś
ci 20 lub 50 m
b.
łatami poligonowymi
c.
drutami inwarowymi Jaederina
d.
metodami paralaktycznymi – przy stałej bazie
e.
dalmierzami elektro-optycznymi
Prosz
ę
poda
ć
dla wy
ż
ej wymienionych metod bł
ę
dy wzgl
ę
dne pomiaru
Bł
ę
dy wzgl
ę
dne dla:
Ta
ś
my stalowej
=
1/2000 – 1/5000 długo
ś
ci mierzonego odcinka
Łaty pomiarowe
=
1/5000 – 1/10000
Druty inwarowe
=
1/1 000 000
Metody paralaktyczne
=
1/10000 – 1/15000
Dalmierz elektro-optyczny =
2 mm + D*10
-6
9. Czemu jest równa ostateczna długo
ść
odcinka pomierzonego ta
ś
m
ą
stalow
ą
z uwzgl
ę
dnieniem poprawek.
Prosz
ę
poda
ć
wzory.
Długo
ść
odcinka D
0
= D
zm
± f
k
± f
t
- f
r
D
zm
– ostateczny pomiar odcinka jako
ś
rednia pomiarów „tam” i „ z powrotem”
R
L
n
D
gdzie
D
D
D
p
t
p
t
zm
+
=
+
=
*
2
)
,
(
f
k
– poprawka komparacyjna na wydłu
ż
enie lub skrócenie ta
ś
my (dlatego f
k
mo
ż
e mie
ć
znak + lub -)
nom
a
rzeczywist
k
k
nom
zm
k
l
l
f
gdzie
f
l
D
f
−
=
∆
∆
=
*
f
t
– poprawka termiczna ze wzgl
ę
du na współczynnik rozszerzalno
ś
ci stali =
Λ
=0,000013 1/1
o
C
oraz temperatur
ę
w jakiej odbywał si
ę
pomiar
)
(
*
*
k
p
zm
t
t
t
D
f
−
Λ
=
gdzie t
p
-temperatura pomiaru
t
k
-temperatura komparacji ta
ś
my
f
r
– poprawka redukcyjna (przy pomiarze terenu nachylonego)
2
sin
*
2
2
β
zm
r
D
f
=
gdzie
β
-k
ą
t nachylenia terenu
10. Co to jest poprawka komparacyjna dla jednej ta
ś
my
f
k
– poprawka komparacyjna na wydłu
ż
enie lub skrócenie ta
ś
my (dlatego f
k
mo
ż
e mie
ć
znak + lub -)
nom
a
rzeczywist
k
k
nom
zm
k
l
l
f
gdzie
f
l
D
f
−
=
∆
∆
=
*
11. Co to jest poprawka termiczna. W jakich jednostkach wyra
ż
ony jest współczynnik rozszerzalno
ś
ci
liniowej.
f
t
– poprawka termiczna ze wzgl
ę
du na współczynnik rozszerzalno
ś
ci stali =
Λ
=0,000013 1/1
o
C
oraz temperatur
ę
w jakiej odbywał si
ę
pomiar
)
(
*
*
k
p
zm
t
t
t
D
f
−
Λ
=
gdzie t
p
-temperatura pomiaru
t
k
-temperatura komparacji ta
ś
my
12. Co to jest poprawka redukcyjna.
f
k
– poprawka komparacyjna na wydłu
ż
enie lub skrócenie ta
ś
my (dlatego f
k
mo
ż
e mie
ć
znak + lub -)
nom
a
rzeczywist
k
k
nom
zm
k
l
l
f
gdzie
f
l
D
f
−
=
∆
∆
=
*
13. Ta
ś
ma stalowa jest za krótka w stosunku do swojej nominalnej długo
ś
ci o 4mm. Oblicz poprawk
ę
komparacyjn
ą
dla odcinka o długo
ś
ci 250 m. Ile wyniesienie długo
ść
tego odcinka po uwzgl
ę
dnieniu tej
poprawki.
∆
f
k
=19,996m – 20,000m = - 0,004 m; f
k
=
m
m
m
05
,
0
)
004
,
0
(
*
20
250
−
=
−
; D
0
= 250
m – 0,05m = 245,95 m
14. Odcinek 200 m zmierzono ta
ś
m
ą
stalow
ą
z bł
ę
dem bezwzgl
ę
dnym 10 cm. Obliczy
ć
bł
ą
d wzgl
ę
dny tego
pomiaru.
Długo
ść
ta
ś
my = 20 m, a wi
ę
c je
ś
li bł
ą
d bezwzgl
ę
dny = 10 cm na 200 m to bł
ą
d wzgl
ę
dny wynosi:
200/20 = 10 przyło
ż
e
ń
⇒
10 cm/10 = 1 cm
15. Bok zmierzono dwukrotnie otrzymuj
ą
c wynik 300,67m oraz 300,82m. Oblicz bł
ą
d wzgl
ę
dny tego pomiaru.
Czy pomiar ten spełnia standardy dokładno
ś
ciowe.
D
zm
=
m
75
,
300
2
82
,
300
67
,
300
=
+
; bł
ą
d dopuszczalny dla odl. 300 m =
m
D
zm
15
,
0
*
2000
1
=
Sprawdzenie: 300,75-300,67=0,08m<0,15m; 300,82-300,75= 0,07m<0,15m
Wniosek: Bł
ą
d wzgl
ę
dny tego pomiaru mie
ś
ci si
ę
w granicach dopuszczalnych.
16. W terenie pomierzono odcinek AB uzyskuj
ą
c
ś
redni
ą
długo
ść
z pomiaru 280,62 m. Oblicz ostateczn
ą
długo
ść
odcinka z uwzgl
ę
dnieniem poprawek komparacyjnej, termicznej, regukcyjnej je
ż
eli:
∆
f
k
= - 0,005;
α
= 6
o
; T
p
= -15
o
C ; T
k
=20
o
C ;
Λ
=0,000013
C
o
1
; L
n
= 20,00m
D
0
= D
zm
± f
k
± f
t
- f
r
m
f
l
D
f
k
nom
zm
k
07
,
0
)
005
,
0
(
*
20
62
,
280
*
−
=
−
=
∆
=
m
D
f
zm
r
54
,
1
537
,
1
2
6
sin
*
62
,
280
*
2
2
sin
*
2
2
2
≈
=
=
=
β
)
(
*
*
k
p
zm
t
t
t
D
f
−
Λ
=
= 280,62*0,000013*(-15-20) = - 0,127
≈
- 0,13 m
D
0
= 280,62 – 0,07 – 1,54 – 0,13 = 278,88 m
17. W wyniku pomiaru odcinka metod
ą
schodkow
ą
ta
ś
ma stalow
ą
o długo
ś
ci nominalnej 20 m uzyskano
ś
redni
ą
długo
ść
D= 200,05m. Oblicz ostateczn
ą
długo
ść
odcinka D
0
je
ż
eli :
∆
f
k
= - 0,005;
α
= 6
o
; T
p
= 20
o
C ; T
k
=20
o
C ;
Λ
=0,000013
C
o
1
; L
n
= 20,00m
UWAGA: przy metodzie schodkowej pomija si
ę
poprawk
ę
redukcyjn
ą
a wi
ę
c k
ą
t nachylenia nie ma
znaczenia dla oblicze
ń
.
D
0
= D
zm
± f
k
± f
t
- f
r
m
f
l
D
f
k
nom
zm
k
05
,
0
)
005
,
0
(
*
20
05
,
200
*
−
=
−
=
∆
=
UWAGĄ
z
zgodnie
f
r
,
00
,
0
=
)
(
*
*
k
p
zm
t
t
t
D
f
−
Λ
=
= 200,05*0,000013*(20-20) = 0,00
D
0
= 200,05 – 0,05 = 200,00 m
18. Rozstaw skrajnych słupów hali według dokumentacji wynosi 200m. Podaj jak
ą
wielko
ść
nale
ż
y odło
ż
y
ć
w
terenie maj
ą
c ta
ś
m
ę
stalow
ą
dla której w T
k
= 20
o
C poprawka komparacyjna jest równa 0,005m. Długo
ść
nominalna ta
ś
my 20m; T
p
= 35,5
o
C;
Λ
=0,000013
C
o
1
;
α
= 0
o
D
0
= D
zm
+ f
k
+ f
t
⇒
Dzm = D
0
- f
k
- f
t
(f
r
=0)
m
f
n
f
k
k
05
,
0
005
,
0
*
10
*
+
=
=
∆
=
)
(
*
*
*
k
p
nom
t
t
t
L
n
f
−
Λ
=
= 20,00*0,000013*(35,5-20) = + 0,04 m
D
zm
= 200,00 – 0,05 – 0,04 = 199,91 m
19. Co nazywamy skal
ą
, a co podziałk
ą
(podaj interpretacj
ę
matematyczn
ą
skali)
Skal
ą
danego planu (mapy) nazywamy stosunek długo
ś
ci (d) dowolnego odcinka narysowanego na mapie
(planie) do poziomego rzutu tej długo
ś
ci w terenie (D). Skal
ę
wyra
ż
amy w postaci ułamka
M
1
, którego
licznikiem jest jedno
ść
, za
ś
mianownik M wskazuje stopie
ń
zmniejszenia liniowego danego odwzorowania w
stosunku do rzeczywistej wielko
ś
ci obiektu w terenie. Wyra
ż
a si
ę
wzorem:
D
d
M
=
1
Podziałka liniowa jest graficznym obrazem skali i dzi
ę
ki niej mo
ż
emy dokonywa
ć
szybkiego pomiaru na
mapie. Zasada jej budowy jest bardzo prosta, a opiera si
ę
na liniii prostej odpowiednio podzielonej i
opisanej, na której jest przedstawiony stosunek odległo
ś
ci na mapie i w terenie.
Podziałka zło
ż
ona (poprzeczna lub transwersalna) jest du
ż
o bardziej skomplikowana ni
ż
podziałka liniowa,
chocia
ż
budowa jej opiera si
ę
wła
ś
nie na bazie podziałki liniowej.
Nie rysuje si
ę
jej jednak na mapach, a tak
ż
e kartografowie rzadko j
ą
rysuj
ą
na nowo, bowiem w swoich
pracach wykorzystuj
ą
gotowe, wygrawerowane na mosi
ęż
nych płytkach podziałki, o wymiarach 250x40 mm.
Najcz
ęś
ciej maj
ą
4 gotowe skale 1:1000, 1:2000, 1:4000, 1:5000
20. Dana jest mapa w skali 1:4000 i podziałka w skali 1:5000. Cyrklem wzi
ę
to odcinek z mapy d, i przyło
ż
ono
do podziałki i odczytano D=125,00m. Jaka jest rzeczywista długo
ść
odcinka.
Obliczamy d (długo
ść
odcinka na mapie) w skali 1:5000
mm
m
m
d
m
d
25
025
,
0
5000
125
125
5000
1
=
=
=
⇒
=
Obliczamy D (rzeczywist
ą
długo
ść
odcinka w terenie) w skali 1:4000
m
mm
mm
D
D
mm
100
100000
4000
*
25
25
4000
1
=
=
=
⇒
=
21 Z jak
ą
minimaln
ą
dokładno
ś
ci
ą
nale
ż
y mierzy
ć
szczegóły w terenie aby mo
ż
na je było umie
ś
ci
ć
na mapie
w skali 1:200 w sposób wyra
ź
ny i wierny.
Dokładno
ść
mapy wykonanej w skali 1:200 wynosi
∆
M=0,1mm*200 = 2 cm i z tak
ą
minimaln
ą
dokładno
ś
ci
ą
nale
ż
y zdejmowa
ć
szczegóły w terenie.
22. Co nazywamy dokładno
ś
ci
ą
skali, a co dokładno
ś
ci
ą
podziałki
Dokładno
ś
ci
ą
skali nazywamy 1/10mm linii mapy wyra
ż
onej w warto
ś
ci terenowej (rzeczywistej)
Dokładno
ść
skali mapy –
∆
M = 0,1mm * M
Np. dla skali 1:500 dokładno
ść
równa jest
∆
M = 0,1mm * 500 = 5 cm
Dokładno
ść
podziałki jest to długo
ść
odcinka w terenie odpowiadaj
ą
ca najmniejszej cz
ęś
ci podstawy
podziałki, która nie mo
ż
e by
ć
mniejsza ni
ż
1 mm.
Np. je
ś
li najmniejsza cz
ęść
podstawy podziałki równa jest 1mm to w skali 1:500 to dokładno
ść
podziałki
równa jest:
m
cm
mm
mm
D
D
mm
50
,
0
50
500
500
*
1
1
500
1
=
=
=
=
⇒
=
23. Prosz
ę
skonstruowa
ć
podziałk
ę
poprzeczn
ą
dla skali 1:5000 i zaznaczy
ć
na niej odcinek 125,5 m
skala 1:5000
obieramy podstaw
ę
podziałki np. 100 m
obliczamy długo
ść
podstawy podziałki na mapie: d =
⇒
=
=
cm
m 2
50
1
5000
100
1mm podziałki = 5 m w terenie
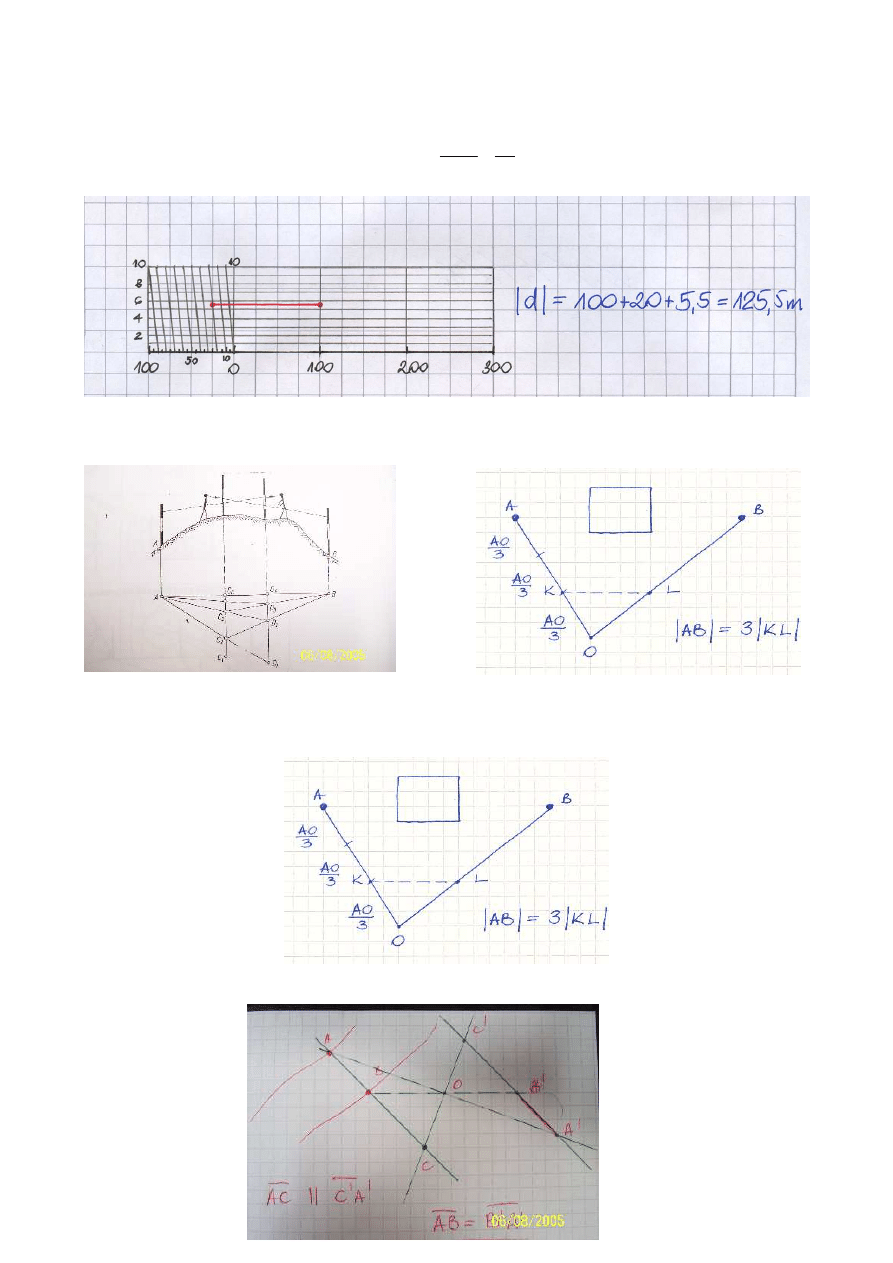
24. Jak mo
ż
na przetoczy
ć
odcinek AB. Do dyspozycji: ta
ś
ma , szpilki, ruletka, tyczki.
25. Jak mo
ż
na okre
ś
li
ć
długo
ść
odcinka AB. Do dyspozycji: ta
ś
ma, szpilki, ruletka, tyczki.
26. Jak mo
ż
na okre
ś
li
ć
szeroko
ść
rzeki
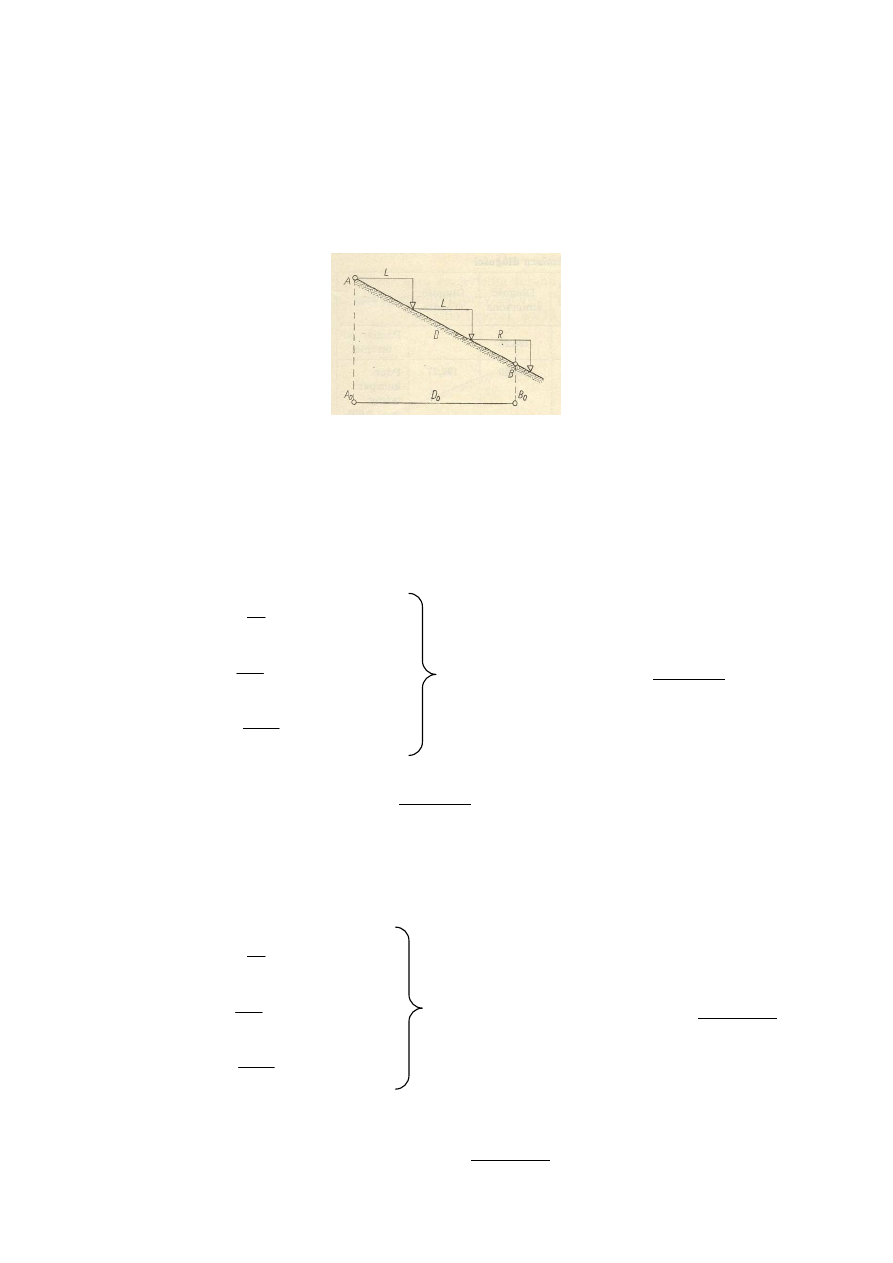
27. Na czym polega pomiar długo
ś
ci metod
ą
schodkow
ą
?
Metoda schodkowa stosowana jest do pomiaru w terenie nachylonym i na znacznych spadkach, polega na
tym,
ż
e zamiast mierzy
ć
długo
ść
D „po terenie” mierzymy rzut poziomy długo
ś
ci D. Wymaga to uło
ż
enia
ta
ś
my w poziomie. W tym celu stosuje si
ę
pion (ci
ęż
arek na sznurku).
Technika pomiaru polega na tym,
ż
e przykładamy zero ta
ś
my w punkcie pocz
ą
tkowym, doprowadzamy
ta
ś
m
ę
do poło
ż
enia poziomego (najbardziej wysuni
ę
te poło
ż
enie pionu w kierunku ko
ń
ca odcinka) i za
pomoc
ą
szpilki oznaczamy poło
ż
enie pionu w terenie. Itd. A
ż
do ko
ń
ca mierzonego odcinka. Pomiary
wykonujemy „tam” i „z powrotem”.
Uwaga w metodzie schodkowej nie uwzgl
ę
dnia si
ę
poprawki redukcyjnej (f
r
=0)
28 Co to jest w
ę
gielnica, jaka jest dokładno
ść
i zasi
ę
g przy zdejmowaniu szczegółów grupy I?
W
ę
gielnica jest to przyrz
ą
d do tyczenia k
ą
tów prostych. Szczególnie u
ż
yteczna jest w sporz
ą
dzaniu
domiarów prostopadłych (prostok
ą
tnych).
Ś
redni bł
ą
d wytyczania k
ą
ta za pomoc
ą
w
ę
gielnic waha si
ę
± 3’-5’
29. Zamie
ń
na stopnie, minuty i sekundy 144
g
48
c
92
cc
1.sposób
144
g
*
'
36
129
6
,
129
10
9
o
o
o
=
=
48
c
*
"
55
'
25
'
92
,
25
100
54
'
=
=
Σ
=
'
36
129
o
+
"
55
'
25
+
"
29
= 130
o
02’25”
92
cc
*
"
30
"
81
,
29
1000
324
"
=
=
2 sposób
144,4892 * 0,9 = 130,04028
o
= 130
o
02’25”
30. Zamie
ń
na grady: 306
o
24’30”
1 sposób
306
o
*
g
g
340
9
10
=
24’
*
c
c
44
,
44
54
100
=
Σ
= 340,00+0,4444+0,0093 = 340,4537= 340
g
45
c
37
cc
30” *
cc
cc
cc
93
59
,
92
324
1000
=
=
2 sposób
306
o
24’30” = 30”+24*60+306*3600= 30+1440+1101600=1103070”
1103070” * 1000 / 324 = 3404537,037
cc
= 340
g
45
c
37
cc
31. Zamie
ń
na miar
ę
łukow
ą
1
o
12’46”
1 sposób
1
o
*
o
o
o
ρ
ρ
0175
,
0
360
2
=
Π
12’
*
'
'
00349
,
0
21600
2
ρ
ρ
=
Π
Σ
= 0,0175+0,00349+0,000223=0,021213
46” *
"
000223
,
0
1296000
2
ρ
=
Π
cc
2 sposób: 1
o
12’46”
⇒
1/57,3 +12/3438 + 46/206265 = 0,0175+0,00349+0,000223= 0,021213
32. Co to jest mapa zasadnicza. Podaj krótk
ą
definicj
ę
.
Mapa zasadnicza - nazywana równie
ż
Podstawow
ą
Map
ą
Kraju to podstawowe opracowanie
geodezyjno-kartograficzne wykonywane w danym kraju. Powinno obejmowa
ć
swoim zasi
ę
giem obszar
całego pa
ń
stwa. Słu
ż
y celom ewidencyjnym, gospodarczym, planistycznym i strategicznym. Jest podstaw
ą
do wykonywania robót budowlanych.
Mapa zasadnicza to mapa wielkoskalowa wykonywana w skalach 1:500 dla obszarów miast, 1:1000 dla
obszarów wiejskich i 1:5000 dla obszarów le
ś
nych. (dodatkowa skala 1:2000)
Tre
ś
ci
ą
mapy s
ą
punkty poziomej i wysoko
ś
ciowej osnowy geodezyjnej, obejmuje ona aktualne dane o:
•
ewidencji gruntów i budynków (katastrze),
•
zagospodarowaniu terenu (ulice, drzewa, obiekty u
ż
yteczno
ś
ci publicznej),
•
podziemnym, naziemnym i nadziemnym uzbrojeniu terenu (Geodezyjna Ewidencja Sieci Uzbrojenia
Terenu),
•
ukształtowaniu terenu (wysoko
ś
ci szczegółów sytuacyjnych, formy ukształtowania terenu).
33. Prosz
ę
wymieni
ć
nakładki mapy zasadniczej i poda
ć
co na ka
ż
dej z nich przedstawiamy.
S – sytuacja nadziemna i naziemna
W – wysoko
ś
ciowa (rze
ź
ba terenu)
U – uzbrojenia terenu i urz
ą
dze
ń
podziemnych
E – ewidencji gruntów (ewentualnie budynków)
R – realizacyjna (przewidywane inwestycje i przewidywane przeznaczenie terenu)
O – osnowy geodezyjnej
34. Prosz
ę
krótko omówi
ć
zasady oblicze
ń
przy pomocy liczb przybli
ż
onych – podaj reguły rachunkowe
Kriłowa-Bradisa
1. Wyniki pomiarów i oblicze
ń
wyra
ż
one liczbami przybli
ż
onymi powinny by
ć
tak obliczane i
zapisywane aby charakteryzowały rz
ą
d wielko
ś
ci liczby i jej dokładno
ść
.
Na przykład, je
ż
eli obliczono długo
ść
odcinka:
- z bł
ę
dem nie przekraczaj
ą
cym 1 m prawidłowym zapisem jest 1614 m
- z bł
ę
dem nie przekraczaj
ą
cym 0,1 m prawidłowym zapisem jest 1613,8 m
- z bł
ę
dem nie przekraczaj
ą
cym 0,01 m prawidłowym zapisem jest 1613,83 m.
2. Cyfry znacz
ą
ce i zera wyst
ę
puj
ą
ce na ko
ń
cu liczby powinny mie
ć
znaczenie dwojakie - wskazywa
ć
rz
ą
d wielko
ś
ci liczby oraz jej dokładno
ść
.
3. Przy dodawaniu i odejmowaniu liczb przybli
ż
onych nale
ż
y w wyniku zachowa
ć
tyle znaków
dziesi
ę
tnych ile zawiera ich liczba przybli
ż
ona o najmniejszej ilo
ś
ci znaków dziesi
ę
tnych.
4. Przy mno
ż
eniu i dzieleniu nale
ż
y w wyniku zachowywa
ć
tyle cyfr znacz
ą
cych, ile zawiera ich liczba
przybli
ż
ona o najmniejszej ilo
ś
ci cyfr znacz
ą
cych.
5. Przy podnoszeniu do kwadratu i sze
ś
cianu nale
ż
y w wyniku zachowywa
ć
tyle cyfr znacz
ą
cych, ile
ich zawiera pot
ę
gowana liczba przybli
ż
ona.
6. Przy wyci
ą
ganiu pierwiastka kwadratowego nale
ż
y w wyniku zachowywa
ć
tyle cyfr znacz
ą
cych, ile
ich zawiera liczba pierwiastkowana.
7. Przy obliczaniu wyników po
ś
rednich stadiów rachunku nale
ż
y bra
ć
zawsze o jedn
ą
cyfr
ę
wi
ę
cej, ni
ż
to wskazuj
ą
zasady podane w ust. 2-6,
8. Je
ż
eli niektóre dane zawieraj
ą
wi
ę
cej znaków dziesi
ę
tnych w działaniach pierwszego stopnia lub
wi
ę
cej cyfr znacz
ą
cych w działaniach drugiego i trzeciego stopnia ni
ż
pozostałe, nale
ż
y je przede
wszystkim zaokr
ą
gli
ć
zachowuj
ą
c przy tym jedn
ą
dodatkow
ą
według reguł cyfr
ę
.
9. Je
ż
eli dane wyj
ś
ciowe do rachunku mo
ż
na bra
ć
z dowoln
ą
dokładno
ś
ci
ą
, wówczas aby otrzyma
ć
wynik o k cyfrach nale
ż
y bra
ć
dane z liczb
ą
cyfr, która zgodnie z regułami 2-6 daje k + 1 cyfr wyniku.
35. W jakich układach odniesienia prowadzona jest mapa zasadnicza
Mapa zasadnicza prowadzona jest w układzie współrz
ę
dnych „1965” pa
ń
stwowej osnowy geodezyjnej.
36. Przy wykonywaniu mapy do celów projektowych geodeta zobowi
ą
zany jest do wykonania tzw. wywiadu
bran
ż
owego. Co to jest wywiad bran
ż
owy, w jakim celu si
ę
go wykonuje i co powinien obj
ąć
swoim zakresem
Wywiad bran
ż
owy jest to wykonanie pomiarów w terenie przedstawiaj
ą
cych aktualny stan
zagospodarowania działki, zmiany w konfiguracji terenu (np. nasypy, doły), istniej
ą
ce sieci uzbrojenia terenu
oraz rosn
ą
ce drzewa i naniesienie tych zmian na map
ę
. Obszar pomiarów obejmuje obszar dotycz
ą
cy
planowanej inwestycji wraz z pasem przyległym szeroko
ś
ci co najmniej 30 metrów.
37. Jakie organy odpowiedzialne s
ą
za prowadzenie ewidencji gruntów i budynków.
Zgodnie z Ustaw
ą
Prawo Geodezyjne i Kartograficzne ewidencj
ę
gruntów i budynków prowadz
ą
starostwa
powiatowe.
38. Co to s
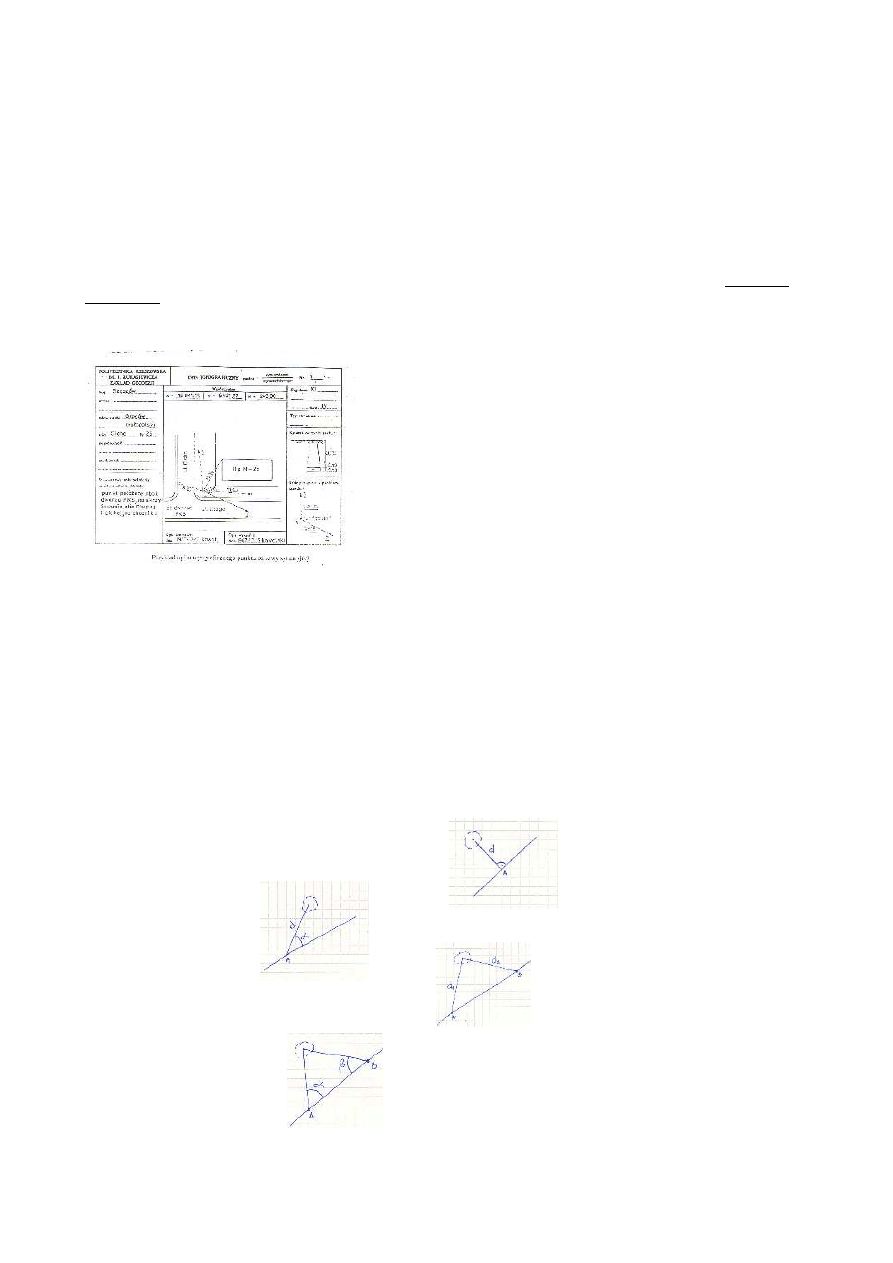
ą
opisy topograficzne punktów osnowy geodezyjnej.
Opis topograficzny punktu osnowy geodezyjnej jest to opisanie
miejsca poło
ż
enia punktu w terenie za pomoc
ą
rysunku na którym
naniesione s
ą
odległo
ś
ci pomi
ę
dzy charakterystycznymi punktami
a punktem osnowy. Jest on pomocny w przypadku, gdy punkt
osnowy zostanie zniszczony lub zabudowany (cho
ć
jest to
prawnie zabronione).
39 Gdzie mo
ż
na uzyska
ć
dane punktów geodezyjnych osnowy znajduj
ą
cej si
ę
na danym terenie.
W starostwie.
40. Jakie znasz dwie podstawowe zasady obowi
ą
zuj
ą
ce przy wykonywaniu pomiarów geodezyjnych i jak je
realizujesz w praktyce.
1. zasada kontroli pomiaru – wykonujemy wszystkie pomiary, nawet te oczywiste, mierzymy
elementy niezb
ę
dne jak i elementy dodatkowe ka
ż
dy pomiar wykonywany jest co najmniej
dwukrotnie
2. zasada przechodzenia od ogółu do szczegółu – zało
ż
enie osnowy pomiarowej (ogólnej),
zdejmowanie szczegółów z nawi
ą
zaniem ich do osnowy pomiarowej
41. Jakie znasz metody zdj
ęć
sytuacyjnych szczegółowych. Prosz
ę
wykona
ć
rysunki zaznaczaj
ą
c wielko
ś
ci
podlegaj
ą
ce pomiarowi.
Metoda domiarów prostok
ą
tnych (prostopadłych)
Metoda biegunowa
Metoda wci
ę
cia liniowego
Metoda wci
ę
cia k
ą
towego
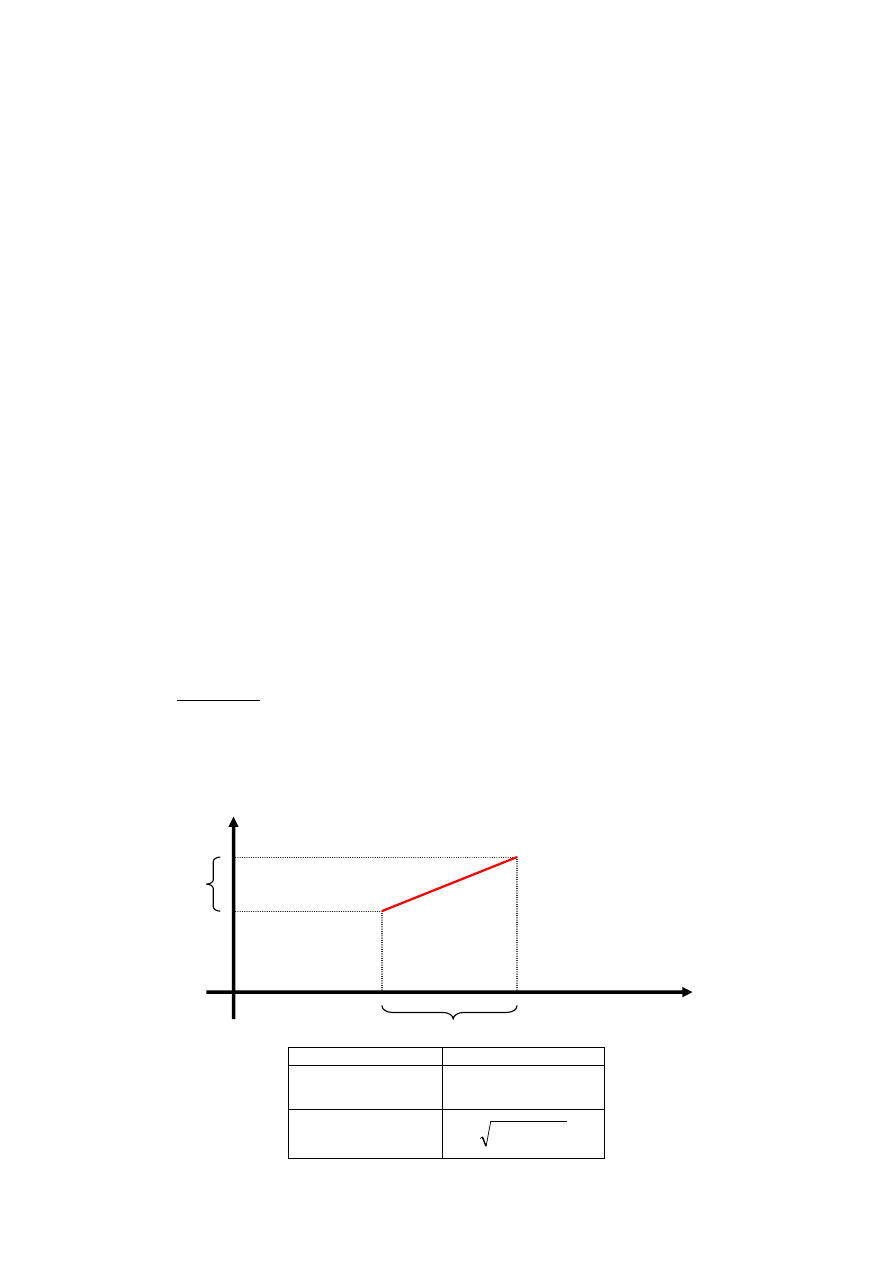
1(x
1
,y
1
)
2 (x
2
,y
2
)
Y
X
d
1-2
∆Y
∆X
y
2
x
2
x
1
y
1
42. Z jak
ą
dokładno
ś
ci
ą
w stosunku do osnowy pomiarowej nale
ż
y zdejmowa
ć
szczegóły sytuacyjne I, II i III
grupy dokładno
ś
ciowej
- dla I grupy szczegółów terenowych ± 0,10 m
- dla II grupy szczegółów terenowych ± 0,30 m
- dla III grupy szczegółów terenowych ± 0,50 m
43. Jakie znasz osnowy pomiarowe. Prosz
ę
wykona
ć
rysunki zaznaczaj
ą
c wielko
ś
ci podlegaj
ą
ce pomiarowi.
1. Linia (baza) pomiarowa
- mierzymy długo
ść
i azymuty
2. Osnowa trójk
ą
tna
- mierzymy długo
ś
ci boków, k
ą
ty i azymuty
3. Osnowa wielok
ą
tna
- mierzymy długo
ś
ci boków, k
ą
ty i azymuty
4. Osnowa w postaci wieloboku zamkni
ę
tego (poligon, ci
ą
g zamkni
ę
ty) – jw.
5. Osnowa w postaci poligonu (ci
ą
gu) otwartego, powi
ą
zanego z osnow
ą
pa
ń
stwow
ą
w :
a. sposób pełny
b. sposób niepełny
c. ci
ą
g wisz
ą
cy
44. Na czym polega zasadnicza ró
ż
nica pomi
ę
dzy ci
ą
giem poligonowym otwartym nawi
ą
zanym do osnowy
szczegółowej
a. w sposób pełny
b. w sposób niepełny
Ci
ą
g poligonowy otwarty nawi
ą
zany do osnowy szczegółowej w sposób pełny pozwala na pełn
ą
kontrol
ę
współrz
ę
dnych , azymutów oraz długo
ś
ci boków.
W ci
ą
gu otwartym nawi
ą
zanym dwustronnie w sposób niepełny , dowi
ą
zanie takie nie pozwala na
sprawdzenie rachunków azymutów, cho
ć
umo
ż
liwia kontrol
ę
współrz
ę
dnych.
45. Co to jest ci
ą
g pomiarowy wisz
ą
cy.
Jest to ci
ą
g jednostronnie dowi
ą
zany do sieci wy
ż
szej klasy. Mo
ż
e mie
ć
co najwy
ż
ej dwa punkty. Ci
ą
g
wisz
ą
cy jest metod
ą
bardzo „niebezpieczn
ą
” i nie gwarantuj
ą
c
ą
dokładno
ś
ci.
46.Ile boków maksymalnie mo
ż
e zawiera
ć
osnowa pomiarowa zało
ż
ona w postaci ci
ą
gu wisz
ą
cego.
Odpowied
ź
zilustruj rysunkiem zaznaczaj
ą
c wielko
ś
ci podlegaj
ą
ce pomiarowi.
Ci
ą
g wisz
ą
cy nie powinien zawiera
ć
wi
ę
cej ni
ż
dwa punkty.
47. Narysuj układ współrz
ę
dnych geodezyjnych i oznacz na nim poło
ż
enie dwóch punktów 1 i 2. Oznacz na
rysunku bok (linii) ł
ą
cz
ą
cej punkty 1 i 2, długo
ść
tego boku, współrz
ę
dne punktów 1 i 2 oraz przyrosty
współrz
ę
dnych mi
ę
dzy tymi punktami. Zapisz wzorami zale
ż
no
ś
ci jakie zachodz
ą
pomi
ę
dzy oznaczonymi na
rysunku wielko
ś
ciami.
Wielko
ść
wzór
przyrosty
∆
X = x
2
– x
1
∆
Y =y
2
– y
2
długo
ść
d
2
2
y
x
∆
+
∆
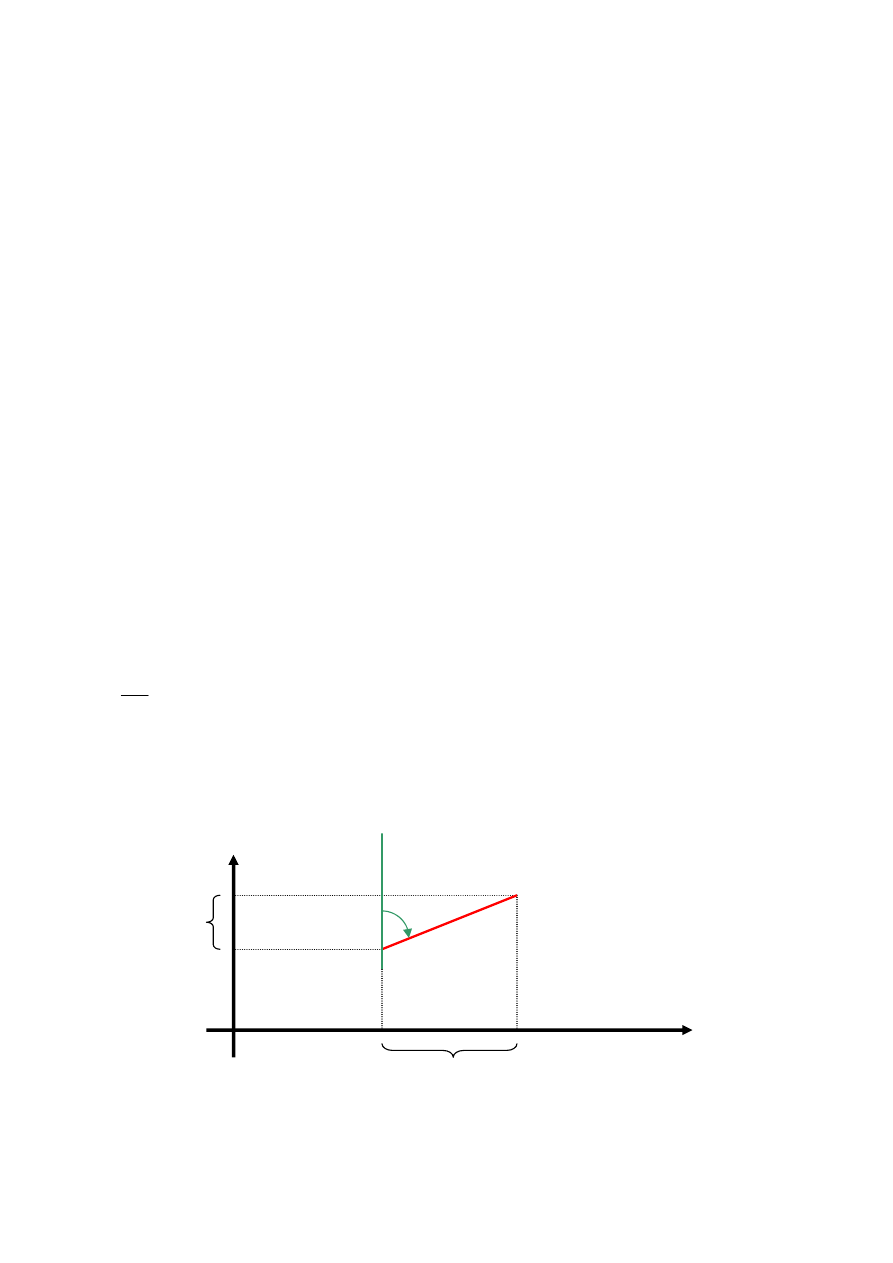
C(x
c
,y
c
)
D
Y
X
d
C-D
∆Y
C-D
∆X
C-D
x
c
y
c
Az
C-D
48. Co to jest azymut:
a. geograficzny
b. topograficzny
c. magnetyczny
Azymut to k
ą
t zawarty mi
ę
dzy północn
ą
cz
ęś
ci
ą
południka odniesienia, a danym kierunkiem poziomym.
Warto
ść
azymutu liczy si
ę
zgodnie z ruchem wskazówek zegara i wyra
ż
a w mierze k
ą
towej. Azymut mo
ż
e
słu
ż
y
ć
do orientacji w terenie i do orientowania pomiarów geodezyjnych.
W zale
ż
no
ś
ci od przyj
ę
tego południka odniesienia wyró
ż
nia si
ę
:
Azymut magnetyczny - k
ą
t mi
ę
dzy północn
ą
cz
ęś
ci
ą
południka magnetycznego a danym kierunkiem
poziomym. Azymut magnetyczny mo
ż
e by
ć
wyznaczony w terenie z u
ż
yciem busoli. Ró
ż
nica mi
ę
dzy
azymutem magnetycznym a azymutem geograficznym to deklinacja magnetyczna
Azymut geograficzny - k
ą
t mi
ę
dzy północn
ą
cz
ęś
ci
ą
południka geograficznego a danym kierunkiem
poziomym. Azymut geograficzny wyznaczany jest w terenie z u
ż
yciem
ż
yroskopu. Ró
ż
nica mi
ę
dzy
azymutem geograficznym a azymutem topograficznym (kartograficznym) to zbie
ż
no
ść
południków.
Azymut topograficzny (kartograficzny) - k
ą
t mi
ę
dzy północn
ą
cz
ęś
ci
ą
południka kartograficznego a danym
kierunkiem poziomym. Azymut kartograficzny mo
ż
e by
ć
wyznaczony k
ą
tomierzem na mapie lub obliczony na
podstawie ró
ż
nic współrz
ę
dnych. Ró
ż
nica mi
ę
dzy azymutem kartograficznym a azymutem geograficznym to
zbie
ż
no
ść
południków.
49. Podaj zale
ż
no
ś
ci mi
ę
dzy azymutami wymienionymi w pytaniu 48.
Ró
ż
nica mi
ę
dzy azymutem magnetycznym a azymutem geograficznym to deklinacja magnetyczna.
Mo
ż
e ona by
ć
wschodnia (dodatnia) lub zachodnia (ujemna).
Ró
ż
nica mi
ę
dzy azymutem geograficznym a azymutem topograficznym (kartograficznym) to zbie
ż
no
ść
południków. Mo
ż
e ona by
ć
wschodnia (dodatnia) lub zachodnia (ujemna).
Ró
ż
nica mi
ę
dzy azymutem kartograficznym a azymutem geograficznym to uchylenie magnetyczne.
Mo
ż
e by
ć
wschodnie (dodatnie) lub zachodnie (ujemne).
50. Oblicz azymut kierunku AB maj
ą
c dane współrz
ę
dne punktu A i B (samodzielnie przerobi
ć
dla własnych
danych)
Maj
ą
c dane współrz
ę
dne punktów A i B obliczamy azymut kierunku AB:
arctg
X
Y
∆
∆
= czwartak azymutu A
A-B
w zale
ż
no
ś
ci od znaków przyrostów X i Y A
A-B
równy jest:
X+;Y+ (I
ć
wiartka)
⇒
A
A-B
= czwartakowi k
ą
ta
X- ;Y+ (II
ć
wiartka)
⇒
A
A-B
= 180
o
- czwartak k
ą
ta
X- ; Y- (III
ć
wiartka)
⇒
A
A-B
= 180
o
+ czwartak k
ą
ta
X+; Y- (IV
ć
wiartka)
⇒
A
A-B
= 360
o
- czwartak k
ą
ta
51. Maj
ą
c dane współrz
ę
dn
ą
punktu C oraz azymut boku CD i długo
ść
boku oblicz współrz
ę
dne punktu D
X
D
= X
c
+
∆
X
C-D
= X
c
+ d
C-D
* cos Az
C-D
Y
D
= Y
c
+
∆
Y
C-D
= Y
c
+ d
C-D
* sin Az
C-D
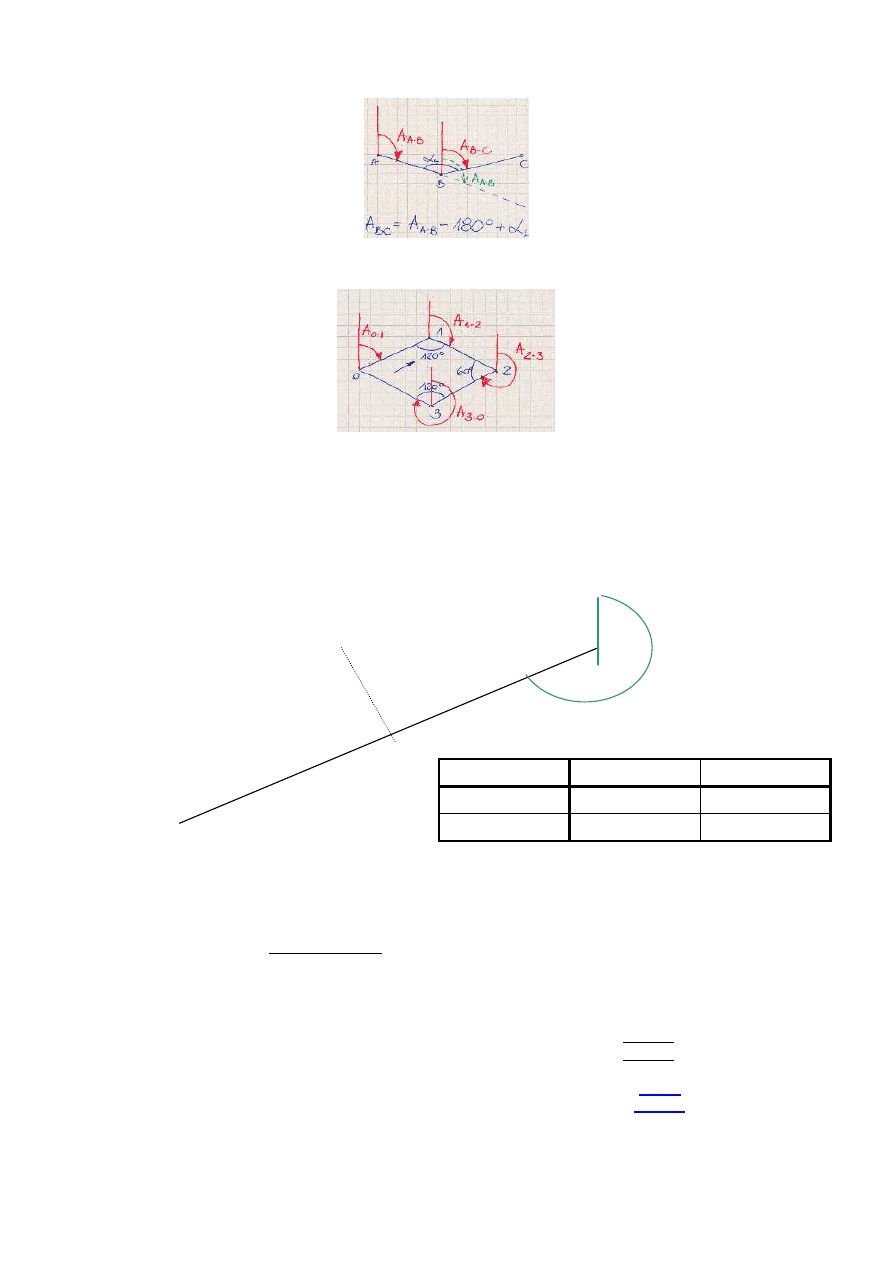
C
C’
A
B
Az
A-B
52. Narysuj rysunek i na jego podstawie napisz wzór na azymut boku nast
ę
pnego maj
ą
c dany azymut boku
poprzedniego i k
ą
t lewy.
53. Maj
ą
c dany azymut boku pocz
ą
tkowego Ap=60” oraz kolejne k
ą
ty prawe 1=120
o
;2=60
o
; 3= 120
o
oblicz
azymut kolejnych boków oraz okre
ś
l znaki przyrostów dla danych boków
A
1-2
=A
0-1
+180
o
-
β
1
= 60+180-120=120
o
A
2-3
=A
1-2
+180
o
-
β
2
=120+180- 60=240
o
A
3-0
=A
2-3
+180
o
-
β
3
=240+180-120=300
o
Znaki przyrostów:
Dla boku 0-1
∆
X+;
∆
Y+
Dla boku 1-2
∆
X-;
∆
Y +
Dla boku 2-3
∆
X -;
∆
Y –
Dla boku 3-4
∆
X+;
∆
Y –
54. Oblicz współrz
ę
dne punktu C na domiarze
1) Obliczamy azymut Az
A-B
∆
X
B-A
= - 113,50 - ( -112,46) = - 1,04
∆
Y
B-A
= - 202,16 - ( -117,26) = - 84,91
tg
Az
A-B
=
- 84,91
= 81,64423077
(III
ć
wiartka)
-1,04
arctg
Az
A-B
= 89,2983 = 89
o
17’54”
Az
A-B
= 180
o
+ 89
o
17’54” =
269
o
17’54”
2) Obliczmy współrz
ę
dne punktów C’ i C
X
C’
= X
A
+
∆
X
A-C’
= X
A
+ d
A-C’
.
cos Az
A-B
= -112,46 + (11,26
.
cos Az
A-B
) = -112,60
Y
C’
= Y
A
+
∆
Y
A-C’
= Y
A
+ d
A-C’
.
sin Az
A-B
= -117,25 + (11,26
.
sin Az
A-B
) = -128,51
Az
C’-C
= Az
A-B
+ 90
o
= 269
o
17’54” + 90
o
=
359
o
17’54”
X
C
= X
C’
+
∆
X
C’-C
= X
C’
+ d
C’-C
.
cos Az
C”-C
= -112,60 + (19,22
.
cos Az
C’-C
) =
-93,38
Y
C
= Y
C’
+
∆
Y
C’-C
= Y
C’
+ d
C’-C
.
sin Az
C’-C
= -128,51 + (19,22
.
sin Az
C’-C
) =
-128,75
55. Oblicz współrz
ę
dne punktu C metod
ą
biegunow
ą
Nr punktu
X
Y
A
- 112,46
- 117,25
B
- 113,50
- 202,16
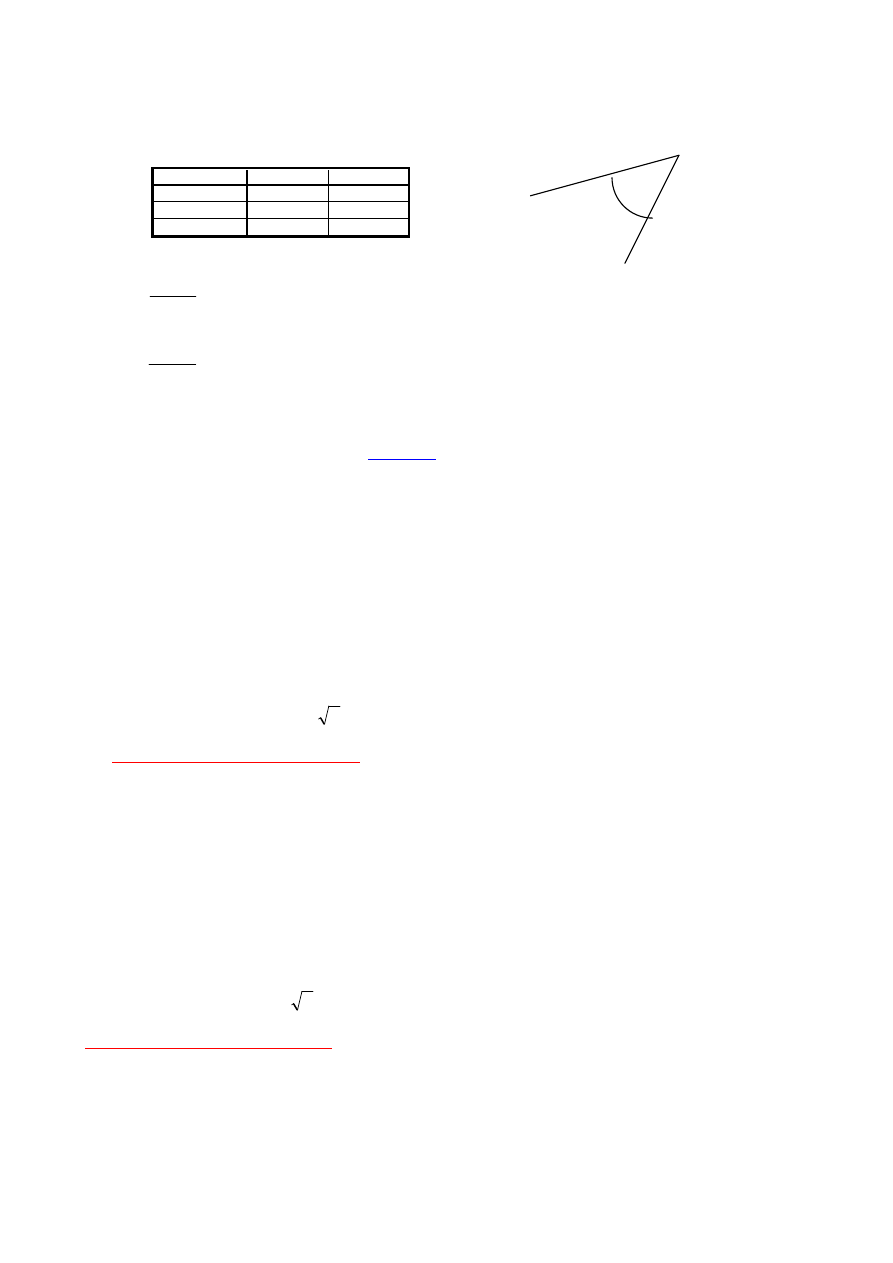
A
B
56. Oblicz współrz
ę
dne punktu C metod
ą
k
ą
towego wci
ę
cia w przód
57. Oblicz współrz
ę
dne punktu C metod
ą
liniowego wci
ę
cia w przód
58. Oblicz k
ą
t ze współrz
ę
dnych.
Nr punktu
X
Y
A
100,10
- 20,10
O
- 200,11
80,42
B
84,62
284,57
1) Obliczamy azymut Az
O-B
tg
Az
O-B
=
0
-
B
0
-
B
X
Y
∆
∆
=0,716995 (I
ć
wiartka)
arctg
Az
O-B
= 35,6403 = 35
o
38’25”
⇒
Az
O-B
=
35
o
38’25”
2) Obliczamy azymut Az
O-A
Obliczamy k
ą
t
β
tg
Az
A-B
=
0
-
A
0
-
A
X
Y
∆
∆
= - 0,334832 (IV
ć
w.)
arctg
Az
O-A
=18,5122 =18
o
30’43”
⇒
Az
O-A
=360-18
o
30’43”=
341
o
29’17”
3) Obliczamy k
ą
t
β’(zewnętrzny)
β’
= Az
O-A
- Az
O-B
= 341
o
29’17” - 35
o
38’25” =
305
o
50’52”
4) Obliczamy k
ą
t
β (wewnętrzny) – wynik ostateczny zadania
K
ą
t AOB =
β
= 360
o
- 305
o
50’52”=
54
o
10’08”
59. Jak sprawdzasz prawidłowo
ść
pomiaru k
ą
tów w ci
ą
gu poligonowym zamkni
ę
tym?
Suma pomierzonych k
ą
tów:
[
β
P
] =
β
1
+
β
2
+
β
3
...... +
β
n
Suma teoretyczna k
ą
tów wewn
ę
trznych w poligonie zamkni
ę
tym zgodnie z wzorem:
[
β
T
] = (n-2)*180
o
(miara stopniowa)
lub
[
β
T
] = (n-2)*200
g
(miara gradowa)
Ró
ż
nica pomi
ę
dzy sum
ą
teoretyczn
ą
k
ą
tów i sum
ą
pomierzonych k
ą
tów daje nam odchyłke nie
zamkni
ę
cia k
ą
towego poligonu
f
k
= [
β
T
] - [
β
P
]
Aby k
ą
ty mo
ż
na było wyrówna
ć
musi zachodzi
ć
nast
ę
puj
ą
ca zale
ż
no
ść
:
f
k
≤
f
kmax
gdzie f
kmax
= 2m
n
Je
ś
li jest zachowany ten warunek mo
ż
emy wyrówna
ć
k
ą
ty („po równo” dla ka
ż
dego k
ą
ta).
Je
ś
li nie to pomiary nale
ż
y powtórzy
ć
60. Jak sprawdzasz prawidłowo
ść
pomiaru k
ą
tów w ci
ą
gu poligonowym otwartym?
Suma pomierzonych k
ą
tów:
[
β
P
] =
β
1
+
β
2
+
β
3
...... +
β
n
Suma teoretyczna k
ą
tów wewn
ę
trznych w poligonie zamkni
ę
tym zgodnie z wzorem:
[
β
T
] = A
pocz
- A
kon
+ n*180
o
(miara stopniowa)
lub
[
β
T
] = A
pocz
- A
kon
+ n*200
g
(miara gradowa)
Ró
ż
nica pomi
ę
dzy sum
ą
teoretyczn
ą
k
ą
tów i sum
ą
pomierzonych k
ą
tów daje nam odchyłk
ę
nie zamkni
ę
cia
k
ą
towego poligonu
f
k
= [
β
T
] - [
β
P
]
Aby k
ą
ty mo
ż
na było wyrówna
ć
musi zachodzi
ć
nast
ę
puj
ą
ca zale
ż
no
ść
:
f
k
≤
f
kmax
gdzie f
kmax
= 2m
n
Je
ś
li jest zachowany ten warunek mo
ż
emy wyrówna
ć
k
ą
ty („po równo” dla ka
ż
dego k
ą
ta).
Je
ś
li nie to pomiary nale
ż
y powtórzy
ć
61. Jak sprawdzasz prawidłowo
ść
pomiaru długo
ś
ci boków w ci
ą
gu poligonowym zamkni
ę
tym?
Podstawowy warunek prawidłowo
ś
ci pomiaru boków w poligonie zamkni
ę
tym :
[
∆
x] = 0 i [
∆
y] = 0 gdzie
∆
x i
∆
y – przyrosty
Dopuszczalna odchyłka wynosi:
0
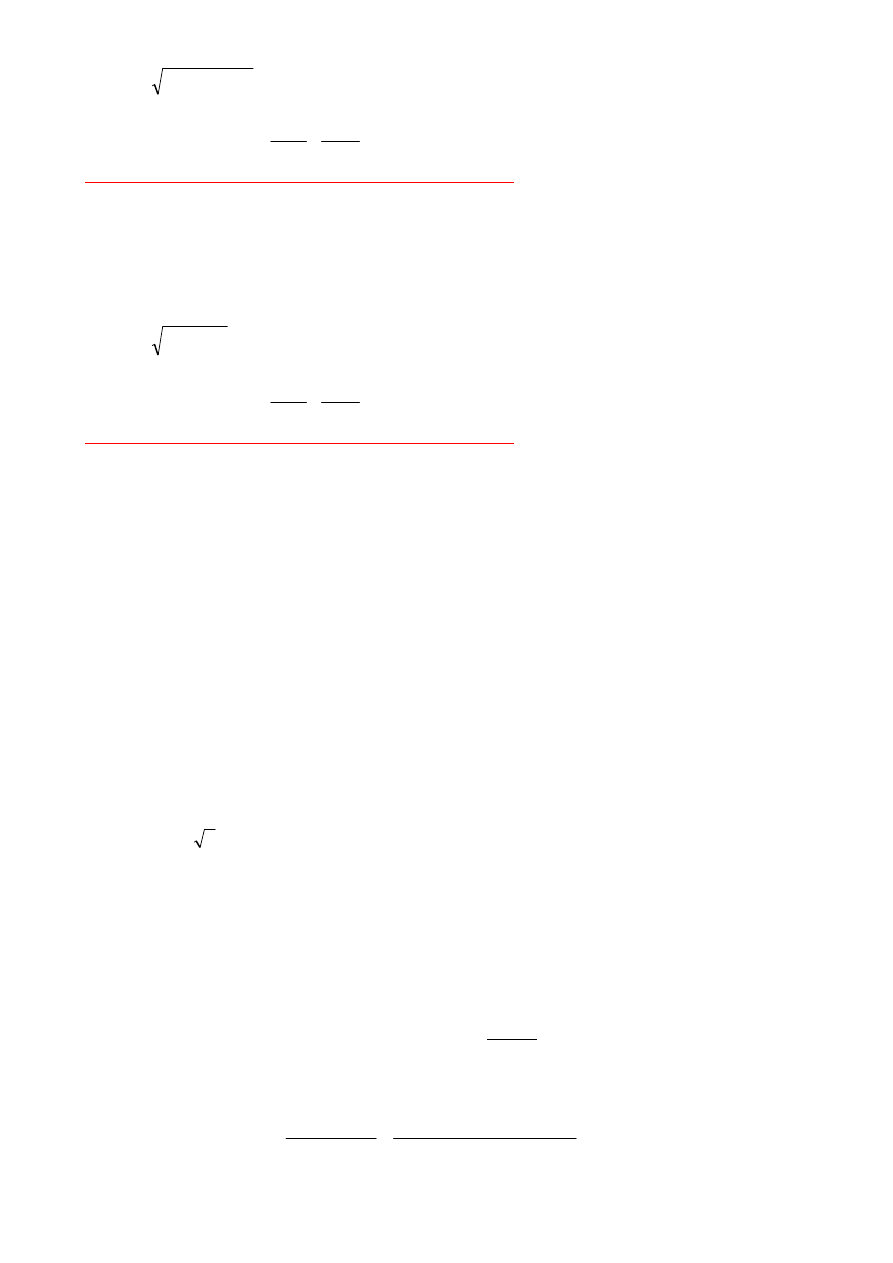
f
l
=
[ ] [ ]
2
2
y
x
∆
+
∆
Aby boki mo
ż
na było wyrówna
ć
musi by
ć
spełniona nast
ę
puj
ą
ca zale
ż
no
ść
:
f
l
≤
f
lmax
gdzie f
lmax
=
−
4000
1
1000
1
Je
ś
li ten warunek nie jest spełniony to pomiary nale
ż
y powtórzy
ć
62. Jak sprawdzasz prawidłowo
ść
pomiaru długo
ś
ci boków w ci
ą
gu poligonowym otwartym?
Podstawowy warunek prawidłowo
ś
ci pomiaru boków w poligonie zamkni
ę
tym :
[
∆
x
P
] = [
∆
x
T
] gdzie niedomkni
ę
cie f
x
=[
∆
x
P
] - [
∆
x
T
]
[
∆
y
P
] = [
∆
y
T
] gdzie niedomkni
ę
cie f
y
=[
∆
y
P
] - [
∆
y
T
]
Dopuszczalna odchyłka wynosi:
f
l
=
2
2
y
x
f
f
+
Aby boki mo
ż
na było wyrówna
ć
musi by
ć
spełniona nast
ę
puj
ą
ca zale
ż
no
ść
:
f
l
≤
f
lmax
gdzie f
lmax
=
−
4000
1
1000
1
[d
i
]
gdzie [di] to suma długo
ś
ci boków
Je
ś
li ten warunek nie jest spełniony to pomiary nale
ż
y powtórzy
ć
63. Oblicz wyrównane współrz
ę
dne dla zał
ą
czonego dziennika współrz
ę
dnych (samodzielnie przerobi
ć
dla
własnych danych) poligon zamkni
ę
ty.
64. Oblicz wyrównane współrz
ę
dne dla zał
ą
czonego dziennika współrz
ę
dnych (samodzielnie przerobi
ć
dla
własnych danych) poligon otwarty.
65. Jak obliczamy odchyłk
ę
liniow
ą
w ci
ą
gu obustronnie nawi
ą
zanym, a jak liniow
ą
odchyłk
ę
dopuszczaln
ą
.
Co uwzgl
ę
dniamy ustalaj
ą
c warto
ść
odchyłki dopuszczalnej.
66. W ci
ą
gu poligonowym składaj
ą
cym si
ę
z czterech punktów pomierzono k
ą
ty prawe których suma
wyniosła 900
g
02
c
. Azymut boku pocz
ą
tkowego równy jest 200
g
, za
ś
azymut boku ko
ń
cowego równy jest
100
g
. Przyjmuj
ą
c dokładno
ść
odczytu 1
c
. Oblicz odchyłk
ę
k
ą
tow
ą
w tym ci
ą
gu i stwierd
ź
czy jest ona
dopuszczalna (czy k
ą
ty mo
ż
na wyrówna
ć
)
β
t
= A
p
– A
k
+ n*200
g
⇒
200
g
– 100
g
+ 4*200
g
= 900
g
β
p
= 900
g
02
c
f
k
=
β
p
-
β
t
= - 2
c
f
kmax
= 1,5
4
= 3
c
K
ą
ty mo
ż
na wyrówna
ć
gdy
ż
odchyłka k
ą
towa jest mniejsza od dopuszczalnej odchyłki k
ą
towej.
67. Obliczy
ć
azymut ko
ń
cowy A
k
gdy dany jest azymut pocz
ą
tkowy A
p
= 128
o
03’, liczba k
ą
tów prawych n=6
oraz ich suma
β
p
= 1075
o
28’
A
p
= 128
o
03’
β
p
= 1075
o
28’
A
k
= A
p
+ n*180
o
-
β
p
⇒
A
k
= 128
o
03’ +6*180
o
-1075
o
28’ = 132
o
35’
68. Z ilu k
ą
tów składa si
ę
ci
ą
g otwarty, w którym azymut pocz
ą
tkowy A
p
= 247
o
19’; A
k
= 142
o
07’, a suma
k
ą
tów lewych
β
l
= 794
o
48’
A
k
= A
p
- n*180
o
+
β
p
⇒
n =
5
180
48'
794
07'
19'-142
247
180
o
o
o
o
=
+
=
+
−
o
l
k
p
A
A
β
69. Co nazywamy k
ą
tem pionowym , a co k
ą
tem poziomym. Zrób rysunek
K
ą
t pionowy - w geodezji, k
ą
t zawarty w płaszczyznie pionowej mi
ę
dzy kierunkiem odniesienia, a
kierunkiem na dany punkt terenowy. Je
ż
eli kierunkiem odniesienia jest poziom, k
ą
t pionowy wyznaczony w
jego oparciu nazywa si
ę
k
ą
tem pochylenia. Je
ż
eli za
ś
kierunkiem odniesienia jest zenit, k
ą
t pionowy
wyznaczony w jego oparciu nazywa si
ę
k
ą
tem zenitalnym.
K
ą
t pionowy mo
ż
e by
ć
mierzony teodolitem lub tachimetrem.
K
ą
t poziomy - w geodezji, k
ą
t dwu
ś
cienny zawarty mi
ę
dzy dwiema płaszczyznami pionowymi
przechodz
ą
cymi przez punkty terenowe. K
ą
t poziomy nie podlega bezpo
ś
redniemu pomiarowi w terenie.
Pomiarem obj
ę
te s
ą
kierunki poziome, których ró
ż
nica daje warto
ść
k
ą
ta poziomego.
K
ą
ty poziome mog
ą
by
ć
mierzone z u
ż
yciem teodolitów lub tachimetrów.
70. Budowa teodolitu – nale
ż
y wykaza
ć
si
ę
znajomo
ś
ci
ą
zasadniczych cz
ęś
ci teodolitu, umie
ć
je wskaza
ć
i
nazwa
ć
.
Teodolit skł
ą
da si
ę
z trzech podstawowych cz
ęś
ci
1) spodarka z limbusem
2) alidada
3) luneta
Spodarka zaopatrzona jest w trzy
ś
ruby nastawcze do poziomowania.
Przechodzi ona w walec (ww) w którego wydr
ąż
eniu obsadzona jest alidada
przekr
ę
cona
ś
rub
ą
. Na alidadzie ustawione s
ą
na stałe dwa d
ź
wigarki lunety
(p1,p2)zako
ń
czone u góry ło
ż
yskami w których obraca si
ę
luneta.
Do unieruchomienia alidady i lunety słu
żą
ś
ruby zaciskowe.
71. Co to jest libela rurkowa, a co pudełkowa. Na czym polega zasadnicza ró
ż
nica w budowie tych libel.
Libella pudełkowa- Jest to naczynie szklane w kształcie walca obsadzonego pionowo, którego górn
ą
powierzchni
ę
stanowi wycinek kuli . Poziomica wbudowana jest w metalow
ą
obudow
ę
, wypełniona jest
lekk
ą
ciecz
ą
(eter, spirytus) który napełnia si
ę
przyrz
ą
d w stanie pogranicznym . Po ostygni
ę
ciu w
zbiornikach tworzy si
ę
wolna przestrze
ń
tzw p
ę
cherzyk libelli
Na
ś
rodku poziomicy znajduje si
ę
punkt zerowy libeli.
Libella rurkowa wykonywana jest w sposób taki jak pudełkowa, lecz w formie podłu
ż
nej rurki zamocowanej
poziomo, mo
ż
e by
ć
ona jednowarstwowa lub dwustronna (rewersyjna). Odchylenie p
ę
cherzyka od punktu
zerowego nazywa si
ę
odskokiem.
Libella pudełkowa jest mniej dokładna i słu
ż
y do zgrubszego (wstepnego) wypoziomowania teodolitu, libella
rurkowa słu
ż
y do ostatecznego spoziomowania teodolitu.
72. Co nazywamy osi
ą
libeli rurkowej.
Osi
ą
libeli rurkowej nazywamy
ś
rodek podziału rurki. Je
ż
eli
ś
rodek p
ę
cherzyka znajduje si
ę
w punkcie
głównym G (w osi libeli) to o
ś
libeli zajmuje w przestrzeni poło
ż
enie pionowe.
73. Co nazywamy osi
ą
celow
ą
.
Osi
ą
celow
ą
lunety nazywamy prost
ą
przechodz
ą
c
ą
przez
ś
rodek optyczny obiektywu i
ś
rodek krzy
ż
a nitek.
74. Co to jest przewaga libeli? W jakich granicach si
ę
ona kształtuje w niwelatorach lub w teodolitach.
Przewaga libeli jest to k
ą
t o jaki nale
ż
y pochyli
ć
libell
ę
, aby jej p
ę
cherzyk przesun
ą
ł si
ę
o jedn
ą
działk
ę
czyli
o 2 mm. Kształtuje si
ę
ona w granicach 5”- 60”
75. Narysuj schematycznie lunet
ę
geodezyjn
ą
oraz omów w punktach jej budow
ę
Luneta składa si
ę
z dwóch współosiowych walców. W jednym
z nich znajduje si
ę
obiektyw, soczewka ogniskuj
ą
ca oraz
płytka ogniskowa. Drugi to okular słu
żą
cy do ustawienia
ostro
ś
ci krzy
ż
a nitek.
76. Na czym polega nastawienie na ostro
ść
w lunecie.
Pierwsz
ą
czynno
ś
ci
ą
jest ustawienie ostro
ś
ci krzy
ż
a nitek. Wykonuje si
ę
to za pomoc
ą
okularu.
Nast
ę
pnie po wst
ę
pnym wycelowaniu lunety za pomoc
ą
muszki i szczerbinki, pokr
ę
camy pier
ś
cieniem
ogniskuj
ą
cym i nastawiamy obraz na ostro.
77.Co nazywamy bł
ę
dem paralaksy.
Bł
ą
d paralaksy wyst
ę
puje przy nastawianiu na ostro
ść
obrazu , jest to tzw. Pozorne pokrycie si
ę
płaszczyzny obrazu z płaszczyzn
ą
krzy
ż
a nitek (obraz widoczny jest ostry, ale płaszczyzny si
ę
nie
pokrywaj
ą
) Paralaks
ę
mo
ż
na łatwo wykry
ć
przesuwaj
ą
c oko z góry na dół.
78. Co jest zadaniem okularu w lunecie geodezyjnej. Do czego on słu
ż
y?
Okular słu
ż
y do ustawienia ostro
ś
ci krzy
ż
a nitek.
79. Co nazywamy osi
ą
celow
ą
lunety, osi
ą
optyczn
ą
lunety, osi
ą
geometryczn
ą
lunety.
Osi
ą
celow
ą
lunety nazywamy prost
ą
przechodz
ą
c
ą
przez
ś
rodek optyczny obiektywu i
ś
rodek krzy
ż
a nitek.
Osi
ą
optyczn
ą
lunety nazywamy prost
ą
przechodz
ą
c
ą
przez
ś
rodek optyczny obiektywu i okularu
Osi
ą
geometryczn
ą
lunety nazywamy prost
ą
ł
ą
cz
ą
ca
ś
rodki pier
ś
cieni lunety, tj. o
ś
symetrii lunety..
80. Jakie znasz systemy odczytowe stosowane w teodolitach?
Noniusze
Mikroskopy odczytowe
Mikrometry odczytowe
Systemy odczytów elektronicznych
81. Narysuj widok w polu widzenia mikroskopu skalowego podziałki horyzontalnej i zaznacz odczyt 122
o
36’
je
ż
eli
δ
= 1’
82. Podaj z jak
ą
dokładno
ś
ci
ą
mo
ż
emy scentrowa
ć
teodolit za pomoc
ą
pionu:
a. sznurkowego
b. dr
ąż
kowego
c. optycznego
sznurkowy: 2-3 mm
dra
ż
kowy: 1 mm
optyczny: 0,3-0,5 mm
83. Narysuj schematycznie układ osiowy teodolitu, oznacz osie i podaj jakie warunki geometryczne musz
ą
spełni
ć
. Nazwij je
C
1. Warunek libeli (zawsze musi by
ć
spełniony) L
┴
V
V 2. Warunek kolimacji (gwarancja płaszczyzny celowej) C
┴
H
H 3. Warunek inklinacji (gwarancja pionowo
ś
ci płaszczyzny celowej) H
┴
V
Osie:
C - o
ś
celowa, H – o
ś
obrotu lunety,
L L – o
ś
libeli rurkowej, V – o
ś
obrotu instrumentu
Pozostałe warunki to:
4. przy pionowym ustawieniu osi obrotu instrumentu kreski krzy
ż
a nitek powinny zajmowa
ć
poło
ż
enie
pionowe i poziome
5. o
ś
obrotu alidady powinna pokrywa
ć
si
ę
z osi
ą
obrotu limbusa
6. przy poziomej osi celowej i spoziomowanej libeli odczyt na kole pionowym powinien by
ć
równy „0”
84. Czy wszystkie warunki teodolitu musz
ą
by
ć
spełnione aby mo
ż
na było mierzy
ć
k
ą
ty.
Musi by
ć
spełniony warunek libelli, czyli o
ś
libelli rurkowej musi by
ć
prostopadła do osi obrotu
instrumentu: L
┴
V
Pozostałe warunki powinny by
ć
spełnione ale nie s
ą
one konieczne.
85. Jak przebiega poziomowanie teodolitu?
Poziomowanie teodolitu:
1. Ustawiamy nogi statywu w taki sposób, aby o
ś
główna teodolitu znajdowała si
ę
w przybli
ż
eniu w pionie i
przechodziła przez punkt geodezyjny. Rozstawione nogi statywu powinny tworzy
ć
trójk
ą
t równoboczny.
Ustawienie instrumentu powinno równie
ż
zapewnia
ć
przybli
ż
one spoziomowanie teodolitu.
2. Patrz
ą
c cały czas