REAKCJE OSCYLACYJNE (przygotował Tomasz Panz)

Zagadnienia do przygotowania:

-podstawowe pojecia kinetyki chemicznej (szybkość reakcji, rząd reakcji,

energia aktywacji)

- kinetyka reakcji enzymatycznych

-prawa termodynamiki, pojecie entropii, reakcje odwracalne

i nieodwracalne

- definicja i przykłady sprzężenia zwrotnego dodatniego i ujemnego

Cel ćwiczenia

a.

obserwacje barwnych reakcji oscylacyjnych

b.

zbadanie wpływu temperatury na kinetykę reakcji

c.

obserwacje struktur dyssypatywnych w roztworach

Wprowadzenie:

Procesy oscylacyjne można obserwować w fizyce, chemii, astronomii i biologii.

Początkowe spostrzeżenia dotyczące oscylacji w układach chemicznych miały charakter

przypadkowy, a ich autorzy narażeni byli na zarzut niestarannego prowadzenia

doświadczeń. Nieufność ta była konsekwencją sprzeczności obserwowanych zjawisk

z klasycznymi regułami termodynamiki ujętymi w XIX w. przez Clausiusa. Reguły te

stwierdzały, że układ pozbawiony dopływu materii i energii z otoczenia nieuchronnie

zmierza do stanu równowagi, zaś entropia w miarę postępu reakcji chemicznej

wzrasta. Periodyczna zmiana własności układu, wskazująca na okresowy wzrost

uporządkowania pewnych reagentów, wydawała się zaprzeczeniem drugiej zasady

termodynamiki.

W roku 1921 William Bray ze Stanów Zjednoczonych badał stężenie jodanu IO

3

–

podczas reakcji katalitycznego rozkładu nadtlenku wodoru (jodan pełni w tej reakcji

funkcję katalizatora):

jodan

H

2

O

2

Y

½ O

2

+ H

2

O

Stężenie katalizatora w toku reakcji okresowo się zmieniało. Prace Bray'a uznano za

artefakty.

W ZSRR w roku 1958 Biełousow badał reakcję kwasu cytrynowego z bromianem

potasu w obecności soli ceru. W tym czasie chemia fizyczna była już lepiej

przygotowana do “przełknięcia pigułki” reakcji oscylacyjnych. Ilia Prirogine z Brukseli

wykazał, że klasyczna termodynamika, a więc to co postulował Clausius, wymaga nie

tylko braku wymiany materii i energii z otoczeniem, ale i bliskości stanu równowagi.

W układach dalekich od tego stanu mogą zachodzić tzw. procesy dyssypatywne,

będące z kolei przyczyną powstawania struktur dyssypatywnych. Procesy

dyssypatywne mogą to być przykładowo zmieniające się okresowo stężenia produktów

pośrednich wspomnianych powyżej reakcji chemicznych. Stężenia substratów

i produktów końcowych nie oscylują, zmierzając ku stanowi równowagi. Systematyczne

badania nad reakcją odkrytą przez Biełousowa podjął w latach sześćdziesiątych

Żabotyński. Określił on dokładnie warunki, w jakich ta reakcja zachodzi, między innymi

wpływ stężeń substratów na charakter drgań (6). Do późnych lat sześćdziesiątych nie

rozumiano właściwie tej reakcji. W uznaniu zasług obydwu uczonych ze Związku

Radzieckiego nazwano tę przemianę reakcją Biełousowa-Żabotyńskiego. Wyjaśnienie

mechanizmu reakcji w sensie chemicznym polega na podaniu sekwencji wszystkich

reakcji elementarnych składających się na cały proces, łącznie ze stałymi równowagi

i stałymi czasowymi poszczególnych etapów. W latach siedemdziesiątych grupa

uczonych amerykańskich, współpracując z Węgrami, zaproponowała schemat

mechanizmu reakcji B-Ż składający się z osiemnastu etapów (2). Schemat ten sprawdził

się m.in poprzez symulacje komputerowe odzwierciedlające kinetykę reakcji

obserwowanej w laboratorium. Wyjaśnienie reakcji B-Ż obudziło nadzieje na głębsze

zrozumienie innych procesów oscylacyjnych. Pod koniec lat siedemdziesiątych

skonstatowano, że przewidywania te nie sprawdziły się – poznano tylko kilka podobnych

reakcji, wszystkie zostały odkryte przypadkowo, nie wiadomo było jakie są warunki

konieczne i wystarczające do zaobserwowania oscylacji.

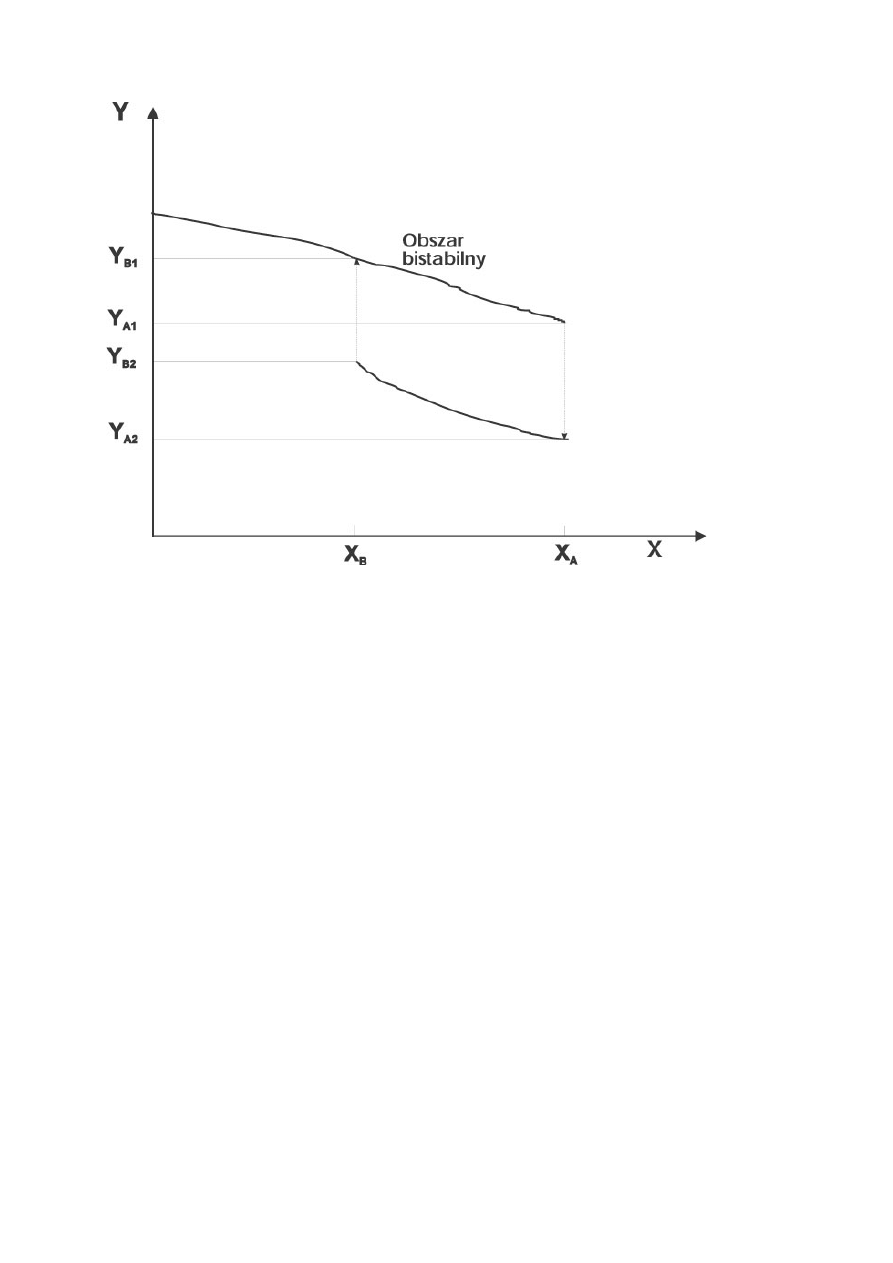
Rysunek 1. Prosty przykład układu bistabilnego

W roku 1979 podjęto próbę zdefiniowania warunków niezbędnych do wywołania

oscylacji chemicznych. Punktem wyjśnia były cechy wspólne wszystkich do tej pory

odkrytych reakcji oscylacyjnych. Oto one:

a.

układ musi być daleko od stanu równowagi

b.

w układzie musi znajdować się pętla sprzężenia zwrotnego - produkt

przynajmniej jednej reakcji powinien kontrolować tempo własnego powstawania

c.

układ musi być bistabilny - znaczy to, że w tych samych warunkach

zewnętrznych możliwe są dwa różne, stabilne stany stacjonarne

Techniką, dzięki której odkryto kilka nowych rodzin reakcji oscylacyjnych, jest

"przepływ ciągły" (w języku angielskim: "continuous flow"). Istotą tej techniki jest

przepływ substratów przez komorę reakcyjną; pozwala ona na łatwe spełnienie warunku

nie zbliżania się do stanu równowagi. Przy zmianie warunków zewnętrznych w

przypadku układu bistabilnego można zobserwować swoistą pętlę histerezy - układ

powraca do stanu wyjściowego po drodze odmiennej od drogi pierwotnej (Rysunek 2).

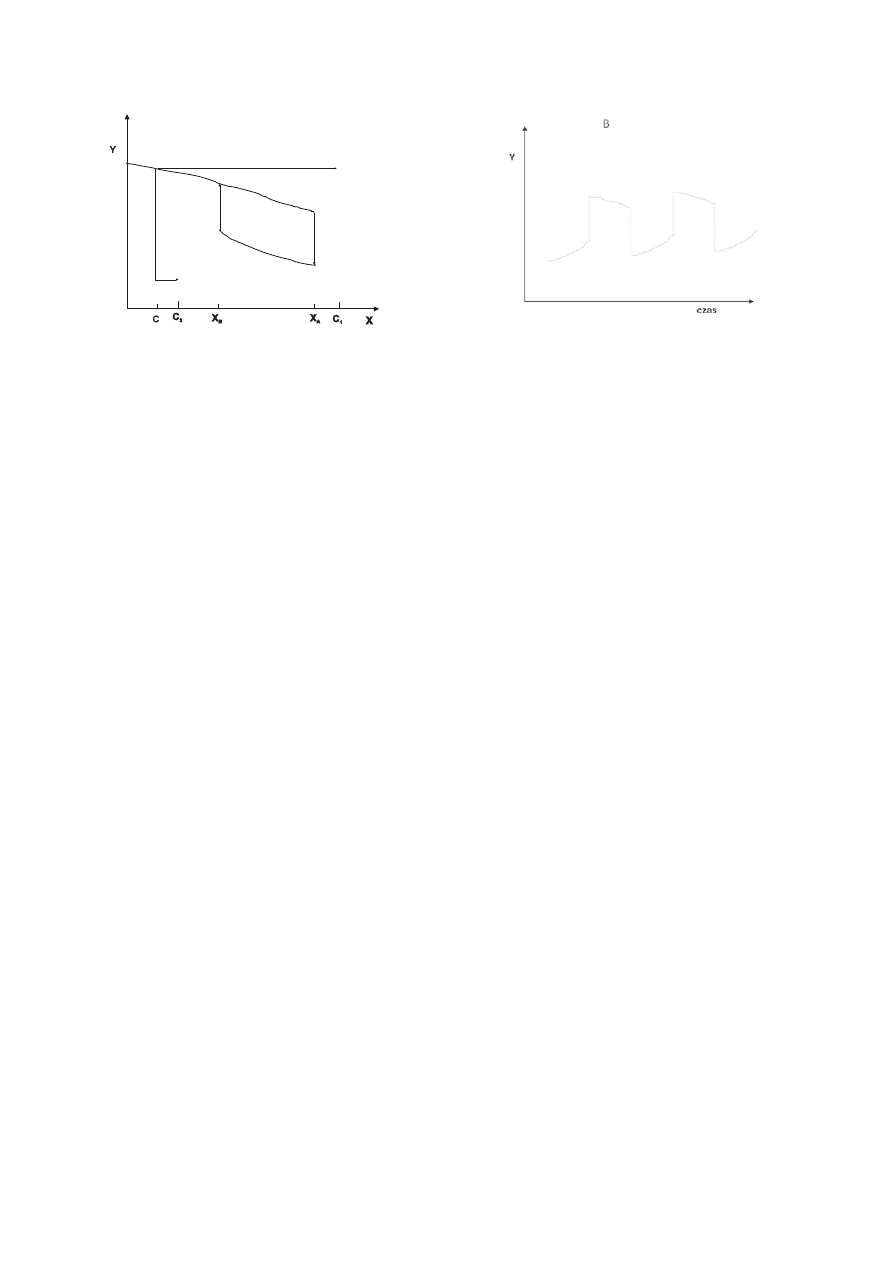
Obszar

bistabilny

A

Rysunek 2. Pętla histerezy w bistabilnym układzie chemicznym.

W miarę gdy stężenie X rośnie, stężenie Y spada wzdłuż krzywej górnej aż do wartości

Y

A1

, a następnie przeskakuje w punkcie X

A

na krzywą dolną. Przy dalszym zwiększaniu

stężenia X ustala się nowy stabilny stan stacjonarny wzdłuż dolnej krzywej. Podczas

zmniejszania stężenia X, po osiągnięciu punktu X

B

, stabilny stan stacjonarny

"przeskakuje" na krzywą górną (wg (2)).

Rysunek 3. Oscylacje w bistabilnym układzie chemicznym.

Oscylacje mogą wystąpić gdy stosowna substancja Z jest dodana do bistabilnego

układu chemicznego, który wykazuje histerezę. Substancja Z wolno reaguje

z substancją Y, przekształcając ją w substancję X, i wówczas efektywne stężenie

substancji X jest wyższe od wartości początkowej, przed dodaniem substancji Z. Efekt

zwiększenia efektywnego stężenia X jest większy na krzywej górnej (przy dużym

stężeniu Y, zgodnie z prawem działania mas) niż na dolnej (A). Wyobraźmy sobie, że

reakcja zaczyna się gdy X=C. Dodajemy odpowiednią ilość Z, tak, że efektywne

stężenie X=C

1

gdy cały układ osiąga stan stacjonarny na krzywej górnej, i C

2

– gdy

"znajduje się" na krzywej dolnej. Dodanie substancji Z powoduje "przesuwanie się"

stanu stacjonarnego wzdłuż krzywej górnej (na skutek przekształcania Y w X). Układ

próbuje osiągnąć punkt C

1

, ale w punkcie A przechodzi gwałtownie do stanu

stacjonarnego na krzywej dolnej. W tym stanie efektywne stężenie X=C

2

, zatem układ

próbuje “dopasować się” do tego stężenia (strzałka w lewo na rysunku 3A). Zanim

jednak osiągnie ten nowy stan stacjonarny, w punkcie X=B wraca na krzywą górną i cykl

się zamyka. Powtórzenie całej sekwencji zdarzeń jest przyczyną oscylacji wartości Y

(Rysunek 3B) (wg 2).

Literatura

1.

O.S.Czernawski i wsp. "Co to jest biofizyka matematyczna", rozdziały I, IV;

Państwowe Wydawnictwo Naukowe, Warszawa 1974 lub jakikolwiek podręcznik

chemii fizycznej, rozdziały o kinetyce chemicznej.

Nieco wiadomości o kinetyce chemicznej i zjawiskach periodycznych.

2.

I.R.Epstein, K. Kustin, P. De Kepper,M. Orban "Oscillating Chemical Reactions"

Scientific American 248(3),1983, str. 96-108

Bardzo ciekawie napisany artykuł w renomowanym czasopiśmie. Głównie na

podstawie tego artykułu została opracowana część teoretyczna instrukcji.

3.

B. Welsh, J. Gomatam, A.E. Burgess "Three-dimensional structures in the

Belousov-Zhabotinski reaction" Nature 304(5927), 1983, str. 611-614

Autorzy prezentują udane fotografie struktur dyssypatywnych w układzie

trójwymiarowym. Niektóre z ich pomysłów posłużyły do zaprojektowania jednego

z doświadczń części praktycznej.

4.

A.T. Winfree "Chemical Systems that Oscillate between One Color and Another"

Scienctific American vol. 239(1), 1978

Artykuł "kuchenny", szereg pomysłów w części praktycznej zostało

zaczerpniętych właśnie od tego autora.

Literatura uzupełniająca:

5.

A. Górski "Indeterminizm, chaos i zjawiska nieliniowe" Problemy 8/85, 14-18,

1985

Ciekawe przedstawienie zjawiska oscylacji w pewnych działach matematyki.

6.

"Koliebatielnyje processy w biołogiczeskijich i chimiczeskich sistiemach", praca

zbiorowa wyd. Nauka, Moskwa 1967

Podstawowa praca dla wszystkich chcących poważnie zająć się studiowaniem

reakcji Biełousowa-Żabotyńskiego.

7.

A. Stasiewicz "Drapieżniki i ofiary" Komputer 3/1988

Prosty przykład programu komputerowego realizującego model "rysi i zająców"

8.

A.T. Winfree "The Geometry of Biological Time", rozdział 13, wyd. Springer-

Verlag, New York - Heidelberg - Berlin 1980, str. 300-314

Wykonanie ćwiczenia

Wariant „A” (wg 2, 3, 4)

Sprzęt laboratoryjny:

a.

spektrometr „Spekol” z wyprowadzeniem sygnału do rejestracji

b.

przystawka do miareczkowania „Micro TI” wraz z zasilaczem

c.

pH-metr

d.

kuwety do przystawki "Micro TI"

e.

małe mieszadełko magnetyczne typu „pcheka”

f.

rejestrator (czas-Y), wymagana czułość 0.5 - 5 mV/cm

g.

kondensator elektrolityczny 100 µF (zakładany pomiędzy wyprowadzenia ze „Spekola”

w celu wytłumienia drgań sieciowych)

h.

pipeta 1 ml lub pipeta automatyczna 200 µl + końcówki

i.

Pipeta automatyczna 20 µl + końcówki

Odczynniki

UWAGA: Poniższe roztwory powinny być przygotowane przed ćwiczeniami przez asystenta

a.

roztwór 0.1 M Ce(SO

4

)

2

w 1 N H

2

SO

4

lub

1.74 g Ce(NO

3

)

3

* 6 H

2

O w 750 ml H

2

0 + 1.5 ml stężonego kwasu siarkowego - 50 ml

b.

roztwór 1.2 M kwasu malonowego w wodzie - 50 ml

c.

roztwór 0.35 M bromianu potasowego w wodzie - 50 ml

d.

stężony kwas siarkowy - 1 ml

e.

stężony kwas solny - 1 ml

f.

1 N kwas siarkowy - 50 ml

Obserwacje oscylacji w różnych warunkach i przy różnych stężeniach substratów:

1.

Odmierzyć do naczynia reakcyjnego po 0.5 ml roztworów a, b i c. Czy bez mieszania

można zauważyć zmiany w barwie roztworu? Włączyć mieszanie. Jakie ma ono

znaczenie w badanym układzie?

Warunki rejestracji: λ = 415 nm, czułość rejestratora 0.5 - 1 mV/cm, szybkość zapisu

60 s/cm. Doświadczenie to uznajemy za standardowe.

2.

Zarejestrować oscylacje przy zmianie stężeń poszczególnych reagentów:

A.

Zmniejszyć dwukrotnie stężenie ceru. W jaki sposób uniknąć błędu zmiany

stężenia pozostałych reagentów? Sprawdź, konsultując swój plan

doświadczenia z asystentem.

B.

Zmniejszyć dwukrotnie stężenie kwasu malonowego.

C.

Zmniejszyć dwukrotnie stężenie bromianu potasu.

3.

Zakwaszanie kwasem siarkowym: do reagentów dodawać po 0.05 ml stężonego

H

2

SO

4

. Zapisać wyniki przy użyciu rejestratora.

4.

Zakwaszanie kwasem solnym: postępować jak wyżej, ale zamiast H

2

SO

4

użyć

stężonego HCl.

Opracowanie wyników:

1.

Na podstawie wyników z punktu 1 spróbować określić który z reagentów pełni rolę

kluczowego w badanej reakcji, uzasadnić dokonany wybór.

2.

Wykreślić zależność szybkości reakcji w zależności od pH dla każdego z kwasów. Czy

zaobserwowana zależność jest taka sama dla każdego z nich?

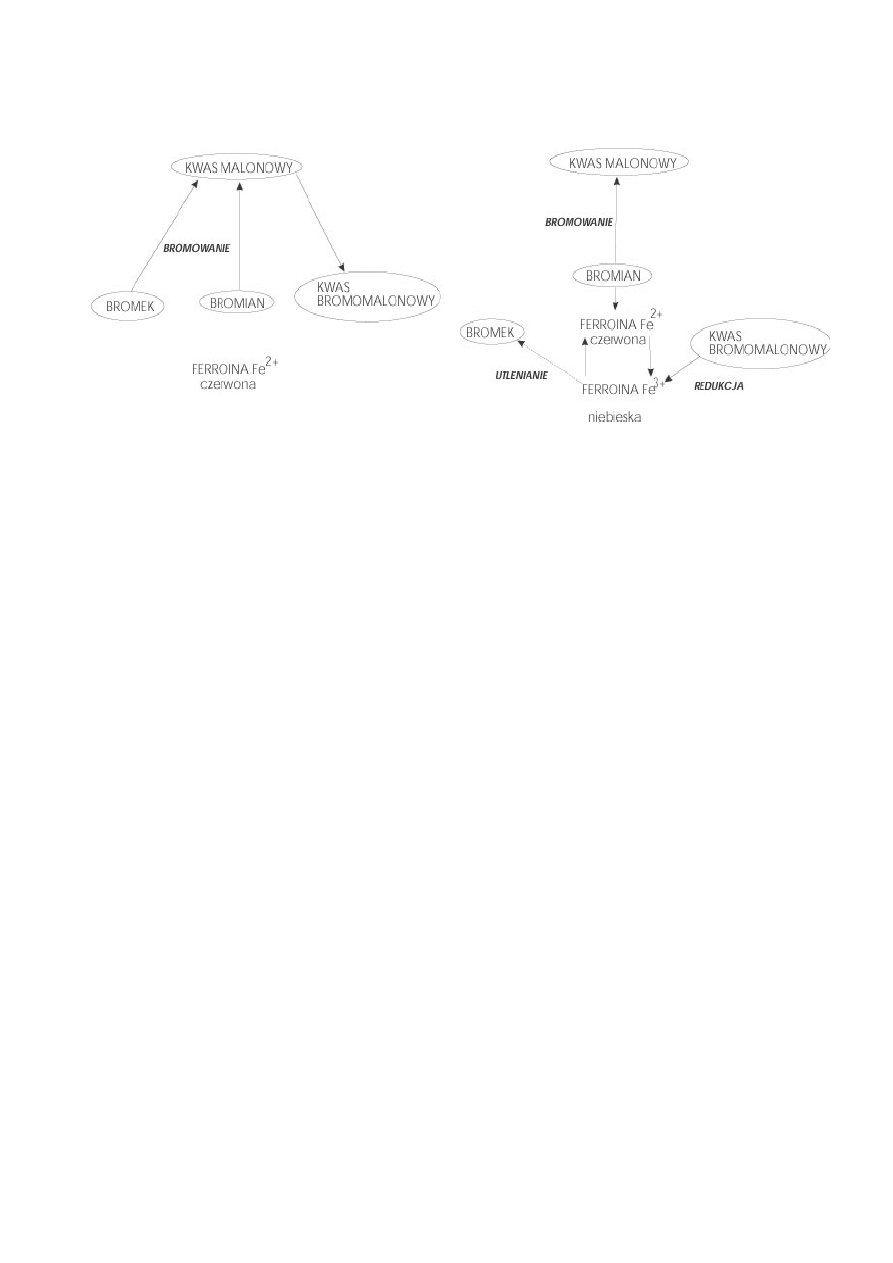
Drugi wariant ćwiczenia — „B”, bez stosowania soli ceru (wg 8)

Rysunek 4. Dwa ciągi reakcji oparte o kwas malonowy mogą wywoływać oscylacje barwne

ferroiny od czerwieni do błękitu i powrót do czerwieni.

Schemat tych reakcji podany jest na powyższych rysunkach. Reakcja zachodzi

pomiędzy bromkiem, bromianem, kwasem malonowym i fenantroliną skompleksowaną

z żelazem. Kompleks fenantroliny z żelazem pełni rolę podwójną - jest katalizatorem

i wskaźnikiem barwnym. Stężenie bromku decyduje, który z dwóch ciągów reakcji

będzie dominował. W jednym przypadku (lewa część rysunku) bromek i bromian

jednocześnie bromują kwas malanowy i tworzy się kwas bromomalonowy. Podczas

tego procesu barwnik fenantrolinowy jest czerwony, z atomem żelaza na drugim

stopniu utlenienia. Jeśli stężenie bromku spadnie poniżej pewnego poziomu, wówczas

drugi ciąg reakcji zaczyna dominować (prawa część rysunku). Bromek zostaje zużyty

do końca i bromian przejmuje bromowanie kwasu malonowego. Równocześnie utlenia

on atom żelaza we wskaźniku barwnym, powodując zmianę jego barwy z czerwonej

(Fe

2+

) na niebieską (Fe

3+

). Nagromadzony kwas bromomalonowy redukuje potem (linia

przerywana) Fe

3+

w kompleksie do Fe

2+

, na powrót pojawia się barwa czerwona.

Podczas tej reakcji uwalnia się bromek (co łatwo poczuć) i dwutlenek węgla. Wysokie

stężenie bromku hamuje tę sekwencję reakcji i powoduje przeskok do ciągu reakcji

przedstawionych po lewej stronie rysunku. Dla uproszczenia pominięto w

rozważaniach reakcje z udziałem tlenu z powietrza.

Wykonanie ćwiczenia:

Sprzęt laboratoryjny:

a.

termostatowane naczynko z mieszadełkiem

b.

łaźnia wodna połączona z termostatowanym naczyniem reakcyjnym

c.

pipety 5 ml, 2 ml i 1 ml

d.

zlewka 400 ml

e.

zlewka 50 - 100 ml - 3 szt.

f.

szklane szalki Petriego - 4 szt.

g.

probówki szklane z dopasowanymi korkami gumowymi - 6 szt.

h.

pipeta półautomatyczna 200

Fl

i.

łaźnia lodowa, lub lód w naczyniu styropianowym

j. termometr lub inny miernik temperatury

n.

stoper

Odczynniki:

a.

ferroina - 25 mM roztwór ortofenantroliny (1,10-Phenantroline) skompleksowanej z Fe

2+

z soli Mohra dodanej w nadmiarze w 1.5 N H

2

SO

4

- 30 ml

b.

roztwór bromku potasu - 5 g/50 ml

c.

roztwór kwasu malonowego - 5 g/50 ml

d.

roztwór bromianu potasu - 134 ml H

2

O + 4 ml stęż. H

2

SO

4

+ 9 g KBrO

3

e.

stężony kwas siarkowy - 1 ml

f.

stężony kwas solny - 1 ml

g.

alkohol etylowy 95% - 5 ml

Protokół doświadczeń:

1.

Odmierzyć do naczyńka reakcyjnego 6 ml roztworu bromianu potasu, 1 ml roztworu

kwasu malonowego, 0.5 ml roztworu bromku potasu. Włączyć mieszanie i poczekać

aż zaniknie całkowicie żółto-brązowy kolor roztworu reakcyjnego. Dodać 1 ml roztworu

ferroiny.

Zaobserwować zmiany barwy (z czerwonej do niebieskiej). Zanotować okres drgań.

Wyniki tego doświadczenia przyjmujemy za standardowe.

2.

Zależność okresu drgań od temperatury.

Odmierzyć do zlewki 50 ml standardowe ilości reagentów. Roztwór reakcyjny umieścić

na mieszadle magnetycznym. Przy stałej szybkości mieszania zmierzyć okresy drgań

tego samego roztworu reakcyjnego w przedziale temperatur 5

o

-50

o

C co 5 stopni. W

tym celu zlewkę z reagentami umieszczać w specjalnym termostatowanym naczyniu

lub, w przypadku braku takiego naczynia, w krystalizatorze wypełnionym wodą o

określonej temperaturze i umieszczonym na mieszadle magnetycznym.

3.

Wpływ etanolu na okres oscylacji.

Odmierzyć do naczynia reakcyjnego standardowe ilości reagentów. Zmierzyć okres

drgań po dodaniu do roztworu reakcyjnego 5 µl etanolu, następnie zwiększać ilość

etanolu do 30 µl porcjami 5 µl, po dodaniu każdej porcji mierzyć okres drgań.

4.

Obserwacje oscylacji chemicznych w układzie dwu- i trójwymiarowym.

A.

Standardowe ilości reagentów mieszać na mieszadle magnetycznym aż do

wystąpienia oscylacji. Następnie roztwór reakcyjny rozlać do szalek Petriego (1-

2 mm warstwa na dnie). Przykryć szalki wieczkami i obserwować.

B.

Powtórzyć postępowanie jak w poprzednim punkcie, lecz roztwór reakcyjny

wlać do probówek i zatkać je korkami gumowymi. Obserwować kształty

obszarów o różnym zabarwieniu.

5.

Zakwaszanie kwasem siarkowym:

Do standardowej ilości reagentów dodać 0.05 ml stężonego H

2

SO

4

.

6.

Zakwaszanie kwasem solnym:

Postępowanie jak w poprzednim punkcie ale zamiast H

2

SO

4

użyć HCl.

Opracowanie wyników:

1.

Sporządzić wykres zależności szybkości reakcji oscylacyjnej (jaki parametr może

posłużyć do tego celu?) w funkcji temperatury we współrzednych standardowych oraz

we współrzędnych Arrheniusa. Czy ciągowi reakcji oscylacyjnych można przypisać

jednoznacznie energię aktywacji?

2.

Wykreślić zależność szybkości reakcji oscylacyjnej od stężenia etanolu.

3.

Opisać zwięźle struktury dyssypatywne w układzie dwuwymiarowym i trójwymiarowym.

Pytania pomocnicze:

1.

Wymień kilka zjawisk periodycznych i postaraj się wskazać, co jest czynnikiem

determinującym ich częstotliwość.

2.

Wyszukaj w instrukcji słowa napisane pogrubioną kursywą. Czy potrafisz podać

definicje tych pojęć?

3.

Co to jest stabilność? Podaj przykłady.

4.

Podaj przykłady sprzężenia zwrotnego dodatniego i ujemnego.

5.

W jaki sposób szybkość reakcji chemicznej zależy od temperatury?

6.

Co to jest energia aktywacji? Jak można wyznaczyć energię aktywacji?

Reakcje oscylacyjne - stanowisko z programem komputerowym do symulacji oscylacji

w liczebności populacji drapieżników (rysi) i ofiar (zającow).

Program EKOLOS3 został napisany w języku QBASIC na podstawie artykułu z czasopisma

BAJTEK. Działanie programu pokazuje model zależności liczebności populacji drapieżników

i ofiar w czasie. Inspiracją do stworzenia modelu zmian liczebności poulacji w czasie była

analiza liczby skór zwierząt futerkowych skupowanych od myśliwych w XIX w. przez faktorie

na terenie dzisiejszej Kanady.

1.

Na stanowisku pracy widoczne są dwa zabytkowe komputery z ubiegłego wieku.

Pierwszy z nich to Amstrad CPC128, zabytek pochodzący z lat 80 wieku XX, a drugi

to Toshiba 100CS z lat 90 XX w.

2.

Mimo tego, że komputery te są przestarzałe, można na nich uruchomić prosty program

symulujący wahania liczebności populacji drapieżników i ofiar.

3.

Niestety, Amstrad CPC128 ma uszkodzoną stację dyskietek, zatem niemożliwe jest

wczytanie programu EKOLOS zapisanego na nietypowej dyskietce o średnicy 3 cali.

4.

Program zapisany został na komputerze Toshiba S100cs (pentium I, 75 MHz, 8 mB na

płycie głównej, pamięć rozszerzona do 16 Mb)

5.

Włącz komputer poczekaj, aż system wystartuje i na ekranie pojawią się ikony

programów.

6.

Uruchom program QBASIC przez dwukrotne kliknięcie na jego ikonę.

7.

Klawiszem ESC wyjdź z krótkiego menu SURVIVAL. Na górnej belce komend wybierz

FILE, a potem OPEN.

8.

Na ekranie ukaże się lista programów napisanych w BASICu. Wybierz kursorem myszy

program EKOLOS3 i otwórz go - przez kliknięcie kursorem myszy lub ENTER.

9.

Komenda RUN uruchamia program. Po podaniu początkowych liczebności

drapieżników i ofiar mamy do wyboru dwie możliwości wyświetlania wyników:

a.

wykres oscylacyjny - czyli tradycyjne liczebności populacji (na osi Y) w funkcji

czasu na osi X

b.

wykres trajektorii - czyli wyświetlanie danych na tzw. płaszczyźnie fazowej. Na

osi X odkreślana jest liczebność jednej populacji, a na osi Y - drugiej. Proszę

zwrócić uwagę, że czas nie występuje explicite (wprost) w tego rodzaju

wykresie, ale można W CZASIE śledzić przesuwanie się punktu oznaczającego

liczebności populacji.

10.

Metodą prób i błędów należy tak dobrać wartości początkowe drapieżników i ofiar, aby

przy wykresie oscylacyjnym oba wykresy znajdowały się w całości na ekranie

komputera. Zanotować wartości, przy których obserwowane jest zjawisko oscylacji,

zarówno na wykresie oscylacyjnym, jaki i na wykresie trajektorii.

11.

Na wykresie oscylacyjnym zaobserwuj:

a.

Czy amplitudy zmian liczebności zająców i rysi są takie same?

b.

Czy okresy oscylacji liczebności obu populacji są takie same?

c.

Czy wykresy zmian liczebności populacji są w tej samej fazie?

12.

Zbadać jak zachowuje się układ w sytuacjach granicznych, np.

a.

brak drapieżników, dużo ofiar

b.

brak ofiar, dużo drapieżników

Czy potrafisz nazwać wykresy otrzymywane w sytuacjach granicznych?

13.

Można zmieniać wartości niektórych parametrów, poprzez skierowanie kursora do

wybranej lini programu i napisanie wartości innych niż początkowe.

UWAGA: Zmiany zapisać POD NOWĄ NAZWĄ, w przeciwnym wypadku program EKOLOS3

może zostać zastąpiony nowym programem, inaczej działającym!

Proszę spróbować zinterpretować obserwowane wyniki i określić jakie założenia

UPRASZCZAJĄCE zostały przez twórców programu przyjęte.

Zachęcam do samodzielnych eksperymentów!

Reakcje oscylacyjne - stanowisko z elektronicznymi modelami świetlika

W krajach tropikalnych po zmierzchu obserwowane jest zjawisko świecenia świetlików

(spokrewnionych z naszymi poczciwymi robaczkami świętojańskimi) w sposób

SYNCHRONICZNY. Prawdopodobnie synchronizacja błysków osiągana jest dzieki detekcji

błysków sąsiadujących owadów i odpowiedniego „nastrajania” własnego aparatu błyskowego.

Umieszczone na stanowisku roboczym dziwne urządzenia z dużą zieloną diodą mają

niezgrabnie przypominać naturalne świetliki.

Zaobserwuj następujące zjawiska:

1.

Obejrzyj uważnie elektroniczny świetlik. Zauważ, że z każdej z czterech stron płytki

zainstalowane są fotodiody, pełniące w tym modelu funkcję fotoreceptorów.

2.

Włącz układ pojedynczego świetlika przy pomocy przełącznika na bocznej ściance

modelu. Zaobserwuj miganie dużej zielonej diody. Ogranicz ilość światła dostarczanego

do fotoreceptorów. Czy częstotliwość migania się zmienia?

3.

W przyciemnionym świetle umieść kilka elektronicznych świetlików obok siebie i włącz

je wszystkie. Pozostaw je włączone przez kilka minut. Co można powiedzieć o

częstotliwości ich błyskania?

4.

Powtórz doświadczenie przy zapalonym świetle górnym. Czy obserwujesz podobne

zachowanie układu jak w poprzednim doświadczeniu?

5.

Przeprowadź doświadczenie jak w punkcie 3, ale oddzielając poszczególne modele od

siebie kartkami papieru. Czy przebieg doświadczenia jest taki sam, jak

w doświadczeniu 3?

Na podstawie dokonanych obserwacji zaproponuj pętlę sprzężenia zwrotnego do kontroli

częstotliwości świecenia świetlików. Co jest sygnałem, co jest szumem, co jest efektem w tej

pętli?