Przekształcenie liniowe

stosowane w analizie obwodów

trójfazowych.

Składowe symetryczne.

EXIT

MENU

WYKŁAD NR 20

Wykład 20

•

•

Metoda składowych symetrycznych.

Metoda składowych symetrycznych.

•

•

Filtry składowych symetrycznych.

Filtry składowych symetrycznych.

MENU

EXIT

Istnieją trzy układy napięć trójfazowych

0

2

1

A

A

A

U

U

U

Wykład 20

Wykład 20

;

;

;

0

0

2

2

1

2

1

A

B

A

B

A

B

U

U

U

a

U

U

a

U

=

=

=

0

0

2

2

2

1

1

A

C

A

C

A

C

U

U

U

a

U

U

a

U

=

=

=

MENU

EXIT

(1)

(2)

(3)

układ zgodny (1), układ przeciwny (2) i układ zerowy (3):

• Idea

metody składowych symetrycznych

polega na tym, że stosując odpowiednie
przekształcenie liniowe zastępujemy układ
trzech wektorów niesymetrycznych przez
trzy równoważne układy symetryczne.

MENU

EXIT

Wykład 20

Wykład 20

• Załóżmy, że dane są trzy napięcia

tworzące układ niesymetryczny. Jeżeli układ tych

wektorów zastępujemy przez trzy układy symetryczne, to
każde z napięć wyrażamy przez sumę trzech napięć po
jednym z każdego układu symetrycznego:

C

B

A

U

U

U

,

,

2

2

1

0

2

1

2

0

2

1

0

A

A

A

C

A

A

A

B

A

A

A

A

U

a

U

a

U

U

U

a

U

a

U

U

U

U

U

U

+

+

=

+

+

=

+

+

=

MENU

EXIT

Wykład 20

Wykład 20

(4)

• Przyjmujemy, że wektorem podstawowym

każdego układu jest wektor odpowiadający fazie
A i wprowadzimy oznaczenia:

• Wektory nazywamy składowymi

symetrycznymi odpowiednio zerową, zgodną i
przeciwną. Uwzględniając składowe symetryczne:

.

;

;

2

2

1

1

0

0

A

A

A

U

U

U

U

U

U

=

=

=

,

,

,

2

1

0

U

U

U

2

2

1

0

2

1

2

0

2

1

0

U

a

U

a

U

U

U

a

U

a

U

U

U

U

U

U

C

B

A

+

+

=

+

+

=

+

+

=

MENU

EXIT

Wykład 20

Wykład 20

(5)

(6)

• Napięcia układu niesymetrycznego wyraziliśmy w funkcji

trzech składowych symetrycznych. W postaci
macierzowej:

• Wprowadzimy oznaczenia:
•

- macierz kolumnowa (wektor) napięć

niesymetrycznych

- macierz kolumnowa (wektor) składowych

symetrycznych

- macierz przekształcenia.

MENU

EXIT

Wykład 20

Wykład 20

⎥

⎥

⎥

⎦

⎤

⎢

⎢

⎢

⎣

⎡

=

C

B

A

U

U

U

U

⎥

⎥

⎥

⎦

⎤

⎢

⎢

⎢

⎣

⎡

=

2

1

0

U

U

U

U

S

⎥

⎥

⎥

⎦

⎤

⎢

⎢

⎢

⎣

⎡

=

2

2

1

1

1

1

1

a

a

a

a

S

(7)

⎥

⎥

⎥

⎦

⎤

⎢

⎢

⎢

⎣

⎡

⎥

⎥

⎥

⎦

⎤

⎢

⎢

⎢

⎣

⎡

=

⎥

⎥

⎥

⎦

⎤

⎢

⎢

⎢

⎣

⎡

2

1

0

2

2

1

1

1

1

1

U

U

U

a

a

a

a

U

U

U

C

B

A

• Równanie (7) można zapisać krótko w postaci
podobnie dla prądów .

Równania (8), (9) stosujemy wtedy, gdy są dane składowe

symetryczne, a należy wyznaczyć układ niesymetryczny.
Przeważnie jednak interesuje nas zagadnienie odwrotne:
wyznaczenie składowych symetrycznych przy danym
układzie niesymetrycznym. W tym celu pomnożymy
lewostronnie równanie (8) przez macierz odwrotną ,
W wyniku czego otrzymamy .

Stąd przy czym:

S

SU

U

=

S

SI

I

=

(8)

(9)

1

−

S

S

SU

S

U

S

1

1

−

−

=

U

S

U

S

1

−

=

⎥

⎥

⎥

⎦

⎤

⎢

⎢

⎢

⎣

⎡

=

−

a

a

a

a

S

2

2

1

1

1

1

1

1

3

1

MENU

EXIT

Wykład 20

Wykład 20

(10)

(11)

(11)

• W postaci rozwiniętej równanie (11) napiszemy tak:

czyli:

⎥

⎥

⎥

⎦

⎤

⎢

⎢

⎢

⎣

⎡

⎥

⎥

⎥

⎦

⎤

⎢

⎢

⎢

⎣

⎡

=

⎥

⎥

⎥

⎦

⎤

⎢

⎢

⎢

⎣

⎡

C

B

A

U

U

U

a

a

a

a

U

U

U

2

2

2

1

0

1

1

1

1

1

3

1

(12)

(

)

(

)

(

)

C

B

A

C

B

A

C

B

A

U

a

U

a

U

U

U

a

U

a

U

U

U

U

U

U

+

+

=

+

+

=

+

+

=

2

2

2

1

0

3

1

3

1

3

1

(13)

Wykład 20

Wykład 20

MENU

EXIT

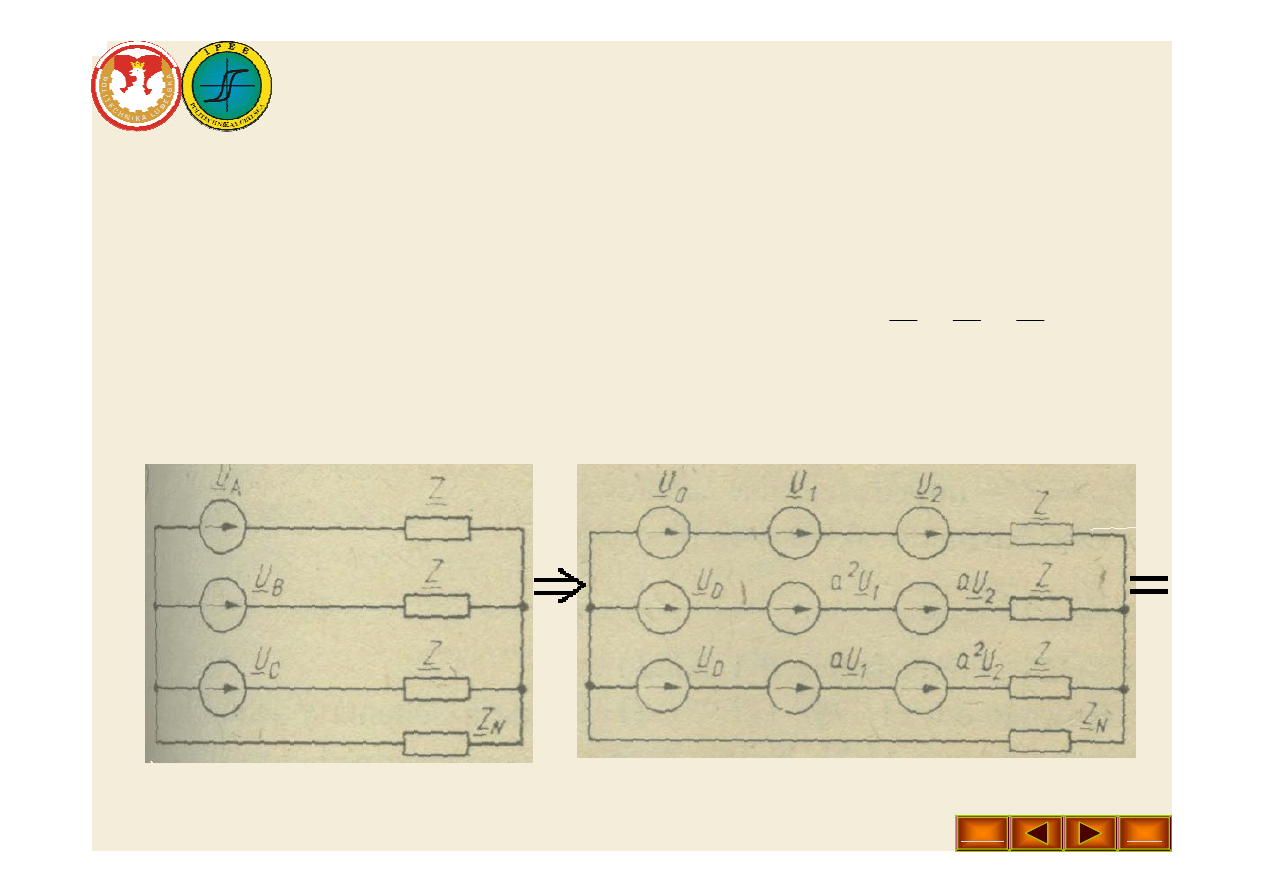
• Dla zilustrowania przedstawionych równań

przeanalizujemy następujące zagadnienie. Załóżmy, że
odbiornik trójfazowy symetryczny jest zasilany ze źródła
trójfazowego niesymetrycznego o napięciach

(rys. 1a). W wyniku rozłożenia niesymetrycznego układu

napięć na składowe symetryczne, obwód pokazany na rys.
1a można zastąpić obwodem jak na rys. 1b.

Wykład 20

Wykład 20

MENU

EXIT

C

B

A

U

U

U

,

,

1a)

1b)

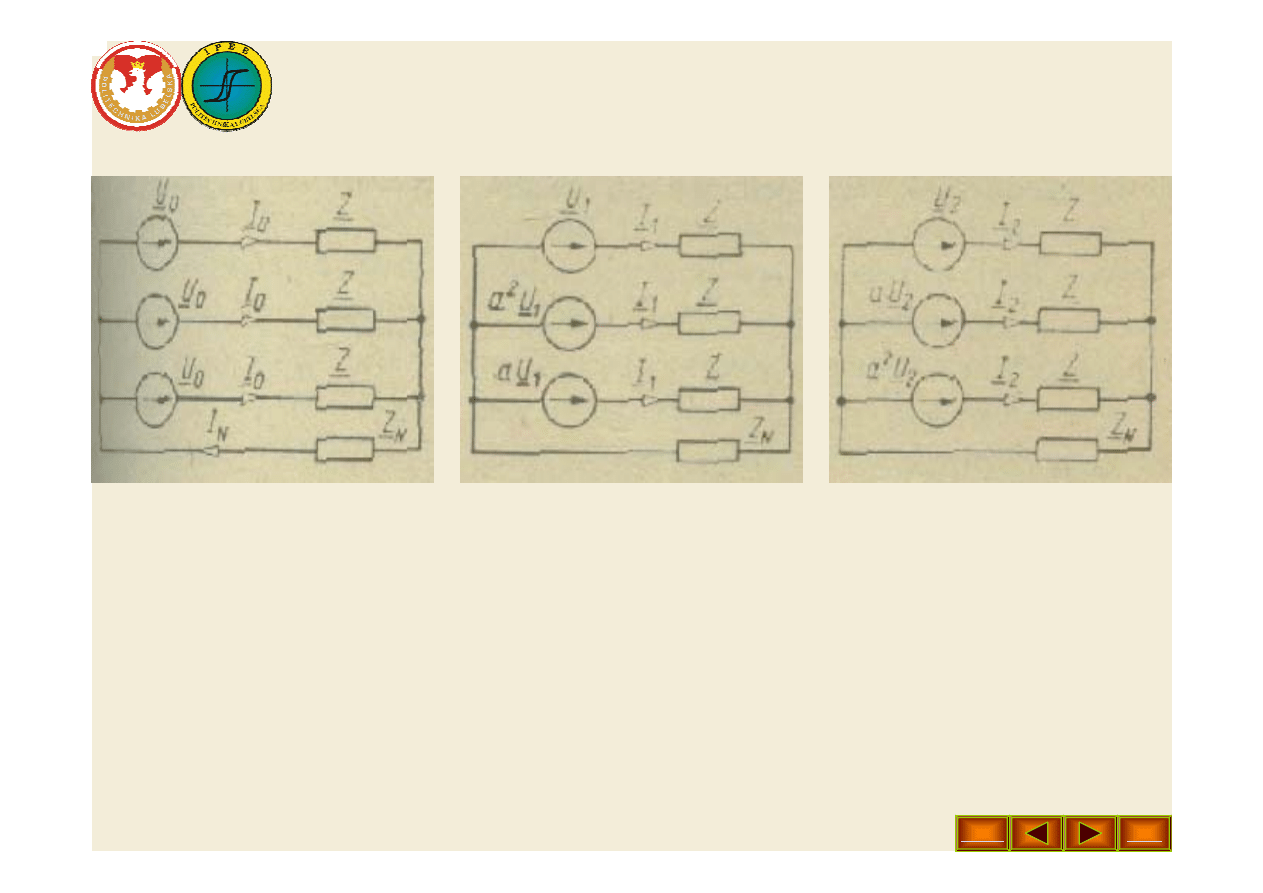
• Rys. 1. Ilustracja metody składowych symetrycznych w

zastosowaniu do układu trójfazowego zasilanego
napięciami niesymetrycznymi: a) układ wyjściowy; b)
układ z zaznaczonymi składowymi symetrycznymi napięć;
c) układy składowe: zerowy, zgodny i przeciwny.

Wykład 20

Wykład 20

MENU

EXIT

=

1c)

+

+

• Jeżeli następnie zastosujemy zasadę superpozycji, to

wydzielimy 3 generatory symetryczne i utworzymy 3
niezależne układy trójfazowe symetryczne zasilane
układem napięć: zerowym, zgodnym i przeciwnym. W
każdym układzie obliczamy rozpływ prądów, przy czym
obliczenia są przeważnie bardzo proste, gdyż dotyczą
układów symetrycznych. Wypadkowy rozpływ prądów
otrzymujemy w wyniku geometrycznego dodania prądów
obliczonych w każdym układzie.

W metodzie składowych symetrycznych oblicza się nie

wszystkie wielkości, lecz wielkości odniesione do fazy
podstawowej, którą jest faza A.

Wykład 20

Wykład 20

MENU

EXIT

•

Napiszemy, zgodnie z drugim prawem Kirchhoffa,

równania dla oczek schematów z rys. 1c obejmujących
fazę A i przewód zerowy.

– Dla schematu składowej zerowej:

przy czym .

Stąd

,

gdzie: - impedancja dla składowej zerowej.
-- Dla schematu składowej zgodnej ,
gdzie - impedancja dla składowej zgodnej.

-- Dla schematu składowej przeciwnej ,

gdzie: - impedancja dla składowej przeciwnej.

Wykład 20

Wykład 20

MENU

EXIT

N

N

I

Z

I

Z

U

+

=

0

0

0

3I

I

N

=

0

0

0

0

0

3

I

Z

I

Z

I

Z

U

N

=

+

=

N

Z

Z

Z

3

0

+

=

1

1

I

Z

U

=

Z

Z

=

1

2

2

I

Z

U

=

Z

Z

=

2

(14)
(15)

(16)

(17)

(18)

•

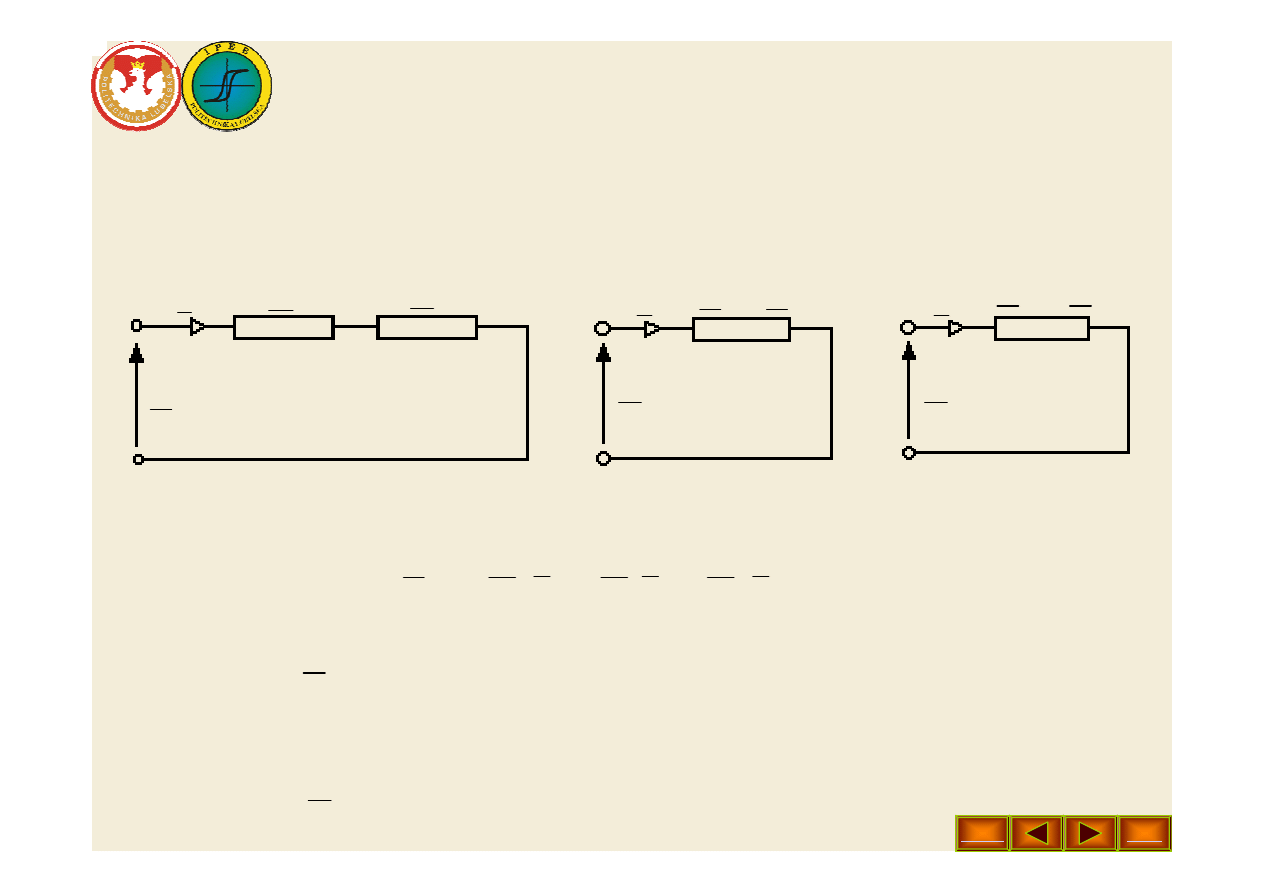
Równaniom (16), (17), (18) odpowiadają schematy

jednofazowe przedstawione na rys. 2:

• Moc pozorna w postaci zespolonej

• Stąd moc czynna

• Moc bierna

Wykład 20

Wykład 20

MENU

EXIT

0

I

1

I

2

I

0

U

1

U

2

U

Z

N

Z

3

Z

Z

=

1

Z

Z

=

2

(

)

*

2

2

*

1

1

*

0

0

3

I

U

I

U

I

U

S

+

+

=

(19)

(

)

2

2

2

1

1

1

0

0

0

cos

cos

cos

3

Re

ϕ

ϕ

ϕ

I

U

I

U

I

U

S

P

+

+

=

=

(20)

(

)

2

2

2

1

1

1

0

0

0

sin

sin

sin

3

Im

ϕ

ϕ

ϕ

I

U

I

U

I

U

S

Q

+

+

=

=

(21)

Praktyczne wnioski z wzorów (13) i (15):

•

(a) w układzie trójfazowym trójprzewodowym składowa zerowa prądu
przewodowego jest równa zeru, ;

•

(b) w układzie trójfazowym czteroprzewodowym prąd w przewodzie
zerowym jest równy potrójnej wartości składowej zerowej,

•

(c) w układzie trójfazowym zarówno trójprzewodowym, jak i cztero-
przewodowym, składowa zerowa napięć międzyfazowych jest równa zeru,
gdyż suma napięć międzyprzewodowych zawsze jest równa zeru;

•

(d) w uzwojeniach źródła lub odbiornika połączonego w trójkąt, może krążyć
składowa zerowa prądów fazowych, ale nie może wyjść poza trójkąt;

•

(e) ponieważ w maszynach elektrycznych trójfazowych układ zgodny prądów
wywołuje pole wirujące zgodne z kierunkiem prędkości obrotowej, a układ
przeciwny prądów wywołuje pole wirujące przeciwne do kierunku prędkości
obrotowej, zatem duża niesymetria w układzie trójfazowym może
spowodować zmianę kierunku wirowania maszyn (przy przewadze składowej
przeciwnej);

Wykład 20

Wykład 20

MENU

EXIT

0

0

=

I

;

3

0

I

I

N

=

Praktyczne wnioski z wzorów (13) i (15):

• (f) występowanie składowej przeciwnej jest dla pracy

maszyn elektrycznych niekorzystne, gdyż pole
magnetyczne wirujące przeciwnie do kierunku wirowania
maszyny indukuje prądy o podwójnej częstotliwości:

• (g) przy przepływie przez linię elektroenergetyczną

składowych zerowych prądu, powstaje w otoczeniu linii
pole magnetyczne, które może wywierać niekorzystny
wpływ na przebiegające w sąsiedztwie inne linie, np. linie
telekomunikacyjne.

Wykład 20

Wykład 20

MENU

EXIT

Filtry składowych symetrycznych

•

Filtrami składowych symetrycznych są nazywane

urządzenia, których zadaniem jest wydzielenie
odpowiednich składowych symetrycznych napięcia i prądu
występujących w układzie trójfazowym. Zaciski
wejściowe filtru są dołączone do odpowiedniej sieci
trójfazowej, a do jego zacisków wyjściowych jest
dołączony przyrząd pomiarowy lub przekaźnik. Zadaniem
przekaźnika jest albo sygnalizowanie niesymetrii, która
może powstać w wyniku występującego w sieci
zakłócenia, albo spowodowanie wyłączenia pewnych
urządzeń wrażliwych na działanie składowych
symetrycznych zerowych lub przeciwnych.

•

Rozróżniamy filtry składowej zerowej, składowej

przeciwnej i składowej zgodnej.

Wykład 20

Wykład 20

MENU

EXIT

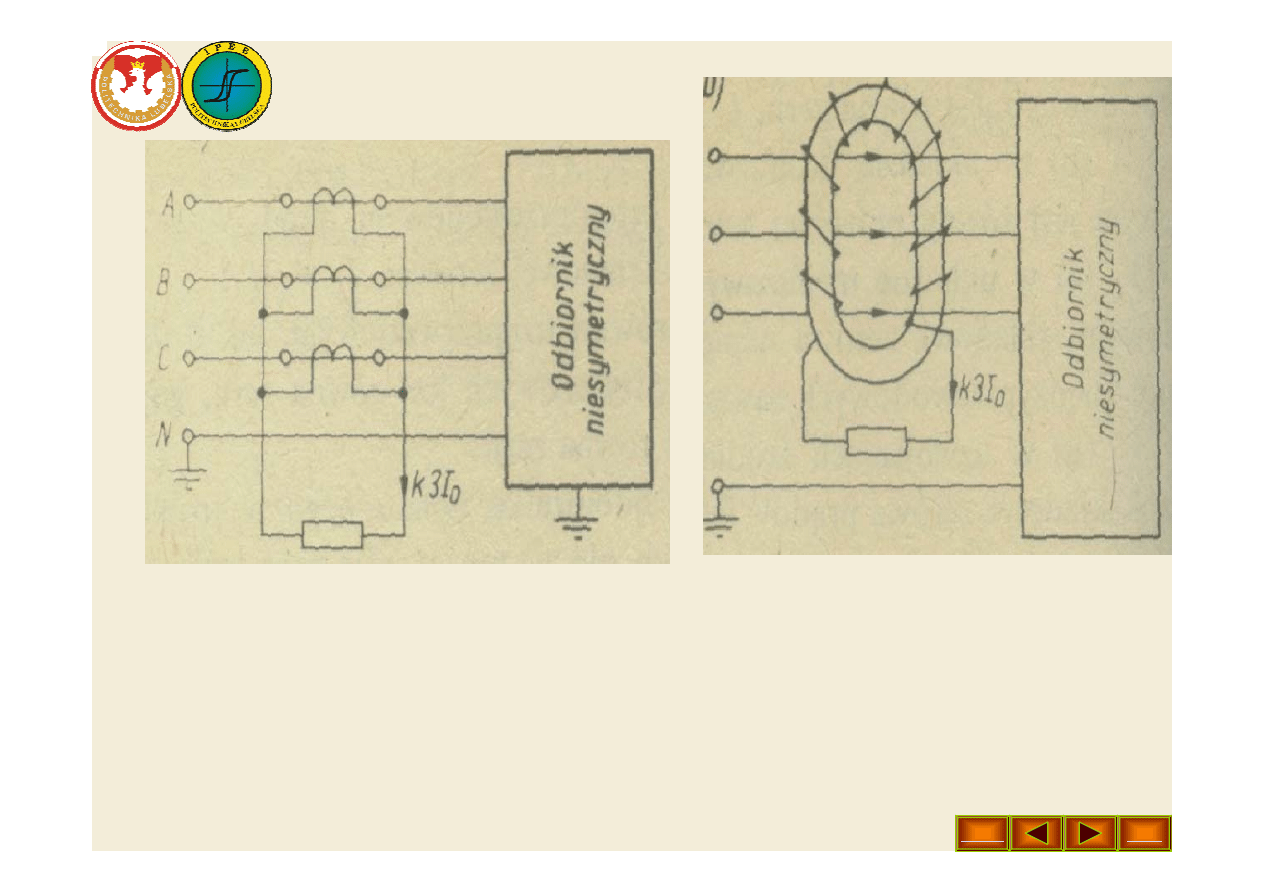
• Rys. 2. Filtry składowej zerowej prądu: a) zastosowanie

trzech przekładników prądowych połączonych równolegle;
b) przekładnik Ferrantiego.

Wykład 20

Wykład 20

MENU

EXIT

2a)

2b)

•

W

układzie trójfazowym czteroprzewodowym

włączenie amperomierza do przewodu zerowego pozwala

stwierdzić, czy istnieje składowa zerowa prądów. Prąd w

przewodzie zerowym jest bowiem równy potrójnej

wartości składowej zerowej prądów przewodowych. Tak

włączony amperomierz spełnia więc rolę filtru składowej

zerowej. W układzie trójfazowym trójprzewodowym

stosuje się filtry składowej prądu jak pokazano na rys. 2.

W układzie z rys. 2a przez amperomierz płynie suma

prądów przetransformowanych przez przekładniki

prądowe. Układ przedstawiony na rys. 2b stosujemy np. w

sieci kablowej, gdy nie ma możliwości włączenia

przekładników do poszczególnych faz sieci. Układ ten nosi

nazwę przekładnika Ferrantiego. Działa on na zasadzie

indukowania w uzwojeniu przekładnika napięcia w

przypadku, gdy w otoczeniu kabla istnieje zmienne pole

magnetyczne.

Wykład 20

Wykład 20

MENU

EXIT

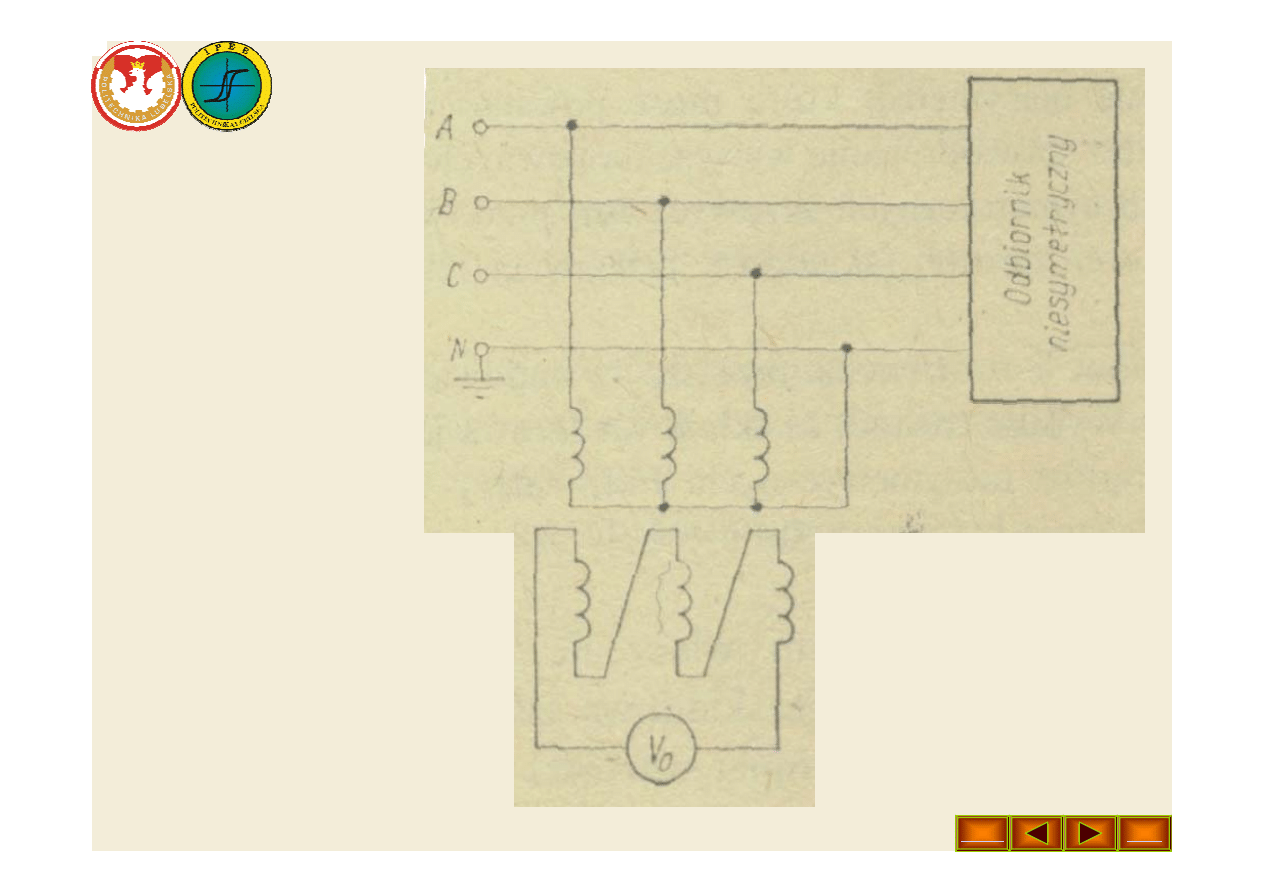
• Na rys. 3 jest

przedstawiony

filtr składowej

zerowej napięcia

fazowego.

Uzwojenie

pierwotne filtru

jest połączone w

gwiazdę z

uziemionym

punktem

zerowym, a

uzwojenie wtórne

w otwarty trójkąt.

Wykład 20

Wykład 20

MENU

EXIT

Rys. 3

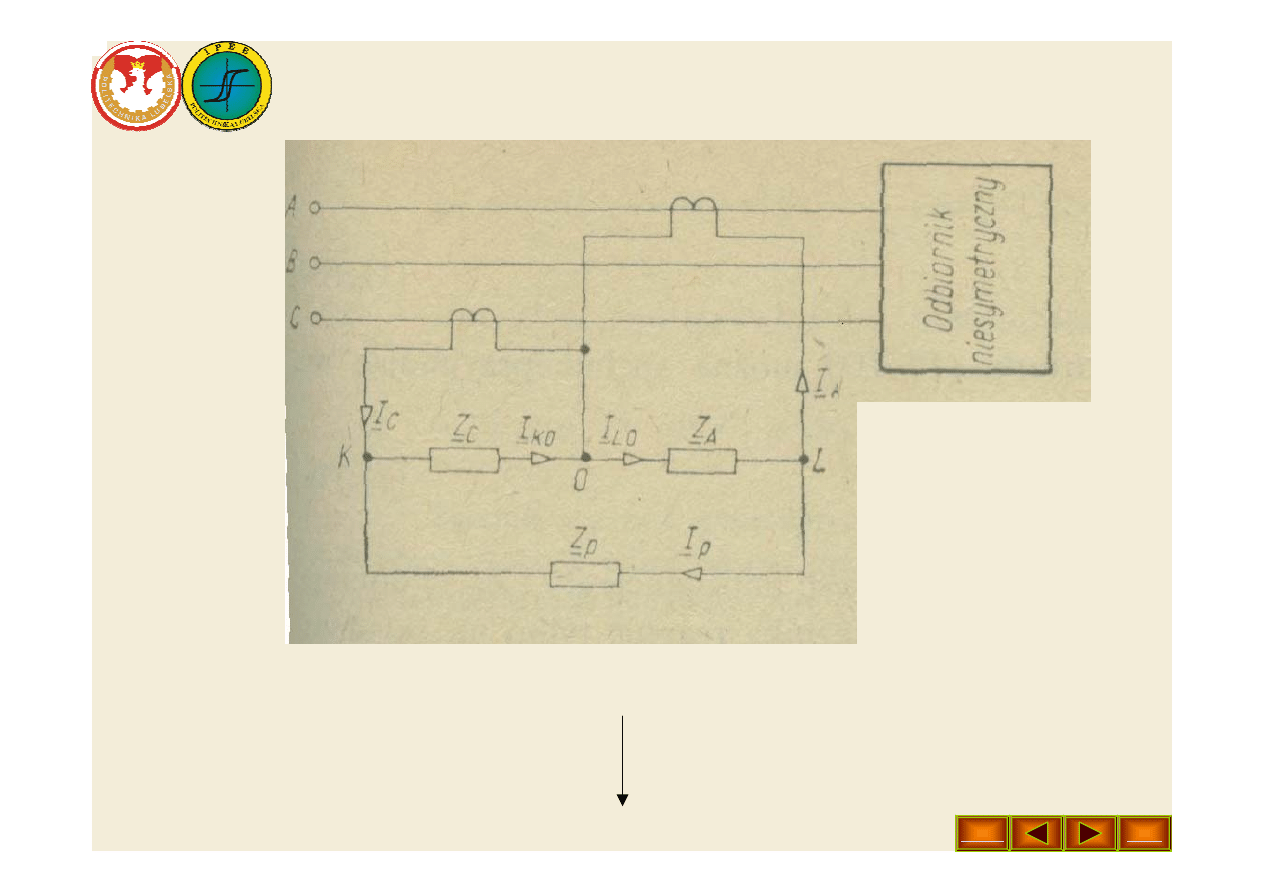
• Rys. 4. Filtr składowej symetrycznej zgodnej i przeciwnej.

Wykład 20

Wykład 20

MENU

EXIT

Rys. 4

• C.d.: Przedstawiamy dla przykładu jeden ze stosowanych

układów (rys. 4). Założymy, że w rozpatrywanym układzie
składowa zerowa prądów jest równa zeru, co jest jak
wiadomo spełnione w układach trójprzewodowych. Ustalimy
warunki, jakie muszą spełniać impedancje i . Impe-
dancję przekaźnika lub innego elementu reagującego na
występowanie określonej składowej symetrycznej oznaczono

•

Na podstawie drugiego prawa Kirchhoffa dla oczka

obejmującego impedancje mamy

•

.

•

Na podstawie pierwszego prawa Kirchhoffa dla węzłów

K i L:

•

Podstawiając prądy i do równania (22)

otrzymamy

Wykład 20

Wykład 20

MENU

EXIT

C

Z

A

Z

p

Z

p

A

C

Z

Z

Z

,

,

0

=

+

+

p

p

LO

A

KO

C

I

Z

I

Z

I

Z

(22)

;

p

C

KO

I

I

I

+

=

.

p

A

LO

I

I

I

+

=

(23)

KO

I

LO

I

p

C

A

C

C

A

A

p

Z

Z

Z

I

Z

I

Z

I

+

+

+

−

=

. (24)

• Prądy oraz są prądami płynącymi po stronie

wtórnej transformatorów prądowych, a więc w pewnej
skali wyrażają prądy przewodowe. Przy przyjętym
założeniu, że w układzie nie występują skłądowe zerowe,
można napisać

• Po podstawieniu prądów oraz wyrażonych za

pośrednictwem skłądowych zgodnej i przeciwnej, do
równania (24) otrzymamy

skąd po przegrupowaniu wyrazów licznika

Wykład 20

Wykład 20

MENU

EXIT

C

I

A

I

;

2

1

I

I

I

A

+

=

.

2

2

1

I

a

I

a

I

C

+

=

(25)

A

I

C

I

,

)

(

)

(

2

2

1

2

1

p

C

A

C

A

p

Z

Z

Z

I

a

I

a

Z

I

I

Z

I

+

+

+

+

+

−

=

(26)

.

)

(

)

(

2

2

1

p

C

A

C

A

C

A

p

Z

Z

Z

Z

a

Z

I

Z

a

Z

I

I

+

+

+

+

+

−

=

(27)

• Prąd przekaźnika reaguje tylko na składową zgodną,

jeśli

czyli

Warunek określony równaniem (29) można spełnić

przyjmując np.

Układ z rys. 4 jest filtrem składowej zgodnej jeśli

impedancje i są dobrane zgodnie z zależnościami
(30): Prąd przekaźnika reaguje tylko na składową
przeciwną, jeśli

czyli

Wykład 20

Wykład 20

MENU

EXIT

p

I

,

0

2

=

+

C

A

Z

a

Z

(28)

.

3

2

Π

=

−

=

j

C

C

A

e

Z

Z

a

Z

(29)

;

R

Z

C

=

.

3

2

2

*

3

R

j

R

e

R

Z

j

A

+

=

=

π

(30)

A

Z

C

Z

p

I

,

0

=

+

C

A

Z

a

Z

(31)

.

3

π

j

C

C

A

e

Z

Z

a

Z

−

=

−

=

(32)

•

Warunek określony równaniem (32) można spełnić

przyjmując np.

• Układ z rys. 4 jest filtrem składowej przeciwnej jeżeli

impedancje i są dobrane zgodnie z zależnościami
(32). W przypadku filtru składowej zgodnej impedancja
ma charakter indukcyjny, w przypadku filtru składowej
przeciwnej impedancja ma charakter pojemnościowy,
przy czym moduły tej impedancji w obu przypadkach są
jednakowe.

Wykład 20

Wykład 20

MENU

EXIT

;

R

Z

C

=

.

3

2

2

*

3

R

j

R

e

R

Z

j

A

−

=

=

−

π

(33)

A

Z

C

Z

A

Z

A

Z