- grupa 1:
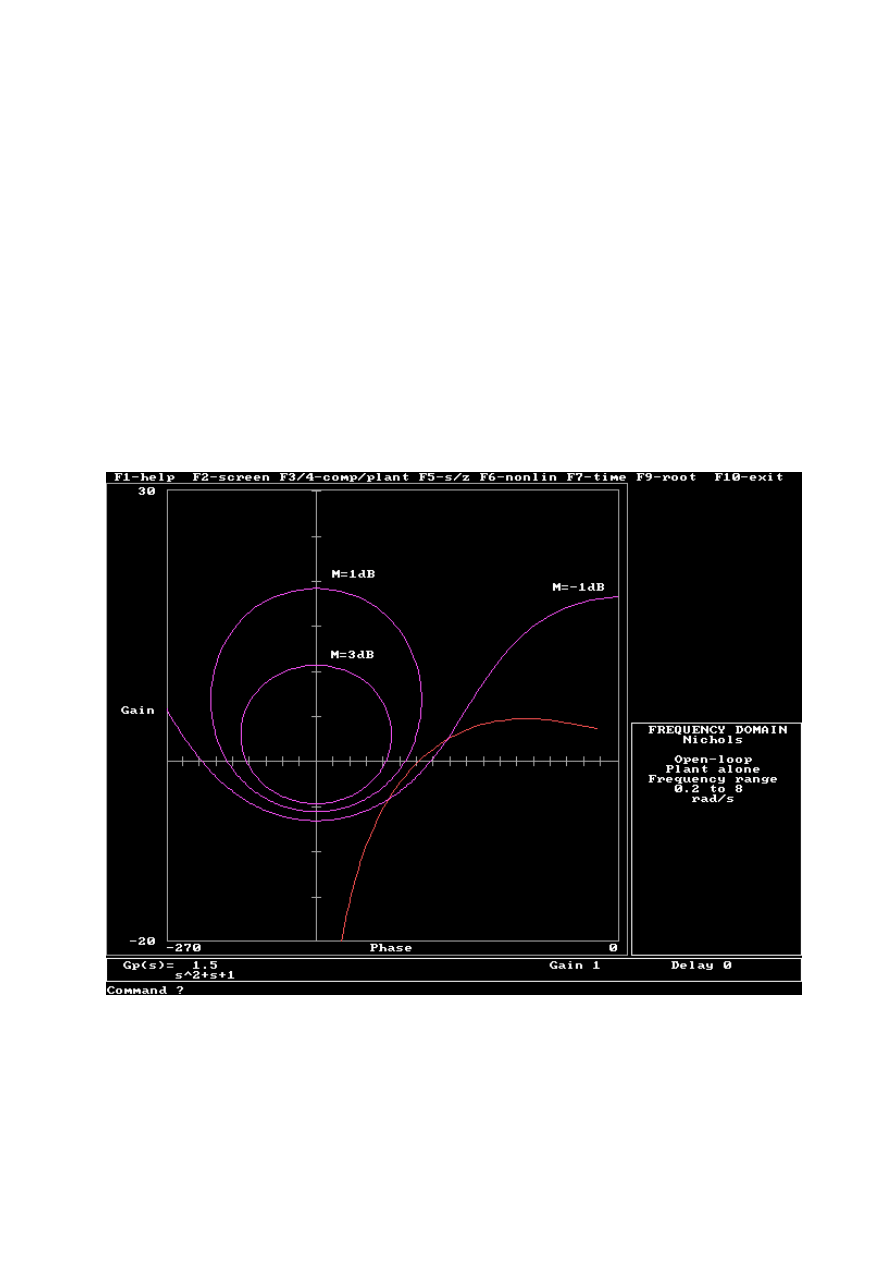
1. Karta Nicholsa, co to jest i do czego służy?

Karta Nicholsa jest to wykres we współrzędnych moduł logarytmiczny -
argument, na który naniesiono siatkę linii stałych wartości modułu transmitancji
układu zamkniętego (M) i fazy układu zamkniętego φ. Rysując na karcie Nicholsa
logarytmiczną charakterystykę częstotliwościową układu otwartego (co jest
parametrem wykresu), można ocenić własności układu zamkniętego nie tylko
pośrednio za pomocą zapasów modułu i fazy, ale od razu także widać, czy wartość
M jest bliska 1 dla małych ω i jaka jest wartość modułu rezonansowego. Jeżeli
charakterystyka amplitudowo -

fazowa nie wchodzi do wnętrza obszaru którego

brzegiem jest na wykresie Nicholsa krzywa odpowiadająca założonym wartości
modułu rezonansowego to układ nie wymaga korekcji. Jeżeli zaś charakterystyka
wchodzi do wnętrza obszaru to należy zastosować człon korekcyjny.

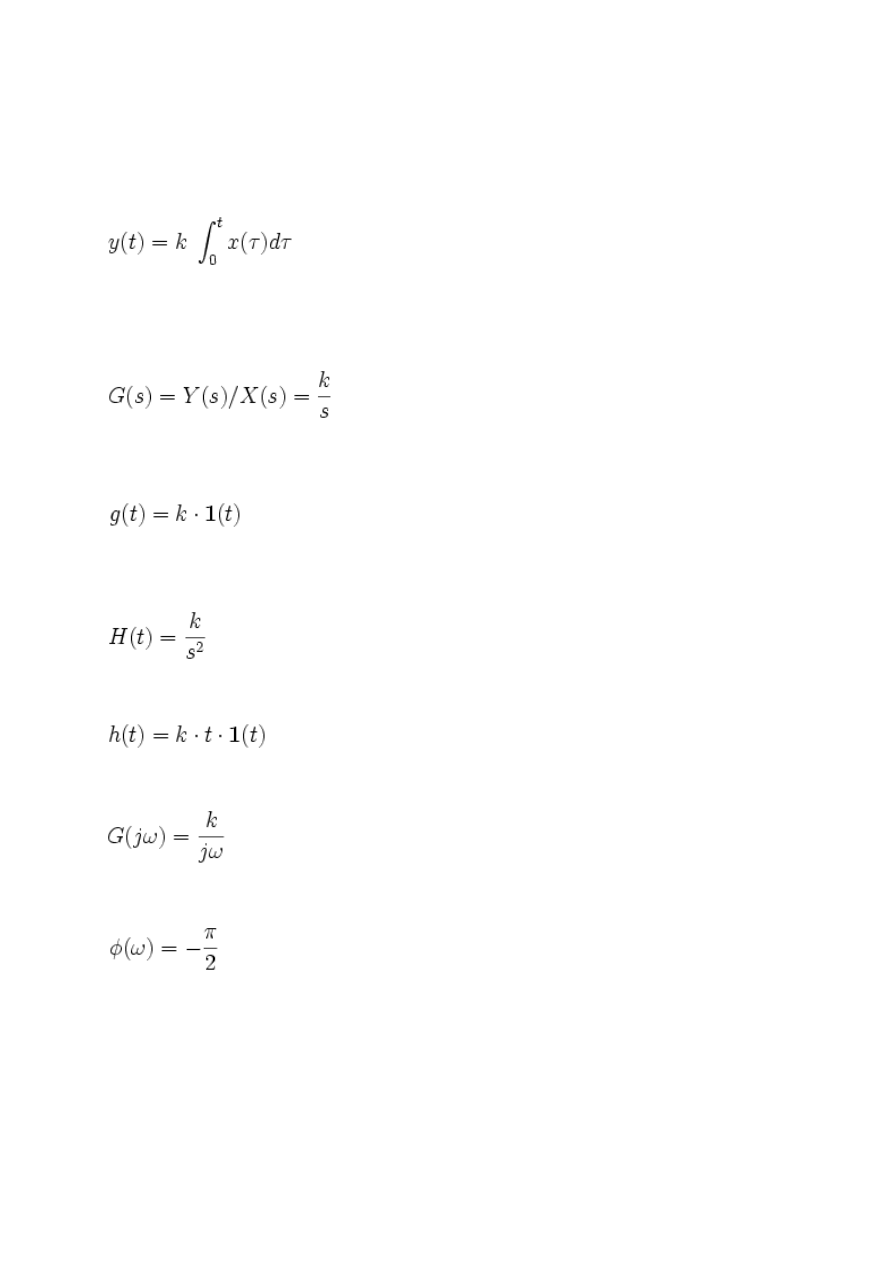
2. Człon całkujący, charakterystyki.

W automatyce człon całkujący I (idealny) (ang. integral term) to człon, którego sygnał
wyjściowy y(t) jest proporcjonalny do całki sygnału wejściowego x(t):

Oznacza to dodawanie na bieżąco wartości sygnału wejściowego w "kolejnych" chwilach.

Transmitancja członu całkującego ma postać:

1/Ts

Jego odpowiedź impulsowa wygląda następująco:

Charakterystyka skokowa:
- w dziedzinie operatorowej

- w dziedzinie czasu

Charakterystyka amplitudowo-fazowa:

Charakterystyka fazowa:

Wzmocnienie maleje o 20 dB na dekadę.

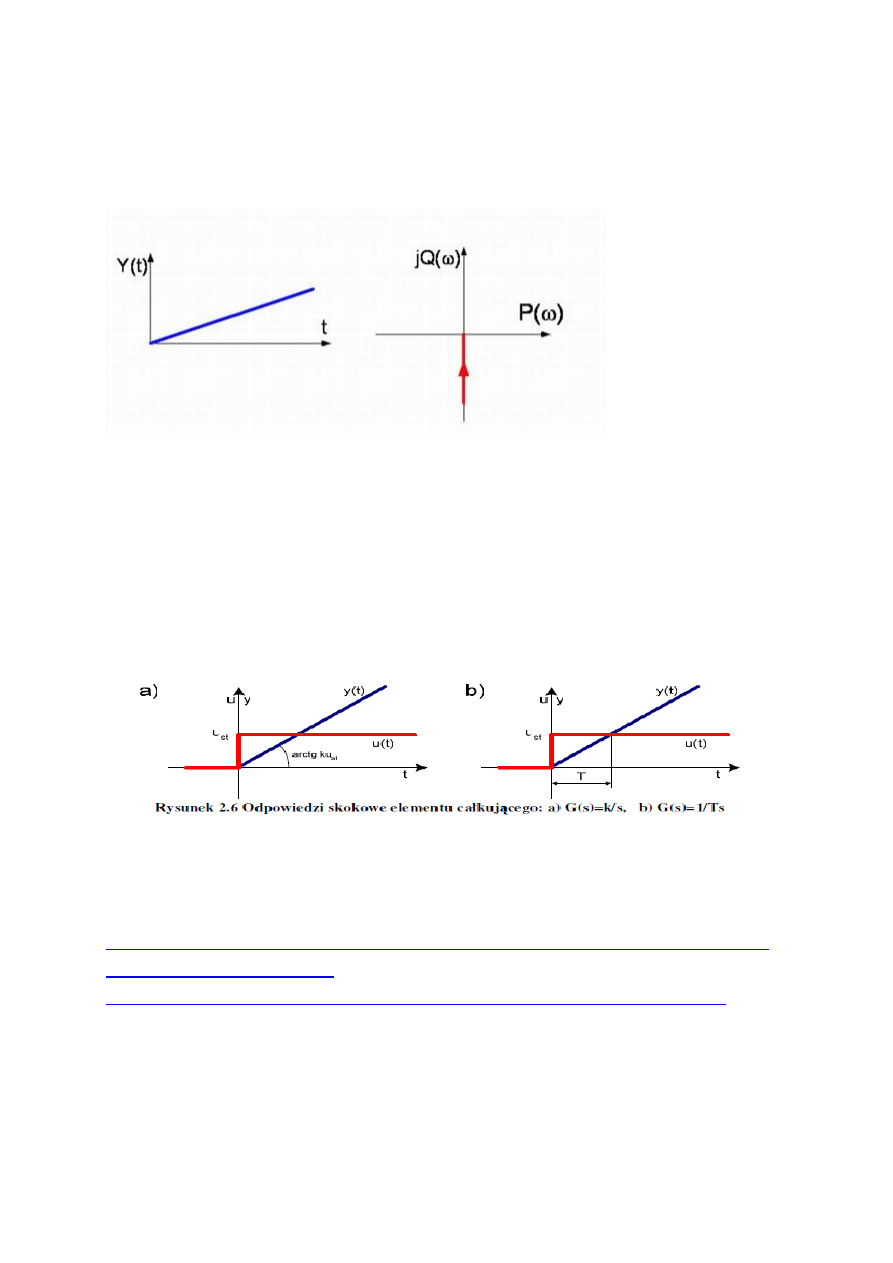
Odpowiedź na skok jednostkowy i charakterystyka amplitudowo - fazowa członu
całkującego:

:

Człony całkujace tworzą obiekty, w których zachodzi przemiana:

- prędkości ruchu w przemieszczenie (położenie)
- przyspieszenia ruchu w prędkość
- liczby obrotów na kąt obrotu (położenie kątowe)
- przepływu medium na wysokość poziomu napełnienia zbiornika
- prądu elektrycznego na ładunek elektryczny zgromadzony np. w kondensatorze
- częstotliwości impulsów na stan licznika zliczającego te impulsy

Charakterystyki

3. Metody doboru nastaw.

http://www.iko.pwr.wroc.pl/PracowDrct/Jan_Syposz/Podstawy_auto
matyki_%28w_3%29_-
_regulatory_podstawy_teoret_ppt_%5Btryb_zgodnosci%5D.pdf

I metoda: Opiera się na identyfikacji obiektu i określeniu jego transmitancji zastępczej,
następnie wymagane parametry oblicza się z odpowiednich wzorów lub odczytuje z
wykresów i koryguje podczas prób.
II metoda (drgań krytycznych Ziglera i Nicholsa): Regulator ustawia się na działanie
proporcjonalne i zwiększa się współczynnik wzmocnienia aż do wystąpienia niegasnących
drgań oscylacyjnych. Wtedy mierzy się okres oscylacji Tosc i współczynnik wzmocnienia
Kkr, a następnie oblicza się parametry nastaw (tu są wzory dla różnych członów
regulacyjnych).

III metoda: Człony regulacyjne dołącza się w określonej kolejności - P->I->D. Wzmocnienie
podnosi się aż do uzyskania najmniejszych oscylacji w układzie, następnie dołącza się człon
całkujący, zaczynając od stosunkowo dużej wartości i stopniowo ją zmniejszając. Po
uzyskaniu zerowego uchybu i krótkiego czasu ustalenia można dokonać jeszcze korekt
poprzez wprowadzenie nastaw różniczkowania.

4. Transmitancja członu inercyjnego i odpowiedzi na standardowe
pobudzenia.

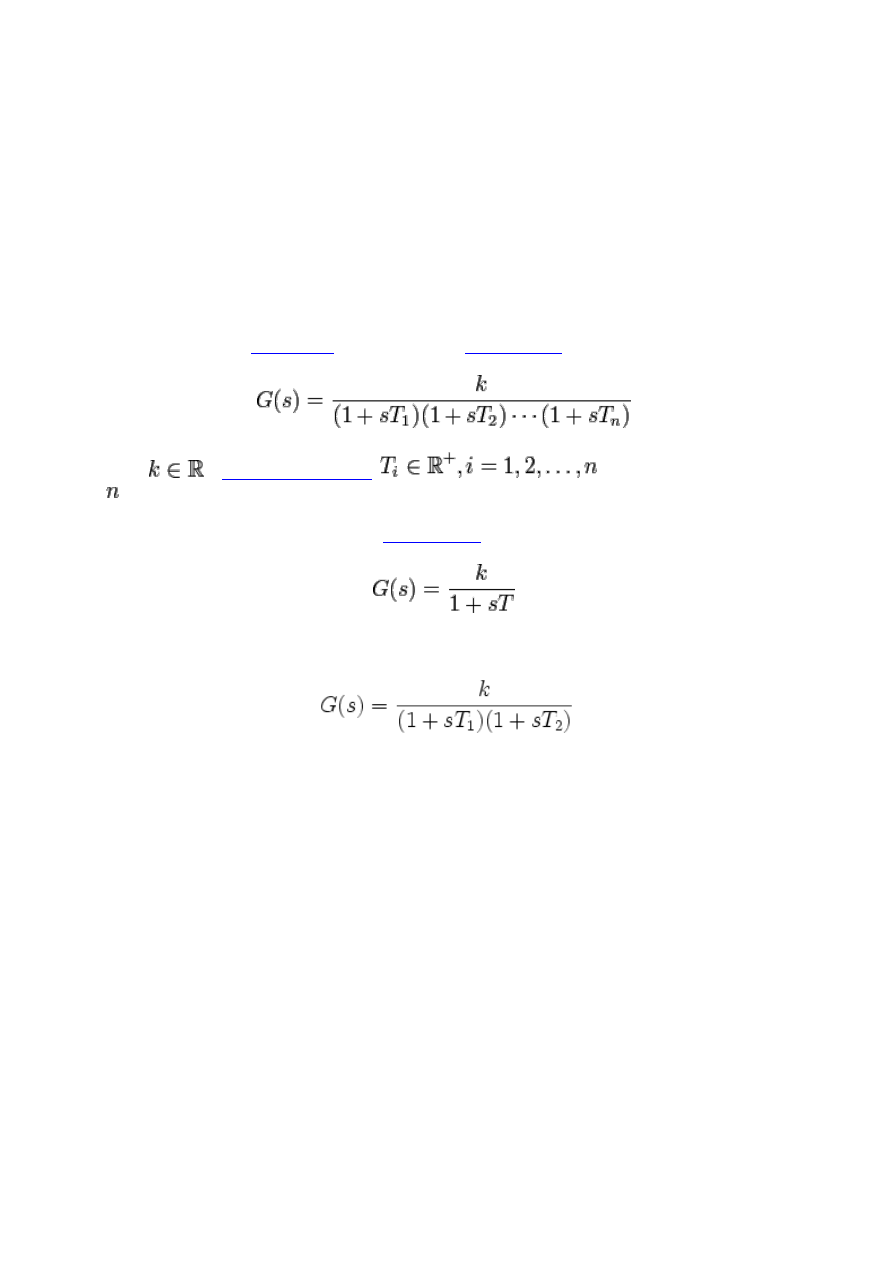
Człon inercyjny w

automatyce

to układ, którego

transmitancja

ma postać

,

gdzie

to

wzmocnienie układu

,

to stałe czasowe inercji, a

to rząd inercji członu.

Człon inercyjny pierwszego rzędu ma

transmitancję

postaci

.

Człon inercyjny drugiego rzędu ma postać

Odpowiedź na skok jednostkowy i charakterystyka amplitudowo - fazowa członu inercyjnego
I rzędu:

F wagi g(t)=k/T e ^(-t/T) odp jednostok y(t)=k(1-e^(=t/T)

5. Rożnica miedzy członem oscylacyjnym drugiego rzędu a
członem inercyjnym drugiego rzędu.

oscylacyjny zawiera względny współczynnik tłumienia, pulsacja drgan tlumionych

- grupa 2:
2. Podać transmitancję członu różniczkującego idealnego i jego
odpowiedzi na podstawowe sygnały pobudzające.

W

automatyce

człon różniczkujący (idealny) (

ang.

derivative term) to człon, który na

wyjściu daje sygnał

proporcjonalny do

pochodnej

sygnału wejściowego

:

Poddanie powyższego związku obustronnej

transformacji Laplace'a

daje związek pomiędzy

transformatami obu sygnałów:

Stąd

transmitancja

członu różniczkującego ma postać:

y(t)= kdelta(t)
G(t)=kddelta(t)/dt

3. Metody przedstawiania układu z daną transmitancją w
przestrzeni zmiennych stanu.

4. Co to jest funkcja wagi układu?

(impuls Diraca jest to inaczej funkcja wagi układu)Delta Diraca (albo funkcja
impulsowa) δ to, mówiąc intuicyjnie, obiekt matematyczny o następujących własnościach:

którego "powierzchnia pod krzywą" jest znormalizowana do 1, czyli wartość

całki

wynosi:

Matematycznie określamy deltę Diraca jako

miarę

albo jako

dystrybucję

, czyli funkcjonał

liniowy określony na odpowiedniej przestrzeni funkcyjnej. Warto tu podkreślić, że spełnienie
warunku normalizacji wymaga w szczególności rozszerzenia definicji całki z funkcji
rzeczywistej.

Delta Diraca jest używana do przedstawienia bardzo krótkiego impulsu o jednostkowym polu
(np. przenoszącego jednostkowy ładunek elektryczny), a w

statyce

- do reprezentowania sił

punktowo obciążających belkę (np. w punktach podparcia). W przypadkach tych, delta Diraca
jest matematycznym modelem nierealizowalnego fizycznie, nieskończenie wąskiego impulsu
występującego w chwili t=0, o nieskończenie dużej

amplitudzie

i polu równym 1.

5. Podstawowe właściwości transformaty Z.

def:

Wyprzedzenie:

Opoznienie:

- grupa 3:
2. Podać definicje transmitancji G(s)

Transmitancja operatorowa (funkcja przejścia,

) – stosunek

transformaty Laplace'a

sygnału wyjściowego do transformaty Laplace'a sygnału wejściowego układu przy zerowych
warunkach początkowych:

.

Transmitancja jest częstotliwościowym modelem układu (w postaci zasadniczej określonym
w

dziedzinie s

). Określa ogólne własności stacjonarnego

układu liniowego

o jednym

wejściu

i

jednym

wyjściu

, niezależne od rodzaju wymuszenia. Dla układu wielowymiarowego o

wejściach i wyjściach można określić x transmitancji wiążących każde wyjście z
każdym wejściem.

Wyk w analizie i syntezie ukla sterowania. Trans pozwala uzyskac nieazbedne w obiekcie
jego zachowa się w przypadku wymuszen.

3. Kryterium stabilności Routha.

algebraiczna

dla układów zamknietych i otwartych

Kryterium Routha - Badany układ musi być przedstawiony w postaci wypadkowej (zastępczej
) transmitancji G(s)= L(s)/M(s) = L(s)/ (anS^n+a(n-1)S^(n-1)+...+a1S+a0)
układ regulacyjny jest stabilny asymptotycznie , jęzeli jego równanie charakterystyczne
(M(s)=0) spełnia dwa warunki :
1. Wszystkie współczynniki an ,... ao są różne od zera i są jednakowego znaku.Jest to
warunek konieczny
2.Wszystkie współczynniki pierwszej kolumny tzw. wyznacznika Routh'a są różne od zera i
są jednakowego znaku.
cecha charakterystyczna kryterium Routh'a:

Ilość zmian znaku wyrazów w 1-szej kolumnie wyznacznika Routh'a jest równa liczbie
biegunów transmitancji leżących w prawej półpłaszczyźnie lub na osi urojonej lm.

KRYTERIUM Michajlowa

4. Podać definicję sygnałów standardowych: skok jednostkowy,
prędkości, delta Diraca.

*delta Dirac'a: δ(t) reprezentuje nieskończenie wielki impuls pojawiający się w chwili t = 0 i
trwający nieskończenie krótko, przy czym efekt działania tego impulsu (mierzony całką po
całej prostej) jest jednostkowy. Inna interpretacja: δ(t) reprezentuje masę jednostkową
skupioną w punkcie 0.
*skok jednostkowy: jest funkcją nieciągłą która przyjmuje wartość 0 dla ujemnych

argumentów i wartość 1 w pozostałych przypadkach. Skok jednostkowy jest wynikiem
całkowania delty Diraca.

*skok prędkości

5. Metody przedstawiania udkładu ze zmienną transmitancją, jak
przedstawić model stanowy (???)

- grupa 4:
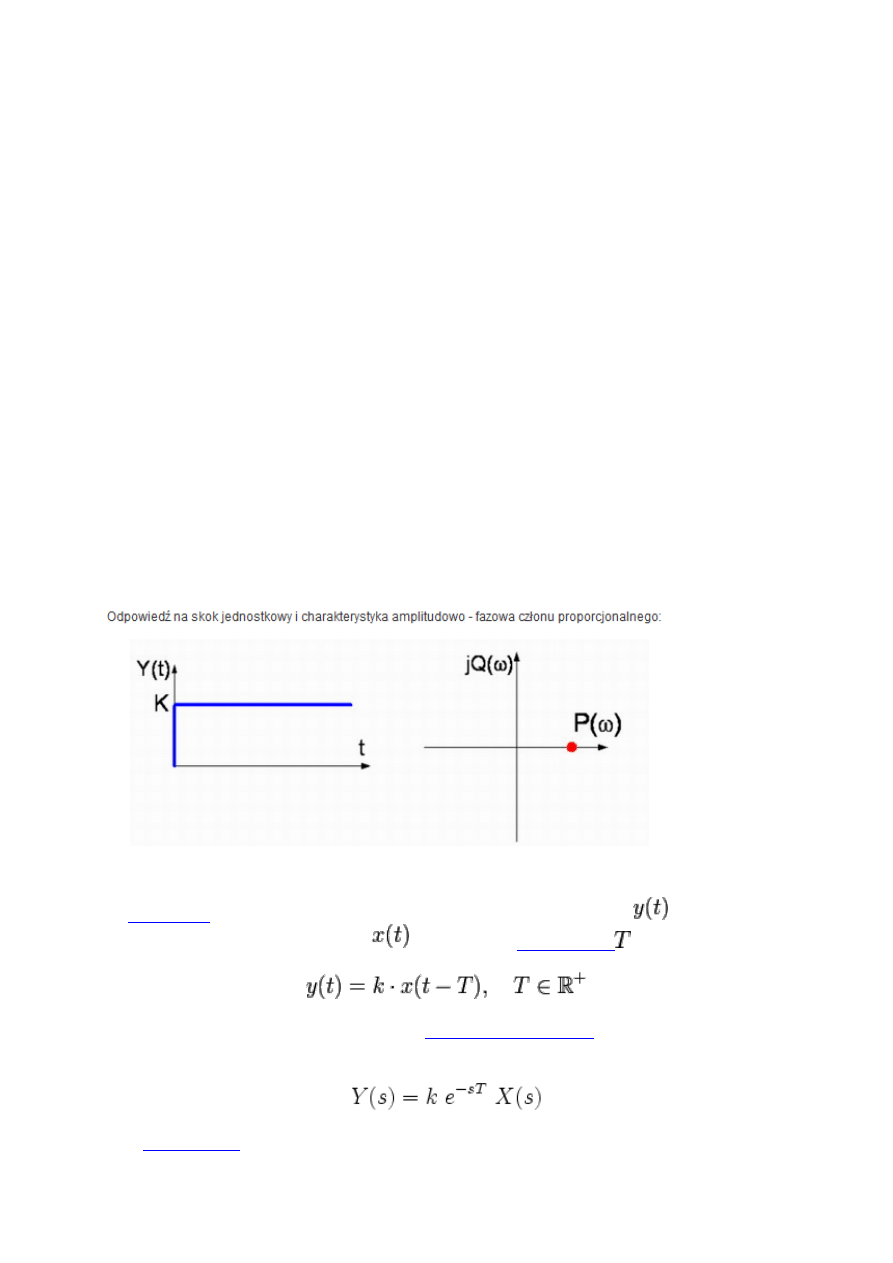
1. Wykres amplitudowo-fazowy członu proporcjonalnego.

2. Transmitancja członu opóźniającego.

W

automatyce

człon opóźniający to człon, który na wyjściu daje sygnał

będący

powtórzeniem sygnału wejściowego

opóźnionym o

stałą wartość

:

Poddanie powyższego związku obustronnej

transformacji Laplace'a

daje związek pomiędzy

transformatami obu sygnałów:

Stąd

transmitancja

członu opóźniającego ma postać

gdzie stała jest czasem opóźnienia.

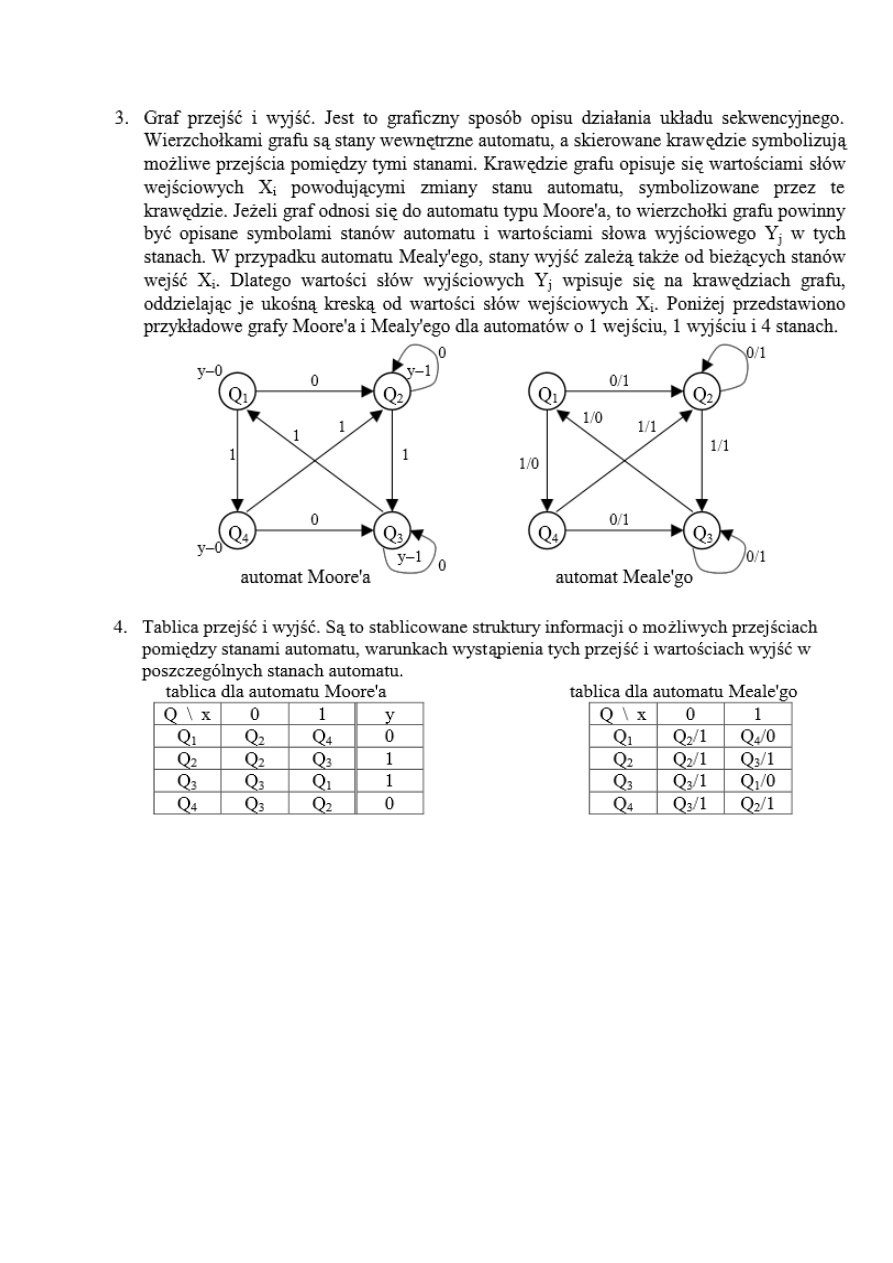
3. Metody opisu automatów. (??? jakoś tak)

4. Stabilność i zapas stabilności.

Zapas stabilności określa praktyczną przydatność

zamkniętego układu automatycznej

regulacji

. Jest miarą odległości danego punktu pracy urządzenia lub algorytmu od granicy

stabilności, określanej przez dowolne z kryterium

stabilności układu automatycznej regulacji

.

Dla zamkniętych układów regulacji zapas stabilności definiuje się na podstawie
charakterystyk układu otwartego jako parę liczb, z których pierwsza określa zapas amplitudy
(nazywany również zapasem modułu), a druga zapas fazy.

W praktyce zapas stabilności powinien być wystarczająco duży, np. większy niż 6

decybeli

i

5. Kryterium Nysquista.

Kryterium Nyquista pozwala na określenie stabilności układu zamkniętego na podstawie
badania

charakterystyki amplitudowo-fazowej

układu otwartego.

Rozważany jest zamknięty układ regulacji:

zamknięty układ regulacji

1. Zakładamy, że rozłączamy sprzężenie zwrotne w układzie.
2. Wyznaczamy

transmitancję operatorową

otrzymanego układu otwartego:

.

3. Zakładamy, że układ ma k biegunów (miejsc zerowych mianownika transmitancji) w

prawej półpłaszczyźnie zespolonej i

biegunów w lewej (nie ma biegunów na

osi urojonej).

4.

Transmitancję widmową

układu otwartego oznaczamy przez

Jeżeli spełnione są powyższe założenia to układ zamknięty jest stabilny wtedy i tylko wtedy,
gdy przyrost argumentu wyrażenia

przy zmianie w zakresie od 0 do

jest

równy

, co zapisujemy następująco:

-grupa 5:
1. Metody doboru nastaw układów przemysłowych. (?)

2. Transmitancja członu inercjalnego I rzędu i odpowiedzi na
standardowe pobudzenia.
4. Człon różniczkujący - charakterystyki logarytmiczno fazowe i
amplitudowe bodajże (wspominał coś chyba, żeby wybrać jeden,
np. oscylacyjny, nie pamiętam dokładnie).
5. Odpowiedź skokowa w układzie regulacyjnym.

-grupa 5: 1. Metody doboru nastaw uk

ładów przemysłowych. (?)

Metody analityczne: metoda linii pierwiastkowych metody doswiadczalne: metoda Zieglera-Nicholsa,
wzmocnienie krytyczne
Przy wyborze typu regulatora konieczna jest znajomo

ść wpływu poszczególnych

cz

łonów: P, I, D na przebieg procesu regulacji.

Cz

łon proporcjonalny P powoduje zmianę

„prędkości” z jaką reaguje regulator, duże wzmocnienie powoduje silniejszą reakcję, jednak nie eliminuje
ustalonego uchybu regulacji.
Cz

łon całkujący I wpływa na ustaloną odchyłkę

regulacji eliminuj

ąc ją.

Cz

łon różniczkujący D odpowiada za to, jak mocno regulator reaguje

na zmiany wielko

ści regulowanej np. czy przy zmianie wartości regulowanej o 2% element

wykonawczy ma zmieni

ć swój stan o 1% czy np. 10%.

Nastawy poszczeg

ólnych członów

w istotny spos

ób wpływają na stabilność układu.

1 metoda: Doboru nastaw dokonuje si

ę po identyfikacji obiektu i określeniu jego transmitancji

zast

ępczej. Optymalne parametry regulatora oblicza się za pomocą odpowiednich wzorów

b

ądź odczytuje z wykresów.

2 metoda: metoda Zieglera-Nicholsa, ktora polega na: I) ustawienie regulatora na dzialanie proporcjonalne i
stopniowe zwiekszanie wspolczynnika wzmocnienia dochodzac do granicy stabilnosci. II) w czasie
wystepowania oscylacji zmierzyc okres oraz wsp. Wzmocnienia przy jakim one wystapily. III) obliczyc
nastaw zaleznie od typu regulatora ze wzorow.
3 metoda: polega na wlaczeniu poszczegolnych czlonow regulatora w nastepujacej kolejnosci: P,I,D.
Wzmocnienie podnosi sie do momentu uzyskania minimalnych oscylacji w ukladzie, przy mozliwie jak
najwiekszym Ti oraz Td=0 (Ti

– czas zdwojenia/calkowania, Td – czas wyprzedzenia/rozniczkowania).

Kolejny krok to dodanie czlonu calkujacego zaczynajac od stosunkowo duzej wartosci, a nastepnie
stopniowo ja zmniejszajac. Po uzyskaniu zerowego uchybu regulacji i krotkiego czasu ustalenia mozna
dokonac korekt dzialania regulatora poprzez wprowadzenie nastaw rozniczkowania.
2. Transmitancja cz

łonu inercjalnego I rzędu i odpowiedzi na standardowe pobudzenia.

G(s) = k/(Ts+1)
T- czas inercji
k

– wspolczynnik wzmocnienia

+ wykres funkcji wagi i odp. jednostkowa (ze slajdow) 3. Karta Nicholsa.(by

ło) 4. Człon różniczkujący -

charakterystyki logarytmiczno fazowe i amplitudowe bodaj

że (wspominał coś chyba, żeby wybrać

jeden, np. oscylacyjny, nie pami

ętam dokładnie).

Slajdy, sa tam el. Rozniczkujacy idealny i rzeczywisty. 5. Odpowied

ź skokowa w układzie regulacyjnym.

http://www.i15.p.lodz.pl/strony/elektrownie/uklady_automatycznej_regulacji.pdf strona 6.
6. Transformata Z - definicja, zastosowanie bodaj

że itp.

http://www.zsir.ia.polsl.pl/~dydaktyka/pa_gliwice/pa_air/transformata_z.pdf strona 1. Tak jak r

ównania

r

óżniczkowe stosowane są do opisu układów z sygnałami analogowymi,

tak r

ównania różnicowe stosowane są dla układów z sygnałami dyskretnymi lub cyfrowymi.

R

ównania różnicowe używane są również do aproksymacji równań różniczkowych w celu zapisania ich w

programach komputerowych wykorzystywanych w r

óżnego rodzaju symulacjach.

Rachunek operatorowy Laplace’a może być stosowany do rozwiązywania liniowych równań
r

óżniczkowych zwyczajnych, natomiast transformata Z jest metodą wykorzystywaną do

rozwiązywania liniowych równań różnicowych i układów liniowych z danymi dyskretnymi lub cyfrowymi.