OBWODY ELEKTRYCZNE i

OBWODY ELEKTRYCZNE i

MAGNETYCZNE

MAGNETYCZNE

ARR1304

ARR1304

Semestr 3

Semestr 3

OBWODY ELEKTRYCZNE i

OBWODY ELEKTRYCZNE i

MAGNETYCZNE

MAGNETYCZNE

‹

‹

Dr inż.. Adam

Dr inż.. Adam

Gubański

Gubański

‹

‹

Pok. 205/7 D1

Pok. 205/7 D1

‹

‹

Konsultacje:

Konsultacje:

wt

wt

. 11

. 11

-

-

13

13

‹

‹

śr

śr

. 9

. 9

-

-

11

11

‹

‹

eportal.eny.pwr.wroc.pl

eportal.eny.pwr.wroc.pl

‹

‹

oeim

oeim

Wprowadzenie

Wprowadzenie

‹

‹

pole elektrostatyczne i

pole elektrostatyczne i

‹

‹

Pole magnetostatyczne i

Pole magnetostatyczne i

‹

‹

Równania materiałowe ( liniowe )

Równania materiałowe ( liniowe )

‹

‹

ε

ε

-

-

przenikalność dielektryczna

przenikalność dielektryczna

‹

‹

µ

µ

-

-

przenikalność magnetyczna

przenikalność magnetyczna

H

B

E

D

ε

=

H

B

μ

=

E

D

r

ε

ε

ε

0

=

r

μ

μ

μ

0

=

Analogie

Analogie

e le k tr y c z n e

m a g n e t y c z n e

p o d s ta w o w e p r a w a

i j

i j

i j

j

i

i j

r

r

r

Q

Q

F

⋅

⋅

Π

=

2

4

1

ε

∫

=

)

( V

s

V

Q

s

d

D

o

3

4

r

r

l

d

I

H

d

×

⋅

Π

=

∫

=

)

( S

L

S

I

l

d

H

o

s ił y

E

q

F

=

B

v

q

F

×

=

ź r ó d ła p o la

d q

l

I d

p o te n c j a ł

∫

=

L

l

d

E

0

o

V

E

− ∇

=

∫

∞

Π

=

r

r

q

r

V

ε

4

)

(

∫

=

)

( S

L

S

I

l

d

H

o

A

r o t

B

=

∫

Π

=

L

r

l

I d

A

4

μ

s tr u m ie ń

∫

=

Ψ

S

s

d

D

o

∫

=

Ψ

S

s

d

B

o

G ę s to ś ć e n e r g ii

E

D

E

o

2

1

=

ω

H

B

E

o

2

1

=

ω

R ó w n a n ie P o is s o n ’ a

ε

V

q

V

−

=

∇

2

j

A

μ

=

∇

2

Układy współrzędnych

Układy współrzędnych

‹

‹

prostokątny, kartezjański (skrót

prostokątny, kartezjański (skrót

-

-

K)

K)

‹

‹

cylindryczny, walcowy, (skrót

cylindryczny, walcowy, (skrót

-

-

C)

C)

‹

‹

sferyczny, kulisty, (skrót

sferyczny, kulisty, (skrót

-

-

S)

S)

Układy współrzędnych

Układy współrzędnych

y

P(x,y,z)

θ

z

r

ρ

ϕ

x

P'(x,y,0)

1

x

1

z

1

y

1

r

1

θ

1

ρ

Układy współrzędnych

Układy współrzędnych

‹

‹

cylindryczny (

cylindryczny (

c

c

→

→

k

k

), x=

), x=

ρ

ρ

cos

cos

ϕ

ϕ

,

,

y=

y=

ρ

ρ

sin

sin

ϕ

ϕ

,

,

z=z

z=z

‹

‹

cylindryczny (

cylindryczny (

k

k

→

→

c

c

),

),

ρ

ρ

=(x

=(x

2

2

+y

+y

2

2

)

)

1/2

1/2

,

,

ϕ

ϕ

=

=

arctg

arctg

(

(

y/x

y/x

)

)

,

,

z=z

z=z

‹

‹

sferyczny (

sferyczny (

s

s

→

→

k

k

),

),

x=r sin

x=r sin

θ

θ

cos

cos

ϕ

ϕ

,

,

y= r

y= r

sin

sin

θ

θ

sin

sin

ϕ

ϕ

,

,

z= r cos

z= r cos

θ

θ

‹

‹

sferyczny (k

sferyczny (k

→

→

s

s

), r=(x

), r=(x

2

2

+y

+y

2

2

+z

+z

2

2

)

)

1/2,

1/2,

θ

θ

=

=

arccos(z

arccos(z

/r),

/r),

ϕ

ϕ

=

=

arctg(y/x

arctg(y/x

)

)

Elementy algebry wektorów

Elementy algebry wektorów

‹

‹

iloczyn liczbowy

iloczyn liczbowy

‹

‹

iloczyn skalarny

iloczyn skalarny

‹

‹

gdzie z definicji przyjęto wartości iloczynu skalarnego

gdzie z definicji przyjęto wartości iloczynu skalarnego

wersorów

wersorów

w

w

v

v

u

u

A

A

A

1

1

1

A

α

α

α

α

+

+

=

(

) (

)

A

B

1

1

1

1

1

1

B

A

⋅

=

+

+

=

+

+

⋅

+

+

=

⋅

w

w

v

v

u

u

w

w

v

v

u

u

w

w

v

v

u

u

B

A

B

A

B

A

B

B

B

A

A

A

0

,

1

=

⋅

=

⋅

=

⋅

=

⋅

=

⋅

=

⋅

u

u

u

u

1

1

1

1

1

1

1

1

1

1

1

1

w

w

v

v

w

w

v

v

Elementy algebry wektorów

Elementy algebry wektorów

‹

‹

iloczyn wektorowy

iloczyn wektorowy

‹

‹

gdzie z definicji przyjęto wartości iloczynu wektorowego

gdzie z definicji przyjęto wartości iloczynu wektorowego

wersorów

wersorów

(

) (

)

(

)

(

)

(

)

w

v

1

1

1

1

1

1

1

1

1

B

A

u

u

v

v

u

w

u

u

w

v

w

w

v

w

w

v

v

u

u

w

w

v

v

u

u

B

A

B

A

B

A

B

A

B

A

B

A

B

B

B

A

A

A

−

+

−

+

−

=

+

+

×

+

+

=

×

v

w

w

w

v

v

w

w

w

v

w

w

v

v

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

u

u

u

u

−

=

×

−

=

×

−

=

×

=

×

=

×

=

×

=

×

=

×

=

×

u

v

u

u

u

v

,

,

0

Elementy algebry wektorów

Elementy algebry wektorów

‹

‹

Wygodny do zapamiętania iloczynu wektorowego jest zapis

Wygodny do zapamiętania iloczynu wektorowego jest zapis

macierzowy w postaci

macierzowy w postaci

‹

‹

iloczyn potrójny skalarny (mieszany) jest skalarem

iloczyn potrójny skalarny (mieszany) jest skalarem

‹

‹

Iloczyn mieszany ma interpretację geometryczna jako objętość

Iloczyn mieszany ma interpretację geometryczna jako objętość

równoległoboku którego krawędziami są odcinki o długości trzech

równoległoboku którego krawędziami są odcinki o długości trzech

wektorów.

wektorów.

A

B

1

1

1

B

A

w

v

u

×

−

=

⎥

⎥

⎥

⎦

⎤

⎢

⎢

⎢

⎣

⎡

=

×

w

v

u

w

v

u

B

B

B

A

A

A

det

(

)

⎥

⎥

⎥

⎦

⎤

⎢

⎢

⎢

⎣

⎡

=

×

⋅

w

v

u

w

v

u

w

v

u

C

C

C

B

B

B

A

A

A

det

C

B

A

Pole magnetyczne

Pole magnetyczne

‹

‹

Hans

Hans

Christian

Christian

Ørsted

Ørsted

(ur.

(ur.

14 sierpnia 1877, zm. 9

14 sierpnia 1877, zm. 9

marca 1851

marca 1851

–

–

duński fizyk i

duński fizyk i

chemik, najbardziej znany z

chemik, najbardziej znany z

odkrycia zjawiska

odkrycia zjawiska

elektromagnetyzmu. W

elektromagnetyzmu. W

prostym eksperymencie

prostym eksperymencie

pokazał, że igła kompasu

pokazał, że igła kompasu

odchyla się pod wpływem

odchyla się pod wpływem

przepływającego

przepływającego

pradu

pradu

w

w

przewodzie a następnie

przewodzie a następnie

oddziaływania wzajemnego

oddziaływania wzajemnego

dwóch przewodów z prądem.

dwóch przewodów z prądem.

Pole magnetyczne

Pole magnetyczne

‹

‹

oddziaływania tego nie opisują prawa pola

oddziaływania tego nie opisują prawa pola

elektrycznego

elektrycznego

‹

‹

do opisu tych zjawisk należało

do opisu tych zjawisk należało

wprowadzić nowe pole zwane polem

wprowadzić nowe pole zwane polem

magnetycznym

magnetycznym

‹

‹

ładunki statyczne

ładunki statyczne

–

–

pole elektrostatyczne

pole elektrostatyczne

‹

‹

Ładunki poruszają się ze stałą prędkością

Ładunki poruszają się ze stałą prędkością

-

-

pole magnetostatyczne

pole magnetostatyczne

Pole magnetyczne

Pole magnetyczne

‹

‹

Zjawiska związane z polem

Zjawiska związane z polem

magnetycznym odgrywają ważną

magnetycznym odgrywają ważną

rolę w naszym życiu:

rolę w naszym życiu:

‹

‹

maszyny elektryczne, mikrofony,

maszyny elektryczne, mikrofony,

głośniki, kineskopy, mierniki

głośniki, kineskopy, mierniki

analogowe, szybkie pojazdy

analogowe, szybkie pojazdy

lewitujące, pamięć magnetyczna,

lewitujące, pamięć magnetyczna,

separatory itd..

separatory itd..

Pole magnetyczne

Pole magnetyczne

‹

‹

Pole magnetyczne w próżni

Pole magnetyczne w próżni

‹

‹

Podstawowe prawa

Podstawowe prawa

1. prawo

1. prawo

Biot’a

Biot’a

-

-

Savart’a

Savart’a

-

-

Laplace’a

Laplace’a

2. prawo

2. prawo

Amper’a

Amper’a

prawo

prawo

Biot’a

Biot’a

-

-

Savart’a

Savart’a

-

-

Laplace’a

Laplace’a

3

4

1

r

r

l

d

H

d

×

⋅

Π

=

∫

×

⋅

Π

=

L

r

r

l

d

H

3

4

1

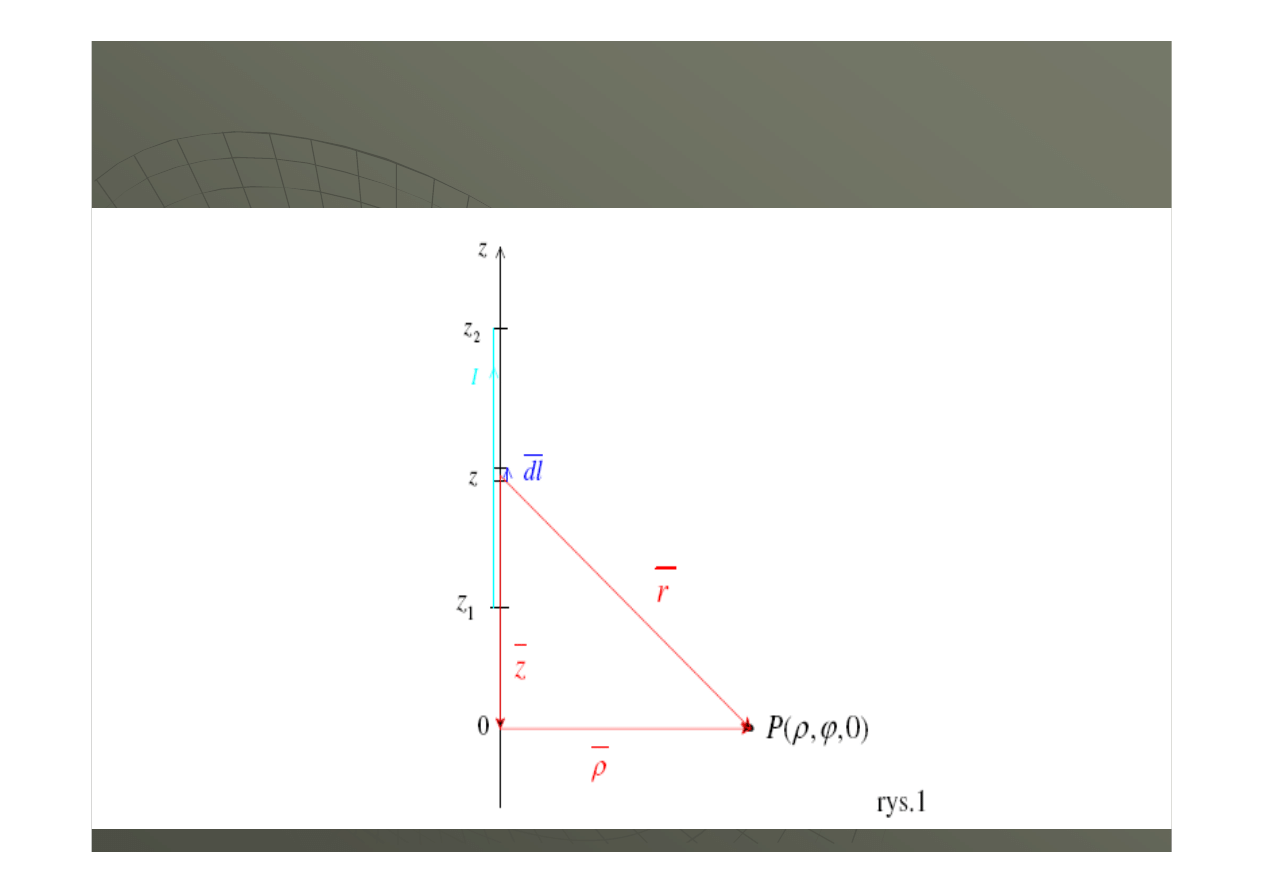
prawo

prawo

Biot’a

Biot’a

-

-

Savart’a

Savart’a

-

-

Laplace’a

Laplace’a

prawo

prawo

Biot’a

Biot’a

-

-

Savart’a

Savart’a

-

-

Laplace’a

Laplace’a

prawo

prawo

Biot’a

Biot’a

-

-

Savart’a

Savart’a

-

-

Laplace’a

Laplace’a

prawo

prawo

Biot’a

Biot’a

-

-

Savart’a

Savart’a

-

-

Laplace’a

Laplace’a

prawo

prawo

Biot’a

Biot’a

-

-

Savart’a

Savart’a

-

-

Laplace’a

Laplace’a

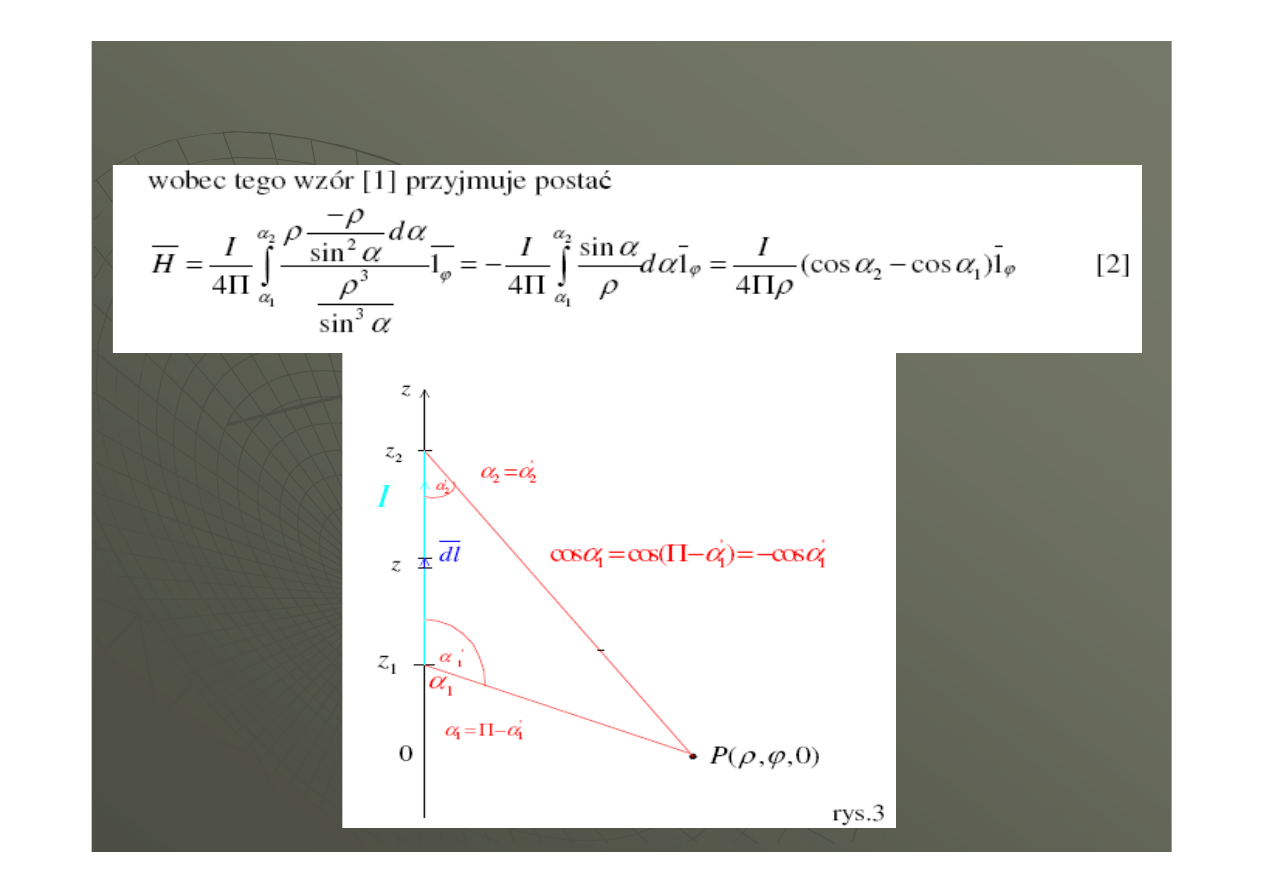
prawo

prawo

Biot’a

Biot’a

-

-

Savart’a

Savart’a

-

-

Laplace’a

Laplace’a

prawo

prawo

Biot’a

Biot’a

-

-

Savart’a

Savart’a

-

-

Laplace’a

Laplace’a

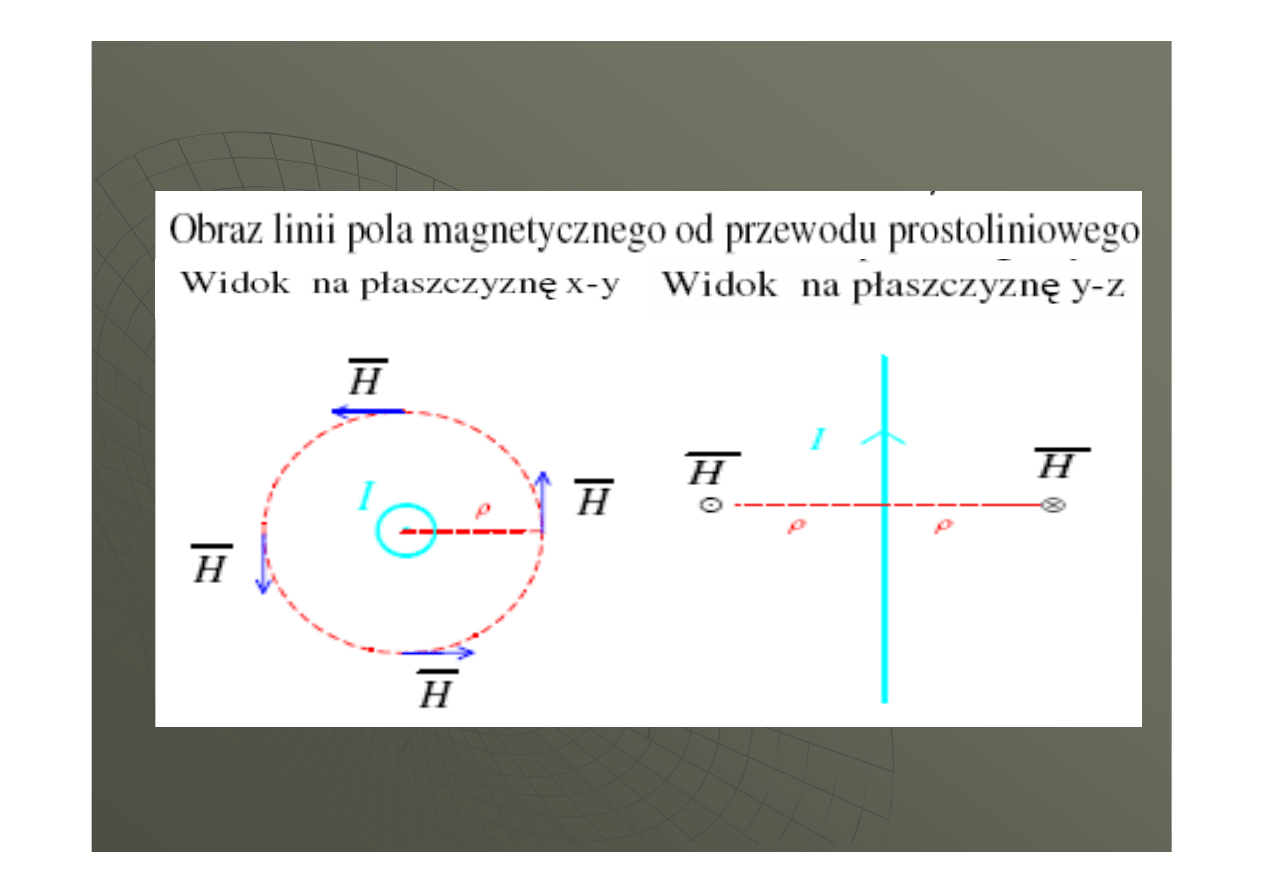
prawo

prawo

Biot’a

Biot’a

-

-

Savart’a

Savart’a

-

-

Laplace’a

Laplace’a