Energia sprzężonych zwojnic

(

)

(

)

(

)

1

2

1

2

1

2

1

2

,

,

1

2

2

1

1 1

2 2

1

1

2

1

0

0

,

,

1 1

1

1

2

2

1

2 2

2

1 1

1

1 2

2 2

2

0

0

2

2

1 1

1 2

2 2

(

)

1

1

2

2

I I

I I

I I

I I

di

di

di

di

W

u i

u i dt

L

M

i

L

M

i dt

dt

dt

dt

dt

L i di

Mi di

Mi di

L i di

L i di

Md i i

L i di

L I

MI I

L I

⎡

⎤ ⎡

⎤

⎛

⎞

⎛

⎞

=

+

=

+

+

+

=

⎜

⎟

⎜

⎟

⎢

⎥ ⎢

⎥

⎝

⎠

⎝

⎠

⎣

⎦ ⎣

⎦

=

+

+

+

=

+

+

=

=

±

+

∫

∫

∫

∫

można również napisać

(

) (

)

2

1 1

2

2

1

2

1 2

1

2

W

L I

L I

L L

M I I

=

±

−

m

energia jest zawsze

0

W

≥

stąd w szczególności gdy

1

2

2

1

I

L

I

L

= +

wynika stąd nierówność

1

2

M

L L

≤

1

2

M

k

L L

=

-- współczynnik sprzężenia zwojnic

Energia sprzężonych zwojnic

Gdy k=1 sprzężenie idealne ( ścisłe ).
Sprzężenie idealne nie jest możliwe, gdyż wówczas otrzymuje się W=0, a w
rzeczywistości zawsze istnieje pole, więc W>0.

Wzór na energię można również zapisać w postaci:

(

)

(

)

(

)

1 1

2

1

2 2

1

2

1 1

2 2

1

1

1

2

2

2

W

L I

MI

I

L I

MI I

I

I

=

±

+

±

=

Ψ + Ψ

lub

(

)

2

1 1

2 2

1 1

2 2

1 2

1

1

1

2

2

2

S

S

M

W

L I

L I

n I

n I

n n

=

+

+

±

Energia i gęstość energii

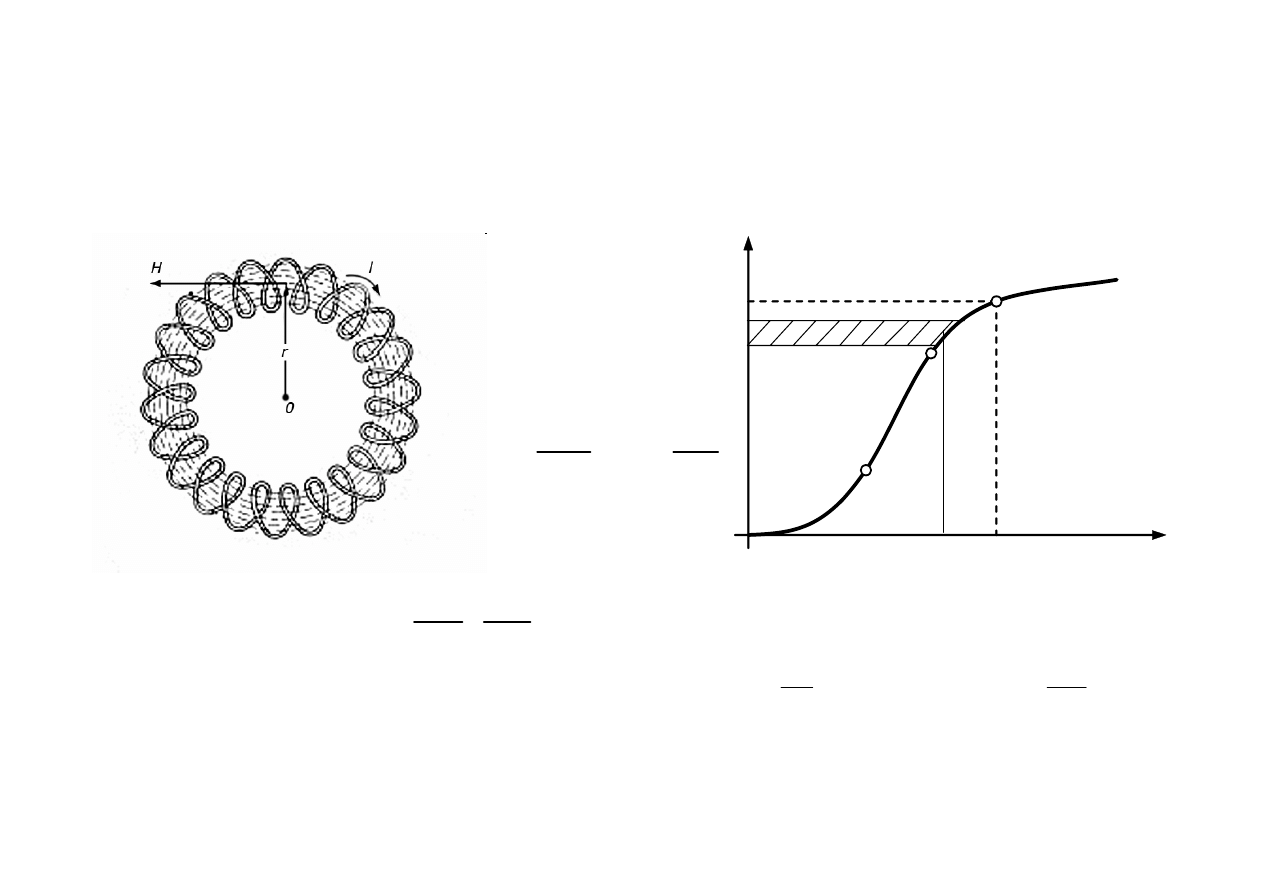
Zwojnicy z rdzeniem ferromagnetycznym

H

B

0

1

2

3

H

n

B

n

dB

H

Hl

ni

BS

d

dB

u

n

nS

dt

dt

=

Φ =

Φ

=

=

dB Hl

W

uidt

nS

dt

SlHdB

dt

n

=

=

⋅

=

∫

∫

∫

0

0

'

'

B

B

W

Sl HdB

V HdB

=

=

∫

∫

Gęstość energii

3

0

'

B

W

J

HdB

V

m

ω

⎡

⎤

= =

⎢

⎥

⎣

⎦

∫

pole nieliniowego trójkata

Energia i gęstość energii

W środowisku liniowym

2

0

0

'

1

'

'

2

B

B

B

B

H

HdB

dB

B

ω

μ

μ

μ

= ⇒

=

=

=

∫

∫

2

2

1

1

1

1

2

2

2

2

B

H

HB

H B

ω

μ

μ

=

=

=

=

o

stąd energia zgromadzona w polu magnetycznym

1

2

V

V

W

dv

H Bdv

ω

=

=

∫

∫

o

Straty energii związane z histerezą

W

HdB

V

ω

=

=

∫

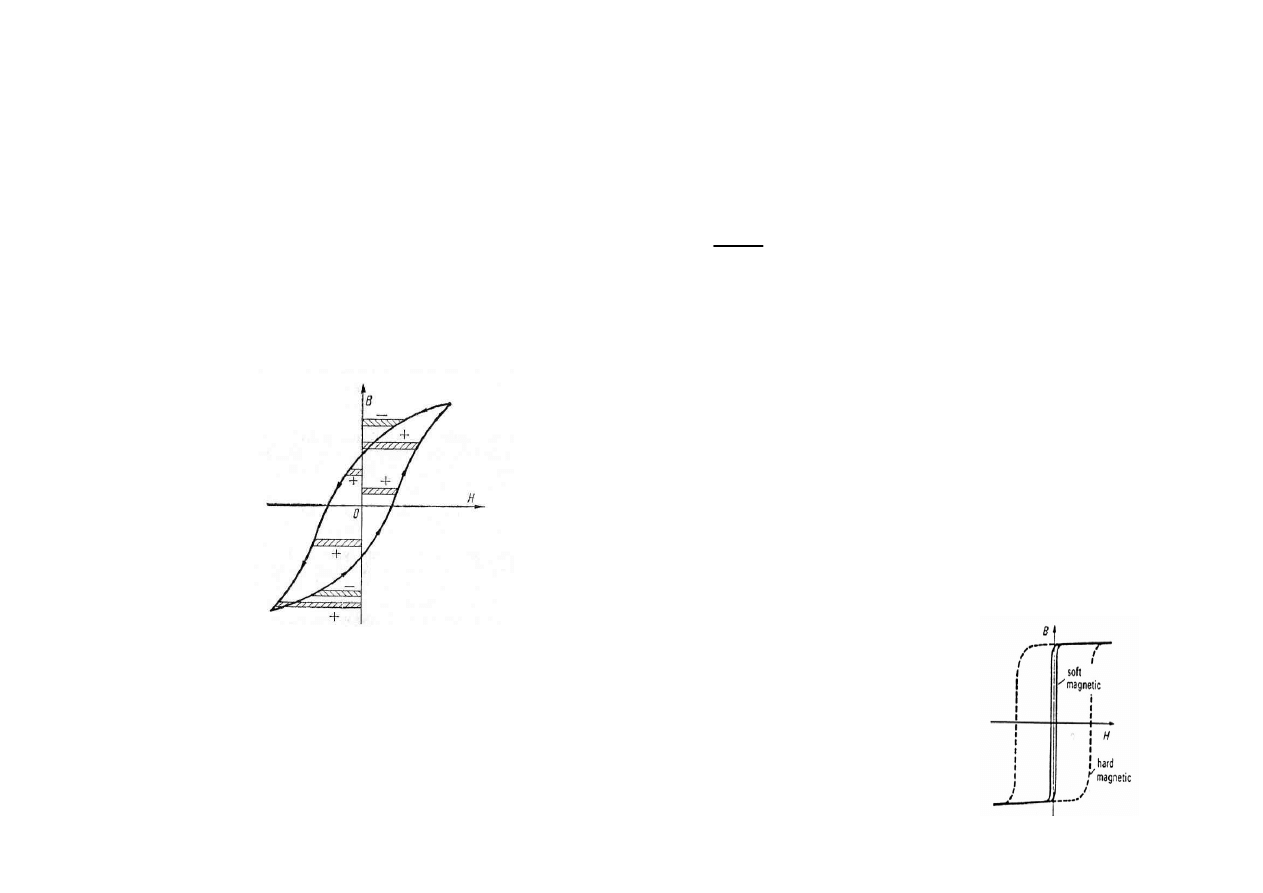
podczas jednego cyklu straty/m

3

są proporcjonalne

do powierzchni wewnętrznej pętli histerezy.
Moc strat na histerezę za okres odniesiona do jednostki
objętości rdzenia

h

P

f

HdB

=

∫

h

h

W

VtP

=

Straty energii

minimalizacja P

h

– ferromagnetyki miękkie

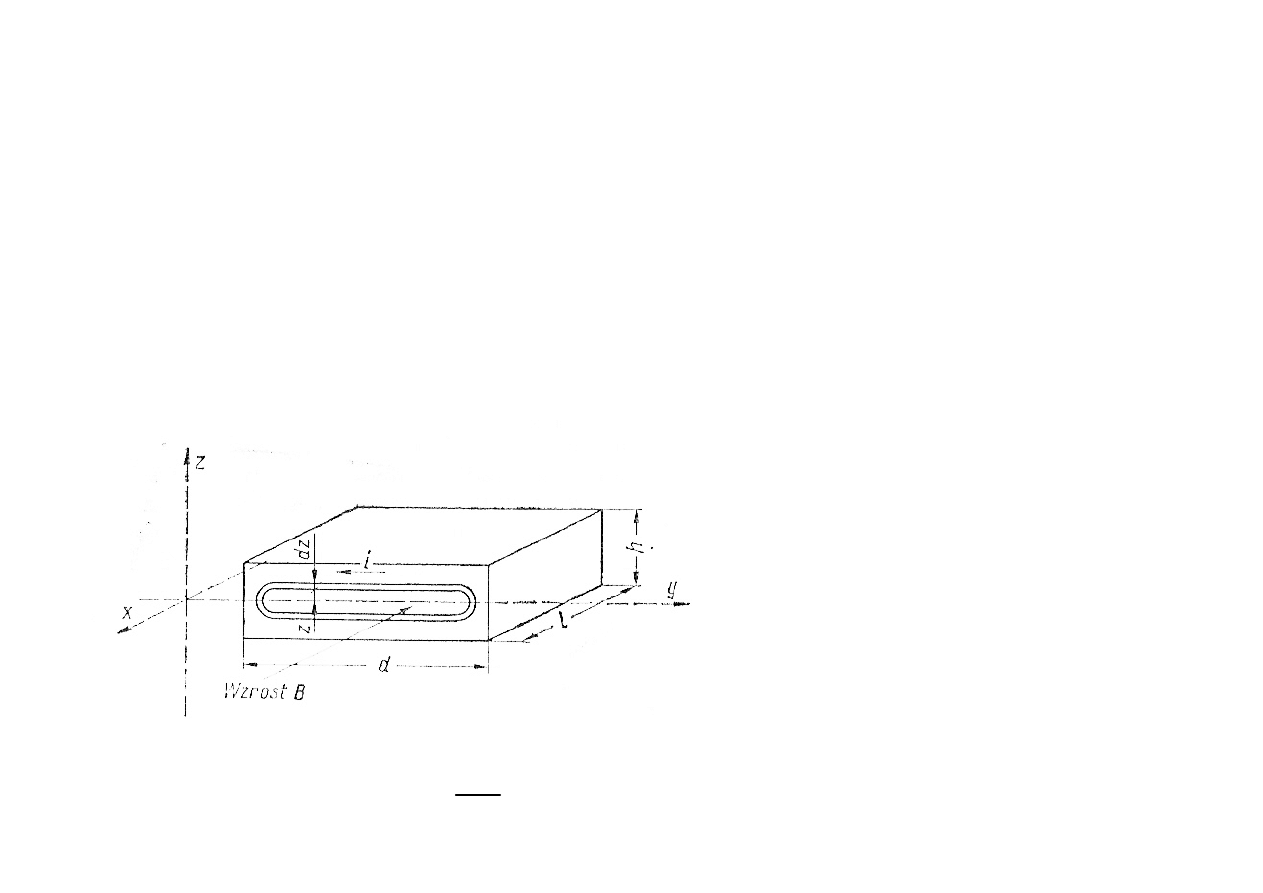
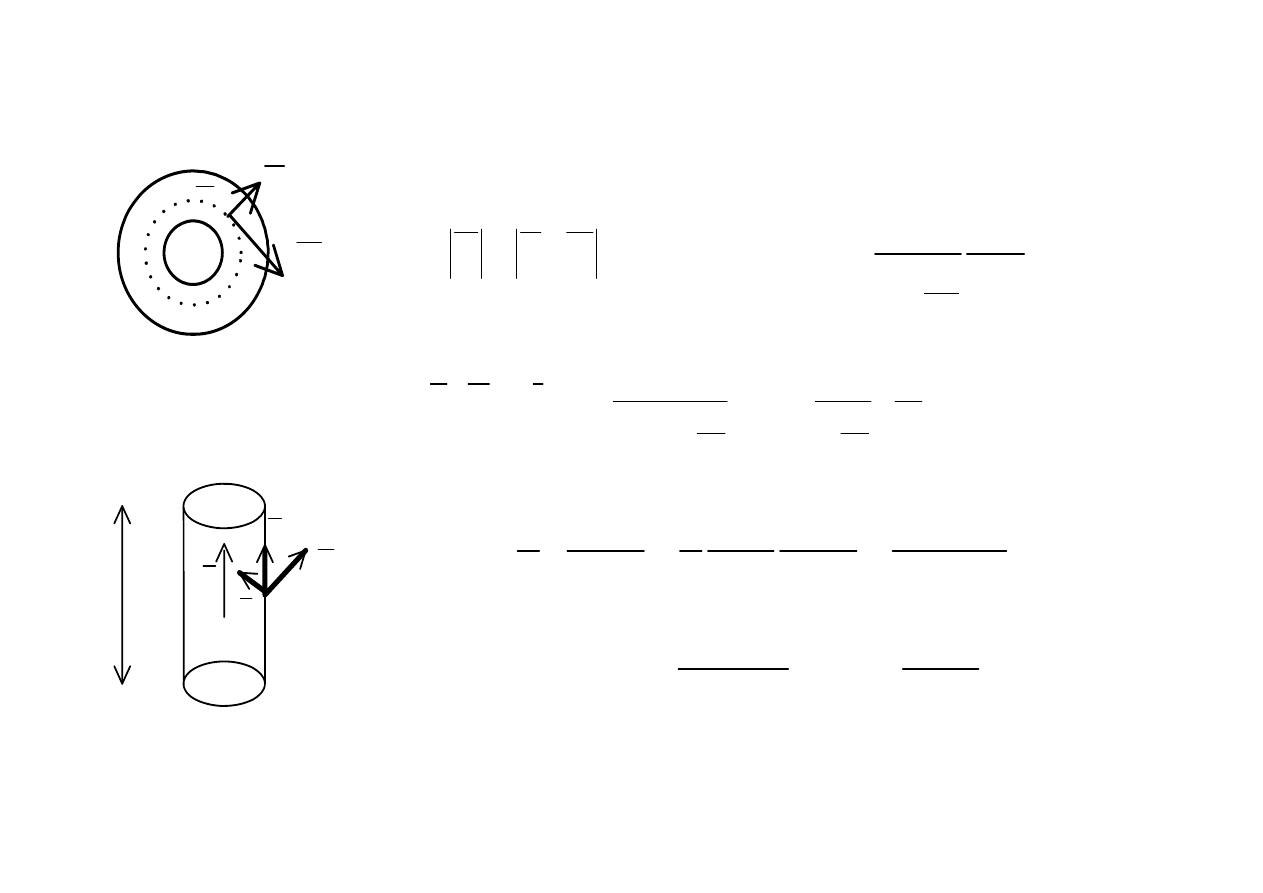
Straty na prądy wirowe

Prądy wirowe są to prądy indukowane w rdzeniu magnetycznym na skutek zmiennego
pola magnetycznego.
Wartość prądów wirowych zależy od:
- częstotliwości zmian pola magnetycznego
- od indukcji magnetycznej w rdzeniu
- od właściwości fizycznych rdzenia, a w szczególności od konduktywności i grubości

Załóżmy:

0

sin

B

B

t

ω

=

h

d

-

-

-pomijamy wpływ „wtórny”
prądów wirowych na „pierwotny”
strumień magnetyczny
- pole magnetyczne w rdzeniu
jest jednorodne

z prawa Faraday’a

0

~

2

cos

d

e

zdB

t

dt

ω

ω

Φ

≈ −

= −

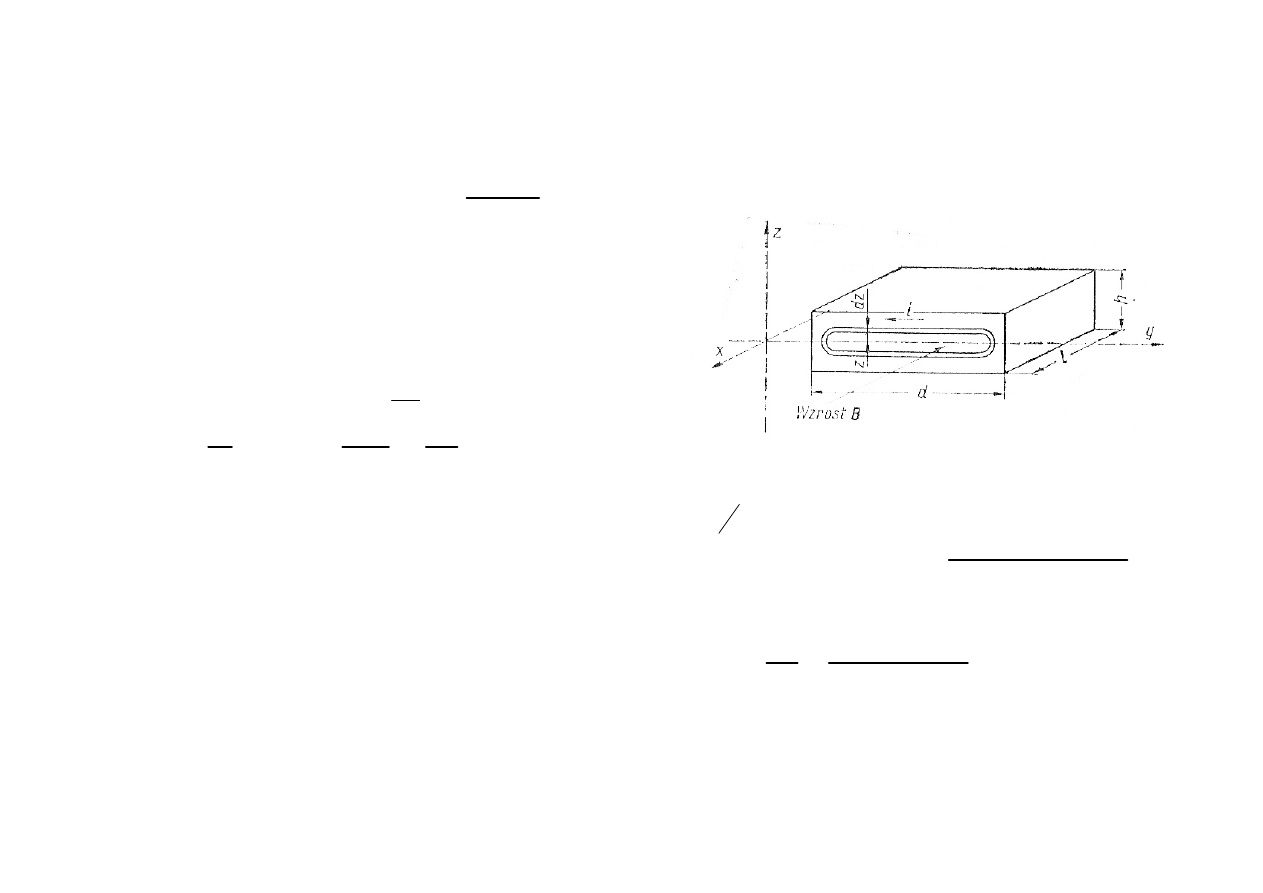
Straty na prądy wirowe

Opór pętli

2d

R

ldz

γ

≈

średnia moc za okres T, tracona
na ciepło w elementarnej pętli

2

2

2

2

2

0

0

0

1

2

T

w

e

dP

eidt

dt

dB lz dz

T

R

ω

ω

ω

γ

Π

=

=

=

Π

∫

∫

Średnia moc tracona w całym rdzeniu

2

2

2

3

2

2

2

2

0

0

0

6

h

w

ldB f

h

P

B ld z dz

γ

ω

γ

Π

=

=

∫

Gęstość mocy tracona na prądy wirowe

2

2

2

2

2

2

2

0

0

6

w

w

P

B f h

p

Kh f

B

V

γ

γ

Π

=

=

=

minimalizacja p

w

: - wykonywać rdzenie z bardzo cienkich blach wzajemnie izolowanych

- stosować materiały magnetyczne o małej konduktywności np. ferryty

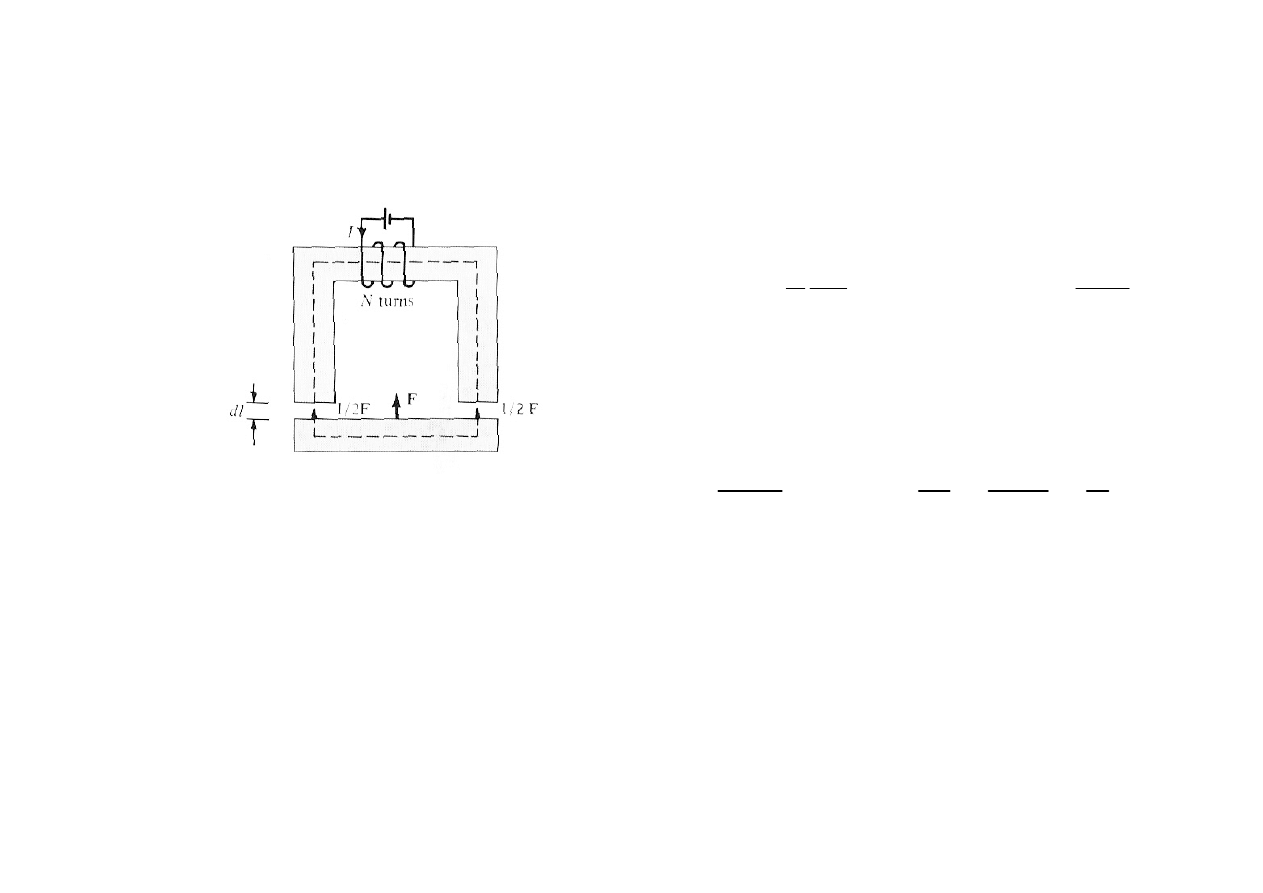
Siły mechaniczne między zwojnicami

1

i

2

i

dx

1

u

2

u

F

Bilans energii przy elementarnym przesunięciu o dx

praca zasilania=wzrost energii pola + praca mech.

1 1

2 2

(

)

x

u i

u i dt

dW

F dx

+

=

+

1

1

2

2

x

i d

i d

dW

Fdx

Ψ +

Ψ =

+

1

1

2

2

1

1

2

2

1

1

2

2

x

i d

i d

d

i

i

Fdx

⎡

⎤

Ψ +

Ψ =

Ψ +

Ψ +

⎢

⎥

⎣

⎦

zakładamy, że i

1

=const. i i

2

= const.

stąd

1

1

2

2

1

(

)

2

x

x

i d

i d

Fdx

czyli

dW

F dx

Ψ +

Ψ =

=

[ ]

1

2

x

i

const

i

const

W

F

N

x

=

=

∂

=

∂

Siły mechaniczne między zwojnicami

rozpiszmy

2

2

1 1

1 2

2 2

1 2

1

1

2

2

x

W

M

F

L i

Mi i

L i

i i

x

x

x

∂

∂

∂

⎛

⎞

=

=

+

+

=

⎜

⎟

∂

∂

∂

⎝

⎠

ponieważ

1

2

0;

0

L

L

x

x

∂

∂

=

=

∂

∂

1 2

x

M

F

i i

x

∂

=

∂

2

1

2

1

R

R

R

d

R

d

(

)

2

2

2

2

0

2

2

0 1 2

1

2

1 1

1

12

3

3

2

2

2

2

2

2

1

1

1

1

2(

)

2

x

x

H

R n

n n R R

i n R

H

M

i

i

R

d

R

d

μ

μ

Π

Π

Φ

=

⇒

=

=

=

+

+

2

2

2

2

0

1 2 1 2

1

2

0

1 2 1 2

1

2

1 2

1 2

5

4

2

2

2

1

3

3

2

2(

)

x

x

i i n n R R d

i i n n R R

M

M

F

i i

F

i i

x

d

d

R

d

μ

μ

Π

Π

∂

∂

=

=

=

= −

≅ −

∂

∂

+

Znak „-” oznacza w tym przypadku wzajemne przyciąganie się cewek,
Co ma zawsze miejsce przy indukcyjności wzajemnej dodatniej
Można powiedzieć, że kierunek wzajemnego oddziaływania cewek
będzie zawsze taki, aby wynikłe stąd przesunięcie powodowało
wzrost indukcyjności wzajemnej.

Siła oddziaływania magnesu

2

2

0

0

1

2

2

2

2

B

B S

Fdl

dW

Sdl

F

μ

μ

⎡

⎤

⎛

⎞

−

=

=

⇒

= − ⎜

⎟

⎢

⎥

⎣

⎦

⎝

⎠

Dla pojedynczej przerwy

2

2

0

0

1

2

2

2

B S

F

B

F

p

HB

S

μ

μ

= −

⇒

=

=

=

Wzór ten pozwala obliczyć siły działające w:
- przekaźnikach
- wirujących maszynach
- lewitacji magnetycznej

Dla B=1T →p=4 KG/cm

2

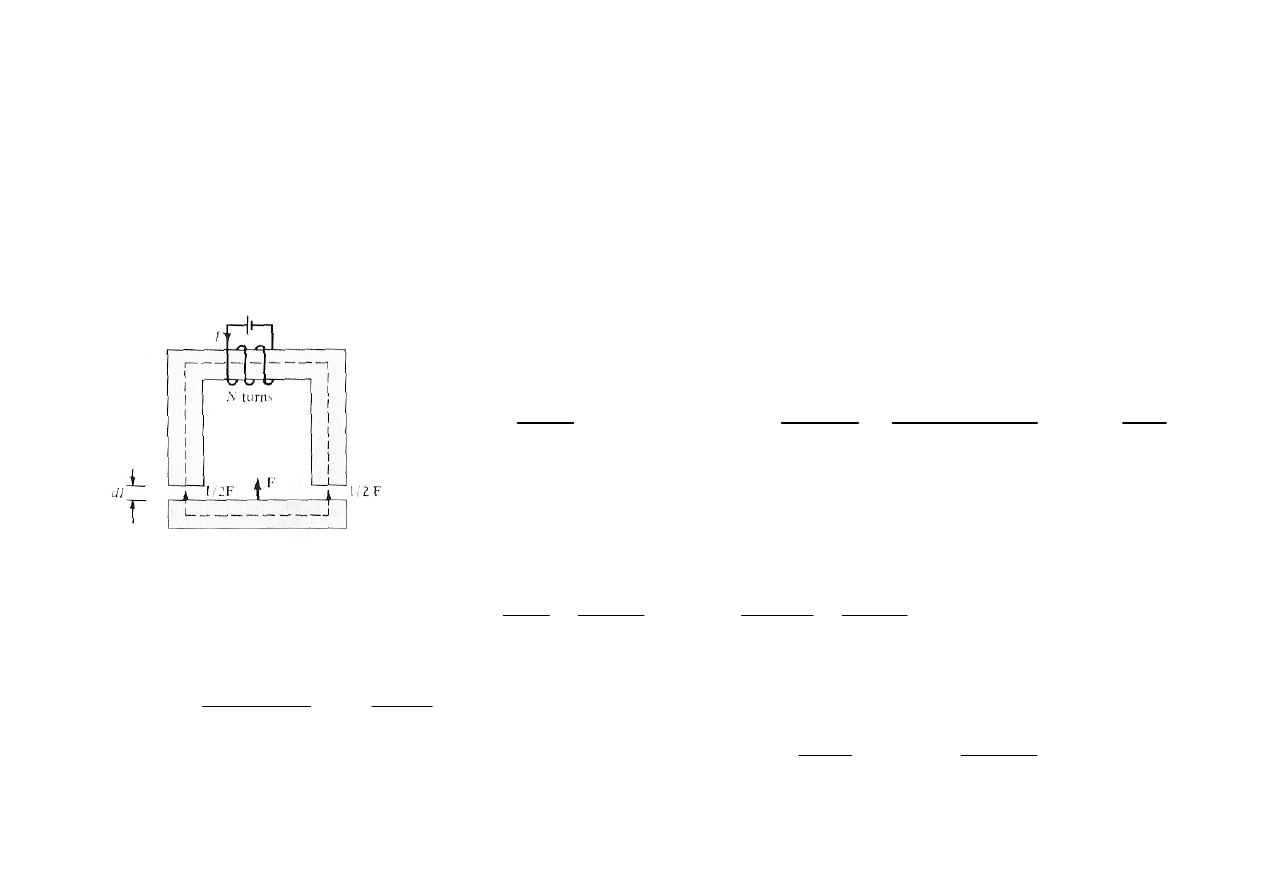
Przykład:
Elektromagnes w kształcie „U” ma dźwignąć masę 400kg ( razem z masą kotwicy
elektromagnesu ). Żelazne jarzmo ( µr=3000 ) ma przekrój 40 cm2 i średnią
długość 50 cm. Przerwa powietrzna wynosi 0,1 mm .
Zaniedbując reluktancję kotwicy obliczyć wymaganą liczbę zwoi cewki przy prądzie
wymuszającym 1 A.

7

4

2

2

400 9,8 4

10

0

2

40 10

0

2

1,11

2

p

p

B S

mg

Wb

F

mg

B

S

m

μ

μ

−

−

×

× Π×

×

=

=

⇒

=

=

=

z teorii obwodów magnetycznych:

(

)

p

NI

j

ε

=

= Φ ℜ + ℜ

6

6

0

0

6 10

5 10

,

48

48

p

j

p

j

r

l

l

S

S

μ

μ μ

⋅

⋅

ℜ =

=

ℜ =

=

Π

Π

6

6 5

p

p

j

NI

p

ε

ε

ℜ

=

=

ℜ + ℜ

+

ponieważ

0

0

11

162

6

p p

p p

p p

p

B l

B l

H l

N

zwoje

I

μ

μ

ε

=

=

⇒

=

−

Indukcyjność torów symetrycznych

N

1

2

3

0

2r

2

N

r

1N

a

2N

a

3N

a

12

a

23

a

31

a

1

1

2

2

3

3

N

N

A

I

B

I

C

I

N

A

B

C

I

I

I

I

=

+ +

l

Indukcyjność torów symetrycznych

Strumień okna: przewód 1; przewód N

1

2

3

1

1

0

12

31

ln

ln

ln

ln

2

2

2

2

N

N

N

N

A

B

C

N

N

N

a

a

a

a

l

l

l

l

I

I

I

I

r

a

a

r

μ

μ

μ

μ

Φ =

+

+

+

Π

Π

Π

Π

Symetryzacja toru

1

1

2

2

3

3

N

N

A

I

B

I

C

I

N

A

B

C

I

I

I

I

=

+ +

/ 3

l

/ 3

l

/ 3

l

A

I

A

I

B

I

B

I

C

I

C

I

Indukcyjność torów symetrycznych

Strumień między prądem fazy A a przewodem neutralnym

1

2

3

'

'

'

?

AN

N

N

N

Φ

= Φ + Φ

+ Φ

=

Cykliczna zmiana indeksów co l/3

1

2

3

1

1

0

12

31

'

ln

ln

ln

ln

6

6

6

6

N

N

N

N

A

B

C

N

N

N

a

a

a

a

l

l

l

l

I

I

I

I

r

a

a

r

μ

μ

μ

μ

Φ

=

+

+

+

Π

Π

Π

Π

2

3

1

2

2

0

23

12

'

ln

ln

ln

ln

6

6

6

2

N

N

N

N

A

B

C

N

N

N

a

a

a

a

l

l

l

l

I

I

I

I

r

a

a

r

μ

μ

μ

μ

Φ

=

+

+

+

Π

Π

Π

Π

3

1

2

3

3

0

31

23

'

ln

ln

ln

ln

6

6

6

2

N

N

N

N

A

B

C

N

N

N

a

a

a

a

l

l

l

l

I

I

I

I

r

a

a

r

μ

μ

μ

μ

Φ

=

+

+

+

Π

Π

Π

Π

stąd

1

2

3

1

2

3

1

2

3

1

2

3

3

3

0

12

23 31

12

23 31

ln

ln

ln

ln

6

6

6

2

N

N

N

N

N

N

N

N

N

N

N

N

A

B

C

N

AN

N

a a a

a a a

a a a

a a a

l

l

l

l

I

I

I

I

r

a a a

a a a

r

μ

μ

μ

μ

Φ

=

+

+

+

Π

Π

Π

Π

Indukcyjność torów symetrycznych

1

0

. Przy obciążeniu symetrycznym

0

0

120

240

;

;

0

j

j

B

A

C

A

N

I

I e

I

I e

I

−

−

=

=

=

12

23 31

1

6

3

0

ln

l

A

A

AN

a a a

I

L I

r

μ

Π

Φ

=

=

[ ]

3

12

23 31

1

2

0

ln

2

a a a

l

L

L

H

r

μ

=

=

Π

Indukcyjność toru dla składowej zgodnej
i przeciwnej

2

0

. Przy obciążeniu zerową kolejnością faz

0

0

;

3

A

B

C

N

I

I

I

I

I

I

=

=

=

=

6

1

2

3

0

0

6

3 9

2

0

12

23 31

(

)

ln

(

)

l

N

N

N

A

AN

N

a a a

I

L I

r r a a a

μ

Π

Φ

=

=

[ ]

2

1

2

3

0

2

2

3

3

0

12

23 31

(

)

ln

(

)

l

N

N

N

A

N

a a a

L

I

H

r r a a a

μ

Π

=

Indukcyjność toru dla składowej
symetrycznej zerowej

Ruch ładunku w jednorodnym polu magnetycznym

×

×

×

×

×

×

q

B

v

ma

qv B

=

×

d v

m

qv B

dt

=

×

Zakładamy, że

(0, 0,

)

z

B

B

=

(

)

,

,

,

, 0

y

x

z

y

z

x

z

dv

dv

dv

m

m

m

q v B

v B

dt

dt

dt

⎛

⎞

=

−

⎜

⎟

⎝

⎠

1)

2)

3)

0

0

x

y

z

x

x

z

z

z

dv

m

qv B

dt

dv

m

qv B

dt

dv

m

v

konst

dt

=

= −

= ⇒

=

=

z 1)

x

y

z

dv

m

v

qB dt

=

i wstawiamy do 2)

2

2

2

2

x

z

x

z

z

d v

qB

m

qv B

qB

dt

m

= −

2

2

2

2

2

0

x

z

x

d v

q B

v

dt

m

+

=

Ruch ładunku w jednorodnym polu magnetycznym

jeżeli oznaczymy

2

2

0

0

2

0

x

z

x

d v

qB

v

m

dt

ω

ω

=

⇒

+

=

równanie to ma rozwiązanie

1

0

2

0

sin

cos

x

v

A

t

A

t

ω

ω

=

+

1

0

2

0

0

1

cos

sin

x

y

dv

v

A

t

A

t

dt

ω

ω

ω

=

=

−

współczynniki A

1

i A

2

wyznaczamy z warunków początkowych,

np. jeśli dla t=0

0

0

0

0

(0)

( , 0, 0)

(cos

, sin

, 0)

v

v

v

v

t

t

ω

ω

=

⇒

=

−

czyli rozpatrywana cząstka porusza się ze stałą prędkością v

0

po leżącym na

płaszczyźnie xy okręgu o promieniu R=v

0

/ω

0

Jeżeli cząstka ma niezerową składową v

z

to tor ruchu cząstki staje się linią śrubową

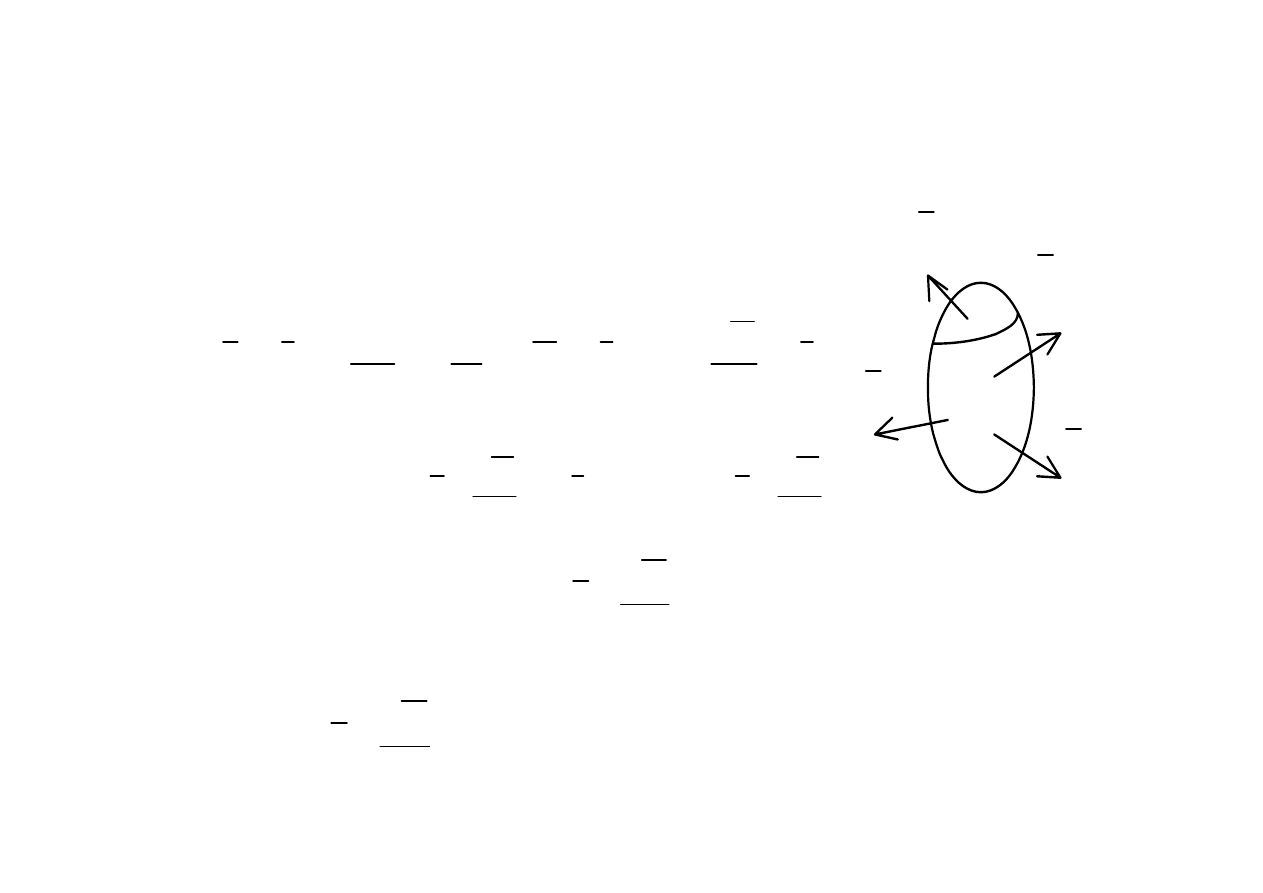
Pole elektromagnetyczne

Pojęcie prądu przesunięcia

( )

S V

j

j

j

j

prąd wypływający z zamkniętej powierzchni S(V) wynosi:

( )

( )

( )

S V

S V

S V

dQ

d

D

j d s

D d s

d s

dt

dt

t

∂

= −

= −

= −

∂

∫

∫

∫

o

o

o

stąd

( )

0

S V

V

D

D

j

d s

div j

dv

dt

dt

⎛

⎞

⎛

⎞

∂

∂

+

= =

+

⎜

⎟

⎜

⎟

⎝

⎠

⎝

⎠

∫

∫

o

Z dowolności V wynika

0

D

div j

dt

⎛

⎞

∂

+

=

⎜

⎟

⎝

⎠

Czyli, wektor

D

j

dt

∂

+

- jest bezźródłowy ( o wymiarze A/m

2

)

Całkując równanie po dowolnej powierzchni S

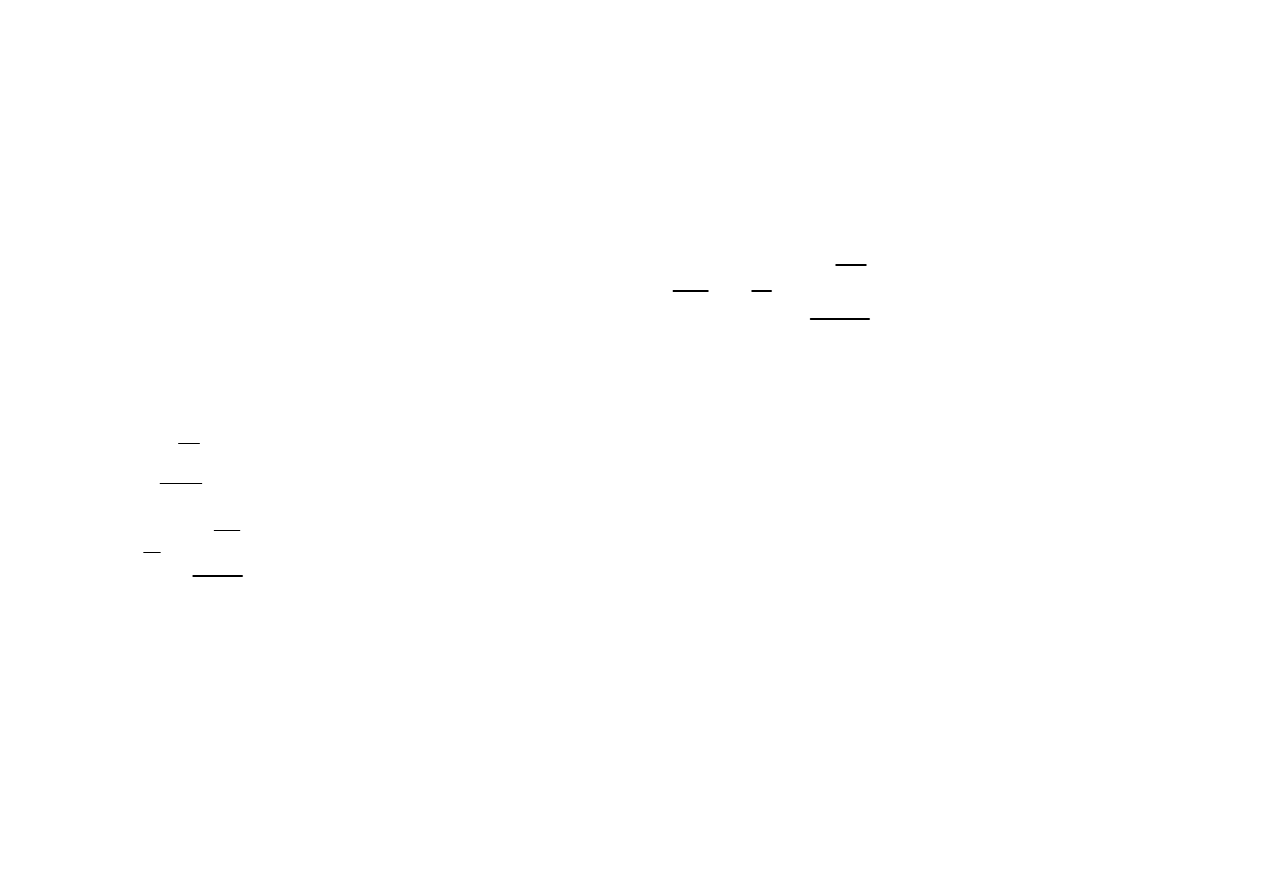
Pole elektromagnetyczne

Maxwell zaproponował rozszerzenie prawa przepływu dla pól zmiennych o
składową prądu przesunięcia

D

rot H

j

t

∂

= +

∂

co stanowi uogólnienie prawa przepływu dla magnetostatyki

D

t

∂

∂

- gęstość prądu przesunięcia

D

j

t

∂

+

∂

- gęstość prądu całkowitego

Jest to II równanie Maxwella dla pól elektromagnetycznych

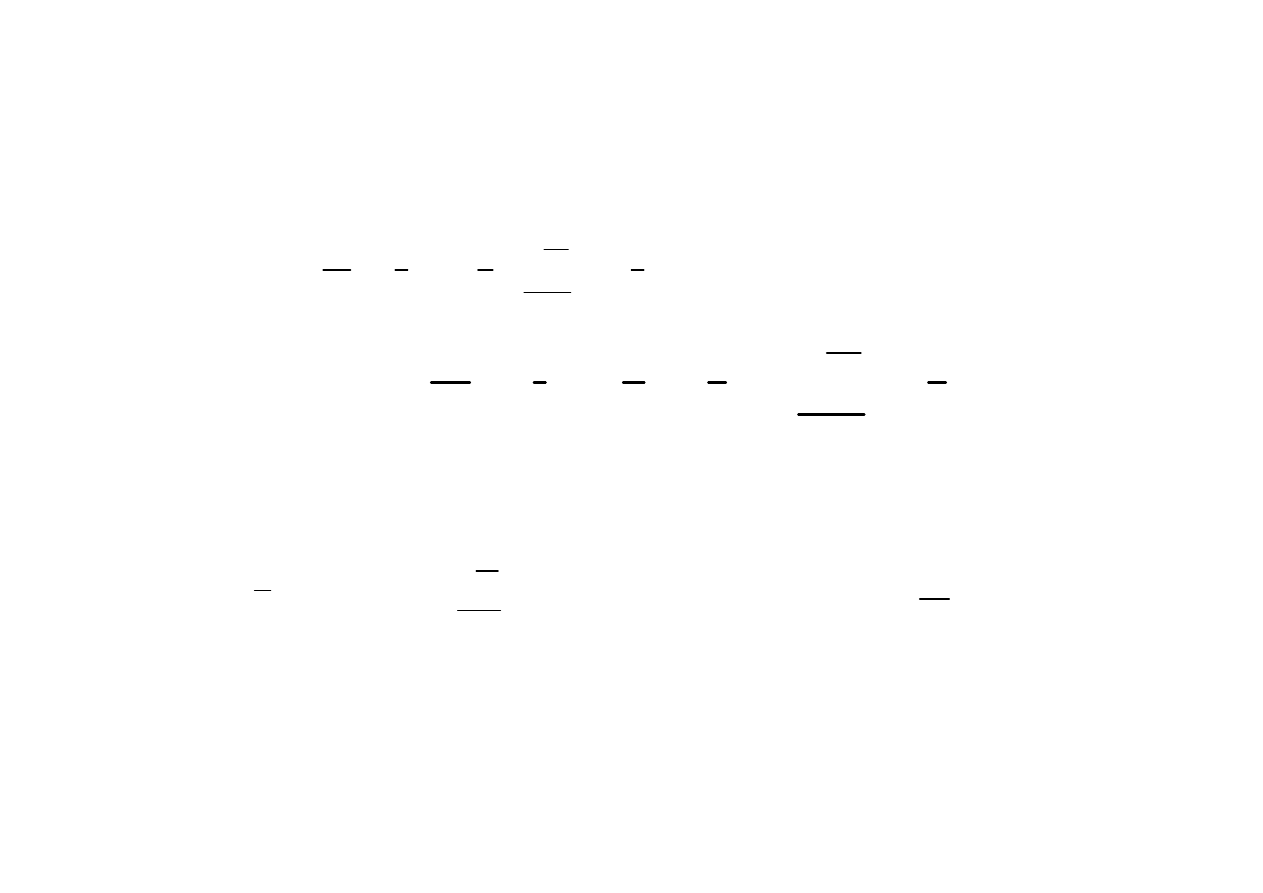
Pole elektromagnetyczne

otrzymamy całkową postać II równania Maxwella

S

S

D

rot H d s

j

d s

czyli

t

⎛

⎞

∂

=

+

⎜

⎟

∂

⎝

⎠

∫

∫

o

o

( )

L S

S

S

D

H d l

j d s

d s

t

∂

=

+

∂

∫

∫

∫

o

o

o

Prąd transportu

Prąd przesunięcia

gdy

0

j

=

to przy

0

D

t

∂

≠

∂

pole H jest wirowe

0

rot H

≠

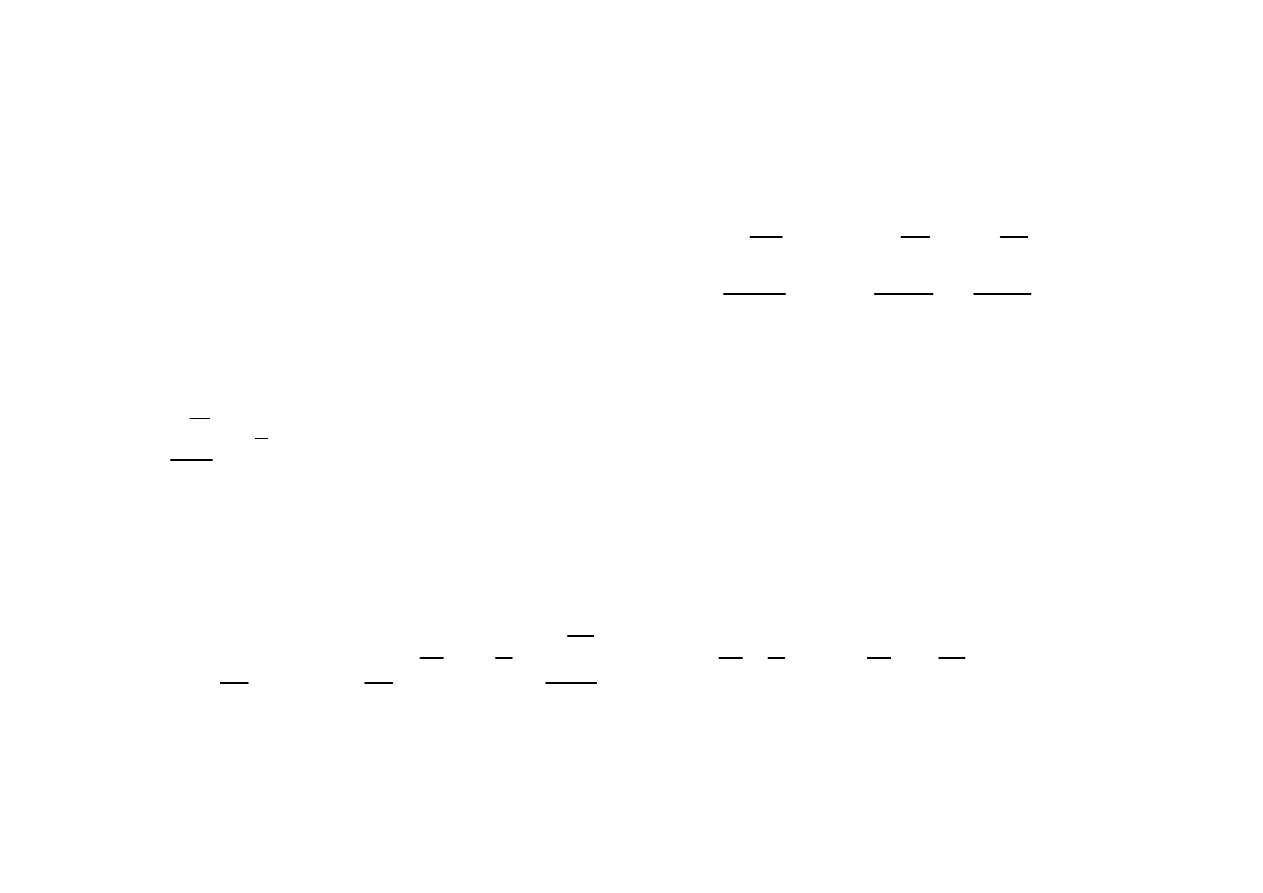
Prąd polaryzacji i straty energii w dielektryku

Prąd przesunięcia składa się z dwóch części

0

D

E

P

t

t

t

ε

∂

∂

∂

=

+

∂

∂

∂

S

P

d s

t

∂

∂

∫

o

-prąd polaryzacji związany z przemieszczaniem i obrotem dipoli
- w próżni jest on zerowy
-ze wzrostem częstotliwości rośnie składowa prądu polaryzacji

obroty dipoli związane są ze stratami energii
Np. dla kondensatora płaskiego w jednostce objętości

1

1

D

uidt

El

j

Sdt

E

jdt

E d D

V

V

t

⎛

⎞

∂

=

+

=

+

⎜

⎟

∂

⎝

⎠

∫

∫

∫

∫

o

o

o

Ciepło Joule’a

Energia pobrana
przez pole w materii

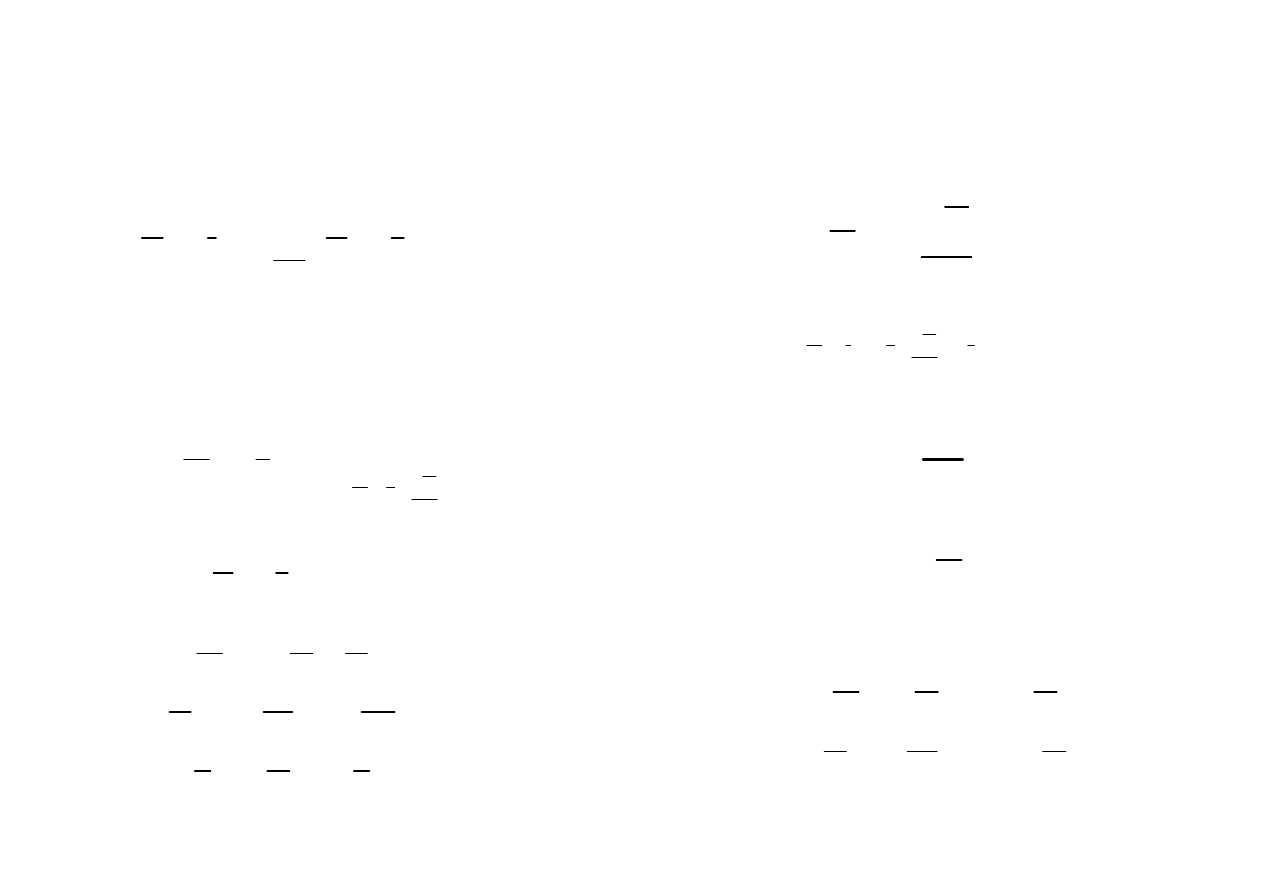
Równania Maxwella

D

rot H

j

t

∂

= +

∂

( )

(

)

L S

S

D

H d l

j

d s

t

∂

=

+

∂

∫

∫

o

o

Postać całkowa

Postać różniczkowa

I równanie Maxwella

( )

L S

S

d

E d l

B d s

dt

= −

∫

∫

o

o

B

rot E

t

∂

= −

∂

II równanie Maxwella

III równanie Maxwella

( )

v

S V

V

D d s

q dv

=

∫

∫

o

v

divD

q

=

IV równanie Maxwella

( )

0

S V

B d s

=

∫

o

0

divB

=

Równania materiałowe

0

0

0

v

D

E

P

B

H

M

j

E

q u

ε

μ

μ

γ

=

+

=

+

=

+

0

0

r

r

D

E

E

B

H

E

ε

ε ε

μ

μ μ

=

=

=

=

Warunki brzegowe

2

1

2

1

t

t

n

n

H

H

K

B

B

−

=

=

1

2

1

2

1

2

1

2

0

n

H

n

H

K

n

D

n

D

×

+ ×

=

+

=

o

o

1

2

2

1

t

t

s

n

n

E

E

q

j

j

t

=

∂

−

= −

∂

Pole elektryczne

1

2

2

1

t

t

n

n

s

E

E

D

D

q

=

−

=

1

2

1

2

1

2

1

2

0

s

n

E

n

E

n

D

n

D

q

×

+ ×

=

+

=

o

o

Pole magnetyczne

Pole przepływowe

1

2

1

2

1

2

1

2

0

s

n

E

n

E

q

n

j

n

j

t

×

+ ×

=

∂

+

= −

∂

o

o

Wektor Poyntinga

V

dV

Energia pobrana przez obszar dV
przez czas dt

(

)

dW

E

jdt

H d B

E d D dV

=

+

+

o

o

o

B

D

dW

E

j

H

E

dVdt

t

t

⎛

⎞

∂

∂

=

+

+

⎜

⎟

∂

∂

⎝

⎠

o

o

o

Moc pobierana przez element dV

dW

B

D

E

j

H

E

dV

dt

t

t

⎛

⎞

∂

∂

=

+

+

⎜

⎟

∂

∂

⎝

⎠

o

o

o

a przez cały obszar V

V

B

D

P

E

j

H

E

dV

t

t

⎛

⎞

∂

∂

=

+

+

⎜

⎟

∂

∂

⎝

⎠

∫

o

o

o

(

)

(

)

(

)

B

D

E

j

H

E

E

j

H

rot E

E

rot H

j

t

t

Erot H

Hrot E

div E H

⎛

⎞

∂

∂

+

+

=

+

−

+

−

=

⎜

⎟

∂

∂

⎝

⎠

=

−

= −

×

o

o

o

o

o

o

Wektor Poyntinga

(

)

(

)

( )

V

S V

P

div E H dV

E H

d s

= −

×

= −

×

∫

∫

o

Moc wyprowadzenia energii poza obszar V

(

)

( )

S V

P

E H

d s

− =

×

∫

o

Strumień wektora

(

)

E H

×

Jest mocą wypromieniowaną z obszaru V

Wektor

(

)

E H

Π =

×

- wektor Poyntinga - wektor gęstości mocy [ W/m

2

]

V

dV

Transport mocy w kablu jedno żyłowym

koncentrycznym

×

I

⊗

E

H

Π

2

1

sin 90

2

ln

o

U

I

E H

EH

EH

R

r

r

R

Π = ×

=

=

=

Π

(

)

2

2

1

1

2

2

2

2

0

1

1

2

ln

ln

R

R

S

R

R

UI

UI

dr

E H

d s

rdrd

UI

P

moc

R

R

r

r

R

R

ϕ

Π

×

=

=

=

= =

Π

∫

∫ ∫

∫

o

2

2

2

3

1

1

1

1

1

1

2

2

2

I

I

I

I

EH

j

R

R

R

R

γ

γ

γ

=

=

=

Π

Π

Π

Π

2

2

2

1

1

2

3

2

1

1

2

2

2

S

I

l

EHds

EH

R l

R l

I

RI

R

R

γ

γ

=

Π

=

Π

=

=

Π

Π

∫

j

E

H

l

Π

Energia płynie do odbiornika przez przestrzeń otaczającą przewody
i częściowo dopływa ( jest tracona na ciepło ) do wnętrza przewodu

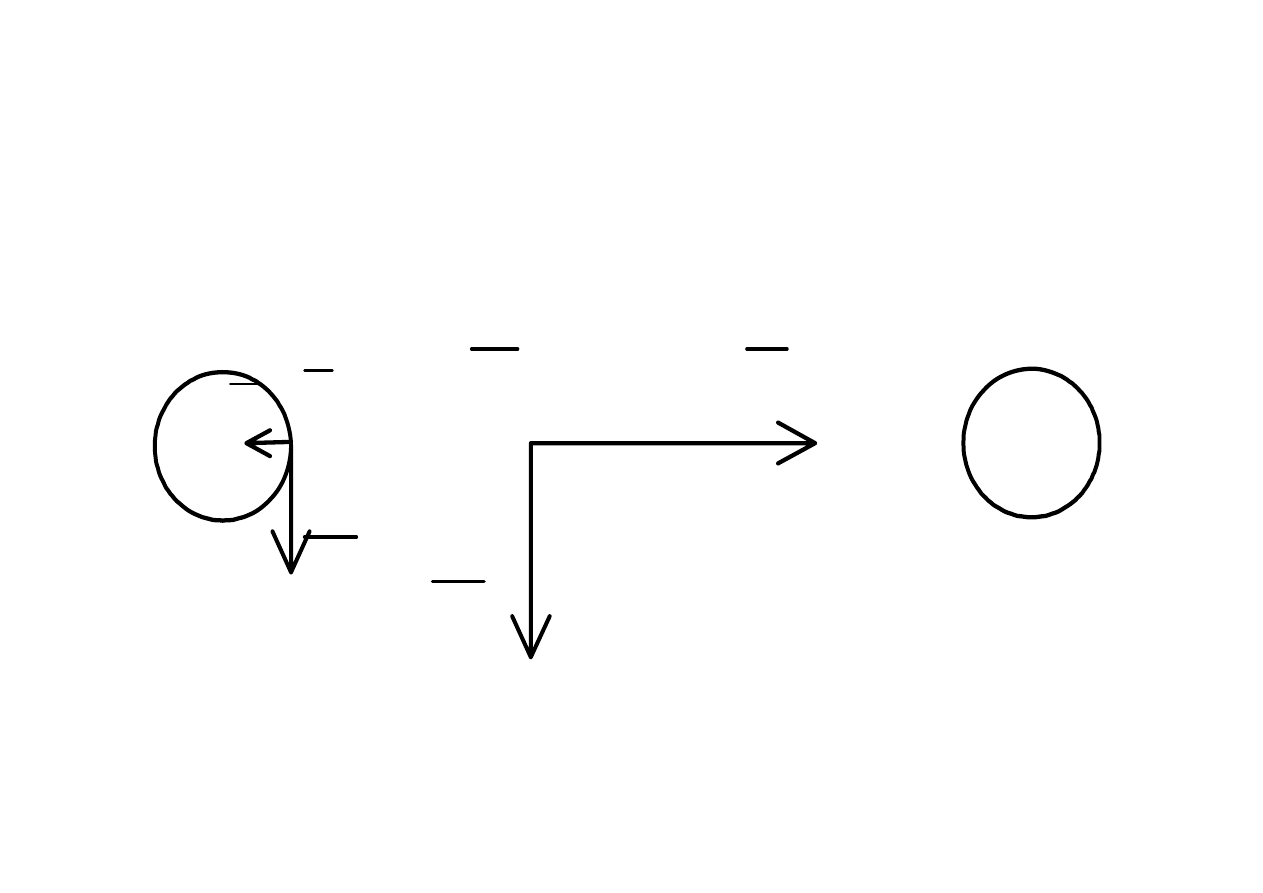
Linia 2 przewodowa

×

•

⊗

E

H

Π

⊗

H

Π

E