zadanie

l

a

=l

b

=977mm, l

c

=343mm, l

s

=0,7621mm,

d=89 mm

1)

Θ

=200A,

µ

r

=4000

→

B

s

=0,13 T

2) B’

s

=0,2T,

µ

r

=4000

→

Θ

= 311 Azwoi

3) B’

s

=0,2T

→

Θ

= 369 Azwoi

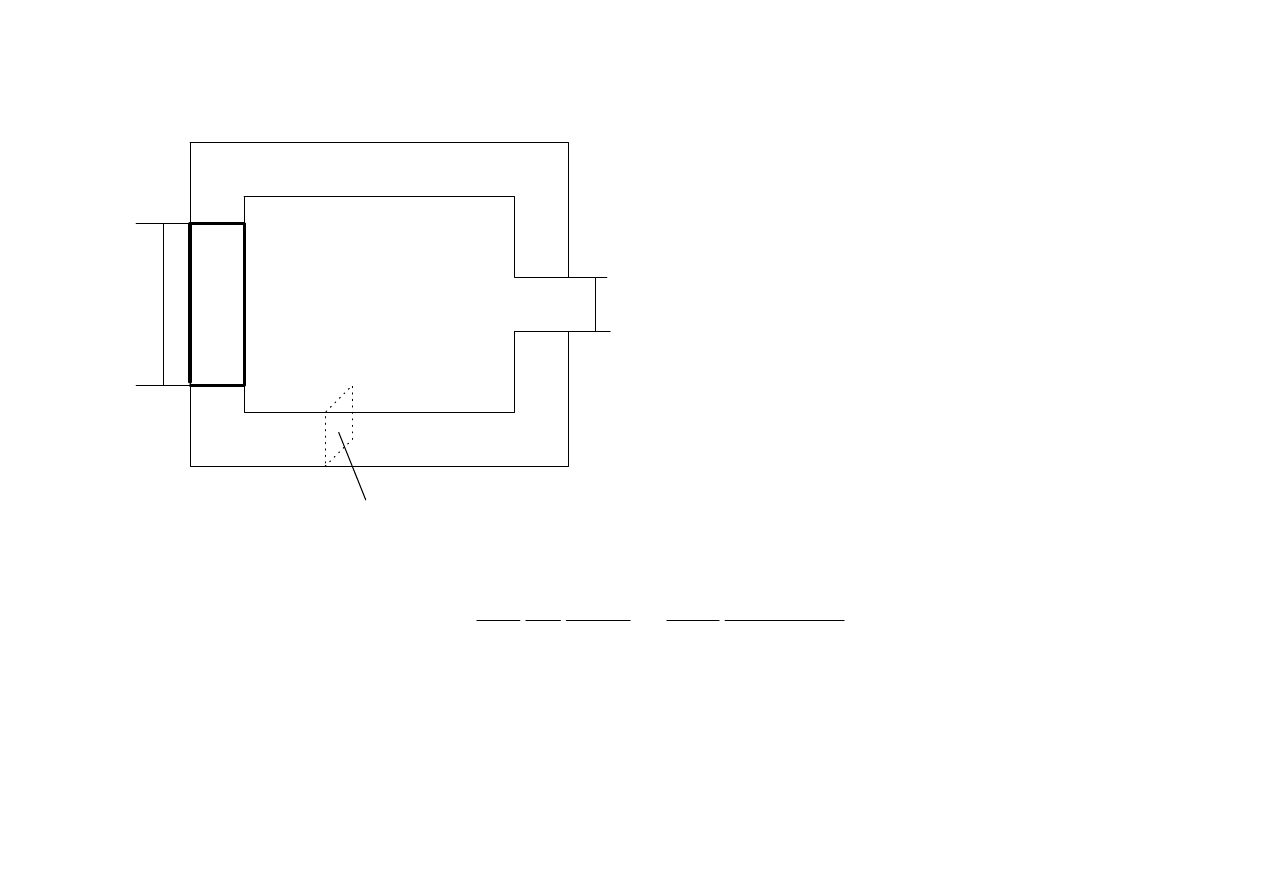
Obwody magnetyczne z magnesem trwałym

δ

m

l

m

S

N

S

Dane: B

p

, S

p

,

δ

Materiał na magnes trwały jest bardzo
drogi, wi

ę

c szukamy V

m

=S

m

l

m

=min

Prawo przepływu:

H

m

l

m

+H

p

δ

=0

Obwód jednooczkowy,to

B

m

S

m

=B

p

S

p

St

ą

d:

2

0

0

min

(

)

p

p

P

P

P

m

m

m

m

m

m

m

B

S

B S

B

V

l S

H

B

H B

δ

δ

µ

µ

=

= −

=

=

−

Kiedy (-H

m

B

m

)=max

Obwody magnetyczne z magnesem trwałym

B

m

B

m

H

H

K

H

R

B

B

m

B

m

m

H B

R

B

St

ą

d, dla takiego punktu pracy uzyskujemy V

m

=min

Indukcja Elektromagnetyczna

Eksperymenty Oersted’a

i innych pokazały,

ż

e „ elektryczno

ść

mo

ż

e by

ć

ź

ródłem magnetyzmu”

Wprowadzili prawa rz

ą

dz

ą

ce polem

magnetycznym zwi

ą

zanych z

przepływem pr

ą

du.

Zmian

ę

strumienia mo

ż

na uzyska

ć

na wiele sposobów:

Przeprowadzono wiele eksperymentów ( bez sukcesu ), które miały potwierdzi

ć

istnienie

efektu odwrotnego. Spodziewano si

ę

uzyska

ć

pr

ą

d stały.

W 1831 roku Faraday pokazał,

ż

e w zamkni

ę

tym obwodzie elektrycznym

płynie pr

ą

d przej

ś

ciowy je

ż

eli

strumie

ń

magnetyczny zwi

ą

zany z obwodem

zmienia si

ę

.

N

S

)

2

)

1

S

N

1) wł

ą

cz/wył

ą

cz zasilanie

2) poruszanie magnesem trwałym

Indukcja Elektromagnetyczna

-

Rozwa

ż

my poruszaj

ą

cy si

ę

przewód w si

ę

stałym polu magnetycznym.

Siła działaj

ą

ca na ładunek w przewodzie:

(

)

F

q u B

=

×

Siła ta na jednostk

ę

ładunku stanowi składow

ą

ź

ródłow

ą

nat

ęż

enia pola elektrycznego

zr

F

E

u B

q

=

= ×

Mo

ż

na stwierdzi

ć

do

ś

wiadczalnie,

ż

e składowa

ź

ródłowa jest ogólnie ró

ż

na od zera

( )

(

)

0

zr

L s

L

e

E

d l

u B

d l

=

=

×

≠

∫

∫

Nazywa si

ę

indukowan

ą

sił

ą

elektromotoryczn

ą

e=e(t) -

ogólnie zmienna w czasie

Indukowane

ź

ródłowe pole elektryczne jest wirowe

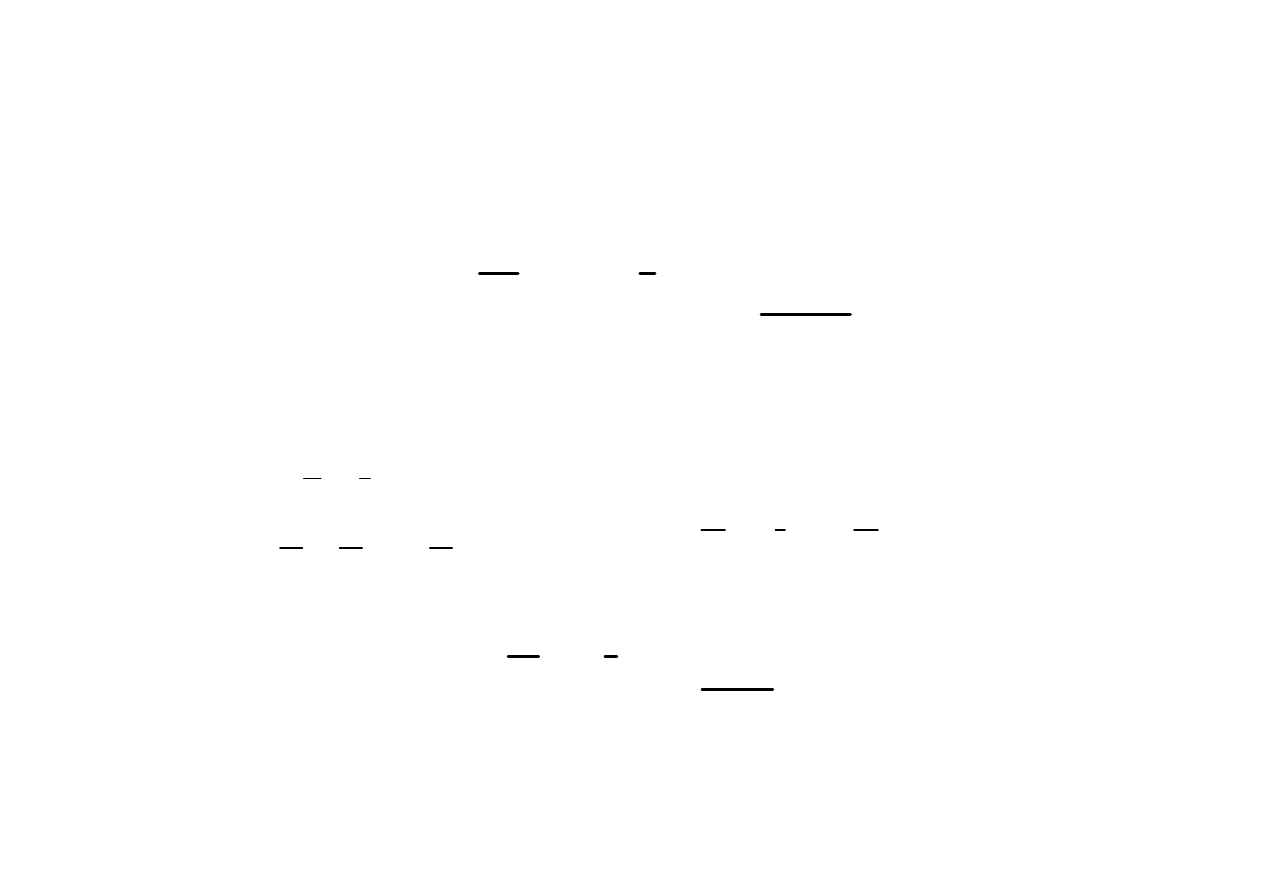
Indukcja Elektromagnetyczna

Mo

ż

na

ś

ci

ś

le udowodni

ć

,

ż

e indukowana siła elektromotoryczna w zamkni

ę

tym

poruszaj

ą

cym si

ę

przewodzie jest równa:

( )

zr

L S

d

e

E

d l

dt

Φ

=

= −

∫

gdzie

S

B d s

Φ =

∫

strumie

ń

indukcji magnetycznej skojarzony z obwodem L

Ogólnie:

pot

zr

E

E

E

=

+

zatem

zr

L

L

E d l

E

e

=

=

∫

∫

czyli

L

d

E d l

dt

Φ

= −

∫

Prawo indukcji magnetycznej – prawo Faraday’a

Indukcja Elektromagnetyczna

Φ

ր

( )

e t

( )

i t

Nie jest istotne co jest przyczyn

ą

zmiany strumienia:

-poruszaj

ą

cy si

ę

przewód

-zmienne pole magnetyczne
-kombinacja tych dwóch składników

Reguła Lenza

Ka

ż

dej zmianie strumienia towarzyszy indukowanie si

ę

siły elektromotorycznej,

która w zamkni

ę

tym obwodzie wywołuje pr

ą

d przeciwdziałaj

ą

cy zachodz

ą

cym

zmianom.

Φ

ց

( )

e t

( )

i t

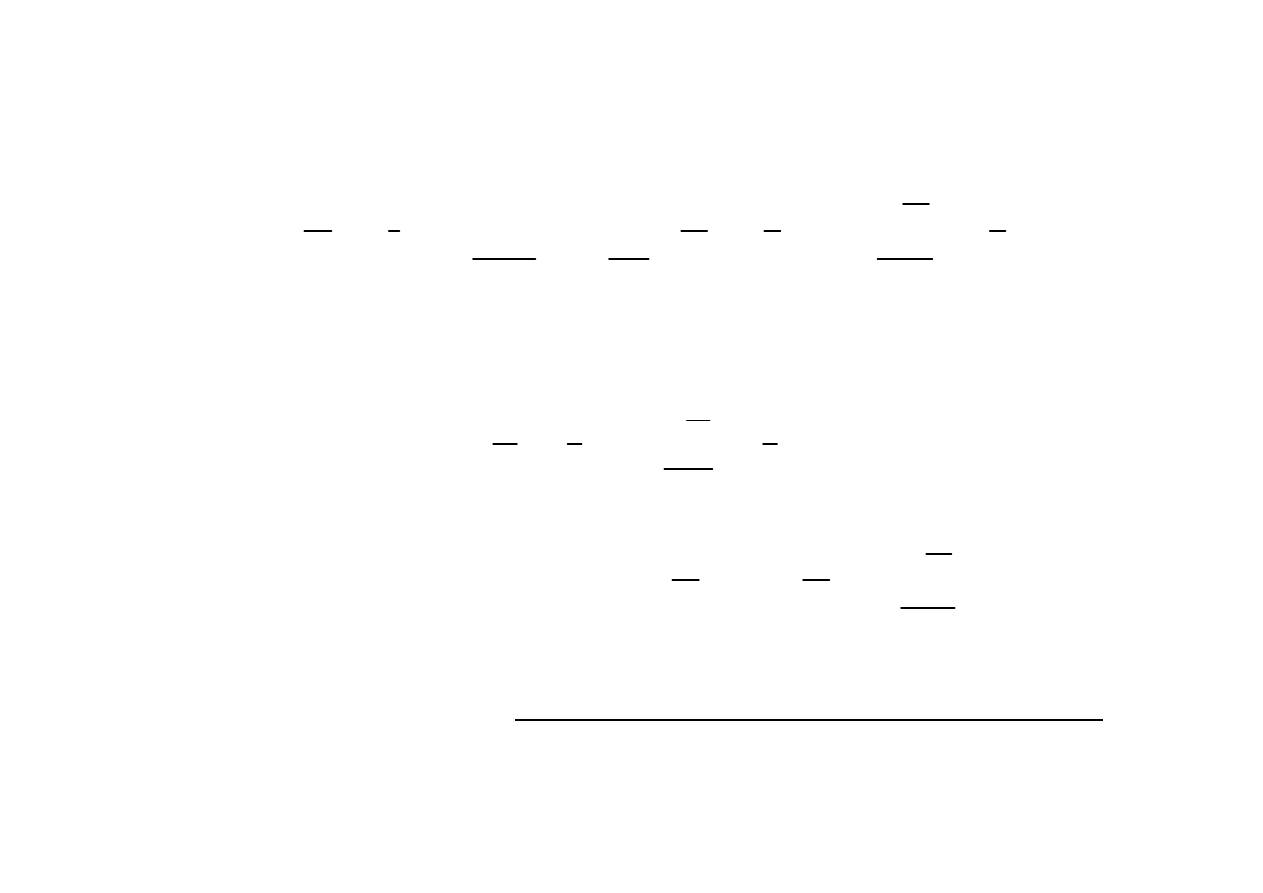
Indukcja Elektromagnetyczna

mo

ż

na napisa

ć

( )

L S

S

S

d

d

B

E d l

B d s

d s

dt

dt

t

Φ

∂

= −

= −

= −

∂

∫

∫

∫

korzystaj

ą

c z twierdzenia Stokes’a

S

S

B

rot E d s

d s

t

∂

= −

∂

∫

∫

a z dowolno

ś

ci powierzchni S

B

rot E

E

t

∂

= ∇× = −

∂

ró

ż

niczkow

ą

posta

ć

prawa indukcji magnetycznej

W obecno

ś

ci zmiennego pola magnetycznego pole elektryczne jest wirowe

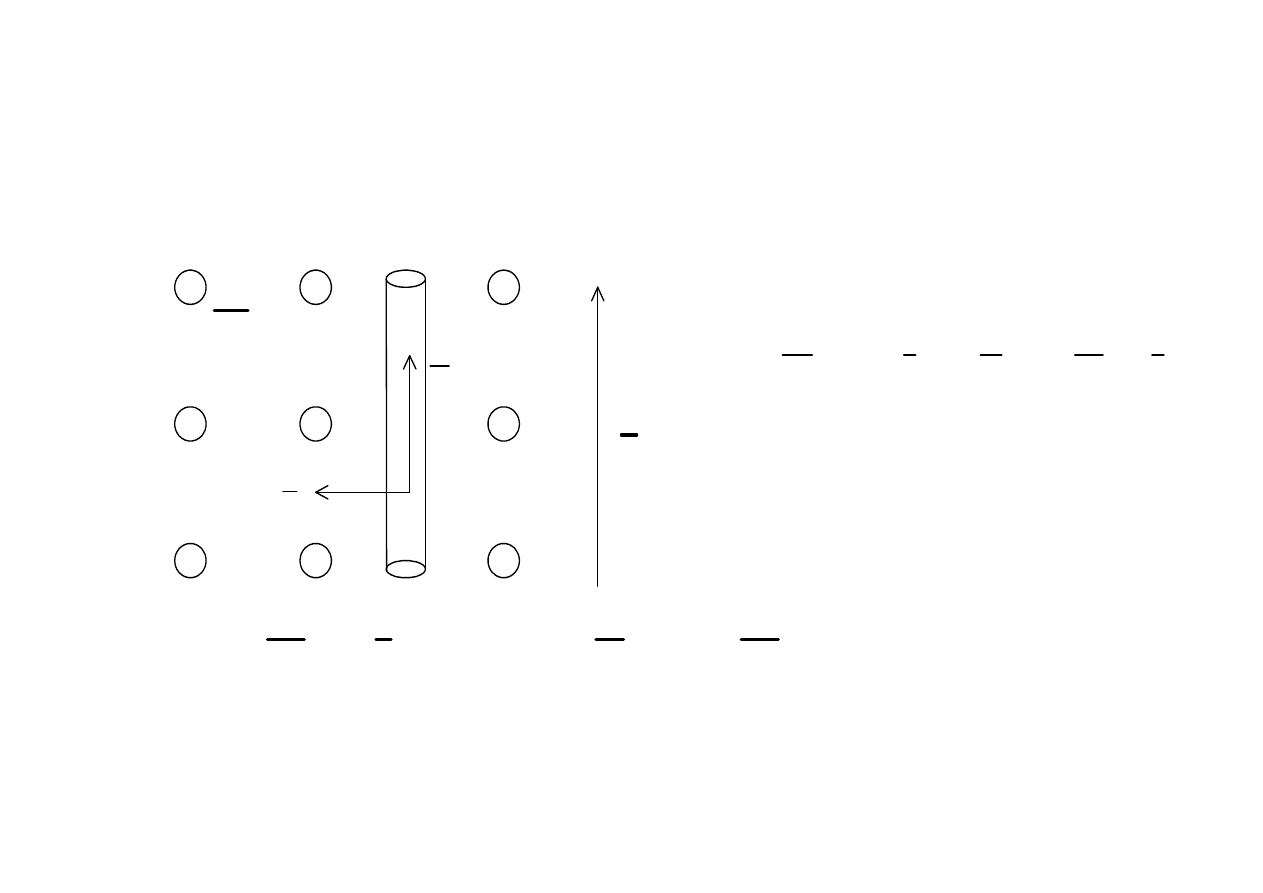
Pr

ą

dnicowa reguła prawej dłoni

•

•

•

•

•

•

•

•

•

B

pr

u

zr

E

l

W odcinku l indukuje si

ę

siła

elektromotoryczna indukcji e

(

)

zr

pr

e

E

d l

u

B

l

=

×

∫

≃

gdy

pr

B

l

i

u

B

e

uBl

⊥

⊥

⇒

=

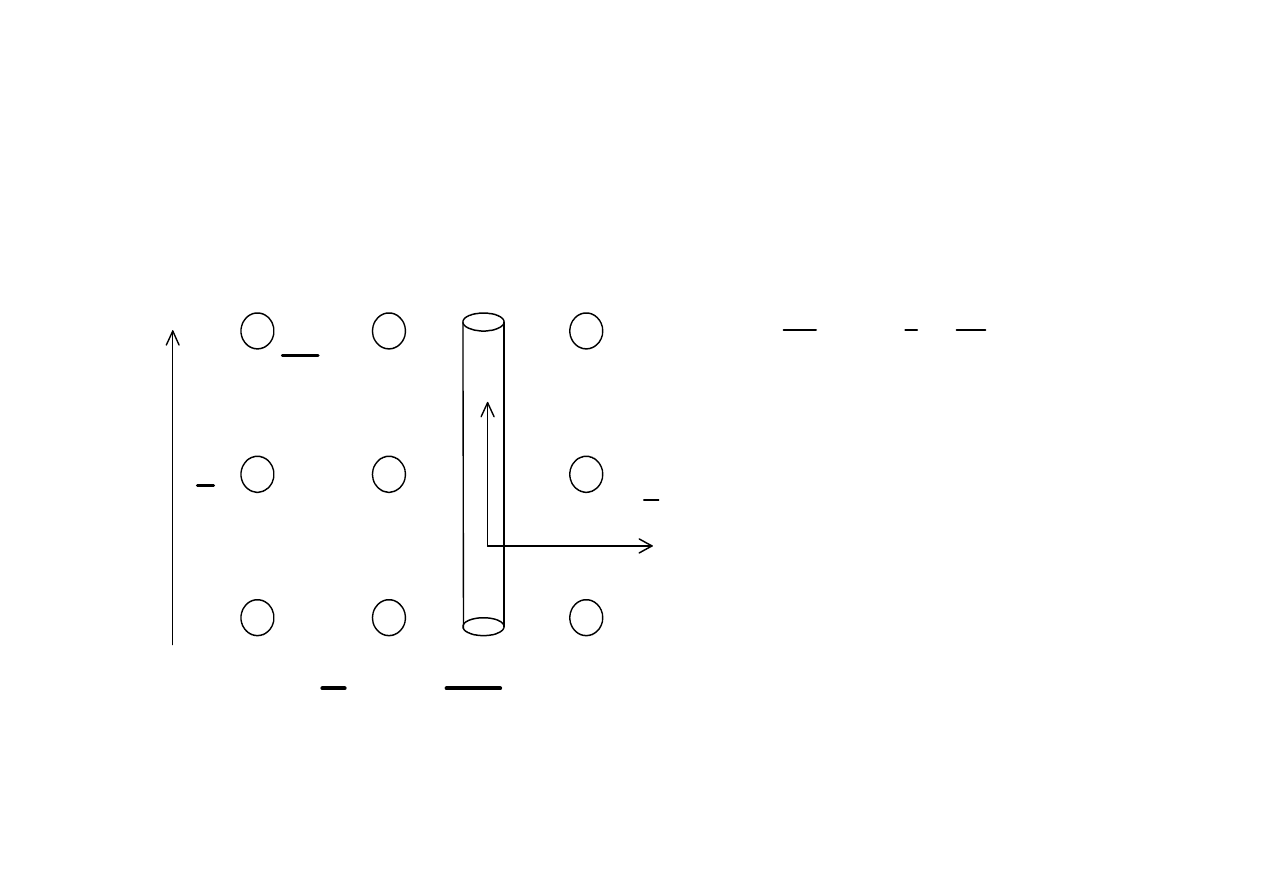
Silnikowa reguła lewej dłoni

Je

ż

eli przez przewód płynie pr

ą

d I, to wtedy na przewód działa siła mechaniczna

•

•

•

•

•

•

•

•

•

B

l

F

I

(

)

F

I l B

=

×

gdy

l

B

F

IlB

⊥

⇒

=

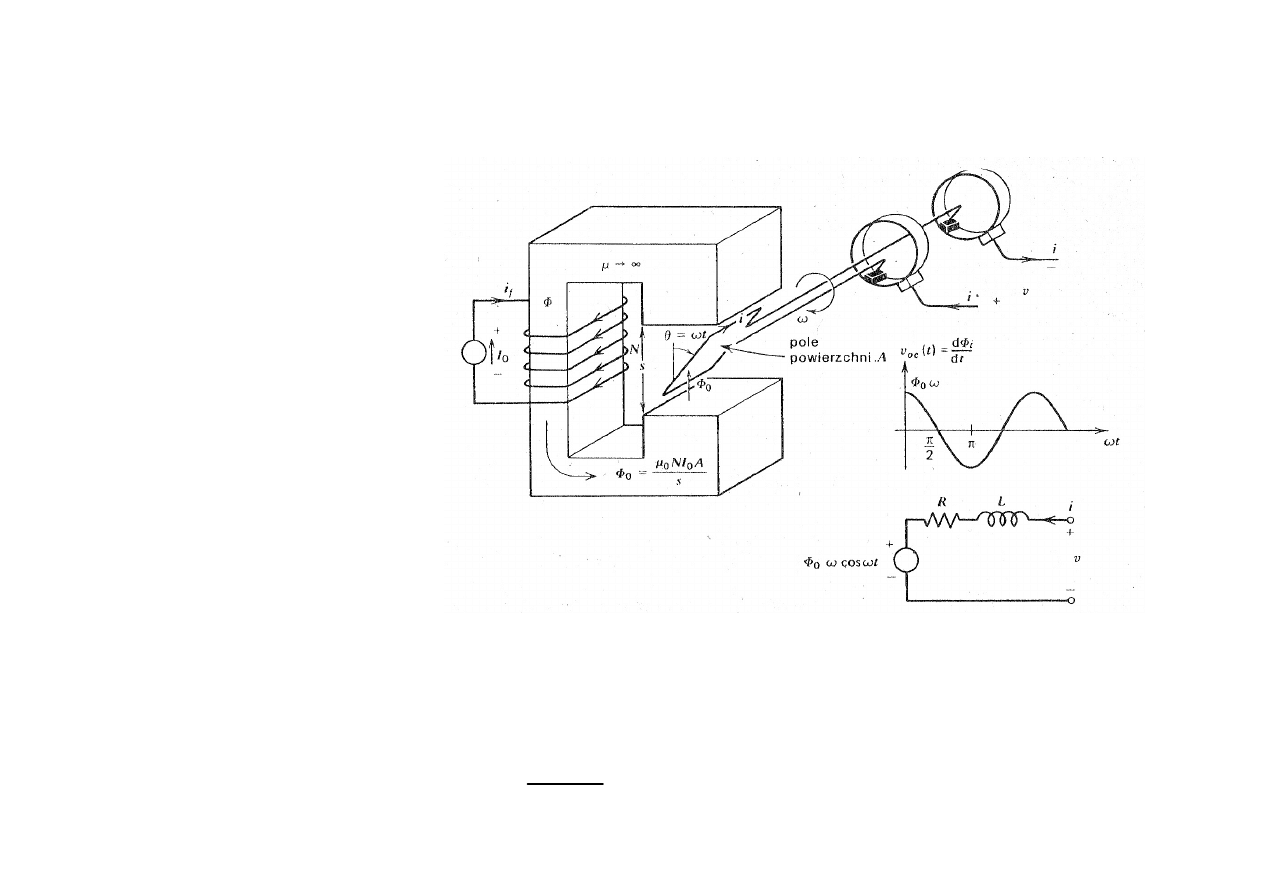
Pr

ą

dnica pr

ą

du przemiennego

0

sin t

ω

Φ = Φ

Zgodnie z prawem Faraday’a

0

( )

cos

e t

t

ω

ω

= Φ

Napi

ę

cie na zaciskach pr

ą

dnicy

0

( )

( )

( )

cos

di t

v t

i t R

L

t

dt

ω

ω

=

+

+ Φ

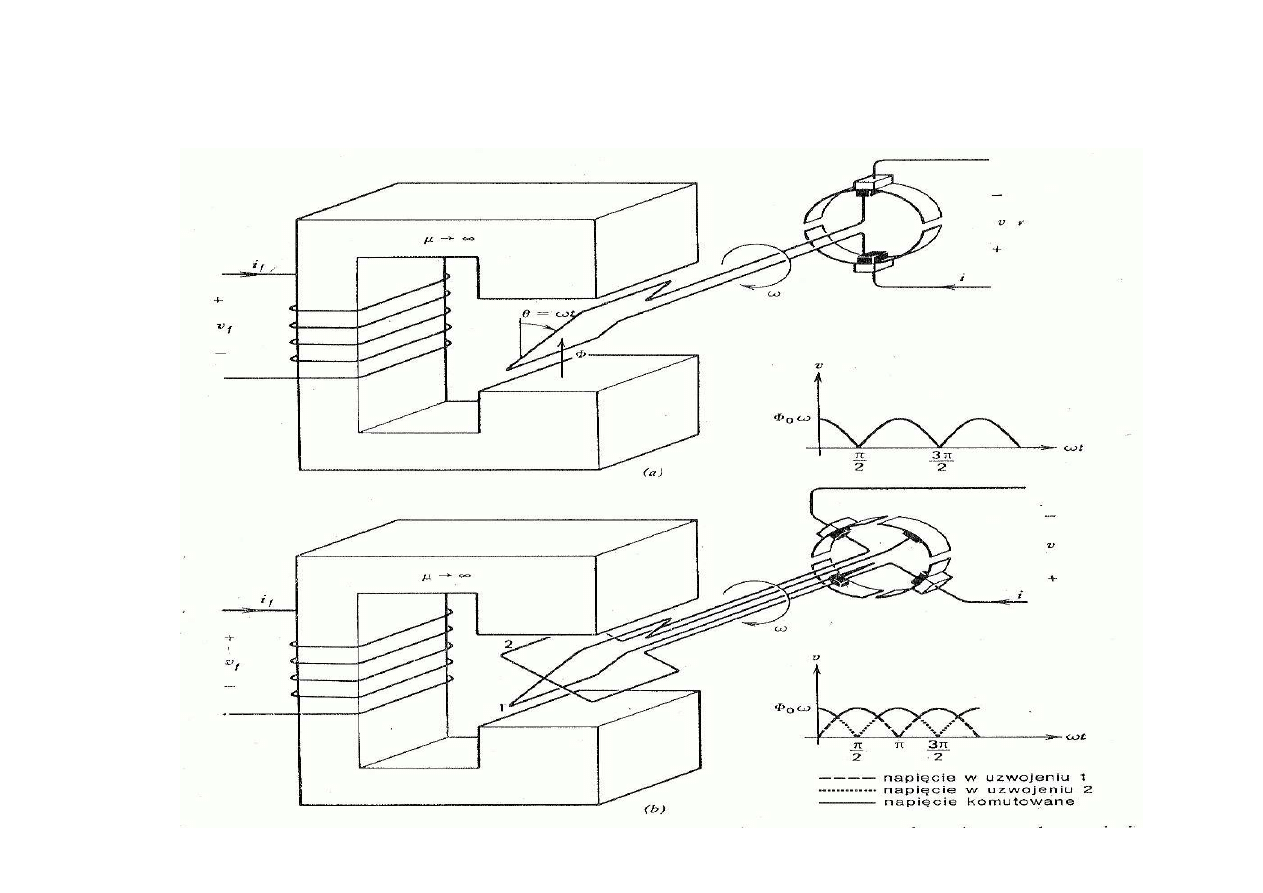
Pr

ą

dnica pr

ą

du stałego

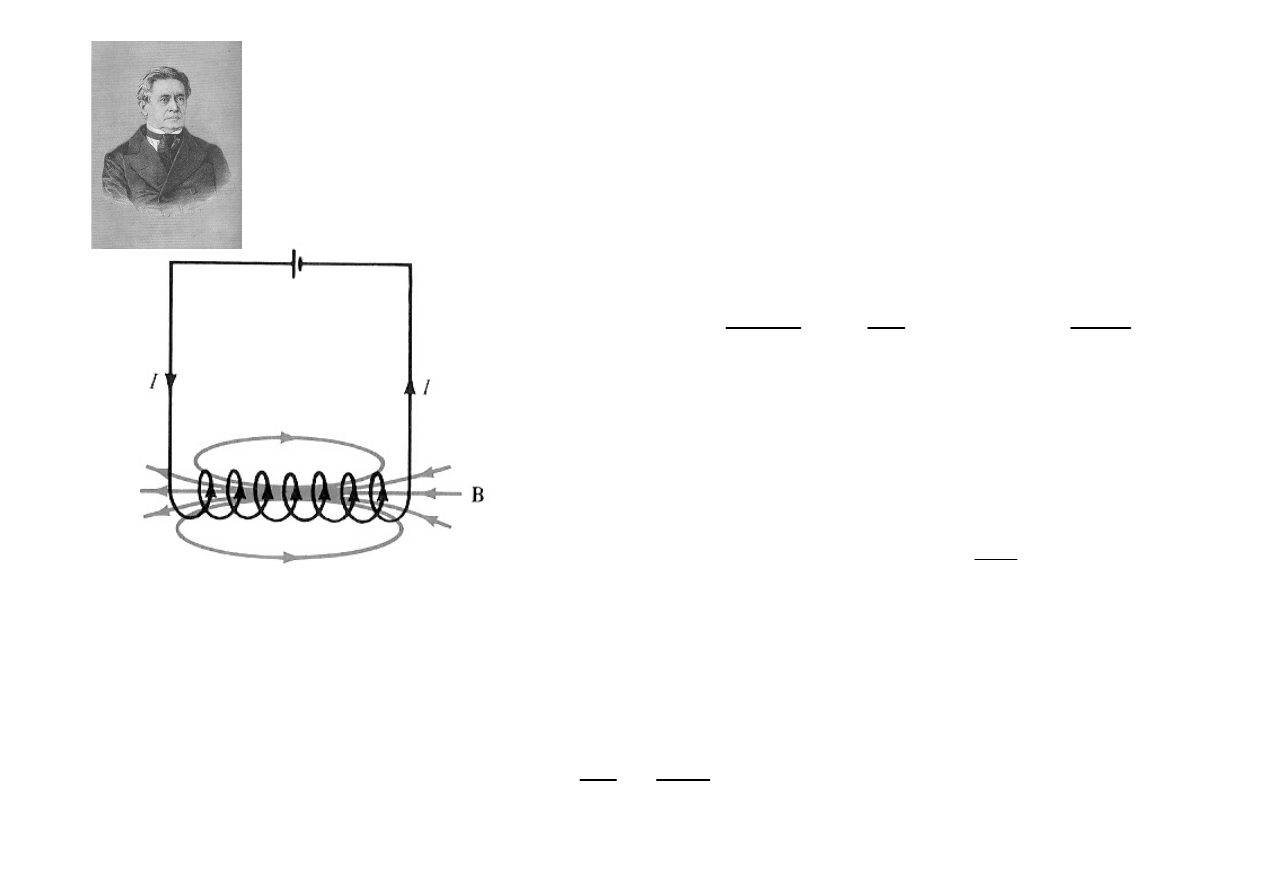
Indukcyjno

ść

własna

Siła indukowana w cewce wielozwojowej jest sum

ą

poszczególnych sił elektromotorycznych

k

k

k

d

d

d

e

e

dt

dt

dt

Φ

Ψ

=

= −

= −

Φ = −

∑

∑

∑

k

Ψ =

Φ

∑

-Strumie

ń

skojarzony cewki

zwojowej

w przypadku gdy

1

2

k

Φ = Φ = ⋅⋅⋅ = Φ = Φ

to

d

e

n

dt

Φ

= −

Strumie

ń

skojarzony cewki jest proporcjonalny do pr

ą

du

~

lub

I

LI

Ψ ∝

Ψ =

Współczynnik proporcjonalno

ś

ci nazywamy indukcyjno

ś

ci

ą

własn

ą

cewki

[ ]

1

L

H

=

n

L

I

I

Ψ

Φ

=

=

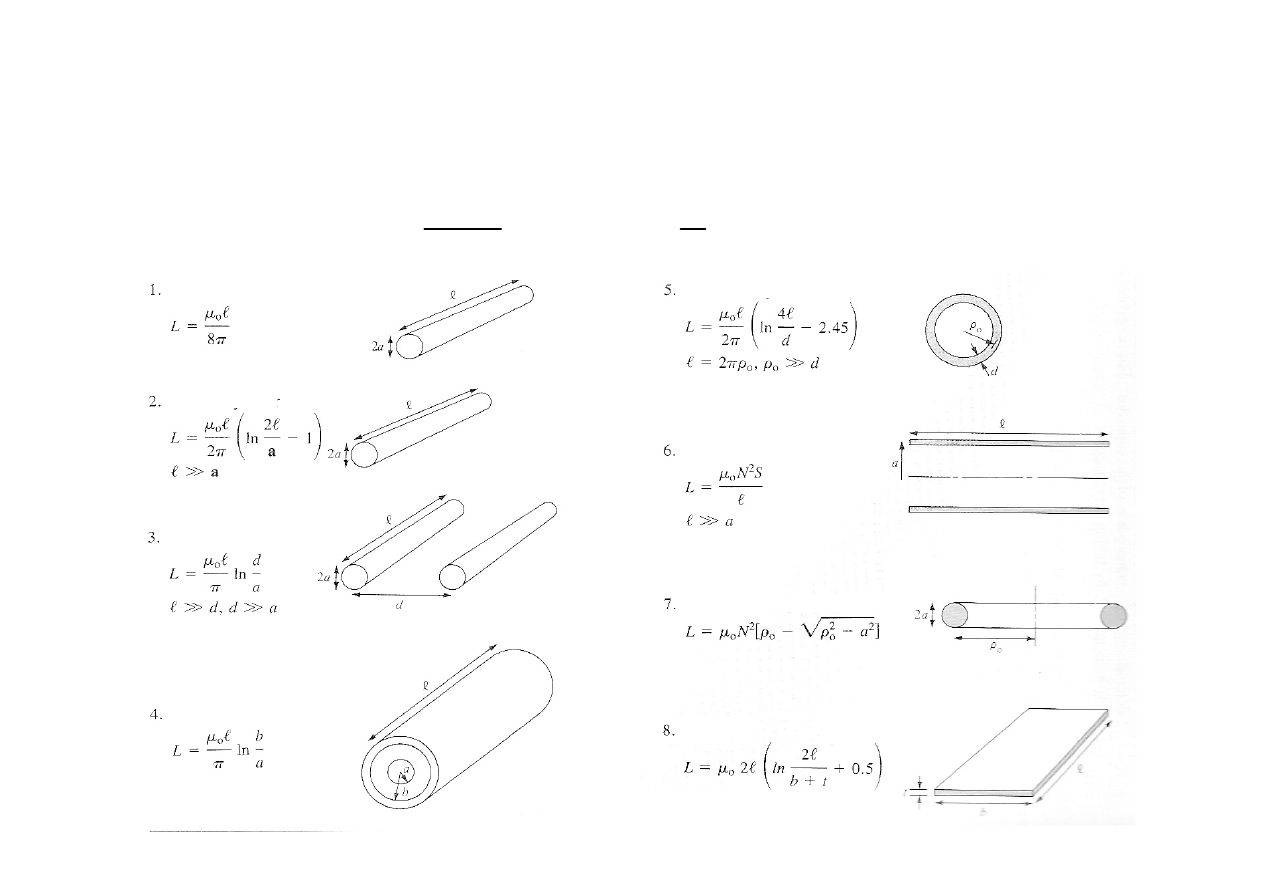
Indukcyjno

ść

własna

Tak jak w przypadku kondensatora, indukcyjno

ść

własn

ą

mo

ż

emy tak

ż

e traktowa

ć

jako zdolno

ść

cewki do magazynowania energii pola magnetycznego

2

2

2

1

2

m

m

W

L

W

LI

I

=

⇒

=

drut

cylinder

Linia 2-przewodowa

Kabel koncentryczny

P

ę

tla kołowa

selenoid

toroid

płyta

Indukcyjno

ść

własna

H.Rawa, PWN W-wa 1994

Obliczy

ć

indukcyjno

ść

własn

ą

drutu o

ś

rednicy 2a i długo

ś

ci l

Korzystaj

ą

c z prawa Ampera

2

( )

1

2

I

B

a

ϕ

µ ρ

ρ

=

Π

ρ

d

ρ

a

•

I

elementarny strumie

ń

2

2

I

d

Bd dz

d dz

a

µ ρ

ρ

ρ

Φ =

=

Π

Strumie

ń

skojarzony

2

3

2

4

2

a

S

I

d dz

d

d

d

S

a

a

ρ

ρ

µ ρ ρ

Π

Ψ = Φ

= Φ

=

Π

Π

3

4

0 0

2

8

a l

I

d dz

Il

a

µ ρ ρ

µ

Ψ =

=

Π

Π

∫ ∫

to

8

l

L

I

µ

Ψ

=

=

Π

Metoda 1

Indukcyjno

ść

własna

Metoda 2

ρ

d

ρ

a

•

I

2

2

m

W

L

I

=

2

1

2

2

m

V

V

B

W

B Hdv

dv

µ

=

=

∫

∫

2

2

2

2

2

2

2

2

4

0 0 0

2

1

2

4

8

a

l

V

B

I

l

L

dv

d d dz

I

I

a

µ ρ

µ

ρ ρ ϕ

µ

µ

Π

=

=

=

Π

Π

∫

∫ ∫ ∫

Wprowadza si

ę

poj

ę

cie indukcyjno

ś

ci na

jednostk

ę

długo

ś

ci – indukcyjno

ść

jednostkowa L’

'

8

L

L

l

µ

= =

Π

Indukcyjno

ść

własna

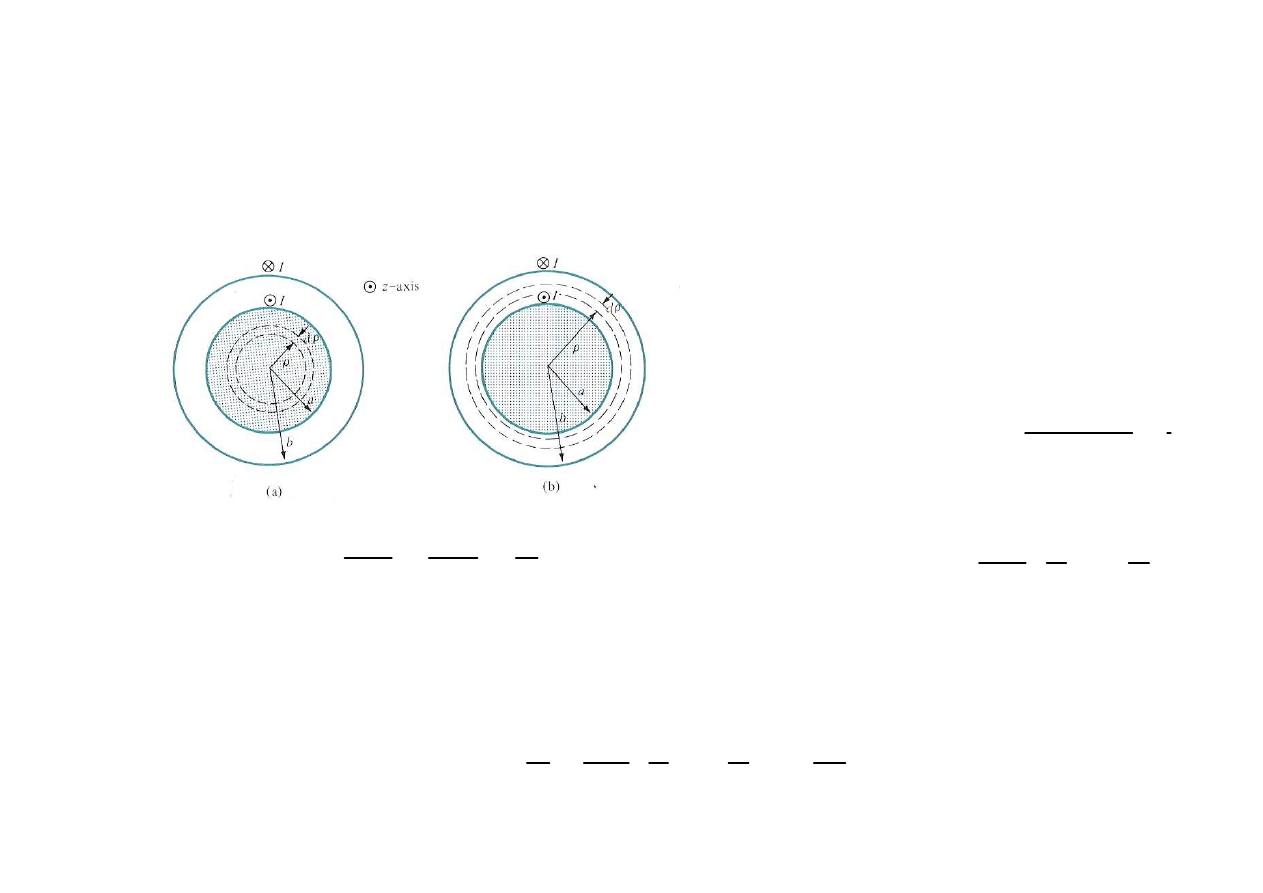
Kabel koncentryczny

Indukcyjno

ść

L

in

ju

ż

policzyli

ś

my

teraz policzymy L

ext

2

2

2

0

2

2

b l

a

Id dz

Il

b

d

B d dz

µ ρ

µ

ρ

ρ

Φ =

⇒

Ψ =

=

Π

Π

∫ ∫

2

ln

2

ext

l

b

L

I

a

µ

Ψ

=

=

Π

st

ą

d

1

ln

2

4

in

ext

l

b

L

L

L

a

µ





=

+

=

+





Π





Indukcyjno

ść

na jednostk

ę

długo

ś

ci L’

1

'

ln

2

4

L

b

H

L

l

a

m

µ





= =

+





Π





Indukcyjno

ść

własna

Dwu

ż

yłowa linia transmisyjna

L

in

tak jak poprzednio

1

8

Il

µ

⇒

Ψ =

Π

dla

0

a

ρ

≤ ≤

dla

a

d

a

ρ

≤ ≤ −

2

0

ln

2

2

d a l

a

I

Il

d

a

d dz

a

µ

µ

ρ

ρ

−

−

Ψ =

=

Π

Π

∫ ∫

Strumie

ń

wytworzony przez jedn

ą

ż

ył

ę

1

2

1

ln

2

4

Il

d

a

a

µ

−





Ψ + Ψ =

+





Π





Ze wzgl

ę

du na symetri

ę

druga

ż

yła wytwarza taki sam strumie

ń

, dlatego całkowity

strumie

ń

jest równy

(

)

1

2

1

2

ln

4

Il

d

a

LI

a

µ

−





Ψ = Ψ + Ψ =

+

=





Π





Je

ż

eli d>>a to indukcyjno

ść

własna wynosi

1

ln

4

l

d

L

a

µ





=

+





Π





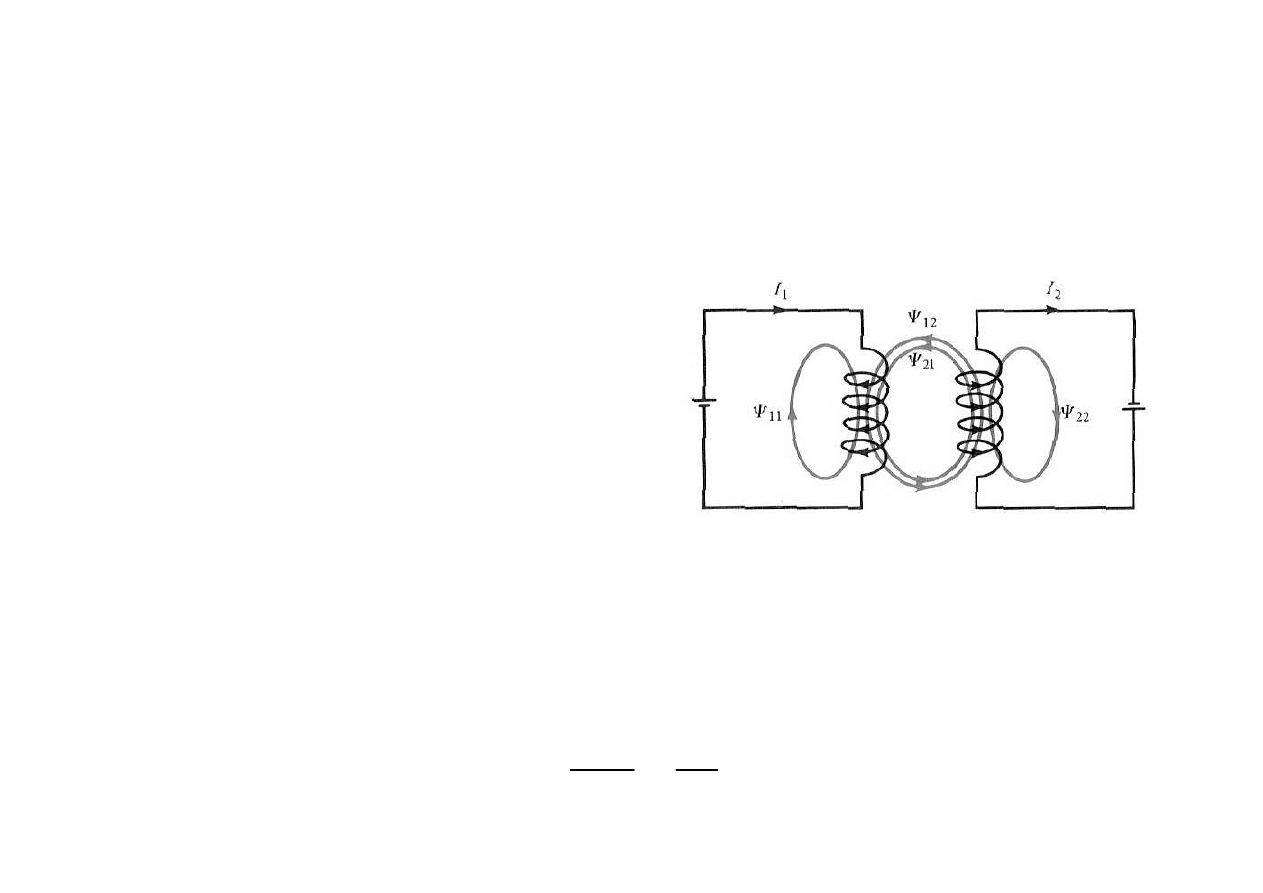
Indukcyjno

ść

wzajemna

Rozwa

ż

my dwie zwojnice o pr

ą

dach I

1

i I

2

w

ś

rodowisku liniowym

1

11

12

1 1

12 2

2

22

21

2 2

21 1

L I

M I

L I

M I

Ψ = Ψ + Ψ =

+

Ψ = Ψ + Ψ =

+

L

1

, L

2

- indukcyjno

ść

własna zwojnic

M

12

, M

21

– indukcyjno

ść

wzajemna zwojnic

[ ] [ ] [ ]

[ ]

Vs

L

M

H

I

A

Ψ

=

=

=

=

Indukcyjno

ść

wzajemna

Je

ż

eli o

ś

rodek wokół obwodów jest liniowy ( bez obecnosci ferromagnetyków ) to

12

21

M

M

=

Strumie

ń

skojarzony z obwodem 1

1

11

12

1 1

12 2

L I

M I

Ψ = Ψ + Ψ =

+

2

22

21

2 2

21 1

L I

M I

Ψ = Ψ + Ψ =

+

Strumie

ń

skojarzony z obwodem 2

Przykład

1

2

2

2

1

12

12

;

4

L

L

I

d l

A d l

A

r

µ

Ψ =

=

Π

∫

∫

st

ą

d

1

2

1

2

1

2

1

2

2

12

12 2

12

21

12

12

4

4

L L

L L

I

d l

d l

d l

d l

M I

M

M

r

r

µ

µ

Ψ =

=

⇒

=

=

Π

Π

∫ ∫

∫ ∫

Indukcyjno

ść

wzajemna

2

I

1

I

W zale

ż

no

ś

ci od zwrotów pr

ą

dów w obwodach L

1

i L

2

strumienie własne i wzajemne

mog

ą

si

ę

dodawa

ć

( sprz

ęż

enie dodatnie albo zgodne ) lub odejmowa

ć

( sprz

ęż

enie

ujemne albo przeciwne ).

1

1 1

12 2

1

1 1

12 2

2

2 2

21 1

2

2 2

21 1

lub

L I

M I

L I

M I

L I

M I

L I

M I

Ψ =

+

Ψ =

−









Ψ =

+

Ψ =

−





⊕

Zaciski jednakoimienne

Je

ż

eli pr

ą

dy do zacisków jednakoimiennych

Jednocze

ś

nie wpływaj

ą

lub wypływaj

ą

to

strumie

ń

własny i wzajemny si

ę

dodaj

ą

.

Wtedy istnieje sprz

ęż

enie dodatnie

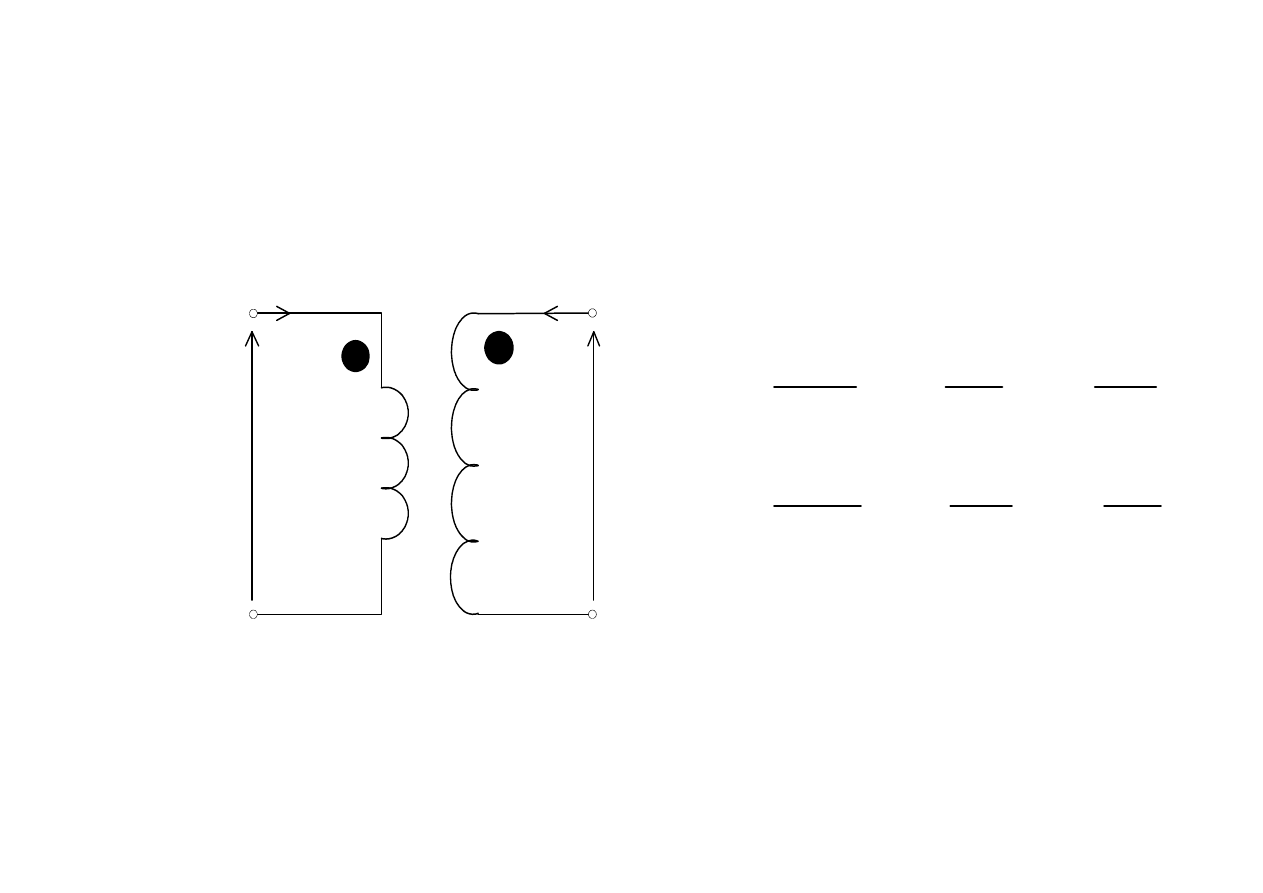
Indukcyjno

ść

wzajemna

Siły indukcyjno

ś

ci własnej i wzajemnej

M

1

I

2

I

1

U

2

U

1

1

2

1

1

2

2

1

2

1

d

dI

dI

U

L

M

dt

dt

dt

d

dI

dI

U

L

M

dt

dt

dt

Ψ

=

=

+

Ψ

=

=

+

Sprz

ęż

enie dodatnie

Strumienie rozproszenia i sprz

ę

gaj

ą

cy ( roboczy )

Sprz

ęż

enie dodatnie

1

1 1

2

1 1

1

1

1

2

2 2

1

2 2

2

2

2

S

M

S

M

S

M

S

M

L I

MI

L I

n

n

L I

MI

L I

n

n

Ψ =

+

=

+ Φ = Ψ + Φ

Ψ =

+

=

+ Φ = Ψ + Φ

Gdzie: L

S1

, L

S2

– indukcyjno

ść

rozproszenia 1,2

1

1 1

2

2 2

,

S

S

S

S

L I

L I

Ψ =

Ψ =

- strumie

ń

rozproszenia

M

Φ

- strumie

ń

sprz

ę

gaj

ą

cy

Mo

ż

na wyprowadzi

ć

:

1

2

1

1

2

2

2

1

;

S

S

n

n

L

L

M

L

L

M

n

n

= −

=

−

(

)

1 1

2

2

1 2

M

M

I n

I n

n n

Φ =

+

Sprz

ęż

enie ujemne

(

)

1 1

2

2

1

1

1

1 2

;

M

S

M

M

I n

I n

n

n n

Φ =

−

Ψ = Ψ + Φ

oraz

2

2

2

S

M

n

Ψ = Ψ − Φ

Pozostałe wzory bez zmian

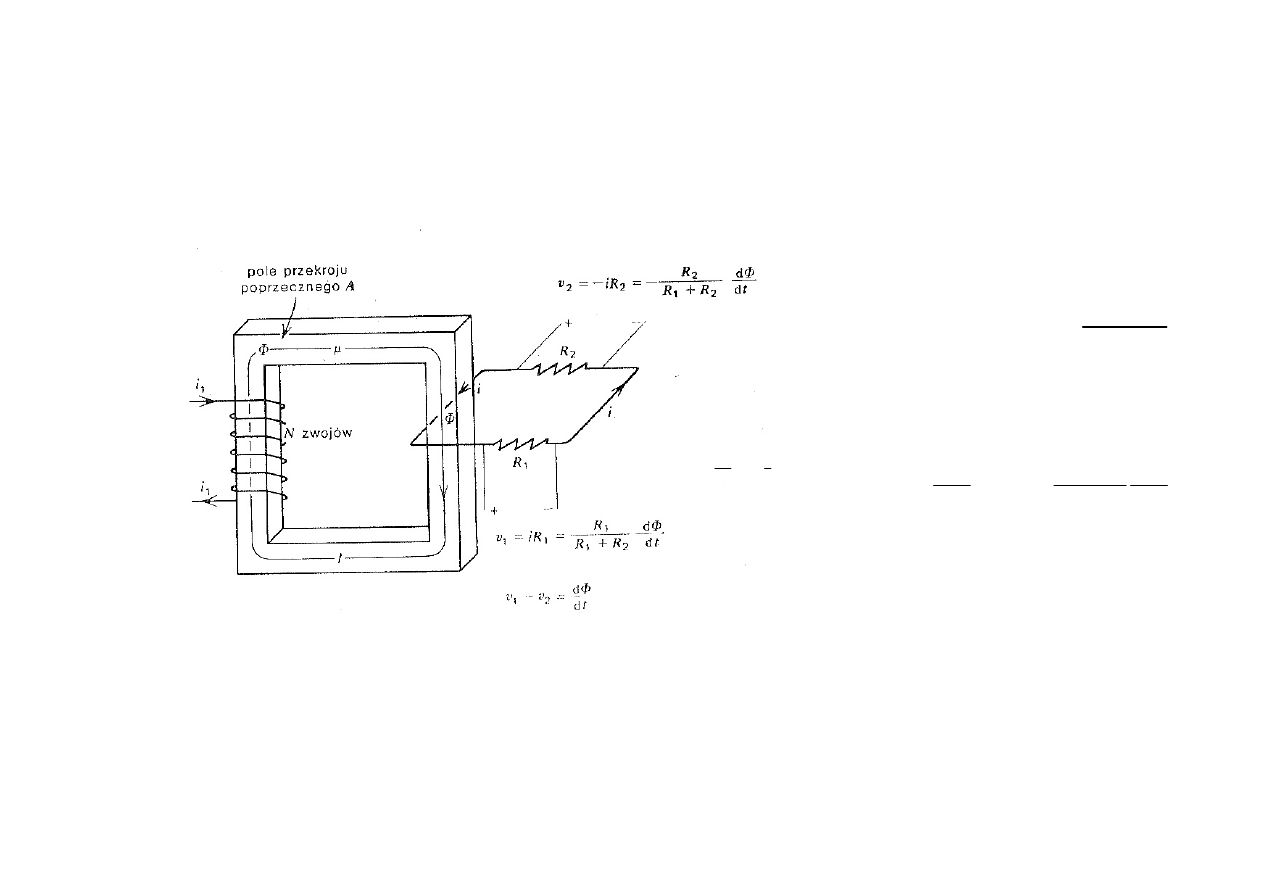
Transformator

Niejednoznaczno

ść

napi

ęć

1

( )

( )

NAI

jeżeli

i t

t

l

µ

⇒

Φ =

Stosuj

ą

c prawo Faraday’a

1

2

1

2

1

(

)

L

d

d

E d l

i R

R

i

dt

R

R

dt

Φ

Φ

=

+

= +

⇒

=

+

∫

paradoks napi

ęć

Niejednoznaczno

ść

napi

ęć

w układzie spowodowana jest faktem,

ż

e pole

elektryczne w tym układzie jest wirowe.

Pomineli

ś

my strumie

ń

własny wytworzony przez

indukowany pr

ą

d

Je

ś

li zmienny w czasie strumie

ń

magnetyczny przecina kontur wyznaczony

przez układ pomiarowy , to ma to wpływ na rozkład pr

ą

dów i napi

ęć

w tym

układzie.

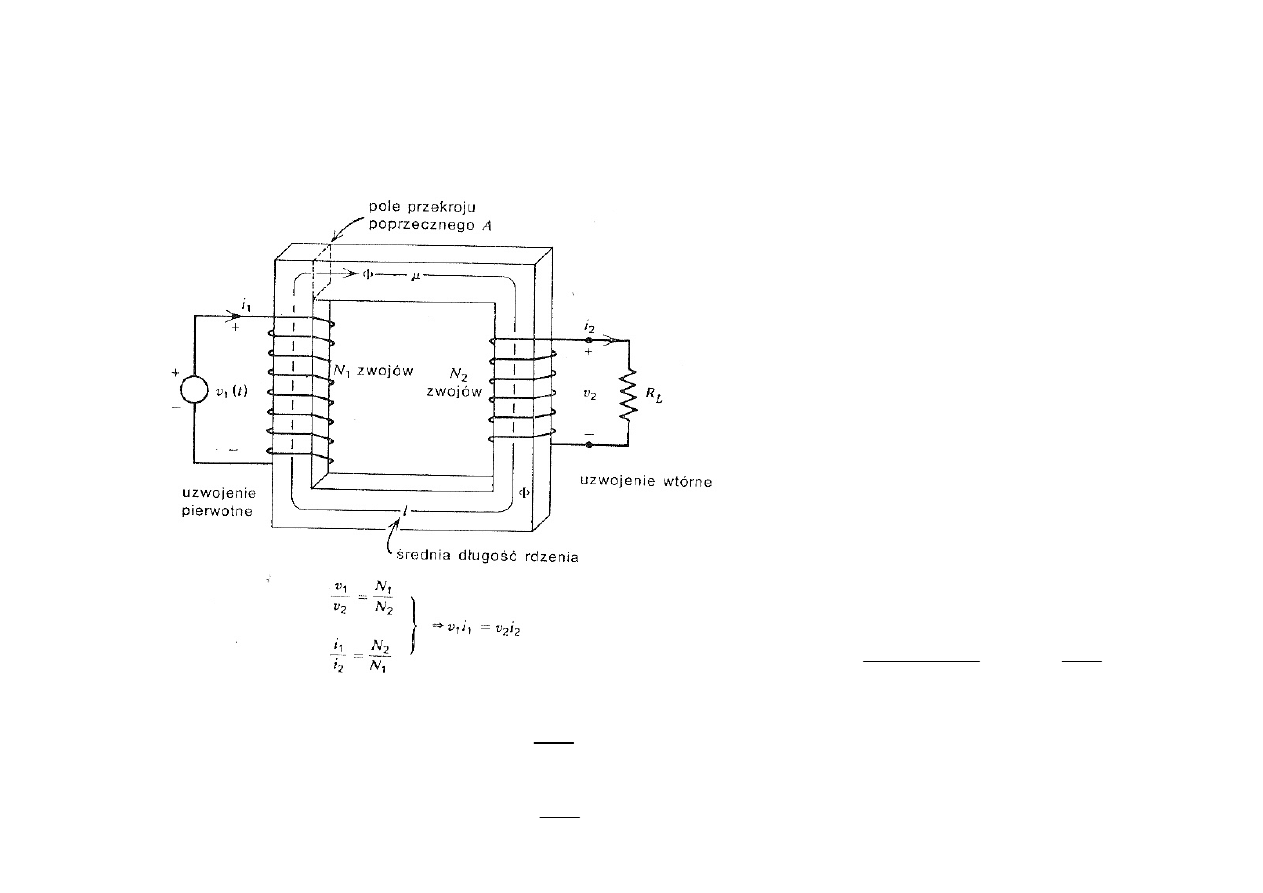
Transformator idealny

µ

→ ∞

Strumie

ń

jest całkowicie zamkni

ę

ty

w obwodzie magnetycznym.

Je

ż

eli zwroty obu pr

ą

dów s

ą

dodatnie , to wytworzone w obu
cewkach strumienie magnetyczne

s

ą

skierowane przeciwnie wzgl

ę

dem

siebie.

Całkowity strumie

ń

magnetyczny

1 1

2 2

,

N i

N i

l

R

R

A

µ

−

Φ =

=

Strumie

ń

skojarzony z cewk

ą

1 i 2

2

1

1

1 1

1

2 2

1 1

2

2

2

2

2 2

1

2 1

2 2

1

(

)

)

(

)

)

A

N

N i

N N i

L i

Mi

l

A

N

N i

N N i

L i

Mi

l

µ

µ

Ψ = Φ =

−

=

−

Ψ =

Φ =

−

=

−

Transformator idealny

2

2

1

1

0

2

2

0

1

2

0

0

,

,

,

A

L

N L

L

N L

M

N N L

L

l

µ

=

=

=

=

W ogólnym przypadku

1

2

1

2

(

)

,

0

1

M

k L L

k

=

≤ ≤

1

1

k

skończone

k

µ
µ

→ ∞

⇒

=

=

⇒

<

Korzystaj

ą

c z prawa Faraday’a

1

1

2

1

1

2

2

1

2

2

d

di

di

v

L

M

dt

dt

dt

d

di

di

v

L

M

dt

dt

dt

Ψ

=

=

−

Ψ

=

=

−

Transformator idealny , to strumie

ń

magnetyczny nie ulega rozproszeniu

1

2

2

1

2

1

N

N

M

L

L

N

N

=

=

I stosunek napi

ęć

na obu cewkach jest równy stosunkowi liczby zwojów

Transformator idealny

1

1

1

2

2

2

v

d

dt

N

v

d

dt

N

Ψ

=

=

Ψ

Gdy µ

→∞

to L

1

i L

2

→∞

i aby v1 i v2 było sko

ń

czone to

1

2

2

1

i

N

i

N

=

Moc wydzielane ze

ź

ródła jest równa mocy pobranej przez odbiornik

1 1

2 2

1

v i

v i

η

=

⇒

=

Je

ż

eli uzwojenie pierwotne zasilimy napi

ę

ciem v

1

(t) a wtórne obci

ąż

ymy rezystancj

ą

R2,

to rezystancja mierzona od strony uzwojenia pierwotnego wynosi

2

1

1

2

1

1

2

1

2

2

1

2

2

(

)

v

N

v

N

R

R

i

N

N

N i

N





=

=

=









2

2

2

v

i R

=

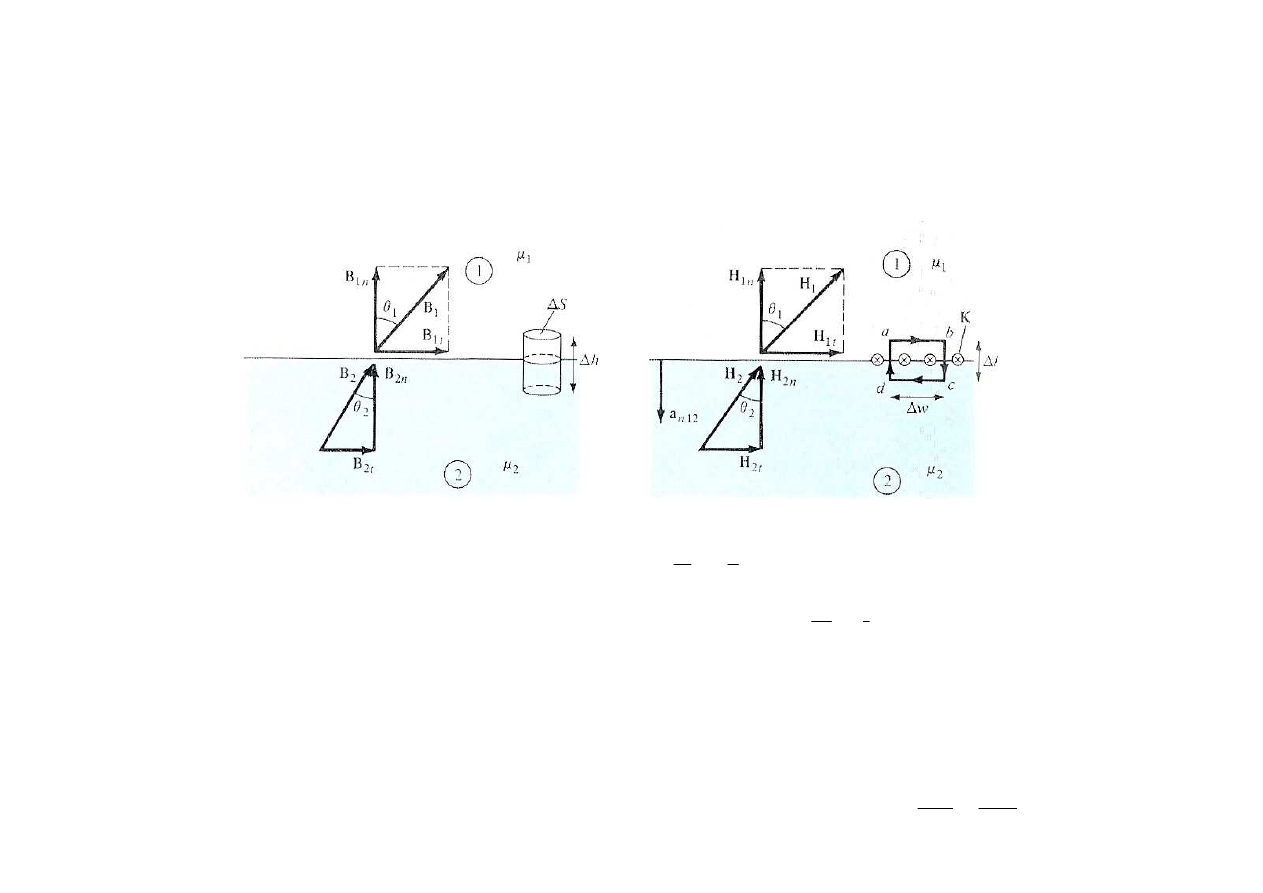
Warunki graniczne

Warunki pola magnetycznego na granicy dwóch o

ś

rodków definiujemy z:

-magnetycznego prawa Gauss’a

-prawa Ampere’a

( )

0

S V

B d s

=

∫

( )

s

L S

H d l

I

=

∫

1

2

1

2

1

1

2

2

0

;

n

n

n

n

n

n

B

B

B

B

H

H

µ

µ

−

=

⇒

=

=

1

2

1

2

1

2

t

t

t

t

B

B

H

H

K

K

µ

µ

−

=

−

=

Warunki graniczne

Je

ż

eli K=0

→

prawo załamania

1

1

2

2

tg

tg

µ

µ

Θ =

Θ

Wnikanie pola do ferromagnetyków µ

1

→∞

0

1

1

2

1

0

90

tg

tg

µ

µ

Θ = Θ

→ ∞

⇒

Θ =