Strumień wektora indukcji magnetycznej

Istotne znaczenie w elektromagnetyźmie posiada strumień

indukcji magnetycznej

S

B

d s

∫

Φ =

B

d s

( )

L S

[ ] [ ][ ]

2

2

1

1

Vs

B S

m

Vs

Wb

m

Φ =

=

=

=

Strumień wektora indukcji magnetycznej

Z bezźródłowości pola magnetycznego wynika, że

( )

S

S

L S

B d s

rot A d s

A d l

∫

∫

∫

Φ =

=

=

( )

0

S V

V

B d s

divB dv

∫

∫

=

⋅

=

do określenia strumienia wystarczy określić potencjał wektorowy na brzegu powierzchni

Bezźródłowość pola magnetycznego w postaci całkowej

0

divB

=

Siły działające między obwodami

wzór Grassmana

2

d l

1

d l

12

B

12

r

1

I

2

I

1

L

2

L

(

)

12

2

0

2

12

12

1

1

1

1

3

1

1

2

12

4

L

L

L

I

d l

r

F

I d l

B

I

d l

r

μ

∫

∫

∫

⎛

⎞

×

=

×

=

×

⎜

⎟

Π

⎝

⎠

12

1

2

0

12

1

2

3

1

2

12

(

)

4

L

L

d l

d l

r

F

I I

r

μ

∫ ∫

×

×

=

Π

czyli

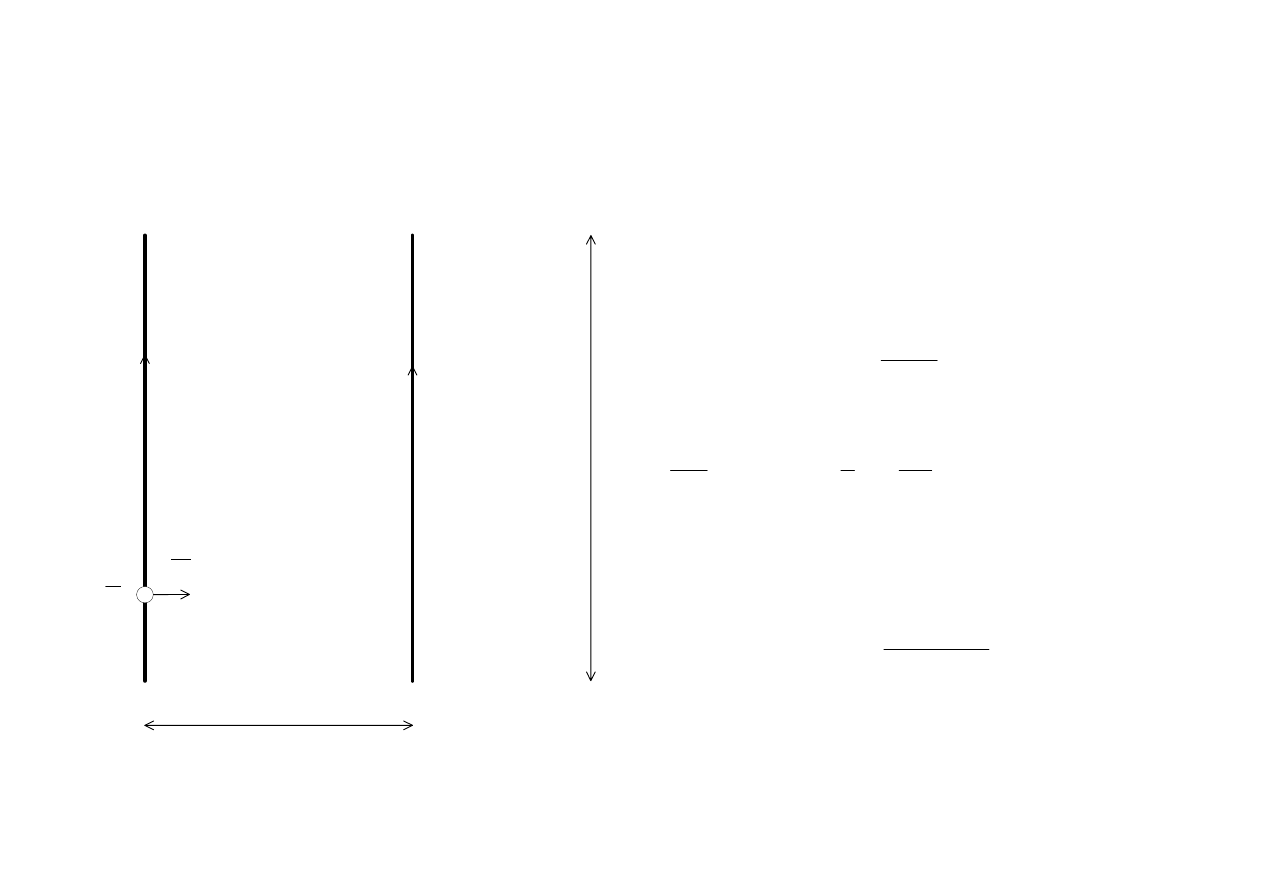
Siły działające między obwodami

•

1

I

12

F

12

B

2

I

l

a

0

2

12

2

I

B

a

μ

=

Π

12

12

1

(

)

F

I l B

=

×

0

1

2

12

2

I I

F

l

a

μ

=

Π

Zasada superpozycji

Stały prąd elektryczny o natężeniu
1 A jest to taki prąd, który płynąc
w dwóch równoległych,
prostoliniowych, nieskończenie
długich przewodach o znikomo
małym przekroju kołowym,
umieszczonych w próżni w
odległości 1 m od siebie,
spowodowałby wzajemne
oddziaływanie przewodów na
siebie z siłą równą 2*10 -7 N na

każdy metr długości przewodu.

7

7

0

0

1 1

2 10

1

4

10

2

1

H

m

μ

μ

−

−

⋅

⋅

=

⋅ →

= Π ⋅

Π ⋅

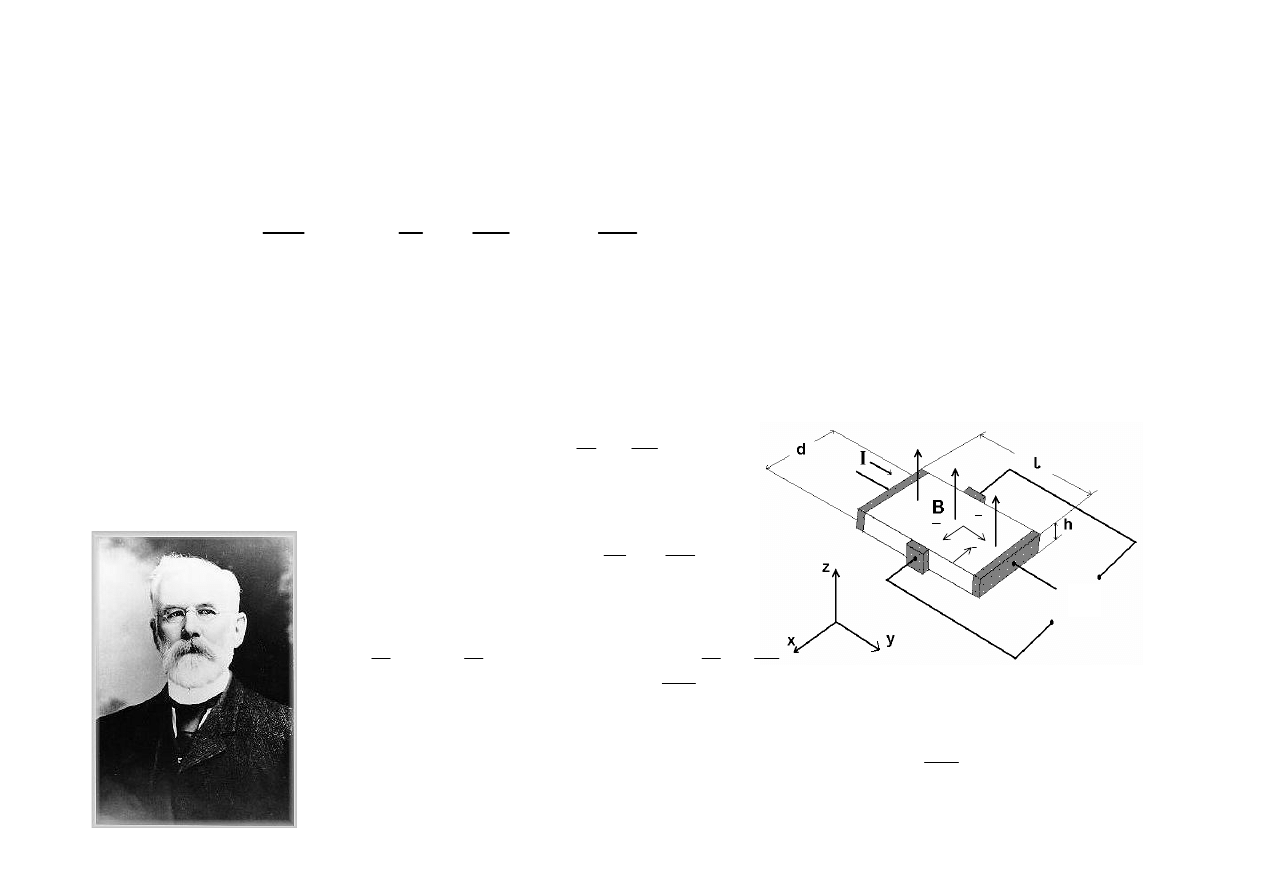
Zjawisko Hall’a

1

V

2

V

+

+
+

−−−

j

m

F

pop

E

W polu elektromagnetycznym na ładunek działa siła

F

qv B

qE

=

× +

W przewodniku lub półprzewodniku siła Lorentz’a jest przyczyną powstawania
Poprzecznego pola elektrycznego znanego jako efekt Hall’a

W stanie równowagi

0

pop

qE

qu B

+

× =

stąd

pop

E

u B

= − ×

1

v

pop

v

j

q u

E

j B

q

=

→

= −

×

1

1

2

2

1

2

1

pop

pop

H

V

E dl

V

V

E d

V

V

U

jBd

q

∫

= − =

→ − =

=

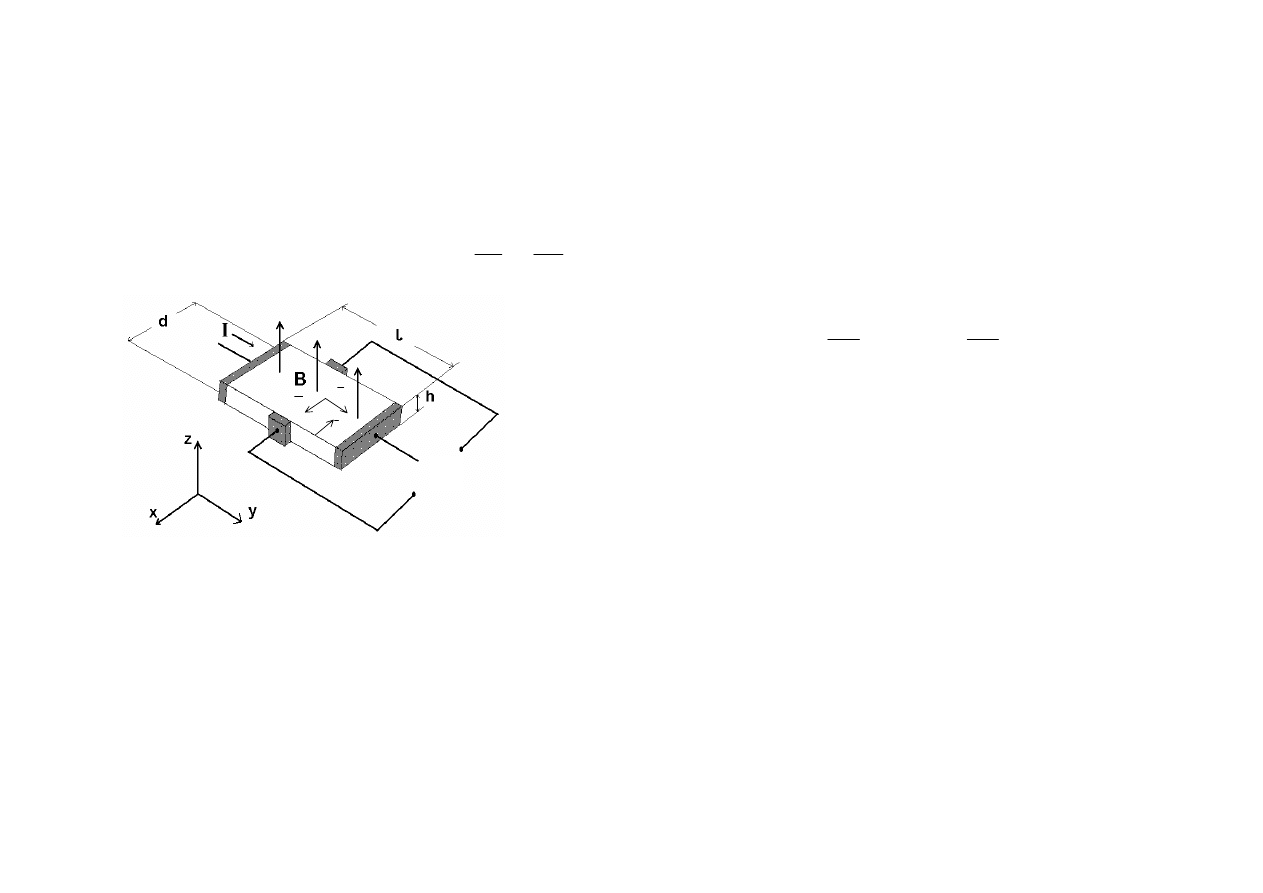
Zjawisko Hall’a

stała Hall’a

1

1

H

V

R

q

en

=

=

H

H

H

H

I

IB

U

R jBd

R

Bd

R

dh

h

=

=

=

1

V

2

V

+

+
+

−−−

j

m

F

pop

E

Napięcie V

2

-V

1

=U

H

może być dodatnie lub ujemne

gdy V

2

-V

1

=U

H

>0 to nośniki prądu dodatnie

metale – beryl, cynk, kadm
półprzewodnik typu „n”

gdy V2-V1=UH<0 to nośniki prądu ujemne
większość metali
półprzewodnik typu „p”

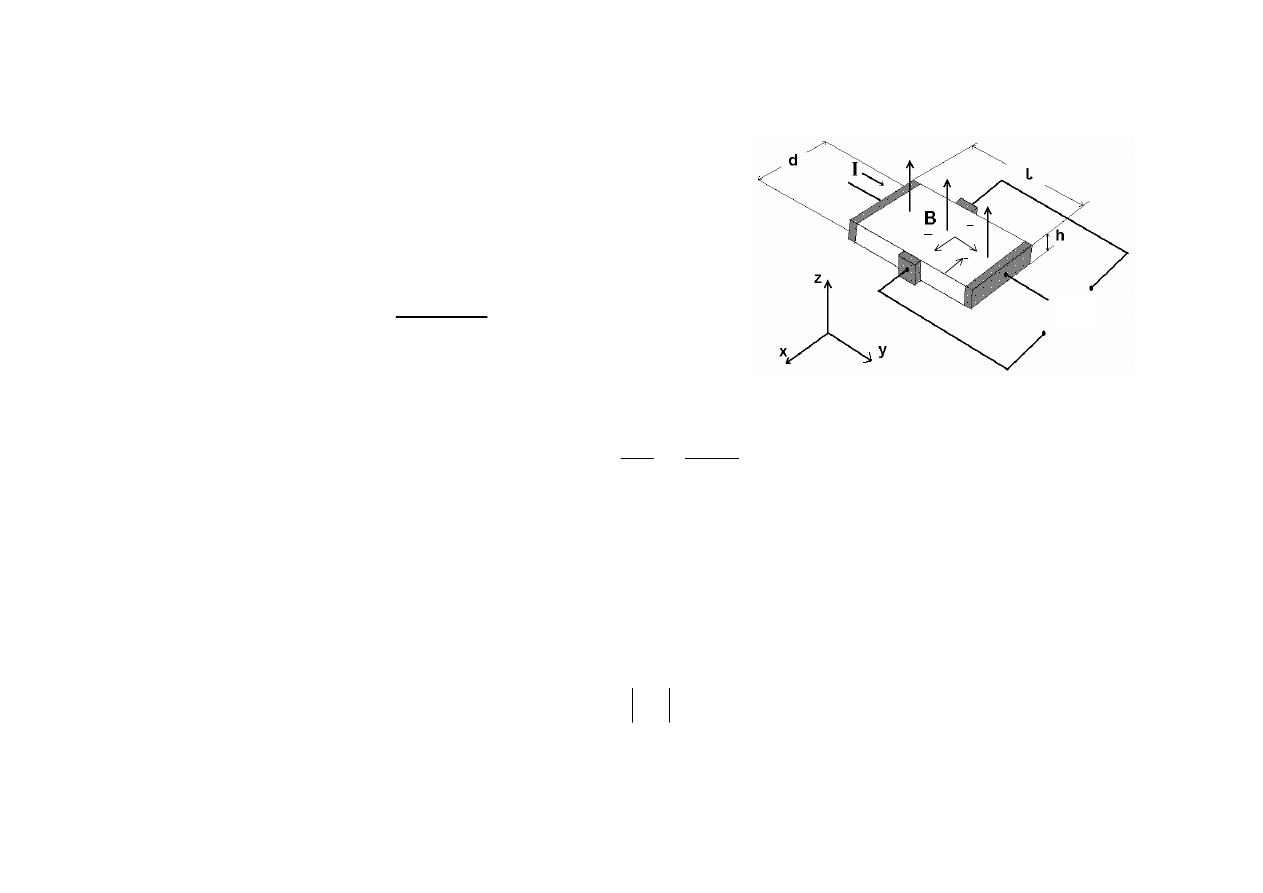
Zjawisko Hall’a

1

V

2

V

+

+
+

−−−

j

m

F

pop

E

Zastosowanie:
- mierniki pola magnetycznego(magnetometry)

H

H

h

B

U

R I

=

- gęstości nośników

1

V

H

H

IB

q

en

R

hU

=

=

=

- znaku nośników

0

( ),

0

( )

H

H

U

U

> → +

< → −

-mierząc konduktywność σ próbki i stałą Hall’a możemy wyznaczyć ruchliwość
nośników

H

R

μ σ

=

Zjawisko Hall’a

0,0044

+24,4

beryl

0,0080

+6,0

kadm

0,0060

+3,3

cynk

0,0030

-7,2

glin

0,0012

-3,0

złoto

0,0056

-8,4

srebro

0,0032

-5,5

miedź

0,0053

-25,0

sód

0,0018

-17,0

lit

m

2

V

-1

s

-1

10

-11

m

3

C

-1

μ

R

H

metal

H

U

B

I

1

L

przew

I

N

zas

U

Pomiar mocy

zas

przew

H

zas

przew

I

U

B

I

U

U

I

⇒

⋅

∼

∼

∼

Pole magnetyczne w środowisku materialnym

-pole magnetyczne oddziałowywuje z materią
-materia może wzmocnić pole magnetyczne
- mikroskopowo wyjaśnia to istnienie „mikroobwodów prądowych” ( w atomach
i cząsteczkach ) związanych z ruchem orbitalnym elektronów oraz istnieniem

tzw. „spinowych momentów magnetycznych” elktronów ( 0,927 10-23 Am2)

-materię można traktować jako zbiór rozłożonych w przestrzeni
dipoli magnetycznych w próżni

Makroskopowo opisuje się ten stan wektorami uśrednionymi

Zgodnie z zasadą SUPERPOZYCJI pole indukcji magnetycznej jest sumą
-pola zewnętrznego od obwodów prądowych i
- wewnętrznego od dipoli w materii

W ujęciu makroskopowym

( )

0

lub

0

S V

divB

B d s

∫

=

=

Wektor magnetyzacji

wprowadza się uśrednioną wartość sumy momentów magnetycznych na

jednostkę objętości ∆V→0

0

lim

V

V

m

M

V

Δ

Δ →

∑

=

Δ

M

- wektor magnetyzacji lub krótko magnetyzacja

[ ] [ ]

[ ]

2

3

1

m

Am

A

M

V

m

m

=

=

=

diamagnetyzm i paramagnetyzm

Pod wpływem zewnętrznego pola magnetycznego B na dipole magnetyczne materii działa

moment mechaniczny dążący do ustawienia momentu magnetycznego dipola
równolegle do tego pola

m B

Jednak w materii ( ze względu na jej budowę mikroskopową) istnieją ograniczenia
uniemożliwiające takie ustawieni.
Równocześnie w zakresie atomu jak i cząsteczki momenty magnetyczne są prawie
całkowicie skompensowane.
Większość substancji w wyniku działąnia nieskompensowanych momentów
magnetycznych wykazuje słabe działanie wzmacniające pole zewnętrzne
są to PARAMAGNETYKI

Istnieją materiały w których występuje efekt osłabiający zewnętrzne pole magnetyczne
-zwany diamagnetyzmem
Elektron na orbicie atomu pod wpływem zewnętrznego pola magnetycznego ( momentu
mechanicznego ) wykonuje ruch precesyjny, który jest źródłem dodatkowego momentu
dipolowego osłabiającego pole zewnętrzne.
Materiały w których stwierdza się występowanie efektu diamagnetyzmu nazywa się
DIAMAGNETYKAMI

Wektor natężenia pola magnetycznego

d l

m

α

( )

L S

dl

ds

d l

( )

L S

Całka z B po krzywej przebiegającej w
materii obejmuje obwody prądowe
makroskopowe oraz mikroobwody
prądów molekularnych

Element drogi przenika pewną liczbę „n”
obwodów molekularnych , których prądy objęte są
krzywą całkowania

Rozważmy kostkę ( dl,ds), w której dipole ( N ) o momencie
tworzą kąt α z przy czym m

d

=s

d

I

d

d

m

d l

k – liczba dipoli w warstwie
n – liczba warstw

to N=nk

cos

d

ds

k

s

α

=

cos

d

s

N

n

N

k

ds

α

=

=

stąd sumaryczny prąd mikroobwodów obejmujący element drogi dl
jest

cos

cos

d

d

d

d

Ns I

Nm

nI

ds

ds

α

α

=

=

Wektor natężenia pola magnetycznego

Ale zgodnie z definicją magnetyzacji

Nm

d

=Mdsdl

cos

cos

d

Mdsdl

nI

Mdl

M d l

ds

α

α

=

=

=

( )

L S

M d l

∫

A na drodze zamkniętej suma prądów molekuł wynosi

uwzględniając wszystkie prądy objęte droga całkowania otrzymamy

0

0

( )

( )

( )

k

L S

L S

L S

B d l

I

M d l

μ

μ

∑

∫

∫

=

± +

( )

( )

0

k

L S

L S

B

M

d l

I

μ

∑

∫

⎛

⎞

−

= ±

⎜

⎟

⎝

⎠

0

B

H

M

μ

=

−

wektor NATĘŻENIA POLA MAGNETYCZNEGO

[ ] [ ]

1

A

H

M

m

=

=

Prawo przepływu- Prawo Ampera

( )

( )

( )

lub

k

S

L S

L S

L S

S

H d l

I

I

H d l

j d s

∑

∫

∫

∫

= ± =

=

j

j

j

H

d l

( )

L S

d s

S

S

rot H d s

j d s

∫

∫

=

wykorzystując twierdzenie Stokes’a

Otrzymamy postać różniczkową prawa przepływu dla pól stałych

rot H

j

=

H

j

∇×

=

Podatność i Przenikalność

(

)

0

0

B

H

M

B

H

M

μ

μ

=

−

→

=

+

0

0

M

B

H

μ

=

→

=

dla próżni

W środowiskach materialnych magnetyzacja M zależy od H

M

H

χ

=

x

xx

xy

xz

x

y

yx

yy

yz

y

z

zx

zy

zz

z

M

H

M

H

M

H

χ

χ

χ

χ

χ

χ

χ

χ

χ

⎡

⎤

⎡

⎤

⎡

⎤

⎢

⎥

⎢

⎥

⎢

⎥

= ⎢

⎥

⎢

⎥

⎢

⎥

⎢

⎥

⎢

⎥

⎢

⎥

⎣

⎦

⎣

⎦

⎣

⎦

χ

- podatność magnetyczna materiałów anizotropowych

większość materiałów jest izotropowa i wóczas

M H

M

H

χ

→

=

Skalar bez jednostki podatność magnetyczna środowiska

Podatność i Przenikalność

(

)

(

)

0

0

0

1

r

B

H

H

H

H

H

μ

χ

μ

χ

μ μ

μ

=

+

=

+

=

=

0

r

μ μ μ

=

0

1

lub

r

r

μ

μ

χ

μ

μ

= +

=

[ ]

2

1

Vs

B

Vs

H

m

A

H

Am

m

m

μ

⎡ ⎤

=

=

=

=

⎢ ⎥

⎣ ⎦

przenikalność magnetyczna środowiska

przenikalność magnetyczna względna

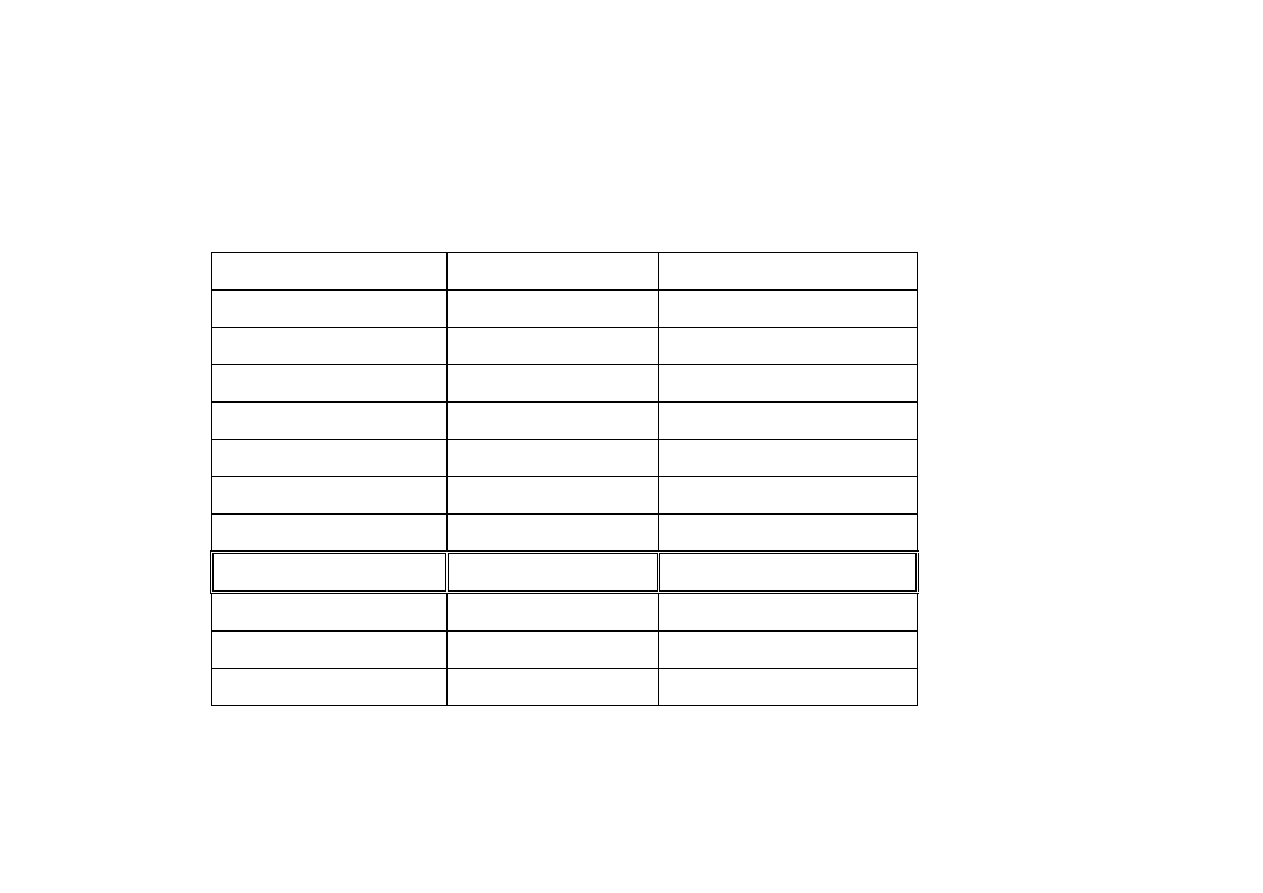
Podatność i Przenikalność

materiał

μ

r

χ

bizmut 0,99983 -1,66

10

-4

złoto 0,999964 -3,6

10

-5

rtęć 0,999968

-3.2

10

-5

srebro 0,99998 -2,6

10

-5

ołów O,999983 -1,7

10

-5

miedź 0,999998 -0,98

10

-5

woda 0,999991 -0,89

10

-5

próżnia 1

0

powietrze 1,00000036 3,6

10

-7

glin 1,000021 2,5

10

-5

pallad 1,00082 8,2

10

-4

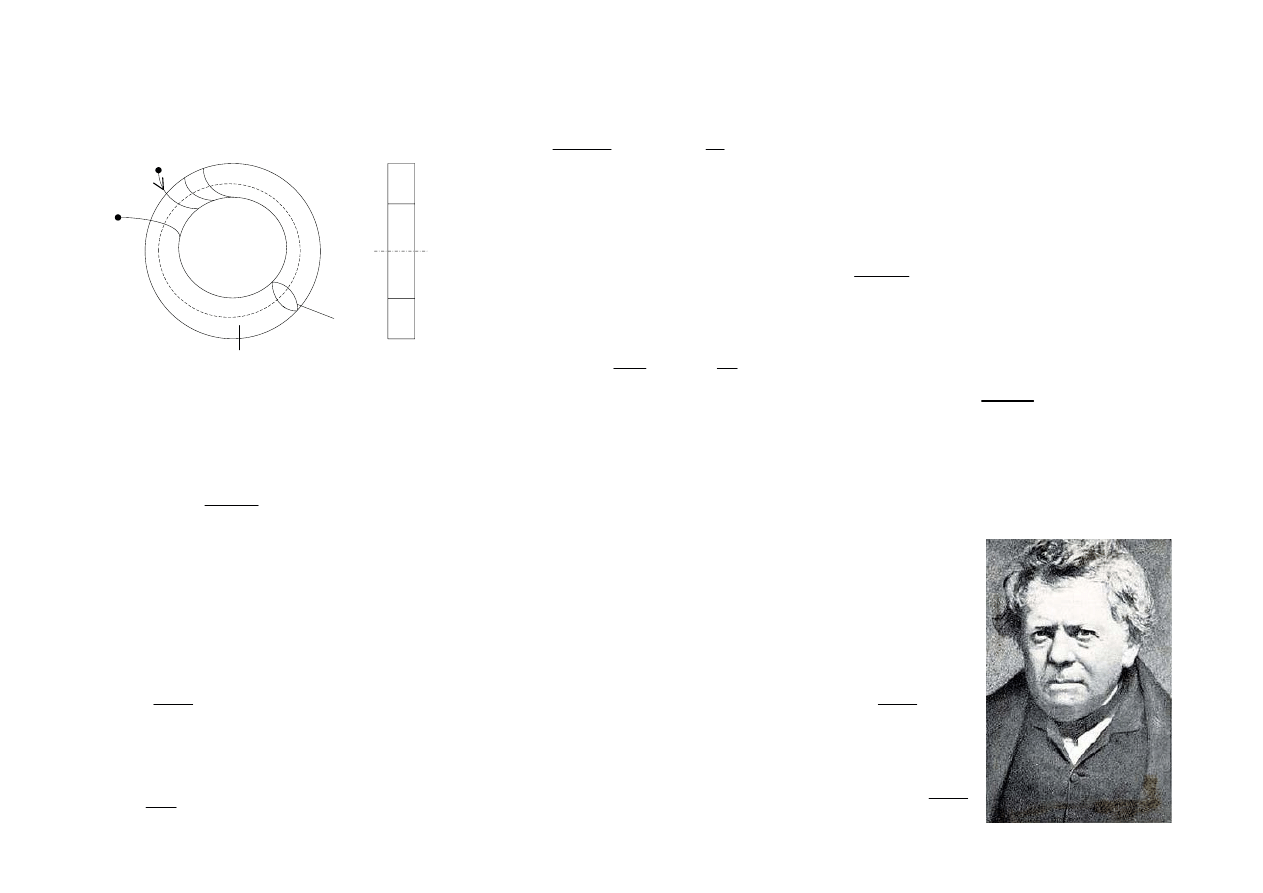
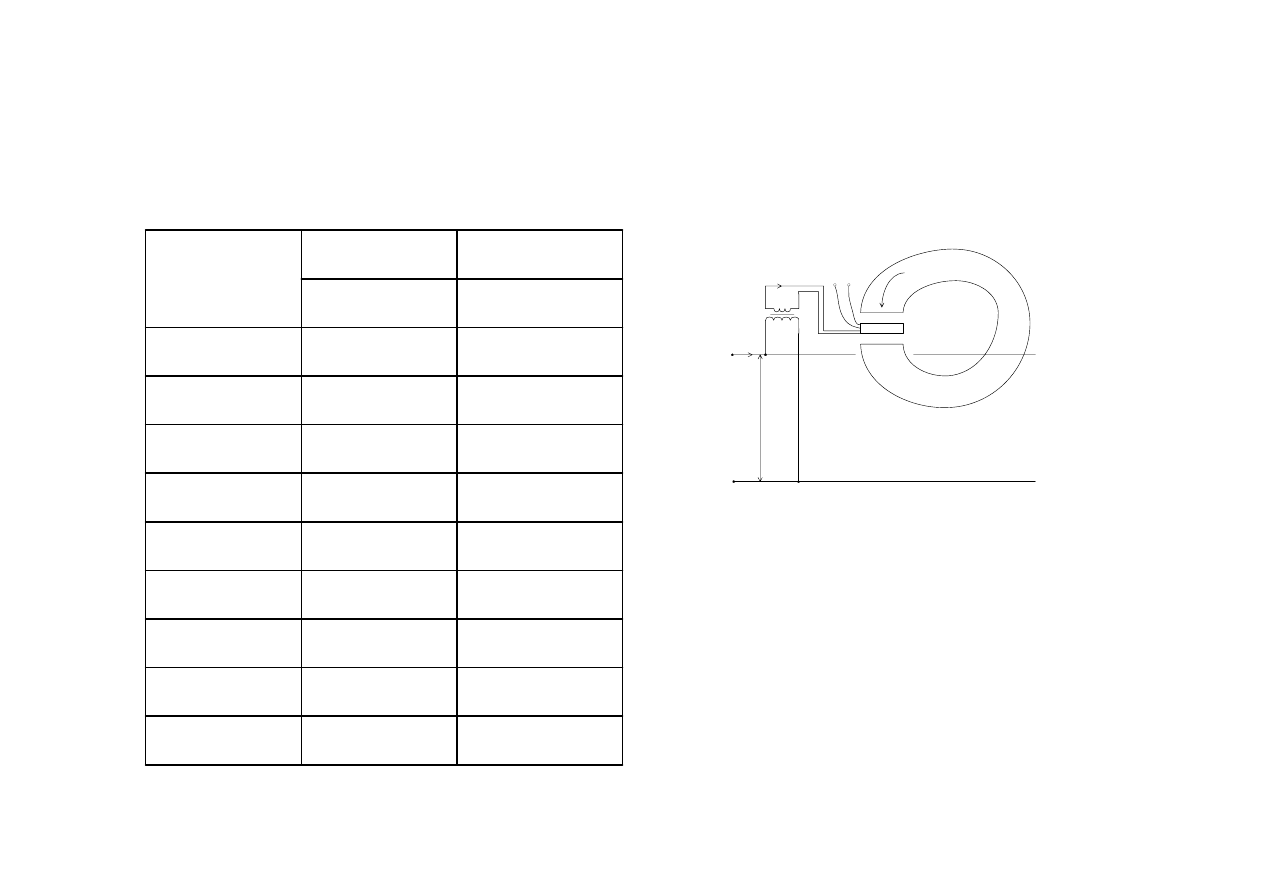
Przykład: toroid

I

( )

L S

S

a

w

r

z

r

n

( )

L S

H d l

Hl

nI

∫

=

=

nI

H

B

H

l

μ

=

=

s

S

nI

B d s

BS

S

l

μ

∫

Φ =

=

l

nI

R

S

μ

μ

=

Φ = Φ

nI

Θ =

R

μ

Θ = Φ

l

R

S

μ

μ

=

1

R

μ

Λ =

1

1

A

R

H

Wb

η

−

=

=

⎡ ⎤

⎣ ⎦

[ ]

1

1

Wb

H

A

Λ =

=

SIŁA MAGNETOMOTORYCZNA

opór magnetyczny - RELUKTANCJA

Przewodność magnetyczna - PERMANENCJA

magnetyczne prawo Ohma