Ferromagnetyki

Ferromagnetykami nazywa się grupę ciał, w których występuje stałe samorzutne
namagnesowanie bez działania obcego pola magnetycznego.

Za zjawisko ferromagnetyzmu, odpowiedzialne są momenty magnetyczne ( spinowe )
elektronów, jeżeli nie są zrównoważone w atomie, cząsteczce.

Jest to możliwe w atomach o niezapełnionych całkowicie powłokach elektronowych.
Np. w atomie żelaza są to cztery nieskompensowane momenty spinowe elektronów w
przedostatniej podpowłoce chmury elektronowej.

Występowanie momentu magnetycznego poszczególnych atomów jest wprawdzie
konieczne, ale nie wystarczające do pojawienia się własności ferromagnetycznych.

Charakterystycznym zjawiskiem dla ferromagnetyków jest zjawisko spontanicznego
porządkowania się sąsiednich atomów, ukierunkowywujące równolegle momenty
magnetyczne. Zjawisko to nie jest wynikiem oddziaływanie elektromagnetycznego, ale
tzw. „wymiennym oddziaływaniem wzajemnym”.

Spontaniczne namagnesowanie pojawia się w bardzo małych obszarach o objętości
10

-6

÷10

-4

cm

3

nazywanych domenami Weissa, oddzielonych strefami przejściowymi –

tzw. ścianami Blocha

1

〉〉

r

μ

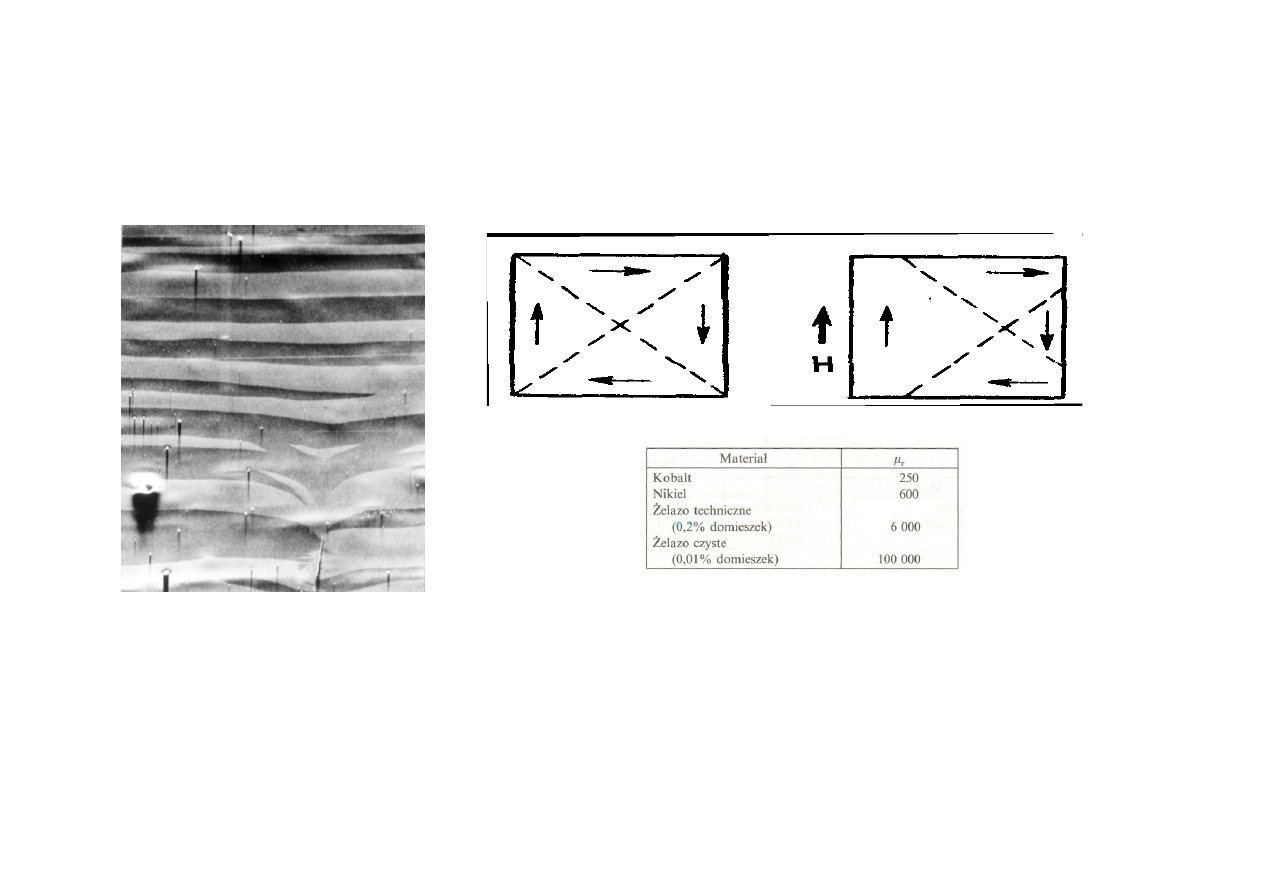
Ferromagnetyki

Przy braku zewnętrznego pola magnetycznego momenty magnetyczne poszczególnych
domen wzajemnie się kompensują.

Pod wpływem zewnętrznego pola następuje uporządkowanie kierunkowe momentów
magnetycznych domen.

Do ferromagnetyków należą : żelazo, kobalt, nikiel ( maja największe znaczenie ).
Ferromagnetykami są także stopy tych metali z nieferromagnetycznymi materiałami
takimi jak np. krzem, aluminium .

Ferromagnetyki

Ferromagnetyzm ujawnia się poniżej pewnej temperatury zwanej punktem Curie.
Żelazo – 1043 K, kobalt – 1393 K, nikiel – 631 K
Powyżej tej temperatury ciało jest paramagnetykiem.

Zjawiska związane z ferromagnetyzmem:

-nieliniowa zależność indukcji magnetycznej od natężenia pola magnetycznego przy
magnesowaniu;

- skokowe zmiany indukcji przy monotonicznym zwiększaniu natężenia pola – zjawisko
Barkhausena;

- występowanie histerezy magnetycznej;

- anizotropowość własności magnetycznych;

- nasycenie magnetyczne objawiające się w zakresie dużych natężeń pola
magnetycznego zanikiem histerezy i małymi przyrostami indukcji przy dużych zmianach
natężenia pola;

Ferromagnetyki

- zależność własności magnetycznych od temperatury i zanikanie tych własności
powyżej temperatury Curie;

-zdolność do długotrwałego zachowywania własności magnetycznych po
namagnesowaniu;

-występowanie własności magnetycznych tylko przy określonej strukturze krystalicznej
ciała i zanikanie tych własności przy jej zmianie oraz przy zmianie stanu skupienia;

- zmiana wymiarów ciała przy magnesowaniu – zjawisko magnetostrykcji; przy czym

obserwuje się zarówno magnetostrykcję podłużną ( w kierunku pola ) jak i poprzeczną;

-zmiana rezystywności ciała przy magnesowaniu – zjawisko Thomsona;

- magnesowanie się ciała wzdłuż osi obrotu pod wpływem ruchu wirowego w przestrzeni
bez zewnętrznego pola magnetycznego – zjawisko Barneta;

- występowanie momentu obrotowego starającego się obrócić ciało wokół osi
równoległej do kierunku magnesowania – zjawisko Einsteina i de Haasa;

- zwiększanie się indukcji nasycenia po napromieniowaniu neutronami.

Istotę ferromagnetyzmu najlepiej wyjaśnia mechanika kwantowa

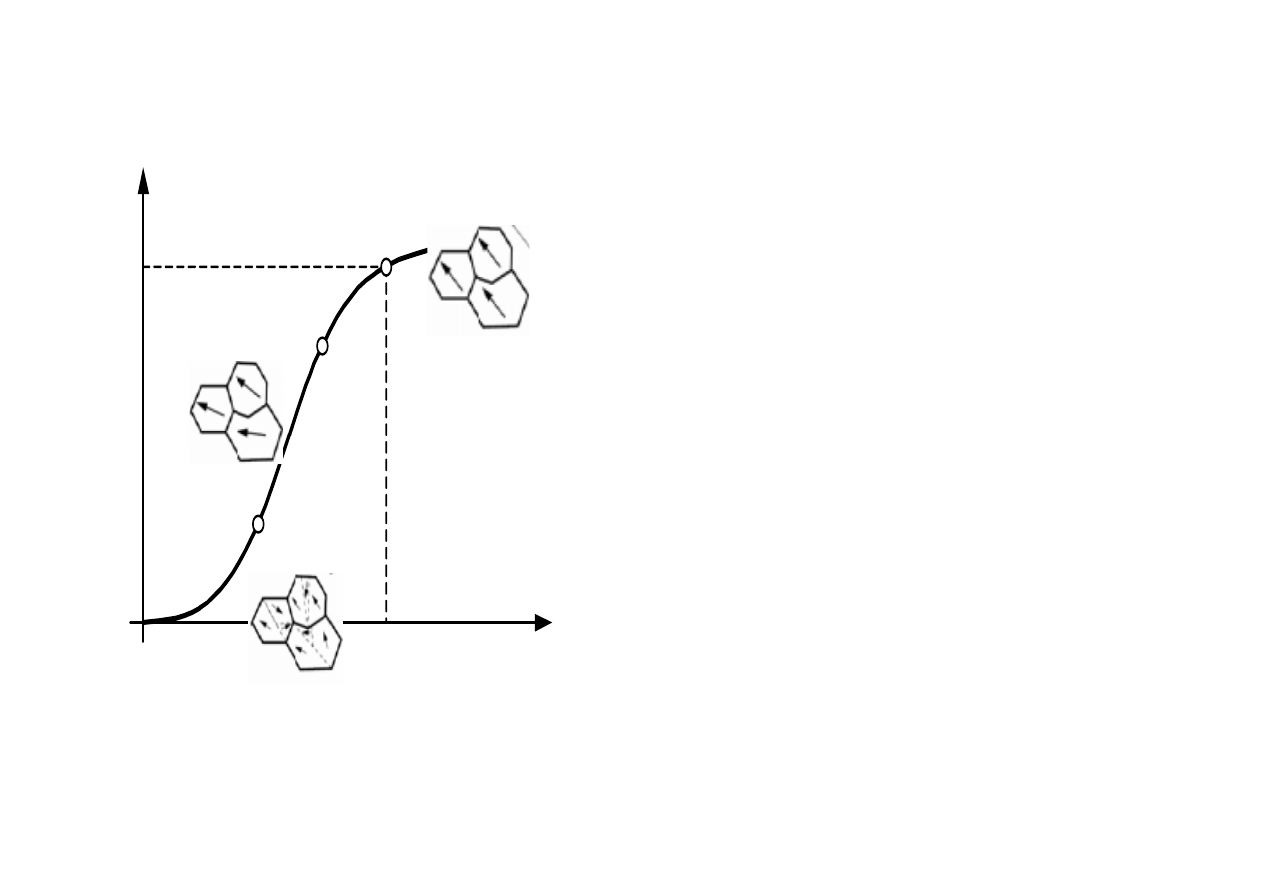
Pierwotna krzywa magnesowania

H

B

0

1

2

3

H

n

B

n

pierwotną krzywą magnesowania otrzymuje się
dla próbki ferromagnetyka magnesowanej po raz
pierwszy.
Można na niej wyróżnić cztery charakterystyczne
części:
- odcinek 0-1, zwany dolnym zagięciem
charakterystyki, na którym przenikalność
magnetyczna µ rośnie,
- odcinek 1-2, będący w przybliżeniu odcinkiem
prostoliniowym o nachyleniu µ

≈ const,

-odcinek 2-3, zwany górnym zagięciem
charakterystyki, na którym µ maleje
- odcinek powyżej punktu 3, będący obszarem
nasycenia; na tym odcinku krzywa ma stałe
nachylenie odpowiadające µ = µ

0

i dalszy wzrost

natężenia pola H powoduje nieznaczny tylko
przyrost indukcji B wg wzoru B = const + µ

0

H.

odwracalne
przesunięcie
ścian Blocha

nieodwracalne przesunięcie
ścian Blocha

Obrotowy ruch
wektorów
magnetyzacji

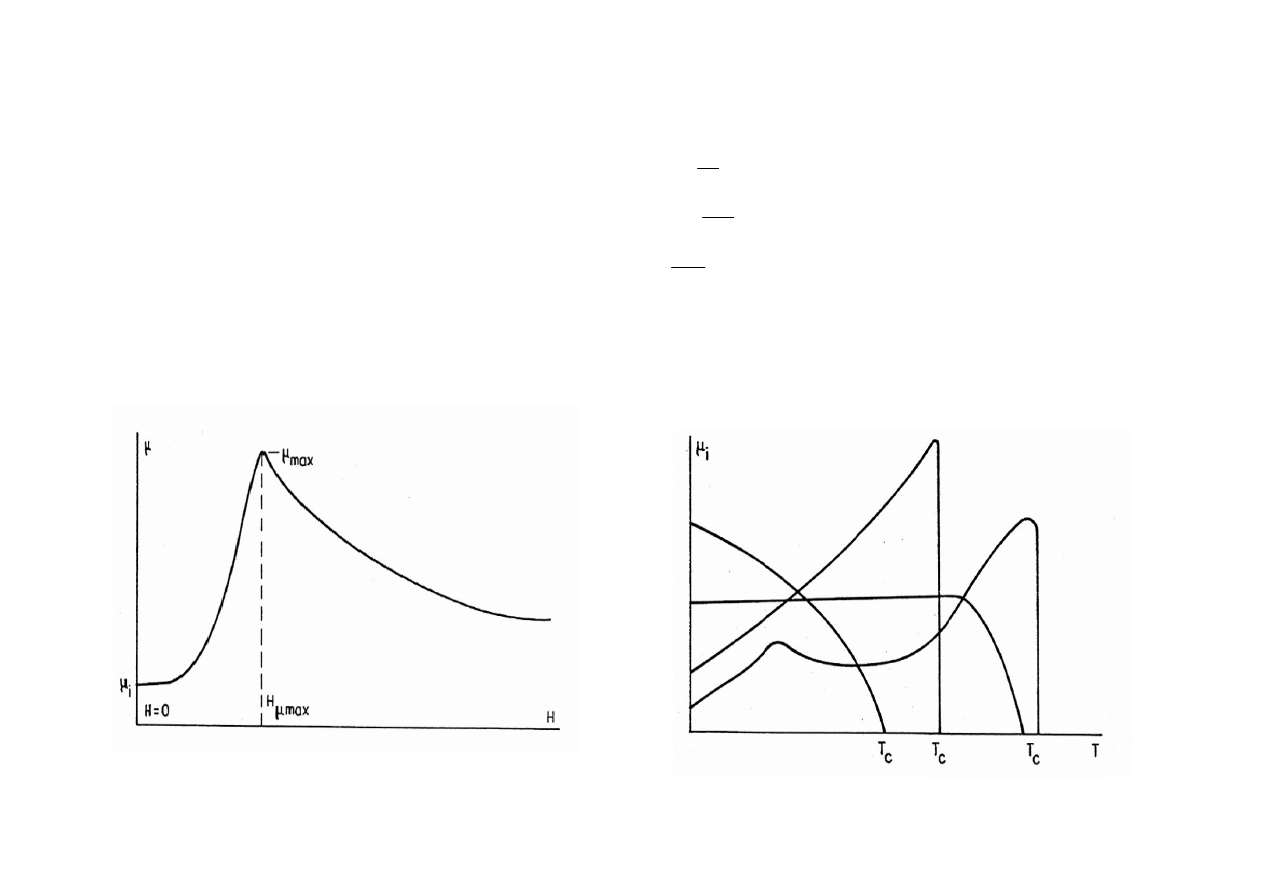
przykład zależności przenikalności
magnetycznej od natężenia pola
magnetycznego

Parametry statyczne i dynamiczne

PRZENIKALNOŚĆ MAGNETYCZNA AMPLITUDOWA

PRZENIKALNOŚĆ POCZĄTKOWA

przykłady zależności przenikalności
magnetycznej od temperatury

Przenikalność statyczna

Przenikalność dynamiczna

Przenikalność przyrostowa

γ

μ

μ

μ

tg

H

B

dH

dB

H

B

dyn

=

Δ

Δ

=

=

=

Δ

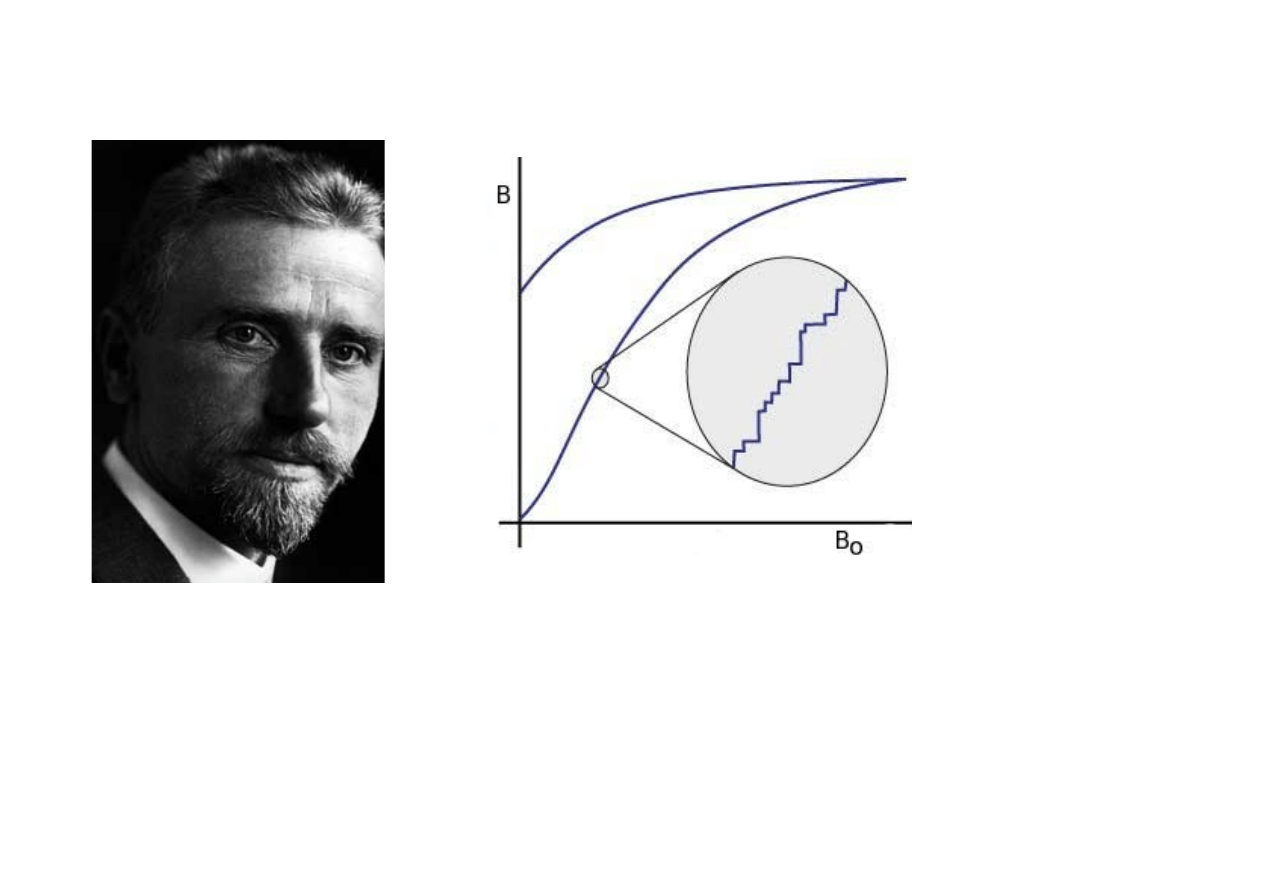
zjawisko Barkhausena

skokowe zmiany namagnesowania ferromagnetyka pod wpływem ciągłej
zmiany natężenia zewnętrznego pola magnetycznego (lub innych warunków
zewnętrznych). Jest ono wynikiem skokowego przesuwania się granic
domen magnetycznych, tzw. ścianek Blocha, ustawiających się w kierunku
zewnętrznego pola magnesującego.

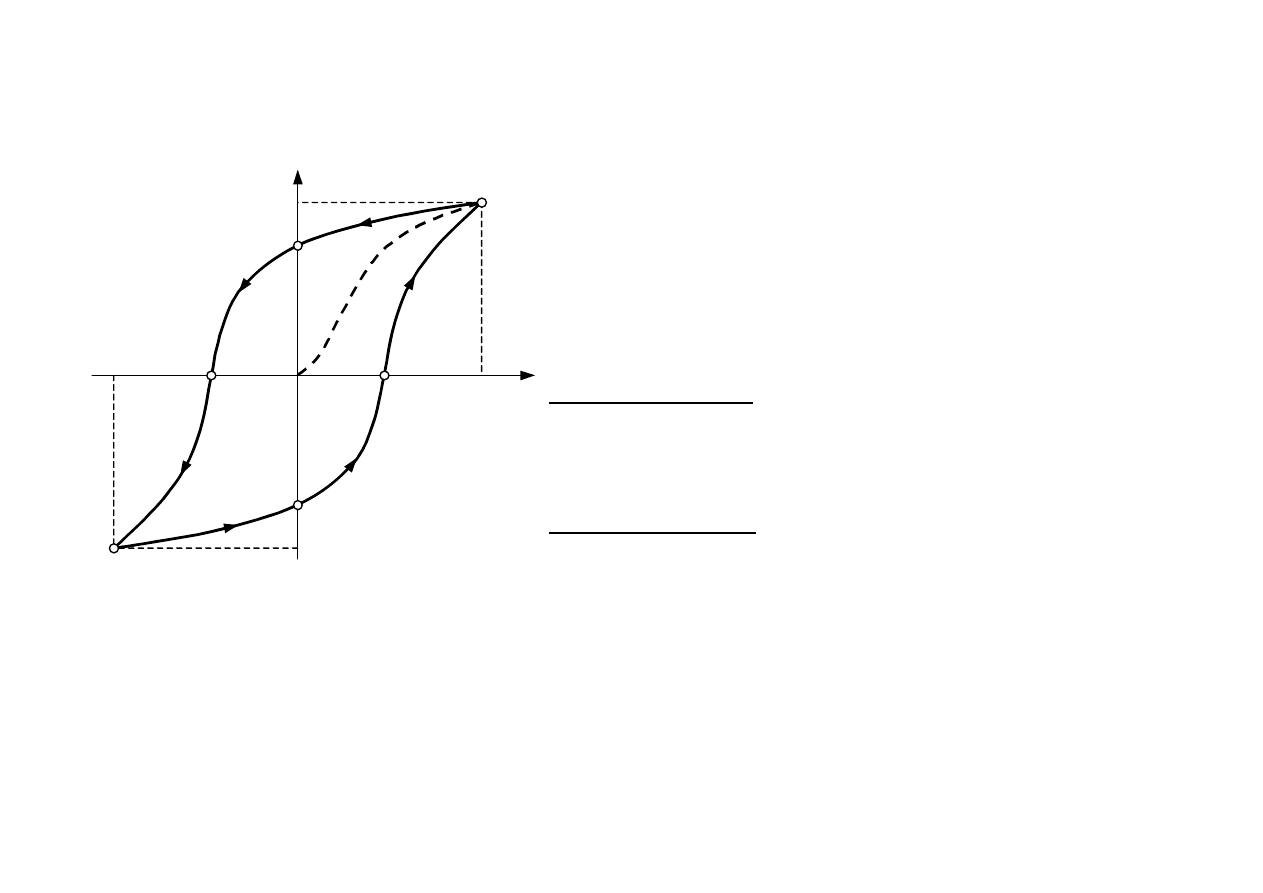
Pętla histerezy

H

B

C

′

C

0

A

A

′

B

n

H

n

–H

n

–B

n

–H

k

B

r

Dokonując wielokrotnego przemagnesowania
ferromagnetyka od wartości –H

n

do +H

n

i z powrotem od +H

n

do –H

n

otrzymuje się

symetryczną krzywą zamkniętą, zwaną pętlą
histerezy
Pętla histerezy odcina na osiach dwa
charakterystyczne odcinki:
odcinek 0A = 0A

′

, którego długość jest równa

indukcji szczątkowej B

r

(remanentu), tj. indukcji

występującej przy braku natężenia zewnętrznego
pola magnetycznego,
odcinek 0C

′

= 0C, którego długość jest równy

natężeniu koercji Hk (natężenie
powściągającego), tj. zewnętrznego natężenia pola
magnetycznego potrzebnego do całkowitego
rozmagnesowania materiału.

Kształt pętli histerezy zależy od wielu czynników, m.in. od składników materiału
ferromagnetycznego i sposobu jego obróbki. Ze względu na szerokość pętli materiały
ferromagnetyczne dzielimy na magnetycznie twarde i magnetycznie miękkie

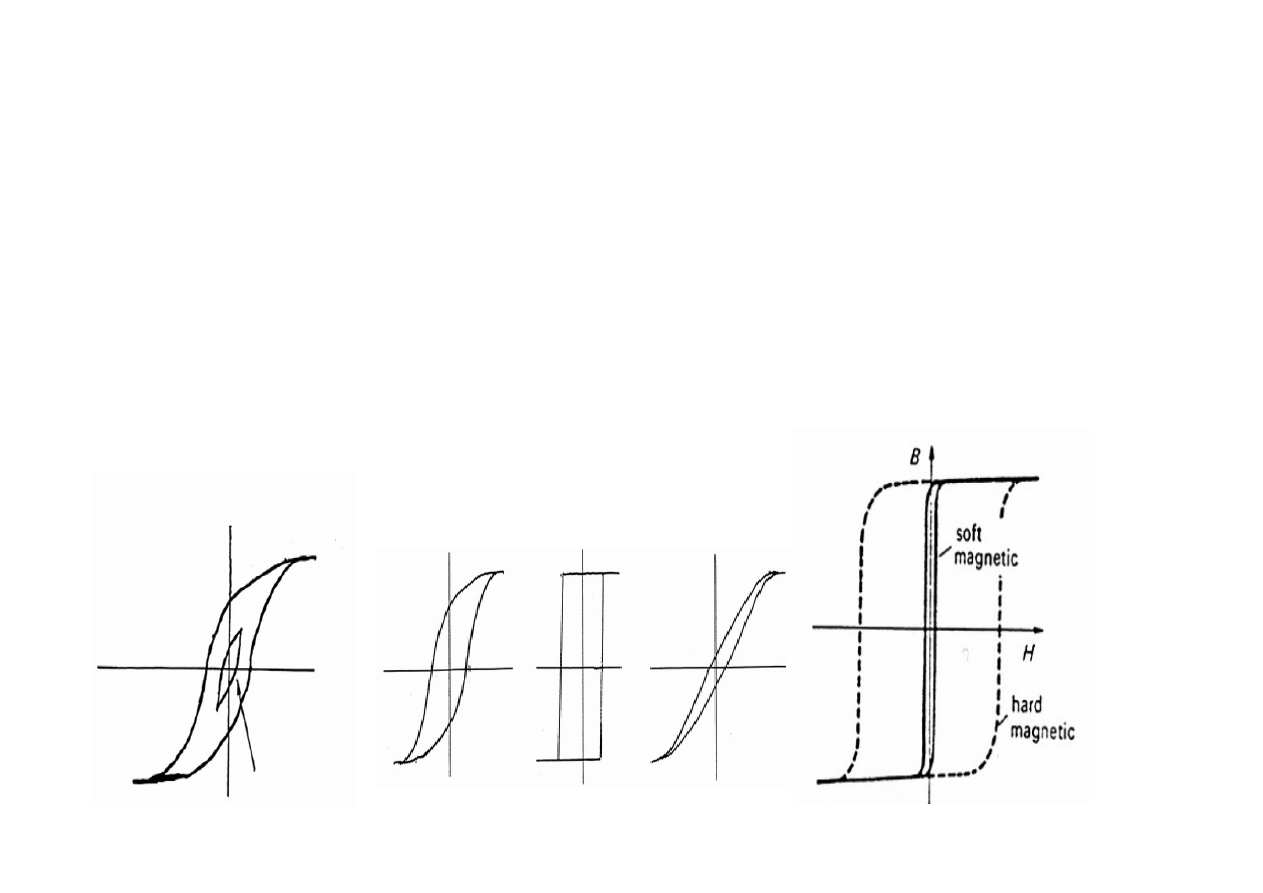
ODDZIAŁYWANIE FERROMAGNETYKÓW Z

POLEM MAGNETYCZNYM

KSZTAŁT PĘTLI HISTEREZY

zależy od:
• rodzaju materiału
• amplitudy i częstotliwości
pola magnetycznego
• stanu obróbki materiału

magnetycznie twardy
magnetycznie miękki

mała amplituda

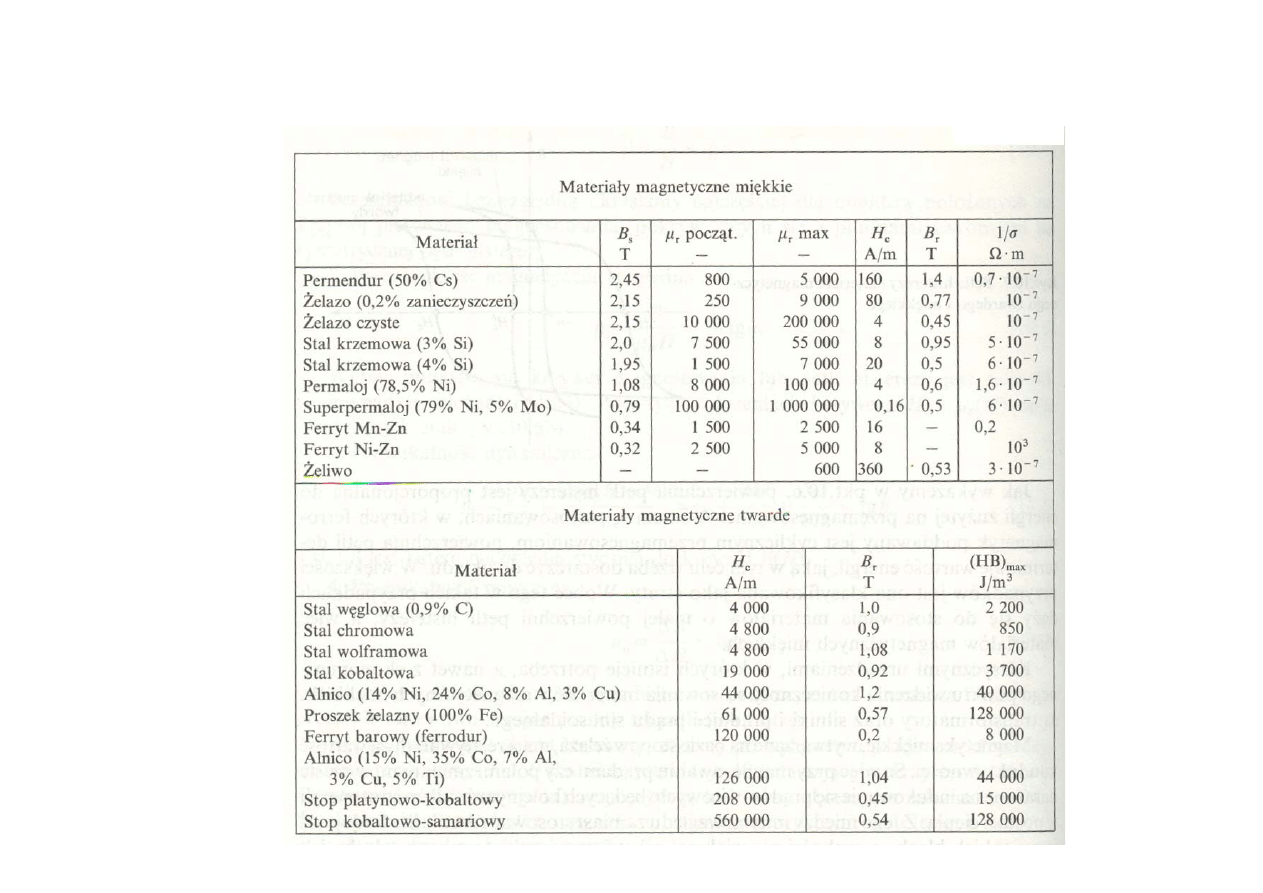
Materiały magnetyczne miękkie

Materiały o małej koercji magnetycznej (o wąskiej pętli histerezy)
: Hc < 10 A/m

Znajdują one zastosowanie do budowy rdzeni transformatorów,elektromagnesów, dławików i
innych elementów elektronicznych, rdzenie elektromagnesów prądu stałego
obwody magnetyczne pracujące przy okresowo zmiennych strumieniach magnetycznych
(maszyny elektryczne ,dławiki, - prądu zmiennego)

Pętla Histerezy Materiałów magnetycznie

miękkich

B [T]

H[

A

/m

]

łatwo i silnie się magnesują (duża podatność

magnetyczna) ale i łatwo się rozmagnesowują (mała
pozostałość magnetyczna)

Żelazo technicznie czyste (armco)
Stale niskowęglowe i krzemowe
Stopy żelaza z niklem (permalloy,
supermalloy)
Stopy żelaza z kobaltem
Stopy żelaza z aluminium
Stopy żelaza z krzemem
stopy niklu z żelazem i kobaltem

ferryty

Materiały magnetyczne miękkie

Obwody

o stałym strumieniu

Obwody

o zmiennym strumieniu

żeliwo
stale niskowęglowe

żelazo armco

stale krzemowe

stale krzemowe

stale bezkrzemowe

stopy żelazo-nikiel

stopy żelazo-kobalt

inne

anizotropowe

izotropowe

szkła metaliczne

ferryty

materiały niemetaliczne

.........................

Podział materiałów magnetycznie miękkich

Cechy dobrego materiału magnetycznie miękkiego

duża wartość indukcji nasycenia B

n

duża wartość przenikalności magnetycznej względnej maksymalnej

μ

wm

małą stratnością magnetyczną
stabilnością powyższych własności w czasie eksploatacji
łatwością kształtowania gotowych wyrobów
niska cena

Materiały magnetyczne twarde

Materiały o dużej koercji magnetycznej (o szerokiej pętli histerezy)
: Hc > 100 A/m

Są one dobrym materiałem do budowy magnesów. Znajdują też zastosowanie w różnych rozwiązaniach pamięci
magnetycznych.

Pętla Histerezy Materiałów m agnetycznie

tw ardych

B [T]

H [

A

/m

]

duża pozostałość magnetyczna
są źródłami pola magnetycznego

Stale węglowe (0,8%-1,5% węgla w

stanie zahartowanym

Stale chromowe

Ferryty Barowe i Strontowe

Stopy żelaza, aluminium, niklu, kobaltu z
domieszkami miedzi lub tytanu (alnico)

Materiały magnetyczne

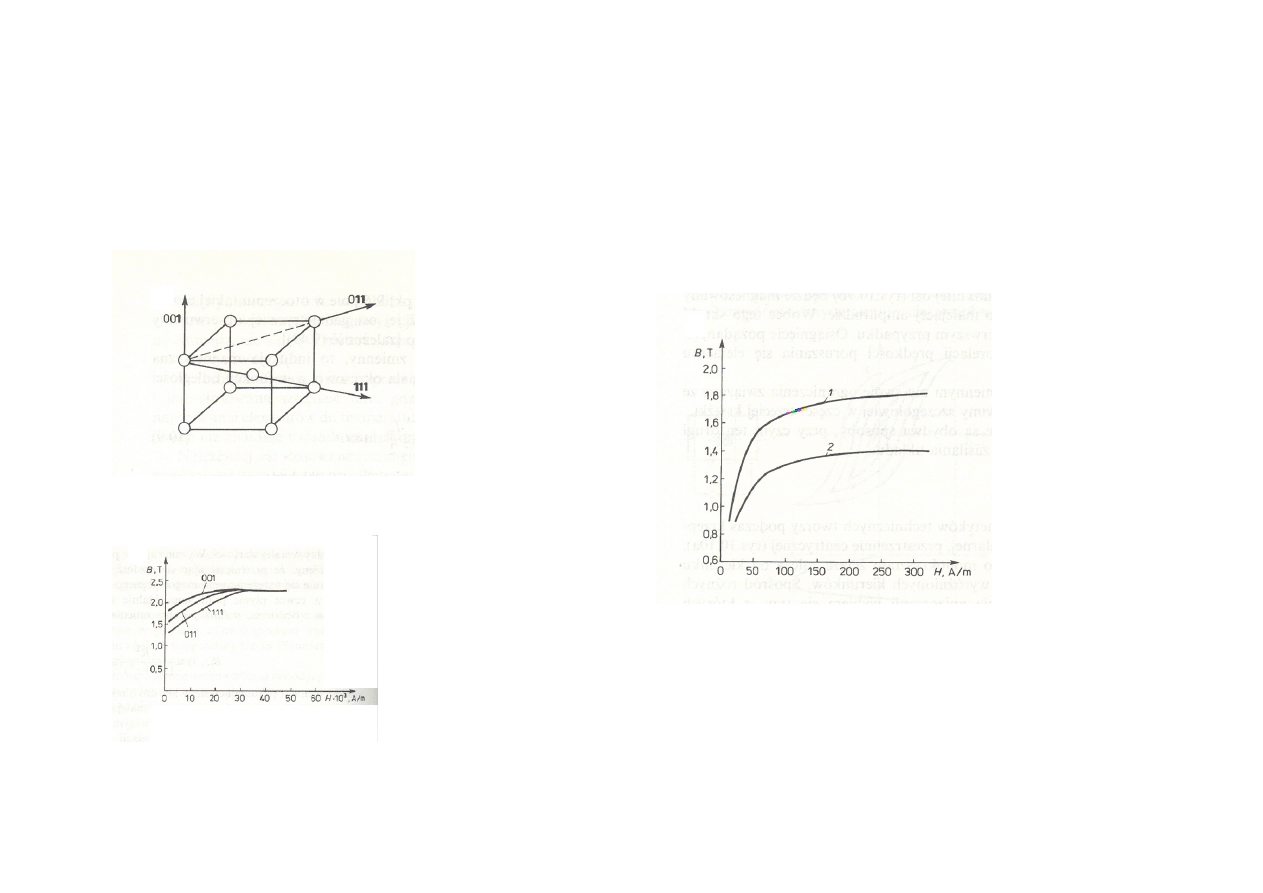
anizotropowość

Głównie występuje w krystalicznych ferromagnetykach
W ciałach polikrystalicznych zanika
Może być także wywołana procesem technologicznym , np.. blachy walcowane na zimno

Struktura krystaliczna żelaza

Przebieg magnesowania w wybranych
Kierunkach anizotropii

Krzywe magnesowaqnia blach transformatorowych
walcowanych „na zimno”

Zgodnie z kierunkiem walcowania

Prostopadle do kierunku walcowania

H.Rawa, PWN W-wa 1994

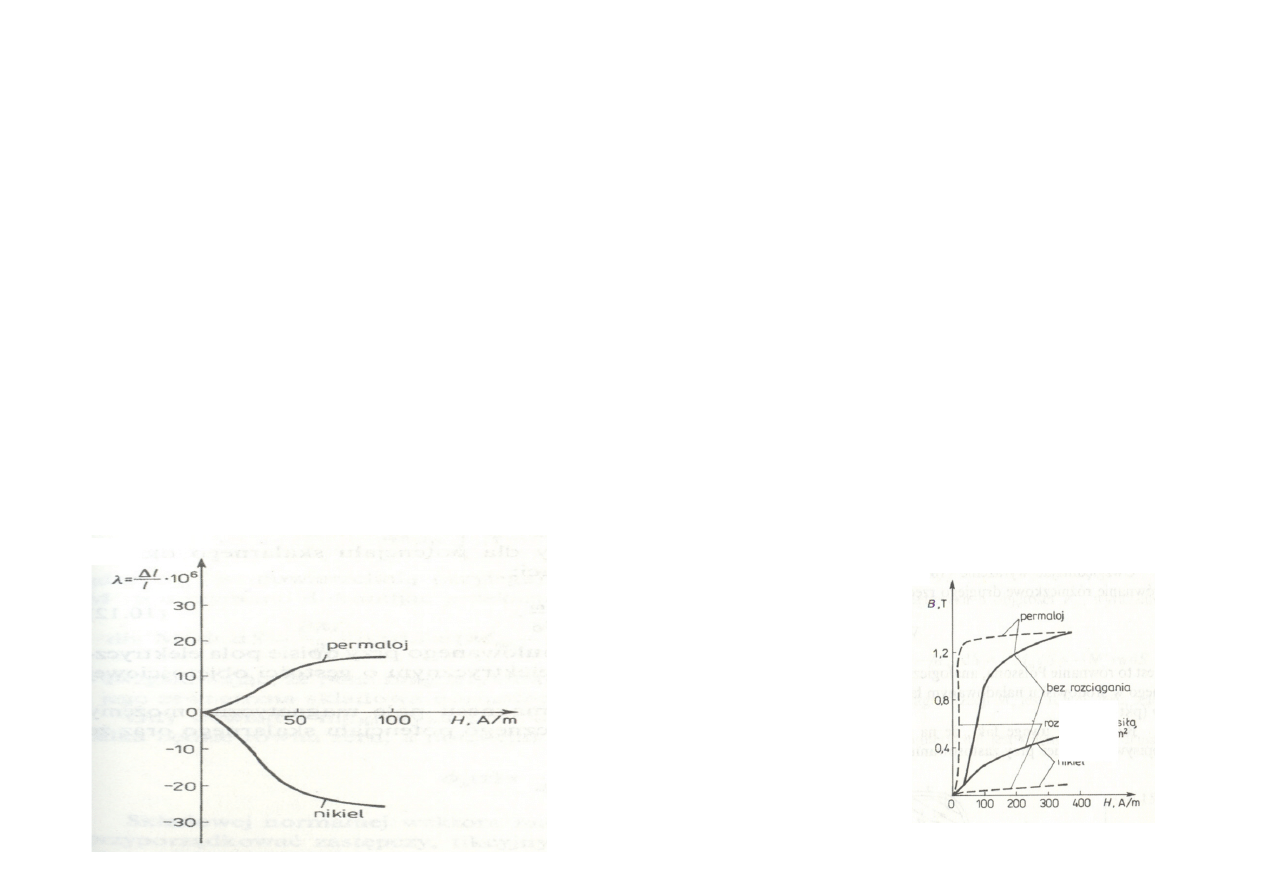
Magnetostrykcja ( efekt Joula )

Historia magnetostrykcji sięga 1842 roku, w którym James Joule zaobserwował zmiany
wymiarów w próbce niklu pod wpływem pola magnetycznego. Podobne zjawisko
zaobserwowano w kobalcie, żelazie i stopach tych metali.
Magnetostrykcja (efekt Joula),
- odkształcenie się ferromagnetyka pod wpływem pola magnetycznego ( bardzo słaby
efekt , rzędu 0,0005 % )
W materiałach ferromagnetycznych wraz z efektem magnetostrykcji występuje efekt
odwrotnej magnetostrykcji (efekt Villariego), który polega na zmianie magnetyzacji
materiału pod wpływem zmiany naprężeń wewnętrznych
materiału.
Zjawisko magnetostrykcji i efekt do niej odwrotny są wykorzystywane do budowy
przetworników i czujników.

Zmiana wymiarów podczas magnesowania

Zmiana charakterystyk magnesowania
pod wpływem rozciągania

Materiały magnetyczne

Szkło metaliczne

Cechy:
-

stop ferromagnetyczny,

-

struktura amorficzna (bezpostaciowa), powstaje gdy szybkość schładzania ciekłego stopu jest

większa od szybkości krystalizacji. W skład takiego stopu wchodzi: Fe, Co, Ni, z dodatkiem B, Si, C (skracają
czas stygnięcia poniżej 10

-6

s)

-

izotropia magnetyczna

-

b. wąska pętla histerezy

-

niższa niż w blachach orientowanych indukcja nasycenia ok. 1,6 T

-

niższa temp. Curie

-

około 3-krotnie niższa stratność

-

wytwarzane w postaci bardzo cienkich taśm 0,03 do 0,05 mm o szerokości 25 do 300 mm.

-

bardzo duża przenikalność początkowa rzędu 10

5

-

poważną wadą jest wysoka cena

Zastosowanie:
-czytniki kart magnetycznych

Magnetodielektryki

Kompozyt z drobinek materiału magnetycznego miękkiego, zatopionego w dielektryku;
niska przenikalność początkowa., nieco lepsza od powietrza.
Wykorzystuje się tu dwa efekty:
magnetorezystancyjny(. – zmiana pola zmienia rezystancję- nie zależy od prędkości zmian pola)
oraz magnetorezystancyjne zjawiko anizotropowe;

czytniki kart magnetycznych;

Materiały magnetyczne

Ferryty

Tlenki żelaza i innych metali:

Cechy:
- własności ferrimagnetyczne i ceramiczne: są twarde, kruche, trudno obrabialne, lekkie, odporne chemicznie
- słabo przewodzą prąd, są prawie dielektrykiem
- duża przenikalność magnetyczna do 6000
- bardzo duża rezystywność 10

2

– 10

8

ohm*cm (np. blachy 10

-5

ohm*cm, 13 rzędów różnicy)

- czarne
- przez odpowiedni dobór składu chemicznego, obróbki termicznej i chemicznej można znacznie zmieniać ich
własności magnetyczne i kształtować odpowiednio pętlę histerezy.
- niska temp Curie
- niska indukcja nasycenia < 1T
-H koercji metali < H koercji ferrytów
-prawie nie występują prądy wirowe

•przy obwodach magnetycznych trzeba ciąć gotowy kształt gdyż nie podlega obróbce.

Zastosowanie:
-

transformatory, dławiki, filtry, przełączniki elektroniczne, pamięci magnetyczne,

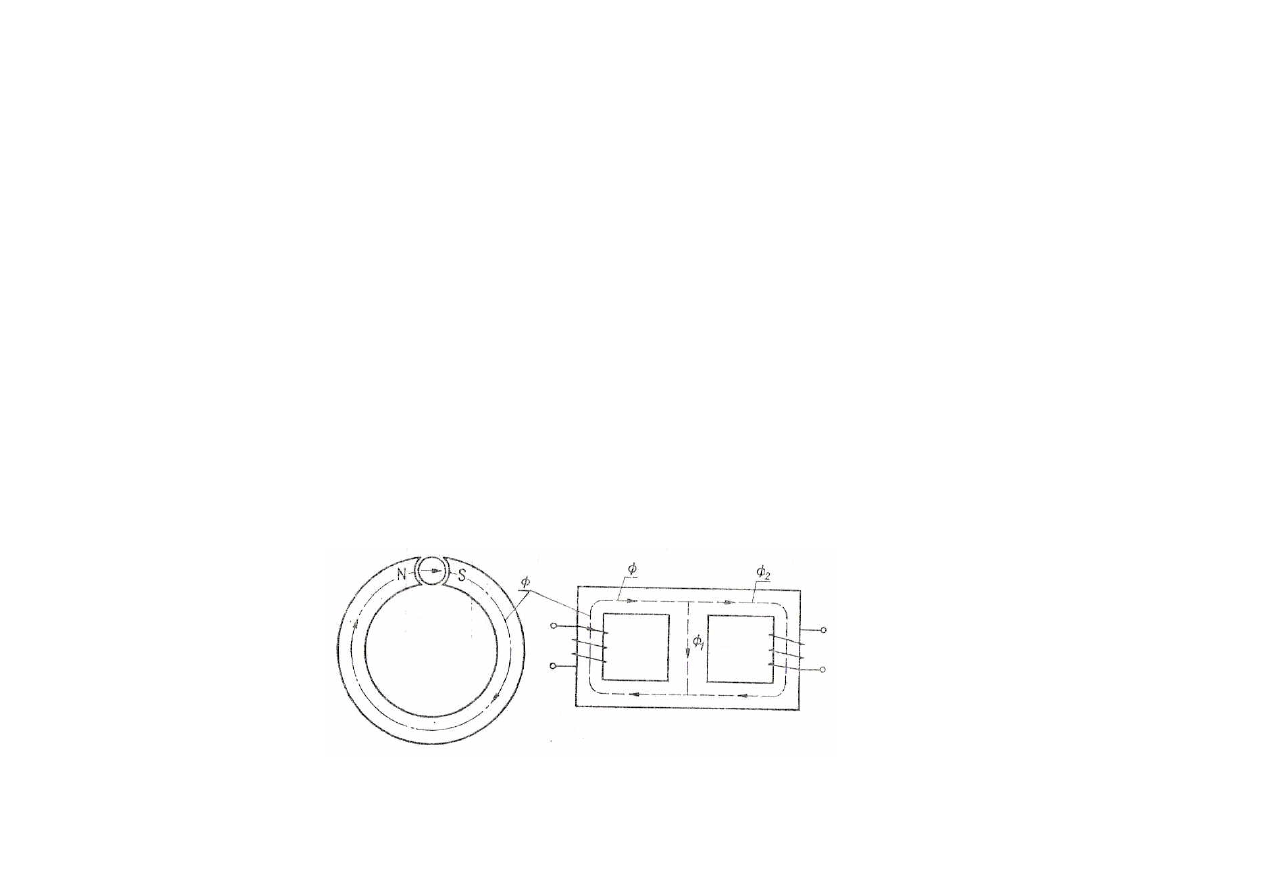
Obwody magnetyczne

Obwodem magnetycznym nazywa się zespół elementów zawierających materiały
magnetyczne służące do skupiania strumienia magnetycznego ( linii indukcji
magnetycznej ) w określonej części przestrzeni. Rozróżnia się obwody z magnesami
trwałymi i obwody z magnetykami stanowiącymi rdzenie dla zwojnic przez, które płynie
prąd elektryczny.

Obwód nazywa się obwodem nierozgałęźnym ( jednooczkowym ) jeżeli strumień
magnetyczny przez każdy przekrój poprzeczny obwodu ( nie uwzględniając niewielkiego
strumienia rozproszenia ) jest jednakowy.

W przeciwieństwie do tego, w obwodzie rozgałęźnym ( wielooczkowym ) strumienie
przechodzące przez różne przekroje obwodu mogą być różne.

Obwód nierozgałęziony
( zastosowany w magneto-elektrycznym przyrządzie
Pomiarowym )

Obwód rozgałęziony
( transformator dwuuzwojeniowy z dwoma okienkami w
rdzeniu )

Obwody magnetyczne

(

)

k

S

L S

H d l

I

∑

∫

= ±

o

[ ]

nI

A

amperozwoje

Θ =

Θ = =

Podstawowym prawem, , które jest punktem wyjścia do teorii obwodów magnetycznych jest prawo
przepływu.

Iloczyn prądu przez liczbę zwojów nazywa się siłą magnetomotoryczną Θ

Zgodnie z prawem przepływu

(

)

L S

H d l

∫

=Θ

o

Gdzie drogę L(S) dobrano tak, że pokrywa się ona z linią pola magnetycznego

wzdłuż całego obwodu

Obwody magnetyczne

0

r

B

H

H

μ μ

μ

=

=

H d l

o

Jeżeli pole rozproszenia można pominąć i w pierwszym przybliżeniu przyjąć dla

materiałów magnetycznych, że spełnione jest równanie materiałowe

oraz zakładając, że wzdłuż linii pola magnetycznego iloczyn

można zastąpić iloczynem skalarów Hdl
oraz zastąpić całkę sumą odpowiednich iloczynów H

ν

l

ν

gdzie indeks ν oznacza kolejny odcinek wzdłuż , którego przyjmuje się, że
pole H i przenikalność μ są stałe, to otrzymamy prawo przepływu w postaci

1

1

n

n

B

H l

l

ν

ν ν

ν

ν

ν

ν

μ

=

=

∑

∑

Θ =

=

gdzie n oznacza liczbę odcinków obwodu magnetycznego

Obwody magnetyczne

(

)

0

S V

B d s

∫

Φ =

=

o

B s

ν

ν ν

Φ = Φ =

Gdzie s

ν

oznacza przekrój poprzeczny ν-tego odcinka obwodu magnetycznego.

Ostatecznie otrzymamy:

Ze względu na bezźródłowość pola magnetycznego, strumień magnetyczny przez
powierzchnię zamknięta S(V) jest równy zero

to dla obwodu magnetycznego nierozgałęźnego strumień magnetyczny jest stały we
wszystkich przekrojach poprzecznych rdzenia.

1

n

m

l

R

s

ν

ν

ν

ν

μ

=

∑

Θ

Θ

Φ =

=

Równanie to opisuje tzw. prawo Ohma dla obwodu magnetycznego

Obwody magnetyczne

1

n

m

l

R

s

ν

ν

ν

ν

μ

=

∑

=

[ ]

1

m

A

R

Wb

=

wielkość tą nazywa się oporem magnetycznym lub reluktancją

Odwrotność reluktancji → przewodność magnetyczna lub permeancja

ze względu na analogię obwodów magnetycznych i elektrycznych można powiedzieć, że dla
każdego węzła ( punktu rozgałęzienia ) rozgałęzionego obwodu magnetycznego będzie
obowiązywało strumieniowe prawo Kirchoffa, analogicznie do prądowego prawa Kirchoffa.

0

=

Φ

±

∑

ν

Obwody magnetyczne

Natomiast dla każdego magnetycznego obwodu zamkniętego będzie obowiązywało
napięciowe prawo

Kirchoffa.

Napięcie magnetyczne można określić jako iloczyn oporu magnetycznego przez
strumień lub iloczyn natężenia pola magnetycznego przez długość .

Obwód elektryczny

Obwód
magnetyczny

żródło

Ε

Θ

opór

R

R

m

Prawo Ohma

I=E/R

Φ=Θ/R

m

PPK

Σ±I

k

=0

Σ±Φ

ν

=0

NPK

Σ±U

k

±E

k

=0

Σ±U

k

±Θ

k

=0

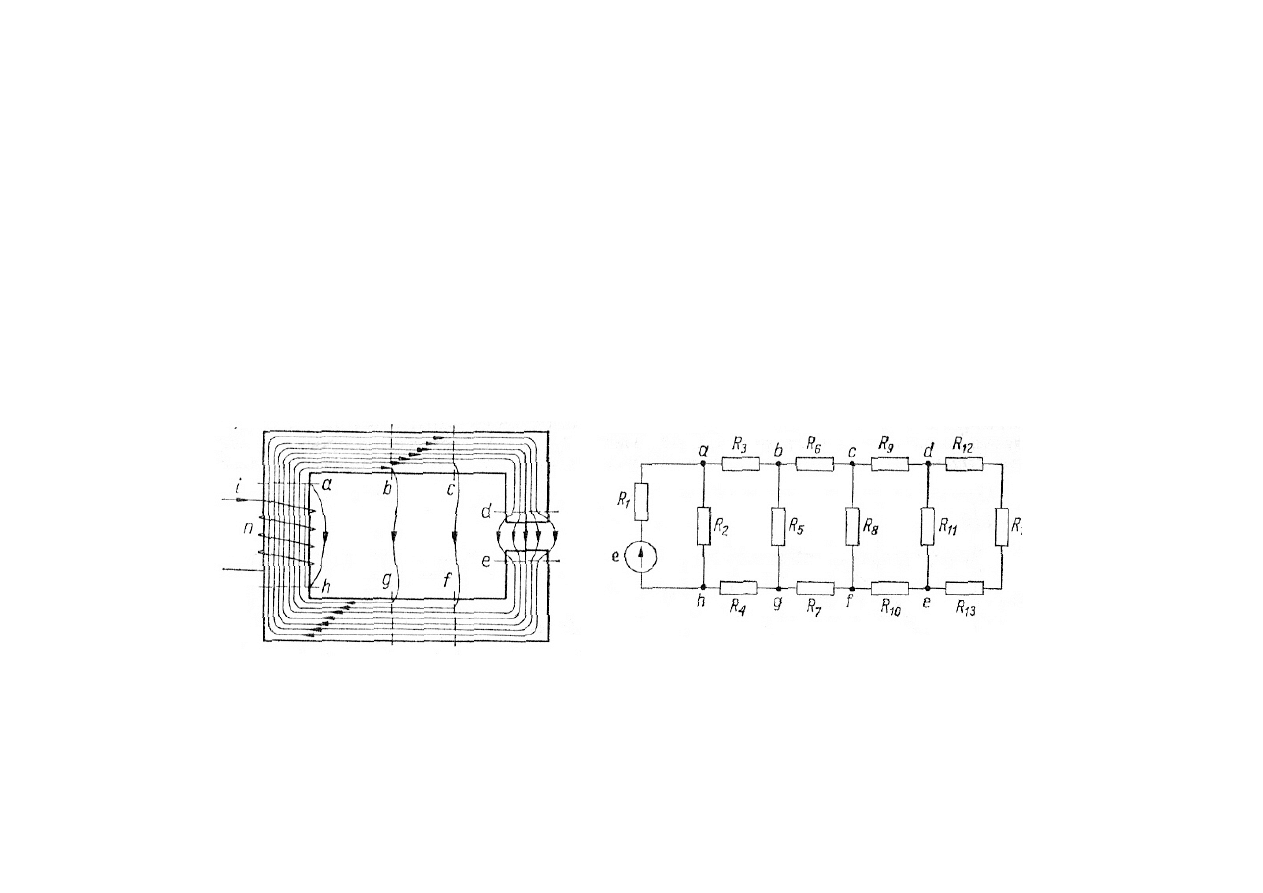
Obwody magnetyczne

W obwodach magnetycznych należy uwzględnić strumień rozproszenia, który
odgrywa dużą rolę w cewkach, transformatorach i maszynach elektrycznych.
W obwodach magnetycznych prawie zawsze zachodzi zjawisko rozpraszania

strumienia magnetycznego, tzn. że nie wszystkie linie pola magnetycznego przebiegają

na całej swej długości przez wyznaczoną ( pożądaną ) drogę, jaką jest na ogół
magnetyk, lecz niektóre z nich bocznikują główną drogę powodując , że strumień
przepływający poprzez poszczególne przekroje nie jest jednakowy.

Chcąc możliwie dokładnie uwzględnić analitycznie wpływ rozproszenia magnetycznego
należałoby badać go jako obwód rozgałęźny ( wielooczkowy ) dodając kilka gałęzi bocznikujących

główny strumień ( jest to jednak przybliżenie ).

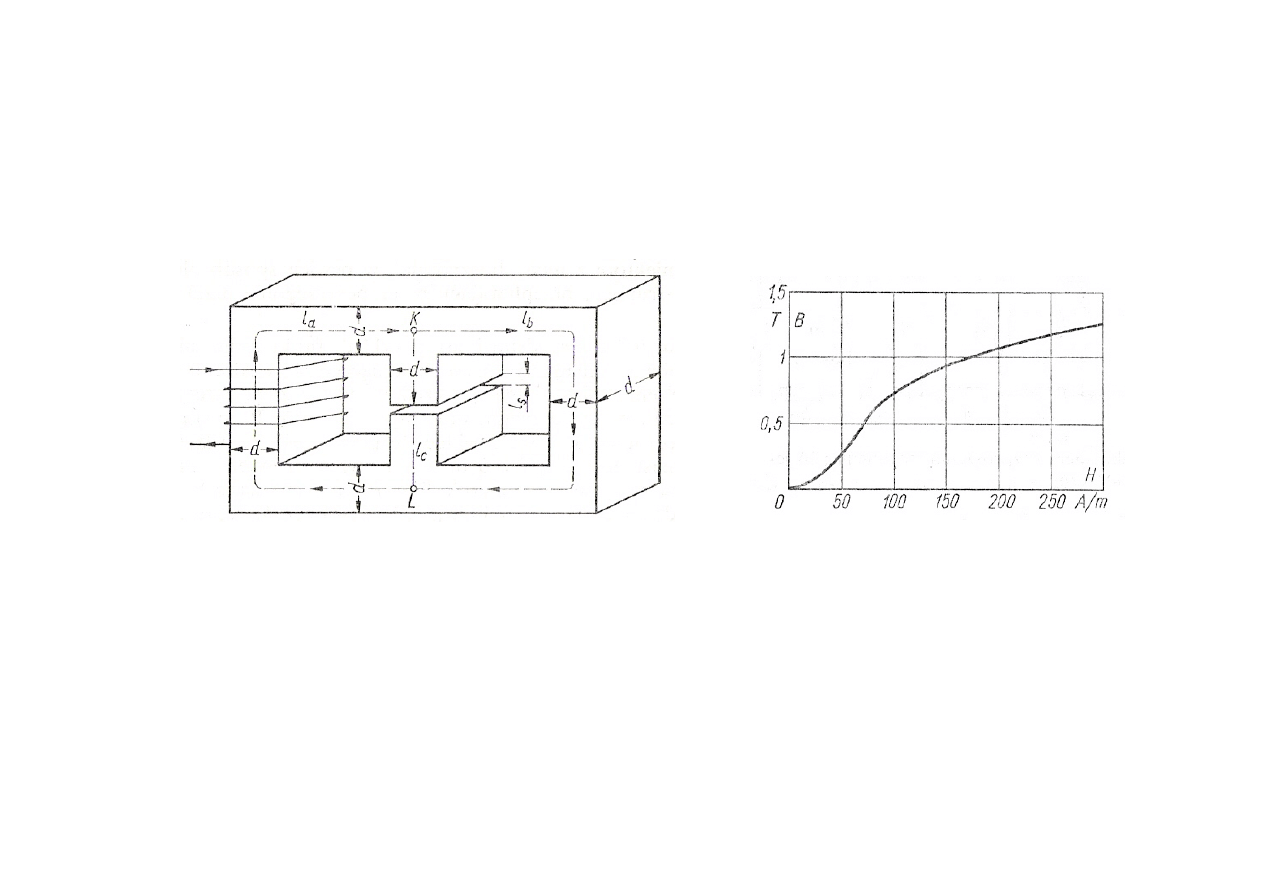
Obwody magnetyczne

Dany jest obwód magnetyczny ( l

a

,l

b

, l

c

, l

s

, d ):

Należy wyznaczyć:
-indukcję magnetyczną B

s

w szczelinie zakładając, ze znamy siłę magnetomotoryczną Θ

i przenikalność względna rdzenia μ

r

-siłę magnetomotoryczną Θ’ w celu uzyskania indukcji w szczelinie B’

s

przy danym μ

r

-siłę magnetomotoryczną Θ’ dla uzyskania indukcji w szczelinie B’

s

jeżeli znamy

charakterystykę magnesowania rdzenia B= f(H)

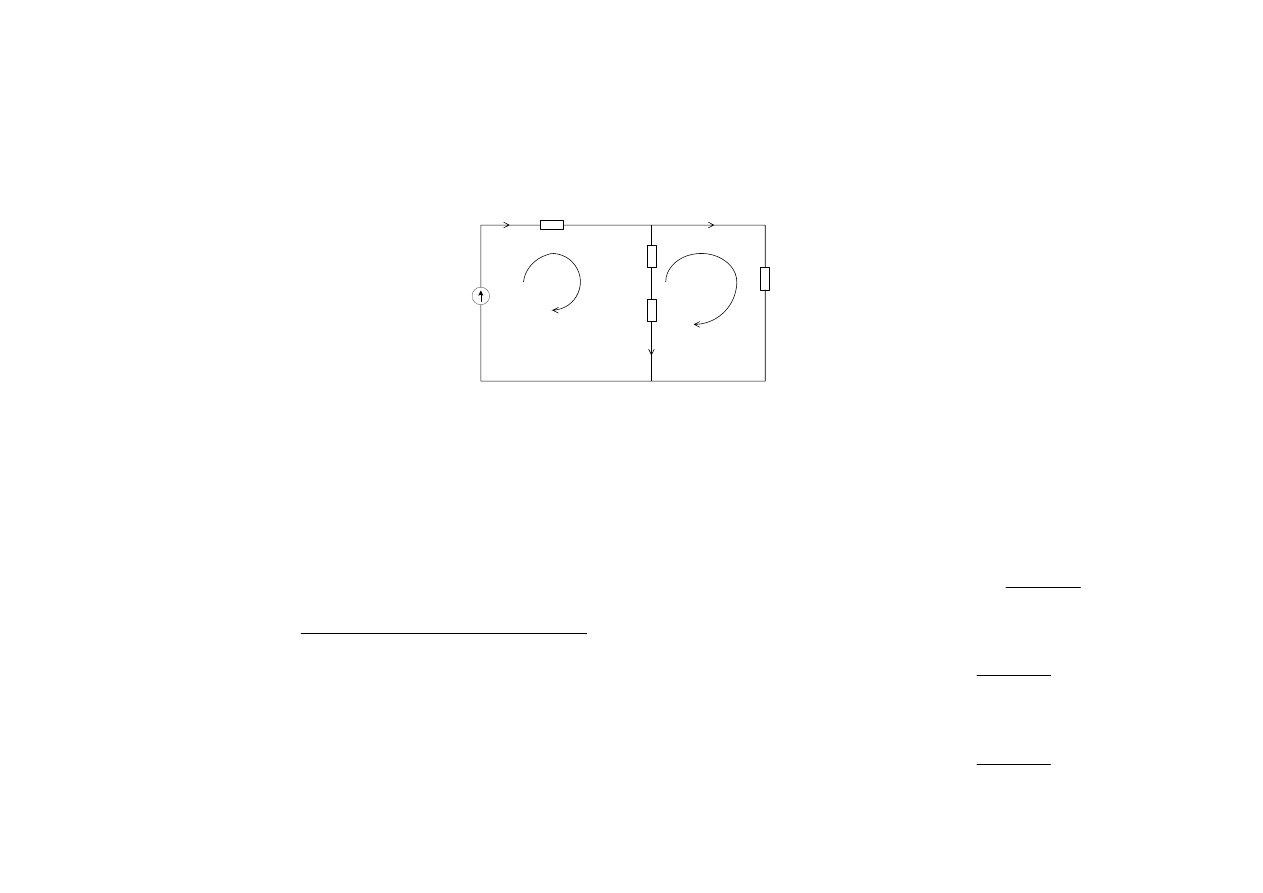
Obwody magnetyczne

1

2

1

2

(

)

(

)

(

)

(

)

0

a

c

s

c

s

a

s

b

c

s

R

R

R

R

R

R

R

R

R

R

Φ

+

+

− Φ

+

= Θ

Φ

+

− Φ

+

+

=

1

2

(

)(

)

b

a

b

c

s

a

b

R

R

R

R

R

R R

Θ

Φ − Φ =

+

+

+

0

0

0

a

a

b

r

a

c

c

r

c

s

s

r

s

l

R

R

s

l

R

s

l

R

s

μ μ

μ μ

μ μ

=

=

=

=

Stąd strumień płynący przez szczelinę

obwód magnetyczny możemy zastąpić analogiem obwodu elektrycznego

Stosując metodę prądów oczkowych

Opory magnetyczne

nI

Θ =

1

Φ

2

Φ

b

Φ

c

Φ

a

Φ

a

R

c

R

s

R

b

R

Obwody magnetyczne

2

(

2 )

s

s

s

d

l

=

+

1

2

s

s

B

s

Φ − Φ

=

s

s

– ze względu na rozproszenie występujące na krawędziach rdzenia przy szczelinie

powietrznej, w praktyce przyjmuje się, ze efektywna powierzchnia szczeliny wynosi:

Zatem:

2) Ponieważ układ podstawowych równań jest liniowy, więc korzystając z zasady
proporcjonalności możemy policzyć Θ’

'

'

s

s

B

B

Θ = Θ

Obwody magnetyczne

0

s

s

s

s

B l

H l

μ

=

s

s

c

c

s

s

c

c

B s

B s

B s

B

s

=

⇒

=

3) Siłę magnetomotoryczną można również policzyć z NPK jako sumę napięć magnetycznych
wzdłuż drogi l

a

-l

c

-l

s

Napięcie na drodze l

s

wynosi

Ze względu na ciągłość strumienia magnetycznego

Zgodnie z krzywą magnesowania indukcji B

c

odpowiada natężenie pola magnetycznego H

c

,

a więc możemy policzyć napięcie na drodze lc →H

c

l

c

W celu wyznaczenia trzeciego składnika NPK H

a

l

a

, należy wyznaczyć indukcję B

a

Zgodnie z PPK dla strumieni

a

b

c

a

c

c

b

b

a

c

b

a

a

B s

B s

B

B

B

s

s

Φ = Φ + Φ

Φ

+

=

=

≅

+

B

b

możemy wyznaczyć z NPK dla drugiego oczka

Obwody magnetyczne

0

s

s

c c

s

s

c c

b b

b

b

H l

H l

H l

H l

H l

H

l

+

+

−

= ⇒

=

Z krzywej magnesowania możemy odczytać wartość B

b

odpowiadająca wartości H

b

wobec tego B

a

=B

b

+B

c

I ponownie z krzywej magnesowania możemy odczytać H

a

odpowiadające wartości B

a

Teraz może3my policzyć napięcie na drodze l

a

→H

a

l

a

I ostatecznie korzystając z NPK dla oczka pierwszego wyznaczyć siłę magnetomotoryczna Θ

s

s

c c

a

a

H l

H l

H l

Θ =

+

+

zadanie

l

a

=l

b

=0,977m, l

c

=0,343m, l

s

=7,6210

-4

m, d=8,910

-2

m

1) Θ=200A, μ

r

=4000

2) B’

s

=0,2T, μ

r

=4000

3) B’

s

=0,2T