
Laboratorium Grafiki Komputerowej
Przekształcenia afiniczne
Wprowadzenie
Transformacja afiniczna jest przekształceniem wzajemnie jednoznacznym prostej w prostą,
płaszczyzny w płaszczyznę i przestrzeni w przestrzeń. Przekształcenie to zachowuje
równoległość linii, nie zachowuje jednak równości kątów oraz długości odcinków.
Przekształcenie afiniczne płaszczyzny zachowuje stosunek długości odcinków równoległych,
a przekształcenie afiniczne przestrzeni zachowuje stosunek pól figur leżących na
płaszczyznach równoległych.
Transformacje afiniczne obejmują w szczególności izometrie (np. przesunięcie równoległe,
obrót, symetrię osiową, symetrię płaszczyznową), jednokładności, czy powinowactwa osiowe.
1. Przekształcenia punktów na płaszczyźnie
1.1 Wprowadzenie
W tej części instrukcji zajmiemy się przekształceniami na płaszczyźnie, będą nas
interesowały transformacje obiektów graficznych. Najczęściej takie obiekty są opisywane
zbiorem wyróżnionych punktów, dlatego omawiane transformacje będą dotyczyły
pojedynczych punktów, a nie np. równań algebraicznych definiujących krzywe.
Pierwszym omówionym przekształceniem będzie przesunięcie (translacja) o dany wektor
]
,
[
y
x
d
d
d =
. Obrazem punktu
)
,
(
y
x
P =
w tym przekształceniu jest punkt
)
'
,
'
(
'
y
x
P =
o
współrzędnych:
y
x
d
y
y
d
x
x
+
=
+
=
'
'
Podstawowym przekształceniem jest także skalowanie, gdzie s
x
oraz s
y
są współczynnikami
skalowania. Obrazem punktu
)
,
(
y
x
P
=
w tym przekształceniu jest punkt
)
'
,
'
(
'
y
x
P
=
o
współrzędnych:
y
s
y
x
s
x
y
x
=
=
'
'
Inną podstawową transformacją jest obrót punktu wokół początku układu o dany kąt α
(dodatni kąt α jest skierowany przeciwnie do ruchu wskazówek zegara). Obrazem punktu
)
,
(
y
x
P
=
po obrocie o dany kąt α wokół początku układu jest punkt
)
'
,
'
(
'
y
x
P
=
o
współrzędnych:

2
α
α
α
α
cos
sin
'
sin
cos
'
y
x
y
y
x
x
+
=
−
=
Jeśli chcemy wykonać obrót nie wokół początku układu, lecz wokół dowolnego punktu
)
,
(
0
0
y
x
, to takie przekształcenie możemy złożyć z poprzednich. Dokładniej, wystarczy
najpierw przesunąć punkt
)
,
(
y
x
P =
o wektor
]
,
[
0
0
y
x −
−
, obrócić punkt
)
,
(
'
0
0
y
y
x
x
P
−
−
=
wokół początku układu, a następnie wykonać przesunięcie o wektor
]
,
[
0
0
y
x
.
Już z tego prostego przykładu widać, że byłoby wygodnie zapisywać w skondensowanej
formie wynik złożenia przekształceń zamiast wszystkich czynników. Narzucającym się
rozwiązaniem jest zapis macierzowy. Kłopot sprawia jedynie translacja. Nie da się jej
przedstawić w formie mnożenia wektora przez macierz, jeśli współrzędne punktu traktujemy
w naturalny sposób jako składowe wektora dwuwymiarowego. Możemy jednak przejść do
współrzędnych jednorodnych uważając punkty z R
2
za elementy przestrzeni R
3
leżące w
płaszczyźnie z = 1, a więc o trzech współrzędnych (x,y,1). W dalszej części instrukcji
wszystkie przekształcenia punktów na płaszczyźnie będą dotyczyły współrzędnych
jednorodnych, w takim podejściu wszystkie przekształcenia można zapisać w postaci mnożeń
macierzy – ułatwia to znacznie składanie przekształceń ze sobą.
1.2 Przesunięcie (translacja)
Zapisem macierzowym przesunięcia we współrzędnych jednorodnych będzie:
•
=
1
1
0
0
1
0
0
1
1
'
'
y
x
d
d
y
x
y
x
1.3 Skalowanie
Zapisem macierzowym skalowania we współrzędnych jednorodnych będzie:
•
=
1
1
0
0
0
0
0
0
1
'
'
y
x
s
s
y
x
y
x
1.4 Obrót o kąt α wokół początku układu współrzędnych
Zapisem macierzowym obrotu wokół początku układu o dany kąt α (dodatni kąt α jest
skierowany przeciwnie do ruchu wskazówek zegara) we współrzędnych jednorodnych będzie:
•
−
=
1
1
0
0
0
cos
sin
0
sin
cos
1
'
'
y
x
y
x
α
α
α
α

3
1.5 Pochylanie
Zapis macierzowy pochylenia wzdłuż osi X wyraża się następująco:
•
=
1
1
0
0
0
1
0
0
1
1
'
'
y
x
a
y
x
Zapis macierzowy pochylenia wzdłuż osi Y wyraża się następująco:
•
=
1
1
0
0
0
1
0
0
1
1
'
'
y
x
b
y
x
gdzie a i b są współczynnikami pochylenia.
1.6 Jednokładność
Przypomnijmy, że jednokładnością o środku
)
,
(
0
0
y
x
S =
i skali
0
≠
k
nazywamy
przekształcenie płaszczyzny, w którym obrazem punktu
)
,
(
y
x
P =
jest taki punkt
)
'
,
'
(
'
y
x
P =
, że
kSP
SP =
'
. Zatem w notacji macierzowej można zapisać:
•
−
−
=
1
1
0
0
)
1
(
0
)
1
(
0
1
'
'
0
0
y
x
y
k
k
x
k
k
y
x
Dla
1
−
=
k
przekształcenie takie jest symetrią względem punktu
)
,
(
0
0
y
x
S =
.
1.7 Powinowactwo prostokątne względem prostej
Niech osią powinowactwa będzie prosta o równaniu
0
=
+
+
c
by
ax
i stosunek
powinowactwa niech wynosi
0
≠
k
. Punkt
)
,
(
y
x
P =
odwzorowujemy więc w taki punkt
)
'
,
'
(
'
y
x
P =
, że
kQP
QP =
'
, gdzie Q jest rzutem prostokątnym punktu P na oś powinowactwa
0
=
+
+
c
by
ax
. W notacji macierzowej takie przekształcenie można zapisać:
•
+
+
=
1
1
0
0
1
1
1
'
'
2
2
y
x
wbc
wb
wab
wac
wab
wa
y
x
gdzie
)
/(
)
1
(
2
2
b
a
k
w
+
−
=
Dla
1
−
=
k
powinowactwo prostokątne jest symetrią względem prostej o równaniu
0
=
+
+
c
by
ax
.
1.8 Składanie przekształceń - obrót o kąt α wokół dowolnego punktu
Wszystkie omówione powyżej przekształcenia podstawowe mogą być dowolnie ze sobą
składane. Wróćmy teraz do obrotu o kąt α wokół dowolnego punktu
)
,
(
0
0
y
x
. Zgodnie z

4
poprzednim opisem punkt P zostanie poddany translacji o wektor
]
,
[
0
0
y
x −
−
, obrotowi wokół
(0,0) o kąt α i przesunięciu o
]
,
[
0
0
y
x
. A zatem
•
−
−
•
−
•
=
1
1
0
0
1
0
0
1
1
0
0
0
cos
sin
0
sin
cos
1
0
0
1
0
0
1
1
'
'
0
0
0
0
y
x
y
x
y
x
y
x
α
α
α
α
Należy zauważyć, iż w takim zapisie wszystkie przekształcenia muszą być zapisane w
odwrotnej kolejności. Mnożenie macierzy odbywa się zawsze od strony lewej do prawej,
kolejność taka jest obowiązkowa, gdyż mnożenie macierzy nie jest przemienne.

5
2. Przekształcenia punktów w przestrzeni R
3
2.1 Wprowadzenie
Do opisu obiektów trójwymiarowych będziemy najczęściej używali układu kartezjańskiego
lewoskrętnego, rysunek 2.1 ilustruje, jakie są zwroty osi.
Rys. 2.1. Układ lewoskrętny współrzędnych kartezjańskich
Przesunięcie, skalowanie i obroty w przestrzeni R
3
są analogiczne do odpowiednich
przekształceń na płaszczyźnie. Dla umożliwienia jednolitego zapisu macierzy tych
transformacji także teraz będziemy posługiwali się współrzędnymi jednorodnymi
)
1
,
,
,
(
z
y
x
punktów.
2.2 Przesunięcie (translacja)
Przesunięcie o wektor
]
,
,
[
z
y
x
d
d
d
punktu
)
,
,
(
z
y
x
P =
daje punkt
)
'
,
'
,
'
(
'
z
y
x
P =
o
współrzędnych:
z
y
x
d
z
z
d
y
y
d
x
x
+
=
+
=
+
=
'
'
'
W notacji macierzowej możemy zapisać to przekształcenie równaniem:
•
=
1
1
0
0
0
1
0
0
0
1
0
0
0
1
1
'
'
'
z
y
x
d
d
d
z
y
x
z
y
x
2.3 Skalowanie
Skalowanie definiuje się wzorami:
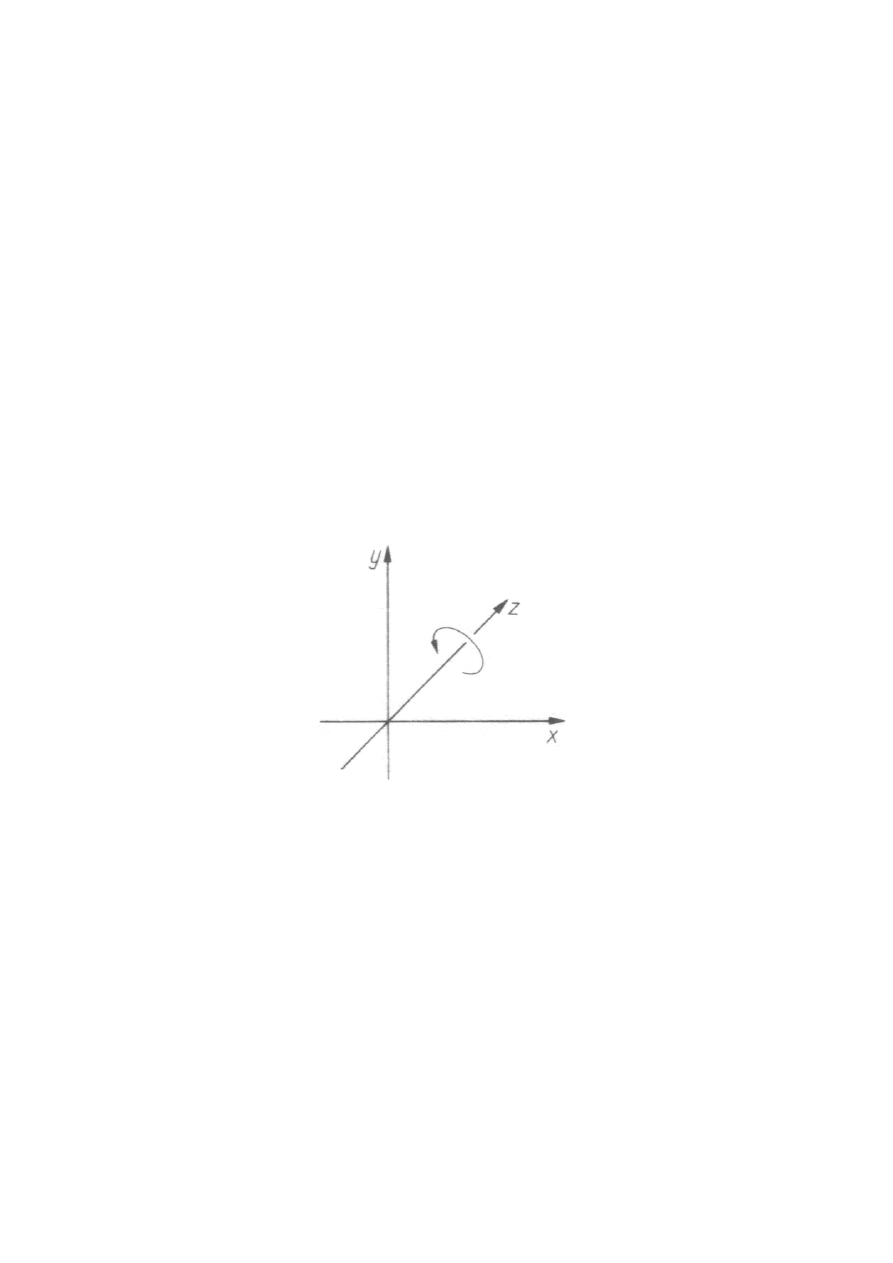
6
z
s
z
y
s
y
x
s
x
z
y
x
=
=
=
'
'
'
W notacji macierzowej możemy zapisać to przekształcenie równaniem:
•
=
1
1
0
0
0
0
0
0
0
0
0
0
0
0
1
'
'
'
z
y
x
s
s
s
z
y
x
z
y
x
2.4 Obrót
Omówienie obrotów wokół osi układu należy rozpocząć od określenia, jakie są zwroty kątów
obrotu. Przypomnijmy, że za podstawowy układ współrzędnych przyjęliśmy lewoskrętny
układ współrzędnych kartezjańskich. Dodatni zwrot kąta obrotu wokół danej osi to zwrot
przeciwny do kierunku ruchu wskazówek zegara, gdy patrzymy na układ współrzędnych w
ten sposób, że oś, wokół której wykonujemy obrót, jest skierowana w głąb kierunku patrzenia.
Zwrot kąta obrotu wokół osi z znajduje się na rysunku 2.2.
Rys. 2.2. Zwrot kąta obrotu wokół osi z.
Obrazem punktu
)
,
,
(
z
y
x
P =
po obrocie o kąt α wokół osi x jest punkt
)
'
,
'
,
'
(
'
z
y
x
P =
gdzie:
α
α
α
α
cos
sin
'
sin
cos
'
'
z
y
z
z
y
y
x
x
+
=
−
=
=
czyli macierzowo:
•
−
=
1
1
0
0
0
0
cos
sin
0
0
sin
cos
0
0
0
0
1
1
'
'
'
z
y
x
z
y
x
α
α
α
α
Obrót wokół osi X
Obracając punkt
)
,
,
(
z
y
x
P =
o kąt α wokół osi y dostajemy punkt
)
'
,
'
,
'
(
'
z
y
x
P =
o
współrzędnych:

7
α
α
α
α
sin
cos
'
'
cos
sin
'
x
z
z
y
y
x
z
x
−
=
=
+
=
czyli macierzowo:
•
−
=
1
1
0
0
0
0
cos
0
sin
0
0
1
0
0
sin
0
cos
1
'
'
'
z
y
x
z
y
x
α
α
α
α
Obrót wokół osi Y
Wreszcie przy obrocie o kąt α wokół osi z punkt
)
,
,
(
z
y
x
P =
jest przekształcany w
)
'
,
'
,
'
(
'
z
y
x
P =
o współrzędnych:
z
z
y
x
y
y
x
x
=
+
=
−
=
'
cos
sin
'
sin
cos
'
α
α
α
α
czyli macierzowo:
•
−
=
1
1
0
0
0
0
1
0
0
0
0
cos
sin
0
0
sin
cos
1
'
'
'
z
y
x
z
y
x
α
α
α
α
Obrót wokół osi Z
Wykorzystanie współrzędnych jednorodnych oraz macierzy przekształceń jest jedną z metod,
która realizuje obroty wokół danej osi. Inna metodą przekształceń punktów, która realizuje to
samo zadanie jest wykorzystanie kwaternionów. Dokładniej to zagadnienie jest opisane w
rozdziale trzecim niniejszej instrukcji.
2.5 Pochylanie
Zapis macierzowy pochylenia na płaszczyznę yz wyraża się następująco:
•
=
1
1
0
0
0
0
1
0
0
0
1
0
0
0
1
1
'
'
'
z
y
x
b
a
z
y
x
Zapis macierzowy pochylenia na płaszczyznę xz wyraża się następująco:
•
=
1
1
0
0
0
0
1
0
0
0
1
0
0
0
1
1
'
'
'
z
y
x
b
a
z
y
x

8
Zapis macierzowy pochylenia na płaszczyznę xy wyraża się następująco:
•
=
1
1
0
0
0
0
1
0
0
0
1
0
0
0
1
1
'
'
'
z
y
x
b
a
z
y
x
gdzie a i b są współczynnikami pochylenia.
2.6 Jednokładność
Jednokładnością o środku
)
,
,
(
0
0
0
z
y
x
S =
i skali
0
≠
k
nazywamy przekształcenie
przestrzeni, w którym obrazem punktu
)
,
,
(
z
y
x
P =
jest taki punkt
)
'
,
'
,
'
(
'
z
y
x
P =
, że
kSP
SP =
'
. Zatem w notacji macierzowej można zapisać:
•
−
−
−
=
1
1
0
0
0
)
1
(
0
0
)
1
(
0
0
)
1
(
0
0
1
'
'
'
0
0
0
z
y
x
z
k
k
y
k
k
x
k
k
z
y
x
Dla
1
−
=
k
przekształcenie takie jest symetrią względem punktu
)
,
,
(
0
0
0
z
y
x
S =
.
2.7 Powinowactwo prostokątne względem prostej
Szczególnym przypadkiem powinowactwa prostokątnego jest symetria osiowa względem
prostej. Prosta ta określona jest w przestrzeni trójwymiarowej poprzez przecięcie dwóch
płaszczyzn P i Q, takich ze P jest prostopadłe do Q. Taka symetria osiowa w przestrzeni jest
złożeniem dwóch symetrii płaszczyznowych S
P
oraz S
Q
.
2.8 Powinowactwo prostokątne względem płaszczyzny
Niech płaszczyzną powinowactwa będzie płaszczyzna o równaniu
0
=
+
+
+
d
cz
by
ax
i
stosunek powinowactwa niech wynosi
0
≠
k
. Punkt
)
,
,
(
z
y
x
P =
odwzorowujemy więc w
taki punkt
)
'
,
'
,
'
(
'
z
y
x
P =
, że
kQP
QP =
'
, gdzie Q jest rzutem prostokątnym punktu P na
płaszczyznę
powinowactwa
0
=
+
+
+
d
cz
by
ax
.
W
notacji
macierzowej
takie
przekształcenie można zapisać:
•
+
+
+
=
1
1
0
0
0
1
1
1
1
'
'
'
2
2
2
z
y
x
wcd
wc
wbc
wac
wbd
wbc
wb
wab
wad
wac
wab
wa
z
y
x
gdzie
)
/(
)
1
(
2
2
2
c
b
a
k
w
+
+
−
=
Dla
1
−
=
k
powinowactwo prostokątne względem płaszczyzny jest symetrią względem
płaszczyzny o równaniu
0
=
+
+
+
d
cz
by
ax
.
2.9 Składanie przekształceń
Wszystkie omówione powyżej transformacje podstawowe mogą być dowolnie ze sobą
składane w przestrzeni R
3
, analogicznie do sposobu składania przekształceń w przestrzeni R
2
.

9
3. Kwaterniony
Kwaterniony odkrył irlandzki matematyk, astronom i fizyk teoretyczny Sir Williams Rowan
Hamilton
(1805-1865).
Hamilton
był
profesorem
i
dyrektorem
obserwatorium
astronomicznego uniwersytetu w Dublinie, członkiem Irlandzkiej Akademii Nauk oraz
autorem wielu prac z dziedziny algebry, rachunku wektorowego, rachunku wariacyjnego,
teorii mechaniki i optyki.
3.1 Postać ogólna
Kwaterniony stanowią uogólnienie liczb zespolonych. Każdy kwaternion można zapisać w
postaci:
3
,
,
]
,
[
,
,
,
,
)]
,
,
(
,
[
,
,
,
,
R
v
R
s
v
s
R
z
y
x
s
z
y
x
s
R
z
y
x
s
zk
yj
xi
s
q
∈
∈
≡
∈
≡
∈
+
+
+
≡
gdzie jednostki urojone
k
j
i ,
,
spełniają następujący układ równań:
j
k
i
i
k
i
j
k
k
j
k
i
j
j
i
k
j
i
k
j
i
=
⋅
−
=
⋅
=
⋅
−
=
⋅
=
⋅
−
=
⋅
−
=
⋅
⋅
=
=
=
1
2
2
2
gdy współczynniki y i z są równe 0 wówczas kwaternion należy do zbioru liczb zespolonych.
3.2 Operacje arytmetyczne
Podstawowe operacje arytmetyczne na kwaternionach wykonane są tak samo jak operacje na
wielomianach, oczywiście z zachowaniem reguł mnożenia jednostek urojonych.
3.2.1 Dodawanie
k
z
z
j
y
y
i
x
x
s
s
k
z
j
y
i
x
s
k
z
j
y
i
x
s
q
q
)
(
)
(
)
(
)
(
)
(
)
(
2
1
2
1
2
1
2
1
2
2
2
2
1
1
1
1
2
1
+
+
+
+
+
+
+
=
=
+
+
+
+
+
+
+
=
+
3.2.2 Odejmowanie
k
z
z
j
y
y
i
x
x
s
s
k
z
j
y
i
x
s
k
z
j
y
i
x
s
q
q
)
(
)
(
)
(
)
(
)
(
)
(
2
1
2
1
2
1
2
1
2
2
2
2
1
1
1
1
2
1
+
−
+
−
+
−
+
=
=
+
+
+
−
+
+
+
=
−
3.2.3 Mnożenie
k
s
z
x
y
y
x
z
s
j
x
z
s
y
z
x
y
s
i
y
z
z
y
s
x
x
s
z
z
y
y
x
x
s
s
k
z
j
y
i
x
s
k
z
j
y
i
x
s
q
q
)
(
)
(
)
(
)
(
)
)(
(
2
1
2
1
2
1
2
1
2
1
2
1
2
1
2
1
2
1
2
1
2
1
2
1
2
1
2
1
2
1
2
1
2
2
2
2
1
1
1
1
2
1
+
−
+
+
+
+
−
+
+
−
+
+
+
−
−
−
=
=
+
+
+
+
+
+
=

10
3.2.4 Sprzężenie
Operacje sprzężenia kwaternionu definiuje następujący wzór:
)]
,
,
(
,
[
)]*
,
,
(
,
[
*
z
y
x
s
z
y
x
s
q
−
−
−
=
=
3.2.5 Normalizacja
Operację normalizacji kwaternionu
)]
,
,
(
,
[
z
y
x
s
q =
(operacja ta jest analogiczna do
normalizacji wektora) przeprowadza się w następujący sposób:
1.
Należy obliczyć długość kwaternionu ze wzoru:
2
2
2
2
|
|
z
y
x
s
q
+
+
+
=
2.
Współczynniki kwaternionu znormalizowanego
)]
,
,
(
,
[
n
n
n
n
n
z
y
x
s
q =
mają postać:
|
|
/
|,
|
/
|,
|
/
|,
|
/
q
z
z
q
y
y
q
x
x
q
s
s
n
n
n
n
=
=
=
=
Normalizacja kwaternionu powoduje przekształcenie go do kwaternionu o długości równej 1.
3.3 Interpretacja geometryczna
Kwaterniony można także przedstawiać jako sumę części rzeczywistej oraz pewnego wektora
v określonego w trójwymiarowej przestrzeni urojonej ijk.
]
,
,
[
z
y
x
s
v
s
q
+
=
+
=
3.4 Wykorzystanie kwaternionów w grafice komputerowej
Kwaterniony wykorzystuje się w grafice komputerowej głównie jako obiekty matematyczne
pozwalające dokonać transformacji współrzędnych danego punktu, która odpowiada obrotowi
wokół dowolnej osi przechodzącej przez środek układu współrzędnych. Kwaterniony tym
różnią się od macierzy prezentowanych w rozdziale drugim, że zapisują obrót jako kąt oraz
wektor, wokół którego obrót następuje. Otrzymujemy dzięki temu naturalny zapis
pozwalający w intuicyjny sposób zrozumieć, w jaki sposób punkt tak naprawdę jest
transformowany. Przy wykorzystaniu trzech macierzy obrotów wokół osi X, Y oraz Z, które
po odpowiednim złożeniu także mogą reprezentować obrót wokół dowolnej osi, intuicyjne
zrozumienie transformacji jest o wiele trudniejsze. Z tych powodów kwaterniony stały się
popularne w grafice komputerowej.
Poniżej przedstawiony jest algorytm, który pozwala wykorzystać kwaterniony w celu
obliczenia współrzędnych punktu
)
,
,
(
p
p
p
z
y
x
P =
obróconego o dany kąt α wokół osi
wyznaczonej przez wektor
]
,
,
[
S
S
S
z
y
x
S =
. Dodatni zwrot kąta obrotu to zwrot przeciwny do
kierunku ruchu wskazówek zegara, gdy patrzymy na układ współrzędnych w ten sposób, że
oś, wokół której wykonujemy obrót, jest skierowana w głąb kierunku patrzenia.

11
1.
Mając dany punkt
)
,
,
(
p
p
p
z
y
x
P =
oraz kąt obrotu α wokół osi wyznaczonej przez
dany wektor
]
,
,
[
S
S
S
z
y
x
S =
można przystąpić do wyliczenia nowych współrzędnych
punktu P.
2.
Należy wyliczyć współrzędne znormalizowane wektora obrotu S (sposób wyliczenia
tych współrzędnych podany został w rozdziale 3.2.5), nowe współrzędne będą opisane
jako wektor
]
,
,
[
A
A
A
z
y
x
A =
3.
Następnie należy wyznaczyć współczynniki kwaternionu obrotu
)]
,
,
(
,
[
z
y
x
s
q =
na
podstawie wzoru:
)
2
/
sin(
)
2
/
sin(
)
2
/
sin(
)
2
/
cos(
α
α
α
α
A
A
A
z
z
y
y
x
x
s
=
=
=
=
W tym momencie kwaternion ten jednoznacznie definiuje obrót o kąt α wokół osi
wyznaczonej przez wektor S.
4.
Wyliczyć szukane współrzędne, można to zrobić w dwojaki sposób:
a.
wyznaczyć współrzędne jako wymnożenie przez siebie trzech kwaternionów
*
]
,
,
,
[
q
p
q
z
y
x
s
w
w
w
w
⋅
⋅
=
=
,
gdzie
q
jest
wyliczonym
wcześniej
kwaternionem obrotu,
]
,
,
,
0
[
p
p
p
z
y
x
p =
, a q* jest kwaternionem sprzężonym
do q (sposób wyliczenia kwaternionu sprzężonego podany został w rozdziale
3.2.4). W ten sposób współczynniki
w
w
w
z
y
x
,
,
otrzymanego kwaternionu są
współrzędnymi szukanego punktu.
b.
wyznaczyć współrzędne jako wymnożenie przez siebie macierzy M,
wyznaczonej na podstawie wzoru
*
]
,
,
,
[
q
p
q
z
y
x
s
w
w
w
w
⋅
⋅
=
=
, przez macierz
punktu P zapisaną we współrzędnych jednorodnych.
=
1
W
W
W
z
y
x
W
+
−
+
+
−
+
−
+
−
+
+
−
+
−
=
1
0
0
0
0
)
(
2
1
2
2
2
2
0
2
2
)
(
2
1
2
2
0
2
2
2
2
)
(
2
1
2
2
2
2
2
2
y
x
yz
sx
xz
sy
yz
sx
z
x
sz
xy
xz
sy
sz
xy
z
y
M
=
1
P
P
P
z
y
x
P
P
M
W
⋅
=
W ten sposób elementy macierzy W
W
W
W
z
y
x
,
,
są współrzędnymi szukanego
punktu.

12
DODATEK 1: Przekształcenia układu współrzędnych
Te same przekształcenia, którym poddawaliśmy punkty na płaszczyźnie, możemy zastosować
do układu współrzędnych. W takim przypadku punkty zachowują swe położenia, natomiast
zmienia się sposób ich opisu, a więc i współrzędne.
Przy przesunięciu (translacji) układu współrzędnych o wektor
]
,
[
y
x
d
d
współrzędne punktu P
w układzie pierwotnym 0xy i przesuniętym 0x’y’ będą spełniały zależności:
y
x
d
y
y
d
x
x
−
=
−
=
'
'
Dokonując obrotu układu współrzędnych 0xy wokół jego początku, otrzymamy układ 0x’y’ o
tym samym początku 0’ = 0 i nowych osiach x’ i y’ tworzących ze starymi osiami x i y dany
kąt α. Dla takich warunków otrzymujemy następujące związki między starymi
współrzędnymi
)
,
(
y
x
punktu P i nowymi
)
'
,
'
(
y
x
:
α
α
α
α
cos
sin
'
sin
cos
'
y
x
y
y
x
x
+
−
=
+
=
DODATEK 2: Reprezentacja szkieletowa brył
Omawiana w tej części reprezentacja dotyczy brzegu bryły i ma hierarchiczną strukturę.
Powierzchnie bryły opisujemy sumą płaskich wielokątnych ścian. Zakładamy, że ściany
przecinają się jedynie we wspólnych krawędziach lub wierzchołkach. Każda ściana jest
określona zbiorem swoich krawędzi (boków swego wielokąta), a te są zdefiniowane parami
wierzchołków.
Klasyczna metoda pamiętania takich danych polega na utworzeniu kilku list. Tablica
wierzchołków
TW
zawiera współrzędne x,y,z tych punktów. W tablicy krawędzi
TK
zapisuje
się parami numery wierzchołków – końców krawędzi. Wreszcie tworzy się listę ścian, jej
elementami są listy (skończone ciągi) numerów krawędzi stanowiących boki wielokątnych
ścian.
W praktyce nierzadko obiekt wielościenny składa się z tysięcy ścian, krawędzi i
wierzchołków. Bardzo istotne staje się wtedy badanie poprawności tak dużej liczby danych.
Nieskomplikowany test polega na sprawdzeniu, czy każdy z wierzchołków występuje w
tablicy krawędzi co najmniej dwukrotnie (bo powinien być końcem przynajmniej dwóch
wychodzących z niego ścian), czy każda krawędź znajduje się w liście ścian itp. Pozytywna
odpowiedź oczywiście nie gwarantuje, że w opisie nie ma innych błędów. Można próbować je
wykryć korzystając z twierdzenia Eulera. Mówi ono, że w każdym zwykłym wielościanie
między liczbą s ścian, liczbą k krawędzi i liczbą w wierzchołków zachodzi związek
2
=
+
−
s
k
w

13
DODATEK 3: Zbiór wszystkich macierzy przekształceń w R
2
Macierz dla przesunięcia (translacji):
1
0
0
1
0
0
1
y
x
d
d
Macierz dla skalowania:
1
0
0
0
0
0
0
y
x
s
s
Macierze pochylania:
1
0
0
0
1
0
0
1
a
Pochylenie wzdłuż osi X
1
0
0
0
1
0
0
1
b
Pochylenie wzdłuż osi Y
Macierz dla obrotu:
−
1
0
0
0
cos
sin
0
sin
cos
α
α
α
α
Macierz dla jednokładności:
−
−
1
0
0
)
1
(
0
)
1
(
0
0
0
y
k
k
x
k
k
Macierz dla powinowactwa prostokątnego względem prostej:
+
+
1
0
0
1
1
2
2
wbc
wb
wab
wac
wab
wa

14
DODATEK 4: Zbiór wszystkich macierzy przekształceń w R
3
Macierz dla przesunięcia (translacji):
1
0
0
0
1
0
0
0
1
0
0
0
1
z
y
x
d
d
d
Macierz dla skalowania:
1
0
0
0
0
0
0
0
0
0
0
0
0
z
y
x
s
s
s
Macierze obrotów:
−
1
0
0
0
0
cos
sin
0
0
sin
cos
0
0
0
0
1
α
α
α
α
Obrót wokół osi X
−
1
0
0
0
0
cos
0
sin
0
0
1
0
0
sin
0
cos
α
α
α
α
Obrót wokół osi Y
−
1
0
0
0
0
1
0
0
0
0
cos
sin
0
0
sin
cos
α
α
α
α
Obrót wokół osi Z
Macierze pochylania:
1
0
0
0
0
1
0
0
0
1
0
0
0
1
b
a
Pochylenie na płaszczyznę yz
1
0
0
0
0
1
0
0
0
1
0
0
0
1
b
a
Pochylenie na płaszczyznę xz

15
1
0
0
0
0
1
0
0
0
1
0
0
0
1
b
a
Pochylenie na płaszczyznę xy
Macierz dla jednokładności:
−
−
−
1
0
0
0
)
1
(
0
0
)
1
(
0
0
)
1
(
0
0
0
0
0
z
k
k
y
k
k
x
k
k
Macierz dla powinowactwa prostokątnego względem płaszczyzny:
+
+
+
1
0
0
0
1
1
1
2
2
2
wcd
wc
wbc
wac
wbd
wbc
wb
wab
wad
wac
wab
wa
Wyszukiwarka
Podobne podstrony:
materialy Przekształcenie afiniczne, materiały
Przeksztalcanie wzorow
5 Przekształcenie Fouriera
Dyskretne przeksztaĹ'cenie Fouriera
GK 9 Przekształcenia geometryczne
10 Laczenie, podzial, przekszta lcanie spolek FOLIE
CPSW4 Z przekszt
Afiniczne odwzorowanie teoria
Afiniczne odwzorowanie ~$teoria
Przekszta?nie wzorów
Jak przekształcono inteligentnych lekarzy w?łkowitych kretynów Jaśkowski
Przekształcenia systemowe polskiej gospodarki
Przeksztaltniki DC DC Prezentacja Kawy
badanie przekształtnika przeciwbieznego
M[1] 5 Przeksztalcenia elementarne macierzy
2 Inf przeksztalcenia liniowe
Przeksztalcenia macierzowe id 4 Nieznany
więcej podobnych podstron