Analiza Sygnałów i Identyfikacja Procesów

Zadanie nr 90

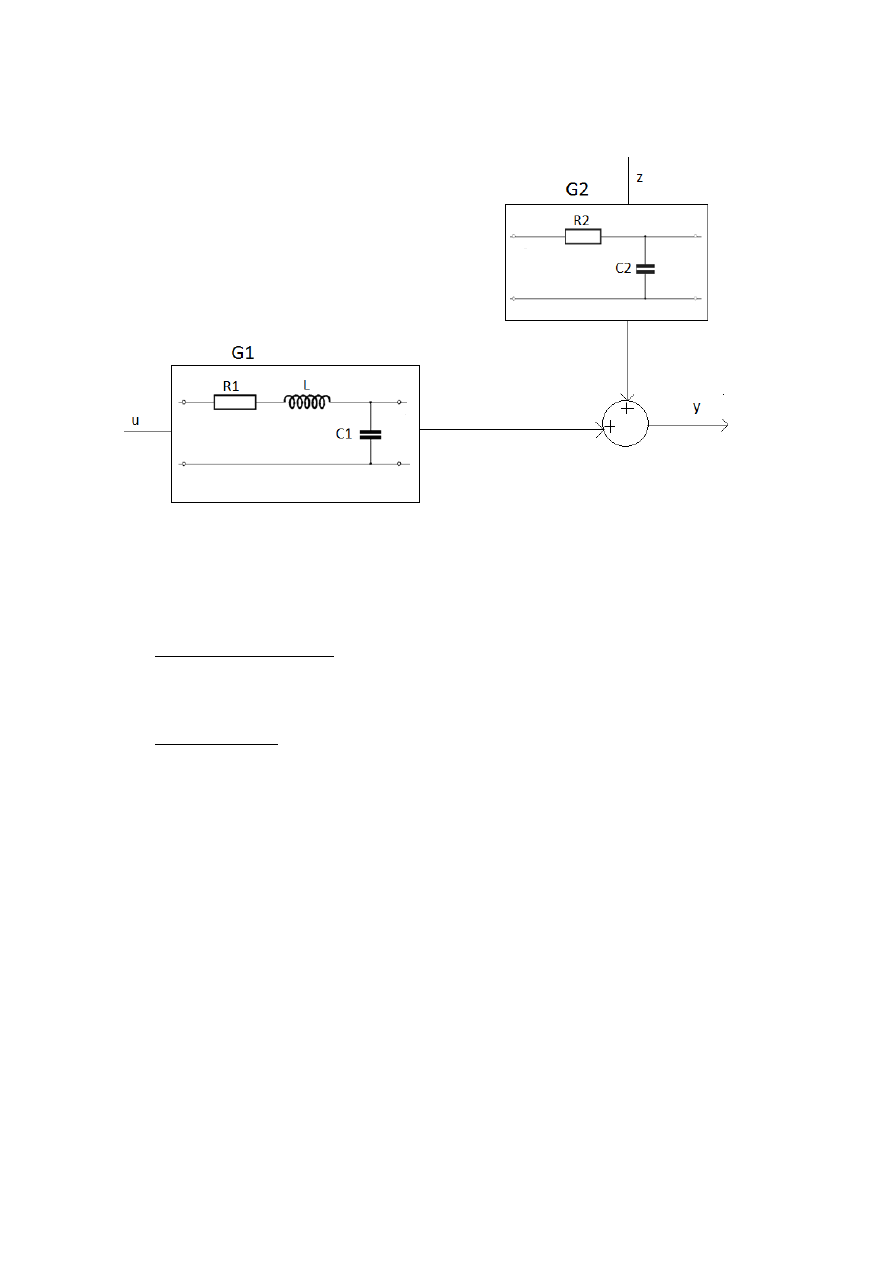
Zadany układ:

gdzie: R1=600Ω

R2=1000 Ω
t

p

=0.0001s

1. Identyfikacja obiektu G1 na podstawie odpowiedzi skokowej układu.

Badany układ jest obwodem RLC wiec jego transmitancja będzie miała postać:

1

1

1

1

1

1

)

(

1

2

+

⋅

⋅

+

⋅

⋅

=

s

C

R

s

C

L

s

G

Do obliczeń wykorzystamy jednak trochę inna postać, mianowicie:

1

2

1

)

(

1

0

2

2

0

+

+

=

s

T

s

T

s

G

ξ

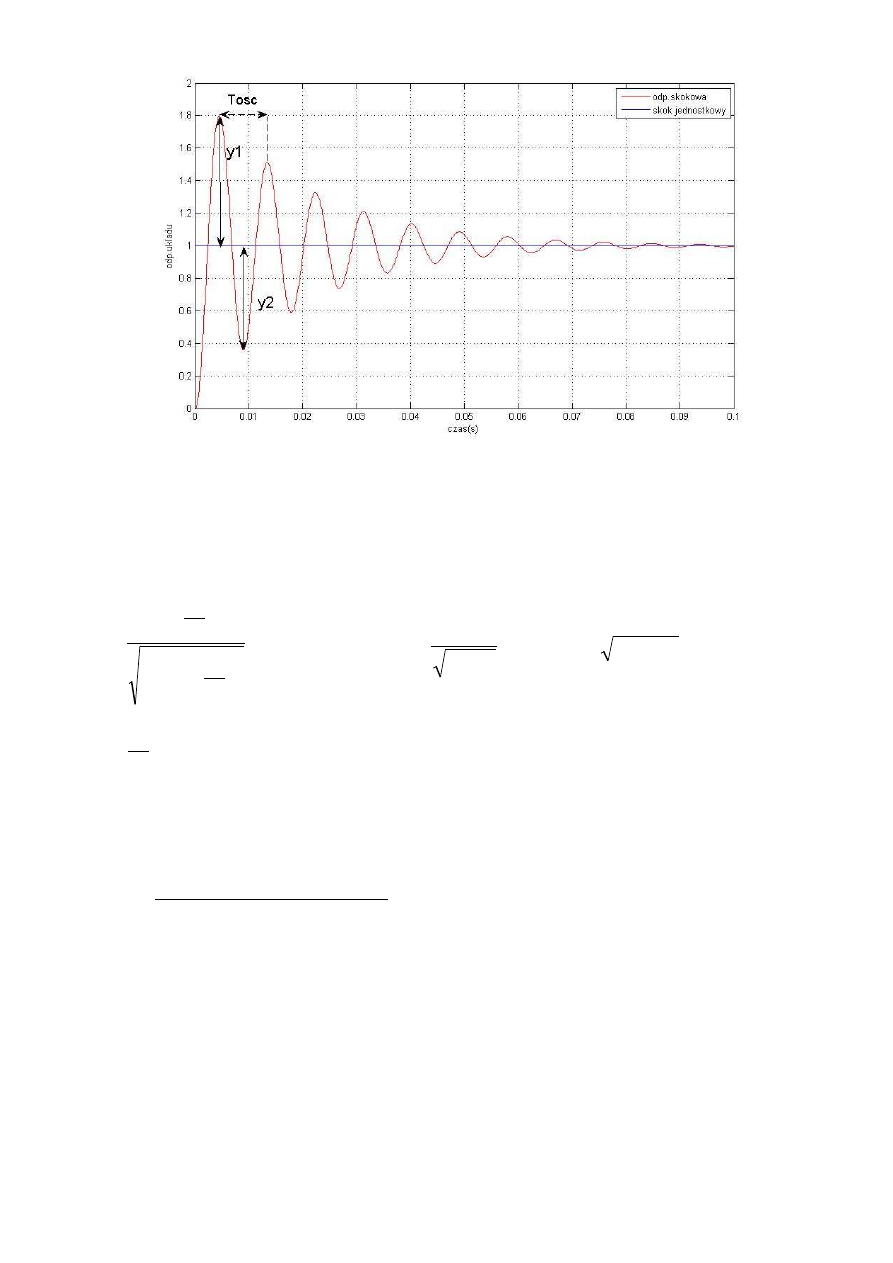
Rys.1 Odpowiedź skokowa układu

Z wykresu odczytujemy:
y1=0.79989 y2=0.6405 Tosc=0.009s

Wzory użyte do obliczenia poszczególnych parametrów :

2

2

1

2

2

1

ln

ln













+

=

y

y

y

y

π

ζ

ω=2π/ Tosc

2

1

ζ

ω

ζ

δ

+

−

=

2

2

0

δ

ω

ω

+

=

0

0

1

ω

=

T

Po wyliczeniu otrzymujemy:

49.386

=

δ

ω

=698.13

696.38

0

=

ω

0.070564

=

ζ

0.001436

0

=

T

Transmitancja przyjmuje postać:

1

0.0002027

10

2.062

1

)

(

1

2

6

-

+

+

⋅

⋅

=

s

s

s

G

Wyliczone parametry układu:

F

C

-7

10

3.378

1

⋅

=

H

6.105

L1

=

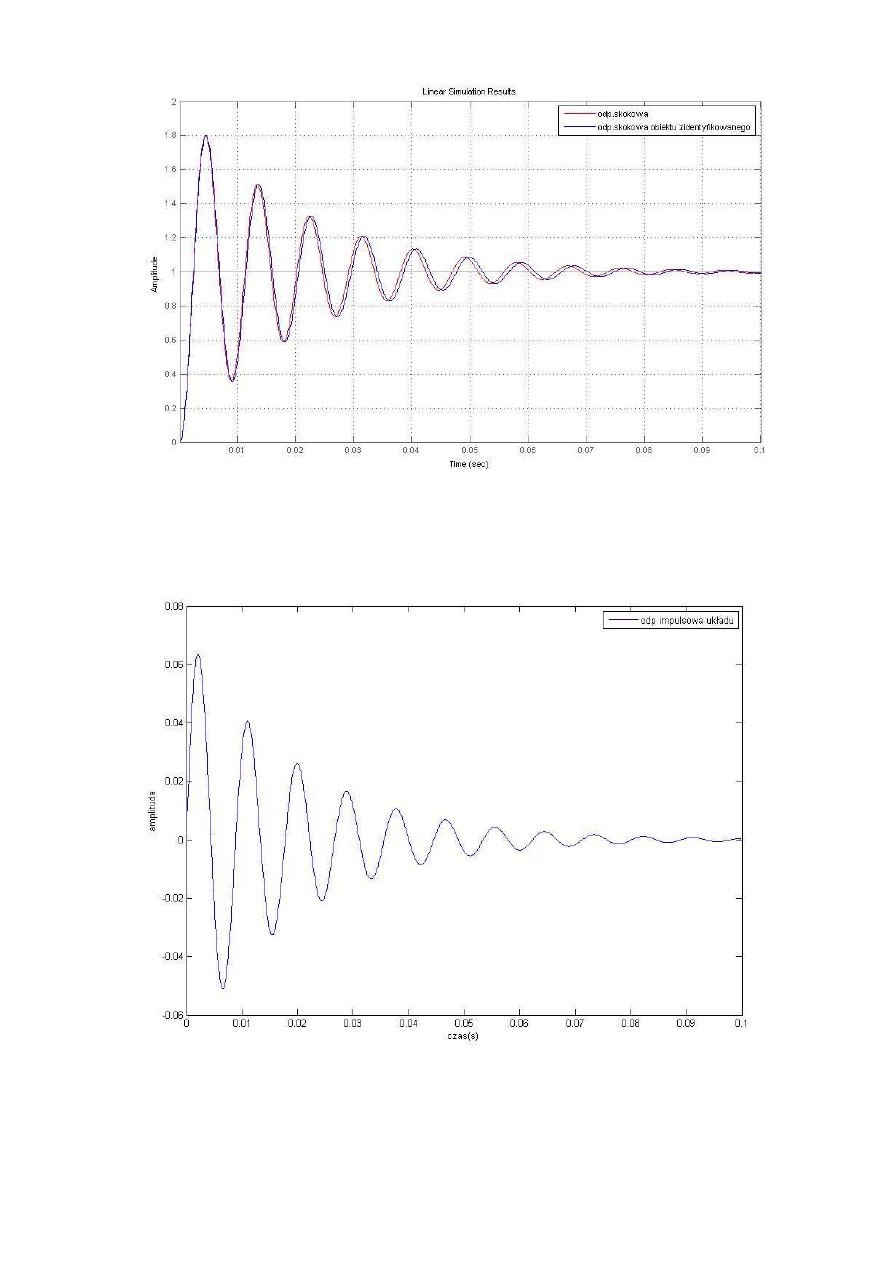
Rys.2 Porównanie odpowiedzi układu zadanego i zidentyfikowanego

2. Identyfikacja obiektu G1 na podstawie char. amplitudowo-częstotliwościowej

Po zróżniczkowaniu odpowiedzi skokowej układu otrzymujemy odp. impulsową:

Rys.3 Charakterystyka impulsowa zadanego ukladu

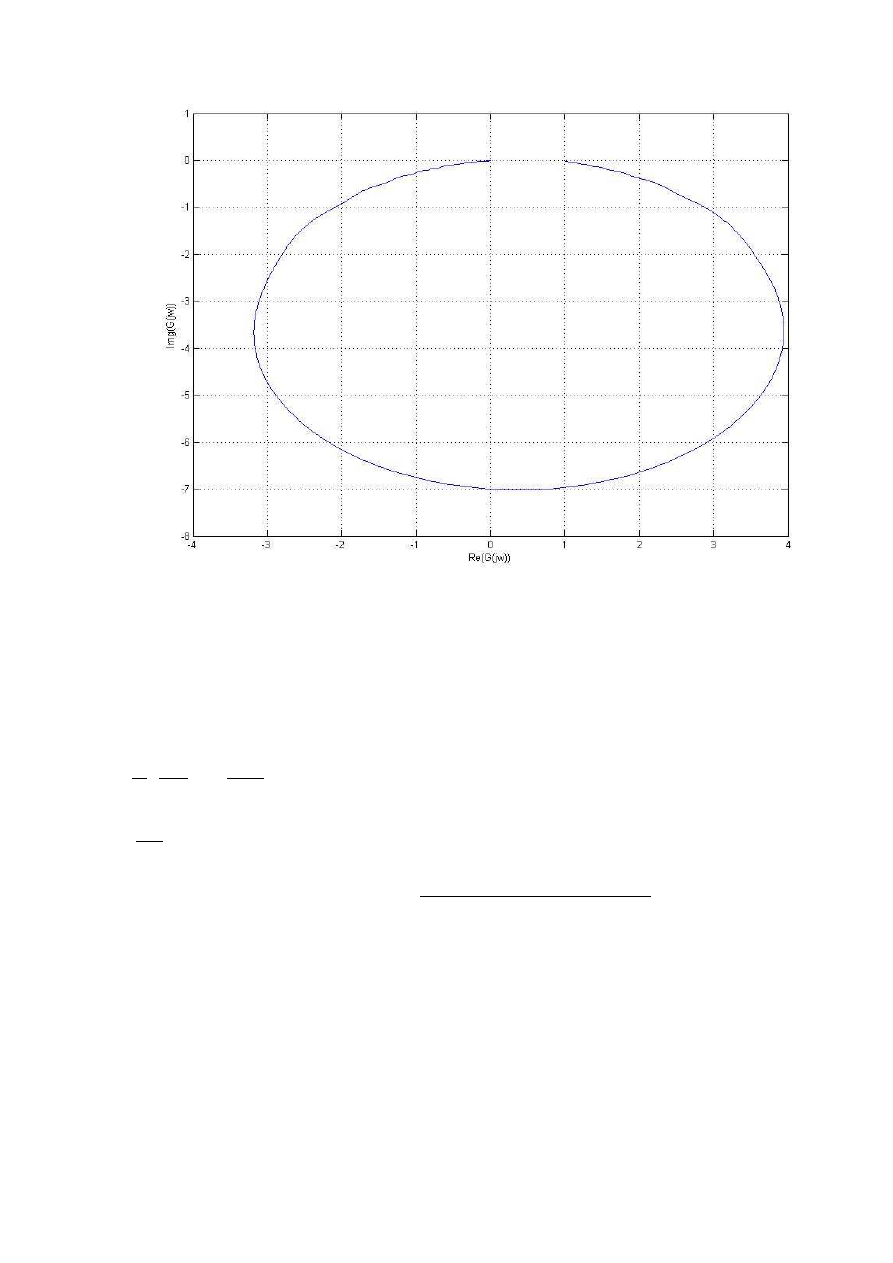
Po poddaniu odpowiedzi impulsowej transformacji Fouriera otrzymujemy wykres:

Rys.4 Charakterystyka amplitudowo-częstotliwościowa zadanego ukladu układu

Wyznaczamy częstotliwości dla których cześć urojona równa się rzeczywistej oraz dla których cześć
rzeczywista się zeruje(wykres przecina się z osią urojoną)
Otrzymujemy:

662.88

1

=

ω

709.37

2

=

ω

Z poniższych wzorów wyliczamy:

0.067843

)

1

(

2

1

2

2

2

1

1

2

=

⇒

−

⋅

=

ζ

ω

ω

ω

ω

ζ

0.0014097

1

0

2

0

=

⇒

=

T

T

ω

Cała transmitancja ma postać:

1

0.0001913

10

1.987

1

)

(

1

2

6

-

+

+

⋅

⋅

=

s

s

s

G

F

C

-7

10

3.188

1

⋅

=

H

6.234

L1

=

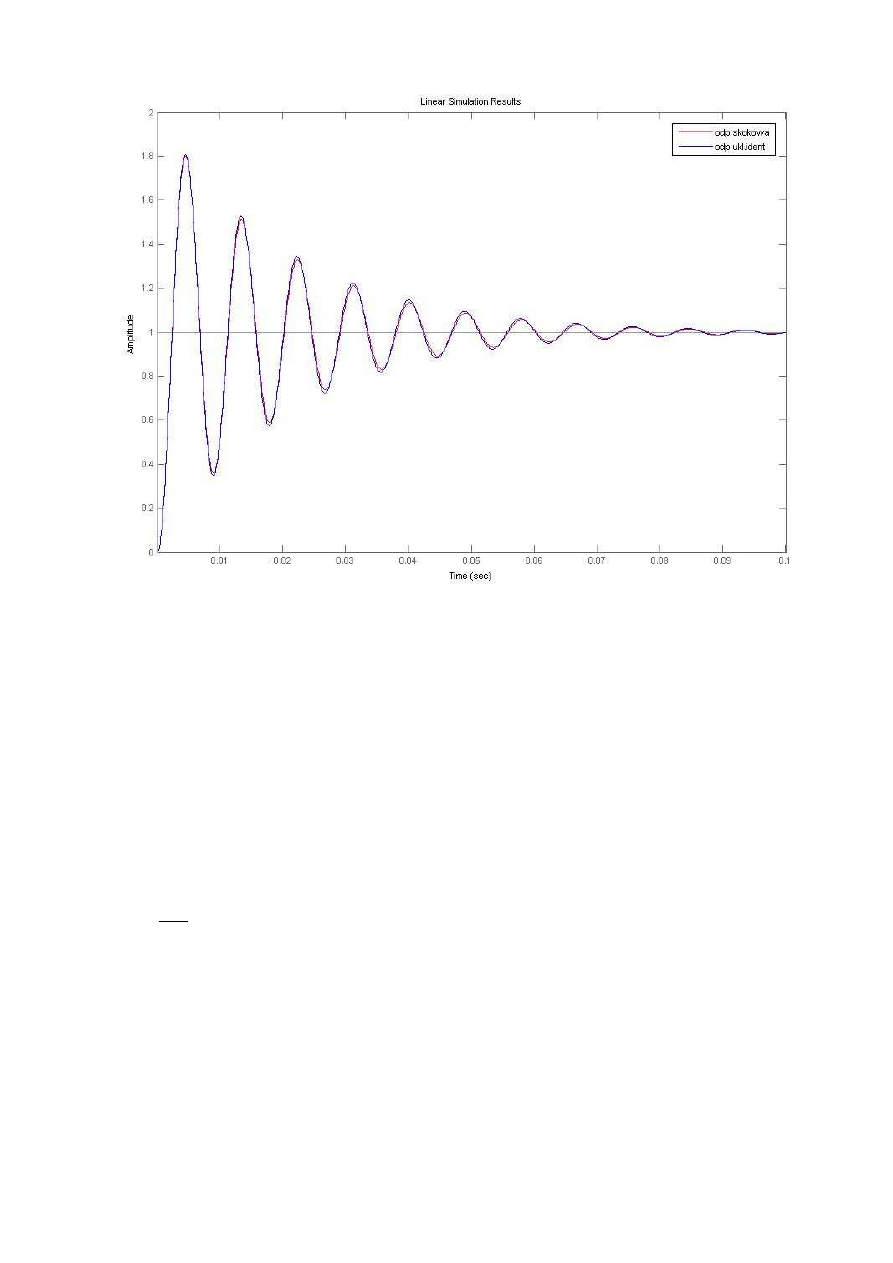
Rys.5 Porównanie odpowiedzi układu zadanego i zidentyfikowanego w pkt. 2

3. Identyfikacja parametrów modelu obiektu SISO

Po poddaniu wejścia i wyjścia układu transformacji Fouriera oraz korzystając z własności funkcji
widmowej mocy wzajemnej i własnej otrzymujemy:

Suu

Suy

j

G

=

)

(

ω

Charakterystyka częstotliwościowa prezentuje się następująco:

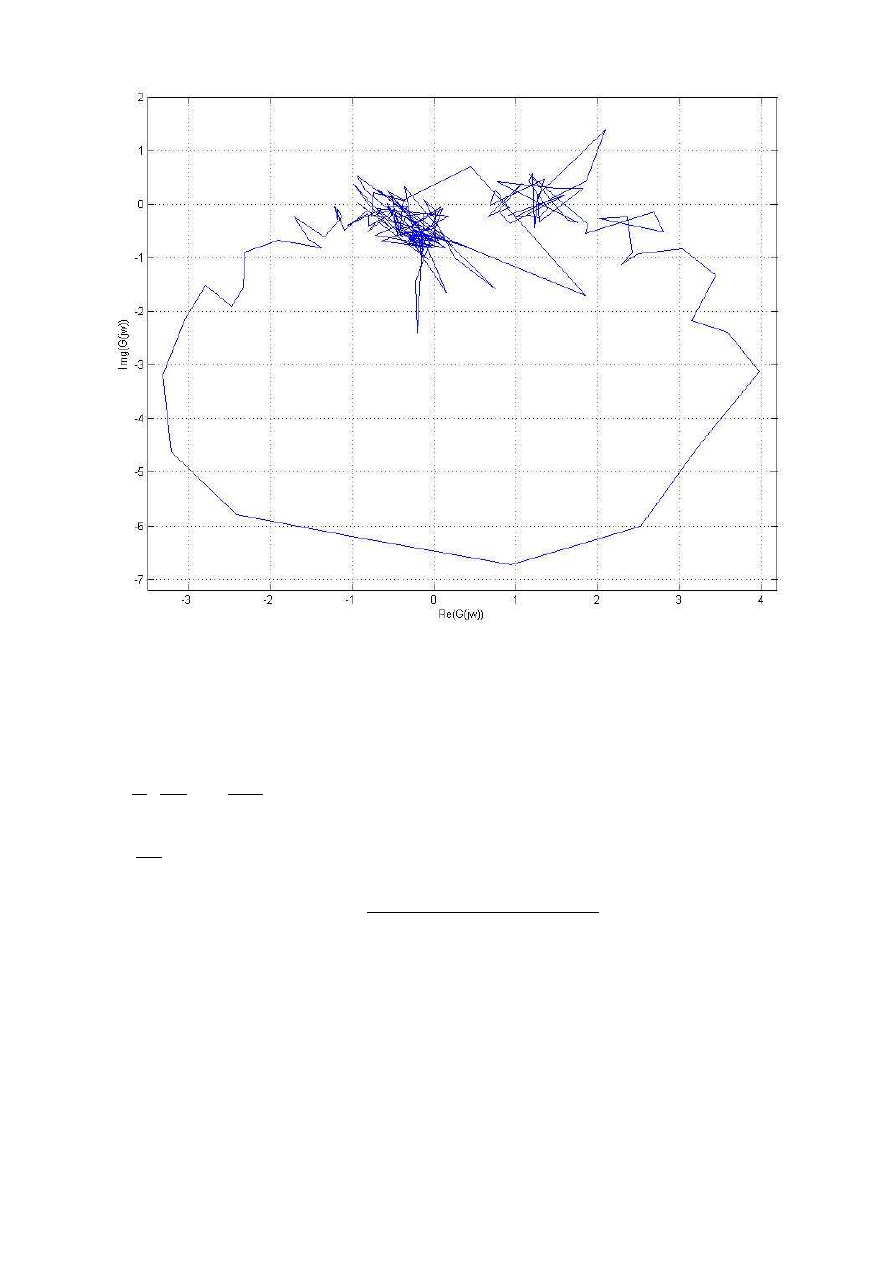
Rys.6 Charakterystyka amplitudowo-częstotliwościowa układu (po uwzględnieniu wejścia i wyjścia)

Podobnie jak w punkcie 2 wyznaczamy częstotliwości

658.24

1

=

ω

703.12

2

=

ω

Dalej otrzymujemy:

0.066006

)

1

(

2

1

2

2

2

1

1

2

=

⇒

−

⋅

=

ζ

ω

ω

ω

ω

ζ

0.0014222

1

0

2

0

=

⇒

=

T

T

ω

Cała transmitancja ma postać:

1

0.0001878

10

2.023

1

)

(

1

2

6

-

+

+

⋅

⋅

=

s

s

s

G

F

C

-7

10

3.129

1

⋅

=

H

6.464

L1

=

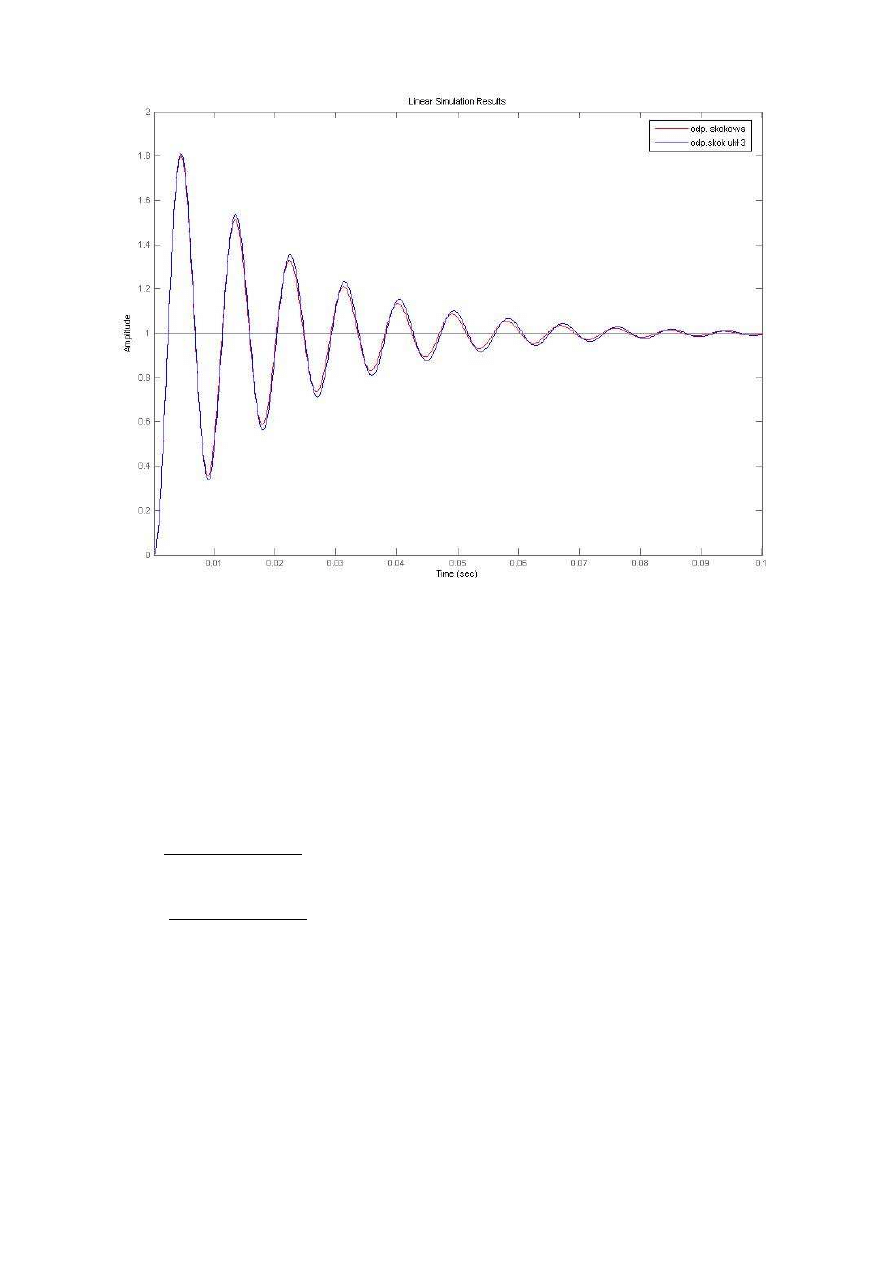
Rys.7 Porównanie odpowiedzi układu zadanego i zidentyfikowanego w pkt. 3

Komentarz:

Widać że otrzymane wyniki nie różnią się zbytnio od siebie a charakterystyki skokowe są zbliżone do

zadanej dlatego tez obliczenia są poprawne. Najbliższy zadanemu jest układ z punktu 2 ponieważ nie
obserwujemy przesunięcia fazowego(rys. 2) ani tez zbytniej różnicy w amplitudzie(rys. 6).

4. Identyfikacja parametrów modelu obiektu MISO

Szu

Suz

Szz

Suu

Szy

Suz

Suy

Szz

j

G

⋅

−

⋅

⋅

−

⋅

=

)

(

1

ω

Szu

Suz

Szz

Suu

Suy

Szu

Szy

Suu

j

G

⋅

−

⋅

⋅

−

⋅

=

)

(

2

ω

Postępujemy podobnie ja powyżej i otrzymujemy wykres:

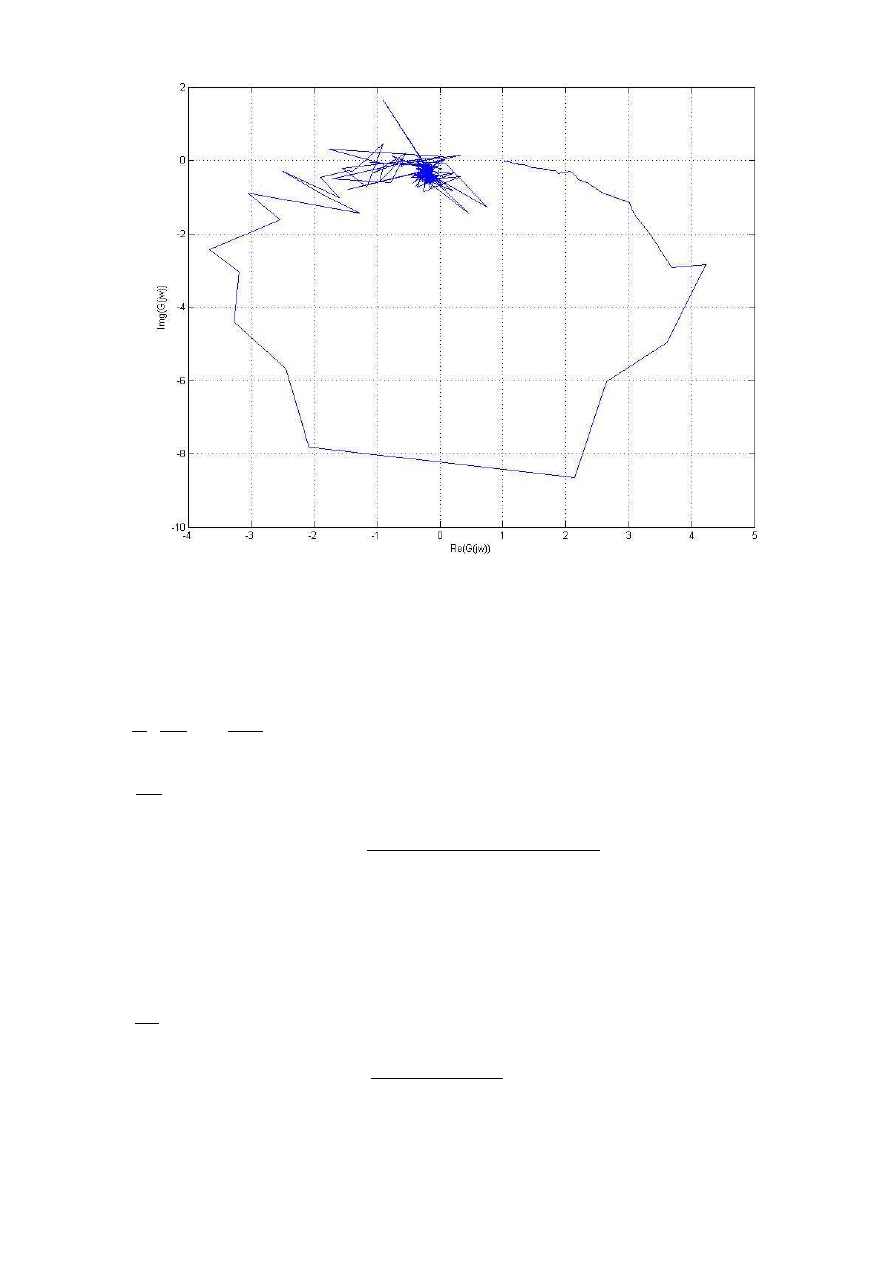
Rys.8 Charakterystyka amplitudowo-częstotliwościowa układu G1

Wyznaczamy:

673.2

1

=

ω

703.12

2

=

ω

Dalej otrzymujemy:

0.043499

)

1

(

2

1

2

2

2

1

1

2

=

⇒

−

⋅

=

ζ

ω

ω

ω

ω

ζ

0.0014222

1

0

2

0

=

⇒

=

T

T

ω

Cała transmitancja ma postać:

1

0.0001237

10

2.023

1

)

(

1

2

6

-

+

+

⋅

⋅

=

s

s

s

G

F

C

-7

10

2.062

1

⋅

=

H

9.809

L1

=

Obliczając transmitancje G2 wystarczy policzyć To gdyż jest to układ inercyjny I rzędu

538.56

1

=

ω

8

0.0.001856

1

0

1

0

=

⇒

=

T

T

ω

Cała transmitancja ma postać:

1

8

0.0.001856

1

)

(

2

+

⋅

=

s

s

G

F

C

-6

10

1.857

2

⋅

=