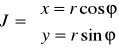Funkcja ciągła w punkcie Funkcja f: Funkcja f jest ciągła w punkcie Rozważmy funkcję dwóch zmiennych. Niech oraz niech funkcja f będzie określona przynajmniej na otoczeniu Funkcja jest ciągłą w punkcie wtedy i tylko wtedy, gdy Pochodna cząstkowa Niech funkcja f będzie określona na obszarze punktu . Pochodną cząstkową pierwszego rzędu funkcji f względem zmiennej x[y] w punkcie określamy wzorem Oznaczamy: f 'x, f `'y Różniczka Niech funkcja f ma pochodne cząstkowe pierwszego rzędu w punkcie . Różniczką funkcji f w tym punkcie nazywamy funkcję zmiennych ∆x, ∆y określona wzorem Oznaczamy ja df Gradient Gradientem funkcji f w punkcie nazywamy wektor określony wzorem Minimum (maksimum) lokalne Mówimy, że funkcja f ma w punkcie minimum (maksimum) lokalne, jeżeli istnieje otoczenie tego punktu takie, że dla każdego (x,y) z tego otoczenia zachodzi nierówność Mówimy że funkcja f ma w punkcie minimum (maksimum) lokalne właściwe jeśli istnieje sąsiedztwo tego punktu takie, że dla każdego (x,y) z tego sąsiedztwa zachodzi nierównośc Współrzędne walcowe (sferyczne) Położenie punktu P w przestrzeni można opisać trójkąt liczb (φ,r,h), {(φ,ψ,r)} gdzie φ -oznacza miarę kąta między rzutem promienia OXY, a dokładnie osią OX 0 ≤φ < albo -Π < φ ≤ Π r-oznacza odległość rzutu punktu P na płaszczyznę OXY od początku układu współrzędnych 0 ≤ ρ < ∞ {ψ-oznacza miarę kąta między promieniem wodzącego punktu P, a płaszczyzną OXY, h- oznacza odległość (dodatnia dla z > 0 i ujemną dla z< 0) punktu P od płaszczyzny OX -∞ < h < ∞ {r - oznacza odległość punktu P od początku układu współrzędnych 0 ≤ r < ∞ } Trójkąt (φ,r,h), {(φ,ψ,T)} nazywamy współrzędnymi walcowymi {sferycznymi} punktu P

Współrzędne biegunowe Położenie punktu P na płaszczyźnie można napisać parę liczb (r , φ) r - oznacza odległość punktu P od początku układu współrzędnych r є [0,+∞] φ - oznacza miarę kąta między dodatnia częścią osi X a promieniem wodzącym punktu P φє[0,2Π] φє[-Π, Π] Parę (r,φ) nazywamy współrzędnymi biegunowymi punktu płaszczyzny. Współrzędne kartezjańskie (x,y) punktu płaszczyzny danego na współrzędnych biegunowych (x,y) określone są wzorami - przekształcenie biegunowe Łuk zwykły Luk zwykły w przestrzeni (rozważać będziemy n=2 lub n=3) jest to zbiór wszystkich punktów o współrzędnych : gdzie są to funkcje ciągłe określone w przedziale <α,β> przy czym różnym wartościom parametru tє(α,β) odpowiadają różne punkty P Interpretacja fizyczna całki krzywoliniowej skierowanej Jeżeli R oznacza wektor siły o zmiennych wzdłuż łuku AB współrzędnych P(x,y), Q(x,y), to całka krzywoliniowa skierowana przedstawia pracę siły R wzdłuż łuku AB Interpretacja geometryczna całki krzywoliniowej nieskierowanej Jeżeli f(x,y)=1 to całka ∫f(x,y)dl przedstawia długość łuku l Jeżeli f - funkcja ciągła i dodatnia, to otrzymujemy pole części powierzchni walcowej

---