Definicja zdania
Zdaniem w logice nazywamy wypowiedź zbudowaną zgodnie z zasadami ustalonego języka, której można przypisać jednoznacznie jedną z dwu ocen: prawdę lub fałsz -nazywane wartościami logicznymi danego zdania i oznaczane odpowiednio symbolami ![]()
, ![]()
.
Definicja formy zdaniowej
Formą zdaniową nazywamy wypowiedź, która może zawierać zmienne, zbudowaną według takich samych reguł gramatycznych jak zdanie. Fakt, że ![]()
jest zmienną formy zdaniowej![]()
oznaczamy pisząc ![]()
.
Uwaga 1. Każde zdanie jest formą zdaniową.
Uwaga 2. Istnieją formy zdaniowe nie będące zdaniami.
Zasada tworzenia zdań z form zdaniowych
Z formy zdaniowej można otrzymać zdanie na dwa sposoby:
Przez podstawienie w miejsce zmiennych, obiektów w stosunku do których będziemy mogli stosować oceny logiczne prawdziwości i fałszu.
Przez stosowanie kwantyfikatorów w odniesieniu do występujących w formie zdaniowej zmiennych. Stosowanie kwantyfikatora dużego do formy
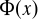
oznacza utworzenie zdania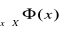
, które czytamy: „ dla każdego elementu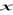
ze zbioru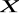
jest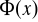
”. Stosowanie kwantyfikatora małego do formy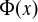
oznacza utworzenie zdania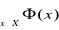
, które czytamy: „ istnieje element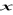
ze zbioru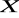
taki, że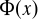
”.
Definicja
Jeśli zakresem zmienności zmiennej ![]()
w formie ![]()
jest zbiór ![]()
, to zbiór tych wszystkich elementów zbioru ![]()
, które podstawione w miejsce zmiennej ![]()
w formie ![]()
dają zdanie prawdziwe oznaczamy jako ![]()
.
Przykład. Przedział domknięty ![]()
gdzie ![]()
, ![]()
są liczbami rzeczywistymi takimi, że ![]()
można zapisać jako ![]()
.
Zasada weryfikacji prawdziwości zdań złożonych
Oceny prawdziwości zdań złożonych dokonujemy na podstawie informacji o prawdziwości ich składników zgodnie z następującymi ustaleniami:
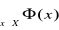
jest prawdą wtedy i tylko wtedy gdy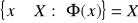
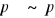
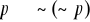
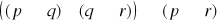
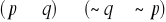




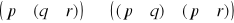
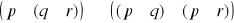



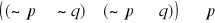

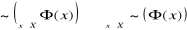
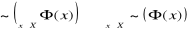
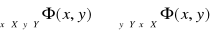
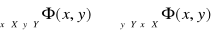
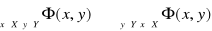
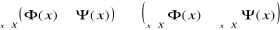
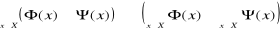
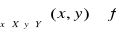
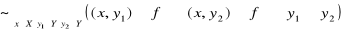
.Jeśli X ⊂ R i Y = R, to funkcję f nazywać będziemy funkcją rzeczywistą zmiennej rzeczywistej.
Jeśli X = N i Y = R, to funkcję f nazywać będziemy nieskończonym ciągiem liczbowym o wyrazach rzeczywistych.
Jeśli X = N i Y = N i f jest funkcją wzajemnie jednoznaczną, to f nazywać będziemy permutacją zbioru liczb naturalnych.
Jeśli X = {1, 2, ..., m}×{1, 2, ..., n} oraz Y = R, to funkcję f nazywać będziemy macierzą o m wierszach i n kolumnach.
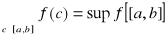
;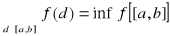
;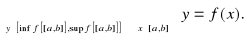
Jeśli
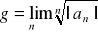
, to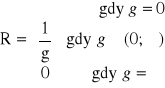
Jeśli
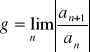
, to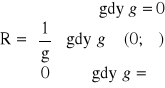
Jeśli
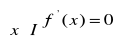
to funkcja f jest stała w przedziale I.Jeśli
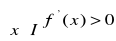
to funkcja f jest rosnąca w przedziale I.Jeśli
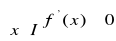
to funkcja f jest niemalejąca w przedziale I.Jeśli
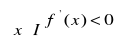
to funkcja f jest malejąca w przedziale I.Jeśli
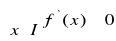
to funkcja f jest nierosnąca w przedziale I.jeśli całka
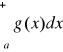
jest zbieżna, to także całka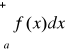
jest zbieżna;jeśli całka
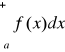
jest rozbieżna, to także całka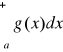
jest rozbieżna.Szeregi Taylora i Maclaurina
funkcja f ma w otoczeniu U(x0) pochodne dowolnego rzędu,
dla każdego x∈U(x0)
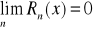
, gdzieCiągi i szeregi ortogonalne
Szereg trygonometryczny Fouriera
f(x) jest przedziałami monotoniczna w (a,b)
f(x) jest ciągła w przedziale (a,b), z wyjątkiem co najwyżej skończonej liczby punktów nieciągłości pierwszego rodzaju (tzn. istnieją skończone granice jednostronne w tych punktach), przy czym w każdym punkcie nieciągłości x0 spełniony jest warunek:
w końcach przedziału [a,b] zachodzą równości:
|
|
|
|
|
|
|
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
![]()
jest prawdą wtedy i tylko wtedy gdy ![]()
Definicja tautologii
Prawem logicznym albo tautologią nazywamy zdanie złożone, które jest prawdziwe niezależnie od wartości logicznych zdań składowych.
Wykaz ważniejszych tautologii
Zasada prowadzenia dowodu
Każdy element rozumowania zwanego dowodem w dowolnej teorii matematycznej daje się uzasadnić tautologią albo aksjomatem tej teorii.
Definicja iloczynu kartezjańskiego zbiorów
Iloczynem kartezjańskim zbiorów ![]()
i ![]()
nazywamy zbiór wszystkich par uporządkowanych ![]()
takich, że ![]()
i ![]()
. Iloczyn kartezjański zbiorów ![]()
i ![]()
oznaczamy jako ![]()
.
Definicja funkcji
Każdy podzbiór ![]()
iloczynu kartezjańskiego ![]()
zbiorów ![]()
i ![]()
nazywamy funkcją odwzorowującą zbiór ![]()
w zbiór ![]()
o ile spełnia on następujące dwa warunki:
Fakt, że ![]()
jest funkcją odwzorowującą zbiór ![]()
w zbiór ![]()
oznaczamy pisząc ![]()
. Zbiór funkcji odwzorowujących ![]()
w ![]()
oznaczamy jako ![]()
.
Definicja funkcji różnowartościowej
Jeśli ![]()
to mówimy, że ![]()
jest różnowartościowa jeśli spełnia następujący warunek:
![]()
Definicja funkcji odwzorowującej zbiór X na zbiór Y
Jeśli ![]()
to mówimy, że ![]()
odwzorowuje zbiór ![]()
na zbiór ![]()
jeśli spełnia następujący warunek:
![]()
.
Definicja funkcji wzajemnie jednoznacznej
Jeśli ![]()
to mówimy, że ![]()
jest funkcją wzajemnie jednoznaczną jeśli jest funkcją różnowartościową odwzorowującą zbiór ![]()
na zbiór ![]()
.
Definicja funkcji odwrotnej
Niech ![]()
będzie funkcją wzajemnie jednoznaczną. Wówczas zbiór ![]()
jest funkcją wzajemnie jednoznaczną odwzorowującą zbiór ![]()
na zbiór ![]()
. Nazywamy go funkcją odwrotną do funkcji ![]()
i oznaczamy jako ![]()
.
Definicja złożenia funkcji
Niech ![]()
, ![]()
przy czym ![]()
. Zbiór ![]()
jest funkcją odwzorowująca zbiór ![]()
w zbiór ![]()
. Nazywamy go złożeniem funkcji ![]()
i ![]()
i oznaczamy jako ![]()
.
Definicja obrazu zbioru przez funkcję
Niech ![]()
. Dla dowolnego zbioru ![]()
zbiór ![]()
nazywamy obrazem zbioru ![]()
przez funkcję ![]()
i oznaczamy jako ![]()
.
Definicja przeciwobrazu zbioru przez funkcję
Niech ![]()
. Dla dowolnego zbioru![]()
zbiór ![]()
nazywamy przeciwobrazem zbioru ![]()
przez funkcję ![]()
i oznaczamy jako ![]()
.
Definicja dziedziny i zbioru wartości funkcji
Niech f : X → Y. Wówczas zbiór X nazywamy dziedziną funkcji i oznaczamy jako Df natomiast f[X] nazywamy zbiorem wartości funkcji i oznaczamy jako Wf.
Przykłady rodzin funkcji
Niech f : X → Y.
Ciągłość. Niech x0 ∈ R.
Definicja otoczenia, sąsiedztwa i punktu skupienia
Niech a, b ∈ R i a < x0 < b. Otoczeniem (otoczeniem lewostronnym, prawostronnym) punktu x0 nazywamy przedział (a, b) ((a, x0], [x0 , b)). Rodzinę zbiorów będących otoczeniami (otoczeniami lewostronnymi, prawostronnymi) punktu x0 oznaczać będziemy symbolem O(x0) (O -(x0), O+(x0)). Każdy zbiór postaci U \ {x0}, gdzie U ∈ O(x0) (U ∈ O -(x0), U ∈ O+(x0)) nazywać będziemy sąsiedztwem (sąsiedztwem lewostronnym, prawostronnym) punktu x0. Rodzinę zbiorów będących sąsiedztwami (sąsiedztwami lewostronnymi, prawostronnymi) oznaczać będziemy symbolem S(x0) (S -(x0), S+(x0)).
Niech X ⊂ R. Mówimy, że x0 jest punktem skupienia (lewostronnym, prawostronnym punktem skupienia) zbioru X, jeśli
![]()
(![]()
, ![]()
).
Zbiór punktów skupienia (lewostronnych, prawostronnych punktów skupienia) zbioru X oznaczamy jako Xd (Xd-, Xd+).
Niech f będzie funkcją rzeczywistą zmiennej rzeczywistej.
Definicja granicy funkcji
Niech x0 ∈ (Df)d (x0 ∈ (Df)d-, x0 ∈ (Df)d+ ). Mówimy, że g ∈ R jest granicą (granicą lewostronną, prawostronną) funkcji f w punkcie x0, gdy
![]()
(![]()
, ![]()
).
Fakt, że g jest granicą (granicą lewostronną, prawostronną) zapisujemy symbolicznie
![]()
(![]()
, ![]()
).
Definicja ciągłości funkcji
Niech x0 ∈ Df.
f jest ciągła w x0 ⇔ x0 ∉ (Df)d ∨ ![]()
f jest lewostronnie ciągła w x0 ⇔ x0 ∉ (Df)d- ∨ ![]()
f jest prawostronnie ciągła w x0 ⇔ x0 ∉ (Df)d+ ∨ ![]()
Niech X ⊂ R. Mówimy, że f jest ciągła w zbiorze X, gdy jest ciągła w każdym punkcie tego zbioru. Zbiór punktów ciągłości funkcji f oznaczać będziemy przez Cf.
Uwaga. Funkcja jest ciągła w punkcie x0 wtedy i tylko wtedy, gdy jest ciągła lewostronnie i prawostronnie w tym punkcie.
Rodzaje nieciągłości - definicja
Niech x0 ∈ Df. Mówimy, że x0 jest punktem nieciągłości pierwszego rodzaju funkcji f, jeśli istnieją i są skończone granice ![]()
, ![]()
przy czym ![]()
lub ![]()
Mówimy, że x0 jest punktem nieciągłości drugiego rodzaju, jeśli x0 ∉ Cf i x0 nie jest punktem nieciągłości pierwszego rodzaju.
Twierdzenia o funkcjach ciągłych
Twierdzenie Weierstrassa-Darboux. Niech a, b ∈ R, a < b, [a, b] ⊂ Cf. Wówczas funkcja f jest ograniczona na [a, b]. Ponadto
Twierdzenie o klasie funkcji ciągłych
Funkcje elementarne są ciągłe. Działania algebraiczne wykonywane na funkcjach ciągłych dają funkcje ciągłe. Złożenia funkcji ciągłych są funkcjami ciągłymi. Funkcje odwrotne do funkcji ciągłych (o ile istnieją) też są funkcjami ciągłymi.
Uwaga. Jeśli x0 ∈ Cf i f(x0) > 0, to ![]()
Definicja ciągłości jednostajnej
Niech X ⊂ Df. Mówimy, że funkcja f jest jednostajnie ciągła na X, jeśli
![]()
Uwaga. Jeśli f jest jednostajnie ciągła na zbiorze X, to jest ciągła w każdym punkcie tego zbioru.
Uwaga. Istnieją funkcje ciągłe w każdym punkcie zbioru X lecz nie będące jednostajnie ciągłymi na tym zbiorze.
Uwaga. Funkcja ciągła na przedziale domkniętym i ograniczonym jest na tym przedziale jednostajnie ciągła.
SZEREGI LICZBOWE
Definicja szeregu
Niech ![]()
będzie ciągiem liczbowym. Szeregiem liczbowym nazywamy ciąg ![]()
gdzie 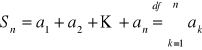
. Taki szereg liczbowy oznaczamy symbolem ![]()
. Liczbę ![]()
nazywamy n-tym wyrazem, a liczbę ![]()
- n-tą sumą tego szeregu.
Definicja szeregu zbieżnego, rozbieżnego i sumy szeregu
Mówimy, że szereg ![]()
jest zbieżny jeśli ciąg ![]()
jest zbieżny do granicy skończonej zwanej w tym przypadku sumą szeregu i oznaczanej symbolem identycznym z symbolem szeregu.
Mówimy, że szereg ![]()
jest rozbieżny gdy nie jest zbieżny.
Twierdzenie o kombinacji liniowej szeregów
Jeśli szeregi ![]()
, ![]()
są zbieżne odpowiednio do liczb ![]()
i ![]()
, to dla dowolnych liczb rzeczywistych ![]()
, ![]()
zbieżny jest również szereg 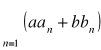
przy czym suma tego szeregu wynosi ![]()
.
Twierdzenie o zbieżności szeregu geometrycznego
Szereg ![]()
zwany szeregiem geometrycznym o podstawie ![]()
jest zbieżny wtedy i tylko wtedy gdy ![]()
.
Twierdzenie o zbieżności szeregu harmonicznego
Szereg ![]()
zwany szeregiem harmonicznym rzędu ![]()
jest zbieżny wtedy i tylko wtedy gdy ![]()
.
Warunek konieczny zbieżności szeregu
Jeśli szereg ![]()
jest zbieżny to ![]()
.
Niech ![]()
i ![]()
oznaczają szeregi liczbowe.
Uwaga. Jeśli ciągi ![]()
i ![]()
różnią się skończoną ilością wyrazów, to oba szeregi ![]()
i ![]()
są jednocześnie zbieżne lub rozbieżne.
KRYTERIA ZBIEŻNOŚCI SZEREGÓW
Kryterium porównawcze
Jeśli ![]()
to ze zbieżności szeregu ![]()
wynika zbieżność szeregu ![]()
i z rozbieżności szeregu ![]()
wynika rozbieżność szeregu ![]()
.
Kryterium ilorazowe
Jeśli ![]()
oraz ![]()
, to oba szeregi ![]()
i ![]()
są jednocześnie zbieżne lub rozbieżne.
Kryterium Cauchy'ego
Jeśli ![]()
to ![]()
jest zbieżny gdy ![]()
i rozbieżny gdy ![]()
.
Kryterium d'Alemberta
Jeśli ![]()
oraz 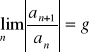
to szereg ![]()
jest zbieżny gdy ![]()
i rozbieżny gdy ![]()
.
Kryterium Raabego
Jeśli ![]()
oraz 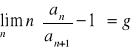
to szereg ![]()
jest zbieżny gdy ![]()
i rozbieżny gdy ![]()
.
Twierdzenie o zagęszczaniu
Jeśli ![]()
jest ciągiem nierosnącym o wyrazach nieujemnych to szeregi ![]()
i 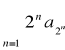
są jednocześnie zbieżne lub rozbieżne.
Kryterium Dirichleta
Jeśli ciąg sum częściowych szeregu ![]()
jest ograniczony oraz ![]()
jest ciągiem nierosnącym zbieżnym do zera to szereg 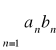
jest zbieżny.
Kryterium Abela
Jeśli szereg ![]()
jest zbieżny i ciąg ![]()
jest monotoniczny i ograniczony, to szereg 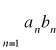
jest zbieżny.
Kryterium Leibniza
Jeśli ![]()
jest ciągiem nierosnącym zbieżnym do 0, to szereg 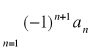
zwany szeregiem naprzemiennym jest zbieżny.
Definicja zbieżności bezwzględnej
Mówimy, że szereg ![]()
jest bezwzględnie zbieżny, gdy zbieżny jest szereg ![]()
.
Uwaga Każdy szereg zbieżny bezwzględnie jest zbieżny.
Uwaga Istnieją szeregi zbieżne lecz nie bezwzględnie zbieżne.
Definicja szeregu zbieżnego warunkowo
Szereg zbieżny lecz nie bezwzględnie zbieżny nazywamy szeregiem zbieżnym warunkowo.
Twierdzenie
Jeśli szereg ![]()
jest bezwzględnie zbieżny, to dla dowolnej permutacji ![]()
liczb naturalnych szereg 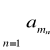
jest zbieżny i ma taką samą sumę jak szereg ![]()
.
Twierdzenie Cauchy'ego
Jeśli szeregi ![]()
i ![]()
są bezwzględnie zbieżne, to szereg ![]()
jest zbieżny przy czym suma tego szeregu wynosi ![]()
gdzie ![]()
oznacza sumę szeregu ![]()
, a ![]()
sumę szeregu ![]()
.
Twierdzenie Riemanna
Niech ![]()
będzie szeregiem warunkowo zbieżnym. Dla dowolnego ![]()
istnieje permutacja ![]()
zbioru liczb naturalnych taka, że ![]()
jest sumą szeregu 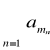
.
CIĄGI I SZEREGI FUNKCYJNE
Przyjmijmy, że ![]()
.
Definicja ciągu funkcyjnego
Ciągiem funkcyjnym określonym na zbiorze ![]()
nazywamy każdą funkcję odwzorowującą zbiór ![]()
w zbiór ![]()
. Załóżmy, że ![]()
. Wówczas dla oznaczenia ciągu funkcyjnego, którego n-tym wyrazem jest funkcja ![]()
używamy oznaczenie ![]()
.
Niech ![]()
oznacza ciąg funkcyjny taki, że ![]()
. Niech ![]()
.
Definicja zbieżności punktowej ciągu funkcyjnego
Mówimy, że ciąg ![]()
jest punktowo zbieżny na zbiorze ![]()
do funkcji ![]()
jeśli ![]()
.
Definicja zbieżności jednostajnej ciągu funkcyjnego
Mówimy, że ciąg ![]()
jest jednostajnie zbieżny na zbiorze ![]()
do funkcji ![]()
jeśli ![]()
.
Fakt, że ![]()
jest punktowo zbieżny do funkcji ![]()
na zbiorze ![]()
oznaczamy pisząc ![]()
.
Fakt, że ![]()
jest jednostajnie zbieżny do funkcji ![]()
na zbiorze ![]()
oznaczamy pisząc ![]()
![]()
![]()
.
Twierdzenie
Jeśli ![]()
![]()
![]()
to ![]()
.
Uwaga Twierdzenie odwrotne nie jest prawdziwe.
Twierdzenie Weierstrassa
Niech ![]()
dla ![]()
. Wówczas ![]()
Twierdzenie
Jeśli ![]()
i ![]()
jest ciągła na X, to również f jest ciągła na X.
Definicja funkcji przedziałami liniowej
Niech ![]()
, ![]()
i niech ![]()
. Funkcję f nazywamy przedziałami liniową na przedziale ![]()
jeśli f jest ciągła na ![]()
oraz jeśli istnieją układy liczb![]()
oraz ![]()
oraz ![]()
takie, że ![]()
Twierdzenie
Każda funkcja ciągła w przedziale domkniętym jest granicą jednostajnie zbieżnego ciągu funkcji przedziałami liniowych na tym przedziale.
Definicja szeregu funkcyjnego
Niech ![]()
będzie ciągiem funkcyjnym takim, że ![]()
. Szeregiem funkcyjnym nazywamy ciąg funkcyjny ![]()
gdzie ![]()
. Taki szereg funkcyjny oznaczamy symbolem ![]()
. Funkcję ![]()
nazywamy n-tym wyrazem a funkcję ![]()
nazywamy n-tą sumą tego szeregu.
Definicja zbieżności punktowej i jednostajnej szeregu funkcyjnego
Szereg funkcyjny ![]()
jest punktowo (jednostajnie) zbieżny na zbiorze X gdy ciąg funkcyjny ![]()
jest punktowo (jednostajnie) zbieżny na tym zbiorze.
Funkcję będącą granicą ciągu funkcyjnego ![]()
o ile ona istnieje nazywamy sumą szeregu ![]()
i oznaczamy tak jak sam szereg.
Wniosek. Szereg funkcyjny ![]()
jest punktowo zbieżny na zbiorze X wtedy i tylko wtedy gdy ![]()
jest zbieżny.
Wniosek. Jeśli szereg funkcyjny ![]()
jest jednostajnie zbieżny na zbiorze X, to jest punktowo zbieżny na tym zbiorze.
Twierdzenie Weierstrassa
Niech ![]()
będzie szeregiem funkcyjnym funkcji określonych na zbiorze X, a ![]()
szeregiem liczbowym zbieżnym takim, że ![]()
.
Wówczas szereg ![]()
jest jednostajnie zbieżny oraz ![]()
jest bezwzględnie zbieżny.
Definicja szeregu potęgowego
Niech ![]()
i niech ![]()
dla ![]()
. Załóżmy, że
![]()
jest funkcją taką, że ![]()
![]()
jest funkcją taką, że ![]()
dla ![]()
i ![]()
.
Szereg funkcyjny ![]()
nazywamy szeregiem potęgowym o środku w punkcie ![]()
i współczynnikach ![]()
. Oznaczamy go symbolicznie jako ![]()
.
Definicja promienia zbieżności szeregu potęgowego
Liczbę 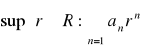
nazywamy promieniem zbieżności szeregu potęgowego ![]()
.
Uwaga. Promień zbieżności szeregu potęgowego nie zależy od jego środka ![]()
a jedynie od współczynników ![]()
dla ![]()
.
Uwaga. Promień zbieżności szeregu potęgowego jest zawsze liczbą nieujemną.
Niech R oznacza promień zbieżności szeregu potęgowego ![]()
.
Twierdzenie Cauchy'ego - Hadamarda
Twierdzenie o punktach zbieżności szeregu potęgowego
Jeśli R = 0, to szereg ![]()
jest zbieżny jedynie dla ![]()
.
Jeśli R = ∞, to szereg ![]()
jest zbieżny bezwzględnie dla dowolnego ![]()
.
Jeśli R ![]()
, to szereg ![]()
jest zbieżny bezwzględnie dla dowolnego ![]()
oraz rozbieżny dla ![]()
.
Definicja przedziału zbieżności szeregu potęgowego
Przedziałem zbieżności szeregu ![]()
nazywamy zbiór 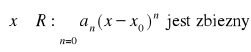
Twierdzenie
Szereg potęgowy ![]()
jest zbieżny jednostajnie w każdym przedziale domkniętym zawartym w przedziale zbieżności szeregu potęgowego.
Niech ![]()
będzie funkcją rzeczywistą zmiennej rzeczywistej
Definicja ilorazu różnicowego
Niech ![]()
oraz ![]()
. Ilorazem różnicowym funkcji ![]()
pomiędzy punktami ![]()
i ![]()
nazywamy liczbę ![]()
.
Załóżmy, że ![]()
wraz z pewnym otoczeniem (otoczeniem lewostronnym, otoczeniem prawostronnym).
Definicja pochodnej .
Pochodną (pochodną lewostronną, prawostronną) funkcji ![]()
w punkcie ![]()
nazywamy granicę ![]()
(![]()
, ![]()
) o ile ona istnieje. Oznaczamy ją wtedy jako ![]()
(![]()
,![]()
).
Definicja różniczkowalności funkcji.
Mówimy, że funkcja ![]()
jest różniczkowalna (różniczkowalna lewostronnie, prawostronnie) w punkcie ![]()
jeśli ma w tym punkcie skończoną pochodną (pochodną lewostronną, prawostronną).
Mówimy, że funkcja ![]()
jest różniczkowalna w przedziale otwartym, jeśli jest różniczkowalna w każdym punkcie tego przedziału.
Mówimy, że funkcja ![]()
jest różniczkowalna w przedziale domkniętym, jeśli jest różniczkowalna w każdym punkcie wewnętrznym tego przedziału, oraz prawostronnie różniczkowalna w lewym krańcu i lewostronnie różniczkowalna w prawym krańcu.
Definicja kąta nachylenia.
Niech ![]()
będzie dowolną prostą na płaszczyźnie![]()
w której![]()
oznacza oś odciętych. Jeśli ![]()
, to przyjmujemy, że kątem nachylenia prostej ![]()
jest zero. Jeśli ![]()
to przyjmujemy, że kątem nachylenia prostej ![]()
jest kąt, którego jednym z ramion jest ![]()
, a drugim odcinek ![]()
przebiegający w górnej półpłaszczyźnie.
Interpretacja geometryczna ilorazu różnicowego i pochodnej.
Prostą przechodzącą przez punkty, ![]()
,![]()
nazywać będziemy sieczną. Zauważmy, że iloraz różnicowy funkcji ![]()
pomiędzy punktami ![]()
i ![]()
jest tangensem kąta nachylenia siecznej. Przy ustalonym ![]()
i ![]()
zmierzającym do ![]()
zauważamy, że sieczne wyznaczone przez te punkty przyjmują w granicy o ile ona istnieje położenie prostej, którą nazwiemy styczną do wykresu funkcji w punkcie![]()
. Pozwala to na spostrzeżenie, że pochodna funkcji jest tangensem kąta nachylenia stycznej do wykresu funkcji w punkcie ![]()
.
Wniosek.
Równanie stycznej do wykresu funkcji w punkcie ![]()
ma postać ![]()
.
Definicja.
Normalną do wykresu funkcji f w punkcie ![]()
nazywamy prostą prostopadłą do stycznej w tym punkcie i przechodzącą przez ten punkt.
Definicja.
Niech funkcje f i g przecinające się w punkcie o odciętej będą różniczkowalne w ![]()
. Kątem przecięcia wykresów funkcji f i g nazywamy nie większy od prostego kąt ![]()
, pomiędzy stycznymi do wykresów tych funkcji w punkcie ich przecięcia.
Wniosek. 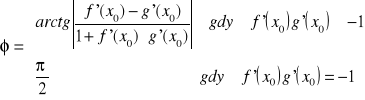
.
Twierdzenie.
Jeżeli funkcja f jest różniczkowalna w pewnym punkcie, to jest w tym punkcie ciągła.
Uwaga. Twierdzenie odwrotne jest fałszywe.
Twierdzenie.
Jeżeli f i g są różniczkowalne w punkcie ![]()
oraz ![]()
, to funkcje
[Author ID0: at Tue Aug 14 13:07:00 2001
][Author ID0: at Tue Aug 14 13:07:00 2001
][Author ID0: at Tue Aug 14 13:07:00 2001
]![]()
[Author ID0: at Tue Aug 14 13:07:00 2001
]są różniczkowalne w tym punkcie, oraz prawdziwe są wzory:
[Author ID0: at Tue Aug 14 13:10:00 2001
][Author ID0: at Tue Aug 14 13:10:00 2001
]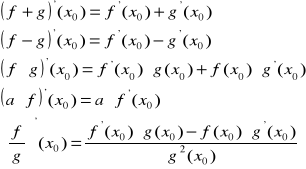
[Author ID0: at Tue Aug 14 13:10:00 2001
]
Ostatni wzór jest prawdziwy przy dodatkowym założeniu, że ![]()
.
Uwaga. Twierdzenie powyższe jest prawdziwe również dla pochodnych jednostronnych oraz dla pochodnych niewłaściwych, o ile nie występują symbole nieoznaczone.
Twierdzenie (o pochodnej funkcji złożonej).
Jeśli funkcja ![]()
jest różniczkowalna w punkcie ![]()
, zaś funkcja ![]()
jest różniczkowalna w punkcie ![]()
to funkcja ![]()
jest różniczkowalna w punkcie ![]()
przy czym [Author ID0: at Tue Aug 14 13:19:00 2001
][Author ID0: at Tue Aug 14 13:19:00 2001
]![]()
[Author ID0: at Tue Aug 14 13:19:00 2001
].
Twierdzenie (o pochodnej funkcji odwrotnej)
Niech ![]()
. Jeśli ![]()
jest ciągłą i różnowartościową funkcją różniczkowalną w punkcie ![]()
, taką, że ![]()
, to funkcja odwrotna ![]()
jest różniczkowalna w punkcie ![]()
i ![]()
.
Uwaga. Twierdzenia o pochodnej funkcji złożonej i pochodnej funkcji odwrotnej są prawdziwe również dla pochodnych jednostronnych i dla pochodnych niewłaściwych, o ile nie występują symbole nieoznaczone.
Wzory na pochodne funkcji elementarnych
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Definicja różniczki .
Niech funkcja f będzie różniczkowalna w punkcie ![]()
. Różniczką funkcji f w punkcie ![]()
nazywamy funkcję liniową, która dowolnej liczbie rzeczywistej ![]()
przypisuje liczbę ![]()
. Różniczkę funkcji f w punkcie ![]()
będziemy oznaczać jako ![]()
.
Uwaga. Zauważmy, że różniczka funkcji identycznościowej obliczana w dowolnym punkcie przypisuje dowolnej liczbie rzeczywistej ![]()
nią samą. Stąd wniosek, że ![]()
. Ponieważ różniczka funkcji f w dowolnym punkcie ![]()
to ![]()
, więc możemy zapisać, że ![]()
. W powyższym wzorze ![]()
jest funkcją, ![]()
jest funkcją, a ![]()
jest liczbą. Wzór ten można zapisać w postaci ![]()
. Jest on oczywiście prawdziwy dla dowolnego argumentu ![]()
i stwierdza, że iloraz dwóch różniczek jest funkcją stałą. Argument ![]()
z przyczyn praktycznych w powyższym wzorze nie występuje.
Definicja pochodnej rzędu n (indukcja).
Załóżmy, że ![]()
wraz z pewnym otoczeniem, oraz że zdefiniowaliśmy już pochodną ![]()
funkcji ![]()
rzędu ![]()
w każdym punkcie wspomnianego otoczenia. Jeśli ![]()
jest funkcją różniczkowalną w punkcie ![]()
to jej pochodną w tym punkcie nazywać będziemy pochodną rzędu ![]()
funkcji ![]()
w punkcie ![]()
. Pochodną rzędu ![]()
funkcji ![]()
w punkcie ![]()
oznaczać będziemy jako ![]()
. Przyjmujemy ponadto, że ![]()
.
Twierdzenie
Jeżeli f i g mają pochodne rzędu ![]()
w punkcie ![]()
, to funkcja ![]()
ma pochodną rzędu n w punkcie ![]()
i wyraża się ona wzorem
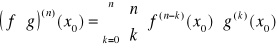
(wzór Leibniza).
Załóżmy, że ![]()
.
Twierdzenie (ROLLE'A)
Jeżeli funkcja f jest ciągła w przedziale [Author ID0: at Tue Aug 14 14:56:00 2001
][Author ID0: at Tue Aug 14 14:56:00 2001
]![]()
[Author ID0: at Tue Aug 14 14:56:00 2001
], różniczkowalna w przedziale [Author ID0: at Tue Aug 14 14:57:00 2001
][Author ID0: at Tue Aug 14 14:57:00 2001
][Author ID0: at Tue Aug 14 14:57:00 2001
]![]()
[Author ID0: at Tue Aug 14 14:57:00 2001
], oraz [Author ID0: at Tue Aug 14 14:58:00 2001
][Author ID0: at Tue Aug 14 14:58:00 2001
]![]()
[Author ID0: at Tue Aug 14 14:58:00 2001
], to istnieje przynajmniej jeden punkt [Author ID0: at Tue Aug 14 14:59:00 2001
][Author ID0: at Tue Aug 14 14:59:00 2001
]![]()
[Author ID0: at Tue Aug 14 14:59:00 2001
] taki, że ![]()
.
Twierdzenie (CAUCHE'EGO )
Jeżeli funkcje ![]()
i ![]()
są ciągłe w przedziale [Author ID0: at Tue Aug 14 14:56:00 2001
][Author ID0: at Tue Aug 14 14:56:00 2001
][Author ID0: at Tue Aug 14 14:56:00 2001
]![]()
[Author ID0: at Tue Aug 14 14:56:00 2001
], różniczkowalne w przedziale [Author ID0: at Tue Aug 14 14:57:00 2001
][Author ID0: at Tue Aug 14 14:57:00 2001
]![]()
[Author ID0: at Tue Aug 14 14:57:00 2001
] to istnieje przynajmniej jeden punkt [Author ID0: at Tue Aug 14 14:59:00 2001
][Author ID0: at Tue Aug 14 14:59:00 2001
]![]()
[Author ID0: at Tue Aug 14 14:59:00 2001
] taki, że![]()
.
Twierdzenie (LAGRANGEA).
Jeżeli funkcja f jest ciągła w przedziale [Author ID0: at Tue Aug 14 14:56:00 2001
][Author ID0: at Tue Aug 14 14:56:00 2001
]![]()
[Author ID0: at Tue Aug 14 14:56:00 2001
]i różniczkowalna w przedziale [Author ID0: at Tue Aug 14 14:57:00 2001
][Author ID0: at Tue Aug 14 14:57:00 2001
]![]()
[Author ID0: at Tue Aug 14 14:57:00 2001
], to istnieje punkt [Author ID0: at Tue Aug 14 14:59:00 2001
][Author ID0: at Tue Aug 14 14:59:00 2001
]![]()
[Author ID0: at Tue Aug 14 14:59:00 2001
] taki, że ![]()
.
Powyższe trzy twierdzenia zwane są twierdzeniami o wartości średniej.
Twierdzenie.
Niech funkcja ![]()
będzie różniczkowalna w przedziale [Author ID0: at Tue Aug 14 14:56:00 2001
][Author ID0: at Tue Aug 14 14:56:00 2001
]![]()
[Author ID0: at Tue Aug 14 14:56:00 2001
].
Twierdzenie.
Jeżeli funkcja ![]()
jest różniczkowalna w przedziale I oraz jest niemalejąca w tym przedziale, to![]()
.
Twierdzenie.
Jeżeli funkcja ![]()
jest różniczkowalna w przedziale I, to jest ona rosnąca w tym przedziale, wtedy i tylko wtedy, gdy ![]()
oraz zbiór ![]()
nie zawiera przedziału.
Twierdzenie.
Niech ![]()
, ![]()
będą funkcjami różniczkowalnymi na przedziale I oraz niech ![]()
. Jeżeli ![]()
oraz ![]()
, to ![]()
.
Twierdzenie. (REGUŁA DE L'HOSPITALA)
Niech ![]()
i ![]()
będą funkcjami różniczkowalnymi w pewnym sąsiedztwie ![]()
punktu ![]()
oraz![]()
. Jeżeli ![]()
, oraz istnieje granica 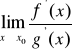
(właściwa lub nie), to istnieje również granica ![]()
przy czym 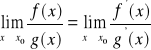
.
Uwaga: twierdzenie odwrotne nie jest prawdziwe.
Twierdzenie (WZÓR TAYLORA)
Jeśli funkcja f ma ciągłą pochodną rzędu ![]()
w przedziale ![]()
oraz pochodną rzędu ![]()
w przedziale ![]()
, to istnieje punkt ![]()
taki, że ![]()
. Ostatni składnik sumy występującej w powyższym wzorze oznaczać będziemy jako![]()
i nazywać resztą w postaci Lagrange'a. Tak więc ![]()
Wniosek. Dla ![]()
otrzymujemy twierdzenie Lagrange'a.
Uwaga Wzory twierdzeń o wartości średniej i wzór Taylora są prawdziwe również w przypadku, gdy ![]()
.
Wniosek. Jeśli we wzorze Taylora przyjmiemy ![]()
, to otrzymujemy wzór Maclaurina ![]()
.
Twierdzenie.
Załóżmy, że funkcja ![]()
ma pochodną dowolnego rzędu ![]()
w przedziale ![]()
. Jeśli ![]()
, to ![]()
.
Uwaga. Założenie istnienia pochodnych dowolnego rzędu ![]()
nie wystarcza do udowodnienia powyższego wzoru nawet wtedy, gdy wzbogacić je założeniem zbieżności szeregu ![]()
.
Wniosek. Załóżmy, że funkcja ![]()
ma pochodną dowolnego rzędu ![]()
w przedziale pomiędzy liczbami ![]()
i ![]()
. Jeśli ![]()
, to ![]()
Twierdzenie.
Jeśli ![]()
, to ![]()
ma pochodną dowolnego rzędu ![]()
w każdym punkcie ![]()
położonym wewnątrz przedziału zbieżności szeregu ![]()
przy czym ![]()
dla ![]()
, oraz ![]()
dla. ![]()
.
Twierdzenie (o różniczkowaniu ciągu funkcyjnego)
Załóżmy, że ![]()
jest ciągiem funkcyjnym złożonym z funkcji mających ciągłe pochodne na przedziale ![]()
. Jeśli ![]()
, oraz ![]()
![]()
![]()
, to ![]()
jest różniczkowalna na ![]()
, przy czym ![]()
.
Załóżmy teraz, że funkcja f jest określona w pewnym otoczeniu punktu ![]()
.
Definicja.
Funkcja f osiąga w punkcie ![]()
maksimum (minimum) lokalne, jeżeli ![]()
(![]()
).
Definicja.
Funkcja f osiąga w punkcie ![]()
maksimum (minimum) lokalne właściwe, jeżeli ![]()
(![]()
).
Maksima i minima funkcji nazywamy ekstremami tej funkcji.
Twierdzenie Fermata. (warunek konieczny istnienia ekstremum).
Jeżeli funkcja f ma ekstremum lokalne w punkcie ![]()
oraz jest różniczkowalna w tym punkcie, to ![]()
.
Twierdzenie. ( I warunek wystarczający istnienia ekstremum lokalnego .
Załóżmy, że ![]()
. Przyjmijmy, że![]()
jest ciągła na ![]()
i różniczkowalna na ![]()
. Jeśli ![]()
to ![]()
ma w punkcie ![]()
minimum właściwe. Jeśli ![]()
to ![]()
ma w punkcie ![]()
maksimum właściwe.
Twierdzenie. (II warunek wystarczający).
Jeżeli funkcja f ma pochodną rzędu ![]()
w pewnym otoczeniu punktu![]()
, ciągłą w punkcie ![]()
, oraz ![]()
, ![]()
, to w przypadku gdy n jest liczbą parzystą, funkcja f ma ekstremum lokalne w punkcie ![]()
. Jest to maksimum właściwe, gdy ![]()
, zaś minimum właściwe, gdy ![]()
. Jeśli n jest liczbą nieparzystą, to f nie ma ekstremum lokalnego w punkcie ![]()
.
Definicja ekstremum absolutnego.
Niech ![]()
i niech f będzie funkcją rzeczywistą taka, że ![]()
. Mówimy, że ![]()
osiąga w punkcie ![]()
maksimum (minimum) absolutne na zbiorze A, jeżeli
![]()
Twierdzenie
Niech ![]()
będzie ciągła w przedziale ![]()
i różniczkowalna w ![]()
. Funkcja ![]()
osiąga w tym przedziale swoje ekstrema absolutne w punktach zbioru ![]()
Definicja.
Załóżmy, że ![]()
jest funkcją różniczkowalną w punkcie![]()
. Funkcję ![]()
nazywamy wypukłą (wklęsłą) w punkcie ![]()
jeśli ![]()
(![]()
). Funkcję ![]()
nazywamy wypukłą (wklęsłą) na przedziale ![]()
, gdy jest wypukła (wklęsła) w każdym punkcie tego przedziału.
Twierdzenie (warunek wystarczający wypukłości (wklęsłości))
Załóżmy, że istnieje druga pochodna funkcji ![]()
w przedziale ![]()
. Jeśli ![]()
(![]()
) to funkcja ![]()
jest wypukła (wklęsła) na ![]()
.
Definicja punktu przegięcia
Mówimy, że funkcja![]()
ciągła w punkcie ![]()
ma w punkcie ![]()
punkt przegięcia, jeśli funkcja ta jest wypukła (wklęsła) na pewnym lewostronnym sąsiedztwie punktu ![]()
i wklęsła (wypukła) na pewnym prawostronnym sąsiedztwie punktu ![]()
.
Twierdzenie (warunek konieczny istnienia punktu przegięcia )
Jeśli funkcja ![]()
ma pochodną rzędu drugiego w pewnym otoczeniu punktu ![]()
ciągłą w ![]()
i ![]()
jest punktem przegięcia funkcji ![]()
to ![]()
.
Twierdzenie ( I warunek wystarczający istnienia punktu przegięcia).
Załóżmy, że ![]()
. Przyjmijmy, że![]()
ma pochodną rzędu pierwszego na ![]()
i pochodną rzędu drugiego na ![]()
. Jeśli ![]()
lub ![]()
to ![]()
ma w punkcie ![]()
punkt przegięcia.
Twierdzenie. (II warunek wystarczający istnienia punktu przegięcia
Jeżeli funkcja f ma pochodną rzędu ![]()
w pewnym otoczeniu punktu![]()
, ciągłą w punkcie ![]()
, oraz ![]()
, ![]()
, to w przypadku gdy n jest liczbą nieparzystą, funkcja f ma w punkcie ![]()
punkt przegięcia.. Jeśli n jest liczbą parzystą, to f nie ma punktu przegięcia w punkcie ![]()
.
Definicja asymptoty pionowej
Załóżmy, że ![]()
jest funkcją określoną na pewnym sąsiedztwie punktu![]()
. Prostą o równaniu ![]()
nazywamy asymptotą pionową funkcji ![]()
gdy ![]()
.
Definicja asymptoty ukosnej
Załóżmy, że ![]()
jest funkcją określoną na pewnym przedziale ![]()
. Prostą o równaniu ![]()
nazywamy asymptotą ukośną w minus nieskończoności (plus nieskończoności) funkcji ![]()
gdy ![]()
(![]()
).
Twierdzenie o współczynnikach asymptoty ukośnej
Prosta o równaniu ![]()
jest asymptotą ukośną funkcji ![]()
w minus nieskończoności (plus nieskończoności) wtedy i tylko wtedy gdy ![]()
(![]()
Definicja (funkcji pierwotnej).
Funkcję F nazywamy funkcją pierwotną funkcji f na przedziale I, jeśli
![]()
Gdy I jest przedziałem domkniętym (I=[a,b]) lub jednostronnie domkniętym (I=[a,b) lub I=(a,b]), to przez pochodną funkcji w punktach a i b należy rozumieć pochodną jednostronną, odpowiednio F'+(a) i F'-(b).
Twierdzenie (Podstawowe własności funkcji pierwotnych)
Niech F będzie funkcją pierwotną funkcji f na przedziale I. Wówczas
(1) każda funkcja postaci F(x)+C, gdzie C=const, jest również funkcją pierwotną funkcji f
(2) jeśli ponadto funkcja G jest też funkcja pierwotną funkcji f na przedziale I, to G=F+C na przedziale I, gdzie C=const.
Uwaga:
Z powyższego twierdzenia wynika, że funkcje pierwotne funkcji f na przedziale I mają postać:
(*) F(x)+C gdzie cR i F jest pewną funkcją pierwotną funkcji f na przedziale I
oraz tylko funkcje postaci (*) są funkcjami pierwotnymi funkcji f na przedziale I.
Definicja (całki nieoznaczonej).
Niech F będzie funkcja pierwotną funkcji f na przedziale I. Całką nieoznaczoną funkcji f na przedziale I nazywamy zbiór funkcji:
{F(x)+C: CR}
i oznaczamy ![]()
.
Uwaga
Działania i operacje na całkach nieoznaczonych oznaczają działania i operacje na funkcjach pierwotnych reprezentujących te całki. Jeśli F jest pewną funkcją pierwotną funkcji f na przedziale I, to zapisujemy ![]()
, gdzie CR.
Bezpośrednio z definicji całki nieoznaczonej wynikają następujące
Wnioski:
Niech funkcja f ma funkcję pierwotną na przedziale I. Wtedy:
(1) ![]()
(2) ![]()
Twierdzenie
Niech dany będzie punkt x0 wewnątrz przedziału I i niech dana będzie dowolna liczba y0R. Jeśli funkcja f posiada funkcję pierwotną w przedziale I, to istnieje tylko jedna funkcja pierwotna F taka, że F(x0)=y0.
Uwaga:
Geometrycznie twierdzenie to oznacza, że przez każdy punkt płaszczyzny o odciętej xI przechodzi krzywa całkowa (tzn. wykres funkcji pierwotnej). Ponieważ krzywe całkowe są do siebie równoległe, więc przez każdy punkt płaszczyzny przechodzić może tylko jedna krzywa całkowa danej funkcji f.
Bezpośrednio z definicji całki nieoznaczonej wynikają następujące wzory na całki nieoznaczone ważniejszych funkcji elementarnych:
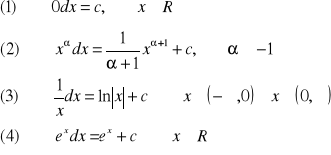
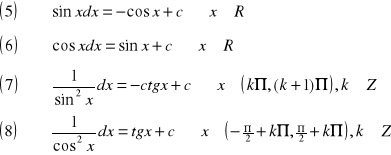
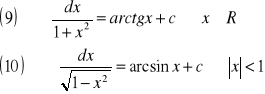
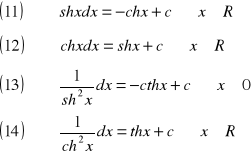
Twierdzenie (o liniowości całki nieoznaczonej)
Jeżeli funkcje f i g mają funkcje pierwotne na przedziale I, to:
(1) ![]()
(2) ![]()
Twierdzenie (o całkowaniu granicy ciągu funkcyjnego)
Jeżeli funkcje fn są ciągłe i posiadają funkcje pierwotne w przedziale I oraz ciąg {fn} jest jednostajnie zbieżny do funkcji f na przedziale I, to funkcja f również posiada funkcję pierwotną i zachodzi równość
![]()
Korzystając z powyższego twierdzenia dowodzi się
Twierdzenie (warunek wystarczający istnienia funkcji pierwotnej)
Każda funkcja ciągła na przedziale I posiada w tym przedziale funkcję pierwotną
Twierdzenie (o całkowaniu szeregu funkcyjnego)
Jeżeli funkcje fn są ciągłe i posiadają funkcje pierwotne w przedziale I oraz szereg funkcyjny ![]()
jest jednostajnie zbieżny do funkcji f na przedziale I, to funkcja f również posiada funkcję pierwotną i zachodzi równość:
![]()
Twierdzenie (o całkowaniu przez części)
Jeżeli funkcje f i g mają ciągłe pochodne, to ![]()
Twierdzenie (o całkowaniu przez podstawienie)
Jeżeli :
1) funkcja f: I→R jest ciągła na przedziale I
2) funkcja ![]()
ma ciągłą pochodną na przedziale ![]()
,
to ![]()
+c , gdzie F jest dowolną funkcją pierwotną funkcji f oraz cR.
Definicja (całki oznaczonej Riemanna).
Niech f będzie funkcją ograniczoną na przedziale [a,b] i niech zbiór Pn={x0, x1,…, xn} oznacza podział odcinka [a,b] na n części, przy czym a= x0< x1<…< xn=b. Niech
xk=xk-xk-1 oznacza długość k-tego odcinka podziału Pn, gdzie 1kn oraz δ(Pn)=max{xk: 1kn} oznacza średnicę podziału Pn, zaś xk*[ xk-1, xk] oznacza punkt pośredni k-tego odcinka podziału Pn, gdzie 1kn.
Sumą całkową funkcji f na przedziale [a,b] odpowiadającą podziałowi Pn oraz punktom pośrednim xk* tego podziału gdzie 1kn, nazywamy liczbę
![]()
.
Całkę oznaczoną Riemanna z funkcji f na przedziale [a,b] definiujemy wzorem;
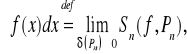
o ile istnieje granica właściwa występująca po prawej stronie znaku równości oraz granica ta nie zależy od sposobu podziałów Pn przedziału [a,b] ani od sposobu wyboru punktów pośrednich xk*, gdzie 1kn. Ponadto przyjmujemy 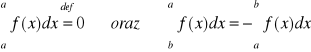
dla a<b.
Funkcję, dla której istnieje całka oznaczona Riemanna na [a,b] nazywamy funkcją całkowalną na [a,b].
Uwaga
Każda funkcja całkowalna jest ograniczona, ale nie każda funkcja ograniczona na przedziale jest na nim całkowalna np. funkcja Dirichleta na przedziale [0,1].
Twierdzenia o funkcjach całkowalnych w sensie (R)
Twierdzenie 1
Jeżeli funkcja f jest całkowalna na przedziale I=[a,b], to jest również całkowalna na każdym podprzedziale [c,d]I.
Twierdzenie 2
Jeśli f jest całkowalna na przedziale I, zaś jest funkcją ciągłą, to funkcja f jest całkowalna na I.
Twierdzenie 3.
Jeśli a=t0< t1<… tn-1< tn=b oraz f jest całkowalna na każdym przedziale [ti,ti+1], i{0,…,n-1}, to f jest całkowalna na [a,b].
Twierdzenie 4 (warunek wystarczający całkowalności)
Jeśli funkcja f jest ograniczona na przedziale [a,b] i ma na tym przedziale skończoną liczbę punktów nieciągłości I rodzaju, to jest na nim całkowalna.
Uwaga *
Z powyższego twierdzenia wynika, że funkcja ciągła na przedziale jest na nim całkowalna. Z drugiej strony funkcja całkowalna na przedziale może mieć nieskończenie wiele punktów nieciągłości.
Twierdzenie 5
Jeśli funkcja f jest monotoniczna i ograniczona na przedziale [a,b], to jest całkowalna na [a,b].
Twierdzenie 6 (Newtona - Leibnitza, I podstawowe twierdzenie rachunku całkowego)
Jeśli funkcja f jest ciągła na przedziale [a,b], to 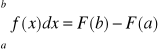
, gdzie F oznacza dowolną funkcję pierwotną funkcji f na tym przedziale. Różnicę F(b)-F(a) oznaczamy ![]()
.
Twierdzenie 7 (o liniowości całki oznaczonej)
Jeżeli funkcja f i g są całkowalne na przedziale [a,b], to
1) 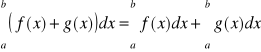
2) 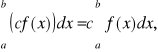
gdzie cR
Twierdzenie 8 (o całkowaniu przez części)
Jeżeli funkcje f i g mają ciągłe pochodne na przedziale [a,b], to
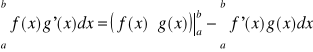
Twierdzenie 9 (o całkowaniu przez podstawienie)
Jeżeli:
1) funkcja ![]()
ma ciągłą pochodną na przedziale [,]
2) ()=a, ()=b,
3) funkcja f jest ciągła na [a,b],
wówczas 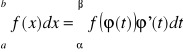
.
Twierdzenie 10 (o równości całek)
Niech funkcja f będzie całkowalna na przedziale [a,b] oraz niech funkcja g różni się od funkcji f tylko w skończonej liczbie punktów tego przedziału. Wtedy funkcja g także jest całkowalna na przedziale [a,b] oraz
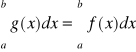
.
Twierdzenie 11 (addytywność całki względem przedziału całkowania)
Jeżeli funkcja f jest całkowalna na przedziale [a,b] oraz c(a,b), to
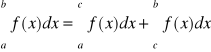
Twierdzenie 12 (o zachowaniu nierówności przy całkowaniu)
Jeżeli funkcja f i g spełniają warunki:
1) są całkowalne na przedziale [a,b],
2) ![]()
to 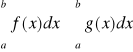
Uwaga
Jeżeli nierówność w założeniu twierdzenia jest ostra, to także nierówność w tezie jest ostra.
Twierdzenie 13 (o całce funkcji nieparzystej, parzystej i okresowej)
Jeżeli funkcja f jest całkowalna oraz
1) jest nieparzysta, to 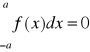
;
2) jest parzysta, to 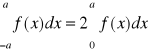
;
3) ma okres T, to 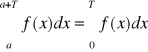
.
Twierdzenie 14
Jeżeli f jest całkowalna na przedziale [a,b] oraz istnieją liczby m, MR takie, że
![]()
wówczas 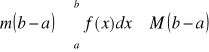
.
Definicja (wartości średniej funkcji)
Niech f będzie całkowalną na przedziale [a,b]. Wartością średnią funkcji f na przedziale [a,b] nazywamy liczbę
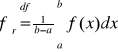
.
Twierdzenie 15 (całkowe o wartości średniej funkcji)
Jeżeli f jest ciągła na przedziale [a,b], to
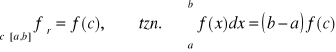
.
Twierdzenie 16 (nierówność Schwartza)
Jeśli f i g są całkowalne na przedziale [a,b], to
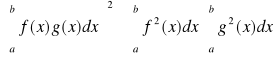
Definicja (funkcji górnej granicy całkowania)
Niech funkcja f będzie całkowalna na przedziale [a,b] oraz niech c[a,b]. Funkcję 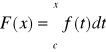
, gdzie x[a,b], nazywamy funkcja górnej granicy całkowania.
Twierdzenie 17 (o ciągłości funkcji górnej granicy całkowania)
Jeżeli funkcja f jest całkowalna na przedziale [a,b] i c[a,b], to funkcja 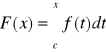
, gdzie x[a,b] jest ciągła na przedziale [a,b].
Twierdzenie 18 (II główne twierdzenie rachunku całkowego)
Jeżeli funkcja f jest całkowalna na przedziale [a,b] oraz ciągła w punkcie x0[a,b], to funkcja 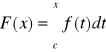
, gdzie c[a,b], ma pochodną właściwą w punkcie x0 oraz ![]()
.
Uwaga
Jeżeli funkcja f jest ciągła na przedziale [a,b], to jej funkcja górnej granicy całkowania F jest funkcją pierwotną funkcji f.
Twierdzenie 19 (O całkowaniu ciągu funkcyjnego)
Jeżeli ciąg {fn}n∈N funkcji ciągłych na przedziale [a,b] jest zbieżny jednostajnie do funkcji f na [a,b], to
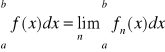
Twierdzenie 20 (O całkowaniu szeregu funkcyjnego)
Jeżeli funkcje fn, dla n=1, 2, …, są ciągłe na przedziale [a,b] i szereg ![]()
jest zbieżny jednostajnie do funkcji f na [a,b], to
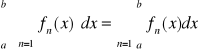
Z powyższego twierdzenia jako bezpośredni wniosek mamy
Twierdzenie 21 (O całkowaniu szeregów potęgowych)
Niech 0<R≤+∞ będzie promieniem zbieżności szeregu potęgowego 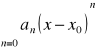
, wówczas 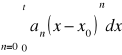
ma ten sam promień zbieżności R oraz
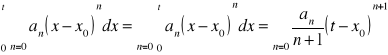
dla każdego t∈(x0-R, x0+R).
Zastosowania geometryczne całki oznaczonej.
1) Pole figury płaskiej
Twierdzenie 1
Niech krzywa AB będzie określona równaniem y=f(x) dla x[a,b], gdzie f jest funkcją dodatnią i ciągłą w przedziale [a,b]. Wtedy pole P trapezu krzywoliniowego ograniczonego krzywa AB z góry oraz prostymi y=0, x=a, x=b, wyraża się wzorem:
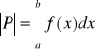
.
Wniosek 1
Jeżeli krzywa AB ograniczająca z góry trapez krzywoliniowy P opisany w twierdzeniu 1 jest określona za pomocą równań parametrycznych:
(*) ![]()
gdzie x=a dla t=, x=b dla t=, funkcje x i y mają ciągłe pochodne i y jest dodatnia w przedziale [,], zaś krzywa AB nie ma punktów wielokrotnych, wówczas pole trapezu krzywoliniowego P wyraża się wzorem:
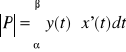
.
Wniosek 2
Jeżeli trapez krzywoliniowy P określony jest następująco:
![]()
gdzie funkcje f1 i f2 są ciągłe na przedziale [a,b] oraz f1(x)f2(x) dla każdego x[a,b], wtedy pole trapezu krzywoliniowego wyraża się wzorem:
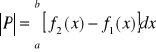
.
Twierdzenie 2
Niech AOB będzie wycinkiem ograniczonym krzywa AB i dwoma promieniami Oa i OB. (z których każdy może być punktem) i niech krzywa AB będzie określona równaniem biegunowym:
![]()
gdzie g jest funkcją ciągłą i dodatnią w przedziale ![]()
. Wtedy pole P wycinka AOB wyraża się wzorem:
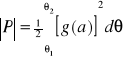
.
Wniosek 3
Jeśli krzywa AB jest określona równaniami parametrycznymi (*) i spełnia założenia z wniosku 1, wówczas pole wycinka AOB wyraża się wzorem:
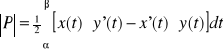
.
2) Długość łuku krzywej
Twierdzenie 3
Jeżeli łuk l dany jest równaniami parametrycznymi:
![]()
przy czym nie ma punktów wielokrotnych oraz funkcje x i y posiadają ciągłe pochodne na przedziale [,], to długość l łuku l wyraża się wzorem:
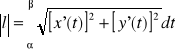
.
Twierdzenie 4
Jeżeli łuk l dany jest równaniem jawnym ![]()
, gdzie f jest funkcją posiadającą ciągłą pochodną na przedziale [a,b], wówczas długość l tego łuku wyraża się wzorem:
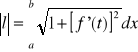
.
Twierdzenie 5
Jeżeli łuk l dany jest równaniem biegunowym ![]()
, gdzie g jest funkcją nieujemną posiadającą ciągłą pochodną na przedziale ![]()
, wówczas długość l łuku l wyraża się wzorem:
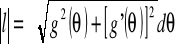
.
3) Objętość bryły obrotowej.
Twierdzenie 6 (objętość bryły)
Niech S(x), gdzie x∈[a.b], oznacza pole przekroju bryły V płaszczyzną prostopadłą do osi OX w przestrzeni X oraz niech S będzie funkcją ciągłą na przedziale [a,b]. Wtedy objętość bryły V wyraża się wzorem;
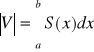
.
Twierdzenie 7 (objętość bryły obrotowej)
Niech ![]()
, gdzie f jest funkcją ciągłą na przedziale [a,b], oznacza trapez krzywoliniowy. Wtedy objętość bryły V powstałej z obrotu trapezu krzywoliniowego D wokół osi 0x wyraża się wzorem:
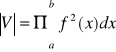
.
4) Pole powierzchni obrotowej.
Twierdzenie 8
Niech krzywa AB będzie dana równaniem ![]()
, gdzie f jest funkcją nieujemną posiadającą ciągłą pochodną na przedziale [a,b]. Wówczas pole powierzchni S powstałej w wyniku obrotu krzywej AB dokoła osi Ox wyraża się wzorem:
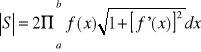
.
Twierdzenie 9
Niech krzywa AB będzie dana równaniami parametrycznymi:
![]()
gdzie funkcje x i y posiadają ciągłe pochodne i y jest nieujemna na przedziale ![]()
, oraz krzywa AB nie posiada punktów wielokrotnych. Wówczas pole powierzchni S powstałej w wyniku obrotu krzywej AB wokół osi Ox wyraża się wzorem:
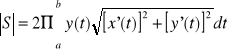
.
Całki niewłaściwe
W rozważaniach tego rozdziału będziemy zakładać, że wszystkie funkcje sa całkowalne na dowolnym przedziale domkniętym zawartym w ich dziedzinie.
Definicja (całki niewłaściwej pierwszego rodzaju)
Niech funkcja f: [a, +∞) →R. Całką niewłaściwą pierwszego rodzaju z funkcji f na półprostej [a, +∞) definiujemy następująco:
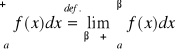
.
Jeżeli granica po prawej stronie znaku równości jest właściwa, to mówimy, że całka niewłaściwa z funkcji f na [a, +∞)jest zbieżna. Jeżeli granica ta jest równa +∞ lub -∞, to mówimy, że całka jest rozbieżna odpowiednio do +∞ lub do -∞. W pozostałych przypadkach mówimy, że całka jest rozbieżna.
Analogicznie definiuje się całkę niewłaściwą pierwszego rodzaju z funkcji f na (-∞,b], a mianowicie:
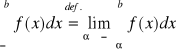
.
Niech f: R→R. Całkę niewłaściwą z funkcji f na prostej (-∞, +∞) definiujemy następująco:
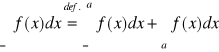
,
gdzie a oznacza dowolną liczbę rzeczywistą. Jeżeli obie całki po prawej stronie znaku równości są zbieżne, to mówimy, że całka niewłaściwa z funkcji f na (-∞, +∞) jest zbieżna.
Uwaga:
Zbieżność całki niewłaściwej na (-∞, +∞) nie zależy od wyboru liczby a.
Wniosek:
Całka niewłaściwa postaci ![]()
, gdzie a>0, jest zbieżna dla p>1 i rozbieżna do +∞ dla p≤1.
Analogiczny fakt jest prawdziwy dla całek ![]()
, gdzie b<0, o ile funkcja podcałkowa jest poprawnie określona.
Kryteria zbieżności całek niewłaściwych pierwszego rodzaju
Twierdzenie 1 (Kryterium porównawcze)
Niech funkcje f i g spełniają warunek:
![]()
Wówczas:
Uwaga:
Twierdzenie to zachodzi także dla funkcji f i g niedodatnich. Ponadto prawdziwe są analogiczne twierdzenie dla całek niewłaściwych na półprostej (-∞,b].
Twierdzenie 2 (Kryterium ilorazowe)
Niech funkcje f i g będą dodatnie (ujemne) na półprostej [a, +∞) oraz niech spełniają warunek:
![]()
, gdzie 0<k<+∞. Wówczas całki 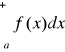
i 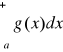
są jednocześnie zbieżne albo rozbieżne.
Definicja (zbieżności bezwzględnej całek niewłaściwych I rodzaju).
Całka niewłaściwa pierwszego rodzaju z funkcji f jest zbieżna bezwzględnie, gdy zbieżna jest całka niewłaściwa z funkcji f.
Twierdzenie 3
Jeżeli całka niewłaściwa z funkcji f jest zbieżna bezwzględnie, to jest zbieżna. Ponadto
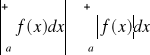
.
Definicja (całek niewłaściwych drugiego rodzaju)
Niech funkcja f: (a,b]→R będzie nieograniczona tylko na prawostronnym sąsiedztwie punktu a. Całką niewłaściwą drugiego rodzaju z funkcji f na (a,b] definiujemy następująco:
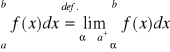
.
Jeżeli granica po prawej stronie znaku równości jest właściwa, to mówimy, że całka niewłaściwa z funkcji f na (a,b] jest zbieżna. Jeżeli granica ta jest równa +∞ lub -∞, to mówimy, że całka jest rozbieżna odpowiednio do +∞ lub -∞. W pozostałych przypadkach mówimy, że całka jest rozbieżna.
Analogicznie definiuje się całkę niewłaściwa drugiego rodzaju z funkcji f:{a,b) i nieograniczonej na lewostronnym sąsiedztwie punktu b:
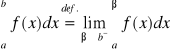
.
Niech funkcja f: [a,c)∪(c,b]→R będzie nieograniczona tylko na obu jednostronnych sąsiedztwach punktu c. Całka niewłaściwą z funkcji f na [a,b] definiujemy następująco:
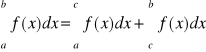
.
Jeżeli obie całki po prawej stronie znaku równości są zbieżne to mówimy, że całka niewłaściwa z funkcji f na [a,b] jest zbieżna.
Analogicznie, jeśli f: (a,b)→R jest nieograniczona na prawostronnym sąsiedztwie punktu a i na lewostronnym sąsiedztwie punktu b, to całkę niewłaściwą z funkcji f na (a,b) definiujemy następująco:
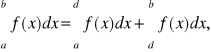
gdzie d jest dowolnym punktem przedziału (a,b), przy czym zbieżność powyższej całki niewłaściwej nie zależy od wyboru punktu d.
Uwaga 1
Dla całek niewłaściwych drugiego rodzaju (analogicznie jak dla całek niewłaściwych pierwszego rodzaju) całka niewłaściwa postaci
![]()
, gdzie b>0
jest zbieżna dla p<1 i rozbieżna do +∞ dla p≥1.
Uwaga 2
Dla całek niewłaściwych drugiego rodzaju z funkcji f na przedziale (a,b] ( lub [a,b) ) prawdziwe są kryteria zbieżności porównawcze i ilorazowe analogiczne jak dla całek pierwszego rodzaju w twierdzeniach 1 i 2.
Twierdzenie 4 (Kryterium całkowe zbieżności szeregów)
Niech funkcja f: [n0, +∞)→[0, +∞), gdzie n0∈N, będzie nierosnąca. Wówczas 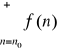
i całka niewłaściwa 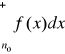
są jednocześnie zbieżne albo rozbieżne.
Wiadomości uzupełniające.
Definicja (Szeregu Taylora)
Niech funkcja f ma w punkcie x0 pochodne dowolnego rzędu. Szereg potęgowy
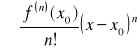
nazywamy szeregiem Taylora funkcji f o środku w punkcie x0. Jeżeli x0=0, to szereg ten nazywamy szeregiem Maclaurina funkcji f.
Uwaga
Ze zbieżności szeregu Maclaurina funkcji f wynika, że jego suma jest równa tej funkcji.
Twierdzenie (O rozwijaniu funkcji w szereg Taylora).
Jeżeli:
![]()
oznacza n-tą resztę we wzorze Taylora dla funkcji f.
Wówczas:
![]()
dla każdego x∈U(x0).
Uwaga
Zamiast założenia (20 można przyjąć:
(2') wszystkie pochodne funkcji f są wspólnie ograniczone, tzn.
![]()
Twierdzenie (O jednoznaczności rozwinięcia funkcji w szereg potęgowy)
Jeżeli ![]()
dla każdego x z pewnego otoczenia U(x0), to ![]()
dla n=0,1,2,…
Niech V={f:[a,b]→R; f-całkowalna w sensie Riemanna na [a,b]}. V jest przestrzenią liniową nad ciałem liczb rzeczywistych z dodawaniem funkcji i mnożeniem funkcji przez liczbę. W przestrzeni V określamy iloczyn skalarny następująco:
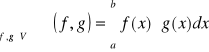
;
oraz określamy normę kwadratową funkcji f:
![]()
.
Definicja
Ciąg funkcyjny {fn}n∈N nazywamy ortogonalnym na [a,b], jeżeli (fn,fm)=0 dla n≠m i ![]()
dla wszystkich n.
Definicja
Jeżeli {cn}n∈N jest ciągiem liczbowym, zaś {fn}n∈N jest ciągiem funkcyjnym ortogonalnym w przedziale [a,b], to szereg funkcyjny ![]()
nazywamy szeregiem ortogonalnym.
Twierdzenie (O szeregu ortogonalnym)
Jeżeli szereg ortogonalny ![]()
jest jednostajnie zbieżny do funkcji f w przedziale [a,b] i funkcja ta jest całkowalna na [a,b], to współczynniki cn wyrażają się wzorami:
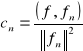
Uwaga
Dla każdego ciągu ortogonalnego w przedziale [a,b] i funkcji f całkowalnej w tym przedziale istnieje więc co najwyżej jeden taki szeteg ortogonalny, który jest jednocześnie zbieżny w tym przedziale do funkcji f. Jeżeli taki szereg istnieje, to jest nim szereg ![]()
, gdzie 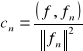
.
Liczby cn określone powyższymi wzorami nazywamy współczynnikami Fouriera funkcji f względem ciągu {fn}n∈N.
Lemat
Ciąg funkcyjny {ϕn}n∈N określony następująco:
![]()
gdzie l>0, jest ciągiem funkcji okresowych o okresie 2l, ortogonalnych w przedziale [-l,l] (ogólniej: w każdym przedziale [a, 2l+a] ), przy czym ![]()
, ![]()
.
Wniosek
Współczynniki Fouriera funkcji f(x) w przedziale [a, 2l+a] względem ciągu ortogonalnego {ϕn}n∈N wyrażają się następująco:
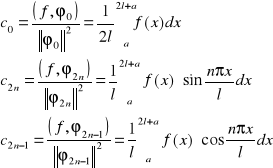
Definicja (Szeregu trygonometrycznego Fouriera)
Szereg Fouriera funkcji f(x) względem ciągu ortogonalnego {ϕn}n∈N w przedziale [-l, l] zapisujemy tradycyjnie:
![]()
,
gdzie a0=c0, an=c2n-1, bn=c2n określone są wzorami z powyższego wniosku. Szereg ten nazywamy trygonometrycznym szeregiem Fouriera funkcji f(x) w przedziale [-l, l] i zapisujemy
f(x)~![]()
Uwaga
Wychodząc od dowolnej funkcji całkowalnej f(x) i określając współczynniki a0, an, bn wzorami Fouriera nie otrzymujemy na ogół w powyższym wyrażeniu równości. Funkcja musi spełniać dość silne warunki, aby równość zachodziła.
Definicja
Mówimy, że funkcja f(x) spełnia w przedziale [a,b] warunki Dirichleta, jeżeli:
![]()
, gdzie ![]()
i ![]()
![]()
.
Uwaga:
Jest wiadome, że funkcja spełniająca warunki Dirichleta w przedziale [a,b] jest całkowalna w sensie Riemanna w [a,b].
Twierdzenie (Dirichleta)
Jeżeli funkcja f(x) spełnia w przedziale [a, 2l+a] warunki Dirichleta, to jest rozwijalna w tym przedziale w szereg trygonometryczny Fouriera
![]()
dla x∈[a, 2l+a] o współczynnikach zadanych wzorami z wniosku powyżej. Jeśli ponadto funkcja f(x) jest okresowa o okresie 2l, to równość powyższa zachodzi dla każdego x z dziedziny funkcji.
Uwaga
Jeśli funkcja f(x) spełniająca w przedziale [-l, l] warunki Dirichleta jest parzysta, to rozwija się w szereg Fouriera postaci:
![]()
.
Jeśli natomiast f(x) jest nieparzysta w [-l, l], to jej szereg Fouriera jest równy:
![]()
.
35
Wyszukiwarka
Podobne podstrony:
Analiza matematyczna 2 Definicje, twierdzenia, wzory
Analiza cz.3
analiza Âci▒ga , Definicje:
Analiza cz 1
Analiza matematyczna 2 Definicje, twierdzenia, wzory (2)
Analiza cz 2
analiza matematyczna 2 definicje twierdzenia wzory
Analiza matematyczna 2 Definicje, twierdzenia, wzory (2)
Analiza cz.2
Analiza matematyczna 1 DEFINICJE, WZORY(2) id 60882
BizAgi Studio Cz, 2 Definiowanie modelu danych
LOGIKA (definicje, zdania)
M Gewert, Z Skoczylas Analiza matematyczna 2 definicje, twierdzenia, wzory
mikroekonomia cz 2 definicje
Analiza matematyczna 1 Definicje, twierdzenia, wzory
analiza matematyczna 2 definicje twierdzenia wzory
Analiza matematyczna 2 Definicje, twierdzenia, wzory
3 cz Definicje i skróty używane w hotelu
więcej podobnych podstron