Definicje z analizy

1. Kres zbioru

Kresem górnym zbioru A jest jego najmniejsze ograniczenie górne. (oznaczamy jako sup A).

Kresem dolnym zbioru A jest jego największe ograniczenie dolne. (oznaczamy jako inf A).

2. Granica ciągu

Granicą ciągu nazywamy taką liczbę g dla której spełnione jest:

 ∂ > 0  N  N  n > N n  N d(x_n, g) < ∂

Ciąg mający granicę jest zbieżny.

3. Granica funkcji

Niech x będzie punktem skupienia zbioru X. Mówimy, że y jest granicą funkcji
w punkcie x gdy:

4. Definicja funkcji

Funkcją
nazywamy przyporządkowanie każdemu elementowi ze zbioru X dokładnie jednego el. ze zbioru Y.

5. Funkcja ciągła

Funkcja
jest ciągła w punkcie
wtedy i tylko wtedy gdy:

Funkcja jest ciągła na przedziale <a,b>, wtedy gdy jest ciągła w każdym jej punkcie.

6. Suma szeregu

Sumą szeregu nazywa się liczbę

o ile granica ta istnieje i jest właściwa. W przeciwnym przypadku szereg nie ma sumy. Najłatwiej przedstawić sumę szeregu jako granicę sum częściowych które wyrażają się wzorem:

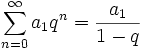
Szereg, który ma sumę nazywa się zbieżnym, który jej nie ma − rozbieżnym.

Przykłady są w 5 wykładzie na stronie prof. Domańskiego

7. Pochodna funkcji

Pochodną w punkcie x₀ nazywamy granicę ilorazów różnicowych:

8. Całka nieoznaczona

Otóż mamy pierwotną funkcji f:

gdzie,

Wyrażenie F(x) + C nazywa się całką nieoznaczoną funkcji podcałkowej f; zmienną x nazywa się w tym kontekście zmienną całkowania.

9. Całka Riemanna Całka dolna Riemanna
z funkcji f na przedziale [a,b] jest określona jako:

Sup {L(f,P): P jest dowolnym(każdym) podziałem [a,b]} a całka górna: Inf {U(f,P): P jest dowolnym(każdym) podziałem [a,b]}

Całkę Reimanna otrzymujemy wtedy kiedy całka dolna Riemanna jest równa całce górnej.

10. Ekstremum lokalne

Ekstremum lokalne to minimalna lub maksymalna wartość funkcji f w danym przedziale, zakładając że, funkcja f jest określona na tym przedziale.

---