Definicje z analizy 2

1. Kres zbioru

Kresem górnym zbioru A jest jego najmniejsze ograniczenie górne. (oznaczamy jako sup A).

Kresem dolnym zbioru A jest jego największe ograniczenie dolne. (oznaczamy jako inf A).

2. Granica ciągu

Granicą ciągu nazywamy taką liczbę g dla której spełnione jest:

Ciąg mający granicę jest zbieżny.

3. Granica funkcji

a) jednej zmiennej

Niech x będzie punktem skupienia zbioru X. Mówimy, że y jest granicą funkcji
w punkcie x gdy:

b) wielu zmiennych

Granica funkcji wg Heinego:

Funkcja f(P) ma w punkcie P₀ granicę g, jeśli dla każdego ciągu punktów {P_k} różnych od P₀, dążącego do P₀, odpowiedni ciąg wartości funkcji {f(P_k)} dąży do liczby g.

jeżeli g jest liczbą skończoną - granica właściwa, jeżeli g→∞ - granica niewłaściwa.

4. Funkcja ciągła

a) jednej zmiennej

Funkcja
jest ciągła w punkcie
wtedy i tylko wtedy gdy:

Funkcja jest ciągła na przedziale <a,b>, wtedy gdy jest ciągła w każdym jej punkcie.

b) wielu zmiennych

Funkcja
jest ciągła w punkcie
wtedy i tylko wtedy gdy:

Funkcja f jest ciągła wtedy i tylko wtedy, gdy wszystkie jej składowe są ciągłe.

5. Suma szeregu

Sumą szeregu nazywa się liczbę

o ile granica ta istnieje i jest właściwa. W przeciwnym przypadku szereg nie ma sumy. Najłatwiej przedstawić sumę szeregu jako granicę sum częściowych które wyrażają się wzorem:

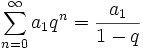
Szereg, który ma sumę nazywa się zbieżnym, który jej nie ma − rozbieżnym.

Przykłady są w 5 wykładzie (Analiza 1) na stronie prof. Domańskiego

6. Pochodna funkcji:

a) jednej zmiennej

Pochodną w punkcie x₀ nazywamy granicę ilorazów różnicowych:

b) wielu zmiennych

Niech
będzie zbiorem otwartym a
będzie odwzorowaniem,
. Jeśli istnieje odwzorowanie liniowe
takie, że:

(*)
,

to mówimy, że przekształcenie f jest różniczkowalne w punkcie x. Odwzorowanie A nazywamy pochodną odwzorowania f w punkcie x i oznaczamy:

f'(x) = A lub Df(x) = A.

Jeżeli f jest różniczkowalna w dowolnym punkcie
, to mówimy, że f jest różniczkowalna na E.

7. Definicja całki:

Całka nieoznaczona

Otóż mamy pierwotną funkcji f:

gdzie,

Wyrażenie F(x) + C nazywa się całką nieoznaczoną funkcji podcałkowej f; zmienną x nazywa się w tym kontekście zmienną całkowania.

Całka Riemanna (oznaczona)

Całka dolna Riemanna
z funkcji f na przedziale [a,b] jest określona jako:

Sup {L(f,P): P jest dowolnym(każdym) podziałem [a,b]} a całka górna: Inf {U(f,P): P jest dowolnym(każdym) podziałem [a,b]}

Całkę Reimanna otrzymujemy wtedy kiedy całka dolna Riemanna jest równa całce górnej.

8. Zbieżność jednostajna ciągu funkcji.

Mówimy, że ciąg funkcji
jest zbieżny jednostajnie na D do funkcji
jeśli jest on zbieżny wg. metryki
tj.

Oznaczenie:
f_n(w tym miejscu są dwie je***e strzałeczki w prawo)f

Warunek Cauchy'ego zbieżności jednostajnej:

Ciąg funkcji (f_n),
lub
jest zbieżny jednostajnie wtedy i tylko wtedy, gdy spełnia warunek Cauchy'ego zbieżności jednostajnej tj.:

9. Współczynniki Fouriera funkcji.

Wzory Eulera-Fouriera:

Jeśli funkcja f na przedziale [-π,π] okresowa o okresie 2π jest sumą jednostajnie zbieżnego szeregu trygonometrycznego to:

Tak wyliczone współczynniki nazywane są współczynnikami Fouriera funkcji f.

Współczynniki Fouriera można wyliczyć dla każdej funkcji całkowalnej (w sensie Riemanna ale także Lebesgue'a) niezależnie od jej okresowości i niezależnie od zbieżności powstałego szeregu.

Definicja Szeregu:

Szeregiem Fouriera funkcji całkowalnej f nazywamy szereg trygonometryczny, którego współczynnikami są współczynniki Fouriera funkcji f i piszemy wtedy:

10. Rozwiązanie równania różniczkowego.

Rozwiązać równanie

F(t, x, x',…, x⁽ⁿ⁾) = 0

lub je scałkować oznacza znaleźć rozwiązanie lub całkę tj. taką funkcję x, że dla każdego t z określonej dziedziny zachodzi:

F(t, x(t), x'(t),…, x⁽ⁿ⁾(t)) = 0.

Czasami mówi się o całce ogólnej równania jakoo wzorze na wszystkie rozwiązania równania i całce szczególnej, jako o poszczególnym rozwiązaniu.

---