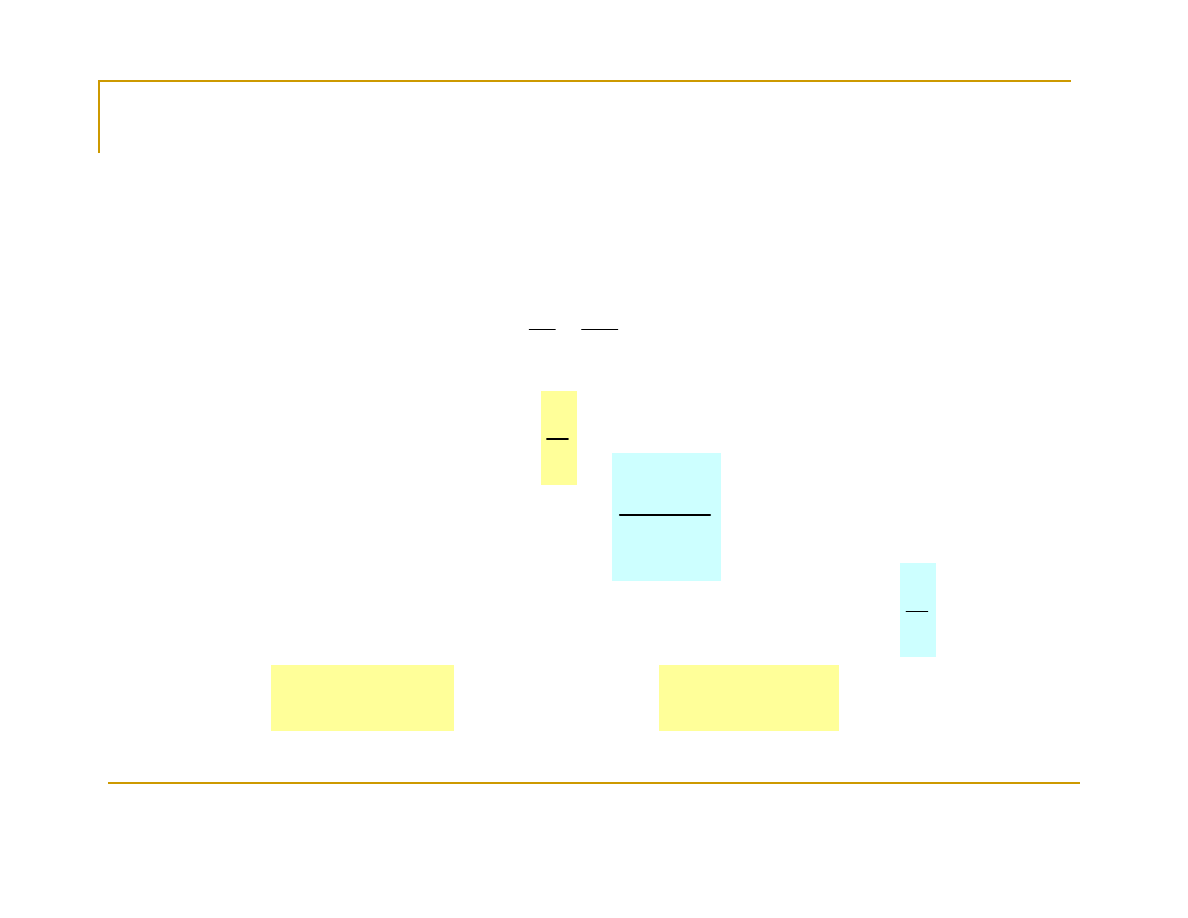
1
WYKŁAD XI
Reguła de l’Hospitala
0
0
( )
( )
x
g
x
f
Mówimy, że iloraz funkcji
w otoczeniu punktu
x=a
jest wyrażeniem nieoznaczonym postaci
, jeżeli
Symbole nieoznaczone:
( )
0
lim
=
→
x
g
a
x
oraz
( )
0
lim
=
→
x
f
a
x
∞
∞
∞
−
∞
⋅
∞
∞
∞
1
,
0
,
,
,
0
,
,
0
0
0
0
1. Symbol nieoznaczony
0
0
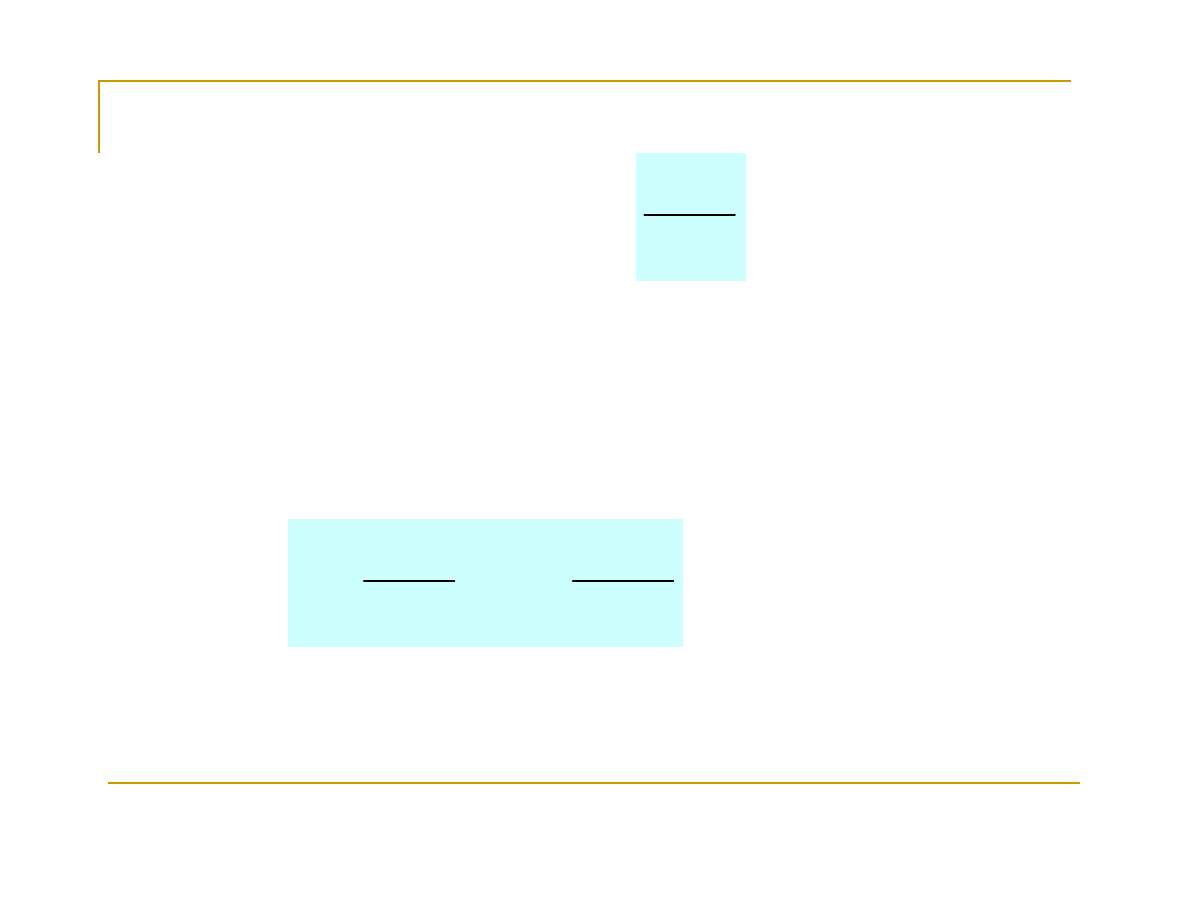
2
Reguła de l’Hospitala mówi, że
( )
( )
x
g
x
f
Granica ilorazu dwóch funkcji
dążących do zera
przy x→a i mających pierwsze pochodne w otoczeniu
punktu x=a jest równa granicy ilorazu pochodnych tych
funkcji przy x→a, jeśli granica ta istnieje, tzn.
( )
( )
( )
( )
x
g
x
f
x
g
x
f
a
x
a
x
′
′
=
→
→
lim
lim
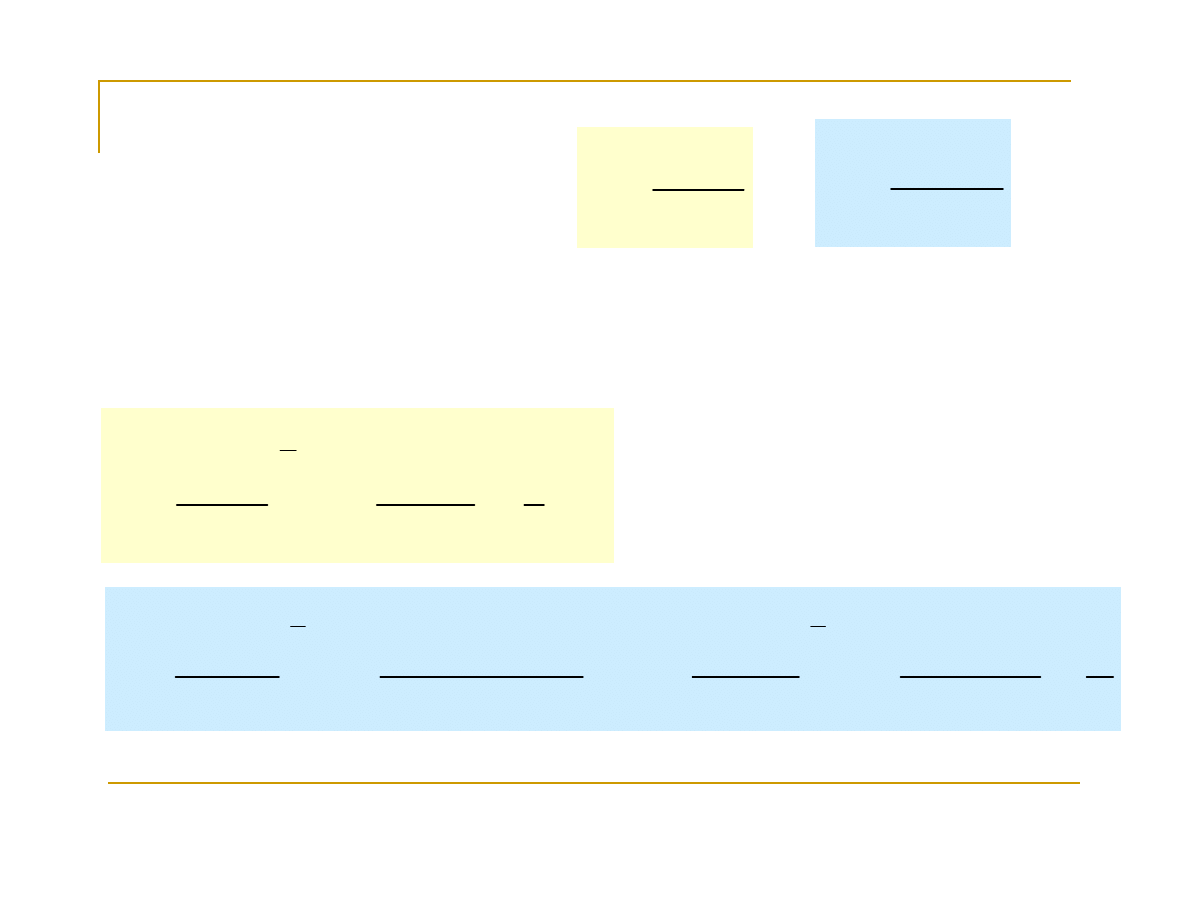
3
Przykład 1.
1
1
1
1
cos
lim
sin
lim
0
0
0
0
=
=
=
→
→
x
x
x
x
x
Ponieważ liczniki i mianowniki obydwu funkcji dążą do
zera przy x→0, do obliczenia granicy wykorzystamy
regułę de l’Hospitala:
Obliczyć granice funkcji:
i
x
x
x
sin
lim
0
→
2
2
0
2
sin
lim
x
x
x→
2
1
4
2
cos
2
lim
4
2
sin
lim
4
cos
sin
2
lim
2
sin
lim
0
0
0
0
0
0
0
2
2
0
=
=
=
=
→
→
→
→
x
x
x
x
x
x
x
x
x
x
x
x
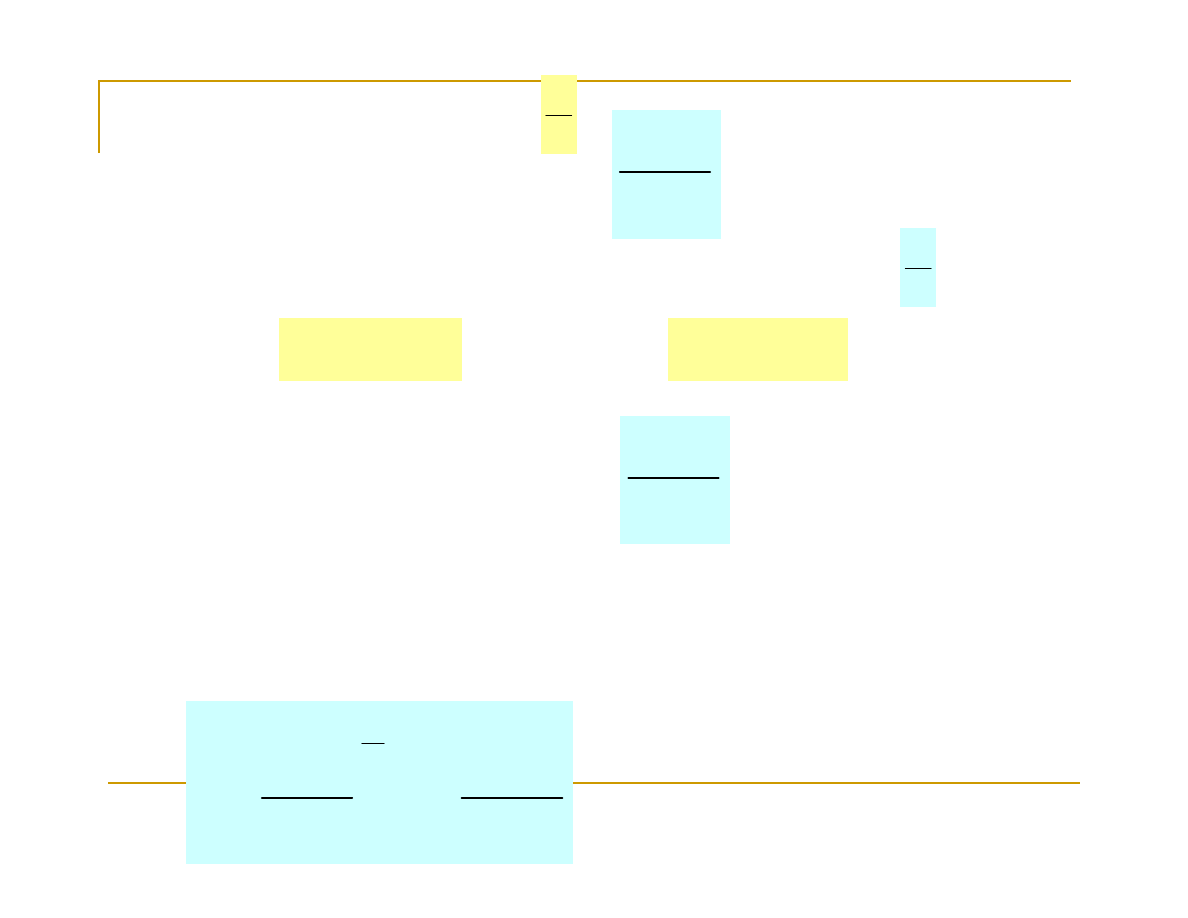
4
∞
∞
( )
( )
x
g
x
f
Mówimy, że iloraz funkcji
w otoczeniu punktu
x=a
jest wyrażeniem nieoznaczonym postaci
, jeżeli
( )
∞
=
→
x
g
a
x
lim
oraz
( )
∞
=
→
x
f
a
x
lim
2. Symbol nieoznaczony
∞
∞
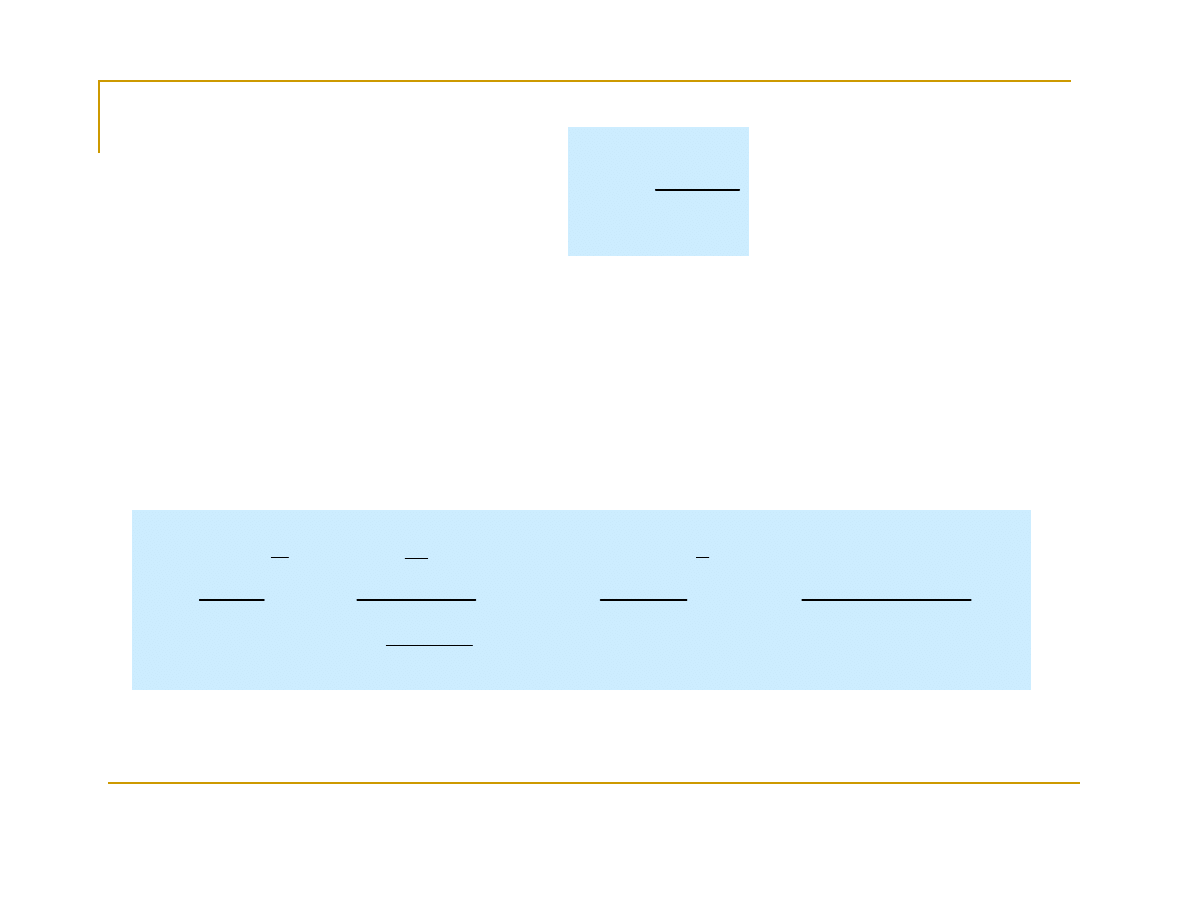
Reguła de l’Hospitala mówi, że:
( )
( )
x
g
x
f
Granica ilorazu dwóch funkcji
dążących do
nieskończoności przy x→a i mających pierwsze pochodne
w otoczeniu punktu x=a jest równa granicy ilorazu
pochodnych tych funkcji przy x→a, jeśli granica ta istnieje,
tzn.
( )
( )
( )
( )
x
g
x
f
x
g
x
f
a
x
a
x
′
′
=
→
∞
∞
→
lim
lim
5
Przykład 2.
Ponieważ licznik i mianownik funkcji dążą do
nieskończoności przy x→0
+
, do obliczenia granicy
wykorzystamy regułę de l’Hospitala:
Obliczyć granicę funkcji:
ctgx
x
x
ln
lim
0
+
→
0
1
cos
sin
2
lim
sin
lim
sin
1
1
lim
ln
lim
0
0
0
2
0
2
0
0
=
−
=
−
=
−
=
+
+
+
+
→
→
→
∞
∞
→
x
x
x
x
x
x
ctgx
x
x
x
x
x
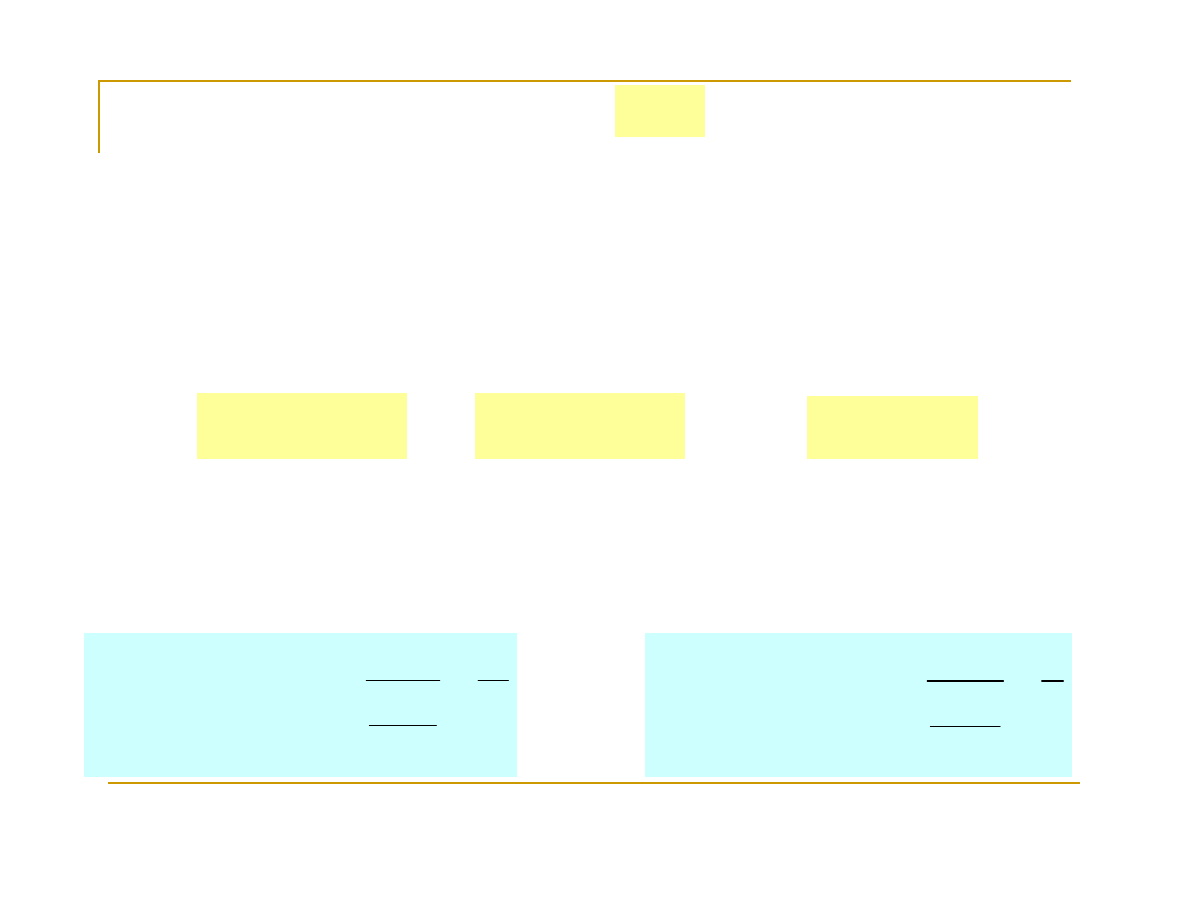
6
3. Symbol nieoznaczony
0
⋅
∞
Wówczas granica iloczynu dwóch funkcji f(x)g(x)
przy x→a może być przedstawiona w postaci granicy
ilorazu:
( ) ( )
( )
( )
∞
∞
=
=
→
⋅
∞
→
x
g
x
f
x
g
x
f
a
x
a
x
1
lim
lim
0
Niech dane będą dwie funkcje f(x) i g(x) określone w
pewnym otoczeniu punktu x=a. Iloczyn f(x)g(x) nazywamy
wyrażeniem nieoznaczonym postaci ∞·0 w punkcie x=a,
jeżeli
lub
( )
0
lim
=
→
x
g
a
x
oraz
( )
+∞
=
→
x
f
a
x
lim
( )
−∞
=
→
x
f
a
x
lim
albo
( ) ( )
( )
( )
0
0
1
lim
lim
0
=
=
→
⋅
∞
→
x
f
x
g
x
g
x
f
a
x
a
x

7
Przykład 3.
Aby wykorzystać regułę de l’Hospitala należy iloczyn
x
3
lnx zapisać w postaci ilorazu:
Obliczyć granicę funkcji:
( )
0
lim
3
1
3
1
lim
1
lim
1
ln
lim
ln
lim
3
0
4
0
3
0
3
0
0
3
0
=
−
=
−
=
′
=
=
+
+
+
+
+
→
→
−
→
∞
∞
→
∞
⋅
→
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
ln
lim
3
0
+
→
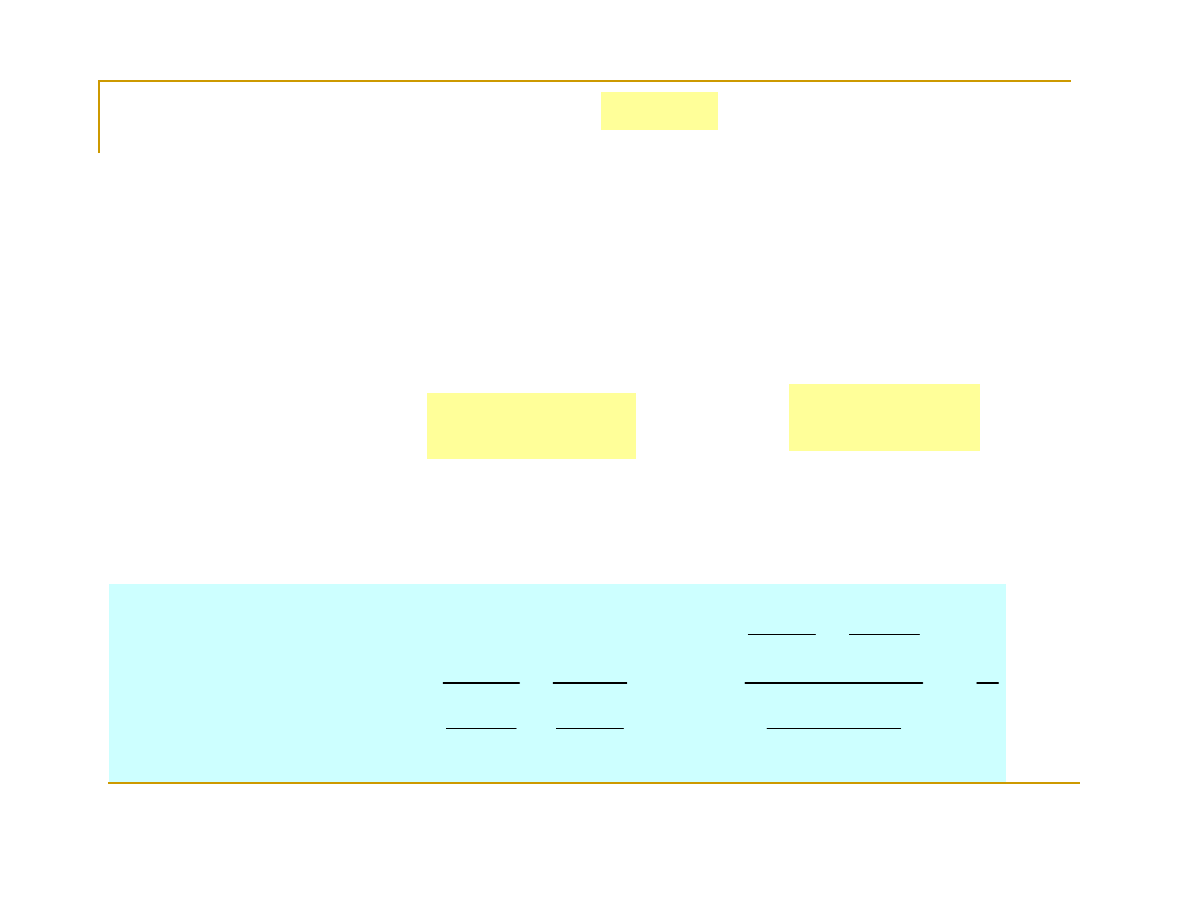
8
4. Symbol nieoznaczony
∞
−
∞
Granicę różnicy dwóch funkcji f(x)-g(x) możemy
przedstawić w postaci granicy ilorazu:
( )
( )
[
]
( )
( )
( )
( )
( ) ( )
0
0
1
1
1
lim
1
1
1
1
lim
lim
=
−
=
−
=
−
→
→
→
x
g
x
f
x
f
x
g
x
g
x
f
x
g
x
f
a
x
a
x
a
x
Niech dane będą dwie funkcje f(x) i g(x) określone w
pewnym otoczeniu punktu x=a. Granicę różnicy f(x)-g(x)
nazywamy wyrażeniem nieoznaczonym postaci ∞-∞ w
punkcie x=a, jeżeli
( )
∞
=
→
x
g
a
x
lim
oraz
( )
+∞
=
→
x
f
a
x
lim
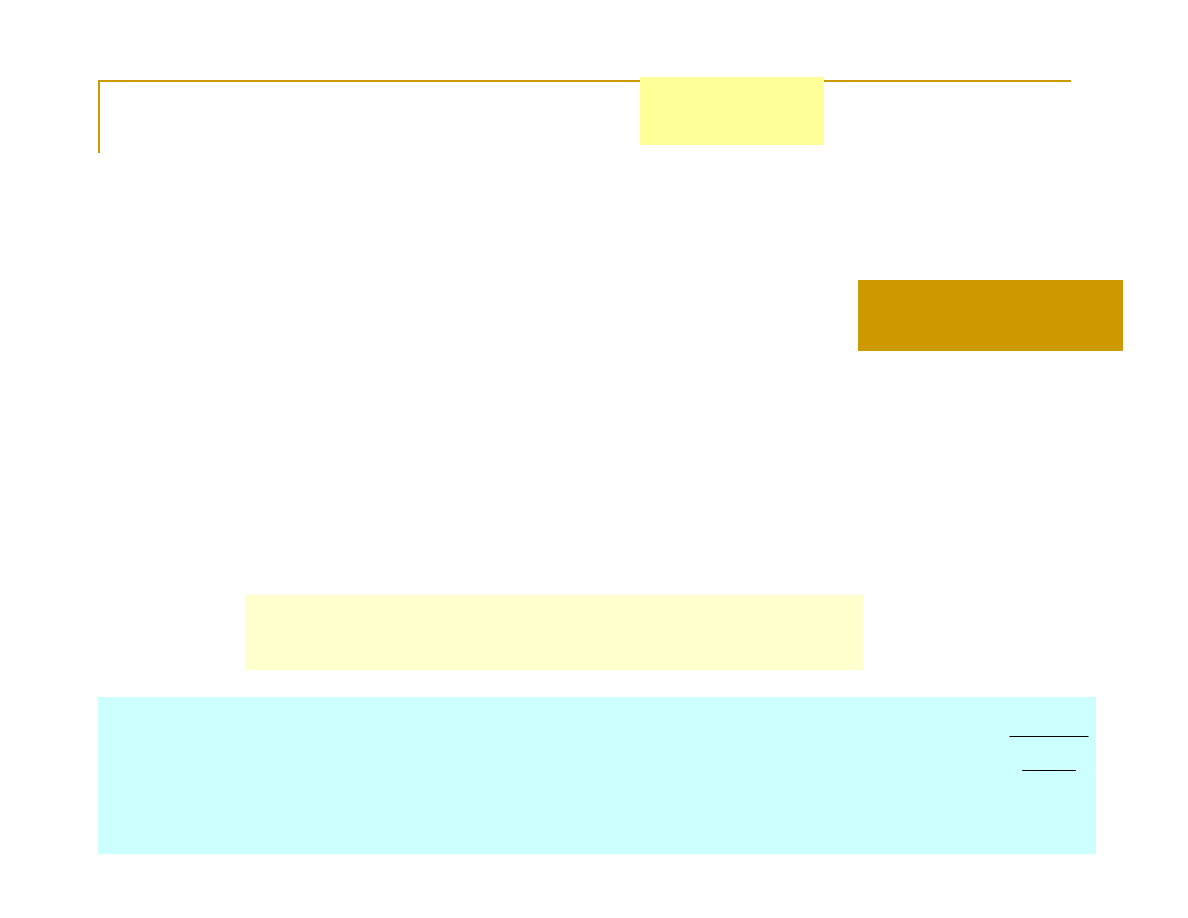
9
5. Symbole nieoznaczone:
∞
∞
1
,
0
,
0
0
Granica funkcji h(x)=f(x)
g
(x)
przy x→a może być jednym z
symboli nieoznaczonych typu: ∞
0
, 0
0
, 1
∞
.
( )
( )
( )
( )
( )
( )
x
f
x
g
x
f
x
h
e
e
e
x
h
x
g
ln
ln
ln
=
=
=
Niech dane będą dwie funkcje f(x) i g(x) określone w
pewnym otoczeniu punktu x=a, przy czym g(x)>0, oraz
posiadające pochodne. Rozważmy wyrażenie:
( )
( )
( )
x
g
x
f
x
h
=
W celu obliczenia granicy funkcji h(x)=f(x)
g
(x)
przy x→a,
przedstawimy funkcję h(x) w postaci:
Wówczas
( )
( )
( )
( )
( )
( )
( )
( )
x
g
x
f
x
f
x
g
x
f
x
h
a
x
a
x
a
x
x
g
a
x
a
x
e
e
e
e
x
h
1
ln
lim
ln
lim
ln
lim
ln
lim
lim
→
→
→
→
=
=
=
=
→
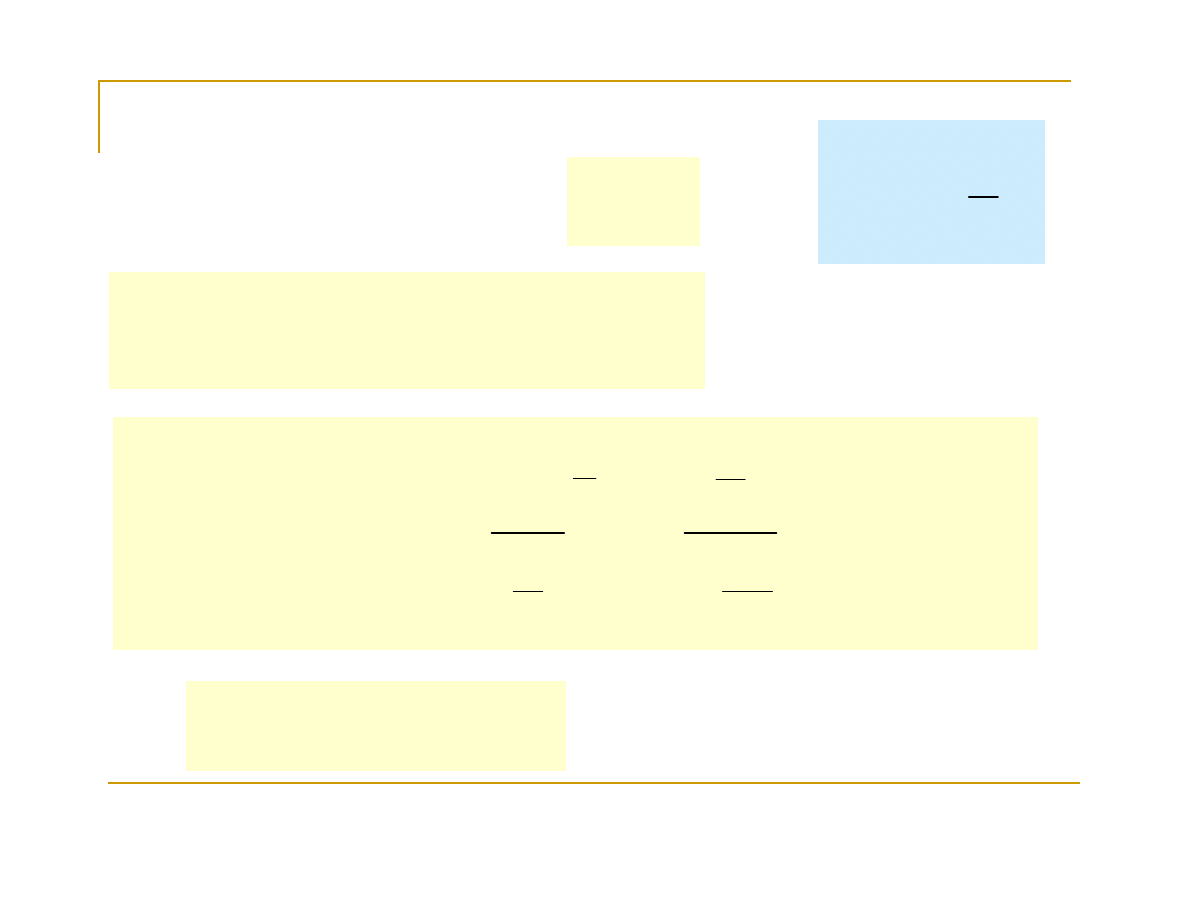
10
Przykład 4.
Obliczyć granice funkcji:
oraz
x
x
x
+
→0
lim
x
x
x
+
∞
→
1
1
lim
g
x
x
x
x
x
e
e
e
x
x
x
x
=
=
=
+
→
+
→
+
→
ln
lim
ln
lim
0
0
0
lim
0
lim
1
1
lim
1
ln
lim
ln
lim
0
2
0
0
=
−
=
−
=
=
=
+
+
+
→
→
∞
∞
→
∞
→
x
x
x
x
x
x
x
g
x
x
x
x
Ostatecznie
1
lim
0
0
=
=
=
+
→
e
e
x
g
x
x
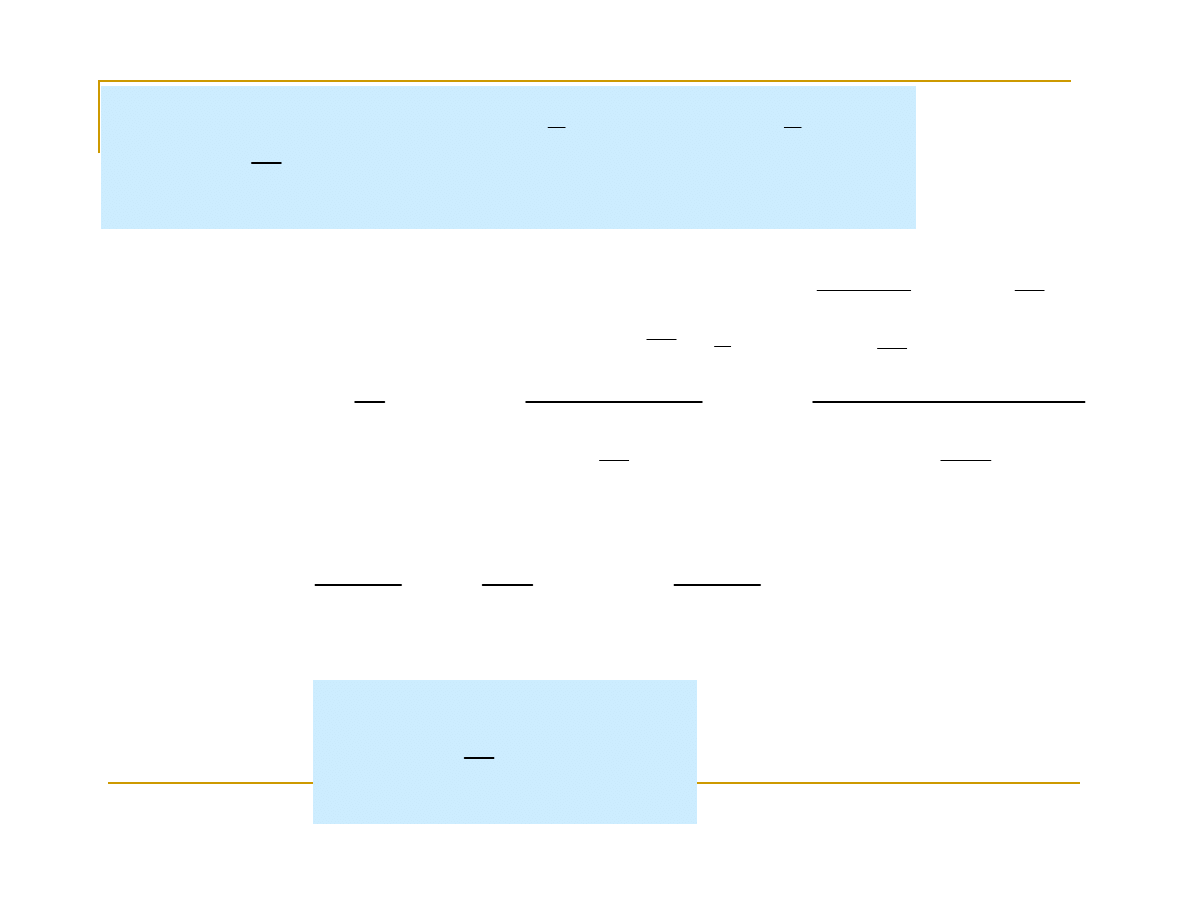
11
g
x
x
x
x
x
x
x
e
e
e
x
x
=
=
=
+
+
+
∞
→
∞
→
→∞
1
1
ln
lim
1
1
ln
lim
1
1
lim
2
0
0
1
1
1
1
1
1
lim
1
1
1
ln
lim
1
1
ln
lim
x
x
x
x
x
x
x
g
x
x
x
−
′
+
⋅
+
=
+
=
+
=
∞
→
∞
→
∞
→
1
1
lim
1
1
lim
2
2
=
+
=
−
⋅
+
⋅
−
=
∞
→
∞
→
x
x
x
x
x
x
x
x
Ostatecznie
e
e
x
x
x
=
=
+
∞
→
1
1
1
lim
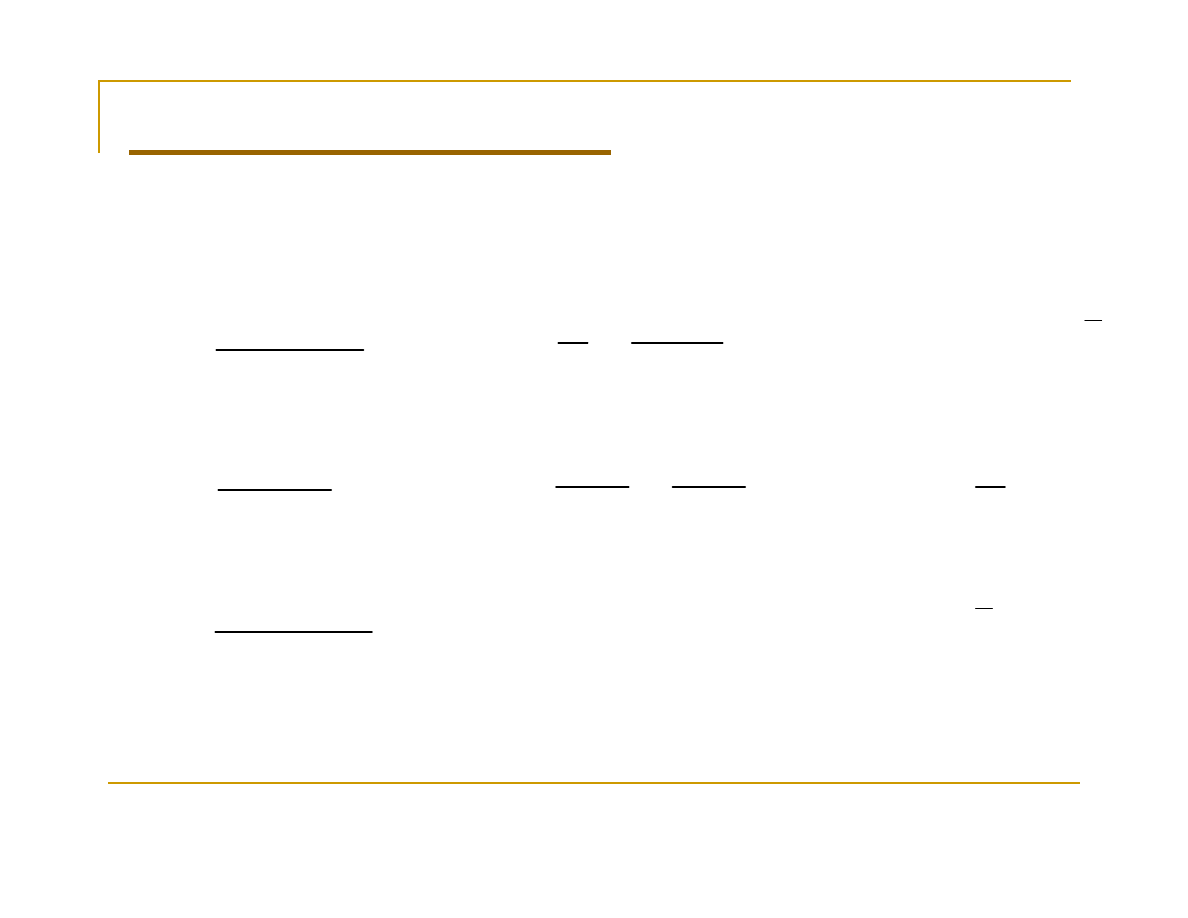
12
Przykłady na ćwiczenia
Wykorzystując regułę de l’Hospitala obliczyć następujące
granice:
x
e
e
x
x
x
−
→
−
0
lim
)
1
x
x
x
2
5
sin
lim
)
2
0
→
2
0
sin
lim
)
3
x
x
x
x
−
→
−
→
x
x
x
sin
1
1
lim
)
4
0
−
→
x
x
x
x
ln
ln
1
lim
)
5
1
x
x
x
1
lim
)
9
∞
→
(
)
x
x
x
x
e
1
2
0
lim
)
7
+
→
x
x
x
sin
0
1
lim
)
8
+
→
(
)
ctgx
e
x
x
2
0
1
lim
)
6
−
→
Wyszukiwarka
Podobne podstrony:
11 Reguła de l Hospitala Równość asymptotyczna
9 Reguła de L'Hospitala Symbole nieoznaczone
9 Regula de LHospitala Symbole nieoznaczone
FGAG explained 2003 11 17 de
Fizjologia& 10 11 Regulacja krazenia
11 regulamin komisji kwalifikac Nieznany (2)
11 Regulamin Mały Szlak Beskidzki compressed
4. Wyrazenia nieoznaczone. Regula de L' Hospitala, uzupelnienie str. 4, 6
11 Regula templariuszy
4 Wyrazenia nieoznaczone Regula de L' Hospitala, uzupelnienie str 4 6
AMI 22 Regula De L'Hospitala i Nieznany (2)
78 Nw 11 Regulator obrotow
11 Regulacja obiektów statycznych
(3655) reguła de l hospitala
więcej podobnych podstron