ANALIZA POJEDYNCZEGO

ZDJĘCIA LOTNICZEGO

ZDJĘCIA LOTNICZEGO

ZAGADNIENIA

1. Podstawowe elementy geometryczne zdjęcia lotniczego
2. Własności punktów i linii szczególnych

p

g

y

3. Zniekształcenia perspektywiczne zdjęcia
3.1 Zniekształcenie liniowe
•

spowodowane deniwelacją terenu

•

spowodowane nachyleniem zdjęcia

3.2 Zniekształcenie kierunków
•

spowodowane rzeźbą terenu,

•

spowodowane nachyleniem zdjęcia

4. Skala zdjęcia lotniczego
4.1 Skala zdjęcia ściśle poziomego
4 2 Sk l

dj i

h l

4.2 Skala zdjęcia nachylonego,
•

wzdłuż poziomych zdjęcia

•

wzdłuż głównej pionowej

•

dla dowolnych kierunków

•

dla dowolnych kierunków

4.3 Wyznaczenie średniej lokalnej skali zdjęcia
5. Czynniki fizyczne wpływające na zniekształcenie obrazu zdjęcia

lotniczego

lotniczego

PUNKTY I LINIE SZCZEGÓLNE ZDJĘCIA LOTNICZEGO

PUNKTY I LINIE SZCZEGÓLNE ZDJĘCIA LOTNICZEGO

PUNKTY I LINIE SZCZEGÓLNE ZDJĘCIA LOTNICZEGO

PUNKTY I LINIE SZCZEGÓLNE ZDJĘCIA LOTNICZEGO

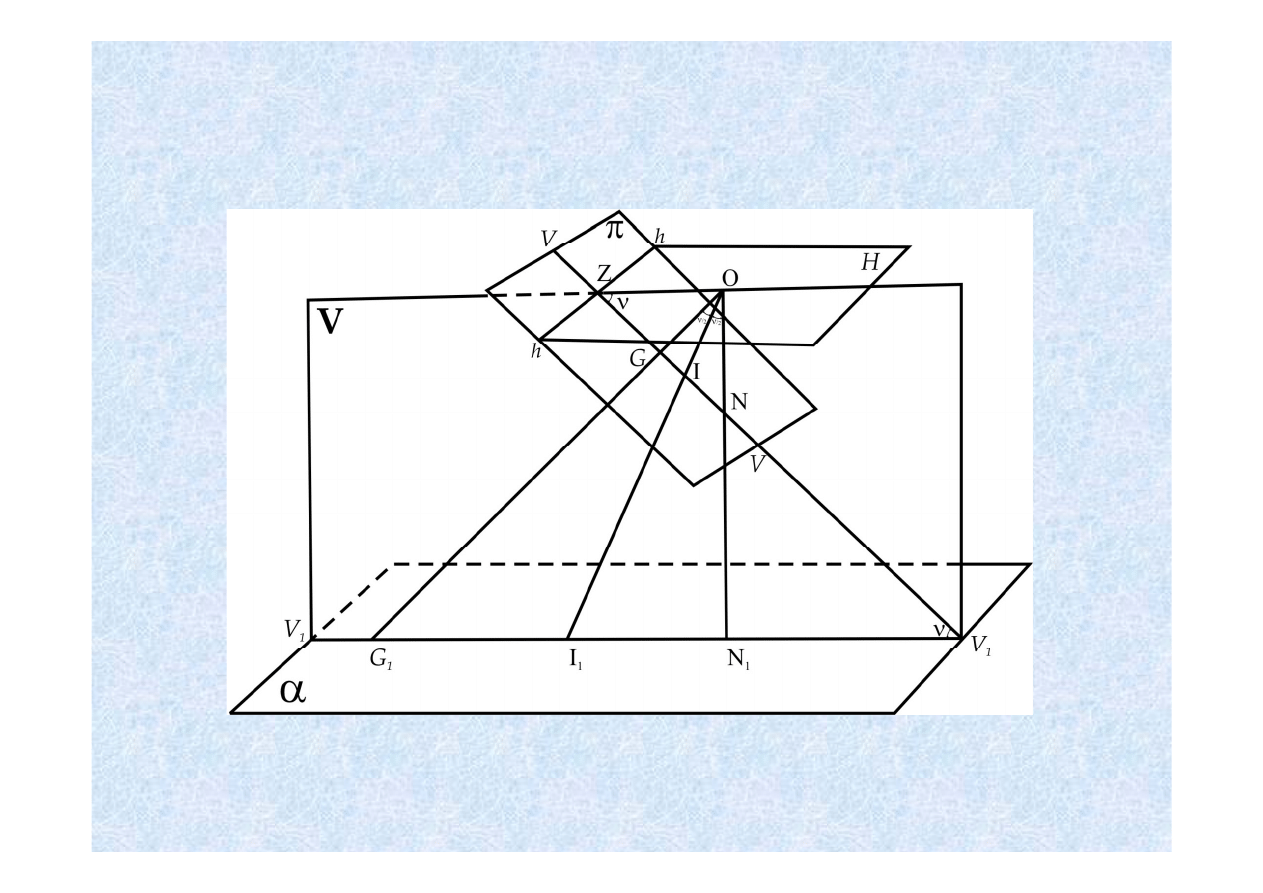
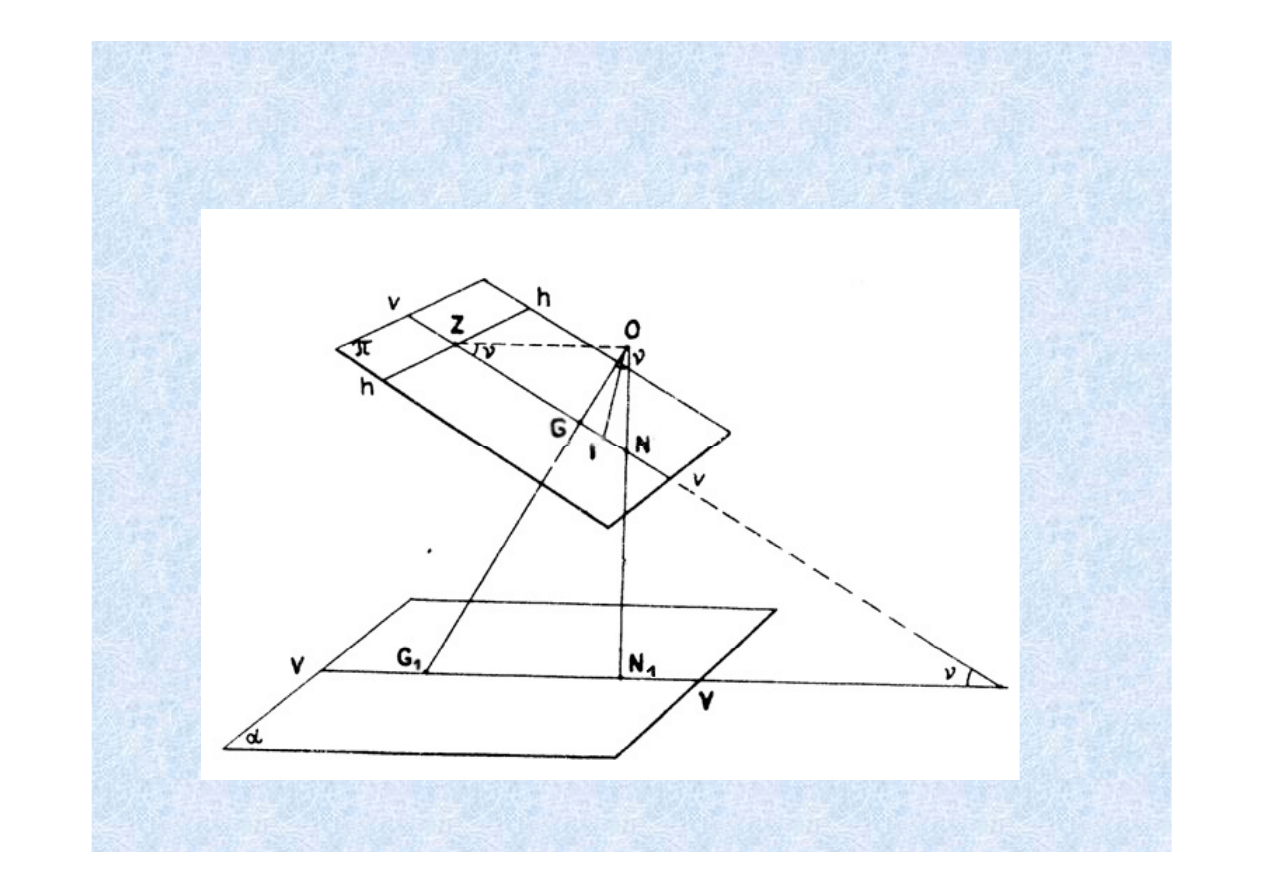
WŁASNOŚCI PUNKTÓW I LINII SZCZEGÓLNYCH

WŁASNOŚCI PUNKTÓW I LINII SZCZEGÓLNYCH

ł

t

α - płaszczyzna terenu
π - płaszczyzna tłowa zdjęcia
ν - płaszczyzna główna prostopadła do płaszczyzny terenu, przechodzi przez

p

y

g

p

p

p

y y

p

p

środek O

Przecięcie

ν z α daje νν - linię kierunku zdjęcia

Przecięcie

ν z α daje νν linię kierunku zdjęcia.

Przecięcie

ν z π daje υυ główną pionową zdjęcia lub prostą największego

spadku.

Płaszczyzna pozioma przechodząca przez środek rzutów płaszczyzna

Płaszczyzna pozioma przechodząca przez środek rzutów - płaszczyzna

horyzontu, przecina się z płaszczyzną zdjęcia wzdłuż prostej hh zwanej linią
horyzontu lub linią zbiegu.

WŁASNOŚCI PUNKTÓW I LINII SZCZEGÓLNYCH

WŁASNOŚCI PUNKTÓW I LINII SZCZEGÓLNYCH

N

i i li ii

i hh l ż

kt bi

Z

Na przecięciu linii

υυ i hh leży punkt zbiegu Z.

Przecięcie linii pionu przechodzącej przez środek rzutów O, z płaszczyzną

ę

p

p

j p

p

y

zdjęcia

π daje punkt nadirowy N i jego odpowiednik w terenie N

1

.

Kąt

ν - kąt dwuścienny pomiędzy płaszczyzną zdjęcia i płaszczyzną terenu

Kąt

ν kąt dwuścienny pomiędzy płaszczyzną zdjęcia i płaszczyzną terenu

określa kąt nachylenia zdjęcia.

Dwusieczna kąta nachylenia przecina płaszczyznę zdjęcia w punkcie

Dwusieczna kąta nachylenia przecina płaszczyznę zdjęcia w punkcie

izocentrycznym I.

Punkty Z, I, N, leżą na linii największego spadku, a ich położenie w

stosunku do punktu głównego określamy ze wzoru

:

WŁASNOŚCI PUNKTÓW I LINII SZCZEGÓLNYCH

v

f

Zo

sin

=

ctgv

f

GZ

⋅

=

v

sin

v

tg

f

GI

⋅

=

f

ON

=

tgv

H

N

O

⋅

=

′

′

1

1

2

tg

f

GI

⋅

=

v

ON

cos

=

tgv

H

N

O

1

1

H

tgv

f

GN

⋅

=

v

H

ZK

sin

=

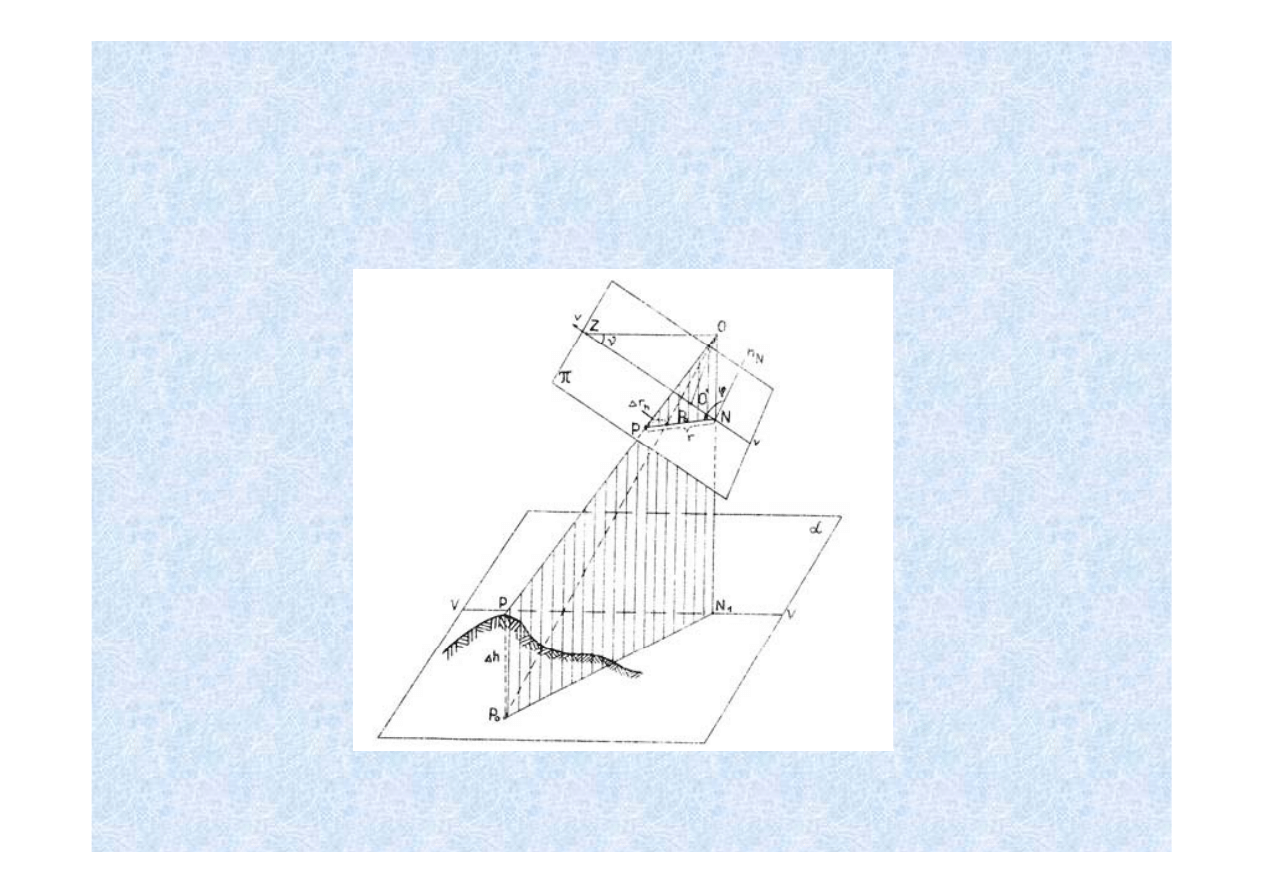
ZNIEKSZTAŁCENIE LINIOWE

SPOWODOWANE DENIWELACJĄ TERENU

ZNIEKSZTAŁCENIE LINIOWE

SPOWODOWANE DENIWELACJĄ TERENU

Dl

k śl i

i lk ś i

i k t ł

i

t k kł d

ół

d

h ( kł d

Dla określenia wielkości zniekształcenia początek układu współrzędnych (układ

biegunowy φ i r ) umieszczamy w punkcie nadirowym N.

v

r

sin

sin

1

ϕ

⋅

h

r

f

v

r

H

h

r

h

i

i

1

2

sin

sin

1

ϕ

δ

⋅

⋅

−

⋅

⋅

=

v

H

f

H

sin

sin

2

1

ϕ

⋅

⋅

−

ZNIEKSZTAŁCENIE LINIOWE

SPOWODOWANE DENIWELACJĄ TERENU

Jeżeli nachylenie zdjęcia jest niewielkie może on być zapisany w formie

uproszczonej:

⎟⎟

⎞

⎜⎜

⎛

⋅

=

v

Y

h

r

h

o

sin

1

δ

⎟⎟

⎠

⎜⎜

⎝

−

=

v

f

H

h

sin

1

δ

ZNIEKSZTAŁCENIE LINIOWE

SPOWODOWANE DENIWELACJĄ TERENU

P

h l i h i

k

j

h 3°

•

Przy nachyleniach nie przekraczających 3°

h

r

⋅

H

h

r

h

=

δ

ZNIEKSZTAŁCENIE LINIOWE SPOWODOWANE

NACHYLENIEM ZDJĘCIA

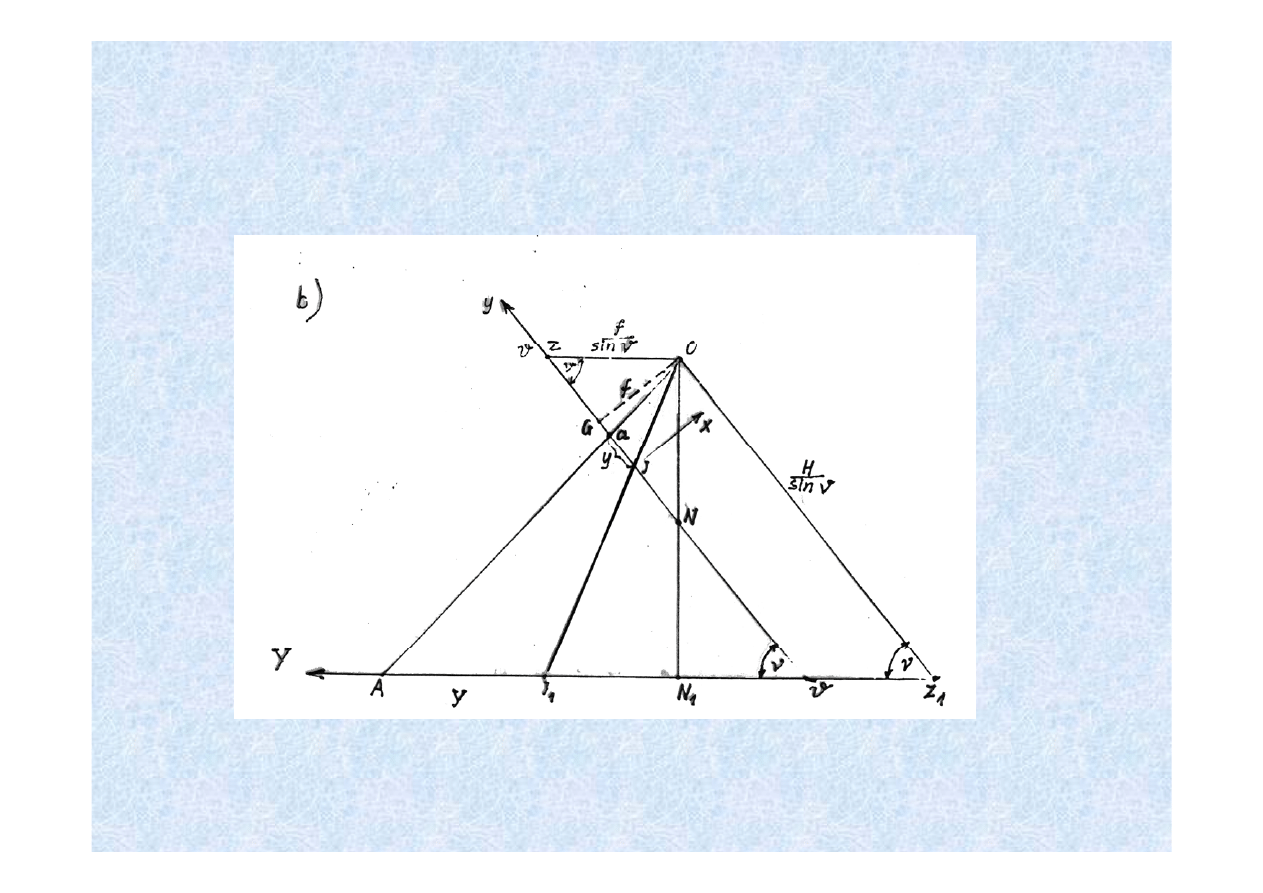
ZNIEKSZTAŁCENIE LINIOWE SPOWODOWANE

NACHYLENIEM ZDJĘCIA

ZNIEKSZTAŁCENIE LINIOWE SPOWODOWANE

NACHYLENIEM ZDJĘCIA

Dl

k śl i

k

t

l ż ś i

i d

ół

d

i dj i i t

Dla określenia wykorzystamy zależności pomiędzy współrzędnymi zdjęcia i terenu,

umieszczając początek układu współrzędnych w punkcie izocentrycznym I na zdjęciu i
I1 w terenie

H

H

v

y

f

H

y

Y

i

v

y

f

H

x

X

sin

sin

⋅

−

⋅

=

⋅

−

⋅

=

A zatem odległość punktu a, od punktu izocentrycznego wynosi:

v

r

f

r

H

v

y

f

r

H

R

Y

X

R

i

y

x

r

sin

sin

sin

2

2

2

2

ϕ

⋅

−

⋅

=

⋅

−

⋅

=

+

=

+

=

v

r

f

v

y

f

sin

sin

sin

ϕ

⋅

−

⋅

−

ZNIEKSZTAŁCENIE LINIOWE SPOWODOWANE

NACHYLENIEM ZDJĘCIA

T

R k śl

d t

i

dj i

i

i i

To samo R określone na podstawie zdjęcia poziomego wyniesie:

R

H

R

r

f

o

o

=

Dzieląc

(

)

i

i

1

∗

=

=

f

f

r

R

R

(

)

ν

ϕ

sin

sin

∗

−r

f

r

R

o

o

ZNIEKSZTAŁCENIE LINIOWE SPOWODOWANE

NACHYLENIEM ZDJĘCIA

Z

i i j

δ

k t ł

i

t

Zamieniając r

0

przez r-

δν po przekształceniu otrzymamy:

2

ν

ϕ

ν

ϕ

δν

sin

sin

sin

sin

2

∗

−

∗

−

=

r

f

r

Po uproszczeniu otrzymujemy postać:

r

2

δν

ϕ

ν

= −

r

f

sin

sin

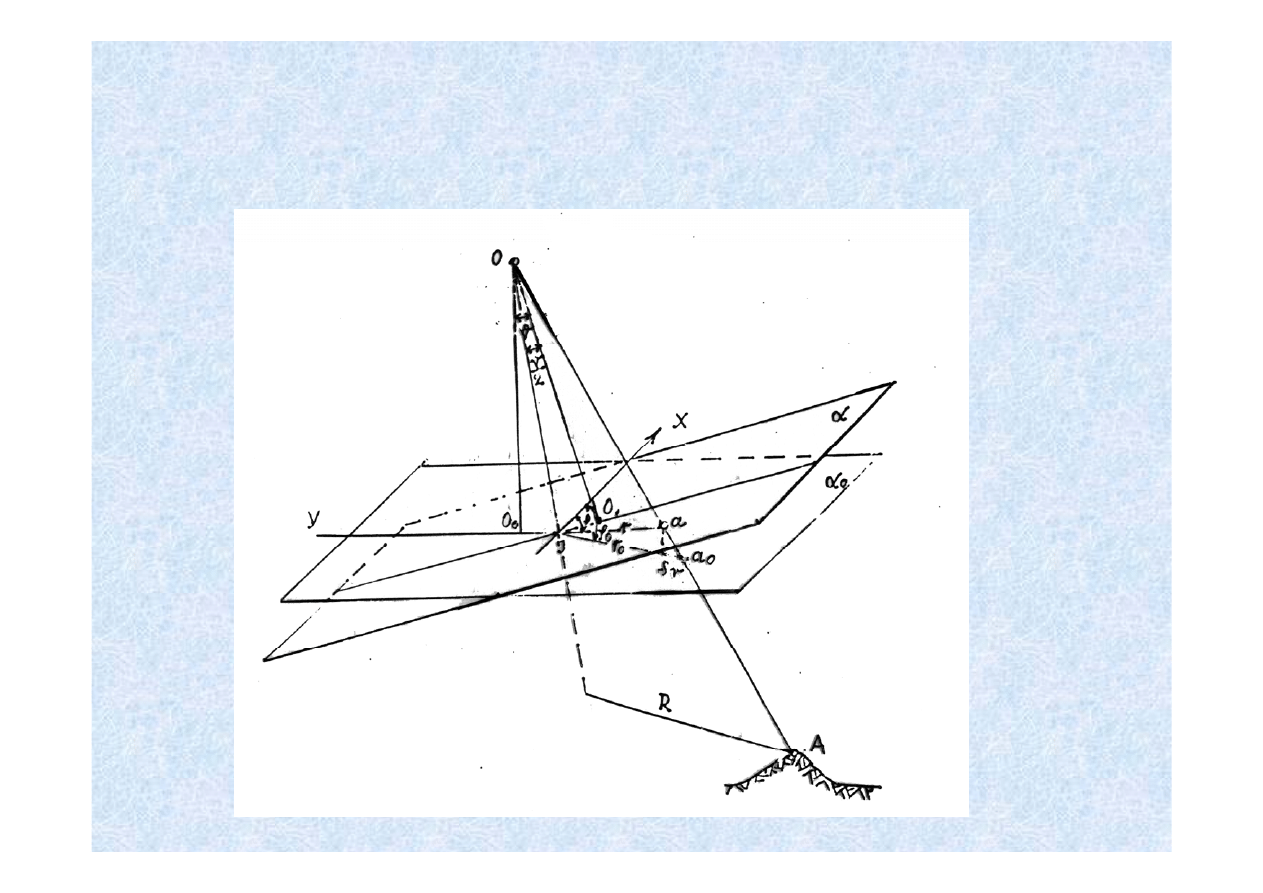
ZNIEKSZTAŁCENIE LINIOWE SPOWODOWANE

NACHYLENIEM ZDJĘCIA

ZNIEKSZTAŁCENIE KIERUNKÓW SPOWODOWANE

RZEŹBĄ TERENU

ZNIEKSZTAŁCENIE KIERUNKÓW SPOWODOWANE

RZEŹBĄ TERENU

h

l

h

h

β

δ

γ

δ

δν

sin

sin

sin

1

2

∗

−

∗

=

o

l

h

a po podstawieniu za i przekształceniu, otrzymamy

H

r

h

h

2

2

2

∗

=

δ

(

) (

) (

) (

)

a

b

b

a

a

b

b

a

h

l

l

f

m

x

y

x

y

h

h

l

l

H

x

y

x

y

h

h

∗

∗

∗

∗

−

∗

∗

−

=

∗

∗

∗

−

∗

∗

−

=

1

2

1

2

δν

o

o

l

l

f

m

l

l

H

∗

∗

∗

∗

∗

ZNIEKSZTAŁCENIE KIERUNKÓW SPOWODOWANE

RZEŹBĄ TERENU

i lk ść h2 h1 j t

ż

i

kt B

d

kt

A

il

wielkość h2 -h1 jest przewyższeniem punktu B nad punktem A, a iloczyn

m·lo odpowiada długości odcinka AB w terenie, dlatego:

μ

- kąt nachylenia linii AB w terenie

μ

tg

m

l

h

h

o

=

∗

−

1

2

Wtedy

μ

δν

tg

sin

l

f

x

y

x

y

a

b

b

a

h

∗

∗

−

∗

=

a ponieważ wielkość najczęściej jest nieznaczna to możemy zapisać :

l

f

a po e a

e ość ajc ęśc ej jest e ac a to o e y ap sać

μ

δν

∗

∗

∗

−

∗

=

l

f

x

y

x

y

a

b

b

a

h

∗ l

f

ZNIEKSZTAŁCENIE KIERUNKÓW SPOWODOWANE

RZEŹBĄ TERENU

Do wyznaczenia wielkości zniekształcenia na podstawie wzoru konieczne

Do wyznaczenia wielkości zniekształcenia na podstawie wzoru konieczne

są współrzędne punktów a, b, o początku układu w punkcie N na zdjęciu.

Omawiane zniekształcenie może być wyrażone również zależnością :

(

)

(

)

(

)

(

)

γ

ϕ

δ

γ

ϕ

δ

δ

δν

−

−

−

∗

∗

−

∗

=

cos

1

sin

h

l

h

r

h

r

tg

h

lub

(

)

(

)

γ

ϕ

δ

∗

−

l

h

r

(

)

δ

h

(

)

(

)

γ

ϕ

δ

δ

δν

−

∗

−

∗

=

sin

l

h

r

h

r

tg

h

zakładając nieznaczne nachylenie zdjęcia otrzymamy wzór uproszczony

(

)

γ

ϕ

δν

−

∗

=

sin

tg

h

r

h

(

)

γ

ϕ

δν

∗

sin

tg

l

H

h

ZNIEKSZTAŁCENIE KIERUNKÓW SPOWODOWANE

RZEŹBĄ TERENU

Dl ki

k

h d

kt

di

i k t ł

i

Dla kierunku przechodzącego przez punkt nadiru = zniekształcenie

nie wystąpi.

Jeżeli analizowane kierunki przechodzą przez inne punkty szczególne,

ϕ

γ

zniekształcenia możemy obliczyć z bardziej prostych zależności:

h

dla kierunku przechodzącego przez punkt główny

γ

ν

δν

cos

tg

m

l

h

h

∗

=

jeżeli kierunek przechodzi przez punkt izocentryczny

γ

ν

ν

cos

2

tg

m

l

h

h

∗

=

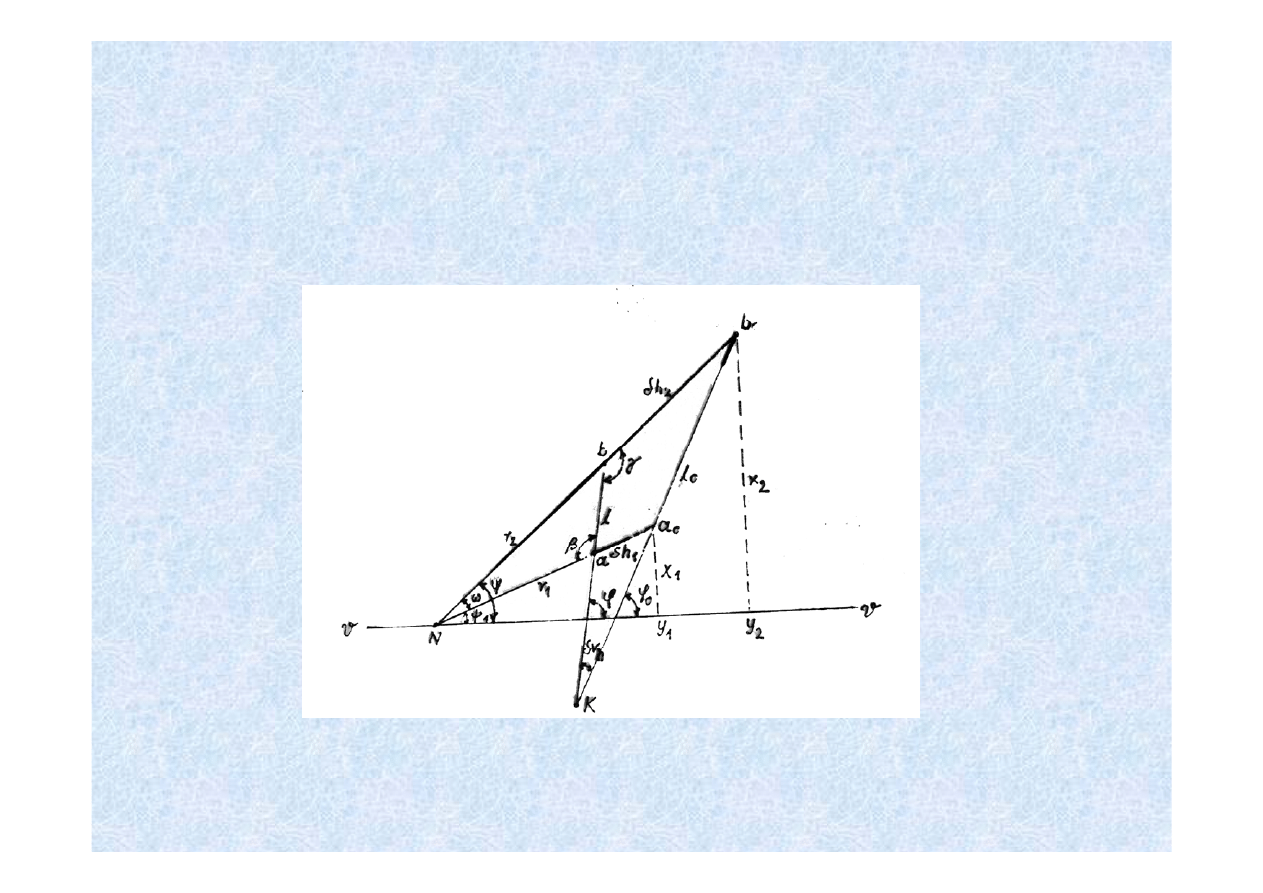
ZNIEKSZTAŁCENIE KIERUNKÓW SPOWODOWANE

NACHYLENIEM ZDJĘCIA

ZNIEKSZTAŁCENIE KIERUNKU SPOWODOWANE

NACHYLENIEM ZDJĘCIA

N

d t

i

k

t

j

Na podstawie rysunku otrzymujemy :

(

)

γ

ϕ

γ

ν

ν

−

∗

−

=

Δ

sin

sin

sin

tg

f

r

Maksymalne zniekształcenie wystąpi jeżeli:

(

)

γ

ϕ

γ

g

f

lub

γ

ϕ

=

2

⎟

⎠

⎞

⎜

⎝

⎛

+

2

90

ϕ

o

⎠

⎝

ν

sin

∗

r

(

)

ϕ

ν

δ

ν

cos

1

2

sin

max

+

∗

=

Δ

f

r

ZNIEKSZTAŁCENIE KIERUNKU SPOWODOWANE

NACHYLENIEM ZDJĘCIA

J ż li ki

k

h d i

kt

ól

O l b N t

Jeżeli kierunek przechodzi przez punkty szczególne np. O lub N, to po

podstawieniu ich współrzędnych tj. r i

ϕ do powyższego wzoru otrzymujemy:

dla kierunku przechodzącego przez punkt O

tg

Δ

ν

ν

γ

= − sin

sin

2

2

2

dl ki

k

h d

k N

dla kierunku przechodzącego przez punkt N

tg

Δ

ν

ν

γ

ν

= − sin

sin

cos

2

2

2

1

ZNIEKSZTAŁCENIE KIERUNKU SPOWODOWANE

NACHYLENIEM ZDJĘCIA

J ż li

kt

któ

h d i

li

ki

k l ż

li ii

Jeżeli punkt przez, który przechodzi analizowany kierunek leży na linii

największego spadku to zależność pomiędzy kierunkiem na zdjęciu i w
terenie wyrazi się wzorem :

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

∗

−

=

f

y

a

p

o

ν

ν

ϕ

ϕ

sin

cos

tg

tg

Maksymalne zniekształcenie kierunku przechodzącego przez punkt O lub N

wyniesie :

⎠

⎝

f

wyniesie :

sin

2

ν

ν

=

Δ

2

sin

max

ν

=

Δ

ZNIEKSZTAŁCENIE KIERUNKU SPOWODOWANE

NACHYLENIEM ZDJĘCIA

M k

l

i k t ł

i dl ki

k

h d

d

l

Maksymalne zniekształcenie dla kierunku przechodzącego przez dowolny

punkt leżący na linii największego spadku wyraża się zależnością :

ν

ρ

ν

sin

2

max

f

r

=

Δ

Jeżeli punkty leżą na poziomej przechodzącej przez punkt izocentryczny |I|

tj. na linii nie zniekształconej skali to:

ν

ρ

ν

sin

max

f

r

=

Δ

ρ

max

f

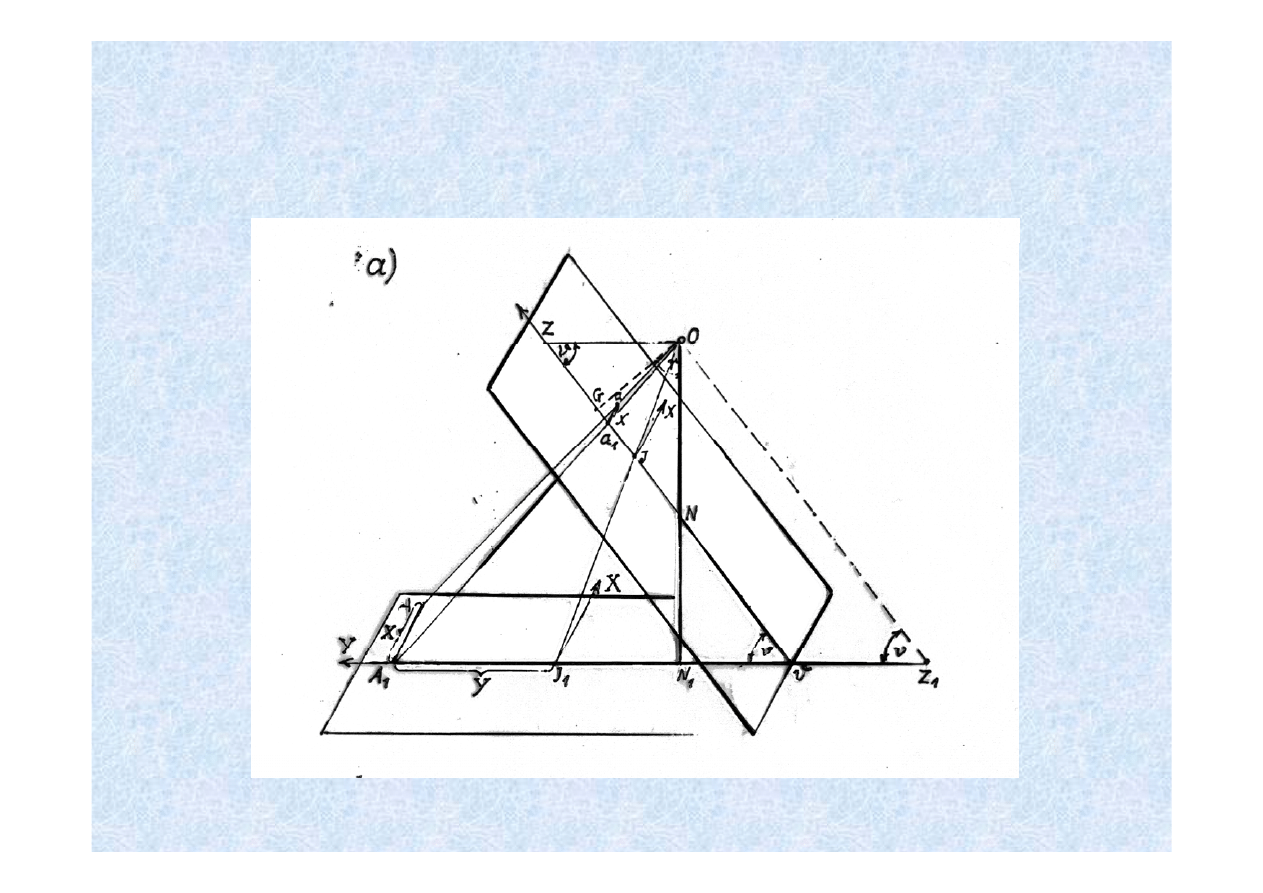
SKALA ZDJĘCIA LOTNICZEGO

SKALA ZDJĘCIA LOTNICZEGO

Sk l

dj i

d

l

k i

dj i

h l

dł ż d

l

Skala zdjęcia w dowolnym punkcie zdjęcia nachylonego wzdłuż dowolnego

kierunku np. prostej „ a” rozumiana jako :

1

l

Δ

1

m

l

L

l

o

=

→

lim

Δ

Δ

Δ

Skala zdjęcia ściśle pionowego, jeżeli

ν = 0 wyraża się wzorem :

1

m

f

H

=

SKALA ZDJĘCIA LOTNICZEGO

SKALA ZDJĘCIA LOTNICZEGO

Sk l

dj i

h l

dł ż ki

kó

di l

h

h d

h

Skala zdjęcia nachylonego wzdłuż kierunków radialnych przechodzących

przez punkt izocentryczny Jeżeli początek układu przyjąć w punkcie
izocentrycznym, to :

γ

ctg

∗

= y

x

a po podstawieniu tej wartości otrzymamy :

1

1

2

m

f

H

y

f

=

−

⎛
⎝

⎜

⎞
⎠

⎟

sin

ν

f

SKALA ZDJĘCIA LOTNICZEGO

SKALA ZDJĘCIA LOTNICZEGO

J ż li

t k kł d

jd j

i

k i

łó

t

Jeżeli początek układu znajduje się w punkcie głównym to :

(

)

x

y

GI ctg

=

+

γ

(

)

x

y

GI ctg

=

+

γ

a po podstawieniu tej wartości otrzymujemy :

1

2

m

f

H

y

f

=

−

⎛
⎝

⎜

⎞
⎠

⎟

cos

sin

ν

ν

m

H

f

⎝

⎠

SKALA ZDJĘCIA LOTNICZEGO

SKALA ZDJĘCIA LOTNICZEGO

Sk l

dł ż

i

h dj i dl

i

h

0

Skala wzdłuż poziomych zdjęcia, dla poziomych

γ = 0

o

1

1

f

y

⎛

⎜

⎞

⎟

i

1

m

f

H

y

f

=

−

⎝

⎜

⎠

⎟

sin

ν

Jeżeli początek układu współrzędnych jest w punkcie I, lub

1

f

y

⎛

⎞

1

m

f

H

y

f

h

=

−

⎛
⎝

⎜

⎞
⎠

⎟

cos

sin

ν

ν

jeżeli początek układu w G.

SKALA ZDJĘCIA LOTNICZEGO

SKALA ZDJĘCIA LOTNICZEGO

W

ż

ż

t

ć j k

t

k

X]

Wzory powyższe można otrzymać jako stosunek x : X]

1

x

x

f

y

f

y

−

⎛

⎜

⎞

⎟

sin

ν

1

1

m

x

X

x

x

H

f

y

f

y

H

f

H

y

f

h

=

=

−

=

=

−

⎛
⎝

⎜

⎞
⎠

⎟

sin

sin

sin

ν

ν

ν

przy początku w punkcie I.

Z przytoczonych wzorów wynika, że skala wzdłuż danej poziomej jest

wielkością stałą, natomiast ze zmianą położenia poziomej (zmiana y) skala
się zmienia i tak na linii horyzontu

1

1

m

h

=

m

h

SKALA ZDJĘCIA LOTNICZEGO

SKALA ZDJĘCIA LOTNICZEGO

W dł ż

i

h

h d

h

kt

ól

k l

ż

Wzdłuż poziomych przechodzących przez punkty szczególne skala wyraża

się prostymi zależnościami :

1

f

dla poziomej przechodzącej przez punkt G

1

m

f

H

h

=

cos

ν

jeżeli pozioma przechodzi przez punkt N

1

f

H

=

m

H

h

cos

ν

niezależnie od tego, w którym punkcie (G lub N) znajduje się początek

układu współrzędnych.

SKALA WZDŁUŻ GŁÓWNEJ PIONOWEJ

SKALA WZDŁUŻ GŁÓWNEJ PIONOWEJ

Zauważmy, że wzory wyrażające skalę wzdłuż kierunków radialnych, wyrażają

również skalę wzdłuż głównej pionowej, gdyż przechodzi ona przez punkt
izocentryczny a = 90

o

W punktach szczególnych otrzymamy :

przy punkcie głównym

1

2

f

ν

=

cos

p y p

g

y

m

H

ν

ν

cos

1

f

przy punkcie nadirowym

1

m

f

H

ν

ν

=

cos

SKALA WZDŁUŻ GŁÓWNEJ PIONOWEJ

SKALA WZDŁUŻ GŁÓWNEJ PIONOWEJ

Dl

i ś d i j k li dj i (t j t

dł ż d

l i

ł ż

Dla wyznaczenia średniej skali zdjęcia (to jest wzdłuż dowolnie położonego

kierunku,

γ od 0° do 360 °) w pobliżu dowolnie położonego na zdjęciu

punktu, korzystamy ze wzoru :

1

1

3

2

m

f

H

y

f

ν

ν

=

−

⎛
⎝

⎜

⎞
⎠

⎟

sin

•

W praktyce skalę zdjęcia najczęściej określamy na podstawie wielkości
pomierzonych na zdjęciu i w terenie lub na mapie Takie położenie

ν

pomierzonych na zdjęciu i w terenie lub na mapie. Takie położenie
odcinków, na podstawie których określamy skalę, umożliwia częściowo
wyeliminowanie wpływu zniekształceń spowodowanych nachyleniem
zdjęcia.

zdjęcia.

•

Skala określona na podstawie elementów a, b, c, d, ....jest skalą lokalną -
miejscową, a z elementów L

1

, L

2

, średnią skalą zdjęcia.

CZYNNIKI FIZYCZNE WPŁYWAJĄCE NA

ZNIEKSZTAŁCENIE OBRAZU ZDJĘCIA LOTNICZEGO

D

ikó fi

h

ł

j

h

i k t ł

i

b

Do grupy czynników fizycznych wpływających na zniekształcenie obrazu

zdjęć lotniczych zaliczamy :

dolność ro d ielc ą fotografic ną

•

zdolność rozdzielczą fotograficzną,

•

dystorsję,

•

nieprzyleganie negatywu do płaszczyzny ramki tłowej oraz niepłaskość

ramki tłowej

ramki tłowej,

•

deformacje materiału światłoczułego,

•

krzywiznę ziemi,

f k j f

fi

•

refrakcję fotograficzną

CZYNNIKI FIZYCZNE WPŁYWAJĄCE NA

ZNIEKSZTAŁCENIE OBRAZU ZDJĘCIA LOTNICZEGO

Zdj i

k j

k

k

i Wild t

RC 5 RC 5

Zdjęcia w kraju są wykonywane kamerami Wilda typu RC - 5, RC - 5a,
RC - 8, RC - 10.

•

zniekształcenia wnoszone przez kamerę nie przekraczają 0,02 - 0,03 mm,

•

dystorsja obiektywu nie przekracza 0,01 mm nawet na skrajach zdjęcia,

•

niedocisk filmu nie przekracza 0,015 mm,

•

wpływ krzywizny ziemi i refrakcji przy nalocie wielkoskalowym - 0,002 -

0,004 mm,

•

deformacja błon firmy Agfa Gevaret nie przekracza 0,02 mm, a po

uwzględnieniu deformacji jednorodnej, deformacja szczątkowa nie

przekracza 0,01 mm.