1

ZALICZANIE STATYSTYKI SEM. 3 (WZMS; A.M.KACZYŃSKI)

13 22 18 22 23 8 21 17 33 22 a) Podać tabelę szeregu rozdzielczego, wykreślić histogram

25 18 16 17 18 24 26 21 19 20 i dystrybuantę empiryczną oraz obliczyć podstawowe
16 22 29 23 22 15 17 19 20 18 statystyki opisowe próbki (średnią

x i odchylenie standardowe s)

16 22 11 21 22 19 26 20 18 38 b) Zweryfikować hipotezę

9

:

1

H





wobec alternatywnej

9

:

1

K





21 16 26 17 15 27 12 19 23 14 przyjmując poziom istotności

0, 04





15 20 17 28 16 22 19 13 21 24 c) Zweryfikować hipotezę





:

,

H X

N x s



przyjmując

0,1





10 26 24 19 17 18 20 21 23 14
17 27 23 25 24 20 15 21 12 30
14 27 20 24 18 24 16 19 17 20
15 18 19 23 28 21 28 11 19 16


Szkic rozwiązania (PATRZ PRZYKŁAD 25, STR. 326):

a)

Grupowanie





klasa

grupowanie

4,5;9,5

7

/

9,5;14,5

12

/ / /

1

/

i

i

x

n

/ / / /



14,5;19,5

17

10

/ / / / / / / / / / / / / / / / / / / / / / / / / / / /



/ /

19,5; 24,5

2

37

2

/ / / / / / / / / / / / / / / / / / / / / / / / / / / /



/

24,5; 29,5

27

36

/ / / / / / / /




13

2

/ / /

29,5;34.5

32

/ /

34,5;39,5

37

/

1

100



Tabela szeregu rozdzielczego

Nr

klasy

Klasa

Środek klasy

Liczność

Częstość

Liczebność

skumulowana

Częstość

skumulowana

i



,

i

i

a b

2

i

i

i

a

b

x





i

n

i

i

n

f

n



:

i

i

j i

cn

n







:

i

i

cn

F

n



1



4, 5; 9,5

7

1

0,01

1

0,01

2



9, 5; 14,5

12

10

0,1

11

0,11

3



14, 5; 19, 5

17

37

0,37

48

0,48

4



19, 5; 24,5

22

36

0,36

84

0,84

5



24, 5; 29, 5

27

13

0,13

97

0,97

6



29, 5; 34,5

32

2

0,02

99

0,99

7 = k



34, 5; 39, 5

37

1

0,01

100

1

2

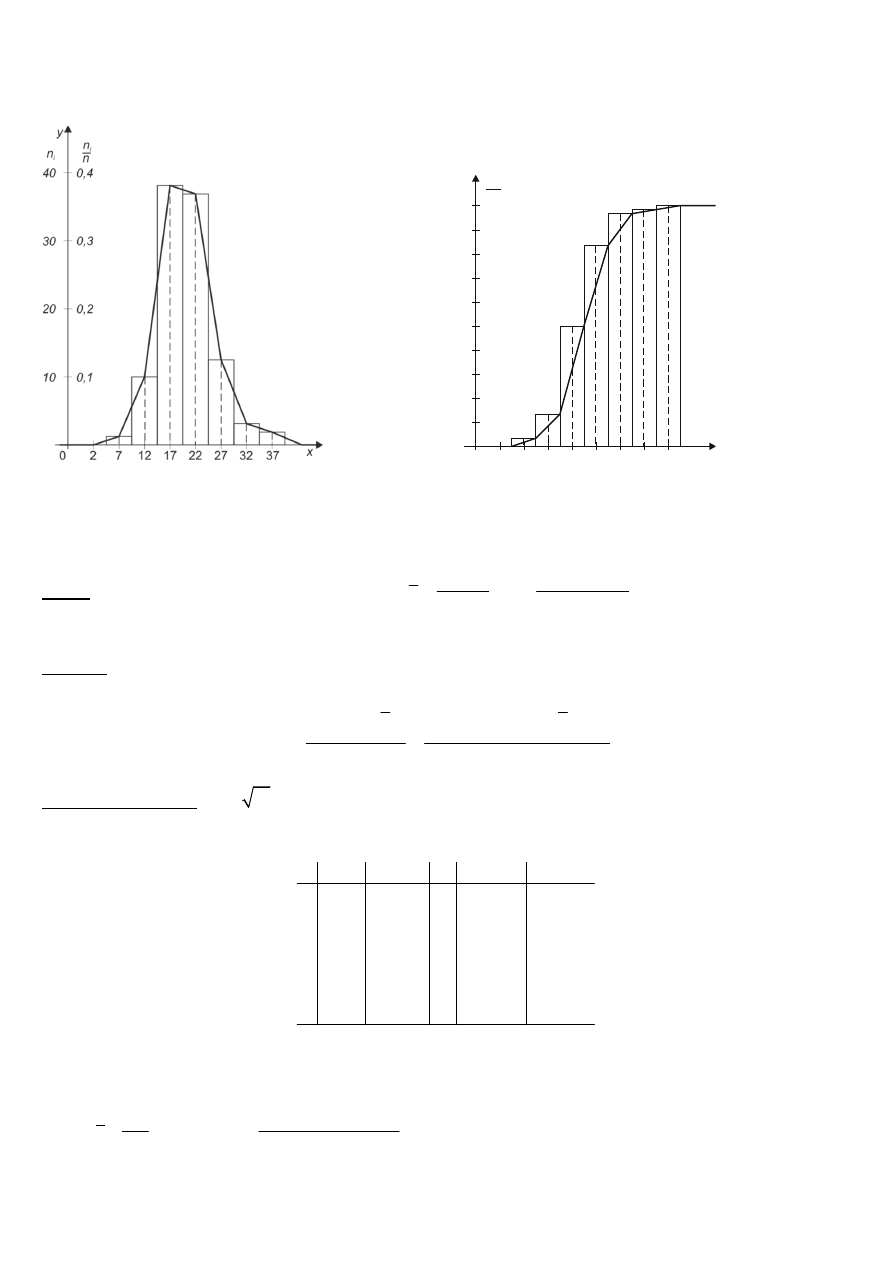
Wykresy

histogram dystrybuanta empiryczna (poprawiona)

Podstawowe charakterystyki (statystyki opisowe próbki)

średnia (ważona) z próbki dla szeregu rozdzielczego:









tw.

1

1

k

k

i

i

i

i

d R

i

i

n x

n x

d

x

d

n

n



















,

gdzie za d wstawia się tzw. dominantę, czyli tę wartość

i

x

, dla której liczebność

i

n

jest największa

wariancja z próbki dla szeregu rozdzielczego:













2

2

2

2

1

1

1

1

k

k

i

i

i

i

i

i

n x

x

n x

d

n x

d

s

n

n

























odchylenie standardowe:

2

s

s



Pomocnicza tabela (

17

d 

):













2

2

17

17

17

17

7

10

100

1

10

100

12

5

25

10

50

250

17

0

0

37

0

0

22

5

25

36

180

900

27

10

100

13

130

1300

32

15

225

2

30

450

37

20

400

1

20

400

100

300

3400

i

i

i

i

i

i

i

i

x

x

x

n

n x

n x



















stąd





2

2

3400 10

20

25, 25

0 17

5, 02

20

300

17

,

,

100

99

5

x

s

s

















.

2

7

12

17

22

27

32

37

0

x

10

40

60

80

0,1

0,4

0,6

0,8

y

cn

i

cn

i

n

20

0,2

100

1,0

= F

i

3

b)

(patrz przykład

29

str. 339 i model 1b) str. 331)

Rozwiązanie dwoma sposobami: za pomocą zbioru krytycznego lub przedziału ufności

 Stawiamy hipotezę zerową

0

:

19

H









wobec hipotezy alternatywnej

9

:

1

K





.

 Statystyka testowa (sprawdzian)





asympt.

~

0,1

/

n

n

n

X

U

N

S

n







.

Wartość sprawdzianu dla zadanej próbki wynosi:

0

obs.

20 19

1,99

5,025

1

:

/

0

n

n

x

u

s

n













.

Zbiór krytyczny

W



, odpowiadający odrzuceniu hipotezy zerowej i przy przyjętej hipotezie alternatywnej,

wyznacza się z warunku:









n

n

P U

W

P U

u















, co prowadzi do





,

,

W

u

u







   



  i

1

1

2

u













  







(z tabl. 4.4 mamy

0,01 0,02 0,03

0,05

2,58

2,33 2,

0

1

,0

7

4

2

1,96

,05

u







).

Równoważnie, dwustronny przedział ufności na średnią

 przy założeniu prawdziwości hipotezy zerowej

otrzymuje się z warunku:





1

n

P U







 

, co daje

;

n

n

n

n

S

S

X

u

X

u

n

n



























.

W obu przypadkach istotna jest więc wartość krytyczna

u



, która dla założonego poziomu istotności

0, 04





wynosi

0,04

2, 05

u



.

Zatem zbiór krytyczny jest postaci:





0,04

; 2,05

2,05;

W

   



 

lub

dla zadanej próbki realizacja 96-procentowanego dwustronnego przedziału ufności na średnią wynosi





pu;

5,025

5,025

20 2,05

; 20 2, 05

18,97; 21, 03

10

10

,

:

n

n

n

n

s

s

x

u

x

u

X

n

n













































.

3. Podejmujemy decyzję:

obs.

0,04

1,99

u

W





lub

0

pu; 0,04

19

X







, więc nie ma podstaw do odrzucenia hipotezy zerowej.

4

c)

(patrz przykład

31 str. 344)

Stawiamy hipotezę zerową





:

~

,

H X

N

  , gdzie nie znamy

2

r 

parametrów  i



. Za ocenę tych

parametrów można przyjąć statystyki opisowe uzyskane na podstawie próbki:

,

20

5

x

s













.

Stosujemy test zgodności

2

 , który wymaga połączenia klas skrajnych ze względu na małą liczność (musi

liczność klasy być przynajmniej 5). Wszystkie obliczenia prowadzące do znalezienia wartości

2

obs.



(przydatny

jest kalkulator) podaje tabelka:

















2

1

2

obs.

,

/

1

,14,5

0,136

13,6

0, 497

2

14,5;19,5

37

0,324

32, 4

0,653

3

19,5; 24,5

36

0,356

35,6

0, 005

4

24,5;

0,184

18, 4

0,313

100 1,000

100,0

1, 468

11

16

i

i

i

i

i

i

i

i

i

i

A

a

a

n

p

n p

n

n p

n p











 





,

Przy

założeniu,

że

hipoteza

jest

prawdziwa,

tzn.





,

~

20 5

X

N

,

wartości

hipotetyczne









ˆ

,

1, 2,3, 4

i

i

p

P X

A

i

k





 



w powyższej tabelce obliczamy tak jak w rozkładzie





20,5

N

:

 





 













1

2

3

4

1

2

3

4

14,5

0,5

0,5

1,1

0,136;

19,5

14,5

0,1

1,1

0,324;

24,5

19,5

0,9

0,1

0,356 ;

24,5

1

0,184 lub

0,5

0,18

20

5

20

20

5

5

20

20

5

5

20

5

4.

p

p

p

p

p

p

p

p









 



 























 

 

 

 































 

 

 

 

























 









 











Przy

0,1





i ˆ

1

2 1

ˆ

4

1

k

n

r



      odczytujemy z tabl. 4.6

1

0,1

2
ˆ

;

2, 7

n











, więc zbiór krytyczny jest

postaci



0,1

2, 7 ;

W





.

Ponieważ

2

obs.

0,1

1, 468 W







, więc

dana próbka nie przeczy hipotezie, że rozkład X jest normalny

.