MO/I - 06

METODY NUMERYCZNE ROZWIĄZYWANIA RÓWNAŃ

METODA BISEKCJI

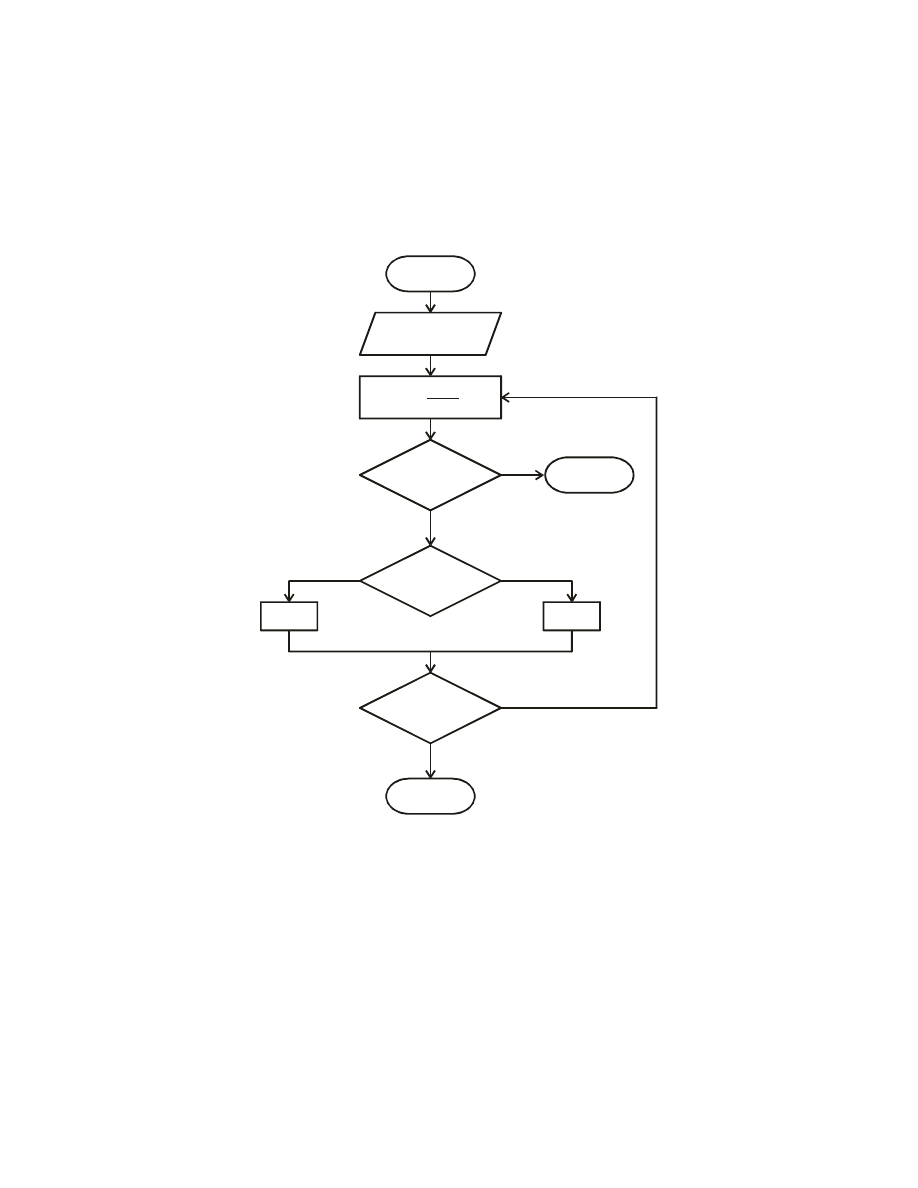
Schemat blokowy

f x a b eps

( ), , ,

Start

T

T

N

N

f x

( ) = 0

f a f x

( ) ( ) < 0

a

x

=

b

x

=

Stop

T

N

|

>

b - a |

eps

Stop

2

b

a

x

+

=

Zadanie 1.

W oparciu o przedstawiony schemat blokowy napisać program do rozwiązywania równań nieliniowych
metodą bisekcji. Działanie programu sprawdzić poszukując rozwiązania równania e

2

0

x

x

−

=

w

przedziale [0,1] z dokładnością

)

1

(

10

Digits

−

. Określić liczbę iteracji.

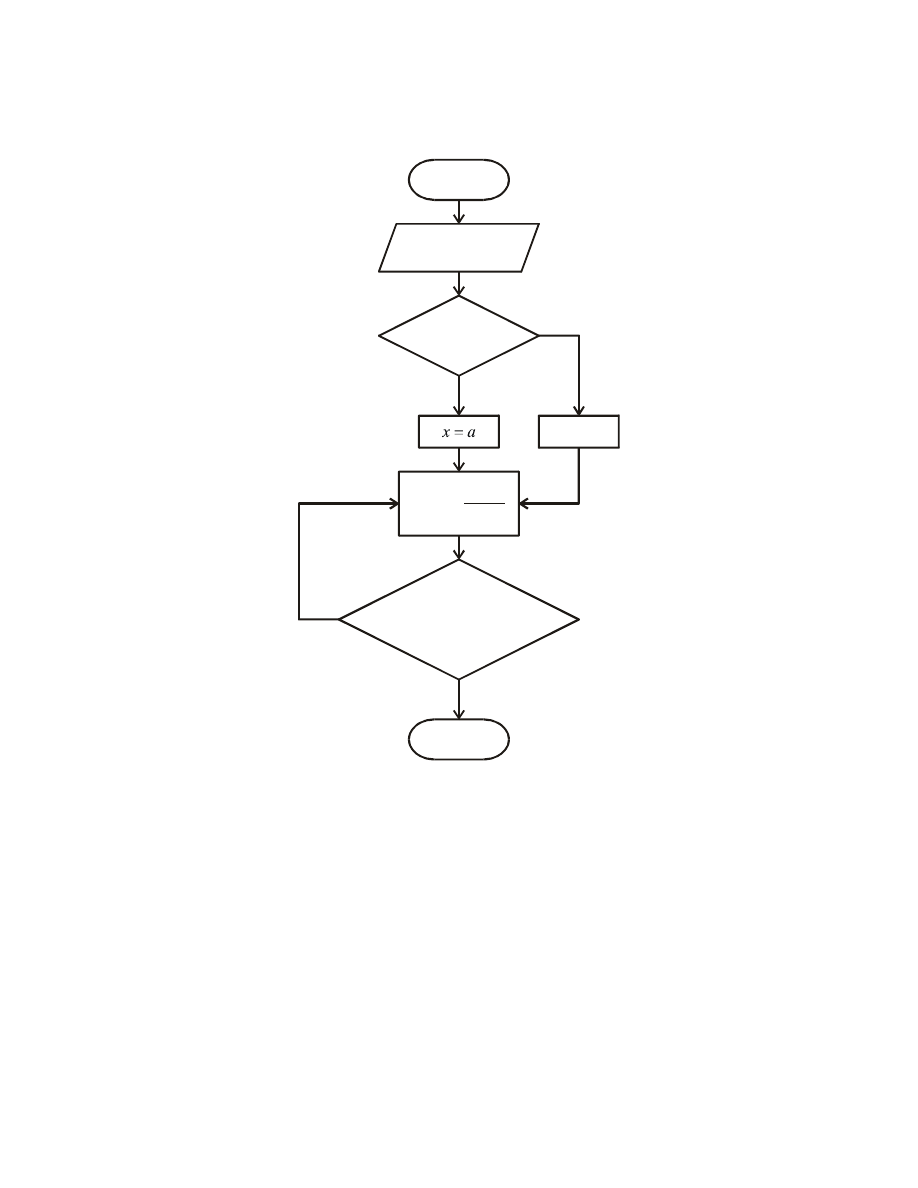
METODA NEWTONA

Schemat blokowy

f x a b eps

( ), , ,

Start

N

T

0

)

(

)

(

>

′

′ a

f

a

f

T

N

Stop

b

x =

)

(

)

(

x

f

x

f

x

x

′

−

=

0

)

(

)

(

0

)

(

)

(

>

+

∧

>

−

e p s

x

f

x

f

e p s

x

f

x

f

Zadanie 2.

W oparciu o przedstawiony schemat blokowy napisać program do rozwiązywania równań nieliniowych
metodą Newtona (stycznych). Działanie programu sprawdzić poszukując rozwiązania równania z zadania
pierwszego. Określić liczbę iteracji.

Zadanie 3.

Powtórzyć obliczenia obydwiema metodami dla zmiennej Digits = 20. Określić w każdym przypadku
liczbę iteracji.