Równania nieliniowe

dr inż. Henryk Olszewski

PWSZ, Elbląg 2003

Elbąg, PWSZ 2002r.

Równania nieliniowe

Algebraiczne równanie nieliniowe ma postać:

gdzie: F(x) jest pewną daną funkcją zmiennej x. Pierwiastkiem
tego równania nazywamy taką wartość zmiennej x, dla której jest
ono spełnione.

Metoda siecznych
W metodzie połowienia kroku dokładną wartość pierwiastka
uzyskano przez dwukrotne zmniejszenie przedziału, w którym
wyznaczono ten pierwiastek.

)

( 

Elbąg, PWSZ 2002r.

Metoda siecznych

Elbąg, PWSZ 2002r.

Metoda siecznych

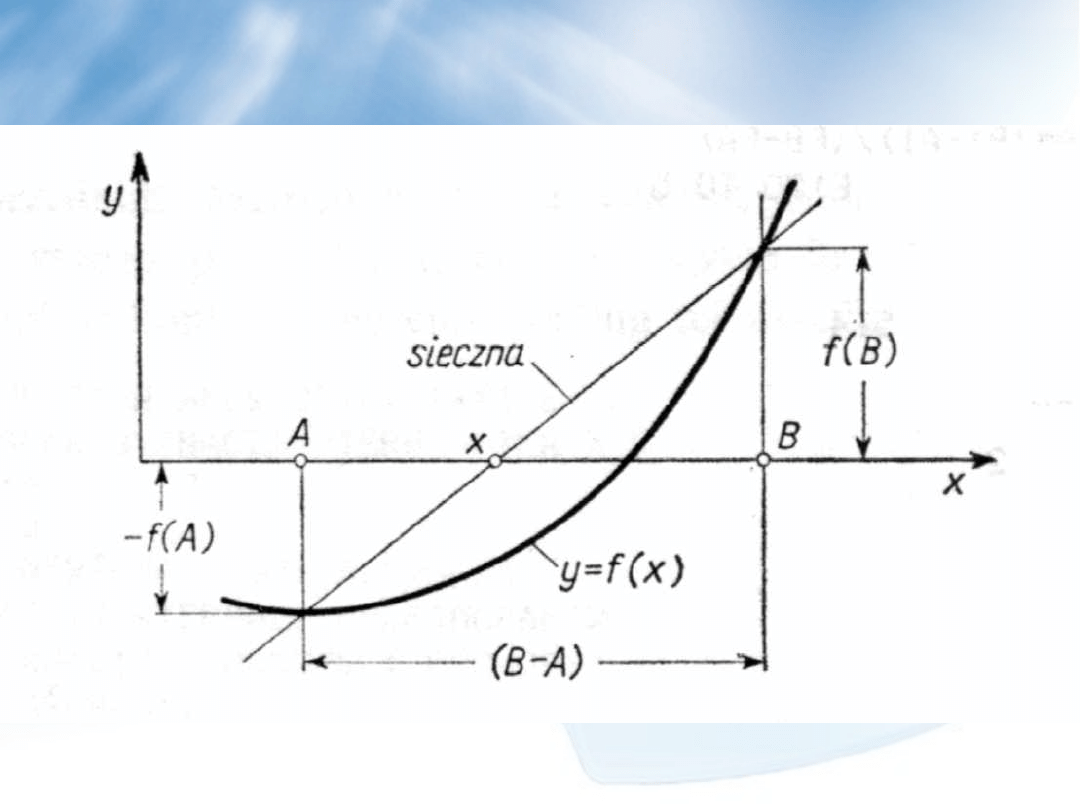
Znacznie szybciej uzyskuje się rozwiązanie stosując metodę
siecznych (reguła falsi).

Reguła falsi polega na tym, aby wykres funkcji f(x)

zastąpić sieczną przechodzącą przez wartości funkcji na końcach
przedziału.

Za najlepsze przybliżenie wartości pierwiastka przyjmuje się
punkt przecięcia tej siecznej z osią x.

Jeśli okaże się, że nie uzyskano zadanej dokładności, do dalszych
obliczeń wybiera się tę wartość przybliżoną, jako nową granicę
przedziału.

Program startuje od metody przeszukiwania, po ustaleniu
przedziału, w którym wartości funkcji na lewym i prawym brzegu
są przeciwnych znaków, przechodzi do metody siecznych.

Elbąg, PWSZ 2002r.

Metoda siecznych

W algorytmie wykorzystujemy n-te i n-1 przybliżenie. Zapisujemy
wzór w następującej postaci:

lub:
x(n+1)=x(n)-(f(x(n))*(x(n)-x(n-1)))/
(f(x(n))-f(x(n-1))), dla n=1,2,...

Przykład 1
Rozwiązać metodą siecznych dane równania nieliniowe:
y =2x-2sin(x)-1 w przedziale <0,2>

     









Elbąg, PWSZ 2002r.

Metoda siecznych – przykład 1

clear all;
blad=0.0001;
i=0 ;
x1(1)=0 ;
x=x1(1) ;
y1(1)=(2*x1(1))-(2*sin(x1(1)))-1;
y=y1(1);
fprintf('iteracja:0\n\n')
fprintf('x=%d y=%.3f\n\n',x,y)
i=1;
x1(2)=2;
x=x1(2);
y1(2)=(2*x1(2))-(2*sin(x1(2)))-1;
y=y1(2);
fprintf('iteracja:1\n\n')
fprintf('x=%d y=%.3f\n\n',x,y)

Elbąg, PWSZ 2002r.

Metoda siecznych – przykład 1

xa=0:0.01:3;
ya=2*xa-2*sin(xa)-1;
plot(xa,ya,'m'); grid on
hold on;

for i=2:30

x1(i+1)=x1(i)-((y1(i)*(x1(i)-x1(i-1)))/(y1(i)-y1(i-

1)));
y1(i+1)=2*x1(i+1)-2*sin(x1(i+1))-1;

x=x1(i+1);
y=y1(i+1);
fprintf('iteracja:%d\n\n',i)
fprintf('x=%.4f y=%.5f\n\n',x,y)

Elbąg, PWSZ 2002r.

Metoda siecznych – przykład 1

a=x1(i-1);
b=x1(i);

xb=[a;b];

c=y1(i-1);
d=y1(i);

yb=[c;d];
line(xb,yb); grid on

hold on;

if abs(y1(i+1))< blad

plot(x,y,'bx');
break;

end

Elbąg, PWSZ 2002r.

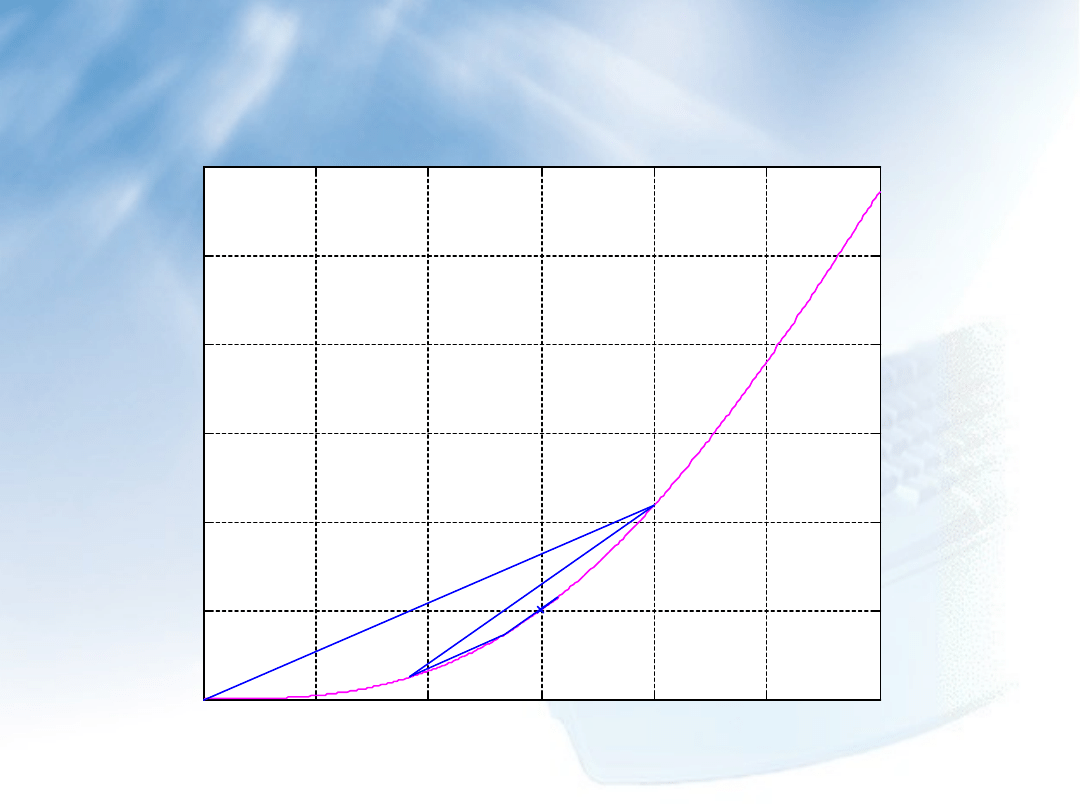
Metoda siecznych – przykład 1

Ilustracja graficzna rozwiązania równania y=2x-sin(x)-1

0.5

1.5

2.5

-1

Elbąg, PWSZ 2002r.

Metoda siecznych – przykład 1

Wynik działania programu:
iteracja:0
x=0 y=-1.000
iteracja:1
x=2 y=1.181
iteracja:2
x=0.9168 y=-0.75369
iteracja:3
x=1.3387 y=-0.26895
iteracja:4
x=1.5728 y=0.14558
iteracja:5
x=1.4906 y=-0.01240
iteracja:6
x=1.4970 y=-0.00049
iteracja:7
x=1.4973 y=0.00000

Elbąg, PWSZ 2002r.

Metoda siecznych – przykład 2

Rozwiązać metodą siecznych dane równania nieliniowe:

y = ln(x

)+4 w przedziale (-0.5,0)U( 0,0.5)

clear all;
blad=0.0001;
fprintf('Obliczenia pierwiastka rownania w(-0.5,0)')
i=0;
x1(1)=-0.5 ;
x=x1(1);
y1(1)=log(x1(1)^(2))+4;
y=y1(1);
fprintf('iteracja:%d\n\n',i)
fprintf('x=%.1f y=%.5f\n\n ',x,y);
i=1;
x1(2)=-0.001;
x=x1(2);
y1(2)=log(x1(2)^2)+4;
y=y1(2);

Elbąg, PWSZ 2002r.

Metoda siecznych – przykład 2

fprintf('iteracja:%d\n\n',i)
fprintf('x=%.3f y=%.5f\n\n ',x,y);
xa=-1:0.01:1;
ya=log(xa.^(2))+4;

plot(xa,ya,'red'); grid on
hold on;

for i=2:30

x1(i+1)=x1(i)-((y1(i)*(x1(i)-x1(i-1)))/(y1(i)-y1(i-1)));
y1(i+1)=log(x1(i+1)^2)+4;

if abs(y1(i+1))< blad
plot(x,y,'bx')

break;

end;

Elbąg, PWSZ 2002r.

Metoda siecznych – przykład 2

x=x1(i+1);
y=y1(i+1);

fprintf('iteracja:%d \n\n',i)
fprintf('x=%.4f y=%.5f\n\n',x,y)

a=x1(i-1);
b=x1(i);

xb=[a;b];

c=y1(i-1);
d=y1(i);

yb=[c;d];

line(xb,yb); grid on
hold on;

end

Elbąg, PWSZ 2002r.

Metoda siecznych – przykład 2

fprintf('Obliczenia nastepnego pierwiastka w (0,0.5)')
i=0;
x1(1)=0.5 ;
x=x1(1);
y1(1)=log(x1(1)^(2))+4;
y=y1(1);
fprintf('iteracja:%d\n\n',i)
fprintf('x=%.3f y=%.5f\n\n ',x,y);
i=1;
x1(2)=0.001;
x=x1(2);
y1(2)=log(x1(2)^2)+4;
y=y1(2);
fprintf('iteracja:%d\n\n',i)
fprintf('x=%.1f y=%.5f\n\n ',x,y);

Elbąg, PWSZ 2002r.

Metoda siecznych – przykład 2

for i=2:30

x1(i+1)=x1(i)-((y1(i)*(x1(i)-x1(i-1)))/(y1(i)-y1(i-1)));
y1(i+1)=log(x1(i+1)^2)+4;

if abs(y1(i+1))< blad
plot(x,y,'bx')

break;

end;

x=x1(i+1);
y=y1(i+1);

fprintf('iteracja:%d \n\n',i)
fprintf('x=%.4f y=%.5f\n\n',x,y)

Elbąg, PWSZ 2002r.

Metoda siecznych – przykład 2

a=x1(i-1);
b=x1(i);

xb=[a;b];

c=y1(i-1);
d=y1(i);

yb=[c;d];

line(xb,yb); grid on
hold on;

end
end

-1

-0.8

-0.6

-0.4

-0.2

0.2

0.4

0.6

0.8

-10

-8

-6

-4

-2

Elbąg, PWSZ 2002r.

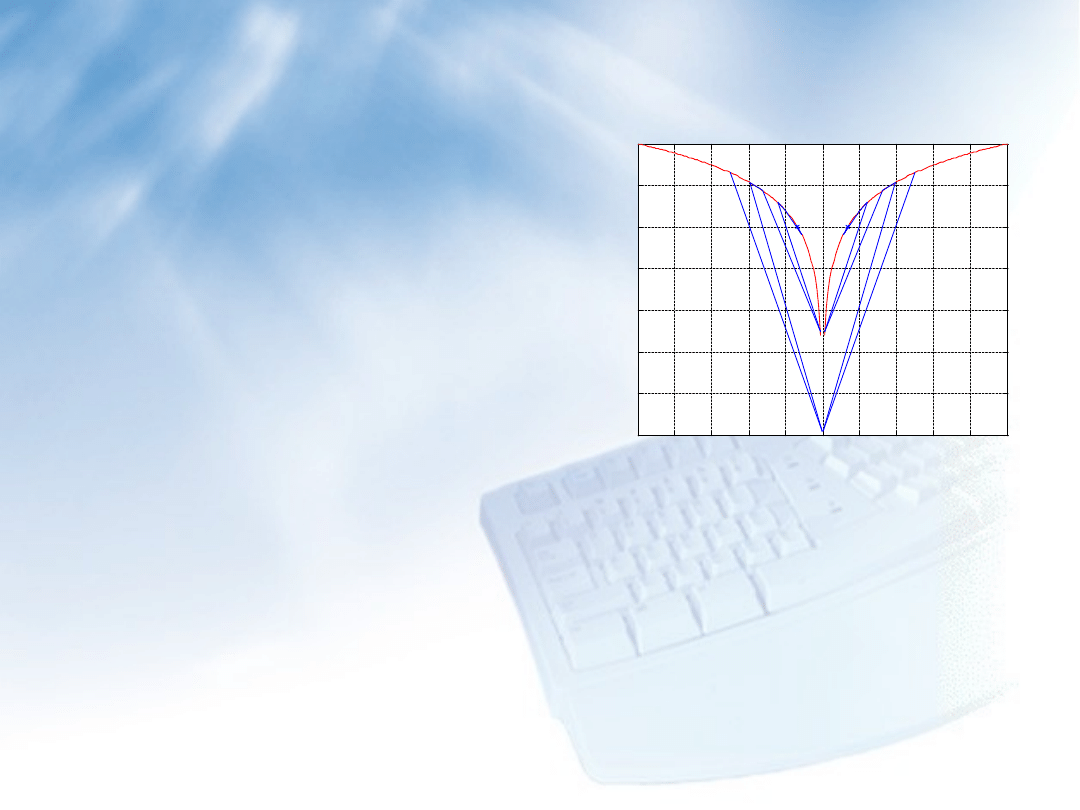
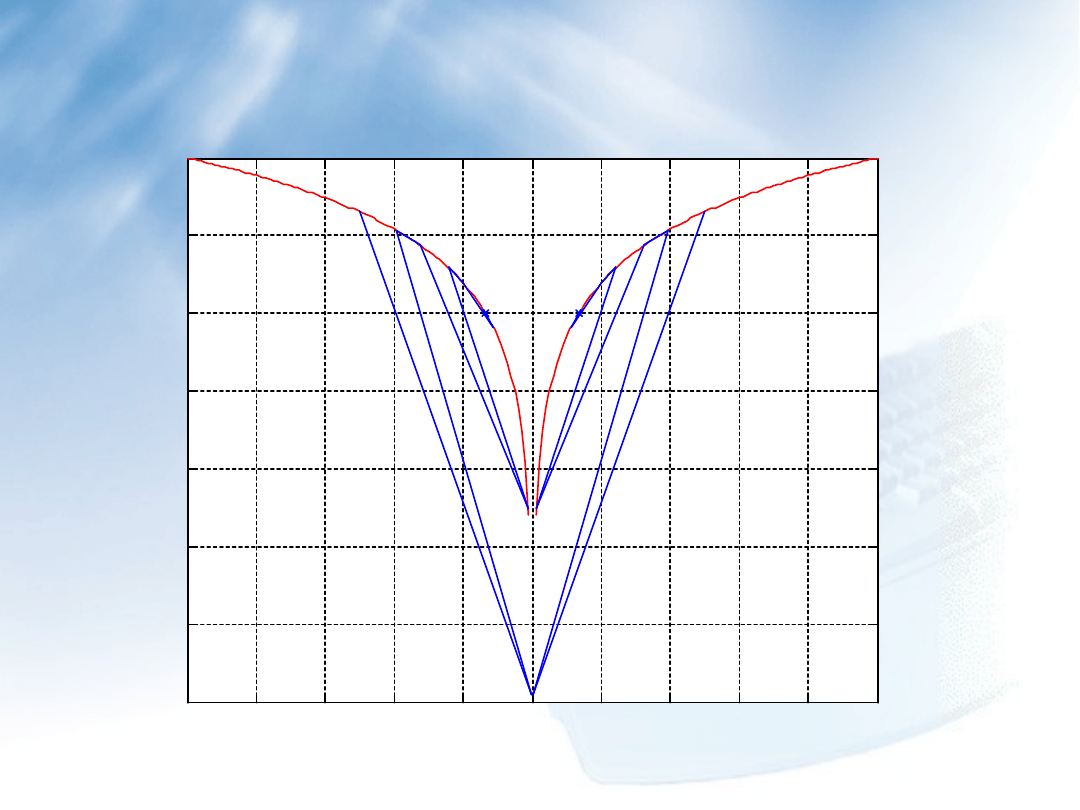
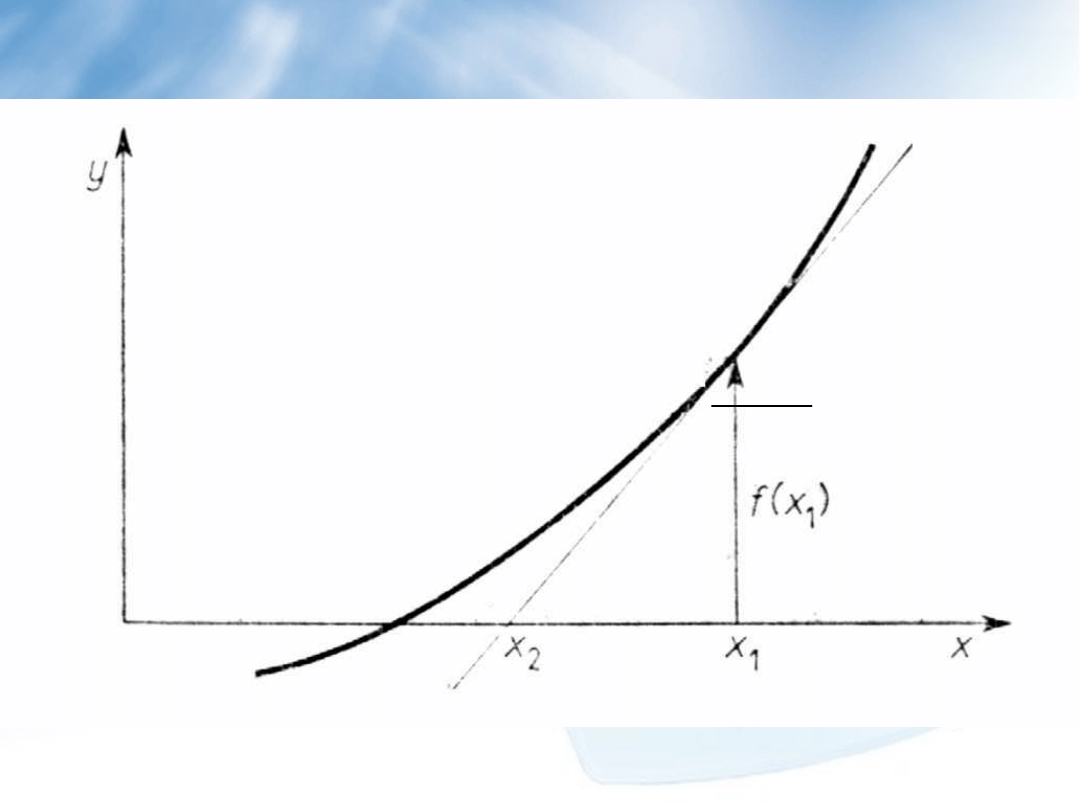
Metoda siecznych – przykład 2

Ilustracja graficzna rozwiązania równania y=ln(x

)+4

-1

-0.8

-0.6

-0.4

-0.2

0.2

0.4

0.6

0.8

-10

-8

-6

-4

-2

Elbąg, PWSZ 2002r.

Metoda siecznych – przykład 2

Obliczenia pierwiastka równania w (-0.5;0)
iteracja:0
x=-0.5 y=2.61371
iteracja:1
x=-0.001 y=-9.81551
iteracja:2
x=-0.3951 y=2.14260
iteracja:3
x=-0.3245 y=1.74881
iteracja:4
x=-0.0109 y=-5.03927
iteracja:5
x=-0.2437 y=1.17616
iteracja:6
x=-0.1996 y=0.77738
iteracja:7
x=-0.1138 y=-0.34738
iteracja:8
x=-0.1403 y=0.07173
iteracja:9
x=-0.1357 y=0.00595
iteracja:10
x=-0.1353 y=-0.00011

Elbąg, PWSZ 2002r.

Metoda siecznych – przykład 2

Obliczenia następnego pierwiastka w (0;0.5)
iteracja:0
x=0.500 y=2.61371
iteracja:1
x=0.0 y=-9.81551
iteracja:2
x=0.3951 y=2.14260
iteracja:3
x=0.3245 y=1.74881
iteracja:4
x=0.0109 y=-5.03927
iteracja:5
x=0.2437 y=1.17616
iteracja:6
x=0.1996 y=0.77738
iteracja:7
x=0.1138 y=-0.34738
iteracja:8
x=0.1403 y=0.07173
iteracja:9
x=0.1357 y=0.00595
iteracja:10
x=0.1353 y=-0.00011

Elbąg, PWSZ 2002r.

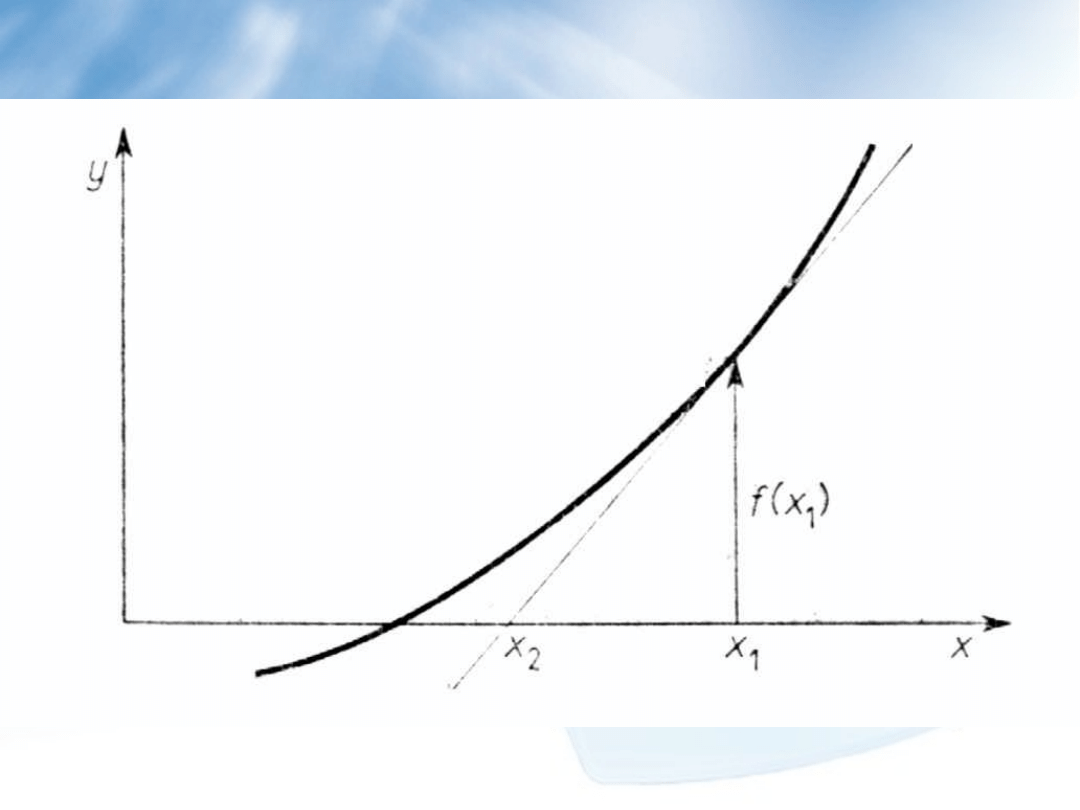
Metoda stycznych (Newtona)

Załóżmy, że x

oznacza oszacowane przybliżenie wartości

pierwiastka równania. Możemy wtedy napisać równanie stycznej
w tym punkcie do krzywej y=f(x):

Punkt x

przecięcia się tej stycznej z osią x uważamy za

następne, lepsze przybliżenie wartości pierwiastka:

Metoda ta znacznie szybciej prowadzi do obliczenia pierwiastka
niż poprzednie. Metoda Newtona wymaga jednak wstępnego
oszacowania pierwszego przybliżenia, co nie zawsze nie jest
łatwe.

 

 

