Spis treści

Część projektowa

1. Opis techniczny do projektu konstrukcyjnego

s.2

2. Schemat szkieletu hali i konstrukcja ramy

s.3

3. Zebranie obciążeń

s.6

4. Przyjęcie przekrojów projektowanych elementów

s.9

5. Przyjęcie belek stężeniowych i obciążenie nimi słupów

s.11

6. Zestawienie poszczególnych obciążeń oraz kombinatoryka obciążeń

s.14

7. Analityczne wymiarowanie rygla stropowego nr 6

s.37

8. Analityczne wymiarowanie słupa nr 1

s.49

9. Wymiarowanie elementów przy użyciu programu RM‐WIN

s.52

9.1. Rygiel nr 6 (7)

s.53

9.2. Rygiel nr 89

s.70

9.3. Słup nr 1 (3)

s.82

9.4. Słup nr 2

s.84

9.5. Słup nr 4 (5)

s.87

9.6. Stopy fundamentowe

s.90

Część rysunkowa

• Rys. nr 4. „Konstrukcja ramy żelbetowej dla hali monolitycznej”

Załączniki

A. Zestawienie stali zbrojeniowej

2 |

S t r o n a

1. Opis techniczny do projektu konstrukcyjnego.

1.1. Podstawa opracowania

A. Zlecenie Politechniki Poznańskiej
B. Plan zagospodarowania przestrzennego miasta Bydgoszcz z 6.09.2001roku
C. Decyzja o warunkach zabudowy i zagospodarowania terenu nr 710/08 UAN‐G‐

7331/63/08

D. Rozporządzenie Ministra Gospodarki Przestrzennej i Budownictwa w sprawie

warunków technicznych jakim powinny odpowiadać budynki i ich
usytuowanie.

1.2. Przedmiot opracowania

Projekt konstrukcyjny ramy żelbetowej obiektu halowego.

1.3. Dane ogólne

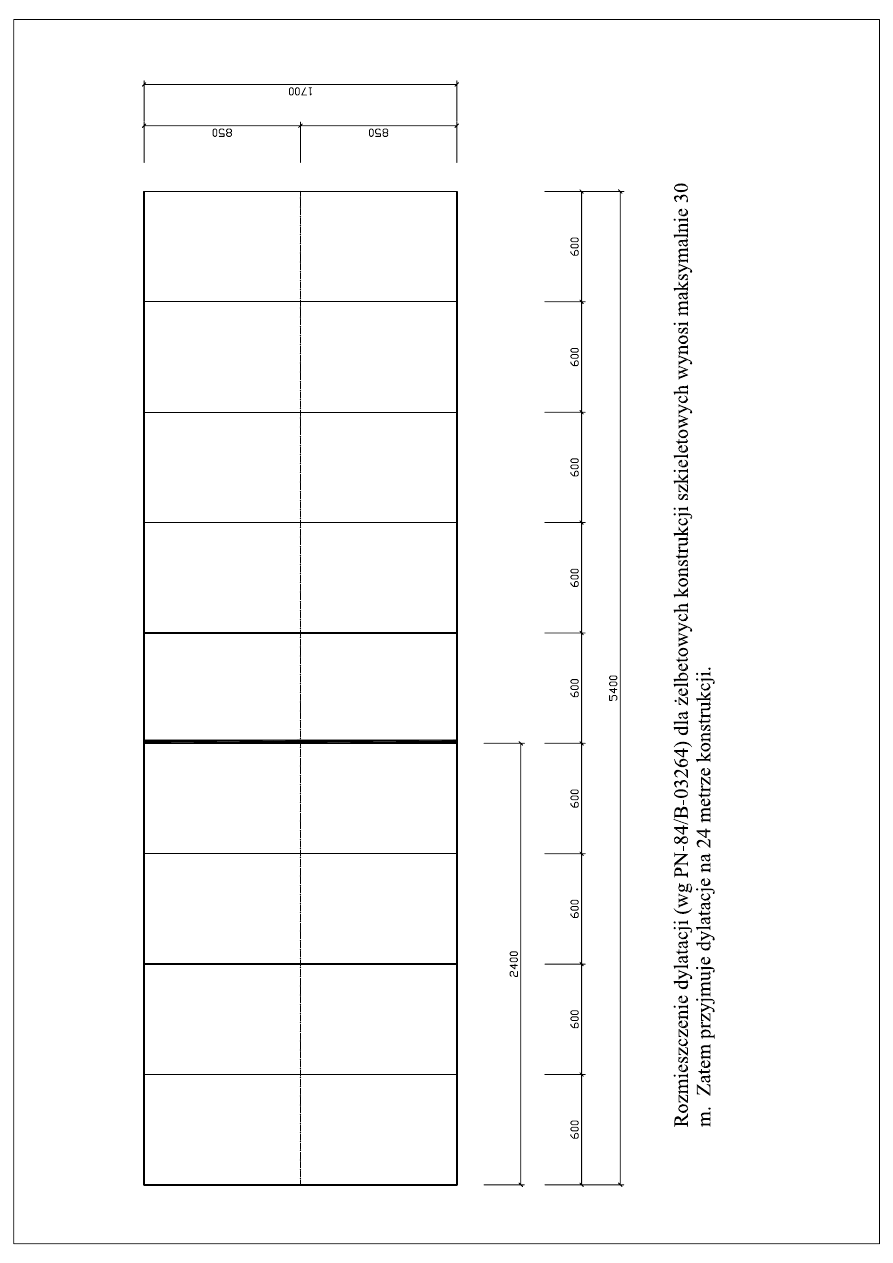
Budynek halowy, przemysłowy. Obiekt o konstrukcji ramowej. Długość obiektu
ramowego wynosi 54,0m, szerokość 17,0m w osiach słupów. Obiekt składa się z 10
ram żelbetowych w odstępach 6,0m. Rama składa się z rygla górnego dwuspadowego
o nachyleniu 8% oraz dwóch rygli dolnych opartych na słupach. Stężenie obiektu
stanowią 4 belki żelbetowe.

1.4. Podstawowe dane geotechniczne

W poziomie posadowienia występują piaski średnie o stopniu zagęszczenia I

0,35.

Badania stanu wilgotności gruntu wykazały, że grunt jest mało wilgotny. Poziom wody
gruntowej znacznie poniżej poziomu posadowienia fundamentów.

1.5. Specyfikacja konstrukcyjno materiałowa

1.5.1. Przekrycie dachowe

Konstrukcję nośną przekrycia dachowego stanowi strop dachowy wykonany z
prefabrykowanych płyt kanałowych SP20 firmy Spiroll. Izolację stanowi warstwa
folii, płyty styropianowe gr.8cm kryte papą oraz podwójna warstwa papy
termozgrzewalnej.

1.5.2. Konstrukcja stropów między‐kondygnacyjnych

Strop wykonany z prefabrykowanych płyt kanałowych SP26.5 firmy Spiroll.
Warstwę wierzchnią stanowi lastrico gr.4cm położone na gładzi cementowej
gr.4cm. Izolacja za pomocą foli, styropianu gr.6cm i warstwy papy.

3 |

S t r o n a

1.5.3. Konstrukcja ścian osłonowych hali

Na konstrukcję ścian zewnętrznych hali wybrano mur z bloczków z betonu
komórkowego gr.25cm, obustronnie otynkowanych tynkiem cementowo‐
wapienny.

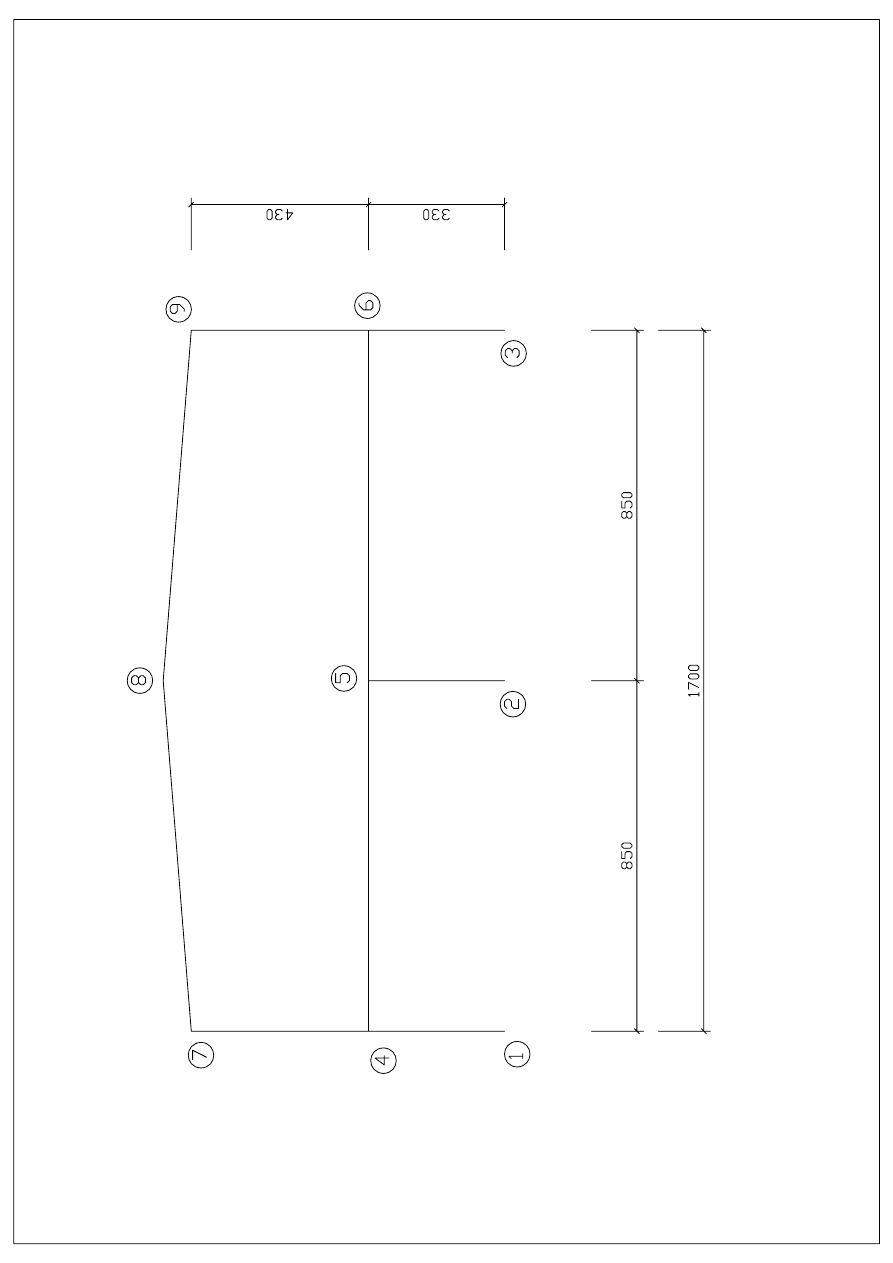
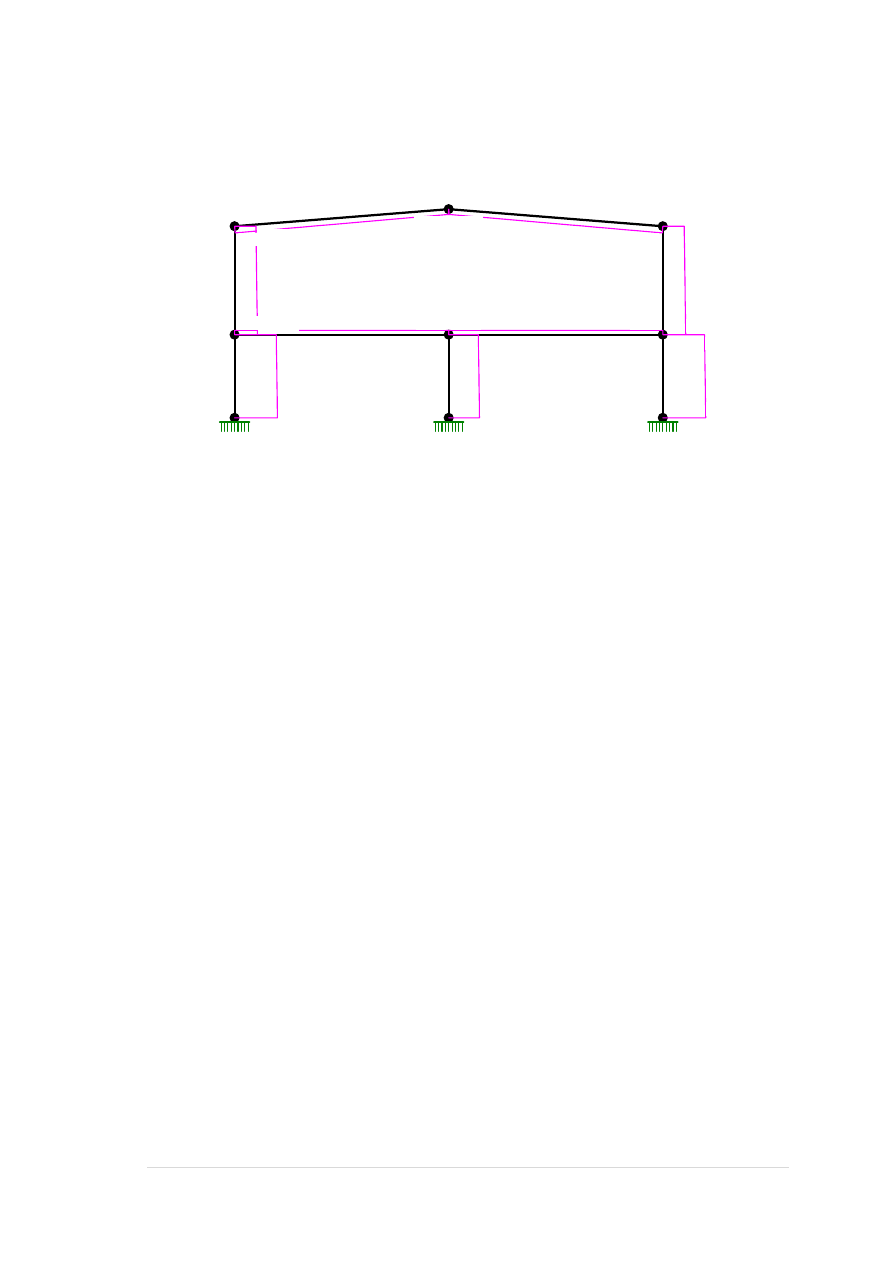
2. Schemat szkieletu hali oraz konstrukcja ramy.

6 |

S t r o n a

3. Zebranie obciążeń.

3.1. Zebranie obciążeń na poszczególne przekrycia poziome:

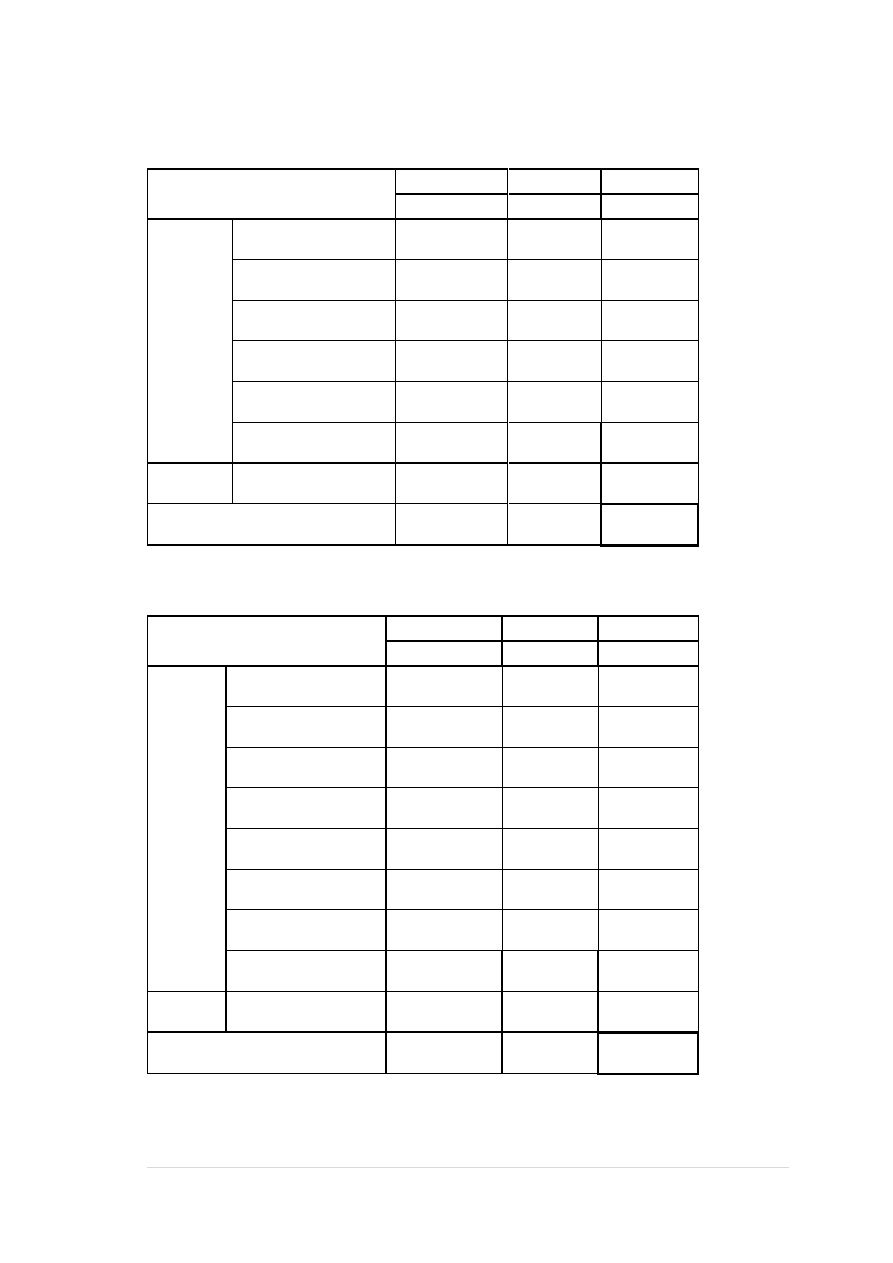
Stropodach

Rodzaj obciążenia

Obc.charakt.

Wsp.bezp.

Obc.oblicz.

[kN/m

]

[‐]

[kN/m

]

obci

ąż

enia

sta

łe

3xpapa gr.0.2cm

3*11*0,002

0,066

1,2

0,08

styropian gr.8cm

0,45*0,08

0,036

1,2

0,04

płyta kan.Spiroll Sp20

2,63

1,1

2,89

płytaG‐K gr.1,2cm

12*0,012

0,144

1,3

0,19

gładź gipsowa gr.1,5cm

12*0,015

0,18

1,3

0,23

RAZEM:

3,056

3,44

2)zmienne

śnieg: S=Q

1,46

1,4

2,04

RAZEM:

4,516

5,48

=0,7kN/m

α=8

C=1,2((60-α)/30)=2,08

Strop między‐kondygnacyjny

Rodzaj obciążenia

Obc.charakt.

Wsp.bezp.

Obc.oblicz.

[kN/m

]

[‐]

[kN/m

]

obci

ąż

enia

sta

łe

lastrico gr.4cm

22*0,04

0,88

1,3

1,14

gładź cementowa

gr.4cm 21*0,04

0,84

1,3

1,09

folia gr.0,2cm

11*0,002

0,022

1,2

0,03

styropian gr.6cm

0,45*0,06

0,027

1,2

0,03

papa o gr.0,2cm

11*0,002

0,022

1,2

0,03

płyta kan. Spiroll Sp26.5

3,65

1,1

4,02

tynk gr.1cm

19*0,01

0,19

1,3

0,25

RAZEM:

5,631

6,58

2)użytk.

7,7

1,2

9,24

RAZEM:

13,33

15,82

7 |

S t r o n a

3.2. Zebranie obciążeń na poszczególne rygle:

obciążenie rygli stropodachu

Rodzaj obciążenia

Obc.charakt.

Wsp.bezp.

Obc.oblicz.

[kN/m]

[‐]

[kN/m]

obci

ąż

enia

sta

łe

3xpapa gr.0.2cm

3*11*0,002*6

0,40

1,2

0,48

styropian gr.8cm

0,45*0,08*6

0,22

1,2

0,26

płyta kan.Spiroll Sp20

15,78

1,1

17,36

płytaG‐K gr.1,2cm

12*0,012*6

0,86

1,3

1,12

gładź gipsowa gr.1,5cm

12*0,015*6

1,08

1,3

1,40

RAZEM:

18,34

20,62

2)zmienne

śnieg: S=Q

*C *6

8,76

1,4

12,26

RAZEM:

27,10

32,88

=0,7kN/m

α=8

C=1,2((60-α)/30)=2,08

obciążenie rygli między‐kondygnacyjnych

Rodzaj obciążenia

Obc.charakt.

Wsp.bezp.

Obc.oblicz.

[kN/m]

[‐]

[kN/m]

obci

ąż

enia

sta

łe

lastrico gr.4cm

22*0,04*6

5,28

1,3

6,86

gładź cementowa

gr.4cm 21*0,04*6

5,04

1,3

6,55

folia gr.0,2cm

11*0,002*6

0,13

1,2

0,16

styropian gr.6cm

0,45*0,06*6

0,16

1,2

0,19

papa o gr.0,2cm

11*0,002*6

0,13

1,2

0,16

płyta kan. Spiroll Sp26.5

21,90

1,1

24,09

tynk gr.1cm

19*0,01*6

1,14

1,3

1,48

RAZEM:

33,79

39,50

2)użytk.

46,20

1,2

55,44

RAZEM:

79,99

94,94

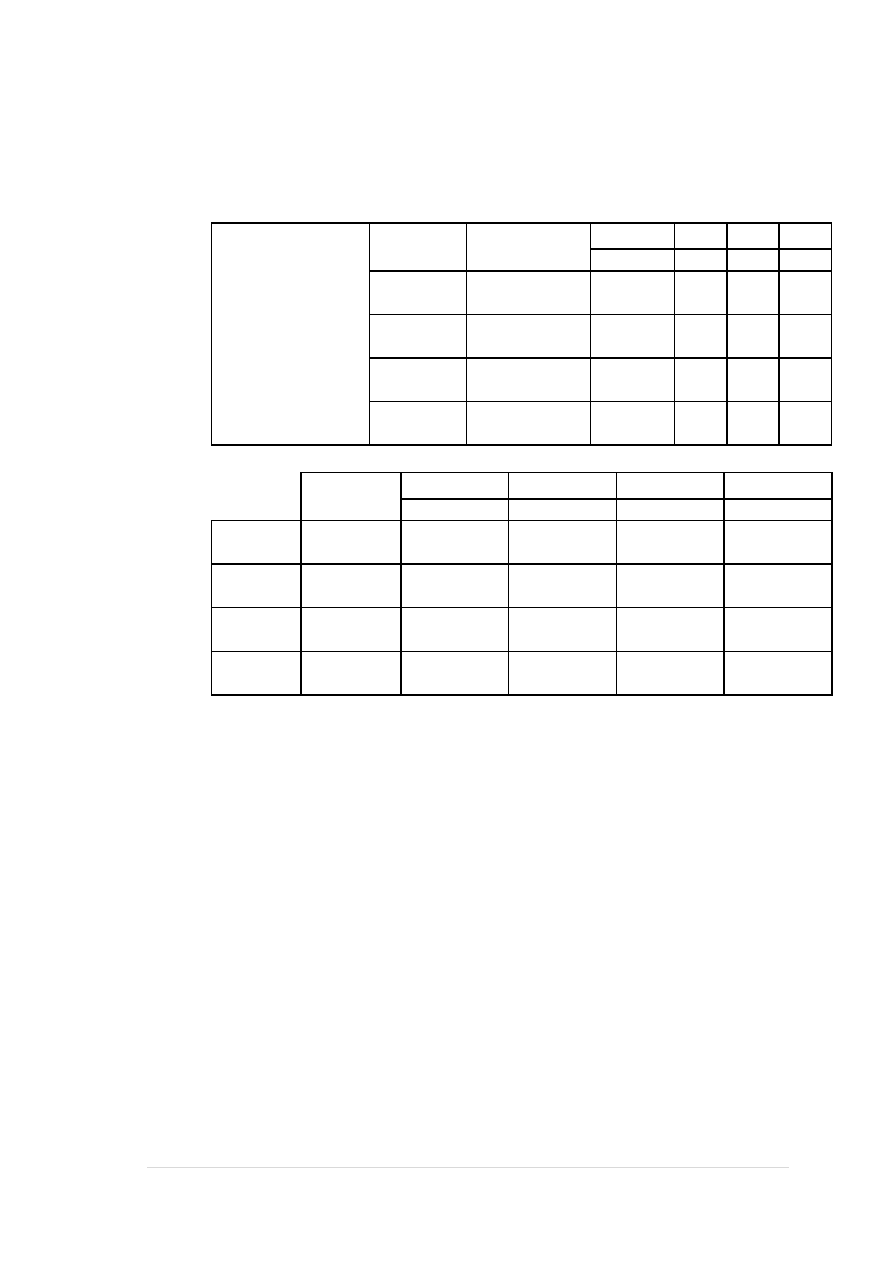
8 |

S t r o n a

3.3. Zebranie obciążeń wiatrowych:

I strefa obciążenia; Teren typu B

[kN/m

]

[‐]

kierunek działania:

→

element

obiektu

0,7

‐1,53

‐0,4

1,8

0,25

0,8

Rodzaj obciążenia

ściana

nawietrzna

połać

nawietrzna

połać

zawietrzna

ściana

zawietrzna

parcie wiatru

*C*β

ssanie wiatru

*C*β

ssanie wiatru

*C*β

ssanie wiatru

*C*β

Obc.charakt

Wsp.bezp.

Obc.oblicz.

Obc.obliczx6m

[kN/m

]

[‐]

[kN/m

]

[kN/m]

‐0,19

1,97

‐4,30

‐1,12

‐0,14

1,3

0,25

‐0,55

0,33

‐0,72

ściana

zawietrzna

Rodzaj

obciążenia

parcie wiatru

*C*β

ssanie wiatru

*C*β

ssanie wiatru

*C*β

ssanie wiatru

*C*β

ściana

nawietrzna

połać

nawietrzna

połać

zawietrzna

9 |

S t r o n a

4. Przyjęcie przekrojów projektowanych elementów:

Zakładam:
Stopień zbrojenia:

Klasa betonu:

B30

→

16,7

1,67

Klasa stali:

AIIIN

→

420

42,0 /

4.1. Rygiel nr 6 (węzeł 4‐5), rygiel nr 7 (węzeł 5‐6):

97,94 8,5

884,52

0,6

0,85

0,7 884,52

619,16

61916

0,01

1,67

0,251

0,5

0,5 0,251

0,875

0,251 0,875

0,220

61916

1,67 35 0,22

69,4

Przyjmuję:

Sprawdzenie ugięcia:

l

δ δ

250

850
250

3,4

gdy l

6,0m

200

3,4

850

0,8

gdy σ

250MPa

250

281,3

0,88

ςdA

61916

0,85 86 30,1

28,13kN cm

⁄

281,3MPa

ρdb

0,01 86 35

30,1cm

850

9,88

0,8 0,88 19

13,37 //warunek spełniony

94,94

10 |

S t r o n a

4.2. Rygiel nr 89 (węzeł 7‐9):

1186,53

1189,53

0,6

0,85

0,7 1189,53

832,67

83267,1

0,01

1,67

0,251

0,5 ξ

0,5 0,251

0,875

0,251 0,875

0,220

b A

83267,1

1,67 35 0,22

80,47cm

Przyjmuję:

Sprawdzenie ugięcia:

l

δ δ

250

1700

250

6,8

gdy l

6,0m

200

6,8

1700

0,8

gdy σ

250MPa

250

250
208

1,19

ςdA

83267,1

0,85 116 40,6

20,8kN cm

⁄

208,0MPa

ρdb

0,01 116 35

40,6cm

1700

116

14,65

0,8 1,19 19

18,08 //warunek spełniony

20,62

12,26

20,62

12,26

11 |

S t r o n a

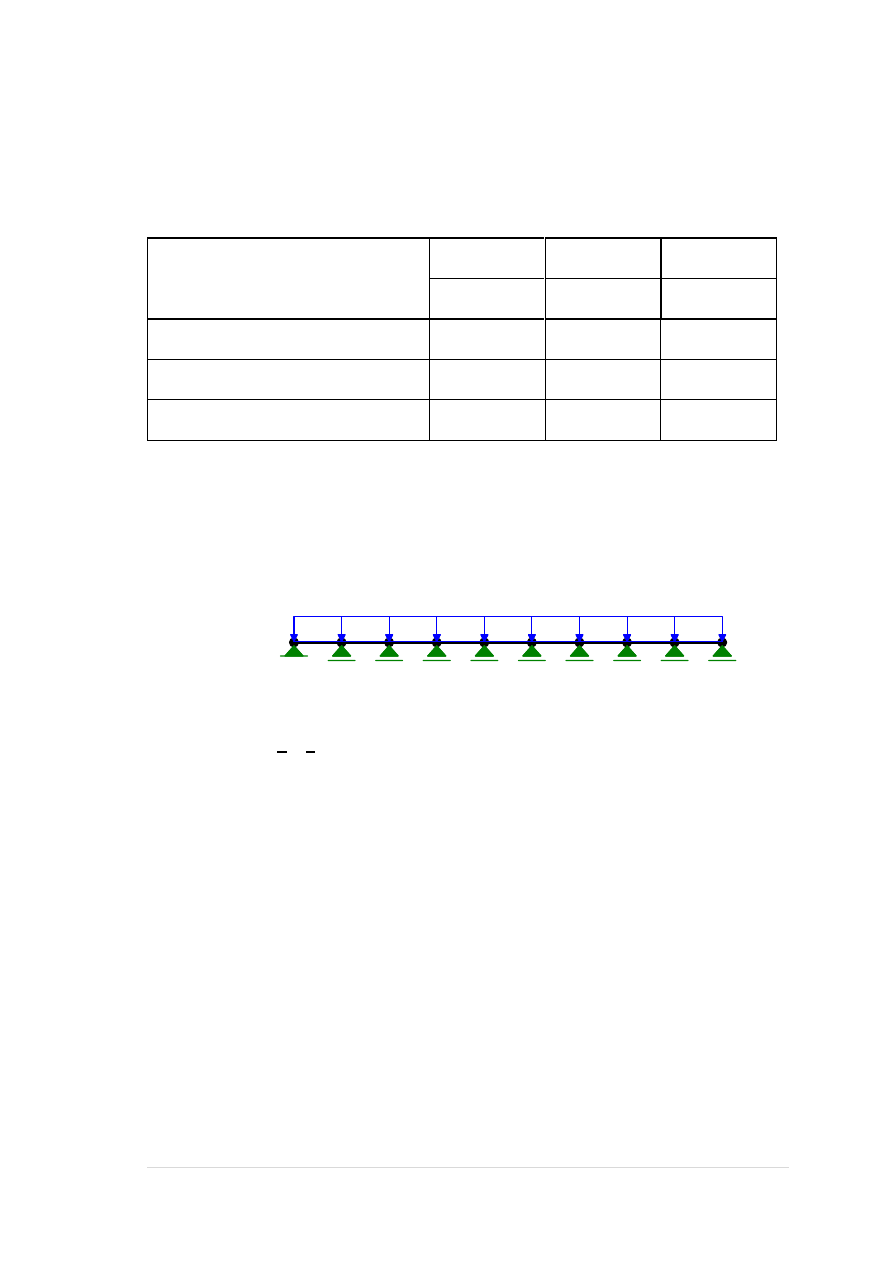
5. Przyjęcie belek stężeniowych i obciążenie nimi słupów:

5.1. Stężenie dolne

5.1.1. Zebranie obciążeń belki stężeniowej

Rodzaj obciążenia

Obc.charakt.

Wsp.bezp.

Obc.oblicz.

[kN/m]

[‐]

[kN/m]

mur z bloczków z betonu komórk. gr. 25cm

0,24m*3,5m*9,0kN/m

7,56

1,1

8,32

obustronny tynk cementowo‐wapienny

2*0,015m*3,5m*19,0kN/m

2,00

1,3

2,59

ciężar własny belki żelbetowej

0,3m*0,5m*25kN/m

3,75

1,1

4,13

RAZEM:

13,31

15,03

5.1.2. Reakcja podporowa belki i moment wywołany jej mimośrodem

1,1

15,03

1,1

99,20

0,15

14,88

//wart. e z rys.3 ‐ str.13

15,03

12 |

S t r o n a

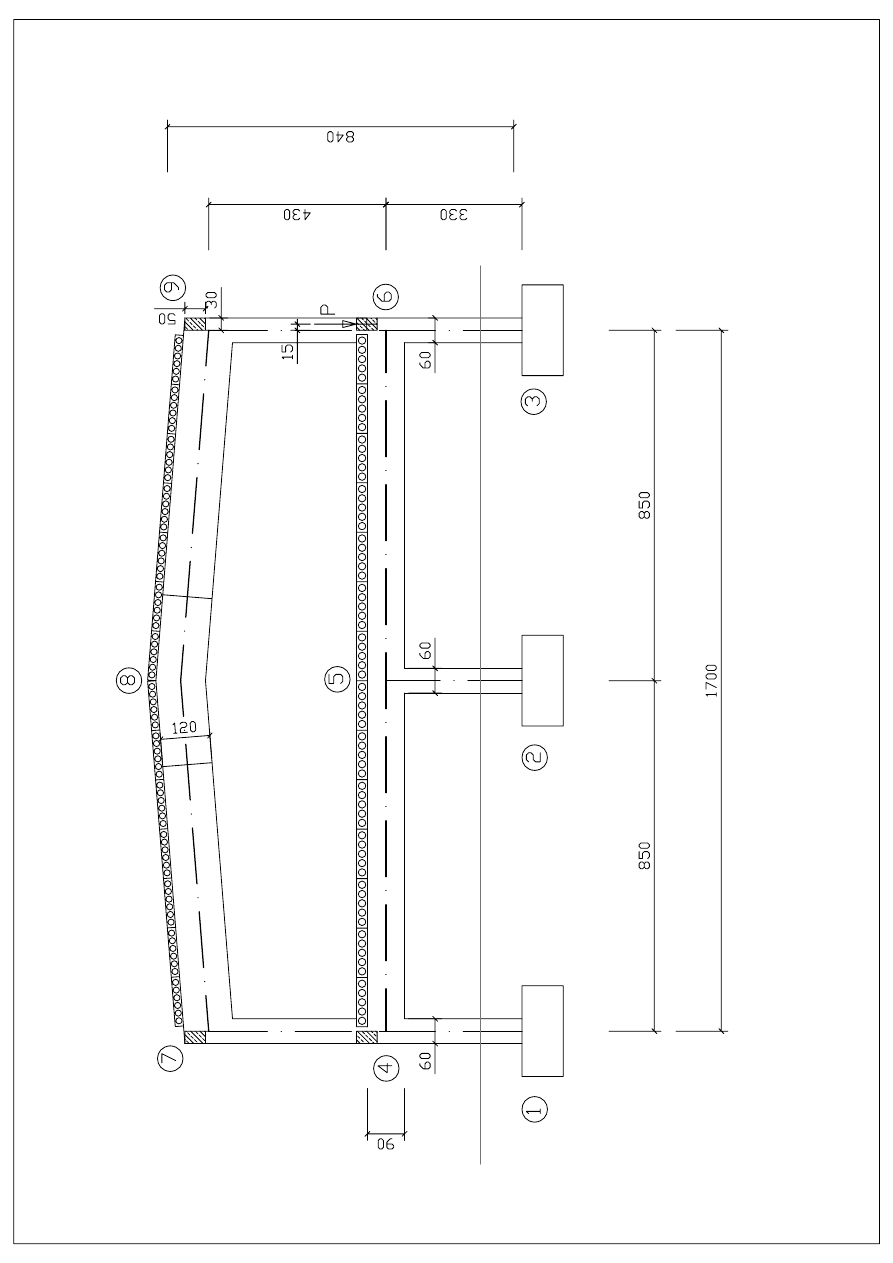
5.2. Stężenie górne

5.2.1. Zebranie obciążeń belki stężeniowej

Rodzaj obciążenia

Obc.charakt.

Wsp.bezp.

Obc.oblicz.

[kN/m]

[‐]

[kN/m]

płyta kanałowa Spiroll SP20

1,2m*2,63kN/m

3,16

1,3

4,10

ciężar własny belki żelbetowej

0,3m*0,5m*25kN/m

3,75

1,1

4,13

RAZEM:

6,91

8,23

5.2.2. Reakcja podporowa belki i moment wywołany jej mimośrodem

1,1

8,23

1,1

54,32

0,15

8,15

//wart. e z rys.3 ‐ str.13

8,23

14 |

S t r o n a

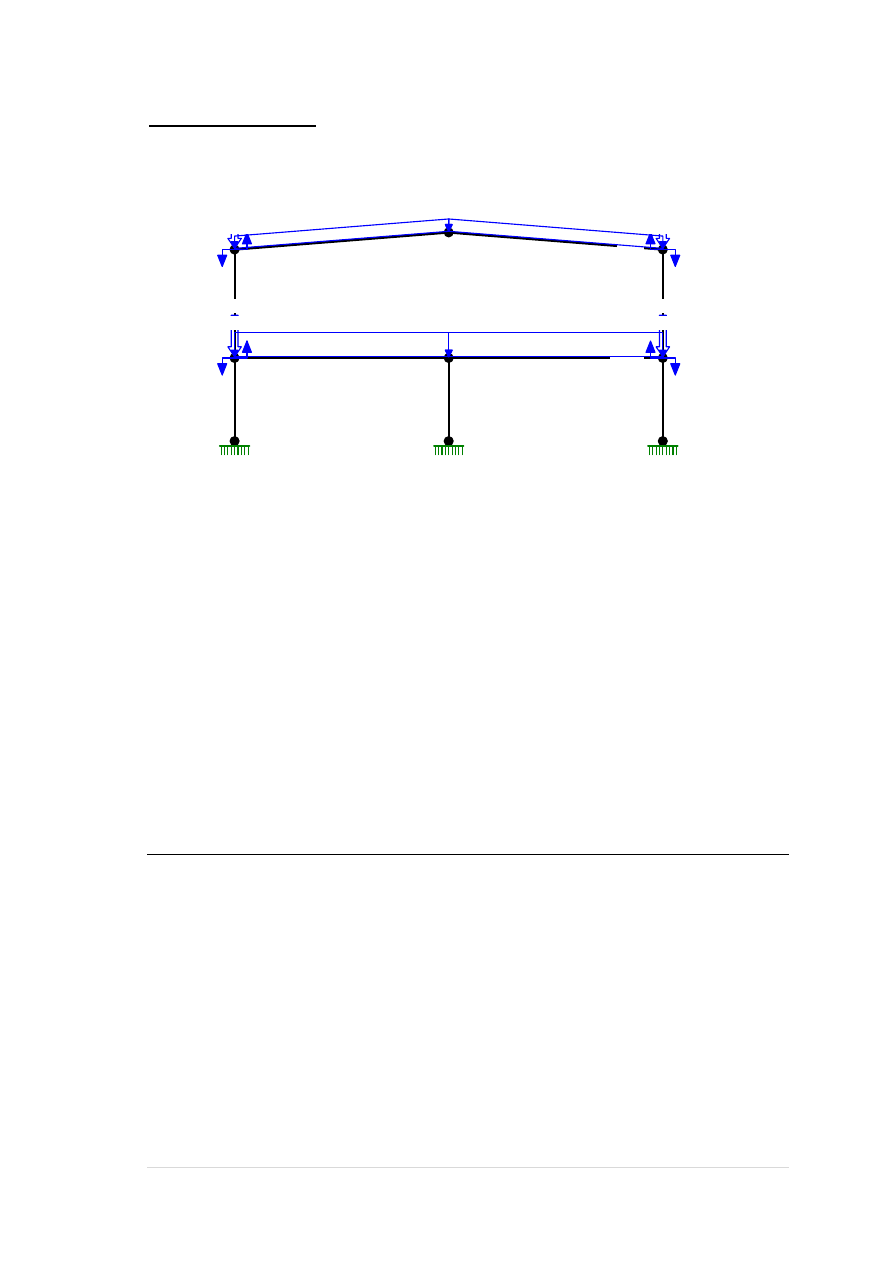
6. Zestawienie poszczególnych obciążeń oraz kombinatoryka obciążeń:

15 |

S t r o n a

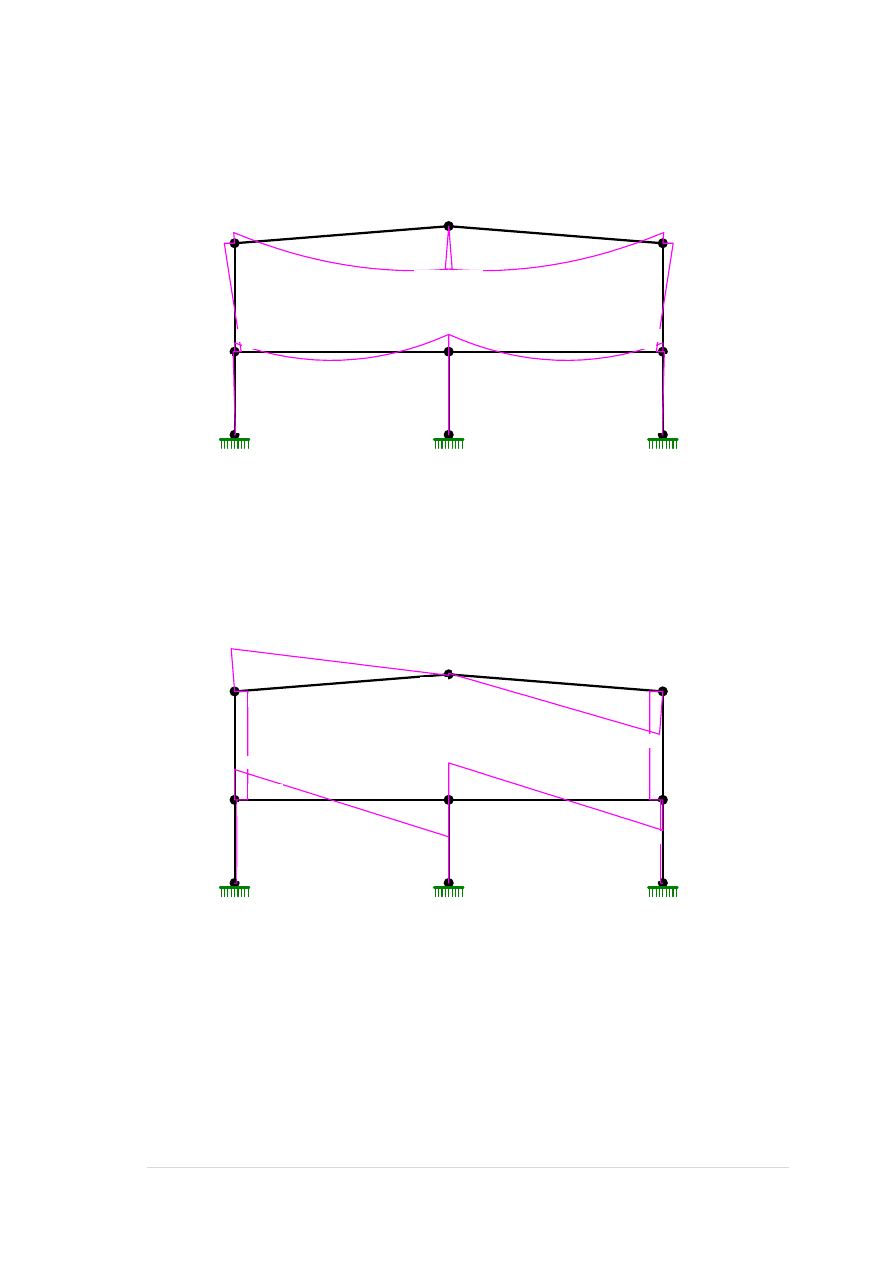
Obciążenia stałe A:

OBCIĄŻENIA: ([kN],[kNm],[kN/m])
------------------------------------------------------------------

Pręt: Rodzaj: Kąt: P1(Tg): P2(Td): a[m]: b[m]:

------------------------------------------------------------------
Grupa: A "obciążenia stałe" Stałe γf= 1,00

4 Skupione 0,0 54,32 4,30

4 Skupione 0,0 99,20 0,00

4 Moment 8,15 4,30

4 Moment 14,88 0,00

5 Skupione 0,0 54,32 4,30

5 Skupione 0,0 99,20 0,00

5 Moment -8,15 4,30

5 Moment -14,88 0,00

6 Liniowe 0,0 39,50 39,50 0,00 8,50

7 Liniowe 0,0 39,50 39,50 0,00 8,50

8 Liniowe 0,0 20,62 20,62 0,00 8,53

9 Liniowe 0,0 20,62 20,62 0,00 8,53

==================================================================

W Y N I K I

Teoria I-go rzędu
==================================================================

OBCIĄŻENIOWE WSPÓŁ. BEZPIECZ.:
------------------------------------------------------------------
Grupa: Znaczenie: ψd: γf:

------------------------------------------------------------------

Ciężar wł. 1,00

A -"obciążenia stałe" Stałe 1,00

------------------------------------------------------------------

54,32

99,20

8,15

14,88

54,32

99,20

-8,15

-14,88

39,50

20,62

16 |

S t r o n a

MOMENTY:

TNĄCE:

29,10

-15,58

29,10

-15,58

-29,10

15,58

-29,10

130,25

-204,63

130,25

-204,63

-130,25

204,63

-130,25

-174,23

-340,37

171,76

-340,37 -340,37

-174,23

171,76

-340,37

-212,78

846,84

-212,78

846,84

-212,78

846,84

-212,78

-13,54

13,54

-77,88

77,88

180,46

-219,55

180,46

-219,55

219,55

-180,46

219,55

-180,46

254,74

-6,21

254,74

-6,21

6,21

-254,74

6,21

-254,74

17 |

S t r o n a

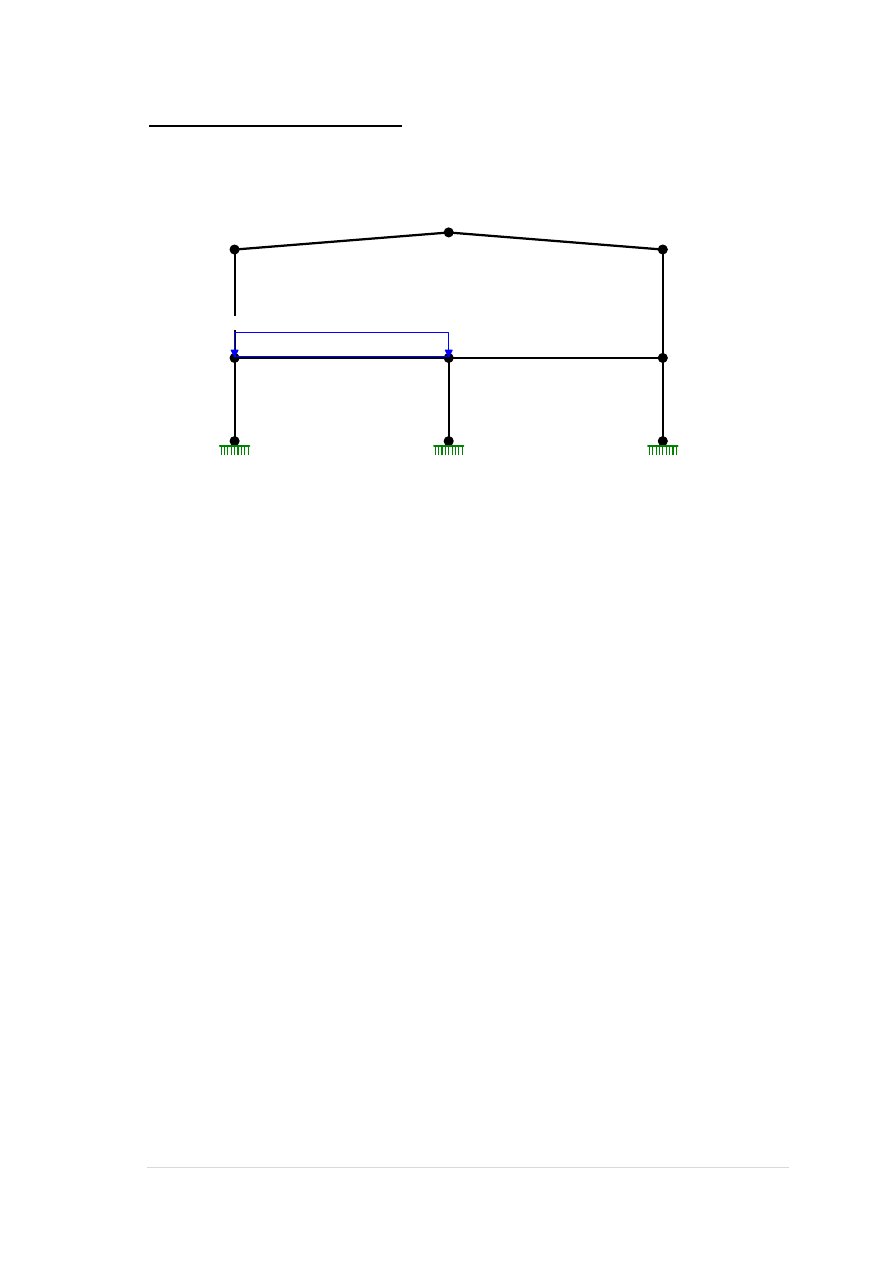
NORMALNE:

SIŁY PRZEKROJOWE:

T.I rzędu

Obciążenia obl. dłg.: Ciężar wł.+A

------------------------------------------------------------------

Pręt: x/L: x[m]: M[kNm]: Q[kN]: N[kN]:

------------------------------------------------------------------

1 0,00 0,000 29,10 -13,54 -617,43

1,00 3,300 -15,58 -13,54 -634,07

2 0,00 0,000 -0,00 0,00 -439,10

1,00 3,300 0,00 0,00 -455,73

3 0,00 0,000 -29,10 13,54 -617,43

1,00 3,300 15,58 13,54 -634,07

4 0,00 0,000 130,25 -77,88 -337,78

1,00 4,300 -204,63 -77,88 -316,10

5 0,00 0,000 -130,25 77,88 -337,78

1,00 4,300 204,63 77,88 -316,10

6 0,00 0,000 -174,23 180,46 64,34

0,45 3,818 171,76* 0,77 64,34
1,00 8,500 -340,37 -219,55 64,34

7 0,00 0,000 -340,37 219,55 64,34

0,55 4,682 171,76* -0,77 64,34
1,00 8,500 -174,23 -180,46 64,34

8 0,00 0,000 -212,78 254,74 -98,51

0,98 8,327 847,47* -0,09 -78,12
1,00 8,527 846,84 -6,21 -77,63

9 0,00 0,000 846,84 6,21 -77,63

0,02 0,200 847,47* 0,09 -78,12
1,00 8,527 -212,78 -254,74 -98,51

------------------------------------------------------------------

* = Wartości ekstremalne

-617,43

-634,07

-617,43

-634,07

-439,10

-455,73

-439,10

-455,73

-617,43

-634,07

-617,43

-634,07

-337,78

-316,10

-337,78

-316,10

-337,78

64,34

-98,51

-77,63

-98,51

-77,63

-98,51

-77,63

-98,51

18 |

S t r o n a

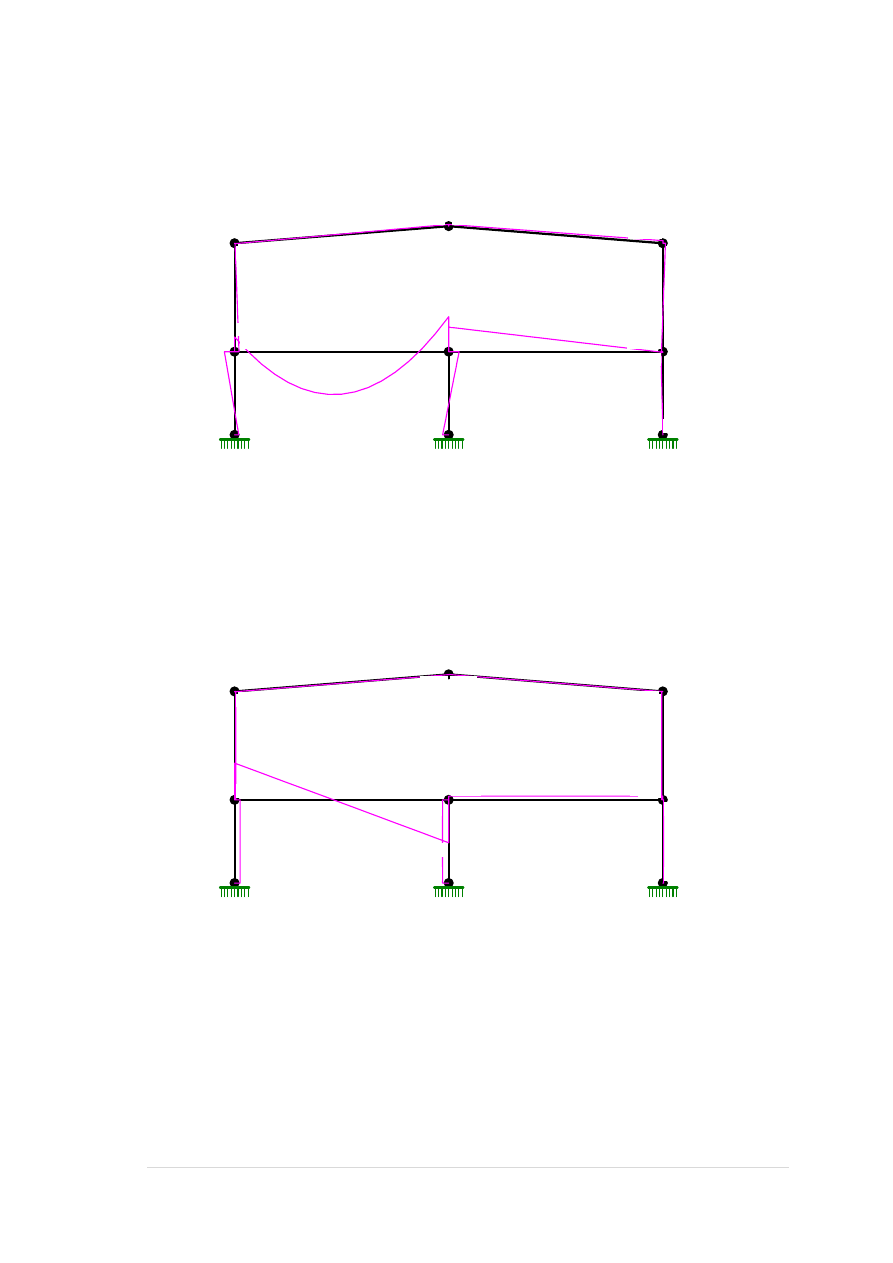
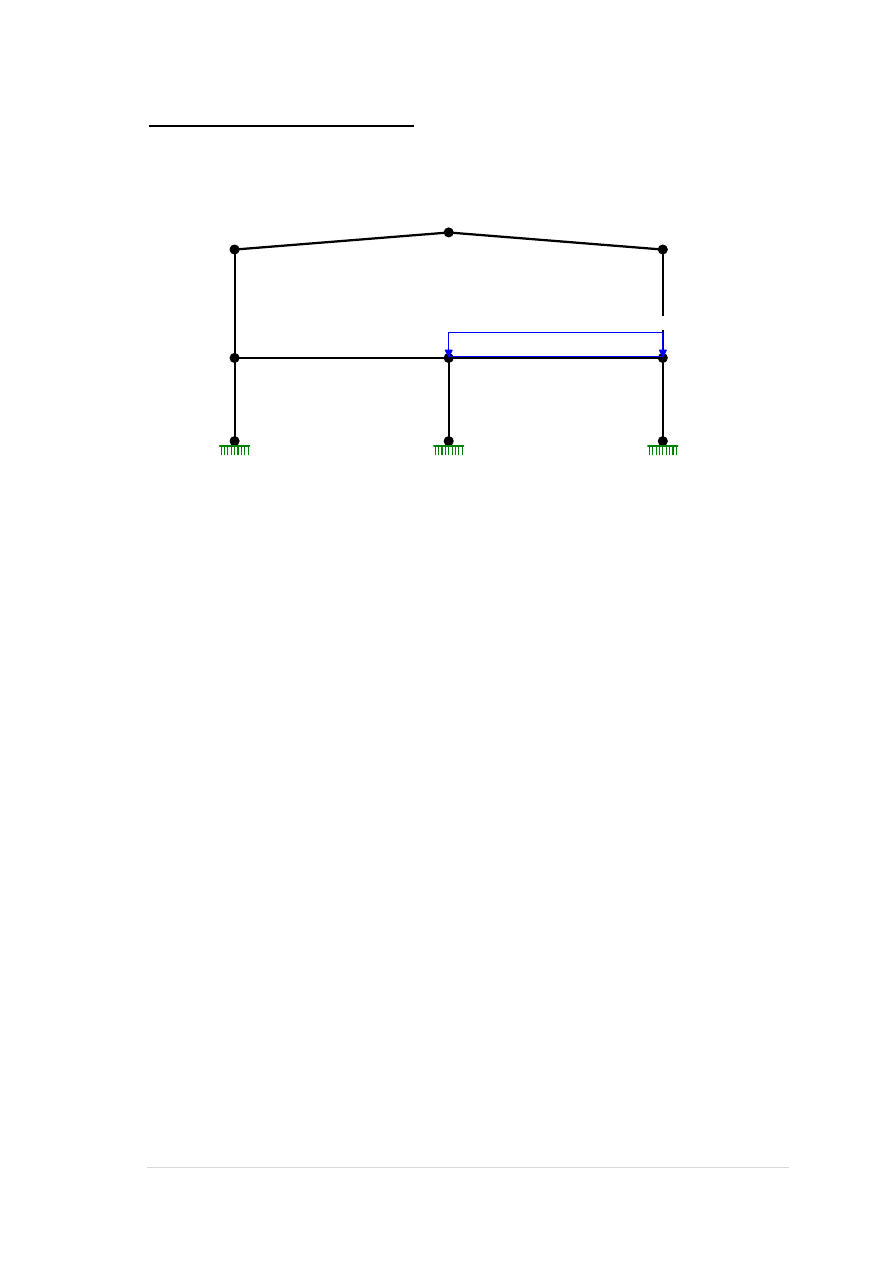
Obciążenia użytkowe lewe B:

OBCIĄŻENIA: ([kN],[kNm],[kN/m])
------------------------------------------------------------------

Pręt: Rodzaj: Kąt: P1(Tg): P2(Td): a[m]: b[m]:

------------------------------------------------------------------
Grupa: B "użytkowe lewe" Zmienne γf= 1,20

6 Liniowe 0,0 46,20 46,20 0,00 8,50

------------------------------------------------------------------

==================================================================

W Y N I K I

Teoria I-go rzędu
==================================================================

OBCIĄŻENIOWE WSPÓŁ. BEZPIECZ.:
------------------------------------------------------------------
Grupa: Znaczenie: ψd: γf:

------------------------------------------------------------------

B -"użytkowe lewe" Zmienne 1 1,00 1,20

------------------------------------------------------------------

46,20

19 |

S t r o n a

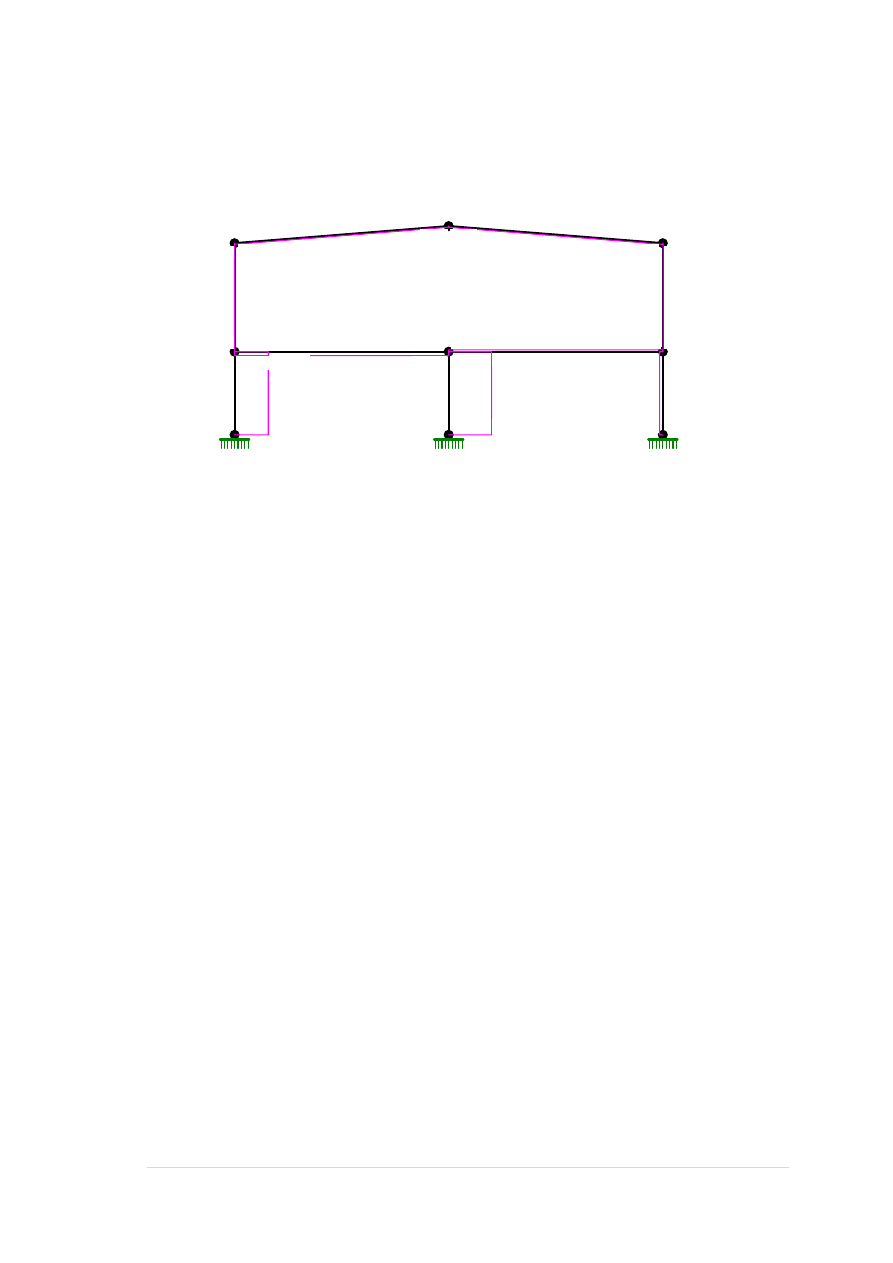
MOMENTY:

TNĄCE:

76,44

-31,08

76,44

-31,08

-77,45

45,46

-77,45

14,87

-0,52

14,87

-0,52

32,89

3,25

32,89

3,25

-10,40

19,25

-10,40

-109,33

-260,40

318,68

-260,40

-182,94

4,48

-182,94

3,25

-12,69

3,25

-12,69 -12,69

-19,25

-12,69

-19,25

-32,58

37,25

-4,66

-6,89

6,89

217,85

-253,39

217,85

-253,39

22,05

-1,87

-0,77

20 |

S t r o n a

NORMALNE:

SIŁY PRZEKROJOWE:

T.I rzędu

Obciążenia obl. dłg.: B

------------------------------------------------------------------

Pręt: x/L: x[m]: M[kNm]: Q[kN]: N[kN]:

------------------------------------------------------------------

1 0,00 0,000 76,44 -32,58 -216,52

1,00 3,300 -31,08 -32,58 -216,52

2 0,00 0,000 -77,45 37,25 -275,44

1,00 3,300 45,46 37,25 -275,44

3 0,00 0,000 14,87 -4,66 20,73

1,00 3,300 -0,52 -4,66 20,73

4 0,00 0,000 32,89 -6,89 1,32

1,00 4,300 3,25 -6,89 1,32

5 0,00 0,000 -10,40 6,89 -1,32

1,00 4,300 19,25 6,89 -1,32

6 0,00 0,000 -109,33 217,85 -25,69

0,46 3,918 318,68* 0,63 -25,69
1,00 8,500 -260,40 -253,39 -25,69

7 0,00 0,000 -182,94 22,05 11,56

1,00 8,500 4,48 22,05 11,56

8 0,00 0,000 3,25 -1,87 -6,77

1,00 8,527 -12,69 -1,87 -6,77

9 0,00 0,000 -12,69 -0,77 -6,98

1,00 8,527 -19,25 -0,77 -6,98

------------------------------------------------------------------

* = Wartości ekstremalne

-216,52

-275,44

20,73

1,32

-1,32

-25,69

11,56

-6,77

-6,98

21 |

S t r o n a

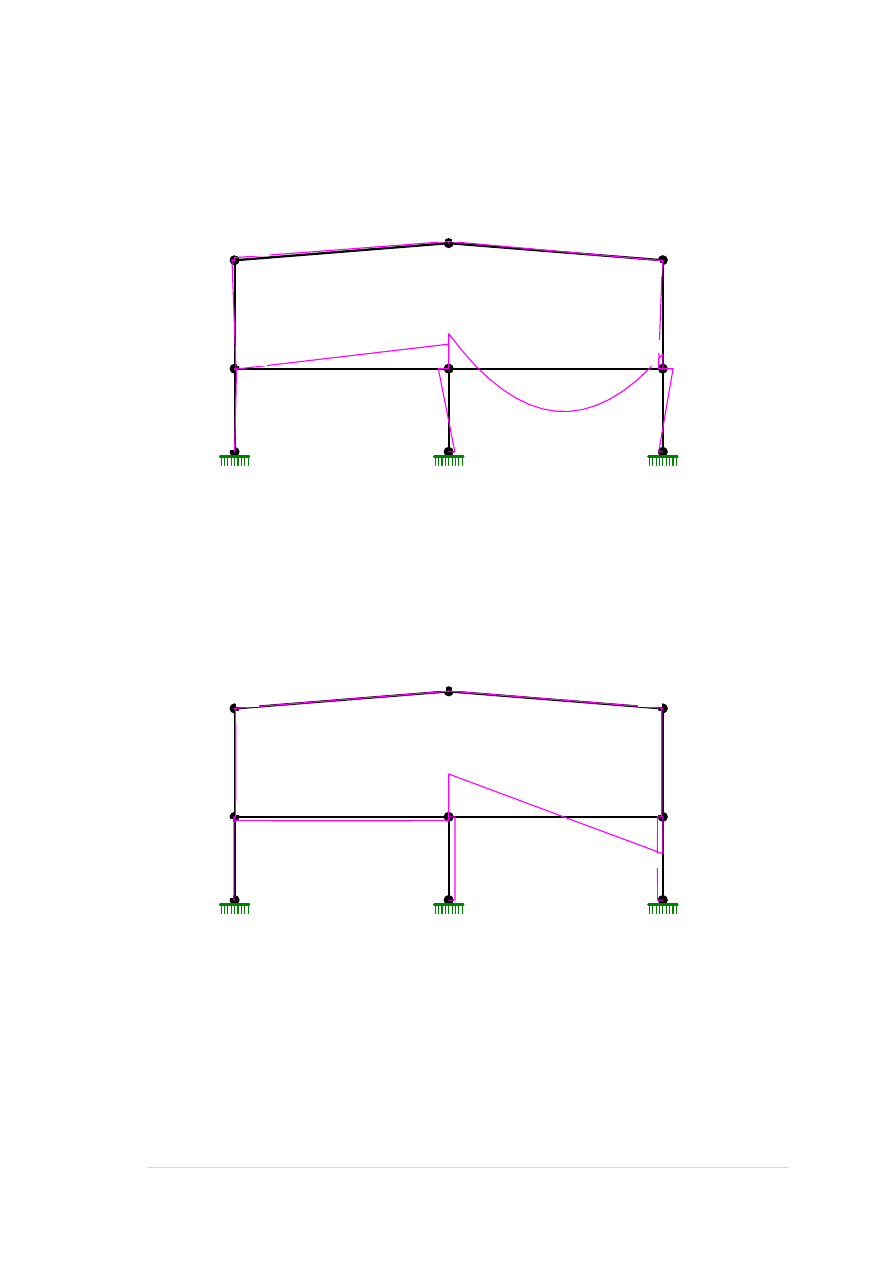
Obciążenie użytkowe prawe C:

OBCIĄŻENIA: ([kN],[kNm],[kN/m])
------------------------------------------------------------------

Pręt: Rodzaj: Kąt: P1(Tg): P2(Td): a[m]: b[m]:

------------------------------------------------------------------
Grupa: C "użytkowe prawe" Zmienne γf= 1,20

7 Liniowe 0,0 46,20 46,20 0,00 8,50

------------------------------------------------------------------

==================================================================

W Y N I K I

Teoria I-go rzędu
==================================================================

OBCIĄŻENIOWE WSPÓŁ. BEZPIECZ.:
------------------------------------------------------------------
Grupa: Znaczenie: ψd: γf:

------------------------------------------------------------------

C -"użytkowe prawe" Zmienne 1 1,00 1,20

------------------------------------------------------------------

46,20

22 |

S t r o n a

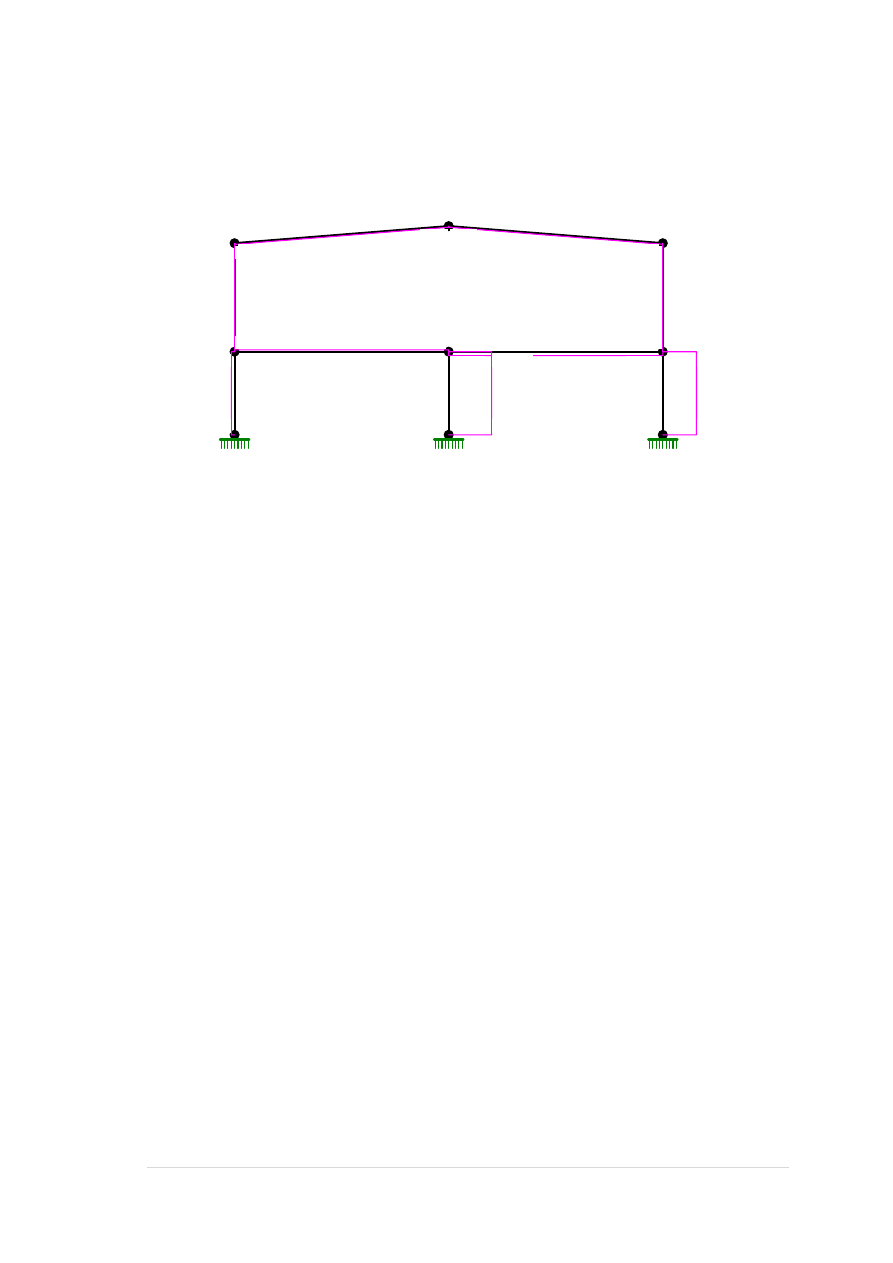
MOMENTY:

TNĄCE:

-14,87

0,52

-14,87

77,45

-45,46

77,45

-45,46

-76,44

31,08

-76,44

10,40

-19,25

10,40

-19,25

-32,89

-3,25

-32,89

4,48

-182,94

4,48

-182,94

-260,40

-109,33

318,67

-260,40

-19,25

-12,69

-19,25

-12,69

3,25

-12,69

4,66

-37,25

32,58

-6,89

6,89

-22,05

253,39

-217,85

253,39

-217,85

0,77

1,87

23 |

S t r o n a

NORMALNE:

SIŁY PRZEKROJOWE:

T.I rzędu

Obciążenia obl. dłg.: C

------------------------------------------------------------------

Pręt: x/L: x[m]: M[kNm]: Q[kN]: N[kN]:

------------------------------------------------------------------

1 0,00 0,000 -14,87 4,66 20,73

1,00 3,300 0,52 4,66 20,73

2 0,00 0,000 77,45 -37,25 -275,44

1,00 3,300 -45,46 -37,25 -275,44

3 0,00 0,000 -76,44 32,58 -216,52

1,00 3,300 31,08 32,58 -216,52

4 0,00 0,000 10,40 -6,89 -1,32

1,00 4,300 -19,25 -6,89 -1,32

5 0,00 0,000 -32,89 6,89 1,32

1,00 4,300 -3,25 6,89 1,32

6 0,00 0,000 4,48 -22,05 11,56

1,00 8,500 -182,94 -22,05 11,56

7 0,00 0,000 -260,40 253,39 -25,69

0,54 4,582 318,68* -0,63 -25,69
1,00 8,500 -109,33 -217,85 -25,69

8 0,00 0,000 -19,25 0,77 -6,98

1,00 8,527 -12,69 0,77 -6,98

9 0,00 0,000 -12,69 1,87 -6,77

1,00 8,527 3,25 1,87 -6,77

------------------------------------------------------------------

* = Wartości ekstremalne

20,73

-275,44

-216,52

-1,32

1,32

11,56

-25,69

-6,98

-6,77

24 |

S t r o n a

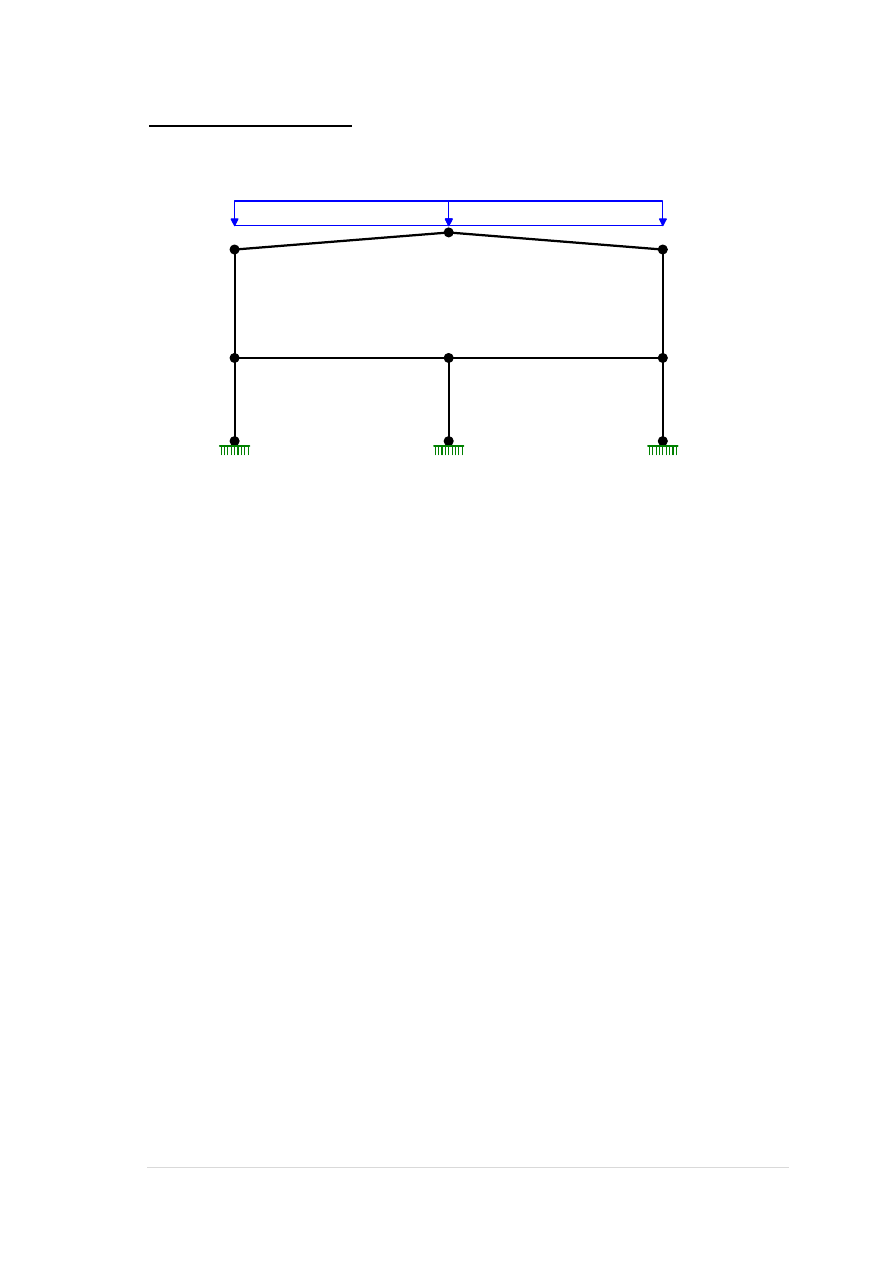
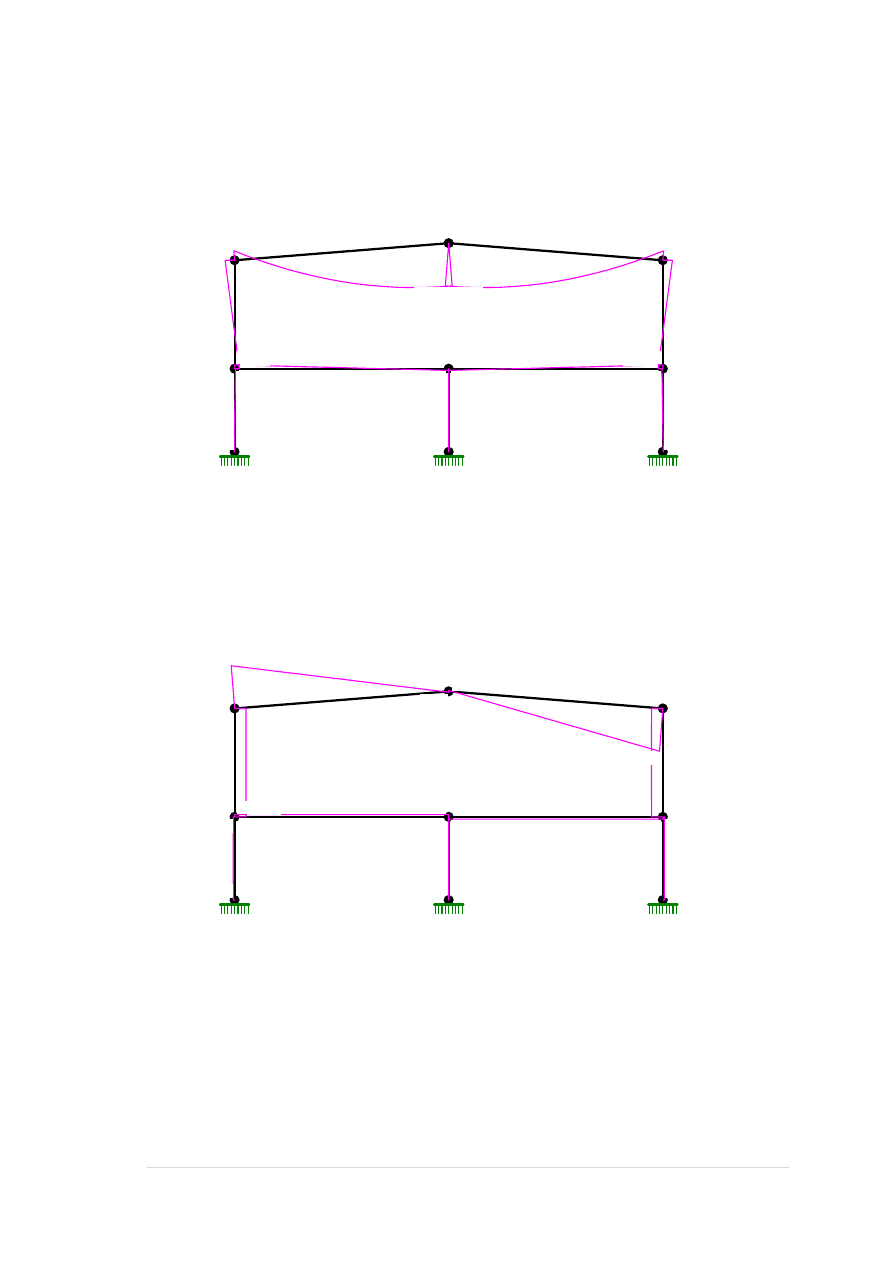
Obciążenie śniegiem D:

OBCIĄŻENIA: ([kN],[kNm],[kN/m])
------------------------------------------------------------------

Pręt: Rodzaj: Kąt: P1(Tg): P2(Td): a[m]: b[m]:

------------------------------------------------------------------
Grupa: D "śnieg" Zmienne γf= 1,40

8 Liniowe-Y 0,0 8,76 8,76 0,00 8,53

9 Liniowe-Y 0,0 8,76 8,76 0,00 8,53

------------------------------------------------------------------

==================================================================

W Y N I K I

Teoria I-go rzędu
==================================================================

OBCIĄŻENIOWE WSPÓŁ. BEZPIECZ.:
------------------------------------------------------------------
Grupa: Znaczenie: ψd: γf:

------------------------------------------------------------------

D -"śnieg" Zmienne 1 1,00 1,40

------------------------------------------------------------------

8,76

25 |

S t r o n a

MOMENTY:

TNĄCE:

-7,88

3,46

-7,88

7,88

-3,46

7,88

-3,46

38,64

-77,28

38,64

-77,28

-38,64

77,28

-38,64

-30,75

13,71

-30,75

13,71

-30,75

13,71

-30,75

-77,28

347,43

-77,28

347,43

-77,28

347,43

-77,28

3,44

-3,44

-26,96

26,96

5,23

-5,23

101,76

-2,15

101,76

-2,15

2,15

-101,76

2,15

-101,76

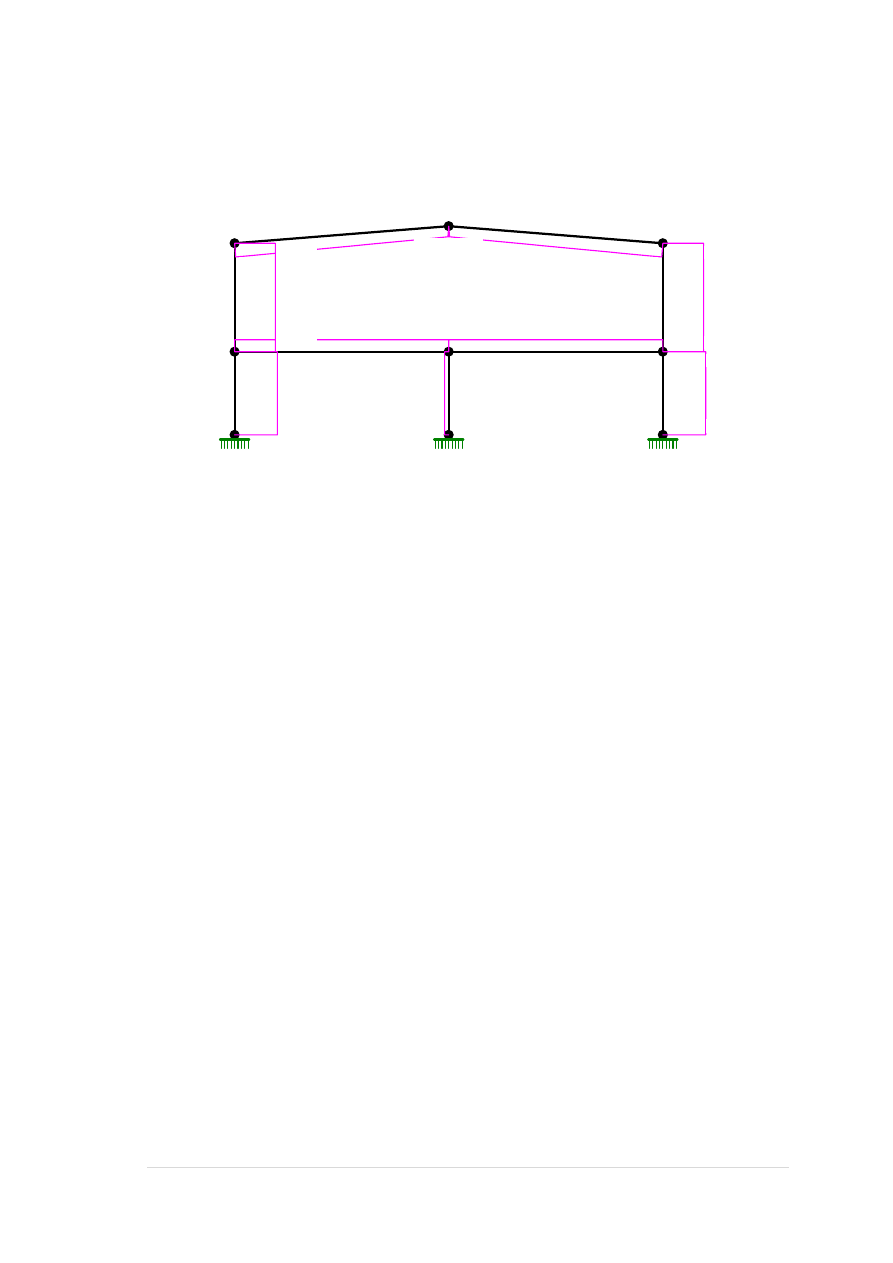
26 |

S t r o n a

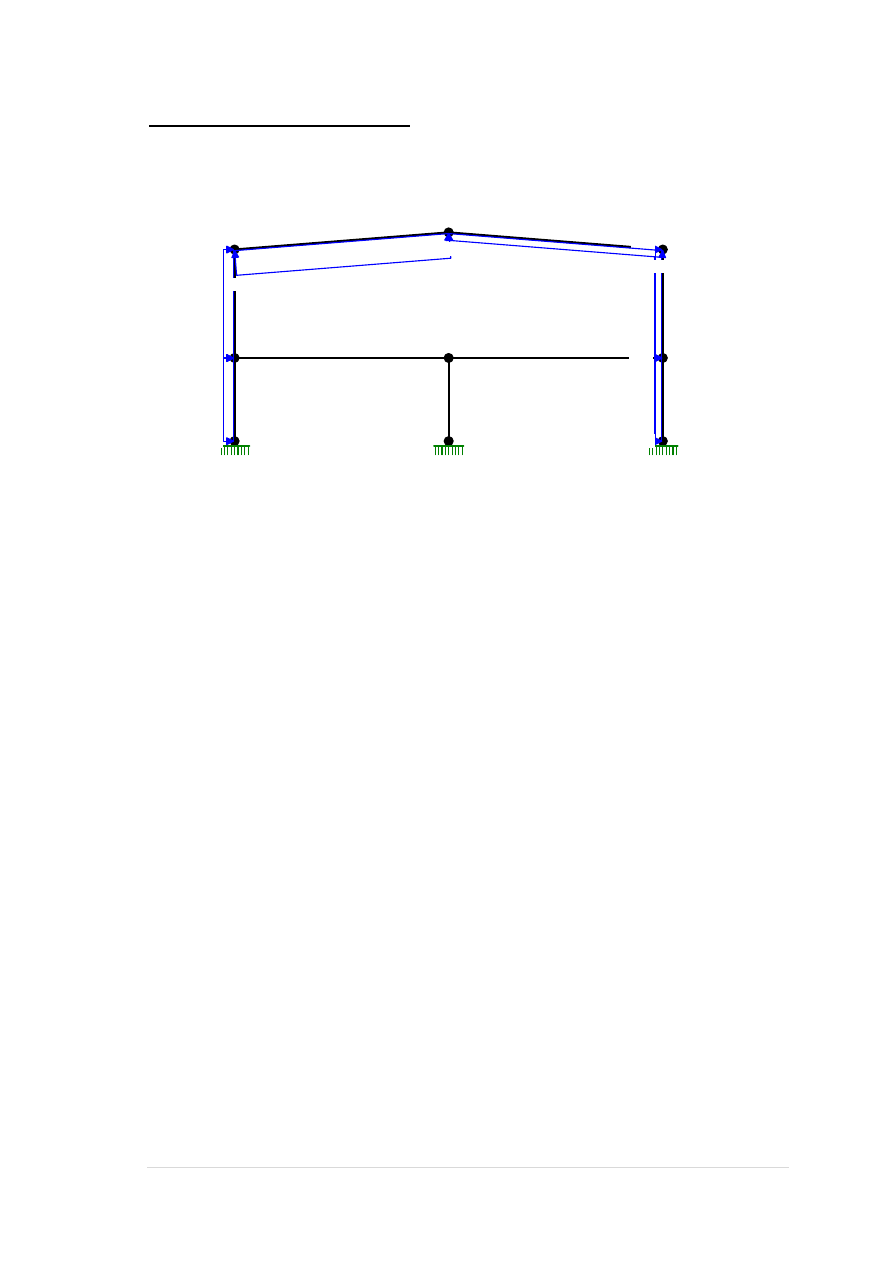
NORMALNE:

SIŁY PRZEKROJOWE:

T.I rzędu

Obciążenia obl. dłg.: D

------------------------------------------------------------------

Pręt: x/L: x[m]: M[kNm]: Q[kN]: N[kN]:

------------------------------------------------------------------

1 0,00 0,000 -7,88 3,44 -109,48

1,00 3,300 3,46 3,44 -109,48

2 0,00 0,000 -0,00 0,00 10,46

1,00 3,300 0,00 0,00 10,46

3 0,00 0,000 7,88 -3,44 -109,48

1,00 3,300 -3,46 -3,44 -109,48

4 0,00 0,000 38,64 -26,96 -104,24

1,00 4,300 -77,28 -26,96 -104,24

5 0,00 0,000 -38,64 26,96 -104,24

1,00 4,300 77,28 26,96 -104,24

6 0,00 0,000 -30,75 5,23 30,39

1,00 8,500 13,71 5,23 30,39

7 0,00 0,000 13,71 -5,23 30,39

1,00 8,500 -30,75 -5,23 30,39

8 0,00 0,000 -77,28 101,76 -35,18

0,98 8,361 347,62* -0,12 -27,03
1,00 8,527 347,43 -2,15 -26,87

9 0,00 0,000 347,43 2,15 -26,87

0,02 0,167 347,62* 0,12 -27,03
1,00 8,527 -77,28 -101,76 -35,18

------------------------------------------------------------------

* = Wartości ekstremalne

-109,48

10,46

-109,48

-104,24

30,39

-35,18

-26,87

-35,18

-26,87

-35,18

-26,87

-35,18

27 |

S t r o n a

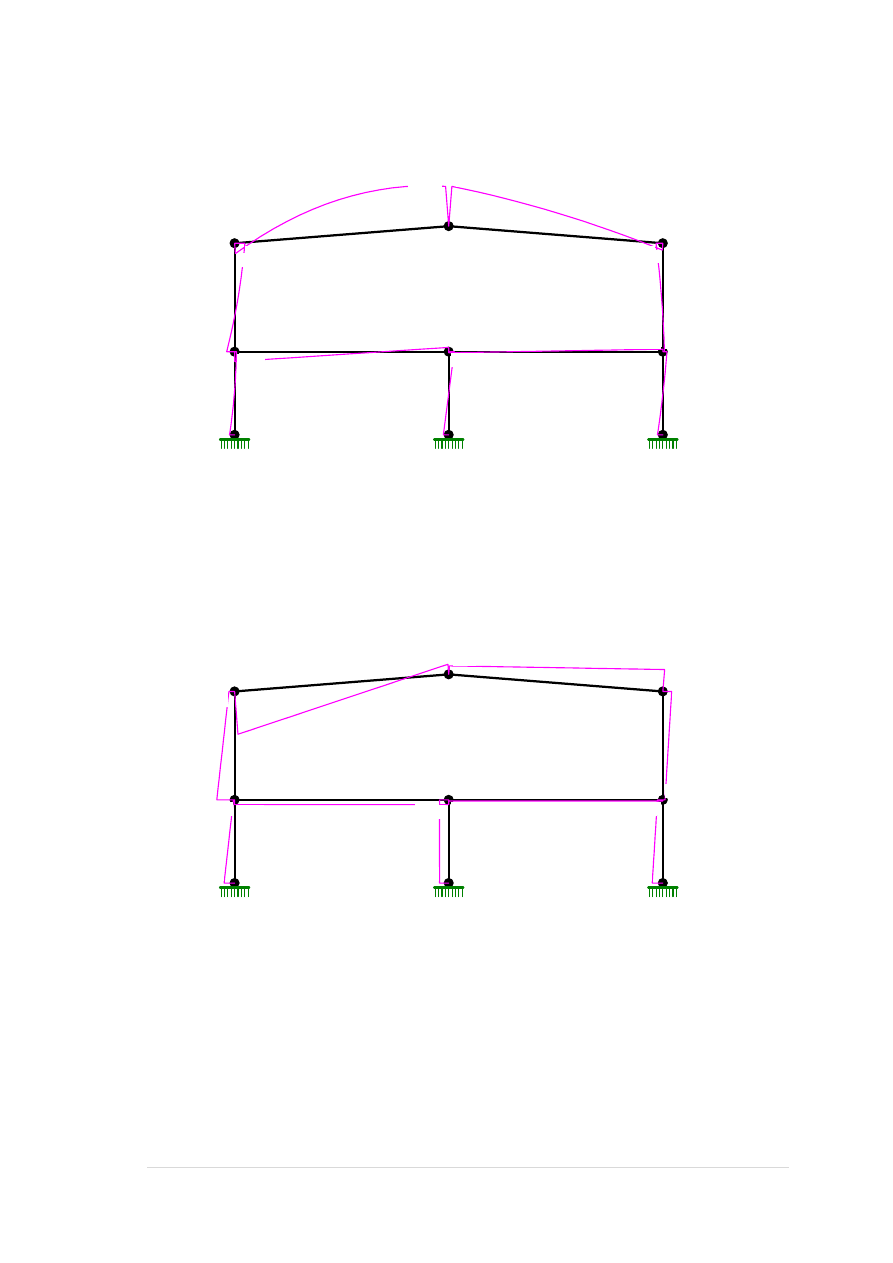
Obciążenie wiatrem z lewej E:

OBCIĄŻENIA: ([kN],[kNm],[kN/m])
------------------------------------------------------------------

Pręt: Rodzaj: Kąt: P1(Tg): P2(Td): a[m]: b[m]:

------------------------------------------------------------------
Grupa: E "wiatr z lewej" Zmienne γf= 1,30

1 Liniowe 90,0 1,50 1,50 0,00 3,30

3 Liniowe 90,0 0,84 0,84 0,00 3,30

4 Liniowe 90,0 1,50 1,50 0,00 4,30

5 Liniowe 90,0 0,84 0,84 0,00 4,30

8 Liniowe -175,4 3,30 3,30 0,00 8,53

9 Liniowe 175,4 0,84 0,84 0,00 8,53

------------------------------------------------------------------

==================================================================

W Y N I K I

Teoria I-go rzędu
==================================================================

OBCIĄŻENIOWE WSPÓŁ. BEZPIECZ.:
------------------------------------------------------------------
Grupa: Znaczenie: ψd: γf:

------------------------------------------------------------------

E -"wiatr z lewej" Zmienne 1 1,00 1,30

------------------------------------------------------------------

1,50

0,84

1,50

0,84

3,30

0,84

28 |

S t r o n a

MOMENTY:

TNĄCE:

-3,60

9,77

-3,60

-10,46

10,36

-10,46

-7,88

10,48

-7,88

-15,29

19,73

-15,29

3,06

-13,18

3,06

-13,18

18,89

-8,38

18,89

-8,38

2,08

-4,83

2,08

-4,83

19,73

-76,71

19,73

-82,39

-76,71

13,18

-76,71

0,83

7,27

0,83

6,31

3,76

7,37

3,76

12,34

3,95

12,34

3,95

-1,43

-6,12

-1,43

-6,12

-3,21

-0,81

-29,60

6,98

-29,60

5,89

15,20

5,89

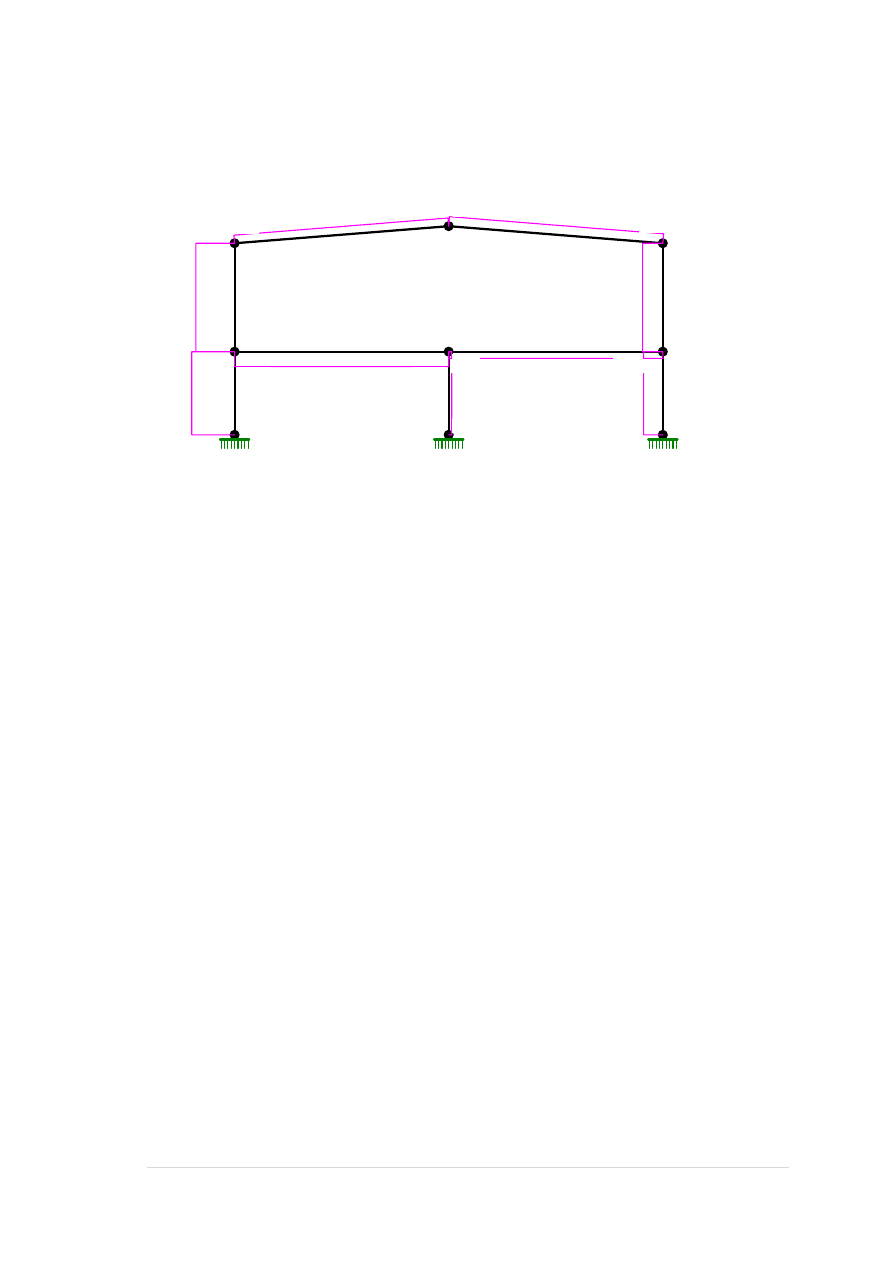
29 |

S t r o n a

NORMALNE:

SIŁY PRZEKROJOWE:

T.I rzędu

Obciążenia obl. dłg.: E

------------------------------------------------------------------

Pręt: x/L: x[m]: M[kNm]: Q[kN]: N[kN]:

------------------------------------------------------------------

1 0,00 0,000 -3,60 0,83 33,22

1,00 3,300 9,77 7,27 33,22

2 0,00 0,000 -10,46 6,31 -2,40

1,00 3,300 10,36 6,31 -2,40

3 0,00 0,000 -7,88 3,76 14,92

1,00 3,300 10,48 7,37 14,92

4 0,00 0,000 -15,29 12,34 30,01

1,00 4,300 19,73 3,95 30,01

5 0,00 0,000 3,06 -1,43 15,74

1,00 4,300 -13,18 -6,12 15,74

6 0,00 0,000 18,89 -3,21 -11,50

1,00 8,500 -8,38 -3,21 -11,50

7 0,00 0,000 2,08 -0,81 -5,19

1,00 8,500 -4,83 -0,81 -5,19

8 0,00 0,000 19,73 -29,60 6,33

0,81 6,895 -82,39* -0,02 6,33

0,00 0,033 18,75 -29,46 6,33*
1,00 8,527 -76,71 6,98 6,33

9 0,00 0,000 -76,71 5,89 7,36

1,00 8,494 12,68 15,16 7,36*

0,02 0,133 -75,91 6,03 7,36*
1,00 8,527 13,18 15,20 7,36

------------------------------------------------------------------

* = Wartości ekstremalne

33,22

-2,40

14,92

30,01

15,74

-11,50

-5,19

6,33

6,33 7,36

7,36

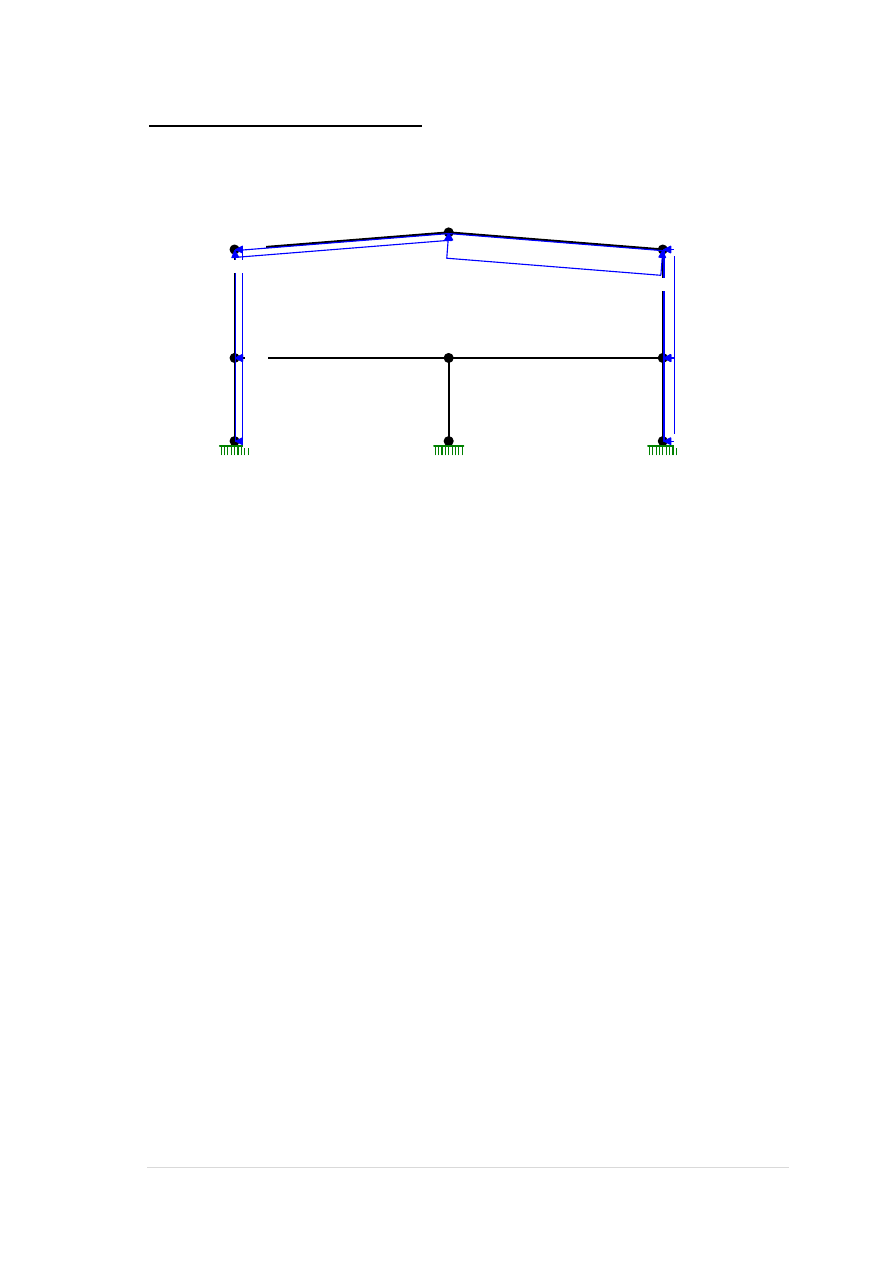
30 |

S t r o n a

Obciążenie wiatrem z prawej F:

OBCIĄŻENIA: ([kN],[kNm],[kN/m])
------------------------------------------------------------------

Pręt: Rodzaj: Kąt: P1(Tg): P2(Td): a[m]: b[m]:

------------------------------------------------------------------
Grupa: F "wiatr z prawej" Zmienne γf= 1,30

1 Liniowe -90,0 0,84 0,84 0,00 3,30

3 Liniowe -90,0 1,50 1,50 0,00 3,30

4 Liniowe -90,0 0,84 0,84 0,00 4,30

5 Liniowe -90,0 1,50 1,50 0,00 4,30

8 Liniowe -175,4 0,84 0,84 0,00 8,53

9 Liniowe 175,4 3,30 3,30 0,00 8,53

------------------------------------------------------------------

==================================================================

W Y N I K I

Teoria I-go rzędu
==================================================================

OBCIĄŻENIOWE WSPÓŁ. BEZPIECZ.:
------------------------------------------------------------------
Grupa: Znaczenie: ψd: γf:

------------------------------------------------------------------

F -"wiatr z prawej" Zmienne 1 1,00 1,30

------------------------------------------------------------------

0,84

1,50

0,84

1,50

0,84

3,30

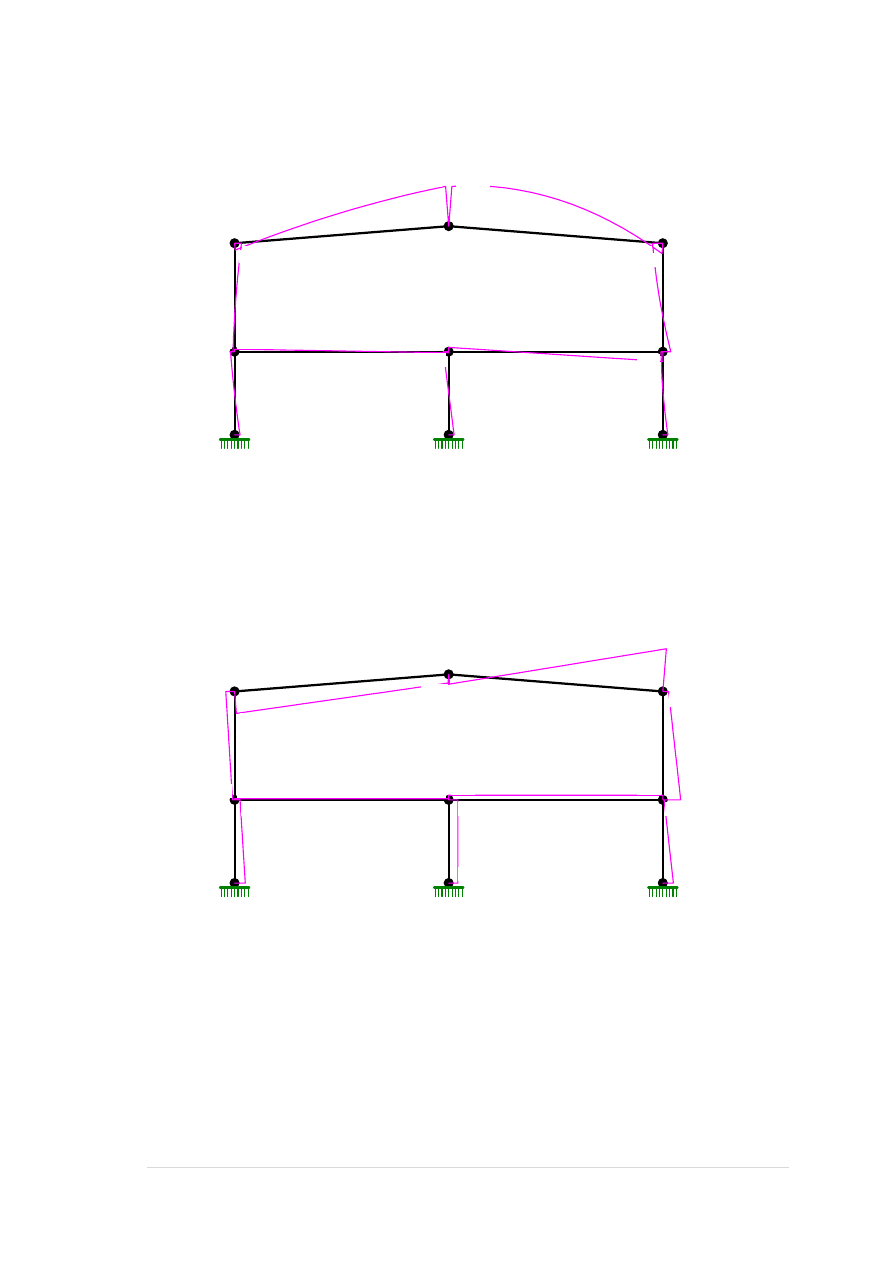
31 |

S t r o n a

MOMENTY:

TNĄCE:

7,88

-10,48

7,88

-10,48

10,46

-10,36

10,46

-10,36

3,60

-9,77

3,60

-9,77

-3,06

13,18

-3,06

15,29

-19,73

15,29

-19,73

-4,83

2,08

-4,83

-8,38

18,89

-8,38

13,18

-76,71

13,18

-76,71

19,73

-82,39

-3,76

-7,37

-3,76

-7,37

-6,31

-0,83

-7,27

-0,83

-7,27

1,43

6,12

1,43

-12,34

-3,95

-12,34

0,81

3,21

-15,20

-5,89

-15,20

-6,98

29,60

-6,98

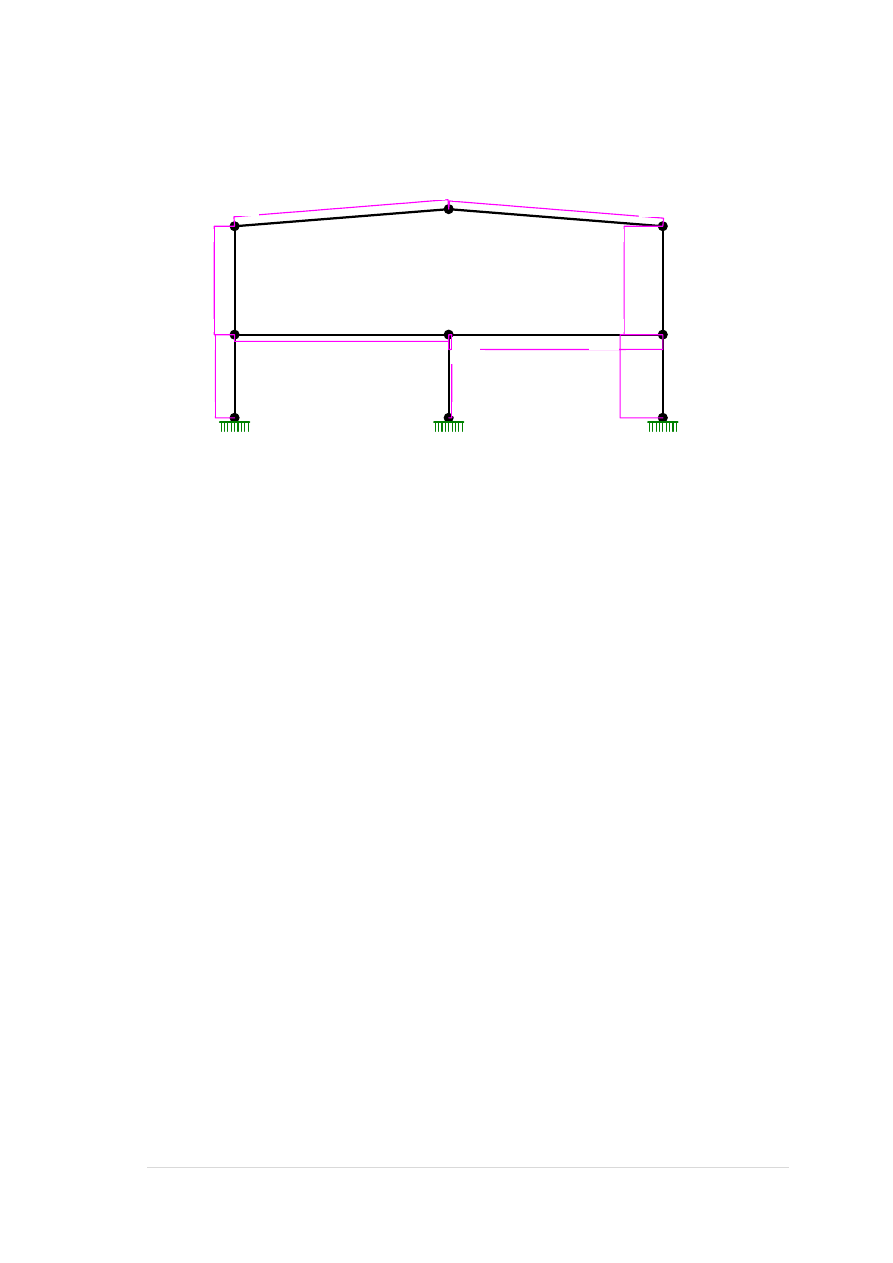
32 |

S t r o n a

NORMALNE:

SIŁY PRZEKROJOWE:

T.I rzędu

Obciążenia obl. dłg.: F

------------------------------------------------------------------

Pręt: x/L: x[m]: M[kNm]: Q[kN]: N[kN]:

------------------------------------------------------------------

1 0,00 0,000 7,88 -3,76 14,92

1,00 3,300 -10,48 -7,37 14,92

2 0,00 0,000 10,46 -6,31 -2,40

1,00 3,300 -10,36 -6,31 -2,40

3 0,00 0,000 3,60 -0,83 33,22

1,00 3,300 -9,77 -7,27 33,22

4 0,00 0,000 -3,06 1,43 15,74

1,00 4,300 13,18 6,12 15,74

5 0,00 0,000 15,29 -12,34 30,01

1,00 4,300 -19,73 -3,95 30,01

6 0,00 0,000 -4,83 0,81 -5,19

1,00 8,500 2,08 0,81 -5,19

7 0,00 0,000 -8,38 3,21 -11,50

1,00 8,500 18,89 3,21 -11,50

8 0,00 0,000 13,18 -15,20 7,36

0,02 0,133 11,17 -15,05 7,36*

1,00 8,494 -76,51 -5,92 7,36*
1,00 8,527 -76,71 -5,89 7,36

9 0,00 0,000 -76,71 -6,98 6,33

0,19 1,632 -82,39* 0,02 6,33

0,00 0,033 -76,94 -6,84 6,33*
1,00 8,527 19,73 29,60 6,33

------------------------------------------------------------------

* = Wartości ekstremalne

14,92

-2,40

33,22

15,74

30,01

-5,19

-11,50

7,36

7,36 6,33

6,33

33 |

S t r o n a

==================================================================

W Y N I K I

Teoria I-go rzędu

Kombinatoryka obciążeń
==================================================================

OBCIĄŻENIOWE WSPÓŁ. BEZPIECZ.:
------------------------------------------------------------------
Grupa: Znaczenie: ψd: γf:

------------------------------------------------------------------

Ciężar wł. 1,00

A -"obciążenia stałe" Stałe 1,00

B -"użytkowe lewe" Zmienne 1 1,00 1,20

C -"użytkowe prawe" Zmienne 1 1,00 1,20

D -"śnieg" Zmienne 1 1,00 1,40

E -"wiatr z lewej" Zmienne 1 1,00 1,30

F -"wiatr z prawej" Zmienne 1 1,00 1,30

------------------------------------------------------------------

RELACJE GRUP OBCIĄŻEŃ:
------------------------------------------------------------------

Grupa obc.: Relacje:

------------------------------------------------------------------

Ciężar wł. ZAWSZE

A -"obciążenia stałe" ZAWSZE

B -"użytkowe lewe" EWENTUALNIE

C -"użytkowe prawe" EWENTUALNIE

D -"śnieg" EWENTUALNIE

E -"wiatr z lewej" EWENTUALNIE

F -"wiatr z prawej" EWENTUALNIE

------------------------------------------------------------------

KRYTERIA KOMBINACJI OBCIĄŻEŃ:
------------------------------------------------------------------

Nr: Specyfikacja:

------------------------------------------------------------------

1 ZAWSZE : A

EWENTUALNIE: B+C+D+E/F

------------------------------------------------------------------

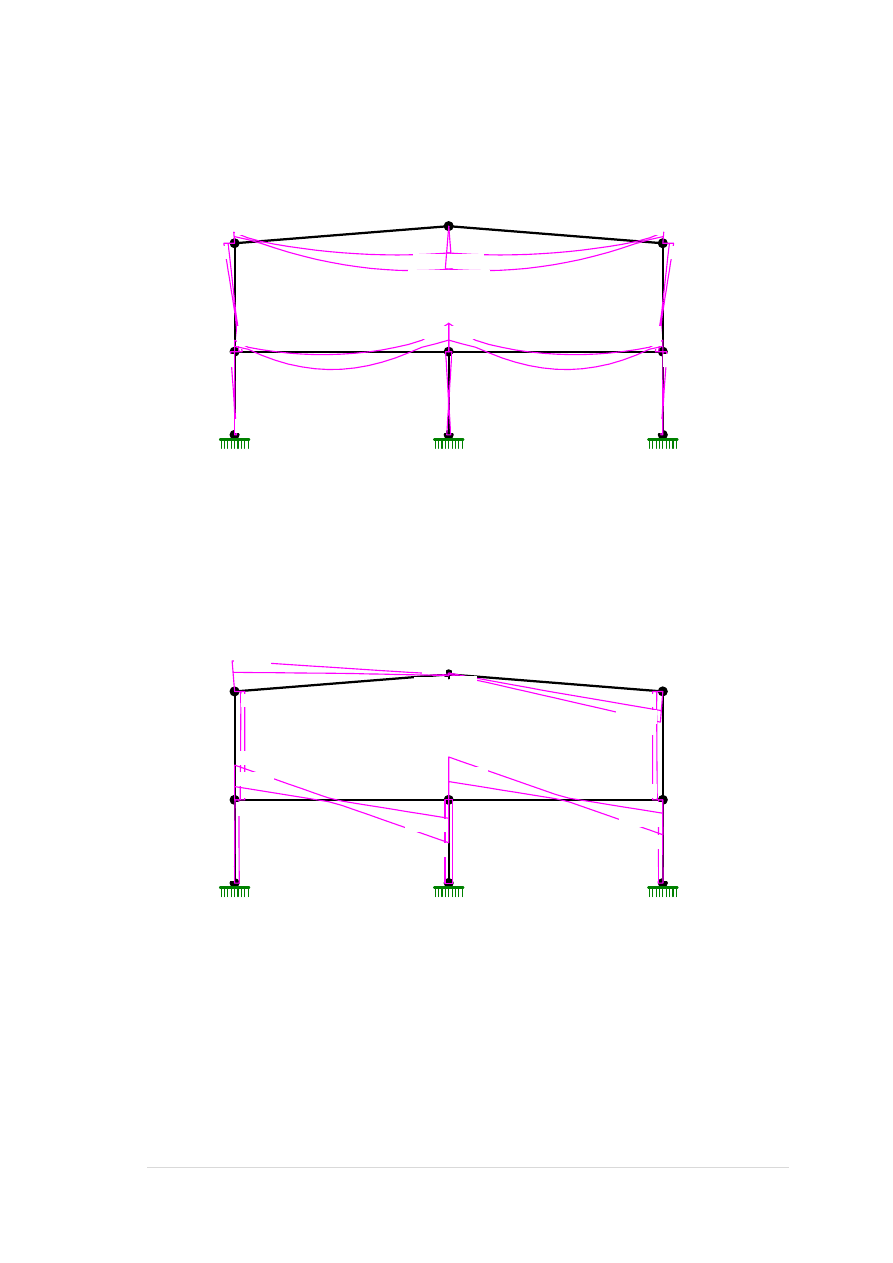
34 |

S t r o n a

MOMENTY-OBWIEDNIE:

TNĄCE-OBWIEDNIE:

113,42

2,75

-1,83

-57,13

87,92 -87,92

55,82 -55,82

-2,75

-113,42

57,13

1,83

212,17

114,96

-181,65

-301,16

-114,96

-212,17

301,16

181,65

-150,86

-319,14

-324,57

-792,09

-324,57

-792,09

-150,86

-319,14

-189,80

-309,31

1194,27

744,76

1194,27

744,76

-189,80

-309,31

-4,60

-49,88

1,83 -53,48

43,56 -43,56

49,88

4,60

53,48 -1,83

-65,54

-118,62

-71,76

-118,62

118,62

65,54

118,62

71,76

404,35

155,20

-213,51

-498,20

498,20

213,51

-155,20

-404,35

357,27

223,27

1,54

-16,11

16,11

-1,54

-223,27

-357,27

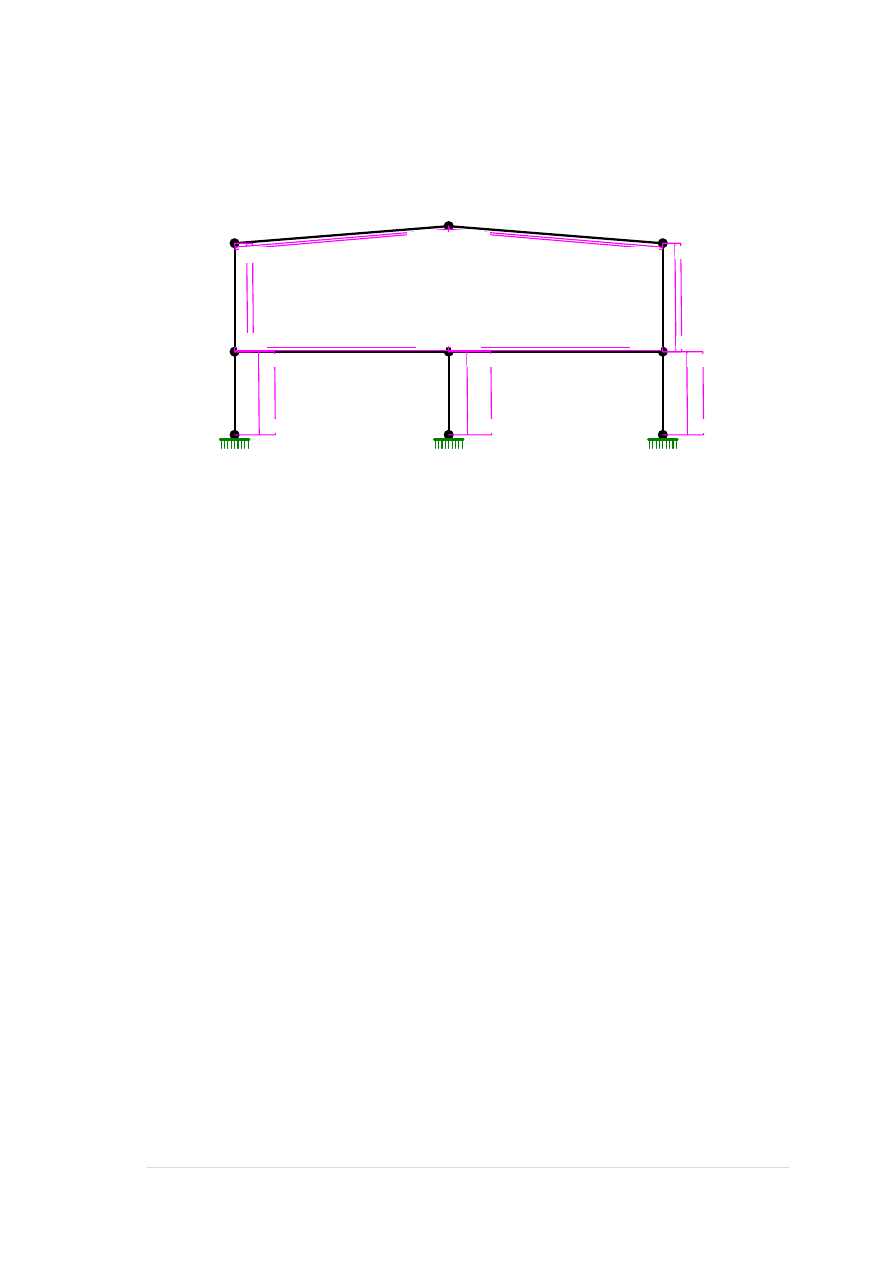
35 |

S t r o n a

NORMALNE-OBWIEDNIE:

SIŁY PRZEKROJOWE - WARTOŚCI EKSTREMALNE:

T.I rzędu

Obciążenia obl. dłg.: Ciężar wł.+"Kombinacja obciążeń"

------------------------------------------------------------------

Pręt: x[m]: M[kNm]: Q[kN]: N[kN]: Kombinacja obciążeń:

------------------------------------------------------------------

1 0,000 113,42* -49,88 -819,04 ABF

3,300 -57,13* -53,48 -835,67 ABF

3,300 -57,13 -53,48* -835,67 ABF

0,000 10,63 -8,04 -563,49* ACE

3,300 -43,20 -42,68 -960,07* ABD

2 0,000 87,92* -43,56 -716,94 ACF

0,000 -87,92* 43,56 -716,94 ABE

0,000 87,92 -43,56* -716,94 ACF

0,000 -87,92 43,56* -716,94 ABE

3,300 55,82 43,56* -733,57 ABE

0,000 -0,00 0,00 -428,64* AD

3,300 10,36 6,31 -1009,01* ABCE

3 3,300 57,13* 53,48 -835,67 ACE

0,000 -113,42* 49,88 -819,04 ACE

3,300 57,13 53,48* -835,67 ACE

0,000 -10,63 8,04 -563,49* ABF

3,300 43,20 42,68 -960,07* ACD

4 0,000 212,17* -118,62 -442,02 ABCD

4,300 -301,16* -111,73 -421,67 ACD

0,000 212,17 -118,62* -442,02 ABCD

4,300 -297,91 -118,62* -420,35 ABCD

4,300 -181,65 -80,82 -284,77* ABE

0,000 179,28 -111,73 -443,34* ACD

-563,49

-943,43

-580,12

-960,07

-428,64

-992,38

-445,27

-1009,01

-563,49

-943,43

-580,12

-960,07

-306,44

-443,34

-284,77

-421,67

-306,44

-443,34

-284,77

-421,67

106,29

27,15

106,29

27,15 106,29

27,15

106,29

27,15

-91,15

-147,43

-70,27

-118,25-70,27

-118,25

-91,15

-147,43

36 |

S t r o n a

5 4,300 301,16* 111,73 -421,67 ABD

0,000 -212,17* 118,62 -442,02 ABCD

4,300 297,91 118,62* -420,35 ABCD

0,000 -212,17 118,62* -442,02 ABCD

4,300 181,65 80,82 -284,77* ACF

0,000 -179,28 111,73 -443,34* ABD

6 3,719 495,86* 13,93 27,15 ABE

8,500 -792,09* -498,20 38,71 ABCE

8,500 -792,09 -498,20* 38,71 ABCE

8,500 -509,60 -236,37 106,29* ACD

3,719 82,63 -11,36 106,29* ACD

8,500 -609,15 -476,15 27,15* ABE

3,719 495,86 13,93 27,15* ABE

7 4,781 495,86* -13,93 27,15 ACF

0,000 -792,09* 498,20 38,71 ABCF

0,000 -792,09 498,20* 38,71 ABCF

0,000 -509,60 236,37 106,29* ABD

4,781 82,63 11,36 106,29* ABD

0,000 -609,15 476,15 27,15* ACF

4,781 495,86 -13,93 27,15* ACF

8 8,527 1194,27* -8,36 -104,50 AD

0,000 -309,31* 357,27 -140,67 ACD

0,000 -309,31 357,27* -140,67 ACD

8,527 770,13 -12,10 -70,27* AF

0,000 -306,06 355,40 -147,43* ABCD

9 0,000 1194,27* 8,36 -104,50 AD

8,527 -309,31* -357,27 -140,67 ABD

8,527 -309,31 -357,27* -140,67 ABD

0,000 770,13 12,10 -70,27* AE

8,527 -306,06 -355,40 -147,43* ABCD
------------------------------------------------------------------

* = Max/Min

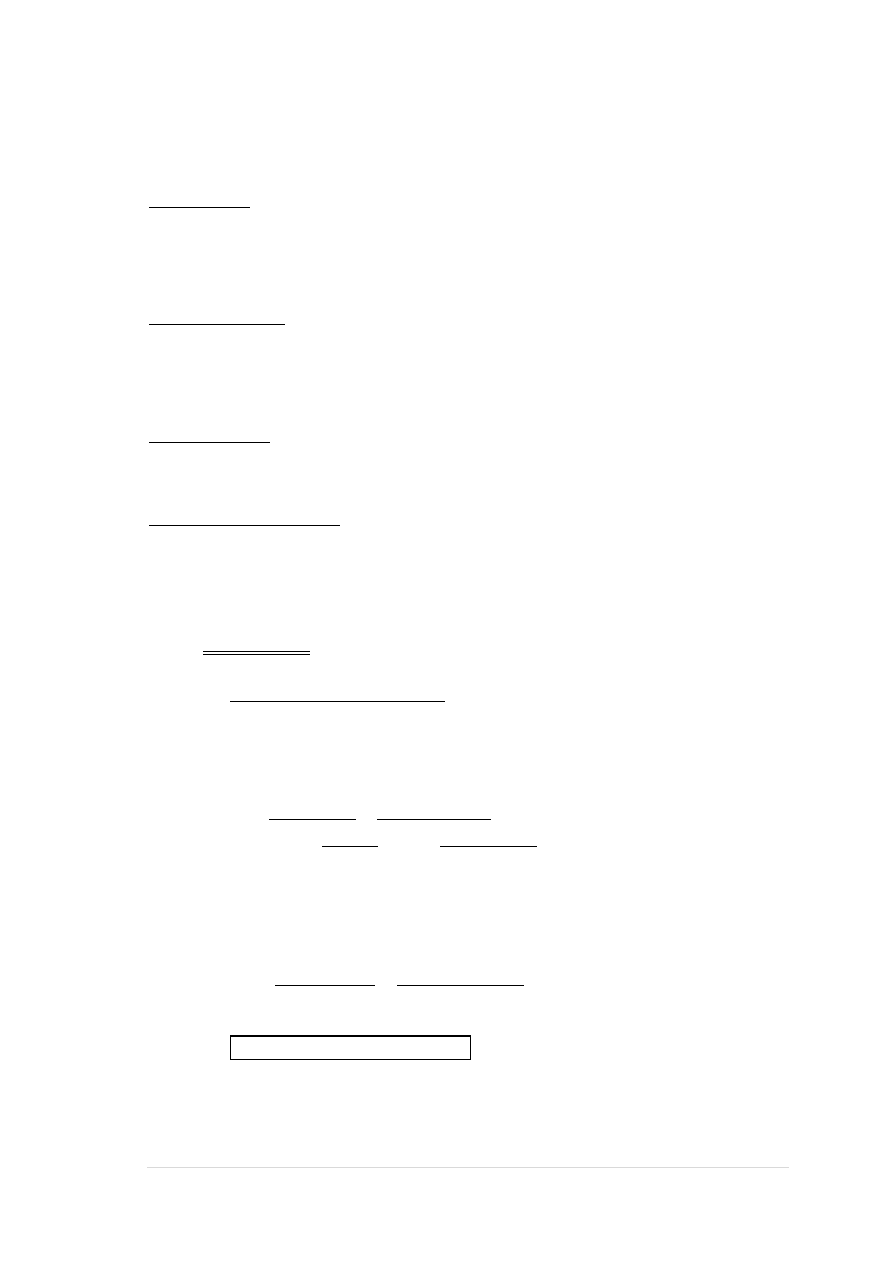
37 |

S t r o n a

7. ANALITYCZNE WYMIAROWANIE RYGLA STROPOWEGO NR 6:

Wymiary rygla:

Beton C25/30 (B30):

16,7

2,6

1,2

Stal A‐IIIN, RB500:

420

500

Stal A‐I, St3S‐b (strzemiona):

210

240

1. Przęsło nr 1:

A. Obliczenie zbrojenia na zginanie

495,86

49586

1,67 35 86

0,115

2 0,115

0,123

0,50

Przekrój może być pojedynczo zbrojony.

0,5

0,5 0,123

0,939

49586

0,939 42,0 86

14,62

Przyjęto: 6 18

15,24

38 |

S t r o n a

B. Sprawdzenie warunku minimalnego pola przekroju zbrojenia podłużnego:

0,0013

0,0013 35 86

3,91

0,26

2,6

500

35 86

4,07

oraz warunku wymaganego z uwagi na ograniczenia szerokości rys
spowodowanych skurczem, osiadaniem podpór itp.

0,4 0,42 0,26

0,5 35 90

24,0

2,867

gdzie:

średnia wytrzymałość betonu na rozciąganie w chwili spodziewanego

zarysowania, przyjęto

2,6

;

współczynnik uwzględniający rozkład naprężeń w chwili poprzedzającej

zarysowanie;

wwspółczynnik uwzględniający wpływ nierównomiernych naprężeń samo

równoważących się w przekroju

pole rozciąg naje strefy w chwili poprzedzającej zarysowanie

0,5

nnaprężenie przyjęte w zbrojeniu rozciąganym natychmiast po

zarysowaniu, zależne od granicznej szerokości rys i średnicy prętów żebrowanych
wg tablicy 13.3

Przyjęty przekrój zbrojenia

15,24

jest większy od minimalnego

wyznaczonego z powyższych warunków.

Stopień zbrojenia w przęśle:

15,24

35 86

0,005

0,5%

C. Sprawdzenie stanu granicznego zarysowania

Moment pochodzący od obciążeń długotrwałych w przęśle żebra:

171,79

17179

Wyznaczenie momentu rysującego:

0,26 47250

12285

122,85

171,79

Nośność przekroju na zarysowanie jest niewystarczająca. Przekrój pracuje jako
zarysowany.

39 |

S t r o n a

Obliczam szerokość rys prostopadłych:

, ‐ zarysowanie spowodowane obciążeniem bezpośrednim

0,8 ‐ pręty żebrowane

0,5 ‐ zginanie

2,5 ;

‐ wysokość strefy ściskanej w fazie II dla przekroju zarysowanego

Współczynniki pełzania betonu dla:

• wiek betonu w chwili obciążenia

90 dni

• wilgotność względna RH=50%
• miarodajny wymiar przekroju

0,252mm

Odczytane z tablicy A.1 A.2:

∞,

2,15

0,56

∞,

2,15 0,56

1,2

30000

1,2

13636,4

200000

13636,4

14,7

15,24 14,7

2 35 86

15,24 14,7

27,39

2,5 4; 90

27,39 /3

10; 20,87

350

15,24

350

0,043

0,25 0,8 0,5

0,043

91,86

40 |

S t r o n a

17229

0,9 86 15,24

14,61

⁄

146,1

1,0 ‐ pręty żebrowane
0,5 – obciążenie długotrwałe

122,85
172,29

0,71

146,1

200000

1 0,5 0,71

5,46 10

Ostateczna szerokość rys:

1,7 91,86 5,46 10

0,1

Dla ekspozycji XC3 graniczna szerokość rysy

0,3

0,1

0,3

D. Ugięcie metodą dokładną

Do obliczeń wykorzystuję wartości parametrów uzyskane przy obliczeniach
szerokości rys.

Faza II zarysowana:

27,39

0,35 0,27

14,7 0,001524 0,86

0,279

9,85 10

Faza I niezarysowana:

0,5

0,5 0,35 0,9

14,7 0,001524 0,86

0,35 0,9

14,7 0,001524

0,48

0,35 0,48

0,35

0,9

0,48

14,7 0,001524

0,86

0,48

0,0247

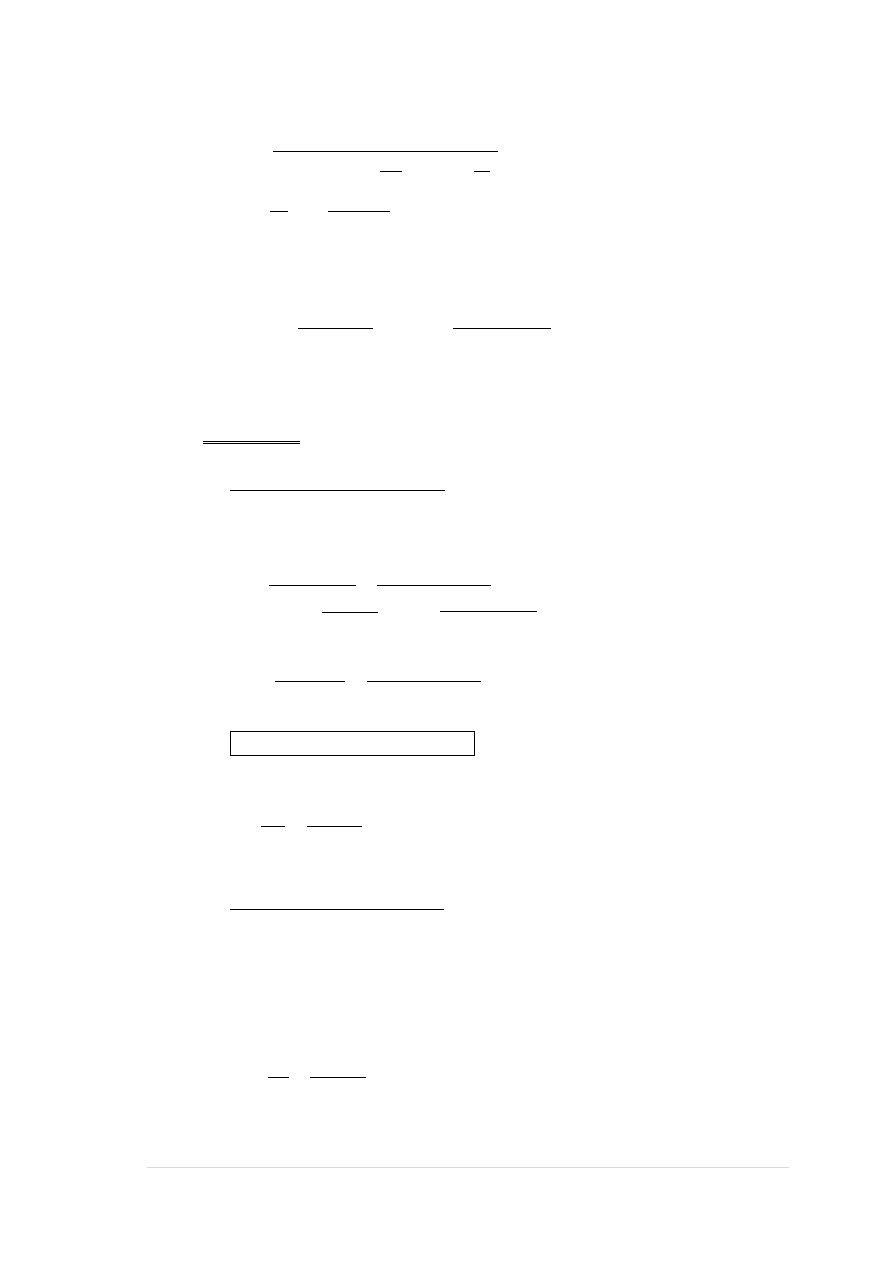
41 |

S t r o n a

Sztywność

0,088

Ostateczna wartość ugięcia:

0,088

172,29 8,5

476

0,023

2. Podpora A:

A. Obliczenie zbrojenia na zginanie

319,14

31914

1,67 35 86

0,074

2 0,074

0,077

0,50

0,5

0,5 0,077

0,962

31914

0,962 42 86

9,18

Przyjęto: 4 18

10,16

Stopień zbrojenia

10,16

35 86

0,003

0,3%

B. Obliczenie zbrojenia na ścinanie

404,35

1,6

0,86

0,74 (do podp. dopr. 4 18,

10,16

)=1,0

10,16

35 86

0,003

1,2MPa

0 ponieważ belka nie jest abc. podłużną siłą ściskającą

42 |

S t r o n a

0,35 1 0,12 1,2

40 0,003

35 86

166,87

404,35

166,87

Konieczne jest obliczenie dodatkowego zbrojenia poprzecznego na odcinku
drugiego rodzaju.

Odcinki drugiego rodzaju:

0,9

0,9 86

77,4

0,6 1

250

0,6 1

250

0,54

0,5 0,54 1,67 35 77,4

1221,48

166,87

404,86

1221,48

404,86

166,87

7,56

39,50

55,44

2,3

Rozstaw strzemion obliczono przyjmując, że:
zbrojenia na ścianie składa się wyłącznie ze strzemion pionowych
strzemiona są dwuramienne 10 ze stali A‐I
strzemiona przeniosą całą siłę poprzeczną

, tak więc

1,00

1,57 21,0 77,4 1,0

404,86

6,3

Rozstaw za mały. Przyjmuję strzemiona czteroramienne w rozstawie 10cm.

Nośność ściskanych krzyżaków betonowych obliczamy ze wzoru:

0,54 1,67 35 77,4

1 1

1221,48

3,14 21

77,4

510,37

225,19

Minimalny stopień zbrojenia strzemion:

0,08

0,08 2,5

24,0

0,0053

43 |

S t r o n a

Stopień zbrojenia strzemionami:

3,14

10 35

0,009

0,9%

Zaprojektowane zbrojenie strzemionami prostopadłymi do osi beli zapewnia
nośność na ścinanie na odcinku drugiego rodzaju.

Sprawdzenie czy zbrojenie podłużne doprowadzone do podpory przeniesie siłę
rozciągającą ∆

obliczoną z uwzględnieniem siły poprzecznej.

∆

0,5

0,5 404,35 1,0

202,18

Do przeniesienia siły ∆

wystarczy zbrojenie podłużne o przekroju ∆

∆

202,18

42,0

4,82

Jest to wartość większa od minimalnego przekrój zbrojenia, które należy
doprowadzić do podpory i odpowiednio zakotwić. Do podpory doprowadzono

4 pręty 18 , których pole przekroju zapewnia przeniesienie siły rozciągającej

∆

, ponieważ

10,16

4,82

C. Obliczenie długości zakotwienia prętów podłużnych 4 18

doprowadzonych do

podpory.

1,0

ę ó

2,7

tabl.5.1

1,8

42,0
0,27

0,3

0,3 70

10 1,8

pole przekroju zbrojenia zastosowanego 4 18

10,16

Wymaganą powierzchnię zbrojenia

należy przyjąć z uwagi na:

‐przekrój potrzebny do przeniesienia siły ∆

, czyli

4,82

1,0 78

4,82

10,16

33,2

21,0

44 |

S t r o n a

Belka podparta bezpośrednio na słupach i wieńcach. Z tego względu długość
zakotwienia zbrojenia poza krawędź podpory można zredukować zgodnie z
warunkiem:

2
3

33,2

Szerokość podpory

, przyjęto

, tak więc ze względu na

ścinanie pręty doprowadzone do skrajnej podpory będą dostatecznie zakotwione.

D. Sprawdzenie stanu granicznego zarysowania

Moment pochodzący od obciążeń długotrwałych w przęśle żebra:

175,53

17553

Wyznaczenie momentu rysującego:

0,26 47250

12285

122,85

175,53

Nośność przekroju na zarysowanie jest niewystarczająca. Przekrój pracuje jako
zarysowany.

Obliczam szerokość rys ukośnych:

404,86

35 86

0,134

0,9%

0,009

0,7 1

4 0,134

0,009 200000 2,5

0,031

0,3

3. Podpora B:

A. Obliczenie zbrojenia na zginanie

792,02

79202

78946

1,67 35 86

0,183

2 0,183

0,203

0,50

45 |

S t r o n a

0,5

0,5 0,203

0,898

78946

0,898 42 86

24,34

Przyjęto: 10 18

25,4

Stopień zbrojenia

25,4

35 86

0,008

0,8%

B. Obliczenie zbrojenia na ścinanie

498,20

1,6

0,86

0,74 (do podp. dopr. 4 18,

10,16

)=1,0

0,008

1,2MPa

0 ponieważ belka nie jest abc. podłużną siłą ściskającą

0,35 1 0,12 1,2

40 0,003

35 86

166,87

498,20

166,87

Konieczne jest obliczenie dodatkowego zbrojenia poprzecznego na odcinku
drugiego rodzaju.

Odcinki drugiego rodzaju:

0,9

0,9 86

77,4

0,6 1

250

0,6 1

250

0,54

0,5 0,54 1,67 35 77,4

1221,48

166,87

497,78

1221,48

497,78

166,87

7,56

39,50

55,44

3,2

46 |

S t r o n a

, tak więc

1,00

1,57 21,0 77,4 1,0

497,78

5,3

Rozstaw za mały. Przyjmuję strzemiona czteroramienne w rozstawie 10cm.

Nośność ściskanych krzyżaków betonowych obliczamy ze wzoru:

0,54 1,67 35 77,4

1 1

1221,48

3,14 21

77,4

510,37

225,19

Minimalny stopień zbrojenia strzemion:

0,08

0,08 2,5

24,0

0,0053

Stopień zbrojenia strzemionami:

3,14

10 35

0,009

0,9%

Zaprojektowane zbrojenie strzemionami prostopadłymi do osi beli zapewnia
nośność na ścinanie na odcinku drugiego rodzaju.

Sprawdzenie czy zbrojenie podłużne doprowadzone do podpory przeniesie siłę
rozciągającą ∆

obliczoną z uwzględnieniem siły poprzecznej.

∆

0,5

0,5 498,20 1,0

248,89

Do przeniesienia siły ∆

wystarczy zbrojenie podłużne o przekroju ∆

∆

248,89

42,0

5,92

Jest to wartość większa od minimalnego przekrój zbrojenia, które należy
doprowadzić do podpory i odpowiednio zakotwić. Do podpory doprowadzono

6 prętów 18 , których pole przekroju zapewnia przeniesienie siły rozciągającej

∆

, ponieważ

15,24

5,92

47 |

S t r o n a

C. Obliczenie długości zakotwienia prętów podłużnych 4 18

doprowadzonych do

podpory.

1,0

ę ó

2,7

tabl.5.1

1,8

42,0
0,27

0,3

0,3 70

10 1,8

pole przekroju zbrojenia zastosowanego 4 18

10,16

Wymaganą powierzchnię zbrojenia

należy przyjąć z uwagi na:

‐przekrój potrzebny do przeniesienia siły ∆

, czyli

5,92

1,0 70

5,92

15,24

27,2

21,0

Belka podparta na słupach i wieńcach. Z tego względu długość zakotwienia
zbrojenia poza krawędź podpory można zredukować zgodnie z warunkiem:

2
3

27,2

Szerokość podpory

, przyjęto

, tak więc ze względu na

ścinanie pręty doprowadzone do skrajnej podpory będą dostatecznie zakotwione.

D. Sprawdzenie stanu granicznego zarysowania

Moment pochodzący od obciążeń długotrwałych w przęśle żebra:

337,62

33762

Wyznaczenie momentu rysującego:

0,26 47250

12285

122,85

33762

Nośność przekroju na zarysowanie jest niewystarczająca. Przekrój pracuje jako
zarysowany.

Obliczam szerokość rys ukośnych:

48 |

S t r o n a

497,89

35 86

0,165

0,9%

0,009

0,7 1

4 0,165 26

0,009 20000 2,5

0,031

0,3

49 |

S t r o n a

8. ANALITYCZNE WYMIAROWANIE SŁUPA NR 1

Wymiary słupa:

3,3

Beton C25/30 (B30):

16,7

2,6

1,2

Stal A‐IIIN, RB500:

420

500

Stal A‐I, St3S‐b (strzemiona):

210

240

Długość obliczeniowa słupa:

1,0 3,25

3,25

Mimośród początkowy:

Obliczenie mimośrodu konstrukcyjnego:

57,13

0,00

1,83

0,00

960,07

43,20

960,07

0,045

580,12

5,28

580,12

0,009

50 |

S t r o n a

113,42

819,04

113,42
819,04

0,138

2,75

672,96

2,75

672,96

0,004

943,43

97,66

943,43

0,104

563,49

10,63

563,49

0,019

Przyjmuję wartość największą.

0,14

Obliczenie mimośrodu niezamierzonego :

600

3,25

600

1
1

0,01

0,6

0,02

Przyjmuję wartość największą.

Wartość mimośrodu początkowego:

0,14

0,02

0,16

Sprawdzenie smukłości słupa:

3,25

0,6

5,42

Słup krępy, w którym można pominąć wpływ wyboczenia i obciążeń długotrwałych.

Mimośrody siły

względem zbrojenia:

0,5

0,16

0,5 0,6

0,04

0,42

0,56

0,42

0,04

0,10

Przyjmuję symetryczne zbrojenie słupa.

0,5 0,56

960,07

1,67 35

16,43

51 |

S t r o n a

16,43

28,0

2 4

960,07

2 1,67 35

5,79

2184

0,003

0,15

960,07

3,43

0,003

0,003 35 56

5,88

Przyjmuję zbrojenie tylko konstrukcyjne w postaci 4 prętów w narożach słupa.

Przyjęto: 4 18

10,16

Stopień zbrojenia przekroju słupa:

10,16

35 56

0,005

0,5%

Rozstaw strzemion:

15 1,8

Przyjmuję rozstaw strzemion 25cm. W miejscu łączenia prętów zagęszczam do 12cm.

52 |

S t r o n a

9. WYMIAROWANIE ELEM. PRZY UŻYCIU PROGRAMU RMWIN

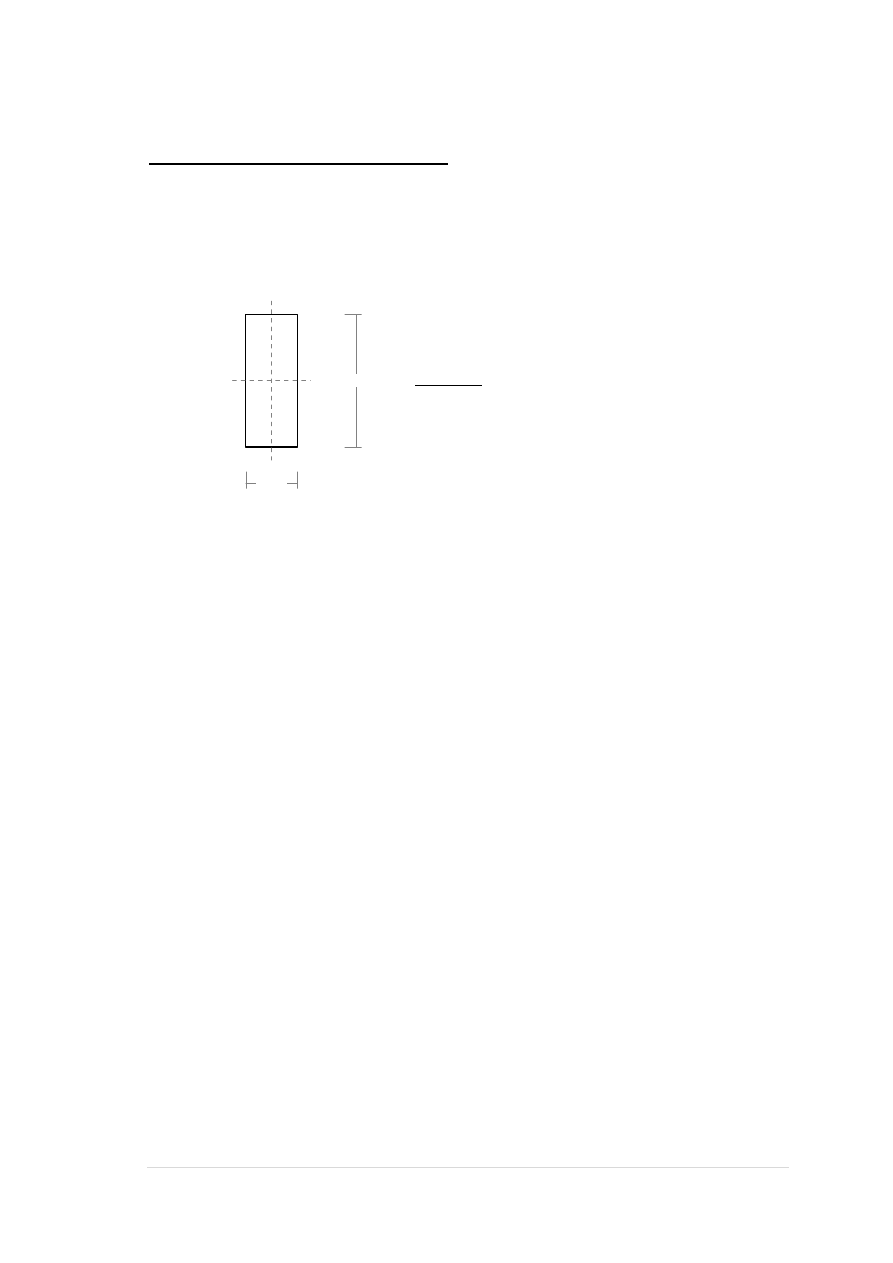
53 |

S t r o n a

9.1. RYGIEL NR 6, (węzeł 45):

ZBROJENIE RYGLA NR 7 (węzeł 5‐6) SYMETRYCZNE DO ZBROJENIA RYGLA
OBLICZANEGO PONIŻEJ.

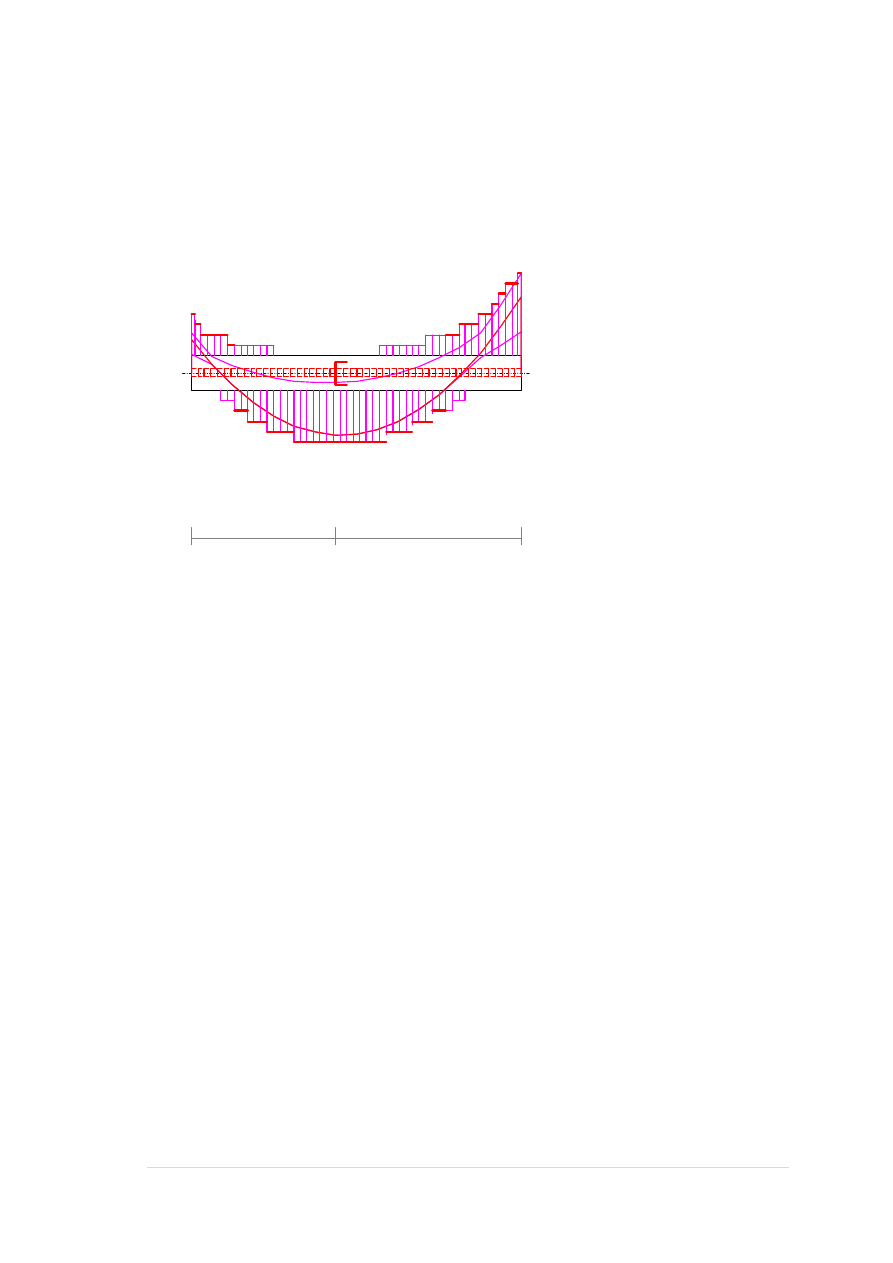
Cechy przekroju:

zadanie hala_monolit, pręt nr 6, przekrój: x

=4,25 m, x

=4,25 m

Wymiary przekroju [cm]:

h=90,0, b=35,0,

Cechy materiałowe dla sytuacji stałej lub
przejściowej
BETON: B30

= 25,0 MPa,

=α·f

=1,00×25,0/1,50=16,7 MPa

Cechy geometryczne przekroju betonowego:

=3150 cm

, J

=2126250 cm

, J

=321563

Siły przekrojowe:

PRZĘSŁO - przekrój: x

=3,72 m, x

=4,78 m

Obciążenia działające w płaszczyźnie układu: ABE
Momenty zginające:

= -495,87 kNm,

= 0,00 kNm,

Siły poprzeczne:

= 13,90 kN,

= 0,00 kN,

Siła osiowa:

N = 27,15 kN = N

, .

PODPORA W WĘŹLE 4 - przekrój: x

=0,00 m, x

=8,50 m

Obciążenia działające w płaszczyźnie układu: ABDF
Momenty zginające:

= 319,14 kNm,

= 0,00 kNm,

Siły poprzeczne:

= 404,35 kN,

= 0,00 kN,

Siła osiowa:

N = 63,86 kN = N

, .

PODPORA W WĘŹLE 5 - przekrój: x

=8,50 m, x

=0,00 m

Obciążenia działające w płaszczyźnie układu: ABCE
Momenty zginające:

= 792,09 kNm,

= 0,00 kNm,

Siły poprzeczne:

= -498,20 kN,

= 0,00 kN,

Siła osiowa:

N = 38,71 kN = N

, .

90,00

35,00

54 |

S t r o n a

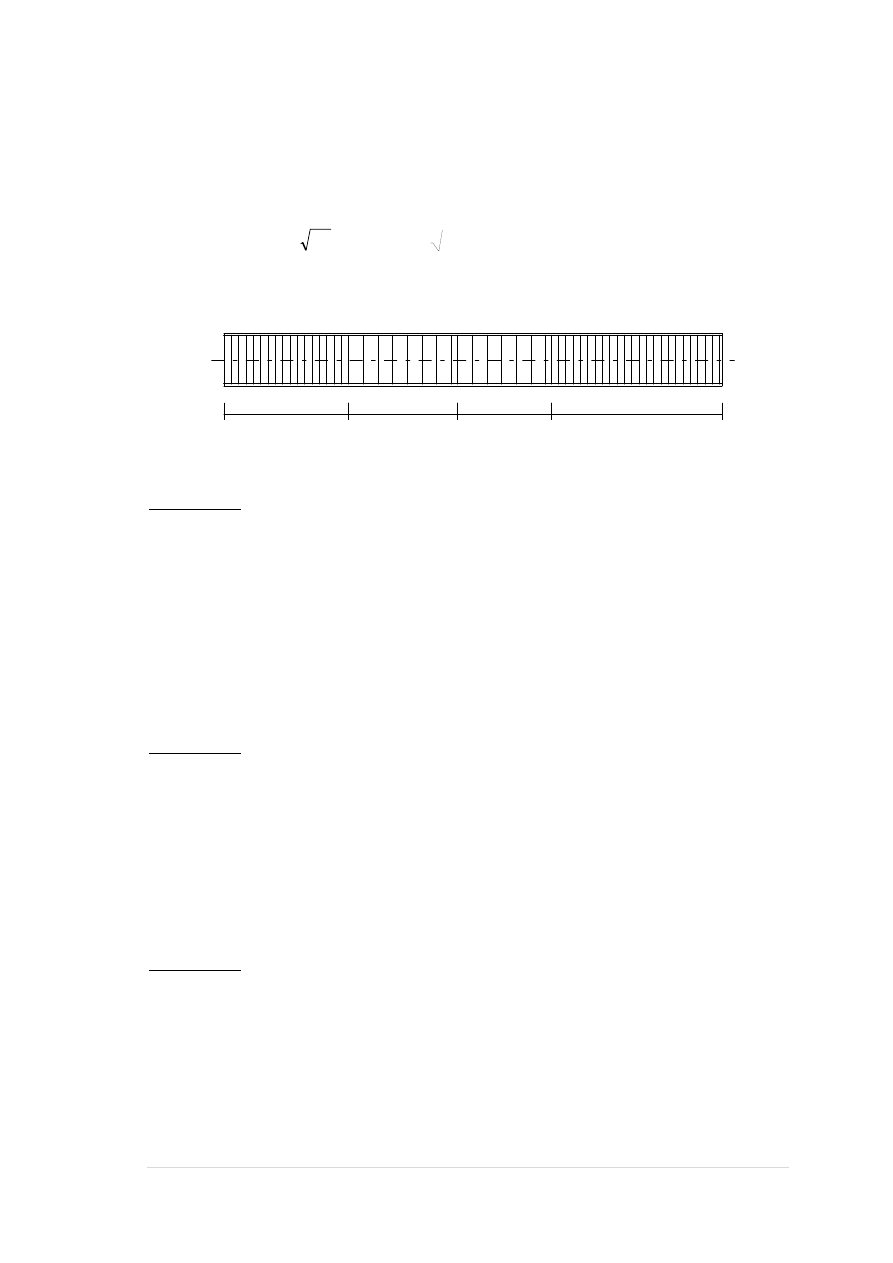
Zbrojenie wymagane:

dla

∅20

222

444

55555555555555

333

3,72

4,78

55 |

S t r o n a

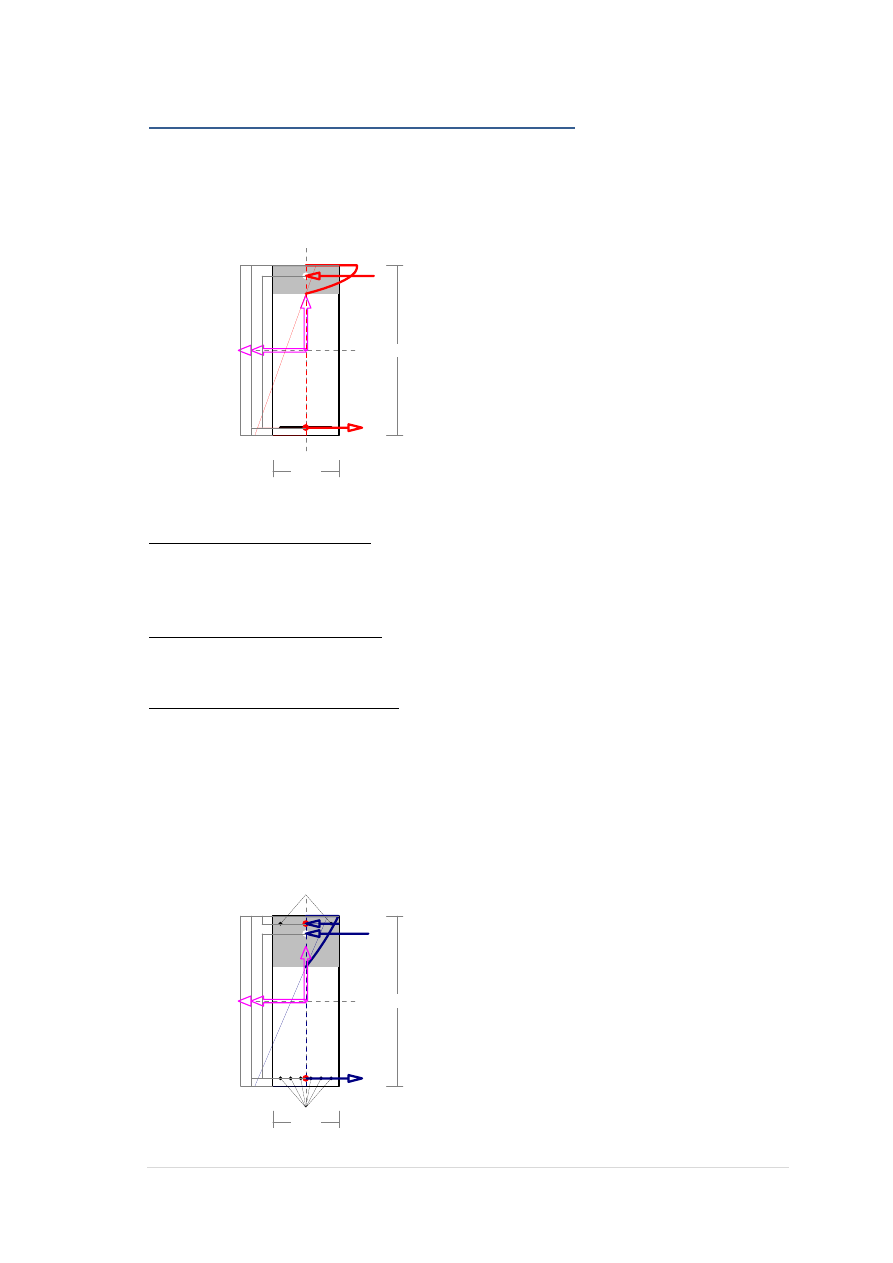
Zbrojenie poprzeczne (strzemiona)

zadanie hala_monolit, pręt nr 6

Na całej długości pręta przyjęto strzemiona o średnicy

φ=10 mm ze stali A-I, dla której

ywd

= 210 MPa.

Minimalny stopień zbrojenia na ścinanie:

w,min

= 0,08

/ f

= 0,08×

/ 500 = 0,00080

Rozstaw strzemion:
Strefa nr 1

Początek i koniec strefy:

= 0,0 x

= 212,5 cm

Maksymalny rozstawy strzemion:

max

= 0,75 d = 0,75×859 = 644 s

max

≤ 400 mm

przyjęto s

max

= 400 mm.

Ze względu na pręty ściskane s

max

= 15

φ = 15×20,0 = 300,0 mm.

Przyjęto strzemiona 4-cięte, prostopadłe do osi pręta o rozstawie 12,5 cm, dla
których stopień zbrojenia na ścinanie wynosi:

= A

/(s b

sin

α) = 3,14 / (12,5×35,0×1,000) = 0,00718

= 0,00718 > 0,00080 =

w min

Strefa nr 2

Początek i koniec strefy:

= 212,5 x

= 398,4 cm

Maksymalny rozstawy strzemion:

max

= 0,75 d = 0,75×859 = 644 s

max

≤ 400 mm

przyjęto s

max

= 400 mm.

Przyjęto strzemiona 2-cięte, prostopadłe do osi pręta o rozstawie 25,0 cm, dla
których stopień zbrojenia na ścinanie wynosi:

= A

/(s b

sin

α) = 1,57 / (25,0×35,0×1,000) = 0,00180

= 0,00180 > 0,00080 =

w min

Strefa nr 3

Początek i koniec strefy:

= 398,4 x

= 557,8 cm

Maksymalny rozstawy strzemion:

max

= 0,75 d = 0,75×859 = 644 s

max

≤ 400 mm

przyjęto s

max

= 400 mm.

Przyjęto strzemiona 2-cięte, prostopadłe do osi pręta o rozstawie 25,0 cm, dla
których stopień zbrojenia na ścinanie wynosi:

= A

/(s b

sin

α) = 1,57 / (25,0×35,0×1,000) = 0,00180

212,5

185,9

159,4

292,2

56 |

S t r o n a

= 0,00180 > 0,00080 =

w min

Strefa nr 4

Początek i koniec strefy:

= 557,8 x

= 850,0 cm

Maksymalny rozstawy strzemion:

max

= 0,75 d = 0,75×859 = 644 s

max

≤ 400 mm

przyjęto s

max

= 400 mm.

Ze względu na pręty ściskane s

max

= 15

φ = 15×20,0 = 300,0 mm.

Przyjęto strzemiona 4-cięte, prostopadłe do osi pręta o rozstawie 12,5 cm, dla
których stopień zbrojenia na ścinanie wynosi:

= A

/(s b

sin

α) = 3,14 / (12,5×35,0×1,000) = 0,00718

= 0,00718 > 0,00080 =

w min

57 |

S t r o n a

WYMIAROWANIE NA MOMENT PRZĘSŁOWY:

Zbrojenie wymagane:

(zadanie hala_monolit, pręt nr 6, przekrój: x

=3,72 m, x

=4,78 m)

Wielkości obliczeniowe:
N

=27,15 kN,

√(M

Sdx

+ M

Sdy

) =

√(-495,87

+0,00

)

=495,87 kNm
f

=16,7 MPa, f

=420 MPa (f

=478 MPa -

uwzgl. wzmocnienia) ,
Zbrojenie rozciągane (

=10,00 ‰):

=14,70 cm

⇒ (5¤20 = 15,71 cm

Dodatkowe zbrojenie ściskane(*As2=0 nie
jest obliczeniowo wymagane.*|* (

2,13 ‰,):
A

=0,00 cm

⇒ (0¤20 = 0,00 cm

) *)

=14,70 cm

ρ=100×A

100

×14,70/3150=0,47 %

Wielkości geometryczne [cm]:
h=90,0, d=85,9, x=15,1 (

ξ=0,175),

=4,1, a

=5,7, z

=80,2, A

=527 cm

=-2,13 ‰,

=10,00 ‰,

Wielkości statyczne [kN, kNm]:
F

= -604,52, F

= 631,67,

= 237,51, M

= 258,35,

Warunki równowagi wewnętrznej:
F

=-604,52+(631,67)=27,15 kN (N

=27,15 kN)

=237,51+(258,35)=495,87 kNm (M

=495,87 kNm)

Nośność przekroju prostopadłego:

zadanie hala_monolit, pręt nr 6, przekrój: x

=3,72 m, x

=4,78 m

Wielkości obliczeniowe:
N

=27,15 kN,

√(M

Sdx

+ M

Sdy

) =

√(-495,87

+0,00

)

=495,87 kNm
f

=16,7 MPa, f

=420 MPa (f

=478 MPa -

uwzgl. wzmocnienia) ,
Zbrojenie rozciągane: A

=18,85 cm

Zbrojenie ściskane: A

=6,28 cm

=25,13 cm

ρ=100×A

100

×25,13/3150=0,80 %

Wielkości geometryczne [cm]:
h=90,0, d=85,9, x=27,0 (

ξ=0,314),

=4,1, a

=9,3, z

=76,6,

90,00

35,00

Fs1

h d

2¤20

6¤20

Fs1

Fs2

h d

90,00

35,00

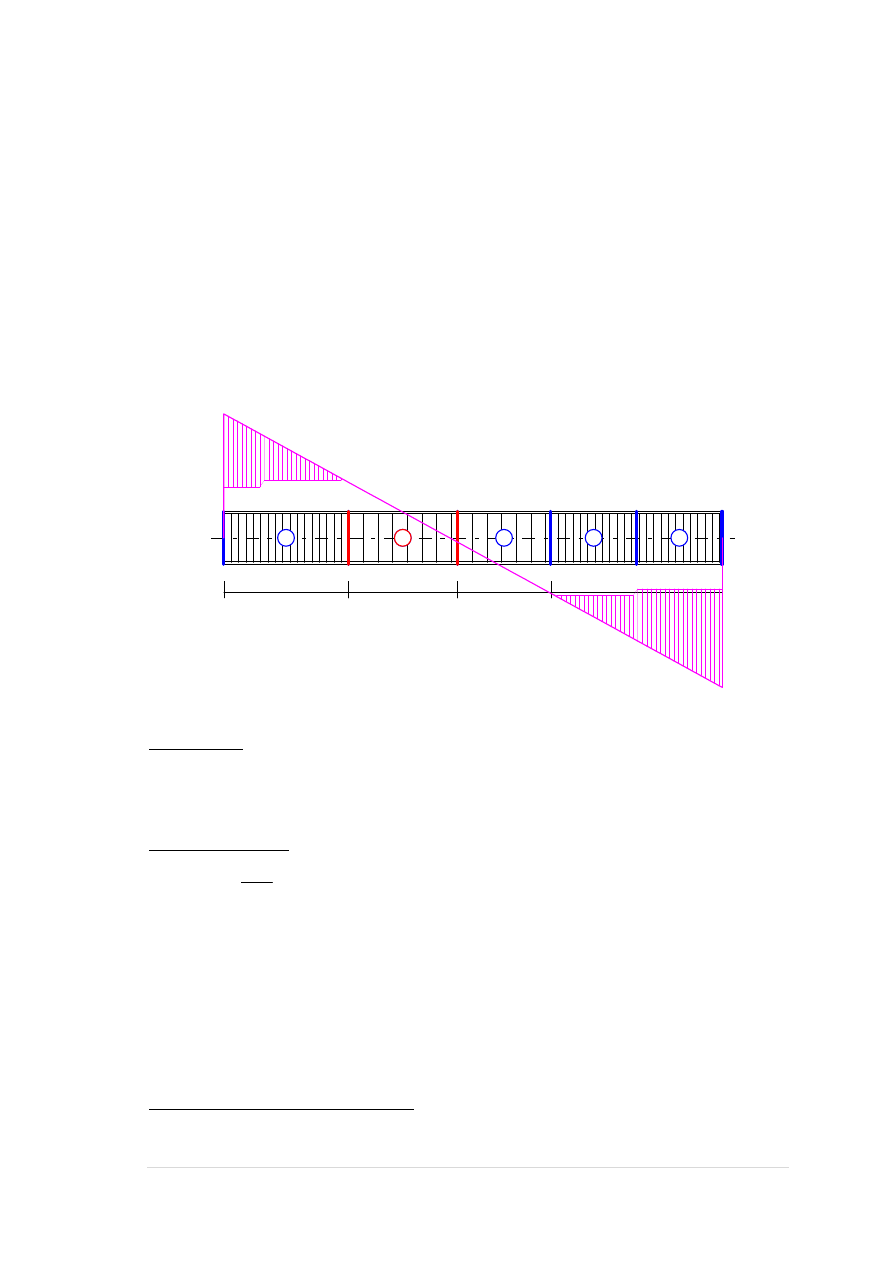
58 |

S t r o n a

=943 cm

=-0,79 ‰,

=-0,67 ‰,

=1,74 ‰,

Wielkości statyczne [kN, kNm]:
F

= -542,71, F

= 654,46, F

= -84,59,

= 193,59, M

= 267,67, M

= 34,60,

Warunek stanu granicznego nośności:

= 639,44 kNm > M

=193,59+(267,67)+(34,60)=495,87 kNm

Ścinanie

zadanie hala_monolit, pręt nr 6.

Przyjęto podparcie i obciążenie bezpośrednie.

Odcinek nr 2
Początek i koniec odcinka: x

= 212,5 x

= 398,4 cm

Siły przekrojowe:

= 27,15;

Sd max

= 177,29 kN

Rodzaj odcinka:

= 0,00627;

≤ 0,01

Przyjęto

= 0,00627.

= N

/ A

= -27,15 / 3150,00 ×10 = -0,09 MPa

≤ 0,2 f

Przyjęto

= 0,00 MPa.

Rd1

= [0,35 k f

ctd

(1,2 + 40

) + 0,15

] b

d =

= [0,35×1,00×1,20×(1,2+40×0,00627) + 0,15×0,00]×35,0×85,9×10

-1

183,19 kN

= 177,29 < 183,19 = V

Rd1

Nośność odcinka I-go rodzaju:

= 177,29 < 183,19 = V

Rd1

212,5

185,9

159,4

292,2

395,10

-476,15

395,10

-476,15

18,85

35,0×85,9

59 |

S t r o n a

ν = 0,6 (1 - f

/ 250) = 0,6×(1 - 25 / 250) = 0,540

Rd2

= 0,5

ν f

z = 0,5×0,540×16,7×35,0×77,3×10

-1

= 1220,07 kN

= 177,29 < 1220,07 = V

Rd2

Nośność zbrojenia podłużnego
Sprawdzenie siły przenoszonej przez zbrojenie rozciągane dla x = 3,719 m:

ΔF

= 0,5 |V

| (cot

θ - V

Rd32

/ V

Rd3

cotα) = 0,5×13,93×(1,000) = 6,96 kN

Sumaryczna siła w zbrojeniu rozciąganym:

= F

td,m

+ ΔF

= 654,45 + 6,96 = 661,41 kN;

≤ F

td,max

= 654,56 kN

Przyjęto F

= 654,56 kN

= 654,56 < 791,68 = 18,85×420 ×10

-1

= A

Zarysowanie

zadanie hala_monolit, pręt nr 6,

Położenie przekroju:

x = 3,719 m

Siły

przekrojowe:

= 441,35 kNm

= 34,09 kN

e = 1294,8 cm

= 12,70 kN

Wymiary

przekroju:

= 35,0 cm

d = h - a

= 90,0 - 4,1 = 85,9 cm

= 3150 cm

= 47250 cm

M i n i m a l n e z b r o j e n i e :
Wymagane pole zbrojenia rozciąganego dla zginania, przy naprężeniach wywołanych
przyczynami zewnętrznymi, wynosi:

= k

k f

ct,eff

s,lim

= 0,4×1,0×2,6×1593 / 500 = 3,31 cm

= 18,85 > 3,31 = A

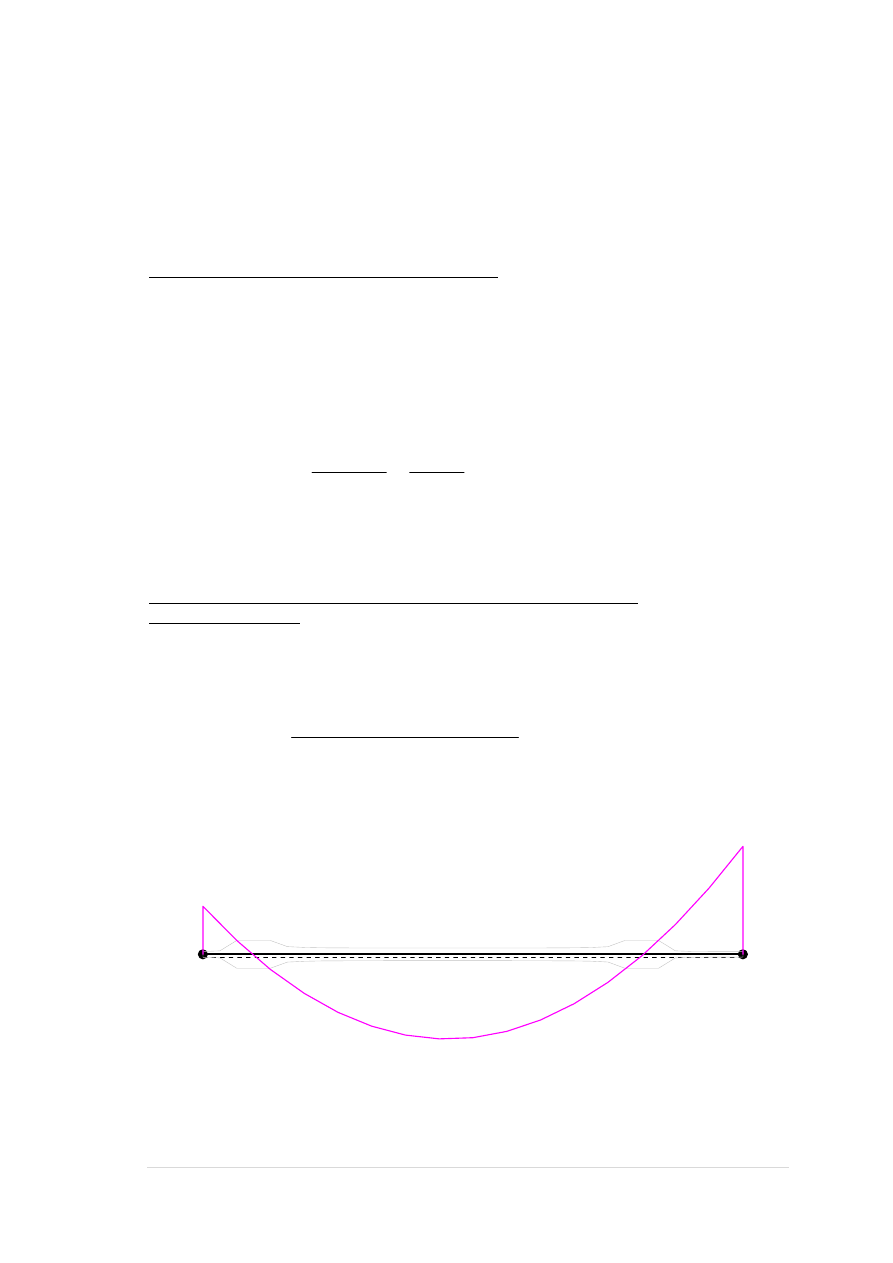
Z a r y s o w a n i e :

= f

ctm

= 2,6×47250 ×10

-3

= 122,85 kNm

×10

-1

= 9,38 kN

= 34,09 > 9,38 = N

Przekrój zarysowany.

S z e r o k o ś ć r o z w a r c i a r y s y p r o s t o p a d ł e j d o o s i p r ę t a :
Przyjęto k

= 0,5.

= A

/ A

ct,eff

= 18,85 / 359 = 0,05254

ctm

2,6

1294,8/47250,00 + 1/3150,00

60 |

S t r o n a

= 50 + 0,25 k

φ / ρ

= 50 + 0,25×0,8×0,50×20/0,05254 = 88,06

/ E

[1 -

(

σsr / σs)

] =

= 310,41/200000 ×[1 - 1,0×0,5×(9,38/34,09)

] = 0,00149

β s

= 1,7×88,06×0,00149 = 0,22 mm

= 0,22 < 0,3 = w

lim

S z e r o k o ś ć r o z w a r c i a r y s y u k o ś n e j :
Rysy ukośne nie występują.

Ugięcia

zadanie hala_monolit, pręt nr 6

Ugięcia wyznaczono dla charakterystycznych obciążeń długotrwałych.
Współczynniki pełzania dla obciążeń długotrwałych przyjęto równy

φ(t,t

) = 1,20.

c,eff

= 14091 MPa

Moment rysujący:

= f

ctm

= 2,6×47250 ×10

-3

= 122,85 kNm

Całkowity moment zginający M

= -563,81 kN powoduje zarysowanie przekroju.

S z t y w n o ś ć d l a d ł u g o t r w a ł e g o d z i a ł a n i a o b c i ą ż e ń
d ł u g o t r w a ł y c h :
Sztywność na zginanie wyznaczona dla momentu M

= -563,81 kNm.

Wielkości geometryczne przekroju:

= 42,9 cm I

= 2707804 cm

= 14,4 cm I

= 519134 cm

B =

×10

-5

= 74582 kNm

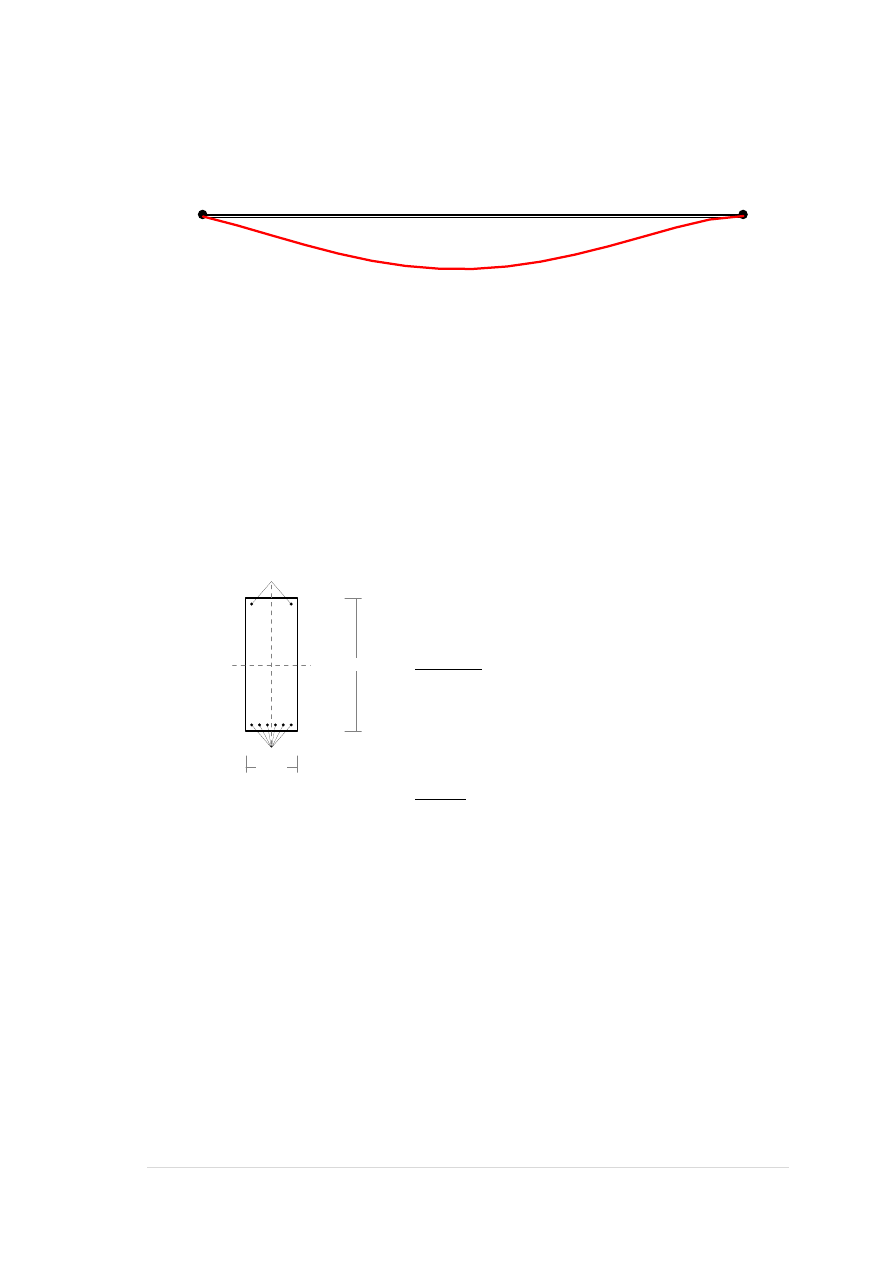
Wykres sztywności i momentów dla obciążeń długotrwałych.

)

(

31000

1 + 1,20

)

(

)

(

eff

−

14091×519134

1 - 1,0×0,5×(122,85/563,81)²×(1 -519134/2707804)

-250,80

-563,81

442,15

-563,81

61 |

S t r o n a

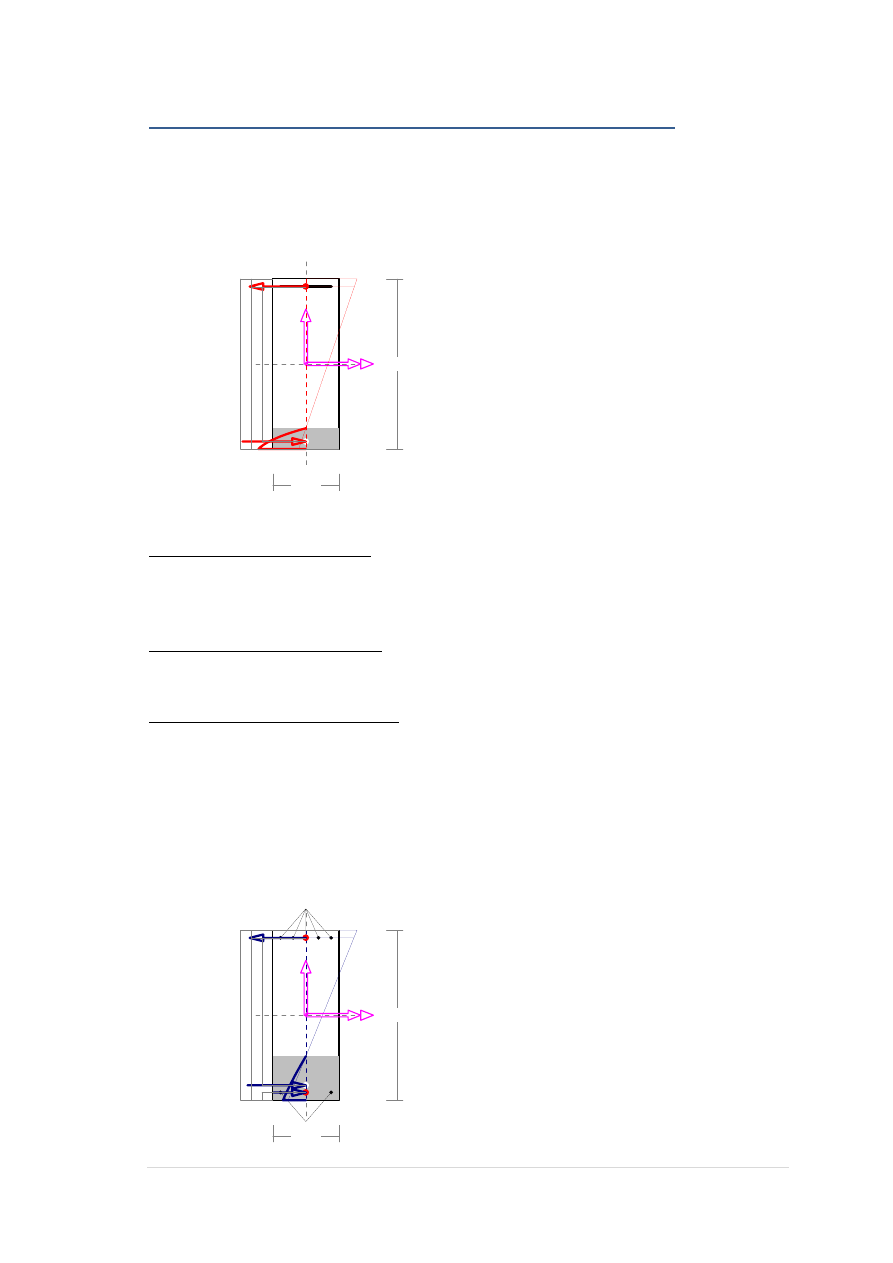
Ugięcia.

Ugięcie w punkcie o współrzędnej x = 3,984 cm, wyznaczone poprzez całkowanie
funkcji krzywizny osi pręta (1/

ρ) z uwzględnieniem zmiany sztywności wzdłuż osi

elementu, wynosi:

a = a

∞,d

= 14,6 mm

a = 14,6 < 34,0 = a

lim

Cechy przekroju:

zadanie hala_monolit, pręt nr 6, przekrój: x

=3,98 m, x

=4,52 m

Wymiary przekroju [cm]:

h=90,0, b=35,0,

Cechy materiałowe dla sytuacji stałej lub
przejściowej
BETON: B30

= 25,0 MPa,

=α·f

=1,00×25,0/1,50=16,7 MPa

Cechy geometryczne przekroju betonowego:

=3150 cm

, J

=2126250 cm

, J

=321563

STAL: A-IIIN (RB 500)

=500 MPa,

=1,15, f

=420 MPa

lim

=0,0035/(0,0035+f

)=0,0035/(0,0035+420/200000)=0,625,

Zbrojenie główne:

=25,13 cm

, ρ=100 (A

)/A

=100×25,13/3150=0,80 %,

=42042 cm

, J

=2708 cm

90,00

35,00

2¤20

6¤20

62 |

S t r o n a

WYMIAROWANIE NA MOMENT PODPOROWY WĘZEŁ 4:

Zbrojenie wymagane:

(zadanie hala_monolit, pręt nr 6, przekrój: x

=0,00 m, x

=8,50 m)

Wielkości obliczeniowe:
N

=63,86 kN,

√(M

Sdx

+ M

Sdy

) =

√(319,14

+0,00

)

=319,14 kNm
f

=16,7 MPa, f

=420 MPa (f

=478 MPa -

uwzgl. wzmocnienia) ,
Zbrojenie rozciągane (

=10,00 ‰):

=9,81 cm

⇒ (4¤20 = 12,57 cm

Dodatkowe zbrojenie ściskane(*As2=0 nie
jest obliczeniowo wymagane.*|* (

1,47 ‰,):
A

=0,00 cm

⇒ (0¤20 = 0,00 cm

) *)

=9,81 cm

ρ=100×A

100

×9,81/3150=0,31 %

Wielkości geometryczne [cm]:
h=90,0, d=85,9, x=11,0 (

ξ=0,128),

=4,1, a

=4,0, z

=81,9, A

=386 cm

=-1,47 ‰,

=10,00 ‰,

Wielkości statyczne [kN, kNm]:
F

= -357,65, F

= 421,51,

= 146,74, M

= 172,40,

Warunki równowagi wewnętrznej:
F

=-357,65+(421,51)=63,86 kN (N

=63,86 kN)

=146,74+(172,40)=319,14 kNm (M

=319,14 kNm)

Nośność przekroju prostopadłego:

zadanie hala_monolit, pręt nr 6, przekrój: x

=0,00 m, x

=8,50 m

Wielkości obliczeniowe:
N

=63,86 kN,

√(M

Sdx

+ M

Sdy

) =

√(319,14

+0,00

)

=319,14 kNm
f

=16,7 MPa, f

=420 MPa (f

=478 MPa -

uwzgl. wzmocnienia) ,
Zbrojenie rozciągane: A

=15,71 cm

Zbrojenie ściskane: A

=6,28 cm

=21,99 cm

ρ=100×A

100

×21,99/3150=0,70 %

Wielkości geometryczne [cm]:
h=90,0, d=85,9, x=23,2 (

ξ=0,270),

90,00

35,00

Fs1

h d

5¤20

2¤20

Fs1

Fs2

h d

90,00

35,00

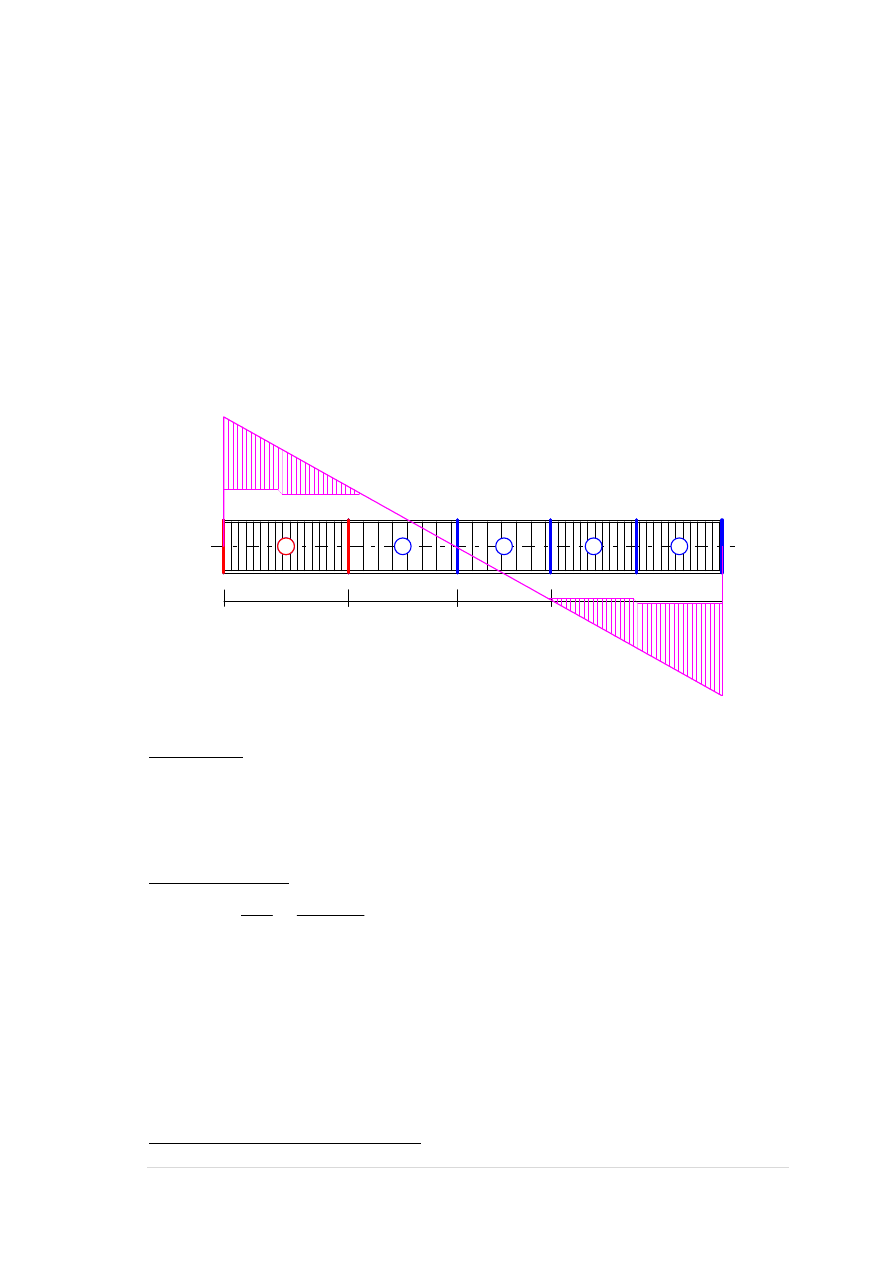
63 |

S t r o n a

=4,1, a

=7,9, z

=78,0, A

=813 cm

=-0,52 ‰,

=-0,42 ‰,

=1,39 ‰,

Wielkości statyczne [kN, kNm]:
F

= -319,82, F

= 437,02, F

= -53,34,

= 118,58, M

= 178,74, M

= 21,82,

Warunek stanu granicznego nośności:

= 508,67 kNm > M

=118,58+(178,74)+(21,82)=319,14 kNm

Ścinanie

zadanie hala_monolit, pręt nr 6.

Przyjęto podparcie i obciążenie bezpośrednie.

Odcinek nr 1
Początek i koniec odcinka: x

= 0,0 x

= 212,5 cm

Siły przekrojowe:

= 63,86;

Sd max

= 404,35 kN

Siła poprzeczna w odległości d od podpory wynosi:

= 316,30 kN

Rodzaj odcinka:

= 0,00209;

≤ 0,01

Przyjęto

= 0,00209.

= N

/ A

= -63,86 / 3150,00 ×10 = -0,20 MPa

≤ 0,2 f

Przyjęto

= 0,00 MPa.

Rd1

= [0,35 k f

ctd

(1,2 + 40

) + 0,15

] b

d =

= [0,35×1,00×1,20×(1,2+40×0,00209) + 0,15×0,00]×35,0×85,9×10

-1

162,08 kN

= 316,30 > 162,08 = V

Rd1

Nośność odcinka II-go rodzaju:

212,5

185,9

159,4

292,2

404,35

-466,90

404,35

-466,90

6,28

35,0×85,9

64 |

S t r o n a

Przyjęto kąt

θ = 45,0°

ν = 0,6 (1 - f

/ 250) = 0,6×(1 - 25 / 250) = 0,540

ΔV

×10

-1

= 0 kN

ΔV

≤

×10

-1

= 0 kN

Przyjęto

ΔV

= 0,00 kN.

Rd2

×10

-1

+ 0,00 = 1220,07 kN

= 404,35 < 1220,07 = V

Rd2

Rd3

= V

Rd31

+ V

Rd32

×10

-1

= 408,03 kN

= 316,30 < 408,03 = V

Rd3

Nośność zbrojenia podłużnego

zadanie hala_monolit, pręt nr 6.

Sprawdzenie siły przenoszonej przez zbrojenie rozciągane dla x = 0,125 m:

ΔF

= 0,5 |V

| (cot

θ - V

Rd32

/ V

Rd3

cotα) = 0,5×404,35×(1,000 - 0,00/408,03

×0,000) = 202,18 kN

Sumaryczna siła w zbrojeniu rozciąganym:

= F

td,m

+ ΔF

= 437,02 + 202,18 = 639,20 kN;

≤ F

td,max

= 437,02 kN

Przyjęto F

= 437,02 kN

= 437,02 < 659,73 = 15,71×420 ×10

-1

= A

Zarysowanie

zadanie hala_monolit, pręt nr 6,

Położenie przekroju:

x = 0,125 m

Siły

przekrojowe:

= -245,95 kNm

= 60,65 kN

e = 405,5 cm

= 354,70 kN

Wymiary

przekroju:

= 35,0 cm

d = h - a

= 90,0 - 4,1 = 85,9 cm

= 3150 cm

= 47250 cm

cos

ywd

cot

0,540×16,7×35,0×77,3 1,000

1 + 1,000²

sin

)

cot

(

cot

ywd

3,14×210

12,5

77,3×1,000

65 |

S t r o n a

M i n i m a l n e z b r o j e n i e :
Wymagane pole zbrojenia rozciąganego dla zginania, przy naprężeniach wywołanych
przyczynami zewnętrznymi, wynosi:

= k

k f

ct,eff

s,lim

= 0,4×1,0×2,6×1517 / 500 = 3,15 cm

= 15,71 > 3,15 = A

Z a r y s o w a n i e :

= f

ctm

= 2,6×47250 ×10

-3

= 122,85 kNm

×10

-1

= 29,21 kN

= 60,65 > 29,21 = N

Przekrój zarysowany.

S z e r o k o ś ć r o z w a r c i a r y s y p r o s t o p a d ł e j d o o s i p r ę t a :
Przyjęto k

= 0,5.

= A

/ A

ct,eff

= 15,71 / 359 = 0,04379

= 50 + 0,25 k

φ / ρ

= 50 + 0,25×0,8×0,50×20/0,04379 = 95,68

/ E

[1 -

(

σsr / σs)

] =

= 217,68/200000 ×[1 - 1,0×0,5×(29,21/60,65)

] = 0,00096

β s

= 1,7×95,68×0,00096 = 0,16 mm

= 0,16 < 0,3 = w

lim

S z e r o k o ś ć r o z w a r c i a r y s y u k o ś n e j :

= 0,00718

= 0,00000

= 0,00718 + 0,00000 = 0,00718

λ =

= 464,20

τ =

= 1,180 MPa

= 0,07 mm

= 0,07 < 0,3 = w

lim

ctm

2,6

405,5/47250,00 + 1/3150,00

3,14

12,5×35,0

sin

⎥

⎦

⎤

⎢

⎣

⎡

3×[0,00718/(1,0×10,0)]

354,70

35,0×85,9

×10

4×1,180²×464,20

0,00718×200000×25

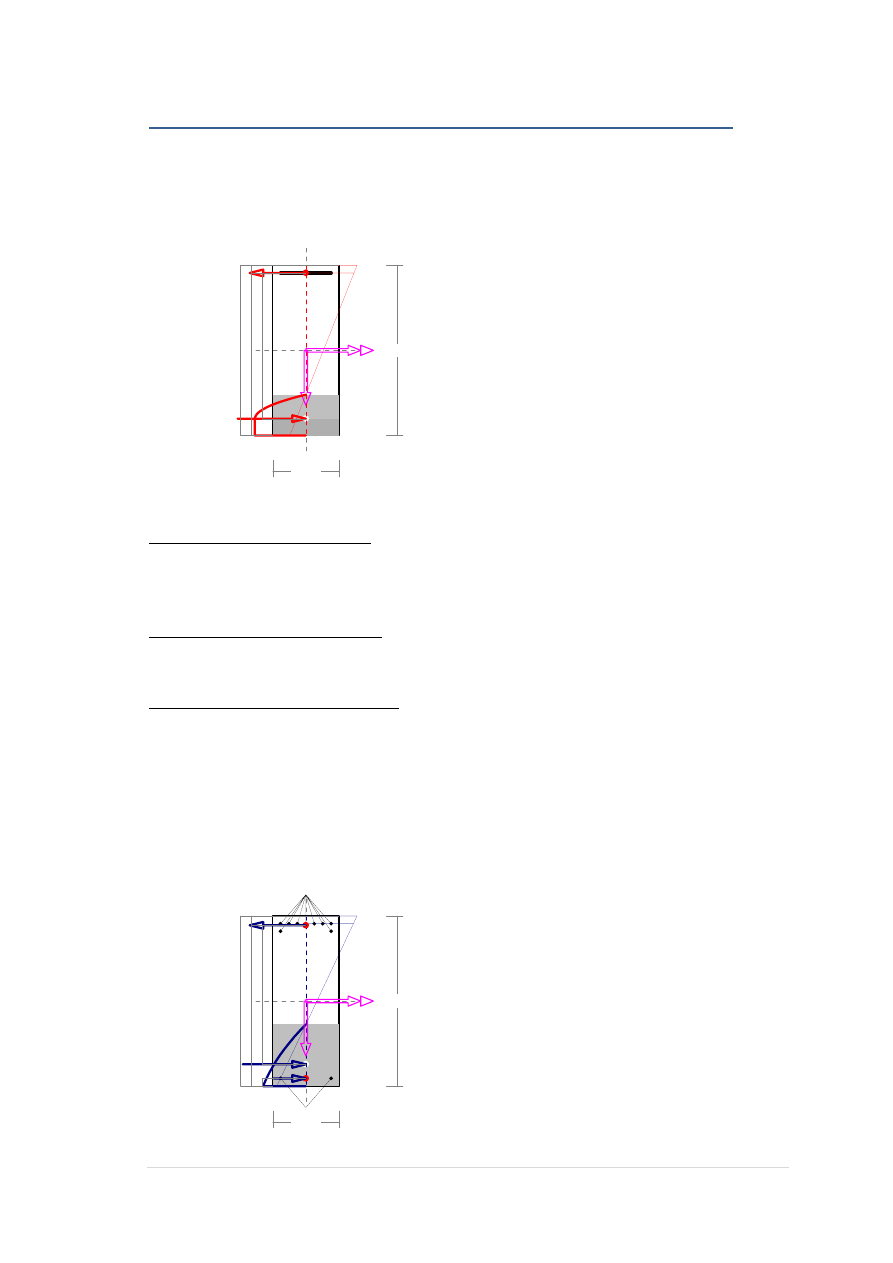
66 |

S t r o n a

WYMIAROWANIE NA MOMENT PODPOROWY W WĘŹLE NR 5:

Zbrojenie wymagane:

(zadanie hala_monolit, pręt nr 6, przekrój: x

=8,50 m, x

=0,00 m)

Wielkości obliczeniowe:
N

=38,71 kN,

√(M

Sdx

+ M

Sdy

) =

√(792,09

+0,00

)

=792,09 kNm
f

=16,7 MPa, f

=420 MPa (f

=478 MPa -

uwzgl. wzmocnienia) ,
Zbrojenie rozciągane (

=10,00 ‰):

=24,36 cm

⇒ (8¤20 = 25,13 cm

Dodatkowe zbrojenie ściskane(*As2=0 nie
jest obliczeniowo wymagane.*|* (

3,35 ‰,):
A

=0,00 cm

⇒ (0¤20 = 0,00 cm

) *)

=24,36 cm

ρ=100×A

100

×24,36/3150=0,77 %

Wielkości geometryczne [cm]:
h=90,0, d=85,9, x=21,5 (

ξ=0,251),

=4,1, a

=8,9, z

=77,0, A

=754 cm

=-3,35 ‰,

=10,00 ‰,

Wielkości statyczne [kN, kNm]:
F

= -1008,00, F

= 1046,70,

= 363,99, M

= 428,10,

Warunki równowagi wewnętrznej:
F

=-1008,00+(1046,70)=38,70 kN (N

=38,71 kN)

=363,99+(428,10)=792,09 kNm (M

=792,09 kNm)

Nośność przekroju prostopadłego:

zadanie hala_monolit, pręt nr 6, przekrój: x

=8,50 m, x

=0,00 m

Wielkości obliczeniowe:
N

=38,71 kN,

√(M

Sdx

+ M

Sdy

) =

√(792,09

+0,00

)

=792,09 kNm
f

=16,7 MPa, f

=420 MPa (f

=478 MPa -

uwzgl. wzmocnienia) ,
Zbrojenie rozciągane: A

=28,27 cm

Zbrojenie ściskane: A

=6,28 cm

=34,56 cm

ρ=100×A

100

×34,56/3150=1,10 %

Wielkości geometryczne [cm]:
h=90,0, d=85,1, x=32,3 (

ξ=0,380),

=4,9, a

=4,1, a

=11,6, z

=73,5,

90,00

35,00

Fs1

h d

9¤20

2¤20

Fs1

Fs2

h d

90,00

35,00

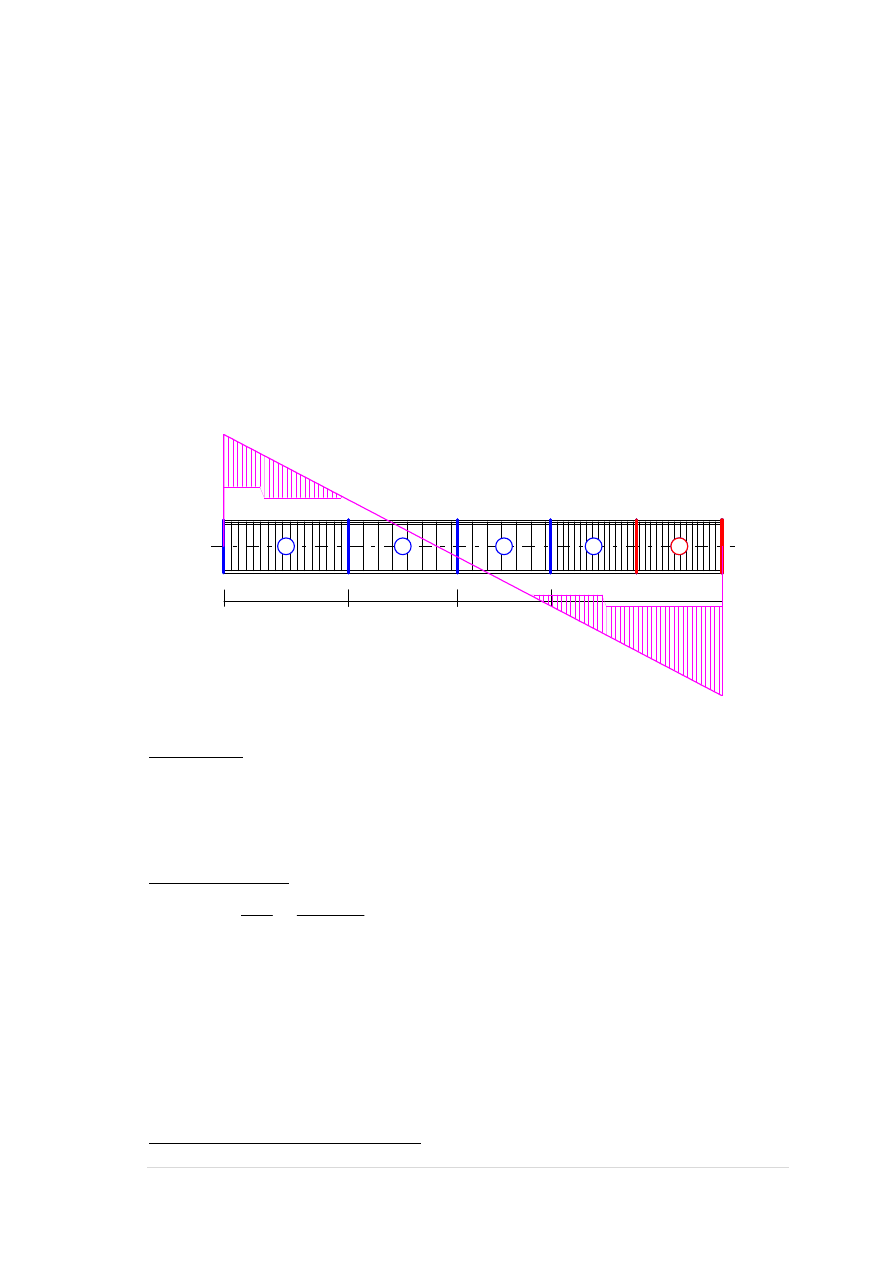
67 |

S t r o n a

=1143 cm

=-1,19 ‰,

=-1,04 ‰,

=1,95 ‰,

Wielkości statyczne [kN, kNm]:
F

= -912,10, F

= 1081,91, F

= -131,10,

= 305,01, M

= 433,46, M

= 53,62,

Warunek stanu granicznego nośności:

= 928,15 kNm > M

=305,01+(433,46)+(53,62)=792,09 kNm

Ścinanie

zadanie hala_monolit, pręt nr 6.

Przyjęto podparcie i obciążenie bezpośrednie.

Odcinek nr 5
Początek i koniec odcinka: x

= 703,9 x

= 850,0 cm

Siły przekrojowe:

= 38,71;

Sd max

= -498,20 kN

Siła poprzeczna w odległości d od podpory wynosi:

= -411,07 kN

Rodzaj odcinka:

= 0,00950;

≤ 0,01

Przyjęto

= 0,00950.

= N

/ A

= -38,71 / 3150,00 ×10 = -0,12 MPa

≤ 0,2 f

Przyjęto

= 0,00 MPa.

Rd1

= [0,35 k f

ctd

(1,2 + 40

) + 0,15

] b

d =

= [0,35×1,00×1,20×(1,2+40×0,00950) + 0,15×0,00]×35,0×85,0×10

-1

197,46 kN

= 411,07 > 197,46 = V

Rd1

Nośność odcinka II-go rodzaju:

212,5

185,9

159,4

292,2

373,05

-498,20

373,05

-498,20

28,27

35,0×85,0

68 |

S t r o n a

Przyjęto kąt

θ = 45,0°

ν = 0,6 (1 - f

/ 250) = 0,6×(1 - 25 / 250) = 0,540

ΔV

×10

-1

= 0 kN

ΔV

≤

×10

-1

= 0 kN

Przyjęto

ΔV

= 0,00 kN.

Rd2

×10

-1

+ 0,00 = 1207,44 kN

= 498,20 < 1207,44 = V

Rd2

Rd3

= V

Rd31

+ V

Rd32

×10

-1

= 504,76 kN

= 411,07 < 504,76 = V

Rd3

Nośność zbrojenia podłużnego

zadanie hala_monolit, pręt nr 6.

Sprawdzenie siły przenoszonej przez zbrojenie rozciągane dla x = 8,500 m:

ΔF

= 0,5 |V

| (cot

θ - V

Rd32

/ V

Rd3

cotα) = 0,5×-498,20×(1,000 - 0,00/504,76

×0,000) = 249,10 kN

Sumaryczna siła w zbrojeniu rozciąganym:

= F

td,m

+ ΔF

= 1081,91 + 249,10 = 1331,01 kN;

≤ F

td,max

= 1081,91 kN

Przyjęto F

= 1081,91 kN

= 1081,91 < 1187,52 = 28,27×420 ×10

-1

= A

Zarysowanie

zadanie hala_monolit, pręt nr 6,

Położenie przekroju:

x = 8,500 m

Siły

przekrojowe:

= -716,27 kNm

= 43,72 kN

e = 1638,3 cm

= -451,55 kN

Wymiary

przekroju:

= 35,0 cm

d = h - a

= 90,0 - 5,0 = 85,0 cm

= 3150 cm

= 47250 cm

cos

ywd

cot

0,540×16,7×35,0×76,5 1,000

1 + 1,000²

sin

)

cot

(

cot

ywd

3,14×210

10,0

76,5×1,000

69 |

S t r o n a

M i n i m a l n e z b r o j e n i e :
Wymagane pole zbrojenia rozciąganego dla zginania, przy naprężeniach wywołanych
przyczynami zewnętrznymi, wynosi:

= k

k f

ct,eff

s,lim

= 0,4×1,0×2,6×1561 / 500 = 3,25 cm

= 28,27 > 3,25 = A

Z a r y s o w a n i e :

= f

ctm

= 2,6×47250 ×10

-3

= 122,85 kNm

×10

-1

= 7,43 kN

= 43,72 > 7,43 = N

Przekrój zarysowany.

S z e r o k o ś ć r o z w a r c i a r y s y p r o s t o p a d ł e j d o o s i p r ę t a :
Przyjęto k

= 0,5.

= A

/ A

ct,eff

= 28,27 / 437 = 0,06477

= 50 + 0,25 k

φ / ρ

= 50 + 0,25×0,8×0,50×20/0,06477 = 80,88

/ E

[1 -

(

σsr / σs)

] =

= 349,79/200000 ×[1 - 1,0×0,5×(7,43/43,72)

] = 0,00172

β s

= 1,7×80,88×0,00172 = 0,24 mm

= 0,24 < 0,3 = w

lim

S z e r o k o ś ć r o z w a r c i a r y s y u k o ś n e j :

= 0,00898

= 0,00000

= 0,00898 + 0,00000 = 0,00898

λ =

= 371,36

τ =

= 1,518 MPa

= 0,08 mm

= 0,08 < 0,3 = w

lim

ctm

2,6

1638,3/47250,00 + 1/3150,00

3,14

10,0×35,0

sin

⎥

⎦

⎤

⎢

⎣

⎡

3×[0,00898/(1,0×10,0)]

-451,55

35,0×85,0

×10

4×1,518²×371,36

0,00898×200000×25

70 |

S t r o n a

9.2. RYGIEL NR 89, (węzeł 79):

Cechy przekroju:

zadanie hala_monolit, pręt nr 8, przekrój: x

=8,53 m, x

=0,00 m

Wymiary przekroju [cm]:

h=120,0, b=35,0,

Cechy materiałowe dla sytuacji stałej lub
przejściowej
BETON: B30

= 25,0 MPa,

=α·f

=1,00×25,0/1,50=16,7 MPa

Cechy geometryczne przekroju betonowego:

=4200 cm

, J

=5040000 cm

, J

=428750

Siły przekrojowe:

PRZĘSŁO – przekrój: x

=8,53 m, x

=0,00 m

Obciążenia działające w płaszczyźnie układu: AD
Momenty zginające:

= -1194,27 kNm,

= 0,00 kNm,

Siły poprzeczne:

= -8,36 kN,

= 0,00 kN,

Siła osiowa:

N = -104,50 kN = N

Uwzględnienie smukłości pręta:
- w płaszczyźnie ustroju:

= M

/N = (-1194,27)/(-104,50)=11,428 m,

Sdx

= η

+ e

) N = 1,011×(0,040 +11,428)×(-104,50) = -1212,08 kNm,.

PODPORA W WĘŹLE NR 7 - przekrój: x

=0,00 m, x

=8,53 m

Obciążenia działające w płaszczyźnie układu: ACD
Momenty zginające:

= 309,31 kNm,

= 0,00 kNm,

Siły poprzeczne:

= 357,27 kN,

= 0,00 kN,

Siła osiowa:

N = -140,67 kN = N

Uwzględnienie smukłości pręta:
- w płaszczyźnie ustroju:

= M

/N = (309,31)/(-140,67)=-2,199 m,

Sdx

= η

+ e

) N = 1,012×(-0,040 -2,199)×(-140,67) = 318,75 kNm,.

PODPORA W WĘŹLE NR 9 - przekrój: x

=8,53 m, x

=0,00 m

Obciążenia działające w płaszczyźnie układu: ABD
Momenty zginające:

= 309,31 kNm,

= 0,00 kNm,

Siły poprzeczne:

= -357,27 kN,

= 0,00 kN,

Siła osiowa:

N = -140,67 kN = N

Uwzględnienie smukłości pręta:
- w płaszczyźnie ustroju:

= M

/N = (309,31)/(-140,67)=-2,199 m,

Sdx

= η

+ e

) N = 1,012×(-0,040 -2,199)×(-140,67) = 318,75 kNm,.

120,00

35,00

71 |

S t r o n a

Zbrojenie wymagane:

dla

∅22

1111

111

2222

3333

44444

55555

66666666777777777777777

8,50

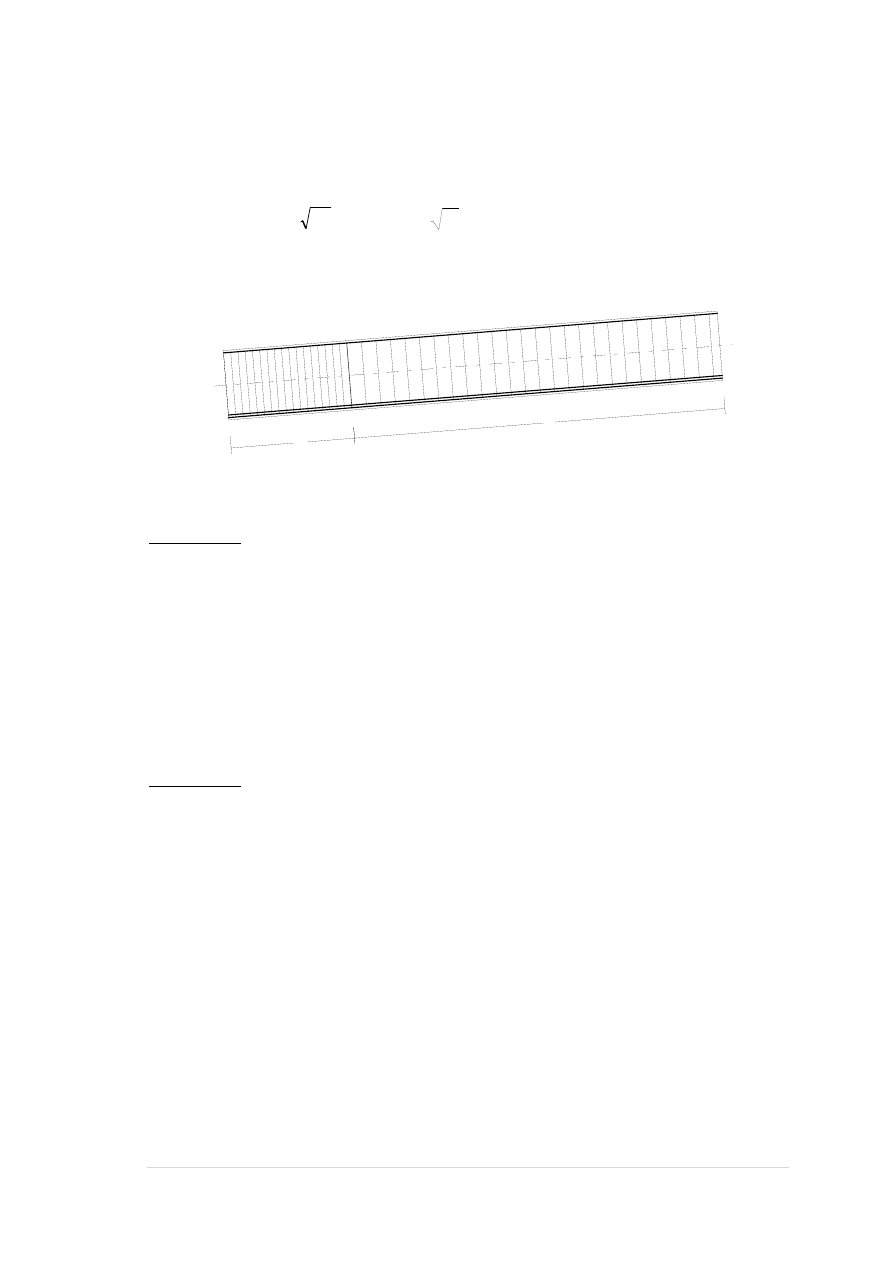
72 |

S t r o n a

Zbrojenie poprzeczne (strzemiona)
Na całej długości pręta przyjęto strzemiona o średnicy

φ=10 mm ze stali A-I, dla której

ywd

= 210 MPa.

Minimalny stopień zbrojenia na ścinanie:

w,min

= 0,08

/ f

= 0,08×

/ 500 = 0,00080

Rozstaw strzemion:
Strefa nr 1

Początek i koniec strefy:

= 0,0 x

= 213,2 cm

Maksymalny rozstawy strzemion:

max

= 0,75 d = 0,75×1147 = 860 s

max

≤ 400 mm

przyjęto s

max

= 400 mm.

Ze względu na pręty ściskane s

max

= 15

φ = 15×22,0 = 330,0 mm.

Przyjęto strzemiona 4-cięte, prostopadłe do osi pręta o rozstawie 12,5 cm, dla
których stopień zbrojenia na ścinanie wynosi:

= A

/(s b

sin

α) = 3,14 / (12,5×35,0×1,000) = 0,00718

= 0,00718 > 0,00080 =

w min

Strefa nr 2

Początek i koniec strefy:

= 213,2 x

= 852,7 cm

Maksymalny rozstawy strzemion:

max

= 0,75 d = 0,75×1147 = 860 s

max

≤ 400 mm

przyjęto s

max

= 400 mm.

Przyjęto strzemiona 4-cięte, prostopadłe do osi pręta o rozstawie 25,0 cm, dla
których stopień zbrojenia na ścinanie wynosi:

= A

/(s b

sin

α) = 3,14 / (25,0×35,0×1,000) = 0,00359

= 0,00359 > 0,00080 =

w min

213,2

639,5

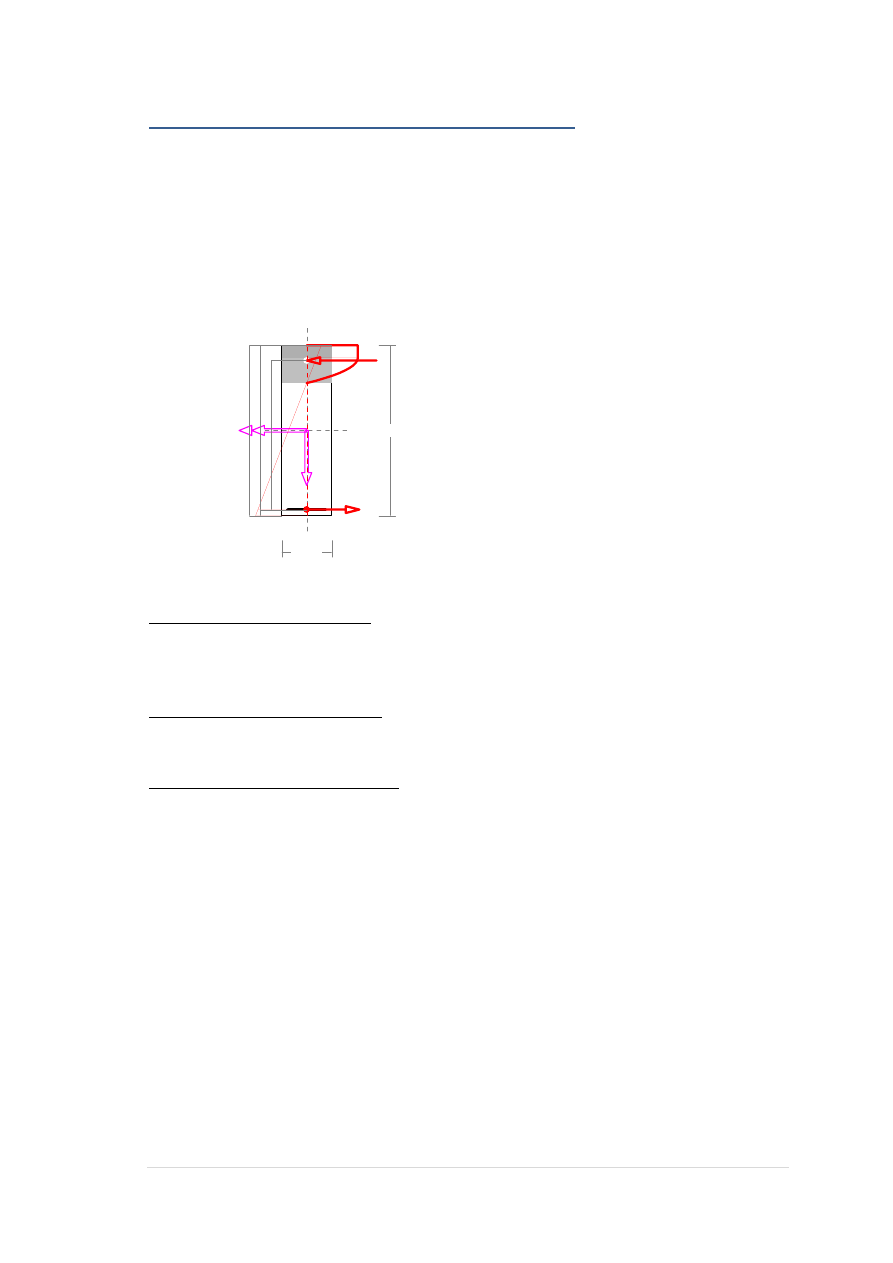
73 |

S t r o n a

WYMIAROWANIE NA MOMENT PRZĘSŁOWY:

Zbrojenie wymagane:

(zadanie hala_monolit, pręt nr 8, przekrój: x

=8,53 m, x

=0,00 m)

Obliczenia wykonano:
- dla kombinacji [AD] grup obciążeń, dla której suma zbrojenia wymaganego jest
największa

Wielkości obliczeniowe:
N

=-104,50 kN,

√(M

Sdx

+ M

Sdy

) =

√(-1213,68

+0,00

)

=1213,68 kNm
f

=16,7 MPa, f

=420 MPa (f

=478 MPa -

uwzgl. wzmocnienia) ,
Zbrojenie rozciągane (

=10,00 ‰):

=25,76 cm

⇒ (7¤22 = 26,61 cm

Dodatkowe zbrojenie ściskane(*As2=0 nie
jest obliczeniowo wymagane.*|* (

2,99 ‰,):
A

=0,00 cm

⇒ (0¤22 = 0,00 cm

) *)

=25,76 cm

ρ=100×A

100

×25,76/4200=0,61 %

Wielkości geometryczne [cm]:
h=120,0, d=115,8, x=26,7 (

ξ=0,230),

=4,2, a

=10,8, z

=105,0, A

=933 cm

=-2,99 ‰,

=10,00 ‰,

Wielkości statyczne [kN, kNm]:
F

= -1211,28, F

= 1106,78,

= 596,10, M

= 617,58,

Warunki równowagi wewnętrznej:
F

=-1211,28+(1106,78)=-104,50 kN (N

=-104,50 kN)

=596,10+(617,58)=1213,68 kNm (M

=1213,68 kNm)

Nośność przekroju prostopadłego:

zadanie hala_monolit, pręt nr 8, przekrój: x

=8,53 m, x

=0,00 m

Obliczenia wykonano dla kombinacji [AD] grup obciążeń, dla której warunek stanu
granicznego nośności przekroju jest najniekorzystniejszy

120,00

35,00

Fs1

h d

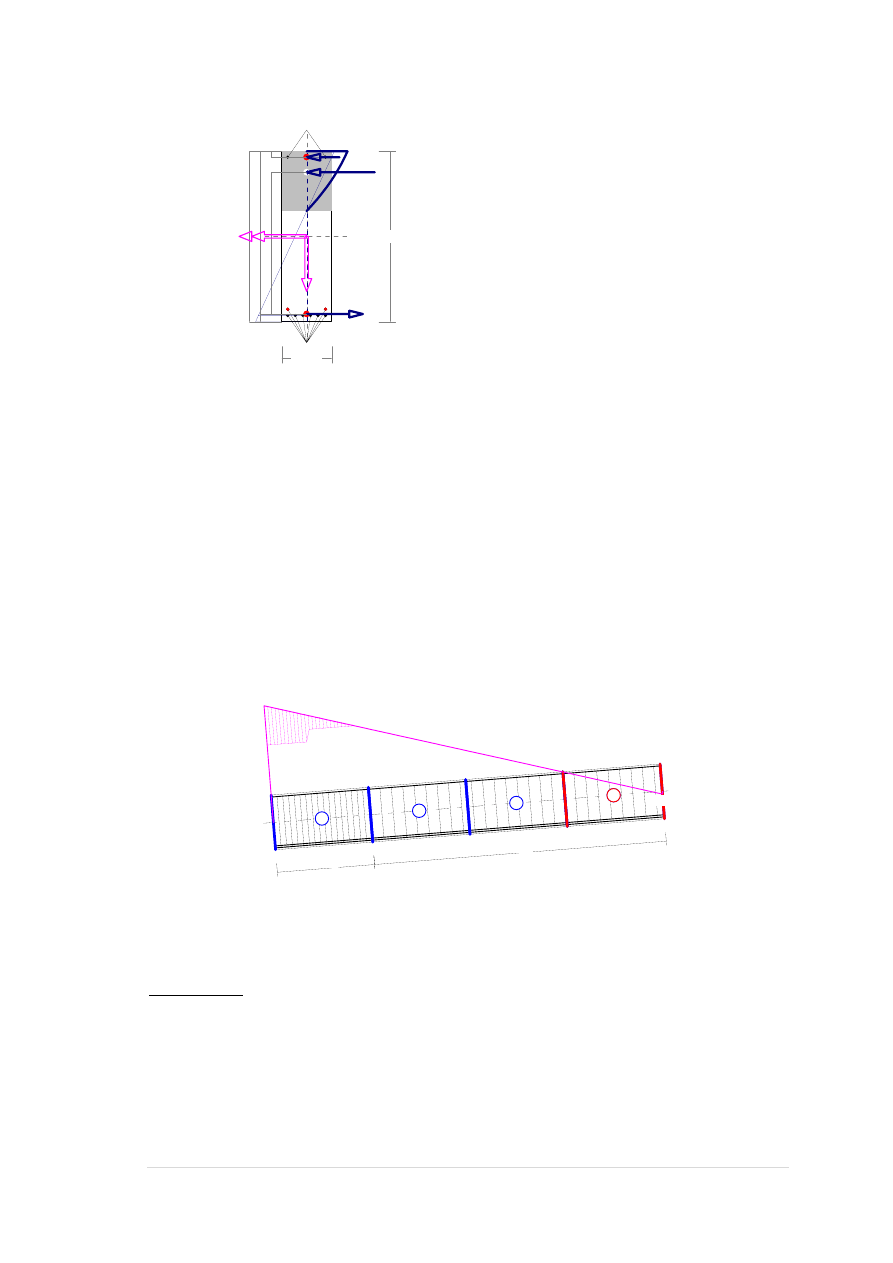
74 |

S t r o n a

Wielkości obliczeniowe:
N

=-104,50 kN,

√(M

Sdx

+ M

Sdy

) =

√(-1213,68

+0,00

)

=1213,68 kNm
f

=16,7 MPa, f

=420 MPa (f

=478 MPa -

uwzgl. wzmocnienia) ,
Zbrojenie rozciągane: A

=30,41 cm

Zbrojenie ściskane: A

=7,60 cm

=38,01 cm

ρ=100×A

100

×38,01/4200=0,91 %

Wielkości geometryczne [cm]:
h=120,0, d=114,8, x=41,8 (

ξ=0,364),

=5,2, a

=4,2, a

=14,8, z

=99,9,

=1475 cm

=-1,10 ‰,

=-0,99 ‰,

=1,92 ‰,

Wielkości statyczne [kN, kNm]:
F

= -1105,46, F

= 1151,42, F

= -150,47,

= 499,32, M

= 630,40, M

= 83,96,

Warunek stanu granicznego nośności:

= 1448,41 kNm > M

=499,32+(630,40)+(83,96)=1213,68 kNm

Ścinanie
Przyjęto podparcie i obciążenie bezpośrednie.

Odcinek nr 4
Początek i koniec odcinka: x

= 639,5 x

= 852,7 cm

Siły przekrojowe:

= -111,80;

Sd max

= 82,86 kN

Siła poprzeczna w odległości d od podpory wynosi:

= 82,86 kN

213,2

639,5

356,50

-8,36

356,50

-8,36

2¤22

8¤22

Fs1

Fs2

h d

120,00

35,00

75 |

S t r o n a

Rodzaj odcinka:

= 0,00758;

≤ 0,01

Przyjęto

= 0,00758.

= N

/ A

= 111,80 / 4200,00 ×10 = 0,27 MPa

≤ 0,2 f

Przyjęto

= 0,27 MPa.

Rd1

= [0,35 k f

ctd

(1,2 + 40

) + 0,15

] b

d =

= [0,35×1,00×1,20×(1,2+40×0,00758) + 0,15×0,27]×35,0×114,7×10

-1

269,45 kN

= 82,86 < 269,45 = V

Rd1

Nośność odcinka I-go rodzaju:

= 82,86 < 269,45 = V

Rd1

ν = 0,6 (1 - f

/ 250) = 0,6×(1 - 25 / 250) = 0,540

Rd2

= 0,5

ν f

z = 0,5×0,540×16,7×35,0×99,9×10

-1

= 1576,75 kN

= 1 +

= 1 + 0,27/16,7 = 1,016

Rd2,red

= α

VRd2 =1,016×1576,75 = 1601,88 kN

Przyjęto V

Rd2,red

= 1576,75 kN

= 82,86 < 1576,75 = V

Rd2,red

Nośność zbrojenia podłużnego
Sprawdzenie siły przenoszonej przez zbrojenie rozciągane dla x = 8,527 m:

ΔF

= 0,5 |V

| (cot

θ - V

Rd32

/ V

Rd3

cotα) = 0,5×-8,36×(1,000) = 4,18 kN

Sumaryczna siła w zbrojeniu rozciąganym:

= F

td,m

+ ΔF

= 1151,42 + 4,18 = 1155,60 kN;

≤ F

td,max

= 1151,82 kN

Przyjęto F

= 1151,82 kN

= 1151,82 < 1277,25 = 30,41×420 ×10

-1

= A

Zarysowanie

zadanie hala_monolit, pręt nr 8,

Położenie przekroju:

x = 8,527 m

Siły

przekrojowe:

= 1095,00 kNm

= -96,82 kN

e = 1134,9 cm

= -7,75 kN

Wymiary

przekroju:

= 35,0 cm

d = h - a

= 120,0 - 5,3 = 114,7 cm

= 4200 cm

= 84000 cm

30,41

35,0×114,7

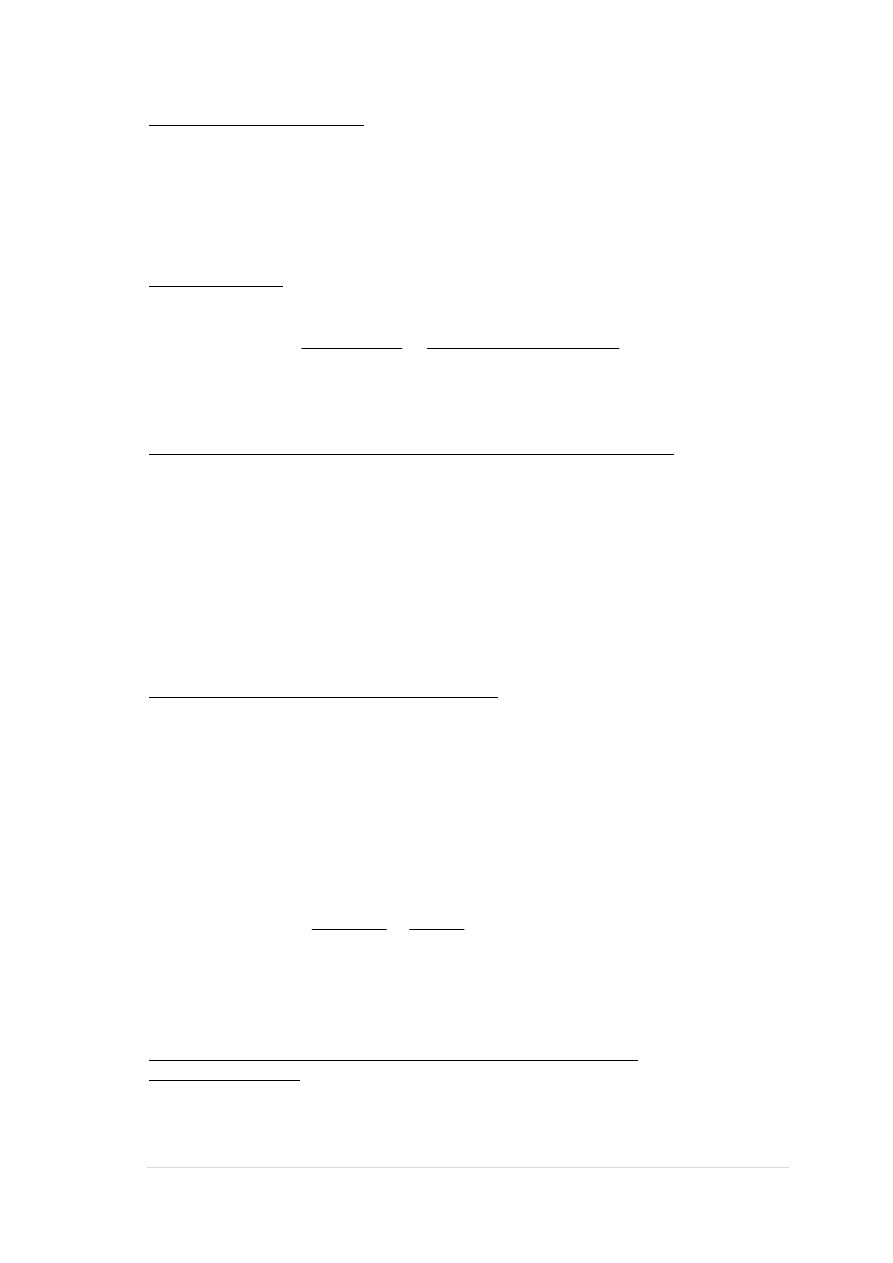
76 |

S t r o n a

M i n i m a l n e z b r o j e n i e :
Wymagane pole zbrojenia rozciąganego dla zginania, przy naprężeniach wywołanych
przyczynami zewnętrznymi, wynosi:

= k

k f

ct,eff

s,lim

= 0,4×1,0×2,6×2063 / 215 = 9,98 cm

= 30,41 > 9,98 = A

Z a r y s o w a n i e :

= f

ctm

= 2,6×84000 ×10

-3

= 218,40 kNm

×10

-1

= -19,59 kN

= 96,82 > 19,59 = N

Przekrój zarysowany.

S z e r o k o ś ć r o z w a r c i a r y s y p r o s t o p a d ł e j d o o s i p r ę t a :
Przyjęto k

= 0,5.

= A

/ A

ct,eff

= 30,41 / 464 = 0,06558

= 50 + 0,25 k

φ / ρ

= 50 + 0,25×0,8×0,50×22/0,06558 = 83,55

/ E

[1 -

(

σsr / σs)

] =

= 349,21/200000 ×[1 - 1,0×0,5×(-19,59/96,82)

] = 0,00171

β s

= 1,7×83,55×0,00171 = 0,24 mm

= 0,24 < 0,3 = w

lim

S z e r o k o ś ć r o z w a r c i a r y s y u k o ś n e j :
Rysy ukośne nie występują.

Ugięcia
W obliczeniach uwzględniono 10 prętów dołem oraz dodatkowe pręty potrzebne
z racji wysokiego przekroju, jako pręty zmniejszające ugiecie.
Ugięcia wyznaczono dla charakterystycznych obciążeń długotrwałych.
Współczynniki pełzania dla obciążeń długotrwałych przyjęto równy

φ(t,t

) = 1,20.

c,eff

= 14091 MPa

Moment rysujący:

= f

ctm

= 2,6×84000 ×10

-3

= 218,40 kNm

Całkowity moment zginający M

= 1095,67 kN powoduje zarysowanie przekroju.

S z t y w n o ś ć d l a d ł u g o t r w a ł e g o d z i a ł a n i a o b c i ą ż e ń
d ł u g o t r w a ł y c h :
Sztywność na zginanie wyznaczona dla momentu M

= 1095,67 kNm.

Wielkości geometryczne przekroju:

= 63,5 cm I

= 7532192 cm

ctm

−

2,6

1134,9/84000,00 - 1/4200,00

)

(

31000

1 + 1,20

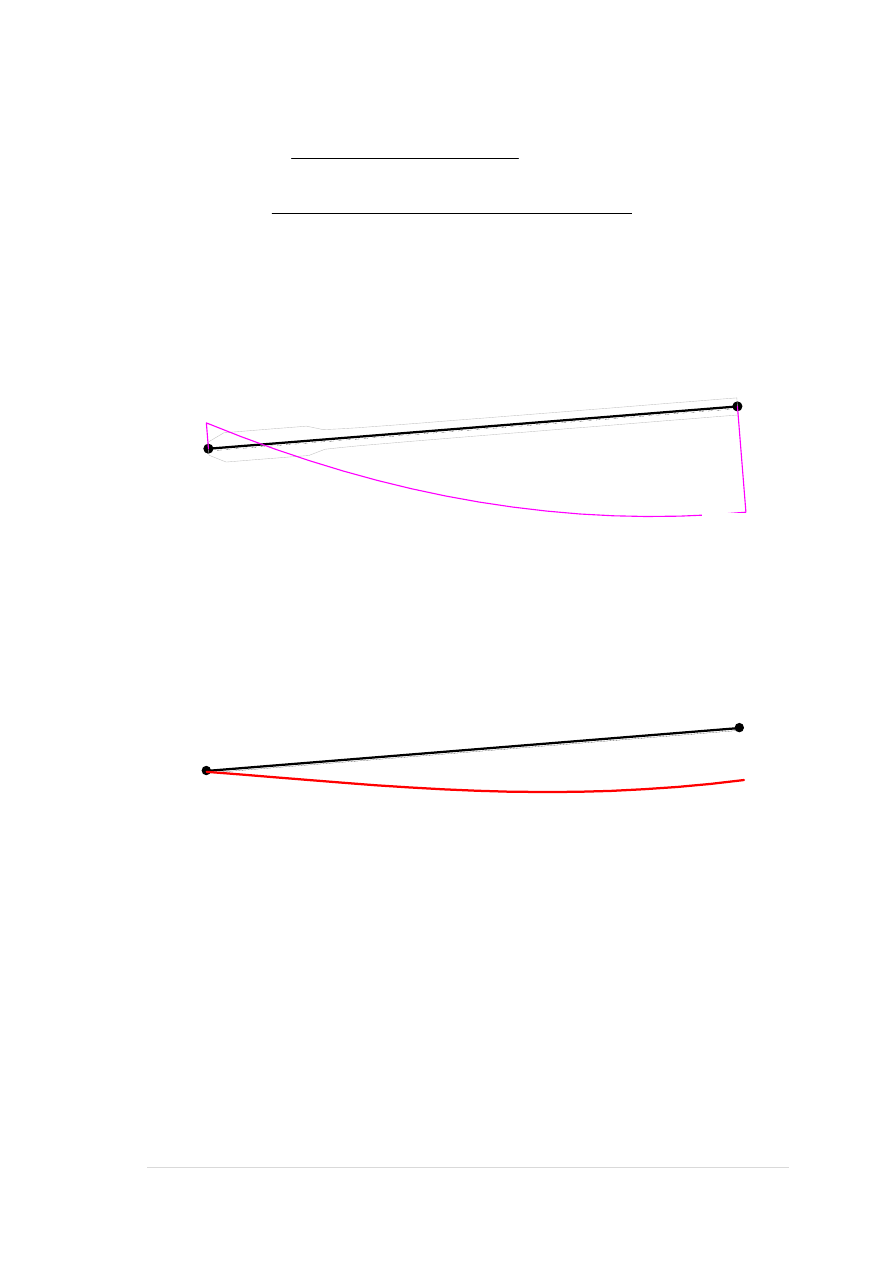
77 |

S t r o n a

= 43,5 cm I

= 4362095 cm

B =

×10

-5

= 619841

kNm

Wykres sztywności i momentów dla obciążeń długotrwałych.

Ugięcia.

Ugięcie w punkcie o współrzędnej x = 7,461 cm, wyznaczone poprzez całkowanie
funkcji krzywizny osi pręta (1/

ρ) z uwzględnieniem zmiany sztywności wzdłuż osi

elementu, wynosi:

a = a

∞,d

= 33,9 mm

a = 33,9 < 34,1 = a

lim

)

(

)

(

eff

−

14091×4362095

1 - 1,0×0,5×(218,40/1095,67)²×(1 -4362095/7532192)

-267,98

1095,00

-267,98

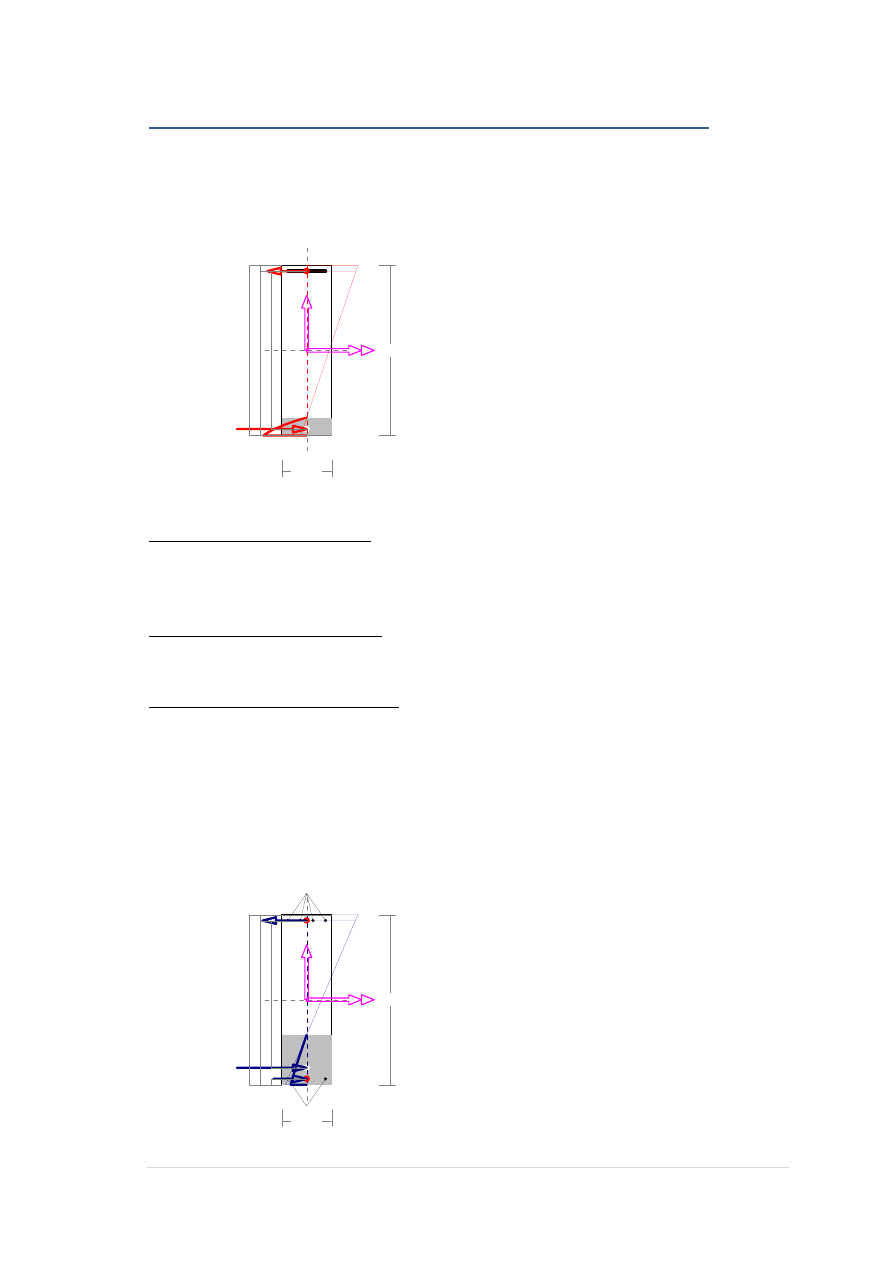
78 |

S t r o n a

WYMIAROWANIE NA MOMENT PODPOROWY WĘZEŁ 7 (9):

Zbrojenie wymagane:

(zadanie hala_monolit, pręt nr 8, przekrój: x

=0,00 m, x

=8,53 m)

Wielkości obliczeniowe:
N

=-140,67 kN,

√(M

Sdx

+ M

Sdy

) =

√(319,91

+0,00

)

=319,91 kNm
f

=16,7 MPa, f

=420 MPa (f

=478 MPa -

uwzgl. wzmocnienia) ,
Zbrojenie rozciągane (

=10,00 ‰):

=5,06 cm

< min A

=6,08 cm

, przyjęto

=6,08 cm

⇒ (2¤22 = 7,60 cm

Dodatkowe zbrojenie ściskane(*As2=0 nie
jest obliczeniowo wymagane.*|* (

1,22 ‰,):
A

=0,00 cm

⇒ (0¤22 = 0,00 cm

) *)

=5,06 cm

ρ=100×A

= 100

×5,06/4200=0,12 %

Wielkości geometryczne [cm]:
h=120,0, d=115,8, x=12,6 (

ξ=0,109),

=4,2, a

=4,5, z

=111,3, A

=441 cm

=-1,22 ‰,

=10,00 ‰,

Wielkości statyczne [kN, kNm]:
F

= -357,85, F

= 217,18,

= 198,73, M

= 121,19,

Warunki równowagi wewnętrznej:
F

=-357,85+(217,18)=-140,67 kN (N

=-140,67 kN)

=198,73+(121,19)=319,91 kNm (M

=319,91 kNm)

Nośność przekroju prostopadłego:

zadanie hala_monolit, pręt nr 8, przekrój: x

=0,00 m, x

=8,53 m

Wielkości obliczeniowe:
N

=-140,67 kN,

√(M

Sdx

+ M

Sdy

) =

√(321,13

+0,00

)

=321,13 kNm
f

=16,7 MPa, f

=420 MPa (f

=478 MPa -

uwzgl. wzmocnienia) ,
Zbrojenie rozciągane: A

=15,21 cm

Zbrojenie ściskane: A

=7,60 cm

=22,81 cm

ρ=100×A

100

×22,81/4200=0,54 %

Wielkości geometryczne [cm]:
h=120,0, d=115,8, x=35,2 (

ξ=0,304),

=4,2, a

=11,9, z

=103,9,

120,00

35,00

Fs1

h d

4¤22

2¤22

Fs1

Fs2

h d

120,00

35,00

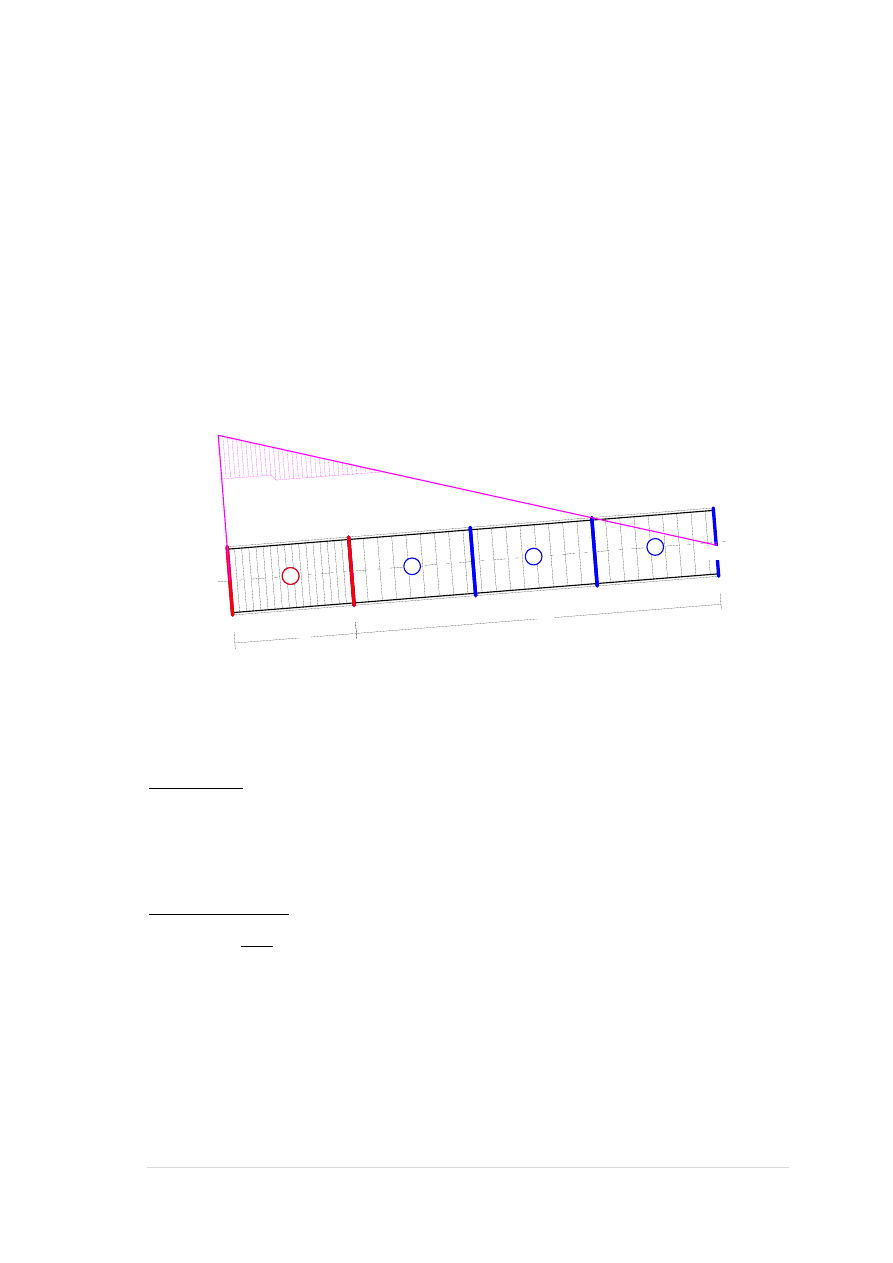
79 |

S t r o n a

=1232 cm

=-0,35 ‰,

=-0,30 ‰,

=0,79 ‰,

Wielkości statyczne [kN, kNm]:
F

= -334,97, F

= 240,57, F

= -46,27,

= 161,08, M

= 134,24, M

= 25,82,

Warunek stanu granicznego nośności:

= 928,23 kNm > M

=161,08+(134,24)+(25,82)=321,13 kNm

Ścinanie

zadanie hala_monolit, pręt nr 8.

Przyjęto podparcie i obciążenie bezpośrednie.

Odcinek nr 1
Początek i koniec odcinka: x

= 0,0 x

= 213,2 cm

Siły przekrojowe:

= -140,67;

Sd max

= 357,27 kN

Siła poprzeczna w odległości d od podpory wynosi:

= 307,72 kN

Rodzaj odcinka:

= 0,00188;

≤ 0,01

Przyjęto

= 0,00188.

= N

/ A

= 140,67 / 4200,00 ×10 = 0,33 MPa

≤ 0,2 f

Przyjęto

= 0,33 MPa.

Rd1

= [0,35 k f

ctd

(1,2 + 40

) + 0,15

] b

d =

= [0,35×1,00×1,20×(1,2+40×0,00188) + 0,15×0,33]×35,0×115,8×10

-1

237,41 kN

= 307,72 > 237,41 = V

Rd1

213,2

639,5

357,27

-7,59

357,27

-7,59

7,60

35,0×115,8

80 |

S t r o n a

Nośność odcinka II-go rodzaju:
Przyjęto kąt

θ = 45,0°

ν = 0,6 (1 - f

/ 250) = 0,6×(1 - 25 / 250) = 0,540

ΔV

×10

-1

= 0 kN

ΔV

≤

×10

-1

= 0 kN

Przyjęto

ΔV

= 0,00 kN.

Rd2

×10

-1

+ 0,00 = 1327,24 kN

= 1 +

= 1 + 0,33/16,7 = 1,020

Rd2,red

= α

VRd2 =1,020×1327,24 = 1353,86 kN

Przyjęto V

Rd2,red

= 1327,24 kN

= 357,27 < 1327,24 = V

Rd2,red

Rd3

= V

Rd31

+ V

Rd32

×10

-1

= 443,88 kN

= 307,72 < 443,88 = V

Rd3

Nośność zbrojenia podłużnego
Sprawdzenie siły przenoszonej przez zbrojenie rozciągane dla x = 0,136 m:

ΔF

= 0,5 |V

| (cot

θ - V

Rd32

/ V

Rd3

cotα) = 0,5×345,87×(1,000 - 0,00/443,88

×0,000) = 172,93 kN

Sumaryczna siła w zbrojeniu rozciąganym:

= F

td,m

+ ΔF

= 152,14 + 172,93 = 325,07 kN;

≤ F

td,max

= 240,57 kN

Przyjęto F

= 240,57 kN

= 240,57 < 638,62 = 15,21×420 ×10

-1

= A

Zarysowanie
Położenie przekroju:

x = 0,201 m

Siły

przekrojowe:

= -218,84 kNm

= -128,82 kN

e = 173,9 cm

= 320,16 kN

Wymiary

przekroju:

= 35,0 cm

d = h - a

= 120,0 - 4,2 = 115,8 cm

cos

ywd

cot

0,540×16,7×35,0×84,1 1,000

1 + 1,000²

sin

)

cot

(

cot

ywd

3,14×210

12,5

84,1×1,000

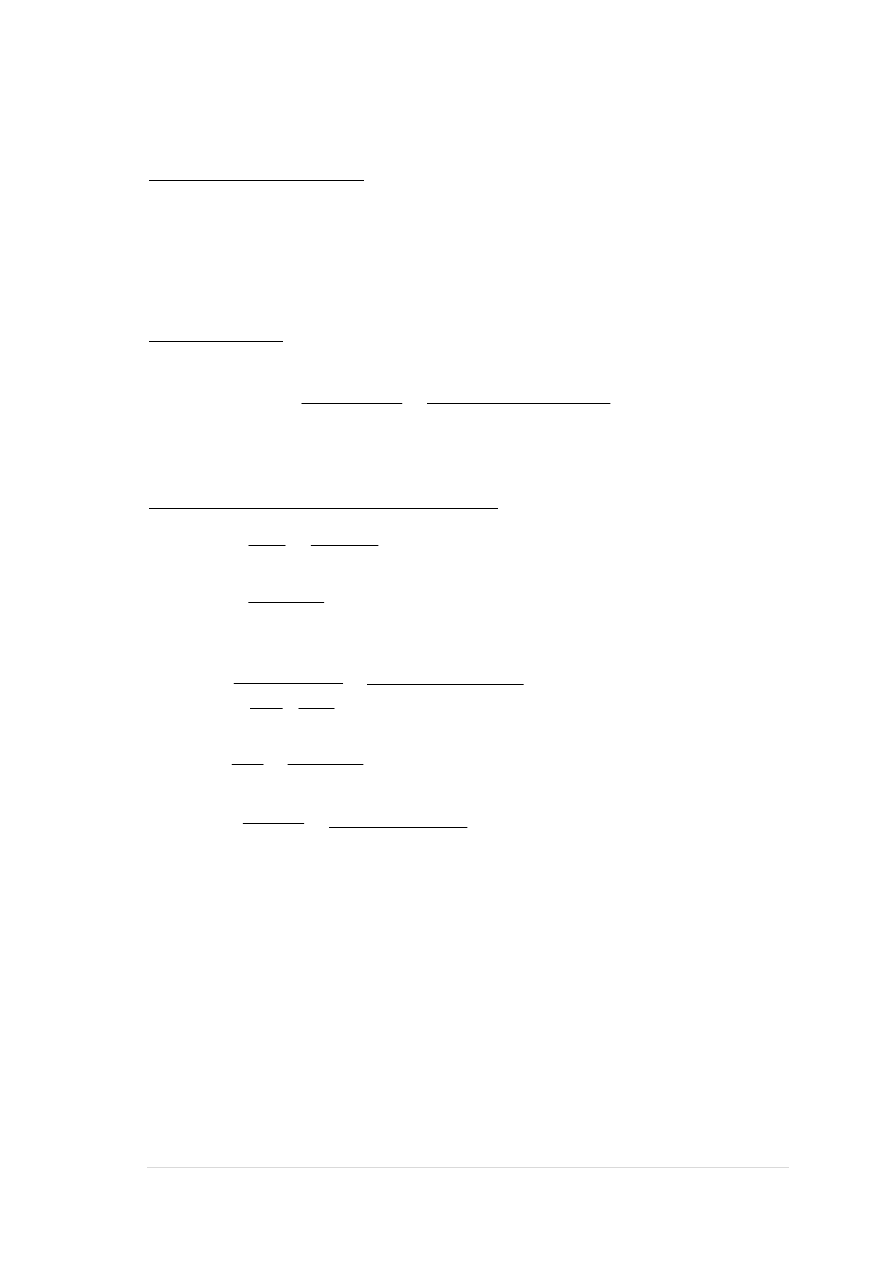
81 |

S t r o n a

= 4200 cm

= 84000 cm

M i n i m a l n e z b r o j e n i e :
Wymagane pole zbrojenia rozciąganego dla zginania, przy naprężeniach wywołanych
przyczynami zewnętrznymi, wynosi:

= k

k f

ct,eff

s,lim

= 0,4×1,0×2,6×2347 / 215 = 11,35 cm

= 15,21 > 11,35 = A

Z a r y s o w a n i e :

= f

ctm

= 2,6×84000 ×10

-3

= 218,40 kNm

×10

-1

= -141,93 kN

= 128,82 < 141,93 = N

Przekrój niezarysowany.

S z e r o k o ś ć r o z w a r c i a r y s y u k o ś n e j :

= 0,00718

= 0,00000

= 0,00718 + 0,00000 = 0,00718

λ =

= 464,20

τ =

= 0,790 MPa

= 0,03 mm

= 0,03 < 0,3 = w

lim

ctm

−

2,6

173,9/84000,00 - 1/4200,00

3,14

12,5×35,0

sin

⎥

⎦

⎤

⎢

⎣

⎡

3×[0,00718/(1,0×10,0)]

320,16

35,0×115,8

×10

4×0,790²×464,20

0,00718×200000×25

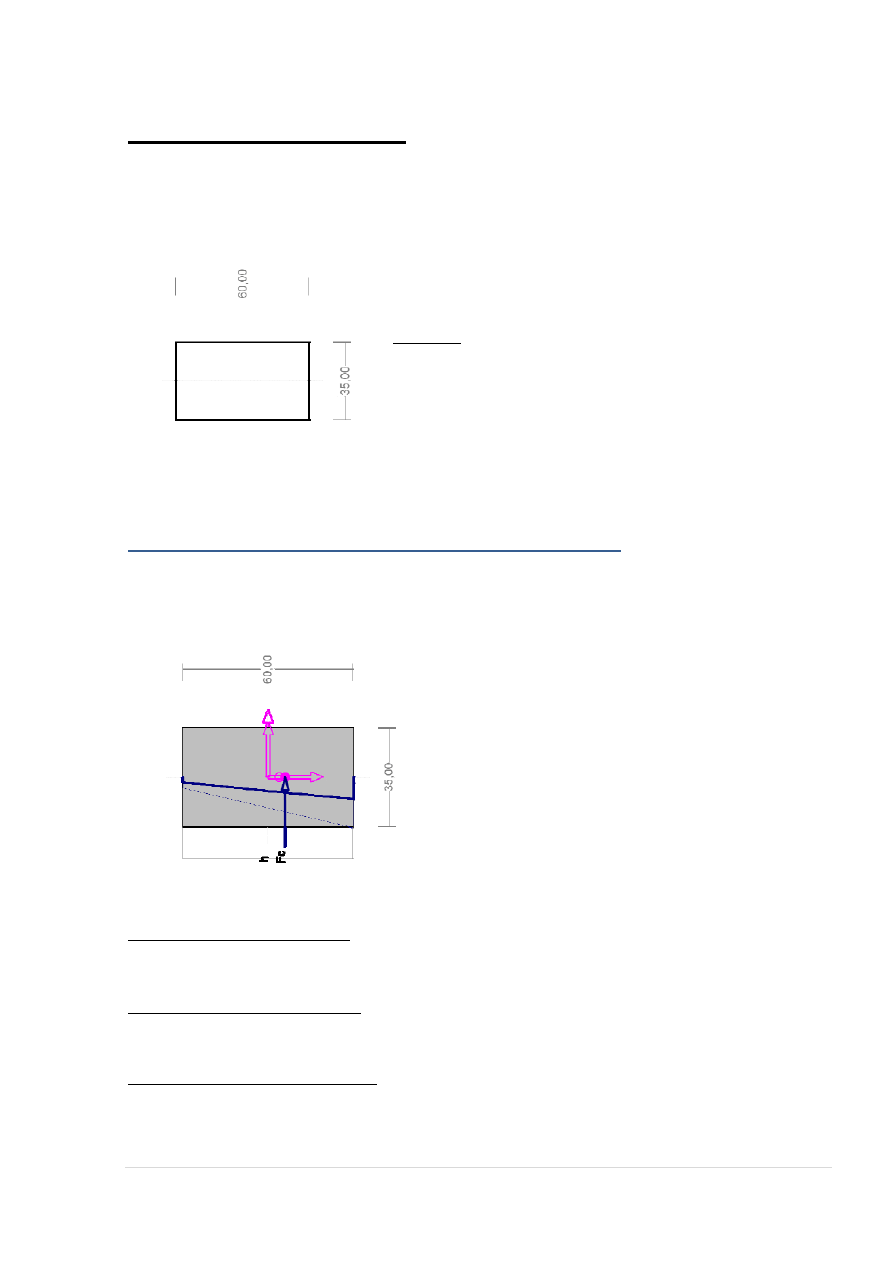
82 |

S t r o n a

9.3. SŁUP NR 1, (węzeł 14):

ZBROJENIE SŁUPA NR 3 (węzeł 3‐6) SYMETRYCZNE DO ZBROJENIA SŁUPA OBLICZANEGO
PONIŻEJ.

Cechy przekroju:

zadanie hala_monolit, pręt nr 1, przekrój: x

=1,65 m, x

=1,65 m

Wymiary przekroju [cm]:

h=60,0, b=35,0,

Cechy materiałowe dla sytuacji stałej lub przejściowej
BETON: B30

= 25,0 MPa, f

=α·f

=1,00×25,0/1,50=16,7 MPa

Cechy geometryczne przekroju betonowego:

=2100 cm

, J

=630000 cm

, J

=214375 cm

WYMIAROWANIE DLA PODSTAWY SŁUPA WĘZEŁ 1:

Zbrojenie wymagane:

(zadanie hala_monolit, pręt nr 1, przekrój: x

=3,30 m, x

=0,00 m)

Wielkości obliczeniowe:
N

=-969,16 kN,

√(M

Sdx

+ M

Sdy

) =

√(57,75

+0,00

)

=57,75 kNm
f

=16,7 MPa, f

=420 MPa (f

=478 MPa - uwzgl.

wzmocnienia) ,
Dodatkowe zbrojenie mniej ściskane nie jest
obliczeniowo wymagane.
Dodatkowe zbrojenie ściskane(*As2=0 nie jest
obliczeniowo wymagane.*|* (

=-0,50 ‰,

0,33 ‰):
A

=0,00 cm

< min A

=3,15 cm

, przyjęto

=3,15 cm

⇒ (1¤20 = 3,14 cm

) *)

Wielkości geometryczne [cm]:
h=60,0, d=60,0, x=82,4 (

ξ=1,373), a

=24,0, A

=2100 cm

=-0,50 ‰,

Wielkości statyczne [kN, kNm]:
F

= -969,13,

= 57,75,

Warunki równowagi wewnętrznej:
F

=-969,13=-969,13 kN (N

=-969,16 kN)

=57,75=57,75 kNm (M

=57,75 kNm)

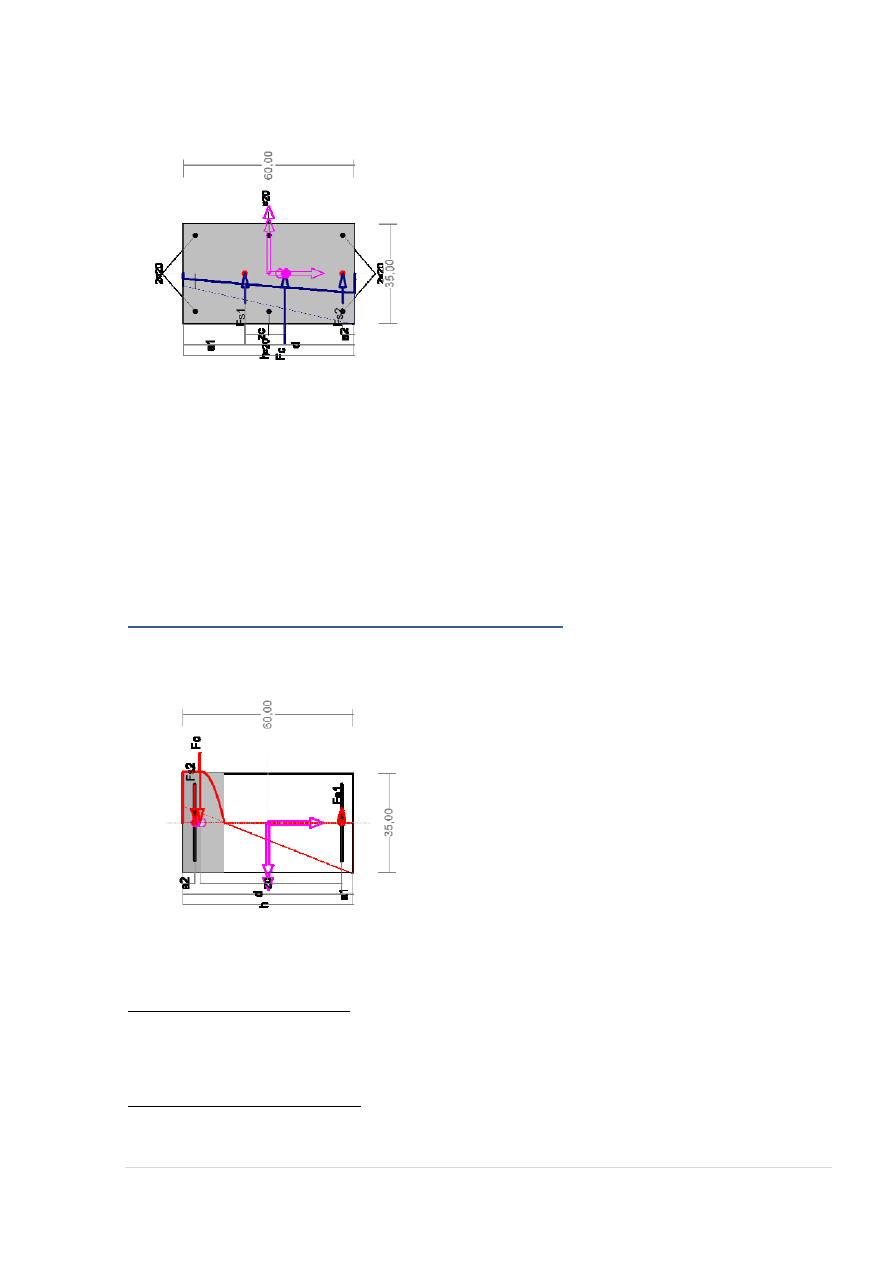
83 |

S t r o n a

Nośność przekroju prostopadłego:

Wielkości obliczeniowe:
N

=-969,16 kN,

√(M

Sdx

+ M

Sdy

) =

√(57,75

+0,00

)

=57,75 kNm
f

=16,7 MPa, f

=420 MPa (f

=478 MPa - uwzgl.

wzmocnienia) ,
Zbrojenie mniej ściskane: A

=12,57 cm

Zbrojenie ściskane: A

=6,28 cm

=18,85 cm

ρ=100×A

100

×18,85/2100=0,90 %

Wielkości geometryczne [cm]:
h=60,0, d=38,4, x=55,0 (

ξ=1,432),

=21,6, a

=4,1, a

=24,4, z

=14,0, A

=2100 cm

=-0,43 ‰,

=-0,41 ‰,

=-0,13 ‰,

Wielkości statyczne [kN, kNm]:
F

= -868,27, F

= -49,86, F

= -51,04,

= 48,74, M

= -4,20, M

= 13,22,

Warunek stanu granicznego nośności:

= -3368,32 kN > N

=-868,27+(-49,86)+(-51,04)=-969,16 kN

WYMIAROWANIE DLA GÓRY SŁUPA WĘZEŁ 4:

Zbrojenie wymagane:

Wielkości obliczeniowe:
N

=-829,31 kN,

√(M

Sdx

+ M

Sdy

) =

√(-211,54

+0,00

)

=211,54 kNm
f

=16,7 MPa, f

=420 MPa (f

=478 MPa - uwzgl.

wzmocnienia) ,
Zbrojenie rozciągane (

=10,00 ‰):

=0,45 cm

< min A

=3,15 cm

, przyjęto

=3,15 cm

⇒ (1¤20 = 3,14 cm

Zbrojenie ściskane(*As2=0 nie jest obliczeniowo
wymagane.*|* (

=-3,50 ‰,):

=3,87 cm

⇒ (2¤20 = 6,28 cm

) *)

=4,32 cm

ρ=100×A

100

×4,32/2100=0,21 %

Wielkości geometryczne [cm]:
h=60,0, d=55,9, x=14,5 (

ξ=0,259),

=4,1, a

=6,0, z

=49,9, A

=507 cm

=-3,50 ‰,

=-2,51 ‰,

=10,00 ‰,

Wielkości statyczne [kN, kNm]:
F

= -685,74, F

= 19,26, F

= -162,83,

= 164,38, M

= 4,99, M

= 42,17,

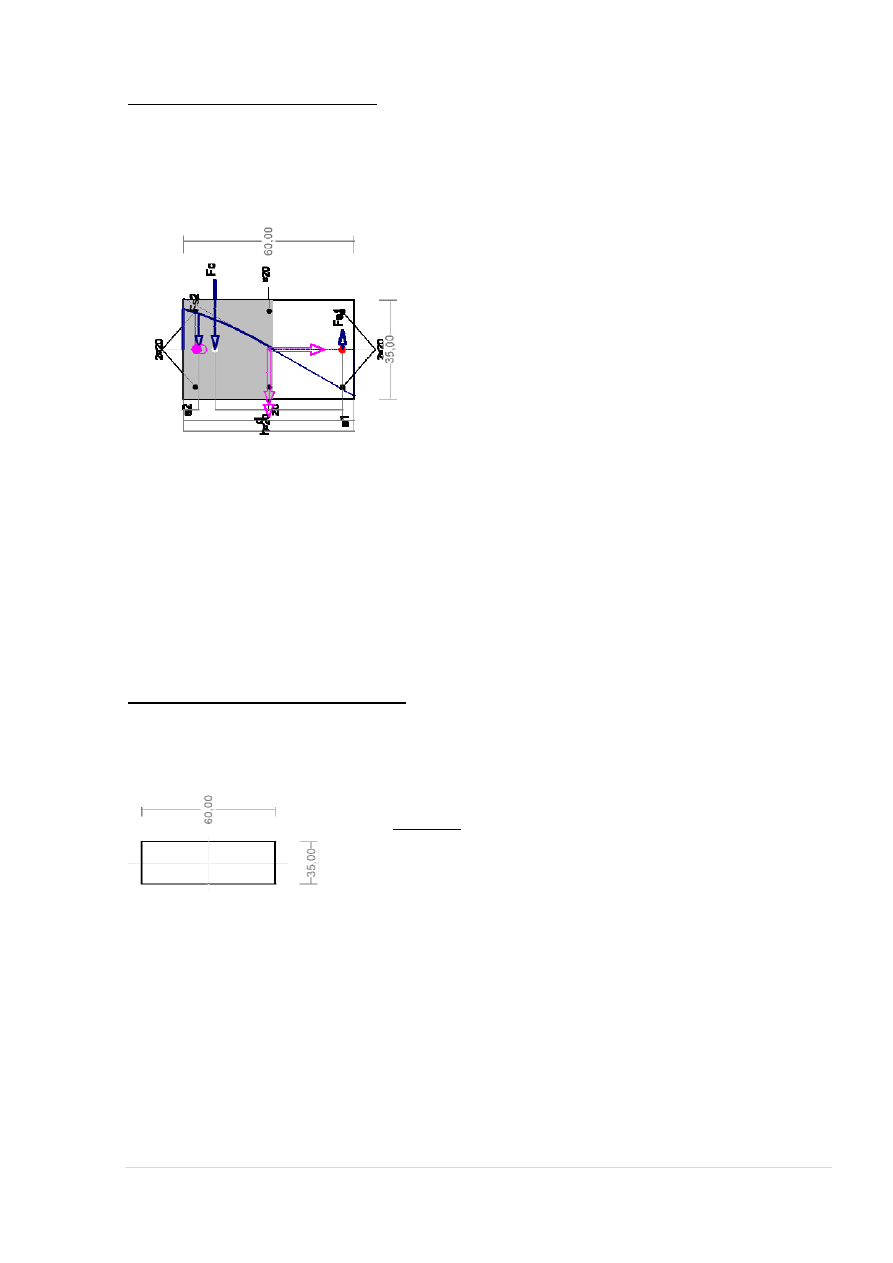
84 |

S t r o n a

Warunki równowagi wewnętrznej:
F

=-685,74+(19,26)+(-162,83)=-829,31 kN (N

=-829,31 kN)

=164,38+(4,99)+(42,17)=211,54 kNm (M

=211,54 kNm)

Nośność przekroju prostopadłego:

Wielkości obliczeniowe:
N

=-829,31 kN,

√(M

Sdx

+ M

Sdy

) =

√(-211,54

+0,00

)

=211,54 kNm
f

=16,7 MPa, f

=420 MPa (f

=478 MPa - uwzgl.

wzmocnienia) ,
Zbrojenie rozciągane: A

=6,28 cm

Zbrojenie ściskane: A

=12,57 cm

=18,85 cm

ρ=100×A

100

×18,85/2100=0,90 %

Wielkości geometryczne [cm]:
h=60,0, d=55,9, x=31,4 (

ξ=0,562),

=4,1, a

=5,4, a

=11,0, z

=44,9, A

=1099 cm

=-1,08 ‰,

=-0,94 ‰,

=0,84 ‰,

Wielkości statyczne [kN, kNm]:
F

= -811,06, F

= 105,48, F

= -123,73,

= 153,75, M

= 27,32, M

= 30,47,

Warunek stanu granicznego nośności:

= -1525,99 kN > N

=-811,06+(105,48)+(-123,73)=-829,31 kN

9.4. SŁUP NR 2, (węzeł 25):

Cechy przekroju:

Wymiary przekroju [cm]:

h=60,0, b=35,0,

Cechy materiałowe dla sytuacji stałej lub przejściowej
BETON: B30

= 25,0 MPa, f

=α·f

=1,00×25,0/1,50=16,7 MPa

Cechy geometryczne przekroju betonowego:

=2100 cm

, J

=630000 cm

, J

=214375 cm

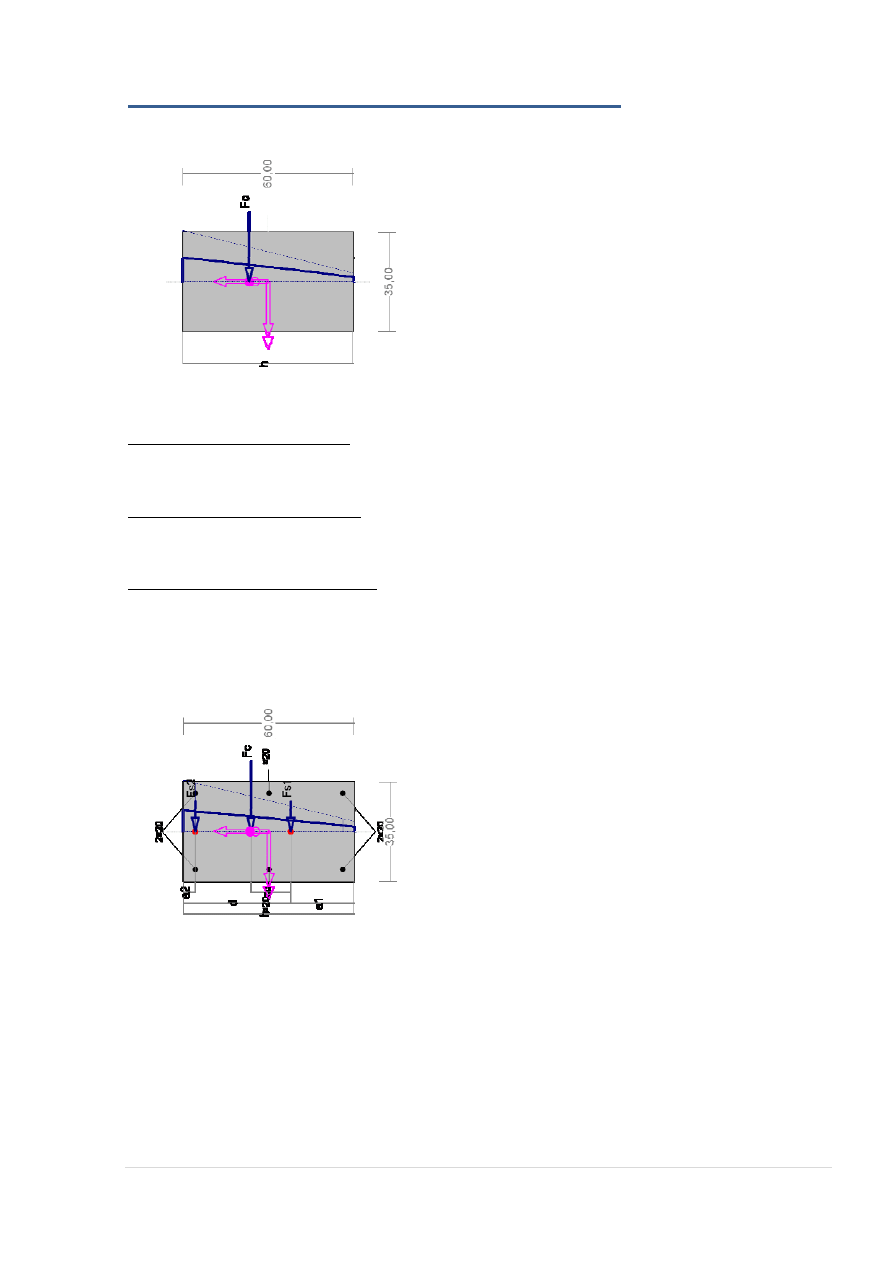
85 |

S t r o n a

WYMIAROWANIE DLA PODSTAWY SŁUPA WĘZEŁ 2:

Zbrojenie wymagane:

Wielkości obliczeniowe:
N

=-996,49 kN,

√(M

Sdx

+ M

Sdy

) =

√(-66,64

+0,00

)

=66,64 kNm
f

=16,7 MPa, f

=420 MPa (f

=478 MPa - uwzgl.

wzmocnienia) ,
Dodatkowe zbrojenie mniej ściskane nie jest
obliczeniowo wymagane.
Dodatkowe zbrojenie ściskane(*As2=0 nie jest
obliczeniowo wymagane.*|* (

=-0,54 ‰,

0,35 ‰):
A

=0,00 cm

< min A

=3,15 cm

, przyjęto

=3,15 cm

⇒ (1¤20 = 3,14 cm

) *)

Wielkości geometryczne [cm]:
h=60,0, d=60,0, x=76,9 (

ξ=1,282), a

=23,3, A

=2100 cm

=-0,54 ‰,

Wielkości statyczne [kN, kNm]:
F

= -996,46,

= 66,63,

Warunki równowagi wewnętrznej:
F

=-996,46=-996,46 kN (N

=-996,49 kN)

=66,63=66,63 kNm (M

=66,64 kNm)

Nośność przekroju prostopadłego:

Wielkości obliczeniowe:
N

=-996,49 kN,

√(M

Sdx

+ M

Sdy

) =

√(-66,64

+0,00

)

=66,64 kNm
f

=16,7 MPa, f

=420 MPa (f

=478 MPa - uwzgl.

wzmocnienia) ,
Zbrojenie mniej ściskane: A

=12,57 cm

Zbrojenie ściskane: A

=6,28 cm

=18,85 cm

ρ=100×A

100

×18,85/2100=0,90 %

Wielkości geometryczne [cm]:
h=60,0, d=37,7, x=50,2 (

ξ=1,335),

=22,3, a

=4,1, a

=23,7, z

=13,9, A

=2100 cm

=-0,46 ‰,

=-0,44 ‰,

=-0,12 ‰,

Wielkości statyczne [kN, kNm]:
F

= -892,29, F

= -49,30, F

= -54,90,

= 56,19, M

= -3,77, M

= 14,22,

Warunek stanu granicznego nośności:

= -3274,23 kN > N

=-892,29+(-49,30)+(-54,90)=-996,49 kN

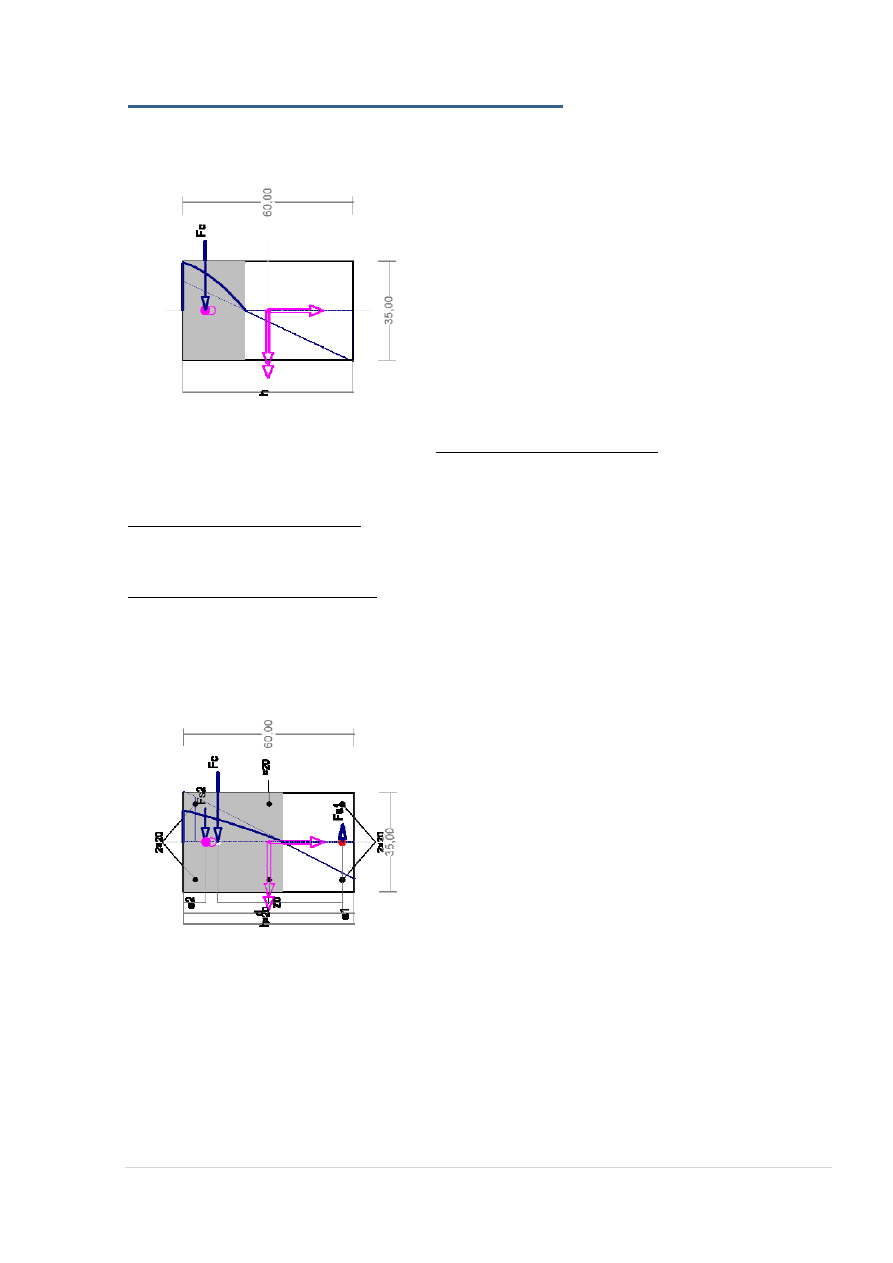
86 |

S t r o n a

WYMIAROWANIE DLA GÓRY SŁUPA WĘZEŁ 5:

Zbrojenie wymagane:

Wielkości obliczeniowe:
N

=-715,91 kN,

√(M

Sdx

+ M

Sdy

) =

√(-158,33

+0,00

)

=158,33 kNm
f

=16,7 MPa, f

=420 MPa (f

=478 MPa - uwzgl.

wzmocnienia) ,
Dodatkowe zbrojenie mniej ściskane nie jest
obliczeniowo wymagane.
Dodatkowe zbrojenie ściskane(*As2=0 nie jest
obliczeniowo wymagane.*|* (

=-1,49 ‰,):

=0,00 cm

< min A

=3,15 cm

, przyjęto

=3,15 cm

⇒ (1¤20 = 3,14 cm

) *)

Wielkości geometryczne [cm]:

h=60,0, d=60,0, x=23,4 (

ξ=0,391), a

=7,9, A

=765 cm

=-1,49 ‰,

Wielkości statyczne [kN, kNm]:
F

= -715,88,

= 158,32,

Warunki równowagi wewnętrznej:
F

=-715,88=-715,88 kN (N

=-715,91 kN)

=158,32=158,32 kNm (M

=158,33 kNm)

Nośność przekroju prostopadłego:

Wielkości obliczeniowe:
N

=-715,91 kN,

√(M

Sdx

+ M

Sdy

) =

√(-158,33

+0,00

)

=158,33 kNm
f

=16,7 MPa, f

=420 MPa (f

=478 MPa - uwzgl.

wzmocnienia) ,
Zbrojenie rozciągane: A

=6,28 cm

Zbrojenie ściskane: A

=12,57 cm

=18,85 cm

ρ=100×A

100

×18,85/2100=0,90 %

Wielkości geometryczne [cm]:
h=60,0, d=55,9, x=34,8 (

ξ=0,623),

=4,1, a

=7,6, a

=12,0, z

=43,9, A

=1219 cm

=-0,76 ‰,

=-0,67 ‰,

=0,46 ‰,

Wielkości statyczne [kN, kNm]:
F

= -676,15, F

= 57,84, F

= -97,60,

= 121,50, M

= 14,98, M

= 21,85,

Warunek stanu granicznego nośności:

= -1762,23 kN > N

=-676,15+(57,84)+(-97,60)=-715,91 kN

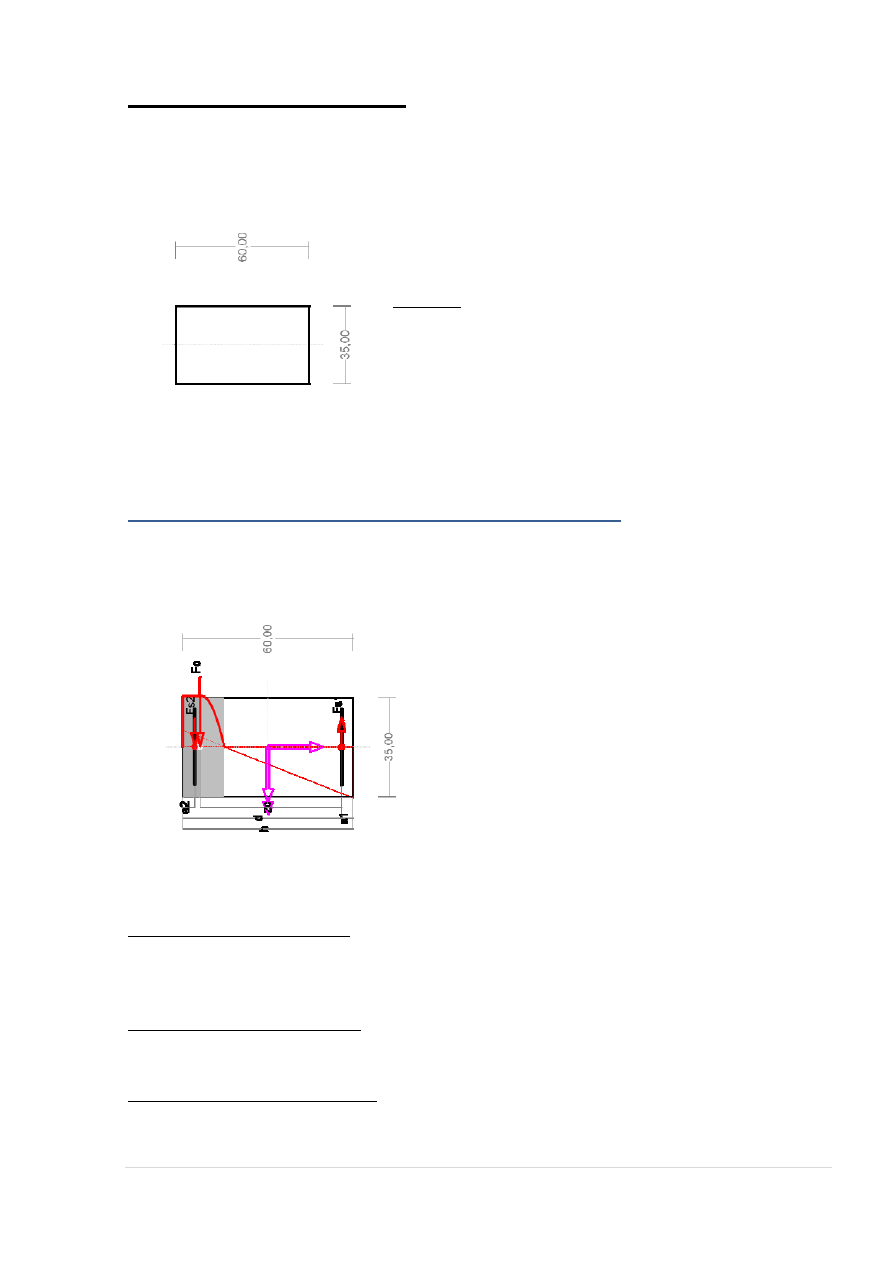
87 |

S t r o n a

9.5. SŁUP NR 4, (węzeł 47):

ZBROJENIE SŁUPA NR 5 (węzeł 6‐9) SYMETRYCZNE DO ZBROJENIA SŁUPA OBLICZANEGO
PONIŻEJ.

Cechy przekroju:

zadanie hala_monolit, pręt nr 4, przekrój: x

=2,15 m, x

=2,15 m

Wymiary przekroju [cm]:

h=60,0, b=35,0,

Cechy materiałowe dla sytuacji stałej lub przejściowej
BETON: B30

= 25,0 MPa, f

=α·f

=1,00×25,0/1,50=16,7 MPa

Cechy geometryczne przekroju betonowego:

=2100 cm

, J

=630000 cm

, J

=214375 cm

WYMIAROWANIE DLA PODSTAWY SŁUPA WĘZEŁ 4:

Zbrojenie wymagane:

(zadanie hala_monolit, pręt nr 4, przekrój: x

=0,00 m, x

=4,30 m)

Wielkości obliczeniowe:
N

=-446,12 kN,

√(M

Sdx

+ M

Sdy

) =

√(-234,13

+0,00

)

=234,13 kNm
f

=16,7 MPa, f

=420 MPa (f

=478 MPa - uwzgl.

wzmocnienia) ,
Zbrojenie rozciągane (

=10,00 ‰):

=5,92 cm

⇒ (2¤20 = 6,28 cm

Zbrojenie ściskane(*As2=0 nie jest obliczeniowo
wymagane.*|* (

=-3,50 ‰,):

=0,35 cm

< min A

=3,15 cm

, przyjęto

=3,15 cm

⇒ (1¤20 = 3,14 cm

) *)

=6,27 cm

ρ=100×A

100

×6,27/2100=0,30 %

Wielkości geometryczne [cm]:
h=60,0, d=55,9, x=14,5 (

ξ=0,259),

=4,1, a

=6,0, z

=49,9, A

=507 cm

=-3,50 ‰,

=-2,51 ‰,

=10,00 ‰,

Wielkości statyczne [kN, kNm]:
F

= -685,74, F

= 254,46, F

= -14,83,

= 164,38, M

= 65,90, M

= 3,84,

Warunki równowagi wewnętrznej:
F

=-685,74+(254,46)+(-14,83)=-446,12 kN (N

=-446,12 kN)

=164,38+(65,90)+(3,84)=234,13 kNm (M

=234,13 kNm)

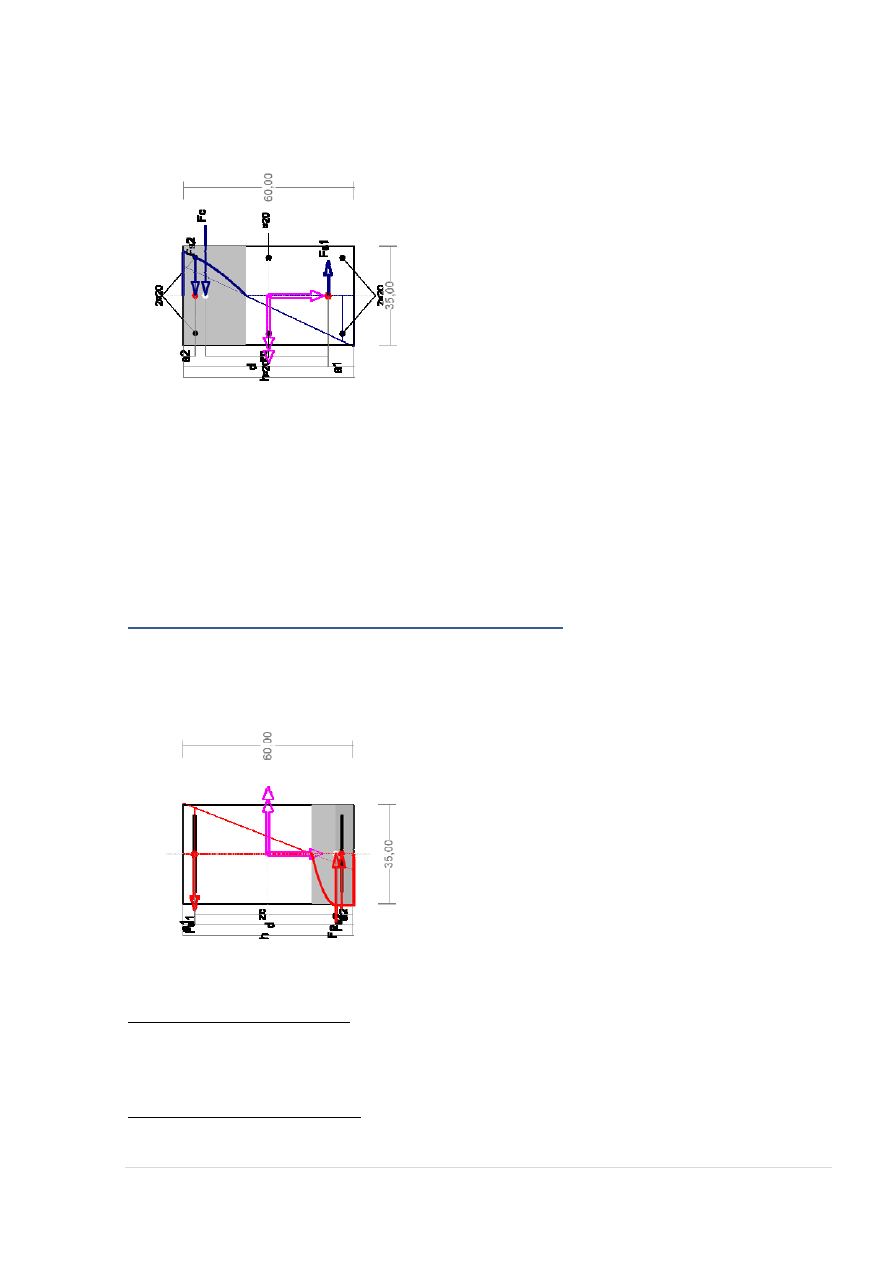
88 |

S t r o n a

Nośność przekroju prostopadłego:

zadanie hala_monolit, pręt nr 4, przekrój: x

=0,00 m, x

=4,30 m

Wielkości obliczeniowe:
N

=-446,12 kN,

√(M

Sdx

+ M

Sdy

) =

√(-234,13

+0,00

)

=234,13 kNm
f

=16,7 MPa, f

=420 MPa (f

=478 MPa - uwzgl.

wzmocnienia) ,
Zbrojenie rozciągane: A

=12,57 cm

Zbrojenie ściskane: A

=6,28 cm

=18,85 cm

ρ=100×A

100

×18,85/2100=0,90 %

Wielkości geometryczne [cm]:
h=60,0, d=50,9, x=19,8 (

ξ=0,389),

=9,1, a

=4,1, a

=7,7, z

=43,1, A

=761 cm

=-1,23 ‰,

=-1,00 ‰,

=1,93 ‰,

Wielkości statyczne [kN, kNm]:
F

= -622,25, F

= 301,75, F

= -125,61,

= 138,65, M

= 62,95, M

= 32,53,

Warunek stanu granicznego nośności:

= 336,38 kNm > M

=138,65+(62,95)+(32,53)=234,13 kNm

WYMIAROWANIE DLA GÓRY SŁUPA WĘZEŁ 7:

Zbrojenie wymagane:

(zadanie hala_monolit, pręt nr 4, przekrój: x

=4,30 m, x

=0,00 m)

Wielkości obliczeniowe:
N

=-426,54 kN,

√(M

Sdx

+ M

Sdy

) =

√(469,06

+0,00

)

=469,06 kNm
f

=16,7 MPa, f

=420 MPa (f

=478 MPa - uwzgl.

wzmocnienia) ,
Zbrojenie rozciągane (

=10,00 ‰):

=16,71 cm

⇒ (6¤20 = 18,85 cm

Zbrojenie ściskane(*As2=0 nie jest obliczeniowo
wymagane.*|* (

=-3,50 ‰,):

=10,91 cm

⇒ (4¤20 = 12,57 cm

) *)

=27,62 cm

ρ=100×A

100

×27,62/2100=1,32 %

Wielkości geometryczne [cm]:
h=60,0, d=55,9, x=14,5 (

ξ=0,259),

=4,1, a

=6,0, z

=49,9, A

=507 cm

=-3,50 ‰,

=-2,51 ‰,

=10,00 ‰,

Wielkości statyczne [kN, kNm]:
F

= -685,74, F

= 717,78, F

= -458,58,

= 164,38, M

= 185,91, M

= 118,77,

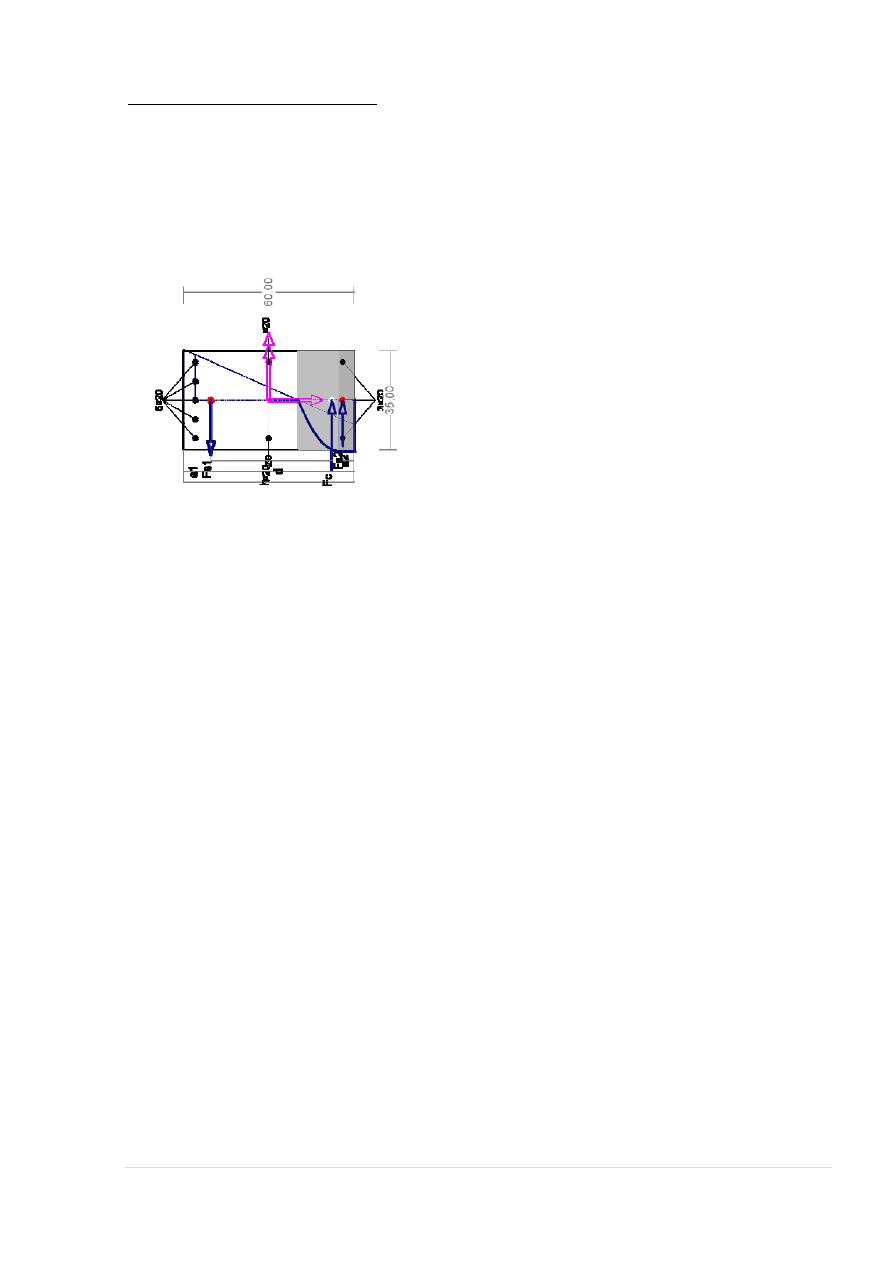
89 |

S t r o n a

Warunki równowagi wewnętrznej:
F

=-685,74+(717,78)+(-458,58)=-426,54 kN (N

=-426,54 kN)

=164,38+(185,91)+(118,77)=469,06 kNm (M

=469,06 kNm)

Nośność przekroju prostopadłego:

zadanie hala_monolit, pręt nr 4, przekrój: x

=4,30 m, x

=0,00 m

Wielkości obliczeniowe:
N

=-426,54 kN,

√(M

Sdx

+ M

Sdy

) =

√(469,06

+0,00

)

=469,06 kNm
f

=16,7 MPa, f

=420 MPa (f

=478 MPa - uwzgl.

wzmocnienia) ,
Zbrojenie rozciągane: A

=21,99 cm

Zbrojenie ściskane: A

=9,42 cm

=31,42 cm

ρ=100×A

100

×31,42/2100=1,50 %

Wielkości geometryczne [cm]:
h=60,0, d=50,4, x=17,8 (

ξ=0,353),

=9,6, a

=4,1, a

=7,9, z

=42,5, A

=691 cm

=-2,78 ‰,

=-2,20 ‰,

=5,09 ‰,

Wielkości statyczne [kN, kNm]:
F

= -877,51, F

= 846,84, F

= -395,96,

= 194,11, M

= 172,35, M

= 102,55,

Warunek stanu granicznego nośności:

= 479,38 kNm > M

=194,11+(172,35)+(102,55)=469,06 kNm

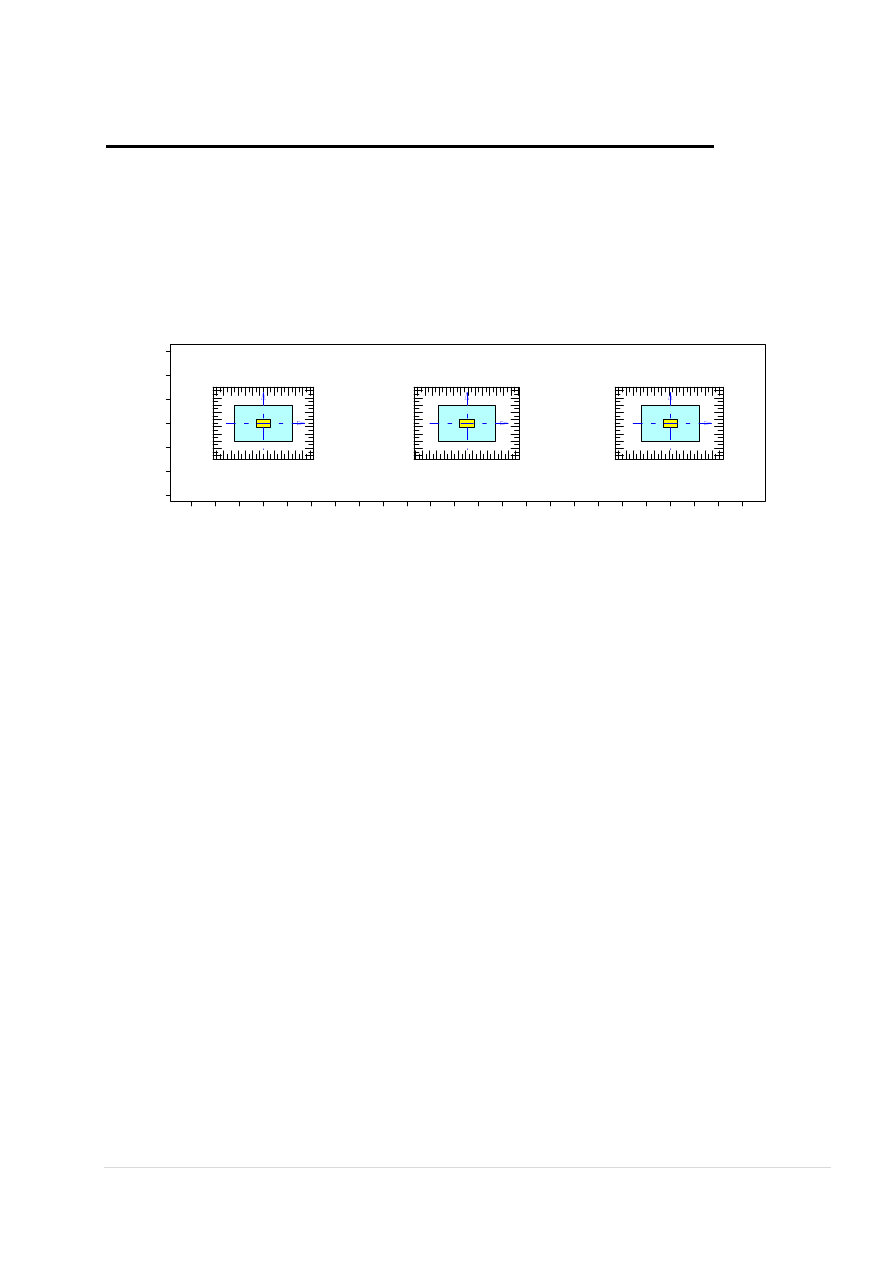
90 |

S t r o n a

9.6. FUNDAMENT NR 1 (węzeł 1), NR2 (węzeł 2), NR3 (węzeł 3):

DANE OGÓLNE PROJEKTU

1. Metryka projektu

Projekt: Hala monolityczna,
Projektant: p.w.,
Komentarz:
Data ostatniej aktualizacji danych: 2008-11-27
Poziom odniesienia: 0,00 m.

2. Fundamenty

Liczba fundamentów: 3

3. Wykopy

Liczba wykopów: 3

3.1. Wykop nr 1

Poziom dna wykopu: z

= 1,60 m,

Współrzędne naroży wykopu:

punkt 0: x = 2,10 m, y = 1,50 m,

punkt 1: x = -2,10 m, y = 1,50 m,

punkt 2: x = -2,10 m, y = -1,50 m,

punkt 3: x = 2,10 m, y = -1,50 m,

3.2. Wykop nr 2

Poziom dna wykopu: z

= 1,60 m,

Współrzędne naroży wykopu:

punkt 0: x = 10,70 m, y = 1,50 m,

punkt 1: x = 6,30 m, y = 1,50 m,

punkt 2: x = 6,30 m, y = -1,50 m,

punkt 3: x = 10,70 m, y = -1,50 m,

3.3. Wykop nr 3

Poziom dna wykopu: z

= 1,60 m,

Współrzędne naroży wykopu:

punkt 0: x = 19,20 m, y = 1,50 m,

punkt 1: x = 14,70 m, y = 1,50 m,

punkt 2: x = 14,70 m, y = -1,50 m,

punkt 3: x = 19,20 m, y = -1,50 m,

-2

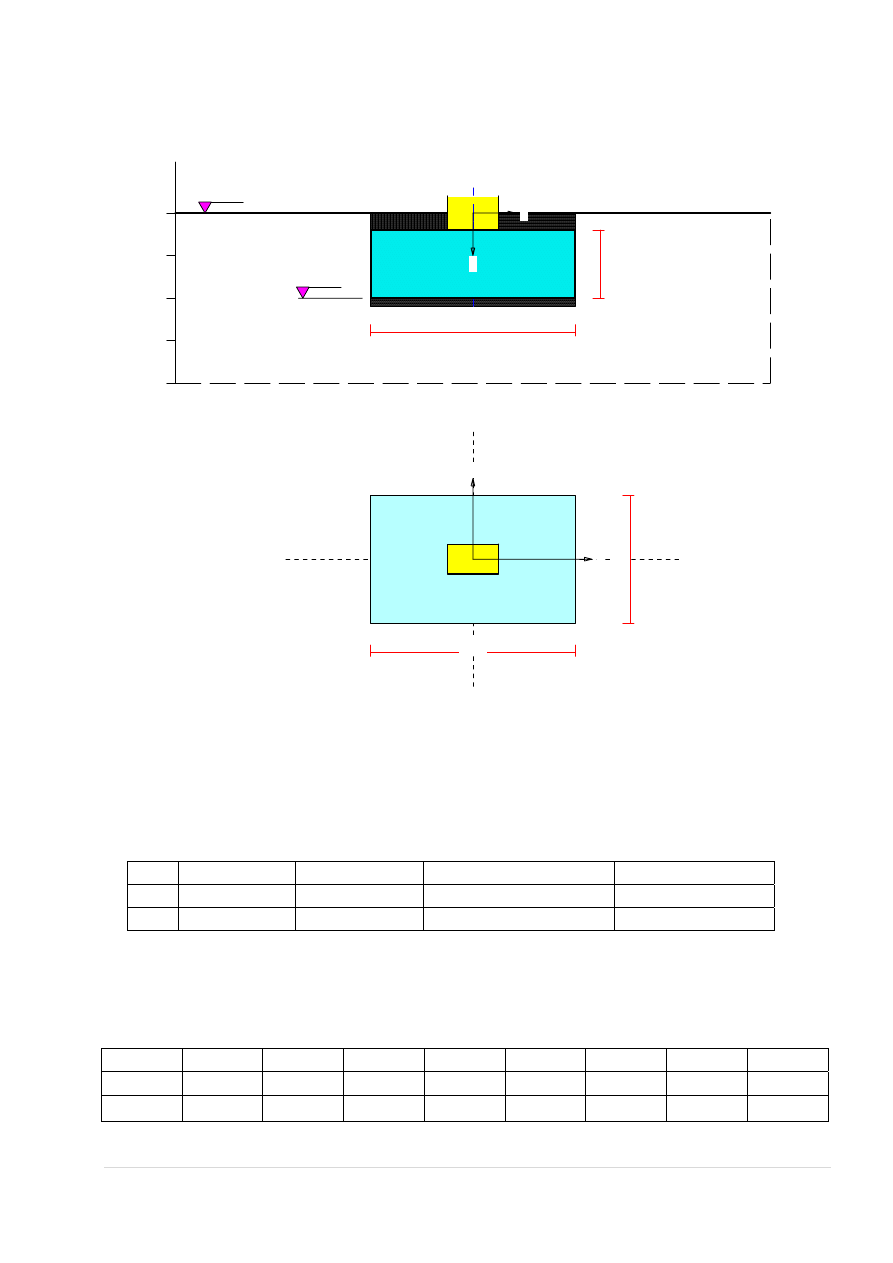
91 |

S t r o n a

FUNDAMENT 1. STOPA PROSTOKĄTNA

1. Podłoże gruntowe

1.1. Teren
Istniejący poziom terenu: z

= 0,00 m,

Projektowany poziom terenu: z

= 0,00 m.

1.2. Warstwy gruntu

Poziom stropu Grubość warstwy Nazwa gruntu

Poz. wody gruntowej

[m]

0,00

nieokreśl.

Piasek średni brak wody

1.3. Zasypka
Charakterystyczny

ciężar objętościowy:

z char

= 20,00 kN/m

Współczynnik obciążenia:

= 1,20.

1.4. Parametry geotechniczne występujących gruntów

Symbol I

stopień

gruntu

[

−]

[

−]

[t/m

]

wilgotn. [kPa]

[

]

[kPa]

0,35

1,70 m.wilg. 0,00 32,1 72494 80549

z [m]

0,00

Skala 1 : 50

2,40

0,80

1,00

2,40

1,50

92 |

S t r o n a

2. Konstrukcja na fundamencie

Typ

konstrukcji:

słup prostokątny

Wymiary

słupa: b = 0,60 m, l = 0,35 m,

Współrzędne osi słupa: x

= 0,00 m, y

= 0,00 m,

Kąt obrotu układu lokalnego względem globalnego:

φ = 0,00

3. Warstwa wyrównawcza pod fundamentem

Grubość: h = 0,10 m,

Charakterystyczny

ciężar objętościowy:

ww char

= 22,00 kN/m

4. Obciążenie od konstrukcji

Poziom przyłożenia obciążenia: z

obc

= 0,60 m.

Lista obciążeń:

Rodzaj

obciążenia

[kN]

[kNm]

[

−]

835,7 -53,5 0,0 0,00 -57,10 1,20

689,6 1,8 0,0 0,00 -1,80 1,20

960,1 -42,7 0,0 0,00 -43,20 1,20

580,1 -1,6 0,0 0,00 -5,30 1,20

D – obciążenia stałe, zmienne długotrwałe,

D+K - obciążenia stałe, zmienne długotrwałe i krótkotrwałe.

5. Materiał

Klasa betonu: B30, nazwa stali: RB 500,

Średnica prętów zbrojeniowych: na kierunku x: d

= 20,0 mm, na kierunku y: d

= 20,0 mm,

Kierunek zbrojenia głównego: x,

Grubość otuliny: 5,0 cm.
Dopuszcza

się zbrojenie strzemionami, jeżeli warunek na przebicie tego wymaga.

6. Wymiary fundamentu

Poziom posadowienia: z

= 1,00 m

Kształt fundamentu: prosty

Wymiary podstawy: B

= 2,40 m, B

= 1,50 m,

Wysokość: H = 0,80 m,
Mimośrody: E

= 0,00 m, E

= 0,00 m.

93 |

S t r o n a

7. Stan graniczny I

7.1. Zestawienie wyników analizy nośności i mimośrodów

Nr obc. Rodzaj obciążenia Poziom [m]

Wsp. nośności

Wsp. mimośr.

1,00

0,59

0,14

1,00

0,45

0,00

* 3

1,00

0,63

0,10

1,00

0,39

0,01

7.4. Analiza stanu granicznego I dla obciążenia nr 3

Wymiary podstawy fundamentu rzeczywistego: B

= 2,40 m, B

= 1,50 m.

Poziom posadowienia: H = 1,00 m.

Rodzaj

obciążenia: D,

Zestawienie

obciążeń:

Pozycja

Obc. char. E

Obc. obl.

Mom. obl. Mom. obl.

[kN]

[m]

[

−] G [kN]

[kNm] M

[kNm]

Fundament

70,63 0,00 0,00 1,10 77,70 0,00 0,00

Zasypka - pole 1

3,39 0,63 -0,39 1,20 4,07 -1,60 2,55

Zasypka - pole 2

3,39 -0,63 -0,39 1,20 4,07 -1,60 -2,55

Zasypka - pole 3

3,39 -0,63 0,39 1,20 4,07 1,60 -2,55

Zasypka - pole 4

3,39 0,63 0,39 1,20 4,07 1,60 2,55

Suma 93,97 0,00 0,00

Obciążenia zewnętrzne od konstrukcji:
siła pionowa: N = 960,10 kN, mimośrody wzgl. podst. fund. E

= 0,00 m, E

= 0,00 m,

siła pozioma: H

= -42,70 kN, mimośród względem podstawy fund. E

= 0,40 m,

siła pozioma: H

= 0,00 kN, mimośród względem podstawy fund. E

= 0,40 m,

moment: M

= 0,00 kNm,

moment: M

= -43,20 kNm.

Sprawdzenie

położenia wypadkowej obciążenia względem podstawy fundamentu

Obciążenie pionowe:

= N + G = 960,10 + 93,97 = 1054,07 kN.

Momenty

względem środka podstawy:

= N·E

− H

·E

+ M

= 960,10·0,00 + (0,00) = 0,00 kNm.

−N·E

+ H

·E

+ M

= -960,10·0,00 + (-42,70)·0,40 + (-43,20) + 0,00 = -60,28 kNm.

Mimośrody sił względem środka podstawy:

= |M

| = 60,28/1054,07 = 0,06 m,

= |M

| = 0,00/1054,07 = 0,00 m.

+ e

= 0,024 + 0,000 = 0,024 m < 0,250.

Wniosek: Warunek położenia wypadkowej jest spełniony.

Sprawdzenie warunku granicznej nośności fundamentu rzeczywistego

Zredukowane wymiary podstawy fundamentu:

′ = B

− 2·e

= 2,40 - 2·0,06 = 2,29 m, B

′ = B

− 2·e

= 1,50 - 2·0,00 = 1,50 m.

Obciążenie podłoża obok ławy (min. średnia gęstość dla pola 1):

średnia gęstość obliczeniowa:

D(r)

= 1,53 t/m

minimalna

wysokość: D

min

= 1,00 m,

94 |

S t r o n a

obciążenie:

D(r)

·g·D

min

= 1,53·9,81·1,00 = 15,01 kPa.

Współczynniki nośności podłoża:
obliczeniowy

kąt tarcia wewnętrznego:

u(r)

u(n)

= 32,10·0,90 = 28,89

spójność: c

u(r)

= c

u(n)

= 0,00 kPa,

= 6,31 N

= 27,62, N

= 16,24.

Wpływ odchylenia wypadkowej obciążenia od pionu:
tg

= |H

|/N

= 42,70/1054,07 = 0,04, tg

/tg

u(r)

= 0,0405/0,5518 = 0,073,

= 0,87, i

= 0,93, i

= 0,93.

= |H

|/N

= 0,00/1054,07 = 0,00, tg

/tg

u(r)

= 0,0000/0,5518 = 0,000,

= 1,00, i

= 1,00.

Ciężar objętościowy gruntu pod ławą fundamentową:

B(n)

·g = 1,70·0,90·9,81 = 15,01 kN/m

Współczynniki kształtu:

= 1

− 0,25·B

′/B

′ = 0,84, m

= 1 + 0,3·B

′/B

′ = 1,20, m

= 1 + 1,5·B

′/B

′ = 1,98

Odpór

graniczny

podłoża:

fNBx

= B

′B

′(m

·N

·c

u(r)

·i

+ m

·N

D(r)

·g·D

min

·i

+ m

·N

B(r)

·g·B

′·i

) = 2084,62 kN.

fNBy

= B

′B

′(m

·N

·c

u(r)

·i

+ m

·N

D(r)

·g·D

min

·i

+ m

·N

B(r)

·g·B

′·i

) = 2065,67 kN.

Sprawdzenie

warunku

obliczeniowego:

= 1054,07 kN < m·min(Q

fNBx

fNBy

) = 0,81·2065,67 = 1673,19 kN.

Wniosek: warunek nośności jest spełniony.

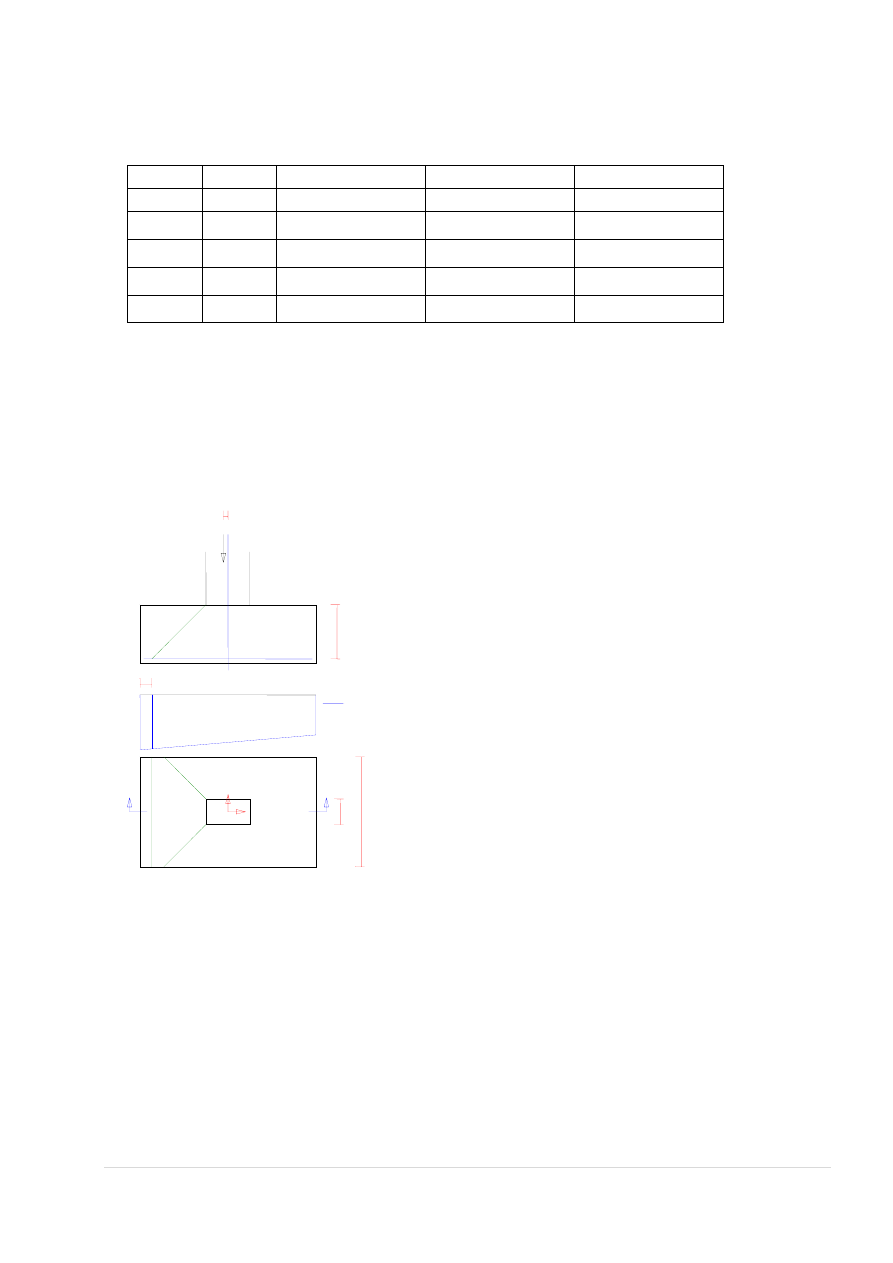
95 |

S t r o n a

8. Wymiarowanie fundamentu

8.1. Zestawienie wyników sprawdzenia stopy na przebicie

Nr obc. Przekrój Siła tnąca

Nośność betonu

Nośność strzemion

V [kN]

[kN]

968

* 3

968

8.4. Sprawdzenie stopy na przebicie dla obciążenia nr 3

Zestawienie

obciążeń:

Obciążenia zewnętrzne od konstrukcji zredukowane do środka podstawy stopy:
siła pionowa: N

= 960 kN,

momenty: M

= 0,00 kNm, M

= -60,28 kNm.

Mimośrody siły względem środka podstawy:

= |M

| = 0,06 m, e

= |M

| = 0,00 m.

Oddziaływanie podłoża na fundament:
Oddziaływania na krawędziach fundamentu w przekroju środkowym A-A:

= 225 kPa, q

= 309 kPa.

Oddziaływanie podłoża w przekroju 1: c = 0,16 m, q

= 303 kPa.

Przebicie stopy w przekroju 1:

Siła ścinająca: V

∫

q·dA = 65 kN.

Nośność betonu na ścinanie: V

= (b+d)·d·f

ctd

= (0,35+0,74)·0,74·1200 = 968 kN.

= 0 kN < V

= 968 kN.

Wniosek: warunek na przebicie jest spełniony.

A-A

96 |

S t r o n a

8.6. Zestawienie wyników sprawdzenia stopy na zginanie

Nr obc. Kierunek Przekrój Moment zginający Nośność betonu

M [kNm]

[kNm]

125

* 3

136

8.11. Sprawdzenie stopy na zginanie dla obciążenia nr 3 na kierunku x

Zestawienie

obciążeń:

Obciążenia zewnętrzne od konstrukcji zredukowane do środka podstawy stopy:
siła pionowa: N

= 960 kN,

momenty: M

= 0,00 kNm, M

= -60,28 kNm.

Mimośrody siły względem środka podstawy:

= |M

| = 0,06 m, e

= |M

| = 0,00 m.

Oddziaływanie podłoża na fundament:
Oddziaływania na krawędziach fundamentu w przekroju środkowym A-A:

= 225 kPa, q

= 309 kPa.

Oddziaływanie podłoża w przekroju 1: s = 0,90 m, q

= 277 kPa.

A-A

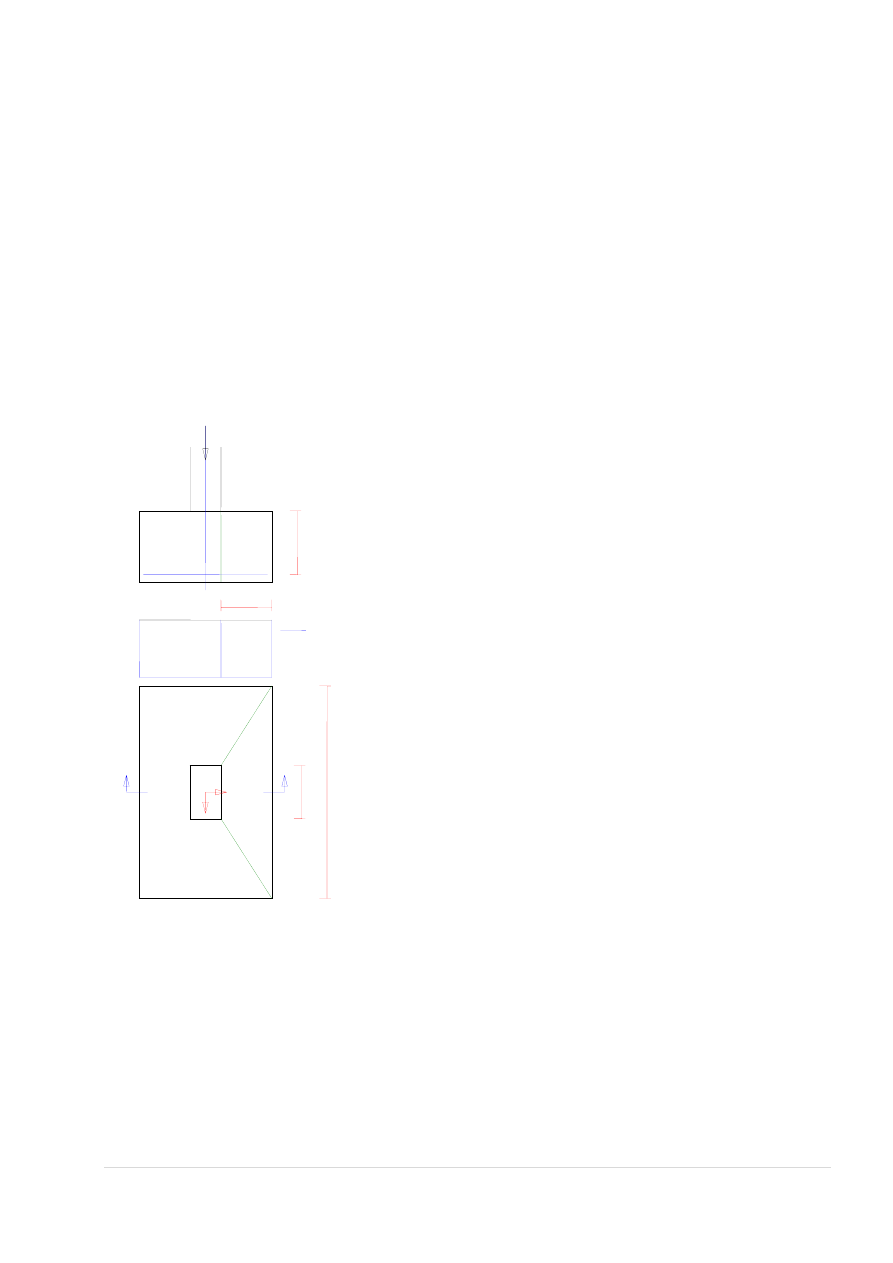
97 |

S t r o n a

Zginanie stopy w przekroju 1:

Moment

zginający:

= [(b+3·B)·q

+ (b+B)·q

]·s

/12 = [(0,35+3·1,50)·309+(0,35+1,50)·277]·0,81/12 = 136 kNm.

Konieczna powierzchnia przekroju zbrojenia: A

= 4,4 cm

Wniosek: warunek na zginanie jest spełniony.

8.12. Sprawdzenie stopy na zginanie dla obciążenia nr 3 na kierunku y

Zestawienie

obciążeń:

Obciążenia zewnętrzne od konstrukcji zredukowane do środka podstawy stopy:
siła pionowa: N

= 960 kN,

momenty: M

= 0,00 kNm, M

= -60,28 kNm.

Mimośrody siły względem środka podstawy:

= |M

| = 0,06 m, e

= |M

| = 0,00 m.

Oddziaływanie podłoża na fundament:
Oddziaływania na krawędziach fundamentu w przekroju środkowym A-A:

= 267 kPa, q

= 267 kPa.

Oddziaływanie podłoża w przekroju 1: s = 0,57 m, q

= 267 kPa.

Zginanie stopy w przekroju 1:

Moment

zginający:

= [(b+3·B)·q

+ (b+B)·q

]·s

/12 = [(0,60+3·2,40)·267+(0,60+2,40)·267]·0,33/12 = 79 kNm.

Konieczna powierzchnia przekroju zbrojenia: A

= 2,7 cm

Wniosek: warunek na zginanie jest spełniony.

A-A

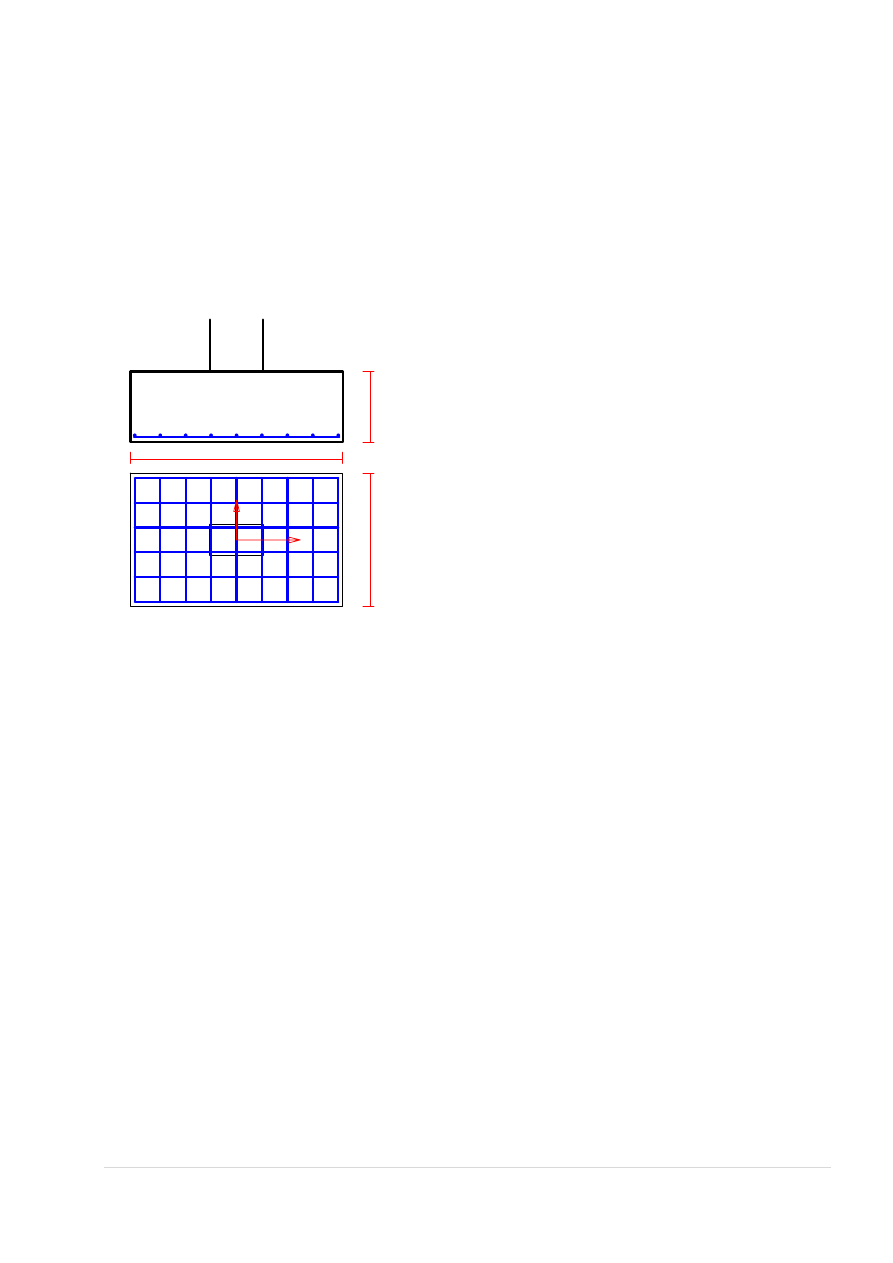
98 |

S t r o n a

9. Zbrojenie stopy

Zbrojenie

główne na kierunku x:

Obliczona powierzchnia przekroju poprzecznego A

= 4,4 cm

Średnica prętów:

φ = 20 mm, rozstaw prętów: s = 28 cm.

Zbrojenie

główne na kierunku y:

Obliczona powierzchnia przekroju poprzecznego A

= 6,5 cm

Średnica prętów:

φ = 20 mm, rozstaw prętów: s = 29 cm.

Ilość stali: 65 kg.

H=0,80

By=1,50

Bx=2,40

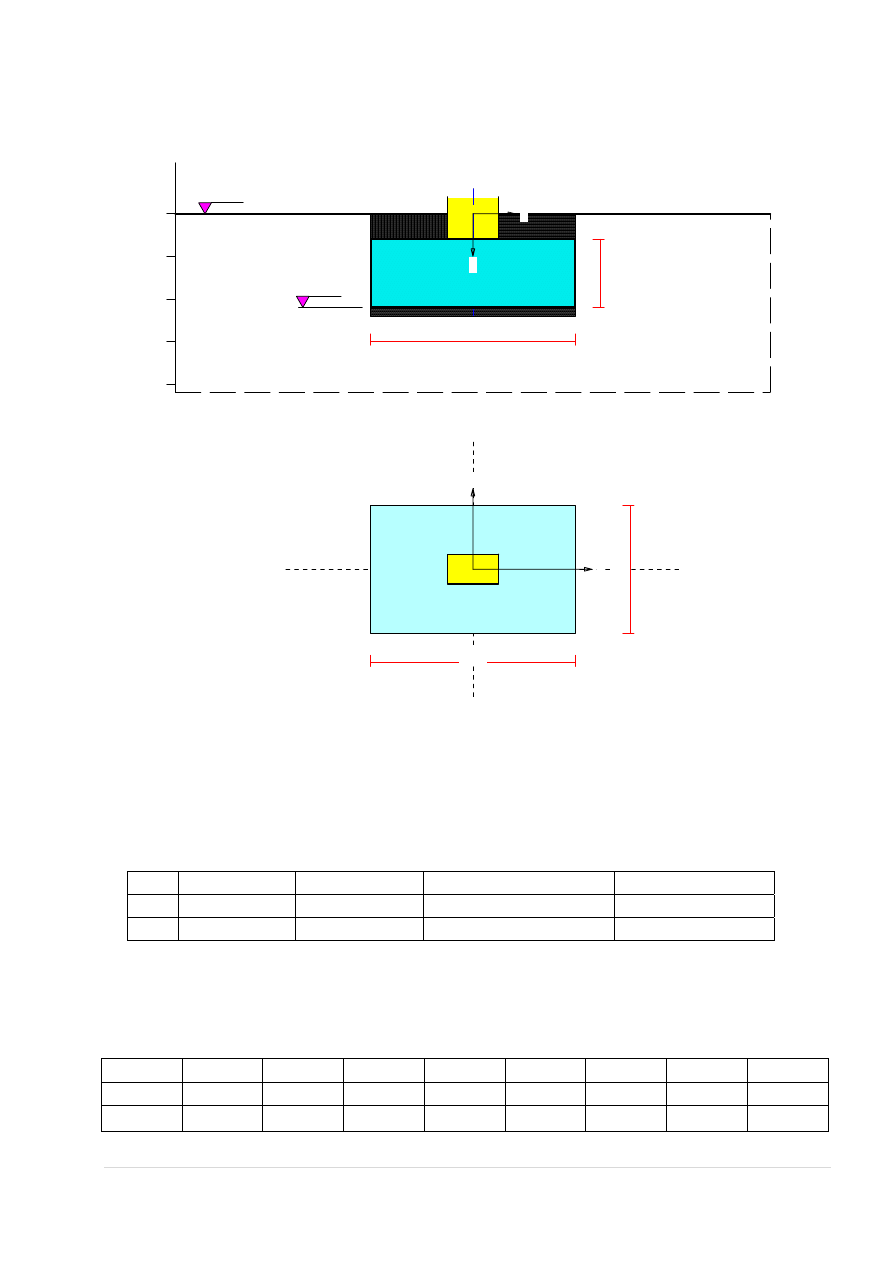
99 |

S t r o n a

FUNDAMENT 2. STOPA PROSTOKĄTNA

1. Podłoże gruntowe

1.1. Teren
Istniejący poziom terenu: z

= 0,00 m,

Projektowany poziom terenu: z

= 0,00 m.

1.2. Warstwy gruntu

Poziom stropu Grubość warstwy Nazwa gruntu

Poz. wody gruntowej

[m]

0,00

nieokreśl.

Piasek średni brak wody

1.3. Zasypka
Charakterystyczny

ciężar objętościowy:

z char

= 20,00 kN/m

Współczynnik obciążenia:

= 1,20.

1.4. Parametry geotechniczne występujących gruntów

Symbol I

stopień

gruntu

[

−]

[

−]

[t/m

]

wilgotn. [kPa]

[

]

[kPa]

0,35

1,70 m.wilg. 0,00 32,1 72494 80549

z [m]

0,00

Skala 1 : 50

2,40

0,80

1,10

2,40

1,50

100 |

S t r o n a

2. Konstrukcja na fundamencie

Typ

konstrukcji:

słup prostokątny

Wymiary

słupa: b = 0,60 m, l = 0,35 m,

Współrzędne osi słupa: x

= 8,50 m, y

= 0,00 m,

Kąt obrotu układu lokalnego względem globalnego:

φ = 0,00

3. Warstwa wyrównawcza pod fundamentem

Grubość: h = 0,10 m,

Charakterystyczny

ciężar objętościowy:

ww char

= 22,00 kN/m

4. Obciążenie od konstrukcji

Poziom przyłożenia obciążenia: z

obc

= 0,60 m.

Lista obciążeń:

Rodzaj

obciążenia

[kN]

[kNm]

[

−]

733,6 -43,6 0,0 0,00 -55,80 1,20

723,1 -43,6 0,0 0,00 -55,80 1,20

733,6 43,6 0,0 0,00 55,80 1,20

723,1 43,6 0,0 0,00 55,80 1,20

1009,0 -6,3 0,0 0,00 -10,40 1,20

1009,0 6,3 0,0 0,00 10,40 1,20

445,3 0,0 0,0 0,00 0,00 1,20

D – obciążenia stałe, zmienne długotrwałe,

D+K - obciążenia stałe, zmienne długotrwałe i krótkotrwałe.

5. Materiał

Klasa betonu: B30, nazwa stali: RB 500,

Średnica prętów zbrojeniowych: na kierunku x: d

= 20,0 mm, na kierunku y: d

= 20,0 mm,

Kierunek zbrojenia głównego: x,

Grubość otuliny: 5,0 cm.
Dopuszcza

się zbrojenie strzemionami, jeżeli warunek na przebicie tego wymaga.

6. Wymiary fundamentu

Poziom posadowienia: z

= 1,10 m

Kształt fundamentu: prosty

Wymiary podstawy: B

= 2,40 m, B

= 1,50 m,

Wysokość: H = 0,80 m,
Mimośrody: E

= 0,00 m, E

= 0,00 m.

101 |

S t r o n a

7. Stan graniczny I

7.1. Zestawienie wyników analizy nośności i mimośrodów

Nr obc. Rodzaj obciążenia Poziom [m]

Wsp. nośności

Wsp. mimośr.

1,10

0,49

0,15

1,10

0,48

0,16

1,10

0,49

0,15

1,10

0,48

0,16

* 5

1,10

0,60

0,02

1,10

0,60

0,02

1,10

0,29

0,00

7.6. Analiza stanu granicznego I dla obciążenia nr 5

Wymiary podstawy fundamentu rzeczywistego: B

= 2,40 m, B

= 1,50 m.

Poziom posadowienia: H = 1,10 m.

Rodzaj

obciążenia: D,

Zestawienie

obciążeń:

Pozycja

Obc. char. E

Obc. obl.

Mom. obl. Mom. obl.

[kN]

[m]

[

−] G [kN]

[kNm] M

[kNm]

Fundament

70,63 0,00 0,00 1,10 77,70 0,00 0,00

Zasypka - pole 1

5,08 0,63 -0,39 1,20 6,10 -2,40 3,83

Zasypka - pole 2

5,08 -0,63 -0,39 1,20 6,10 -2,40 -3,83

Zasypka - pole 3

5,08 -0,63 0,39 1,20 6,10 2,40 -3,83

Zasypka - pole 4

5,08 0,63 0,39 1,20 6,10 2,40 3,83

Suma 102,10 0,00 0,00

Obciążenia zewnętrzne od konstrukcji:
siła pionowa: N = 1009,00 kN, mimośrody wzgl. podst. fund. E

= 0,00 m, E

= 0,00 m,

siła pozioma: H

= -6,30 kN, mimośród względem podstawy fund. E

= 0,50 m,

siła pozioma: H

= 0,00 kN, mimośród względem podstawy fund. E

= 0,50 m,

moment: M

= 0,00 kNm,

moment: M

= -10,40 kNm.

Sprawdzenie

położenia wypadkowej obciążenia względem podstawy fundamentu

Obciążenie pionowe:

= N + G = 1009,00 + 102,10 = 1111,10 kN.

Momenty

względem środka podstawy:

= N·E

− H

·E

+ M

= 1009,00·0,00 + (0,00) = 0,00 kNm.

−N·E

+ H

·E

+ M

= -1009,00·0,00 + (-6,30)·0,50 + (-10,40) + (0,00) = -13,55 kNm.

Mimośrody sił względem środka podstawy:

= |M

| = 13,55/1111,10 = 0,01 m,

= |M

| = 0,00/1111,10 = 0,00 m.

+ e

= 0,005 + 0,000 = 0,005 m < 0,250.

Wniosek: Warunek położenia wypadkowej jest spełniony.

Sprawdzenie warunku granicznej nośności fundamentu rzeczywistego

Zredukowane wymiary podstawy fundamentu:

102 |

S t r o n a

′ = B

− 2·e

= 2,40 - 2·0,01 = 2,38 m, B

′ = B

− 2·e

= 1,50 - 2·0,00 = 1,50 m.

Obciążenie podłoża obok ławy (min. średnia gęstość dla pola 1):

średnia gęstość obliczeniowa:

D(r)

= 1,53 t/m

minimalna

wysokość: D

min

= 1,10 m,

obciążenie:

D(r)

·g·D

min

= 1,53·9,81·1,10 = 16,51 kPa.

Współczynniki nośności podłoża:
obliczeniowy

kąt tarcia wewnętrznego:

u(r)

u(n)

= 32,10·0,90 = 28,89

spójność: c

u(r)

= c

u(n)

= 0,00 kPa,

= 6,31 N

= 27,62, N

= 16,24.

Wpływ odchylenia wypadkowej obciążenia od pionu:
tg

= |H

|/N

= 6,30/1111,10 = 0,01, tg

/tg

u(r)

= 0,0057/0,5518 = 0,010,

= 0,98, i

= 0,99, i

= 0,99.

= |H

|/N

= 0,00/1111,10 = 0,00, tg

/tg

u(r)

= 0,0000/0,5518 = 0,000,

= 1,00, i

= 1,00.

Ciężar objętościowy gruntu pod ławą fundamentową:

B(n)

·g = 1,70·0,90·9,81 = 15,01 kN/m

Współczynniki kształtu:

= 1

− 0,25·B

′/B

′ = 0,84, m

= 1 + 0,3·B

′/B

′ = 1,19, m

= 1 + 1,5·B

′/B

′ = 1,95

Odpór

graniczny

podłoża:

fNBx

= B

′B

′(m

·N

·c

u(r)

·i

+ m

·N

D(r)

·g·D

min

·i

+ m

·N

B(r)

·g·B

′·i

) = 2505,56 kN.

fNBy

= B

′B

′(m

·N

·c

u(r)

·i

+ m

·N

D(r)

·g·D

min

·i

+ m

·N

B(r)

·g·B

′·i

) = 2286,90 kN.

Sprawdzenie

warunku

obliczeniowego:

= 1111,10 kN < m·min(Q

fNBx

fNBy

) = 0,81·2286,90 = 1852,39 kN.

Wniosek: warunek nośności jest spełniony.

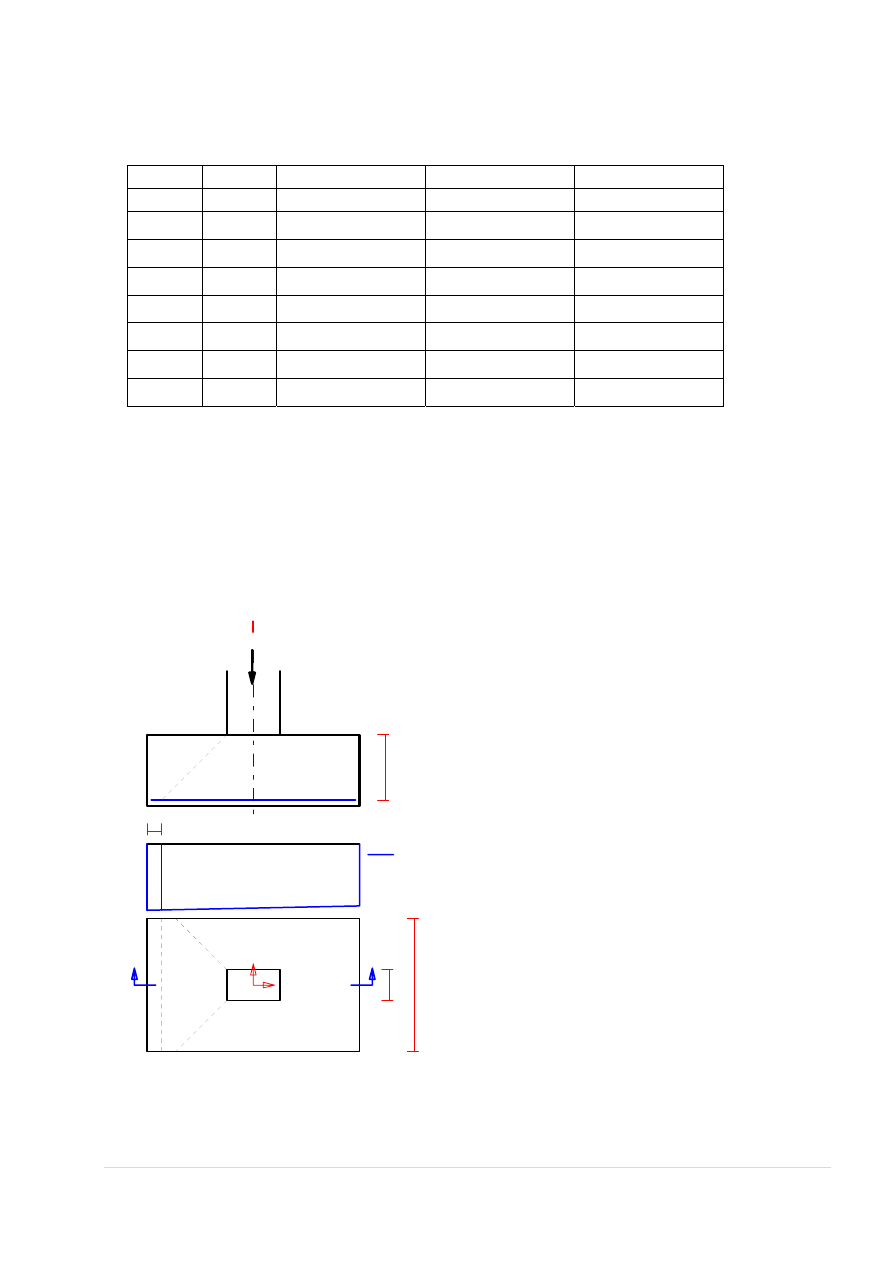
103 |

S t r o n a

8. Wymiarowanie fundamentu

8.1. Zestawienie wyników sprawdzenia stopy na przebicie

Nr obc. Przekrój Siła tnąca

Nośność betonu

Nośność strzemion

V [kN]

[kN]

968

* 5

968

8.6. Sprawdzenie stopy na przebicie dla obciążenia nr 5

Zestawienie

obciążeń:

Obciążenia zewnętrzne od konstrukcji zredukowane do środka podstawy stopy:
siła pionowa: N

= 1009 kN,

momenty: M

= 0,00 kNm, M

= -13,55 kNm.

Mimośrody siły względem środka podstawy:

= |M

| = 0,01 m, e

= |M

| = 0,00 m.

q2 qc

A-A

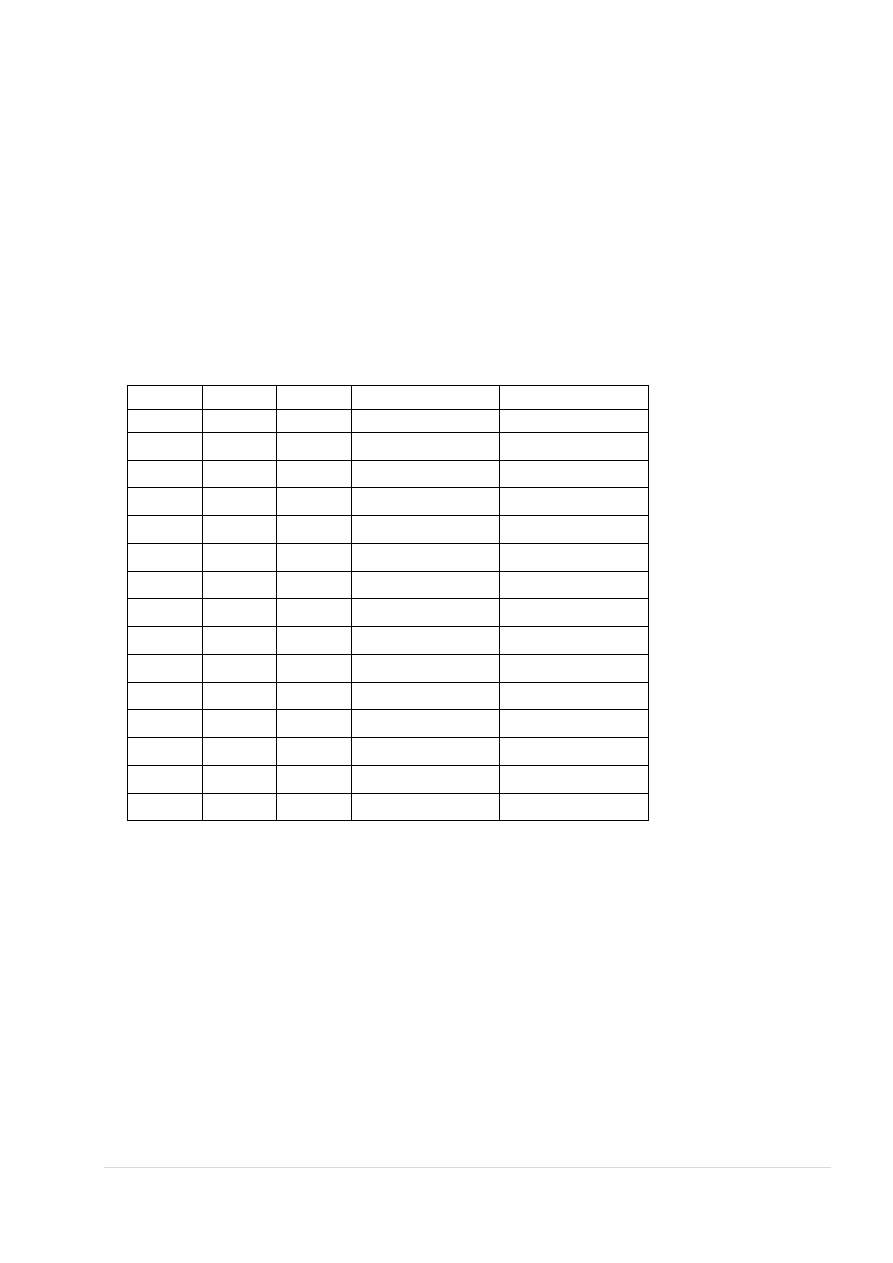
104 |

S t r o n a

Oddziaływanie podłoża na fundament:
Oddziaływania na krawędziach fundamentu w przekroju środkowym A-A:

= 271 kPa, q

= 290 kPa.

Oddziaływanie podłoża w przekroju 1: c = 0,16 m, q

= 288 kPa.

Przebicie stopy w przekroju 1:

Siła ścinająca: V

∫

q·dA = 62 kN.

Nośność betonu na ścinanie: V

= (b+d)·d·f

ctd

= (0,35+0,74)·0,74·1200 = 968 kN.

= 0 kN < V

= 968 kN.

Wniosek: warunek na przebicie jest spełniony.

8.9. Zestawienie wyników sprawdzenia stopy na zginanie

Nr obc. Kierunek Przekrój Moment zginający Nośność betonu

M [kNm]

[kNm]

111

110

111

110

* 5

130

8.18. Sprawdzenie stopy na zginanie dla obciążenia nr 5 na kierunku x

Zestawienie

obciążeń:

Obciążenia zewnętrzne od konstrukcji zredukowane do środka podstawy stopy:
siła pionowa: N

= 1009 kN,

momenty: M

= 0,00 kNm, M

= -13,55 kNm.

Mimośrody siły względem środka podstawy:

= |M

| = 0,01 m, e

= |M

| = 0,00 m.

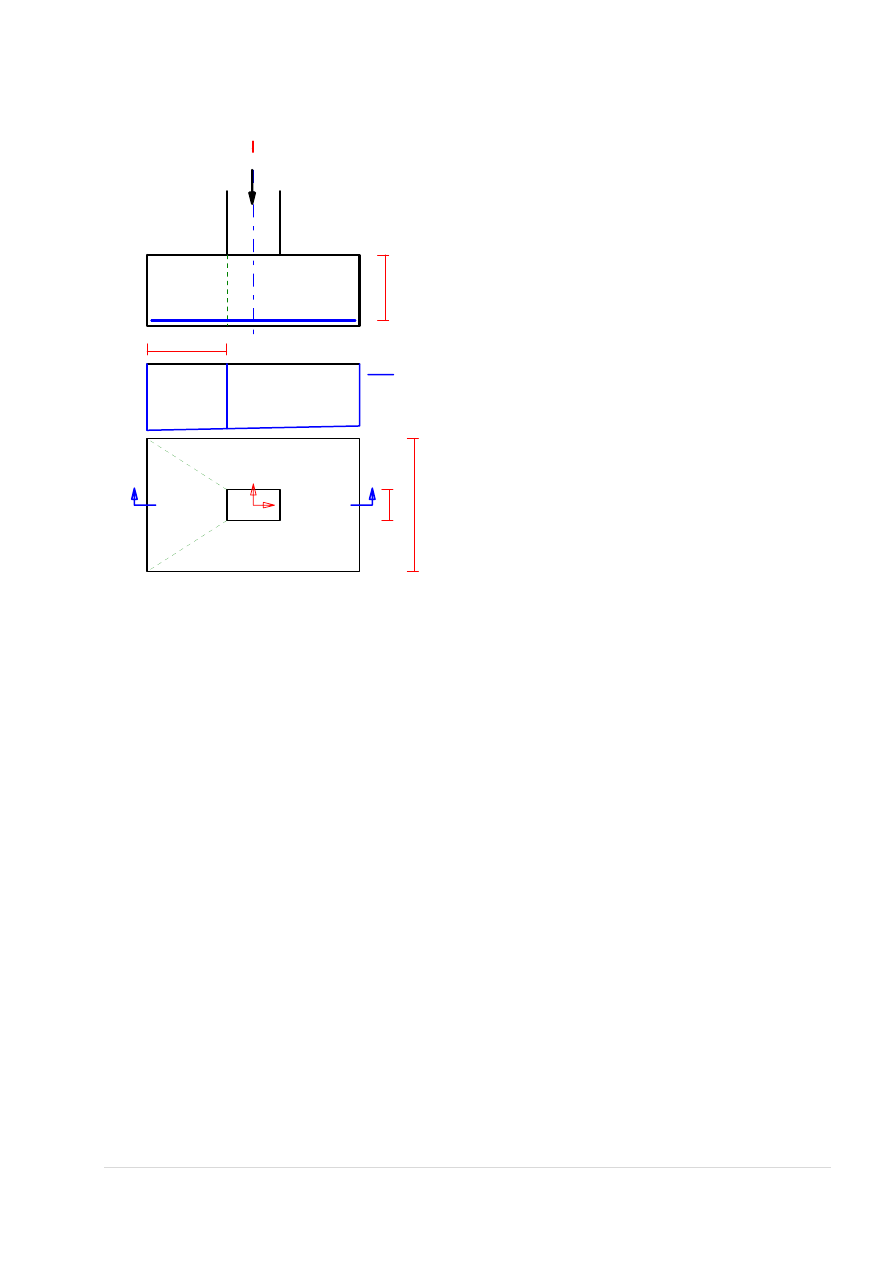
105 |

S t r o n a

Oddziaływanie podłoża na fundament:
Oddziaływania na krawędziach fundamentu w przekroju środkowym A-A:

= 271 kPa, q

= 290 kPa.

Oddziaływanie podłoża w przekroju 1: s = 0,90 m, q

= 283 kPa.

Zginanie stopy w przekroju 1:

Moment

zginający:

= [(b+3·B)·q

+ (b+B)·q

]·s

/12 = [(0,35+3·1,50)·290+(0,35+1,50)·283]·0,81/12 = 130 kNm.

Konieczna powierzchnia przekroju zbrojenia: A

= 4,3 cm

Wniosek: warunek na zginanie jest spełniony.

8.19. Sprawdzenie stopy na zginanie dla obciążenia nr 5 na kierunku y

Zestawienie

obciążeń:

Obciążenia zewnętrzne od konstrukcji zredukowane do środka podstawy stopy:
siła pionowa: N

= 1009 kN,

momenty: M

= 0,00 kNm, M

= -13,55 kNm.

Mimośrody siły względem środka podstawy:

= |M

| = 0,01 m, e

= |M

| = 0,00 m.

A-A

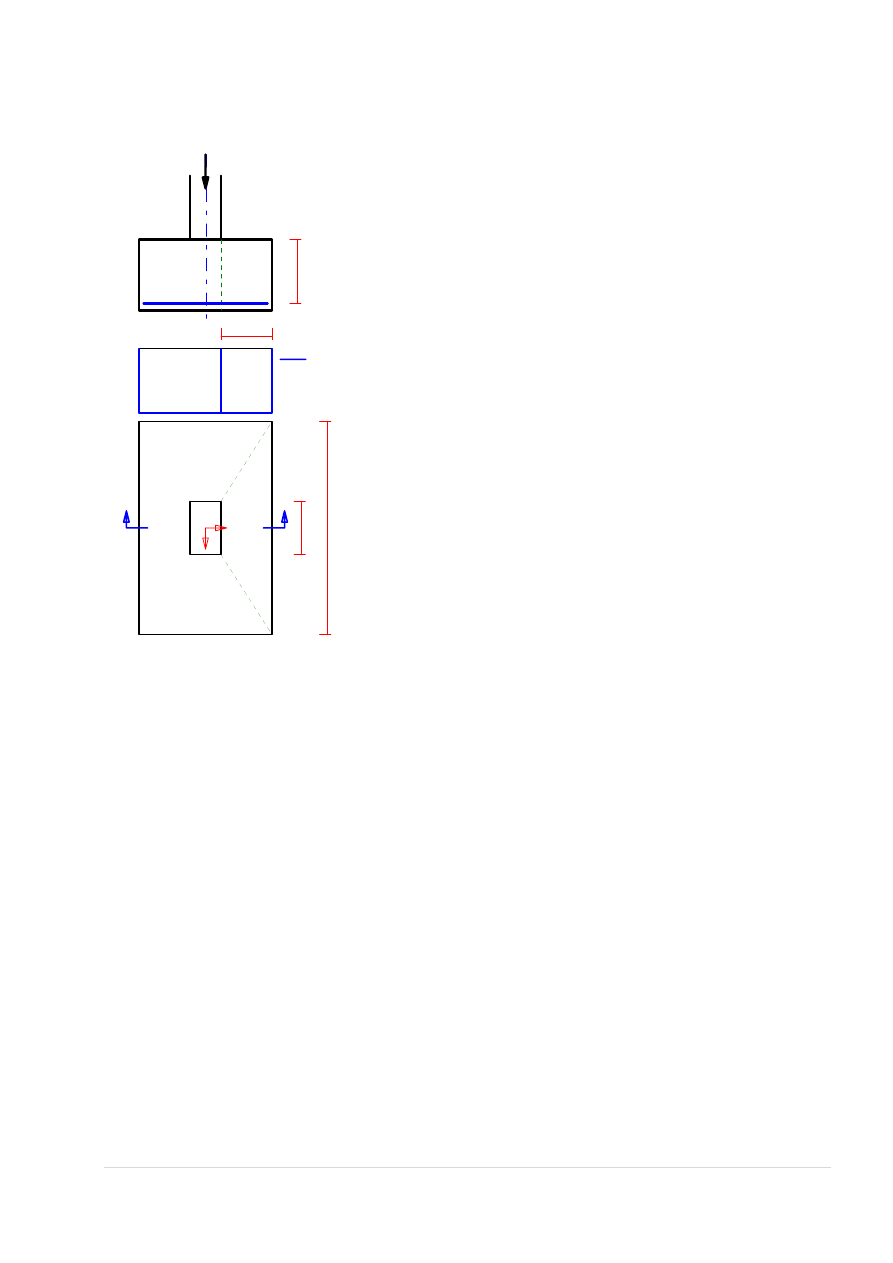
106 |

S t r o n a

Oddziaływanie podłoża na fundament:
Oddziaływania na krawędziach fundamentu w przekroju środkowym A-A:

= 280 kPa, q

= 280 kPa.

Oddziaływanie podłoża w przekroju 1: s = 0,57 m, q

= 280 kPa.

Zginanie stopy w przekroju 1:

Moment

zginający:

= [(b+3·B)·q

+ (b+B)·q

]·s

/12 = [(0,60+3·2,40)·280+(0,60+2,40)·280]·0,33/12 = 83 kNm.

Konieczna powierzchnia przekroju zbrojenia: A

= 2,8 cm

Wniosek: warunek na zginanie jest spełniony.

A-A

107 |

S t r o n a

9. Zbrojenie stopy

Zbrojenie

główne na kierunku x:

Obliczona powierzchnia przekroju poprzecznego A

= 4,3 cm

Średnica prętów:

φ = 20 mm, rozstaw prętów: s = 28 cm.

Zbrojenie

główne na kierunku y:

Obliczona powierzchnia przekroju poprzecznego A

= 6,5 cm

Średnica prętów:

φ = 20 mm, rozstaw prętów: s = 29 cm.

Ilość stali: 65 kg.

H=0,80

By=1,50

Bx=2,40

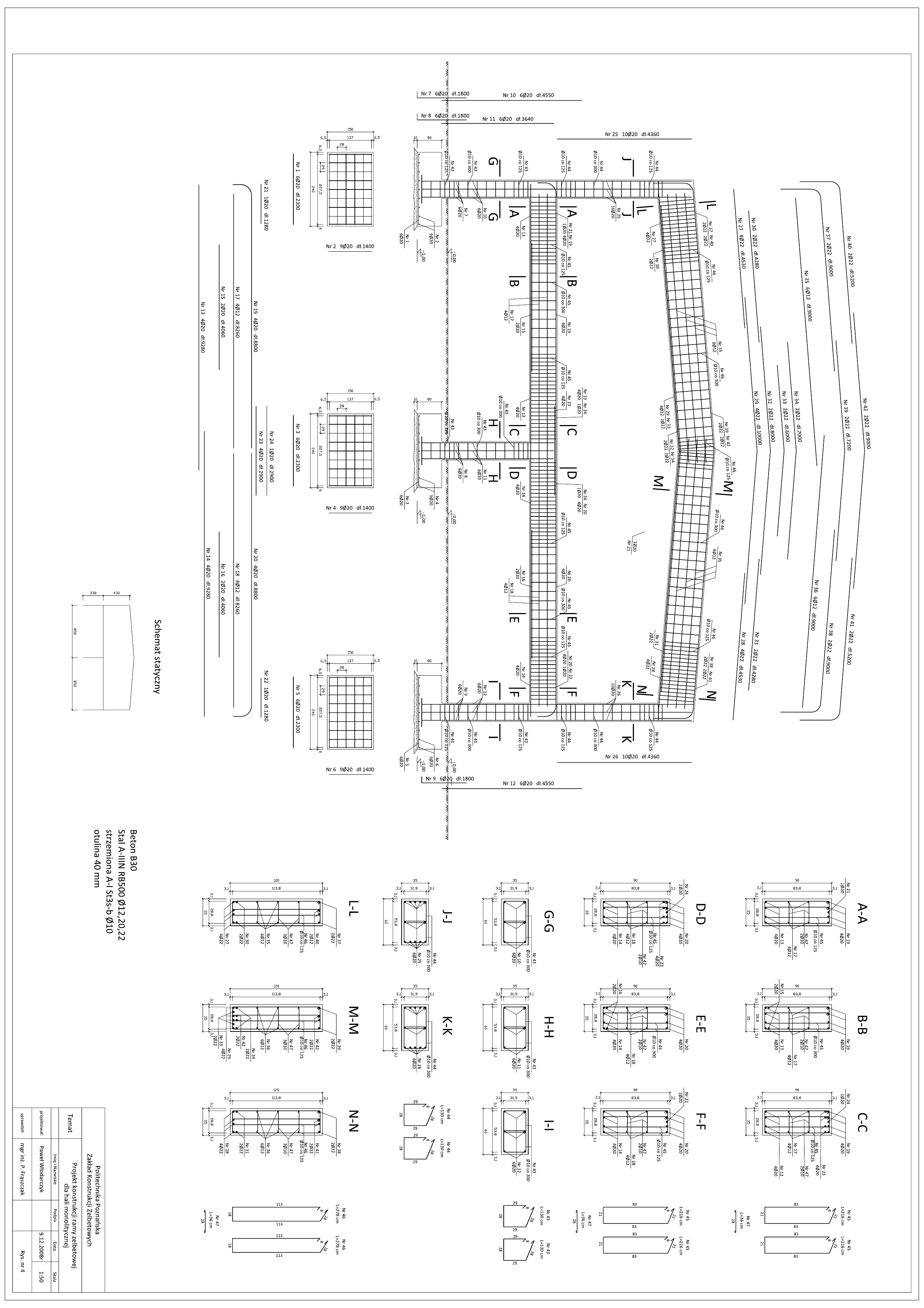
St3s-b

∅10

∅12

∅20

∅22

[mm]

[m]

[‐]

2,3

13,8

1,4

12,6

2,3

13,8

1,4

12,6

2,3

13,8

1,4

12,6

1,8

10,8

4,55

27,3

1,3

1,8

10,8

3,64

21,84

1,3

1,8

10,8

4,55

27,3

1,3

41,6

9,28

37,12

4,06

8,12

8,26

33,04

8,8

35,2

1,28

2,9

11,6

2,9

2,16

211,68

0,28

11,2

9,28

37,12

4,06

8,12

8,26

33,04

8,8

35,2

1,28

20 pop/b

pop/b

20 pop/b

pop/b

2,16

211,68

0,28

11,2

4,36

43,6

1,3

41,6

4,36

43,6

1,3

41,6

4,53

18,12

4,53

18,12

4,28

8,56

4,28

8,56

7,2

14,4

5,2

10,4

5,2

10,4

2,78

140

389,2

0,36

28,8

[m]

1066,6

174,08

453,18

224,56

[kg]

0,617

0,888

2,47

2,98

[kg]

658,07

154,58

1119,4

669,19

[kg]

658,07

[t]

1943,13

2,60

WYKAZ ZBROJENIA

Długość ogólna wg średnic

Masa 1m pręta

Masa prętów wg średnic

Masa prętów wg rodzajów stali

Masa całkowita

NAZWA ELEMENTU

PRĘT

REDNICA

UGO

ŚĆ

Słup nr3

Rygiel nr 6

Rygiel nr 7

Słup nr 4

Słup nr 5

Rygiel dachowy

nr 89

Słup nr1

Słup nr 2

Stopa

fundamentowa

ELEMENT

Stopa

fundamentowa nr1

ILOŚĆ

SZTUK

DŁUGOŚĆ OGÓLNA

RB500

[m]

Stopa

fundamentowa

PRĘTY ZBROJENIOWE

Document Outline

ff.pdf
- calosc.pdf
  - spis tresci.pdf
  - Rysunek1.pdf
  - Rysunek2.pdf
  - Rysunek4.pdf
  - PROJECT POPR.pdf
  - wspomaganie - rygle.pdf
  - wspomaganie - słupy.pdf
  - fundamenty.pdf
- drukdobry.pdf
wykaz stali.pdf

Wyszukiwarka

Podobne podstrony:
Projekt rama zelbetowa
Rama żelbetowa
OPIS TECHNICNY(rama żelbetowa) 2
~$ojekt rama zelbetowa doc
samouczek rama
Prezentacja ZPR MS Project
14 TIOB W14 zelbet i klasyfikacja deskowan
82 Nw 06 Drewniana rama
33 Rama zamknięta ze ściągiem
Free Energy Projects 2
przekroj podłużny przez most żelbetowy
Żelbet obliczenia
Microsoft Office Project Project1 id 299062
Proejtowanie słupa zelbetowego
mes rama
zpp rama, zpp rama 2
Druk podania o rejestrację na semestr letni 2010-2011, Nauka, budownictwo, żelbet EC przykłądy

więcej podobnych podstron

PROJECT rama żelbetowa 1

Document Outline