6

L

ABORATORIUM FIZYCZNE

Instytut Fizyki Politechniki Krakowskiej

ĆWICZENIE

20

Zastosowanie oscyloskopu do badania sygnałów

przemiennych

Ćwiczenie20

2

ĆWICZENIE

20

Zastosowanie oscyloskopu do badania sygnałów
przemiennych

B.Oleś i J.Brzezowska

1.

Wprowadzenie

Celem ćwiczenia jest obserwacja i pomiar napięcia prądu przemiennego za pomocą oscylosko-

pu oraz zapoznanie się z metodami prostowania tego prądu. Oscyloskop posłuży również do anali-
zowanie figur Lissajous, powstających ze złożenia dwóch sinusoidalnych sygnałów, wzajemnie do
siebie prostopadłych.

1.1

Budowa oscyloskopu analogowego

Oscyloskop jest urządzeniem elektronicznym powszechnie stosowanym w wielu dziedzinach na-

uki i techniki, szczególnie w elektronice. Służy do obserwacji i pomiarów zmiennych w czasie sygna-
łów elektrycznych lub innych wielkości fizycznych, przetworzonych na sygnały elektryczne (zazwyczaj
na napięcie). Można za jego pomocą również porównywać częstotliwości, fazy napięć i mierzyć krót-
kie odstępy czasu.

Rozróżniamy oscyloskopy analogowe i cyfrowe

1

. W oscyloskopie analogowym zasadniczym ele-

mentem jest

lampa oscyloskopowa

z układem zasilania, której schemat budowy przedstawiono na

rys. 1. Jest to opróżniona z powietrza rura szklana o odpowiednim kształcie. W jej wąskiej części znaj-
duje się pośrednio żarzona katoda K emitująca elektrony. Katodę otacza metalowy cylinder Wehnelta
CW znajdujący się na ujemnym względem niej potencjale. Reguluje on ilość elektronów dochodzą-
cych do anody i zapobiega ich rozpraszaniu. Elektrony po przejściu przez otwór w cylindrze Wehnelta
są przyspieszane dodatnim potencjałem anod A

1

i A

2

. Elektrody te mają kształt cylindrów i dodatko-

wo odgrywają rolę soczewek elektrostatycznych skupiając elektrony w wąską wiązkę, ogniskowaną
w jednym punkcie ekranu. Stanowi go płaska ścianka szerszego końca lampy pokryta od wewnątrz
warstwą substancji fluoryzującej pod wpływem padających elektronów. Jasność tej plamki reguluje

1

W oscyloskopie cyfrowym lampa oscyloskopowa została wyeliminowana. Badany przebieg sygnału przetwa-

rzany jest na postać cyfrową, zapamiętywany w układzie pamięci, a następnie po wykonaniu operacji przetwa-
rzania cyfrowo-analogowego odtwarzany na ekranie ciekłokrystalicznym.

K

E

P

3

P

1

P

4

P

2

A

2

A

1

C

Ż

P

3

P

1

P

4

P

2

Rys.1. Schemat budowy lampy oscyloskopowej i układu elektrod odchylających. Oscyloskop analogowy

Zastosowanie oscyloskopu

3

się potencjałem cylindra Wehnelta, a ostrość poprzez zmianę potencjału anod. Układ dwóch par elek-
trod odchylających X (P

3

i P

4

) i Y (P

1

i P

2

) pozwala odchylać strumień elektronów w kierunku pozio-

mym X i pionowym Y poprzez przyłożenie zewnętrznego sygnału. Wewnętrzne ściany lampy pokryte
są warstwą grafitu lub są metalizowane i uziemione w celu odprowadzenia ładunków elektrycznych
gromadzących się na ekranie i w przedniej części lampy.

Badanie charakterystyki czasowej sygnału umożliwia

wbudowany w oscyloskop

generator podstawy czasu

(GPCz). Generator ten wytwarza sygnał piłokształtny
(rys.2), którego napięcie przykładane jest do płytek od-
chylania poziomego X. W czasie narastania napięcia
plamka wychyla się proporcjonalnie do jego chwilowej
wartości. Dzięki temu uzyskujemy przesuwanie się na
ekranie świecącej plamki ze stałą szybkością w kierunku
poziomym. Powrotny ruch plamki, odpowiadający spad-
kowi napięcia, jest niewidoczny, ponieważ odpowiednie sprzężenie układu regulacji jasności z gene-
ratorem podstawy czasu wygasza wówczas obraz. Częstotliwość generatora podstawy czasu może
być płynnie zmieniana i zsynchronizowana z częstotliwością zmian badanego sygnału. Jeśli okres sy-
gnału badanego przyłożonego do płytek odchylania pionowego Y będzie równy okresowi podstawy
czasu, to obserwujemy na ekranie jeden cykl, jeśli będzie n-krotnie mniejszy, to zaobserwujemy n
cykli.

Generator podstawy czasu można wyłączyć i do płytek odchylania pionowego Y przyłożyć sygnał

zewnętrzny, podczas gdy do płytek odchylania poziomego X przykłada się drugi sygnał. Pracując w
tym tzw. układzie xy możemy porównywać ze sobą częstotliwości różnych sygnałów.

Następnym podstawowym elementem oscyloskopu jest

wzmacniacz szerokopasmowy

sygnału

wejściowego. Umożliwia on regulację wzmocnienia i badanie napięć zmiennych o bardzo małych
amplitudach. Nowoczesne oscyloskopy posiadają wzorcowane układy elektroniczne. Oznacza to, że
przy jednym ze skrajnych położeń pokrętła regulacji ciągłej wzmacniacza amplituda sygnału obser-
wowanego na ekranie jest proporcjonalna do amplitudy sygnału wejściowego, a współczynnik pro-
porcjonalności jest podany na pokrętle skokowej zmiany wzmocnienia (np. 10 mV/cm). Podobnie
wzorcowana jest podstawa czasu.

1.2

Prostowanie prądu przemiennego

Prostowniki

są to urządzenia elektroniczne pozwalające z prądu zmiennego uzyskać prąd stały.

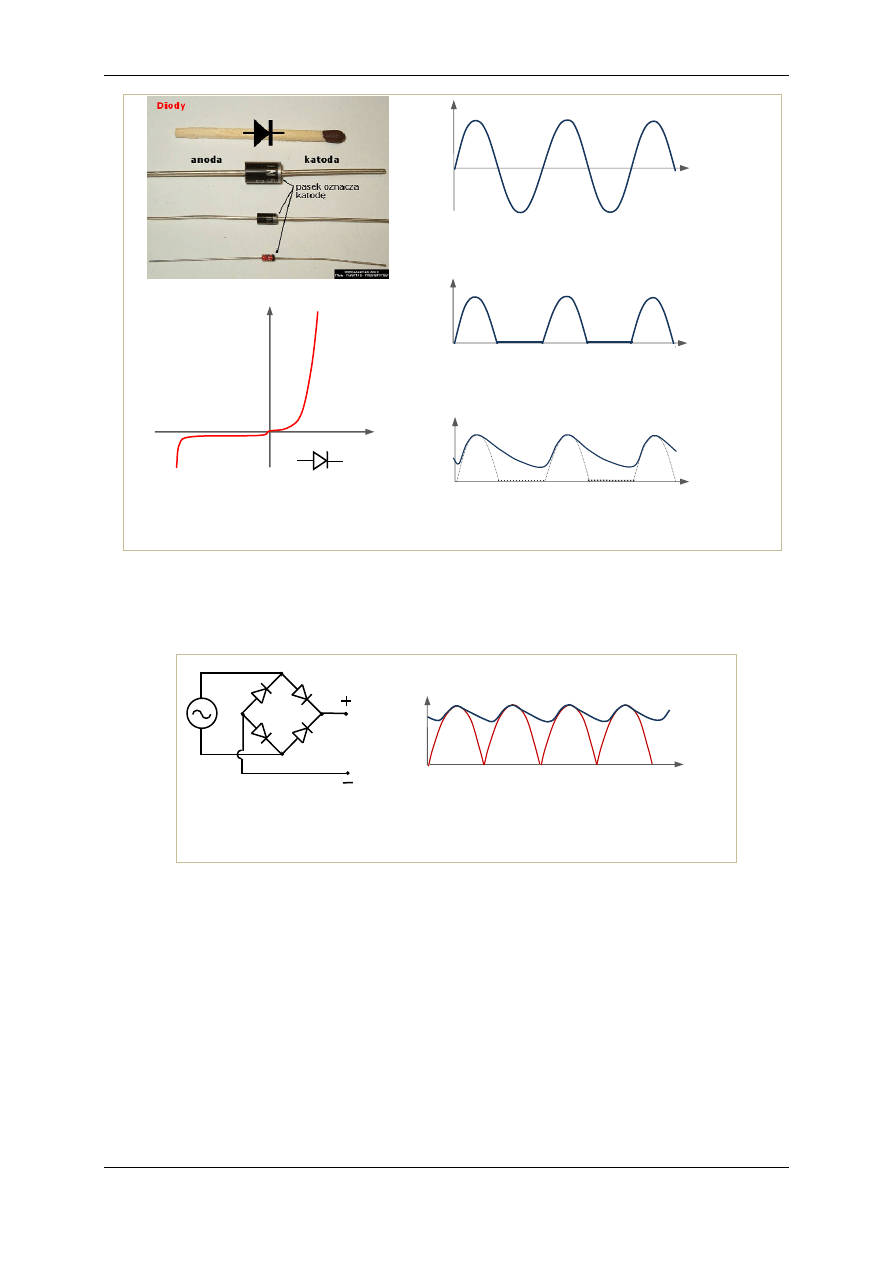
Proces ten nazywamy prostowaniem prądu zmiennego. Elementami prostującymi mogą być diody
półprzewodnikowe, które mają tę własność, że opór ich bardzo silnie zależy od kierunku spadku po-
tencjału na elemencie (rys.3a). Półprzewodnikowa dioda prostownicza włączona w obwód zasilany
sieciowym napięciem sinusoidalnym (rys.3b) przepuszcza prąd tylko w jednym kierunku, kiedy jest
spolaryzowana w kierunku przewodzenia i pozwala to otrzymać prąd jednokierunkowy o zmiennym,
pulsującym napięciu, jak na rys.3c. Wahania napięcia można zmniejszyć przez włączenie równolegle z
oporem R kondensatora C o dużej pojemności. Kondensator rozładowuje się w przerwach między im-
pulsami i wygładza napięcie (rys.3d).

Rys.2. Piłokształtny sygnał generatora
podstawy czasu

U

t

Ćwiczenie20

4

Rys. 4a przedstawia schemat prostownika dwukierunkowego (dwupołówkowego). Sygnał sinuso-

idalny po wyprostowaniu wygląda tak jak na rys. 4b (czerwona linia). Dodatkowo można go wygładzić
stosując kondensatory o odpowiedniej pojemności (niebieska linia na rys. 4b).

1.3

Krzywe Lissajous

Krzywą (figurą) Lissajous

nazywamy tor, jaki zakreśla punkt drgający harmonicznie w dwóch wza-

jemnie prostopadłych kierunkach. Ogólne równania krzywych Lissajous, w których parametrem jest
czas, mają postać:

= cos

+

i = cos

+

, 1

gdzie i oznaczają amplitudy drgań odpowiednio w kierunkach osi i ,

ω

x

i

ω

y

to częstości, a

ϕ

x

i

ϕ

y

to fazy początkowe tych drgań. Występująca w równaniach częstość

ω

wyraża się poprzez często-

tliwość (podawaną w hercach) wzorem

= 2 .

U

t

Rys.3 c. Prostowanie prądu przemiennego
przez diodę prostowniczą

U

t

Rys.3 b. Przebieg czasowy napięcia prą-
du przemiennego

U

t

Rys.3 d. Prostowanie prądu przemiennego
przez diodę prostowniczą i kondensator

Kierunek
przewodzenia

Kierunek
zaporowy

+

−

Rys.3 a. Różne typy diod prostowni-
czych oraz charakterystyka prądo-
wo-napięciowa diody prostowniczej

http://kunio13.elektroda.eu/rysunki/diody2.jpg

Rys.4 a. Schemat prostownika dwukierunkowego (dwupołówkowego). Sygnał
sinusoidalny po wyprostowaniu wygląda tak jak na rysunku b (linia czerwona).
Dodatkowo można go wygładzić stosując kondensatory (linia niebieska).

U

t

a)

b)

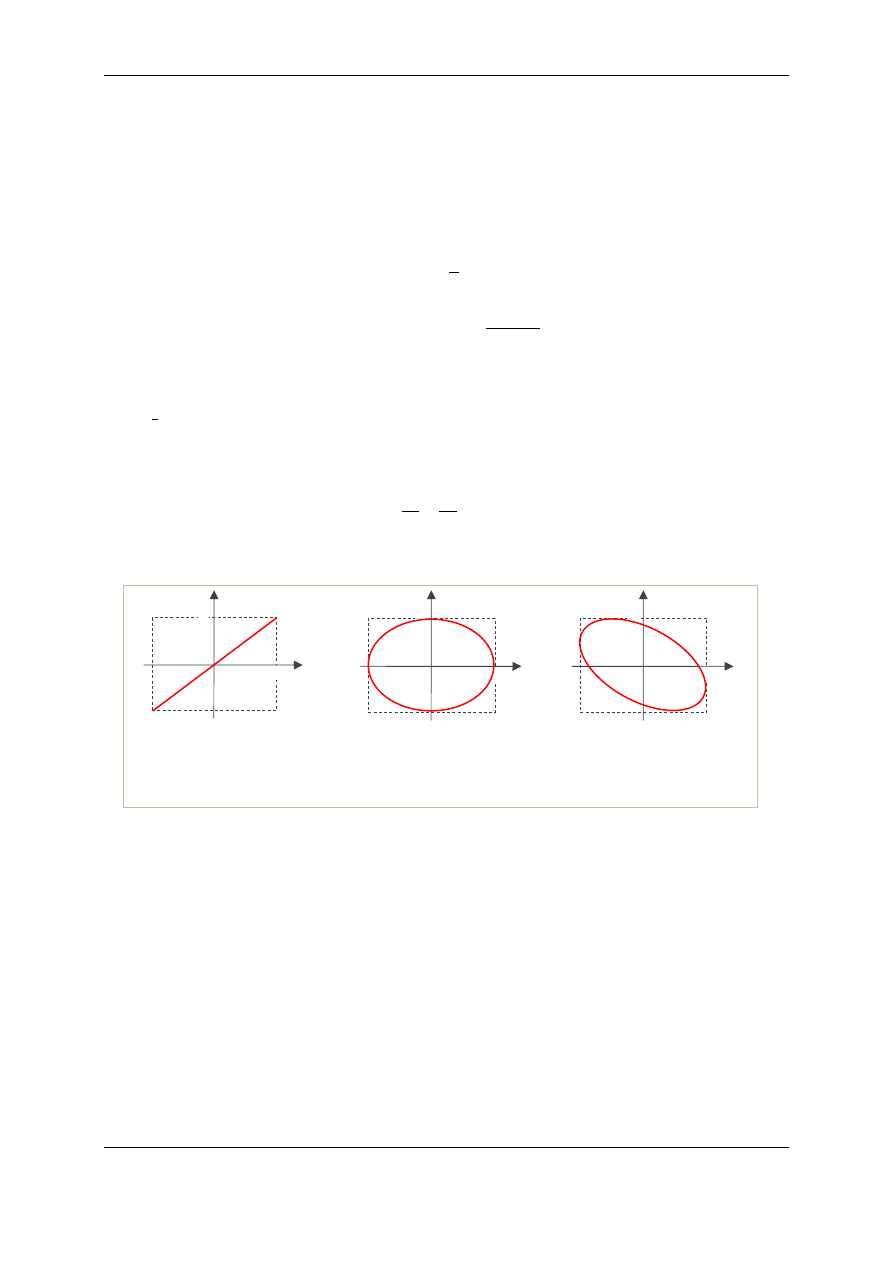
Zastosowanie oscyloskopu

5

Sprawdźmy, jaką figurę Lissajous otrzymuje się ze złożenia drgań o jednakowych częstościach,

ω

x

=

ω

y

=

ω

. Jeśli przyjmiemy

ϕ

x

= 0, a

ϕ

y

=

ϕ

, to z równań (1) dostajemy równania:

= cos

i = cos

+

, 2

z których po wyeliminowaniu czasu dostaje się równanie toru punktu. Łatwo zauważyć, że dla

ϕ

= 0

otrzymuje się równanie prostej:

=

,

a wypadkowy ruch punktu jest ruchem harmonicznym z częstością

ω

po odcinku tej prostej, którego

długość jest równa podwojonej amplitudzie drgań, tj.

2√

+

(rys.5a).

Dla innych kątów

ϕ

, zawartych w przedziale od zera do 2

π

, krzywe Lissajous mają kształty elips

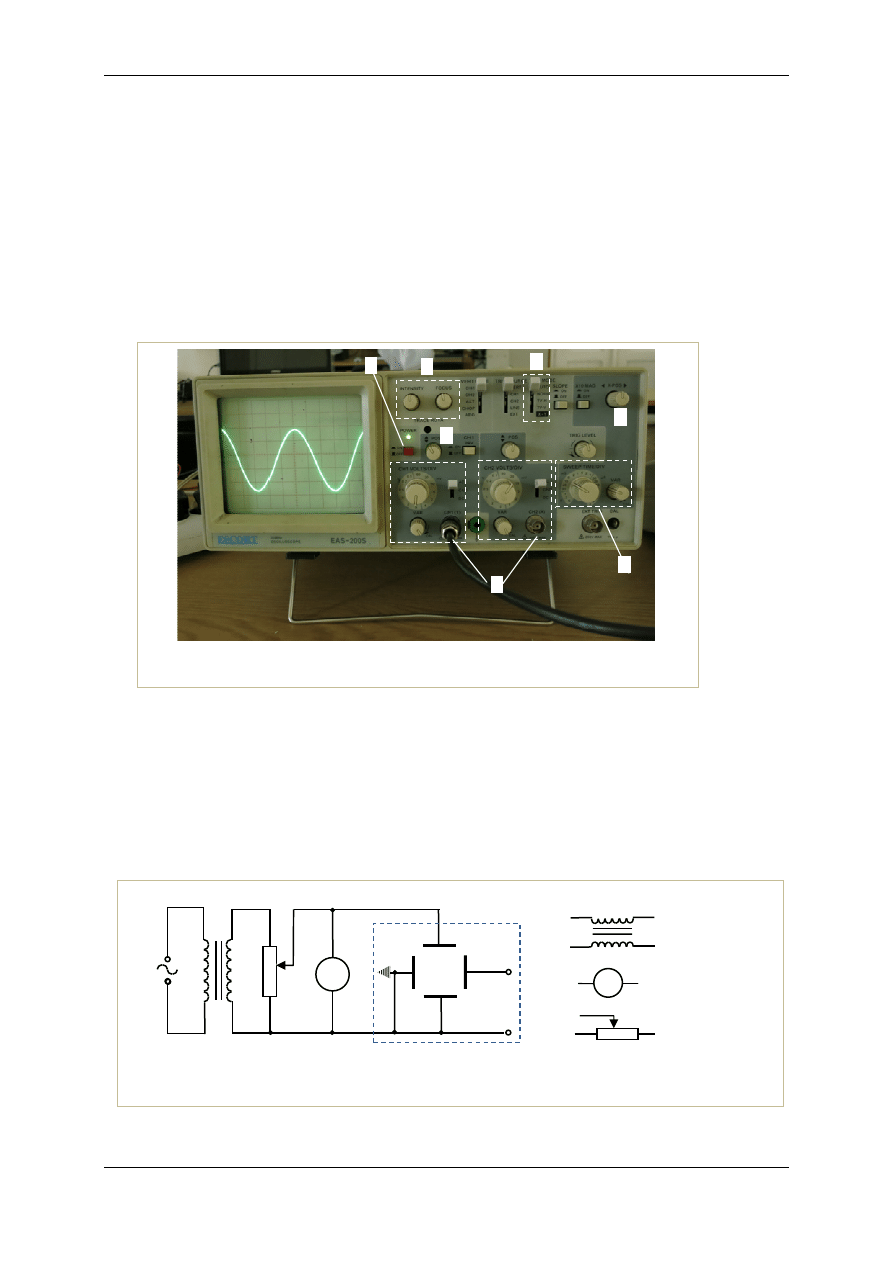
mniej lub bardziej wydłużonych i ustawionych pod różnymi kątami (rys.5c). W szczególnym przypad-
ku

ϕ

=

punkt porusza się po elipsie w kierunku zgodnym z ruchem wskazówek zegara, a osie syme-

trii krzywej pokrywają się z kierunkami drgań składowych

, (rys.5b). Jest ona dana równaniem otrzy-

manym z równań (2) po wyeliminowaniu czasu

+

= 1.

Gdy

= , równanie elipsy przechodzi w równanie okręgu o promieniu równym .

Jeżeli częstości drgań różnią się nieznacznie, wypadkowy ruch zachodzi po wolno zmieniającej

swój kształt krzywej, przyjmującej formy od odcinka do elipsy.

W przypadku, gdy częstości drgań są różne i ich stosunek da się wyrazić przez stosunek liczb cał-

kowitych, torem ruchu wypadkowego jest dość złożona krzywa zamknięta. Przykłady takich figur Lis-
sajous znajdziesz na rys.12 w Uzupełnieniu.

Krzywe Lissajous (rys.5) można obserwować na oscyloskopie, sterując wychyleniem wiązki elek-

tronów w kierunku i poprzez odpowiednią zmianę częstotliwości i amplitudy sygnałów podawa-
nych na wejścia i .

a.

=

,

=

= 0

b.

=

,

= 0,

= /2

c.

=

Rys.5. Przypadki figur Lissajous, gdy częstości drgań składowych są jednakowe

,

=

Ćwiczenie20

6

2.

Wykonanie ćwiczenia

2.1

Zapoznanie się z elementami regulacyjnymi oscyloskopu.

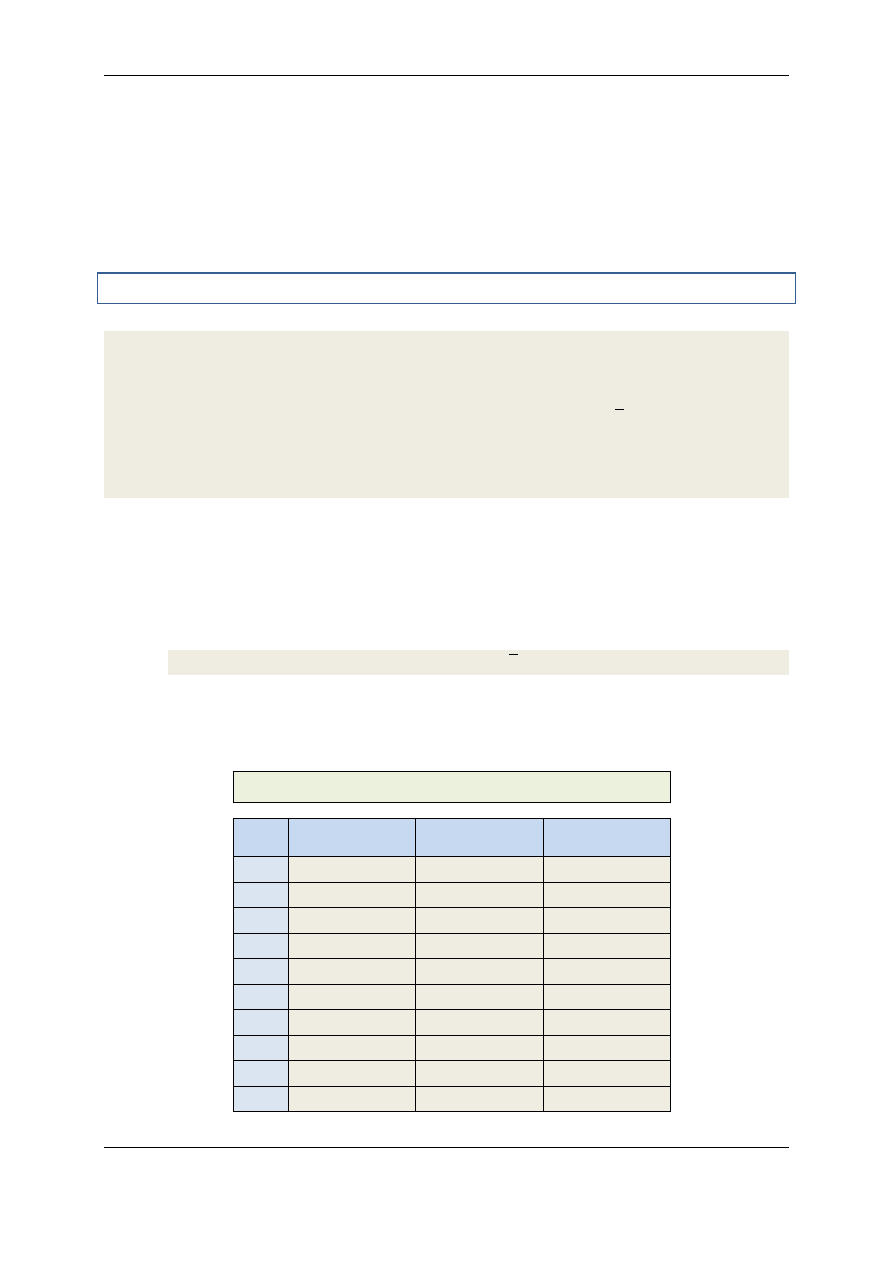
Korzystając z instrukcji obsługi umieszczonej bezpośrednio przy ćwiczeniu należy zapoznać się z

głównymi elementami regulacyjnymi oscyloskopu (zaznaczonymi na rys.6). Są nimi: wyłącznik zasila-
nia (a), pokrętło jasności i pokrętło ostrości plamki (b), pokrętło położenia plamki na osiach x i y (c i
d), wyłącznik generatora podstawy czasu (e), regulator częstotliwości generatora podstawy czasu
(skokowy i ciągły) (f), pokrętło synchronizacji częstotliwości generatora podstawy czasu (GPCz) z czę-
stotliwością badanego sygnału, gniazdka (g), do których załączamy badane napięcie.

3.

Przebieg pomiarów

3.1

Obserwacja napięcia prądu przemiennego i obliczanie czułości
oscyloskopu

1.

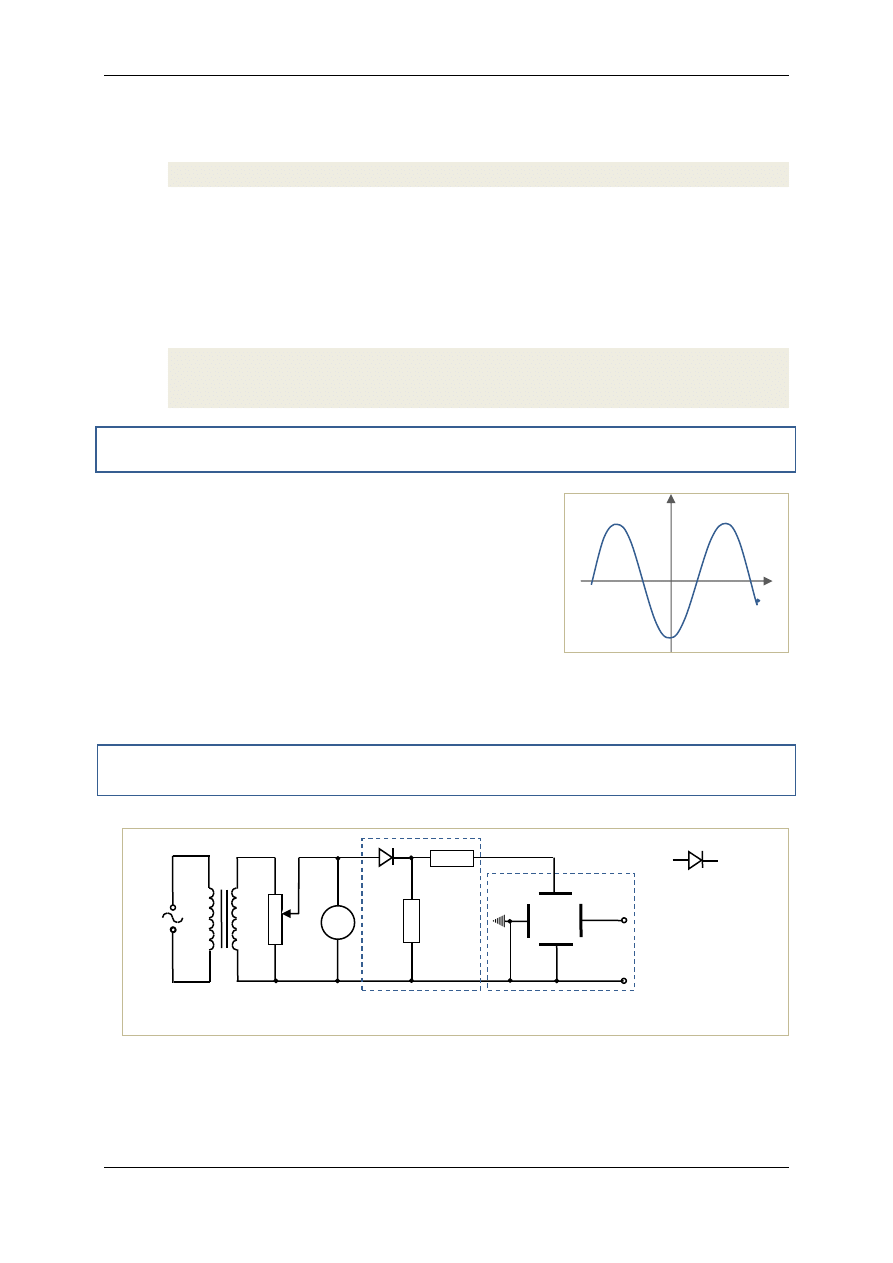
Połącz obwód elektryczny według schematu przedstawionego na rys. 7.

a

f

g

b

c

d

e

Rys.6. Fotografia płyty czołowej oscyloskopu

Rys.7. Schemat obwodu elektrycznego służącego do
obserwacji zmiennego napięcia z sieci

V

woltomierz

transformator

opornik
suwakowy

V

Oscyloskop

Sieć

GPCz

Zastosowanie oscyloskopu

7

2.

Po sprawdzeniu obwodu przez opiekuna ćwiczenia włącz transformator do sieci. Za pomocą
opornika suwakowego dobierz odpowiednią wysokość sygnału obserwowanego na ekranie
oscyloskopu oraz ustaw zakres woltomierza.

3.

Następnie zrównaj częstotliwość generatora podstawy czasu z częstotliwością badanego
sygnału tak, by na ekranie pojawił się przebieg w czasie jednego okresu. Naszkicuj przebieg
napięcia sieciowego obserwowanego na ekranie oscyloskopu na papierze milimetrowym.

Możesz wykonać zdjęcia obserwowanych na ekranie sygnałów i dołączyć do sprawozdania.

Zapamiętaj

Woltomierz mierzy

napięcie skuteczne

$%

prądu przemiennego, czyli napięcie takiego prądu stałego,

który wydziela w tym samym czasie tą samą ilość energii, co dany prąd przemienny. Napięcie sku-
teczne związane jest z napięciem maksymalnym

&

zależnością

$%

=

&

/√2.

Oscyloskop pozwala zmierzyć maksymalne napięcie

&

, czyli amplitudę prądu przemiennego opisa-

nego wzorem

=

&

sin 2π +

α

, gdzie – częstotliwość prądu,

α

– faza początkowa.

4.

Wyłącz GPCz. Na ekranie będziesz wówczas obserwować pionowy jasny odcinek, którego
długość równa jest podwojonej amplitudzie sygnału, tj.

= 2(.

5.

Przy ustalonym wzmocnieniu zmierz amplitudę

( (w działkach skali oscyloskopu) obserwo-

wanego na ekranie wychylenia plamki, odpowiadającą napięciu skutecznemu

$%

wskazy-

wanemu przez woltomierz. Oblicz maksymalne napięcie

&

ze wzoru:

&

=

)*

√2.

6.

Zmieniając wartość napięcia

$%

za pomocą opornika suwakowego, powtórz ok. dziesięć ra-

zy pomiary z punktu 5.

Wyniki wpisz do Tabeli 1.

Tabela 1. Ćwiczenie 20. Dane pomiarowe

Lp.

$%

[V]

( = /2 [dz]

&

[V]

1.

2.

3.

4.

5.

6.

7.

8.

9.

10.

Ćwiczenie20

8

7.

Amplituda

( sygnału jest wprost proporcjonalna do napięcia

&

, a współczynnik proporcjo-

nalności nosi nazwę

czułości oscyloskopu

+:

( = +

&

,

Wymiarem + jest dz/V.

Sporządź wykres zależności amplitudy ( od napięcia

&

, ( =

&

, dopasowując prostą

=

do punktów pomiarowych metodą regresji liniowej za pomocą programu Wykres

Lab.

Czułość oscyloskopu oraz jej niepewność otrzymamy z powyższego dopasowania prostej do
punktów pomiarowych i, jak łatwo zauważyć, jest ona równa współczynnikowi kierunko-
wemu prostej.

Znając czułość oscyloskopu dla danego wzmocnienia możemy przeliczyć wysokość sygnału obser-
wowanego na ekranie na jednostki napięcia (wolty).

8. Korzystając z wyznaczonej czułości uzupełnij wartości

napięcia na sporządzonym wykresie.

3.2

Obserwacja jednopołówkowego efektu prostowania prądu
zmiennego w obwodzie z diodą półprzewodnikową

W poniższych zadaniach zaobserwowany na ekranie oscyloskopu przebieg sygnału narysuj na papie-
rze milimetrowym. Przelicz wysokość sygnału na jednostki napięcia.

1.

Połącz układ według schematu przedstawionego na rys.8. Obserwuj zjawisko prostowa-
nia prądu przemiennego przy tym samym wzmocnieniu, co w poprzednim zadaniu.

2,0

–

1,0 −

-2,0

–

-1,0 −

U [V]

t [s]

dioda
prostownicza

Rys.8. Schemat obwodu do badania prostowania jednopołówkowego

V

Oscyloskop

Element z diodą
prostowniczą

Sieć

GPCz

Zastosowanie oscyloskopu

9

2.

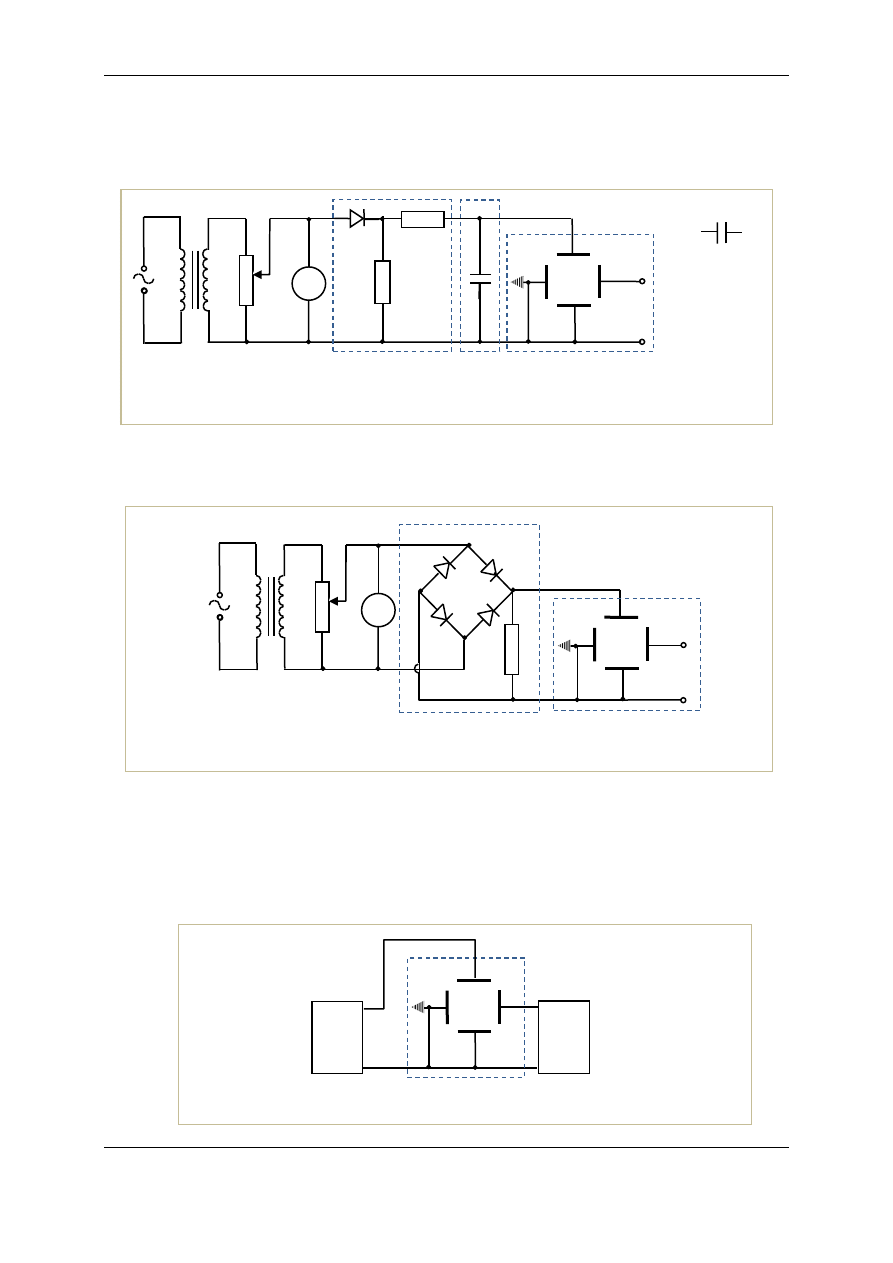
Do obwodu elektrycznego z rys.8 dołącz płytkę z kondensatorami o różnej pojemności,
jak przedstawiono na schemacie na rys.9. Następnie obserwuj efekt wygładzania prądu
przez włączanie kondensatorów o coraz to większej pojemności.

3.

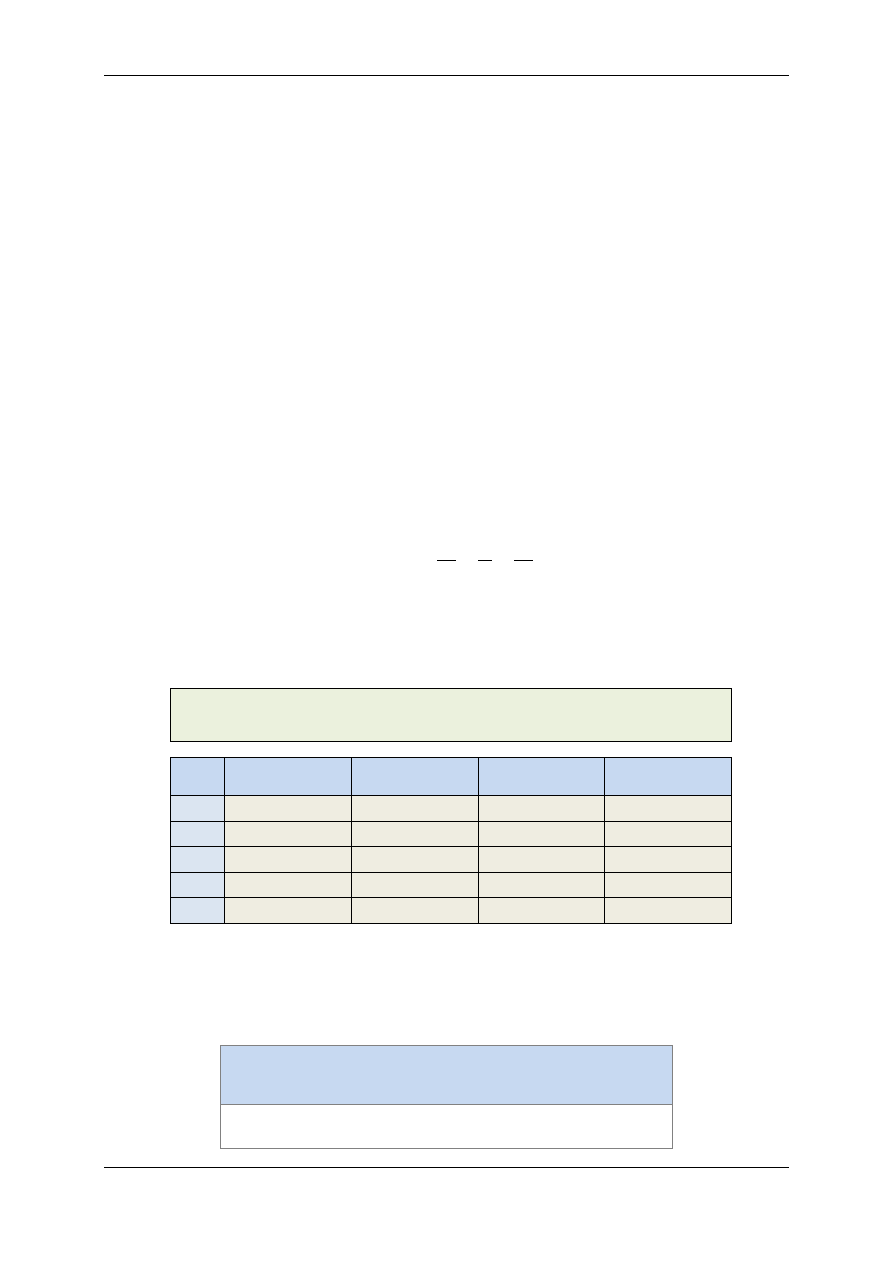
Połącz układ według schematu przedstawionego na rys.10 celem obserwacji prostowa-
nia dwupołówkowego.

3.3

Obserwacja krzywych Lissajous

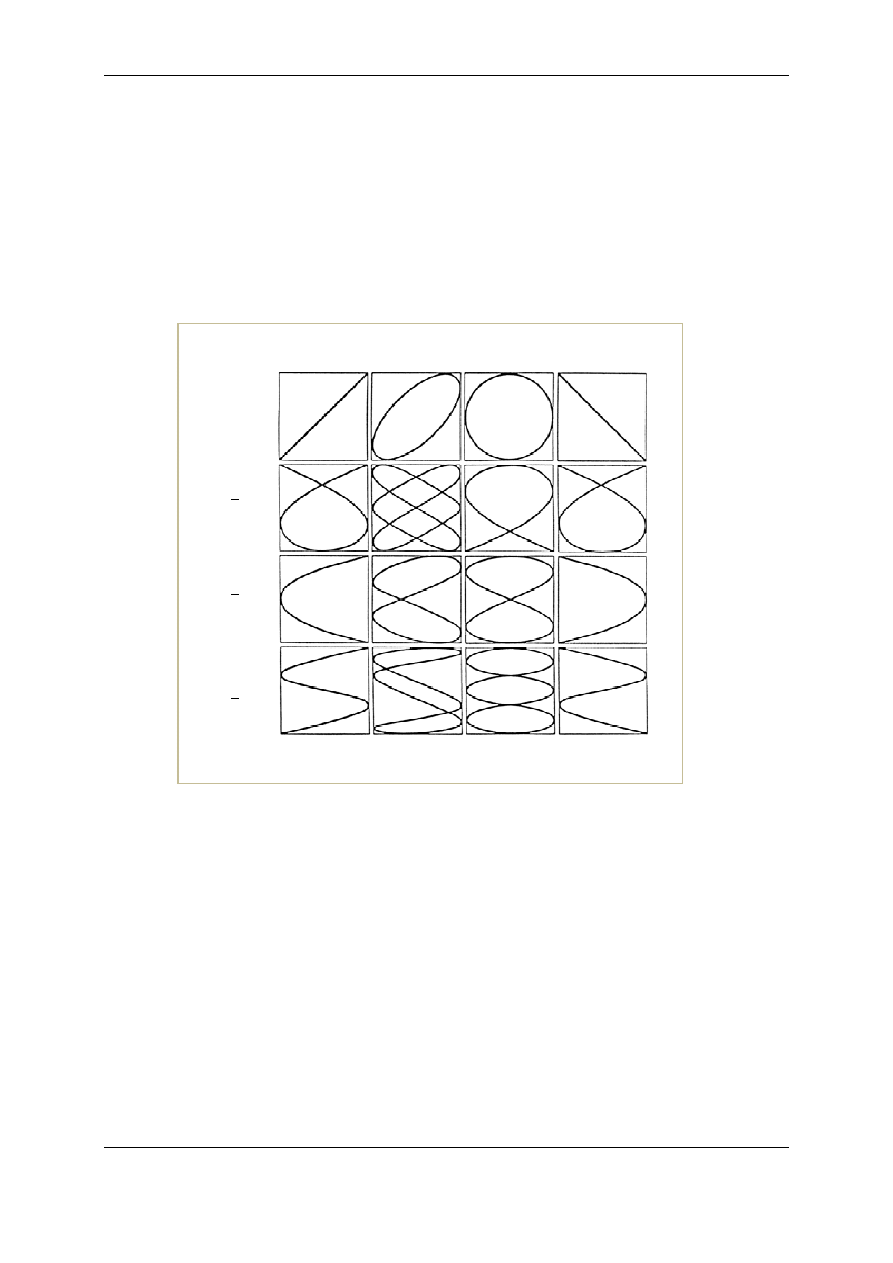
1.

Połącz obwód według schematu przedstawionego na rys.11. Na płytki odchylania piono-
wego oscyloskopu podaj napięcie

z generatora sygnału G

2

, zaś na płytki odchylania

poziomego – napięcie

z drugiego generatora G

1

. Generator G

1

posiada dodatkowo

kondensator

Rys.9. Schemat obwodu do badania prostowania jednopołówkowego z kondensatorem
wygładzającym prąd

V

Oscyloskop

Element z diodą
prostowniczą

Element z kondensatorem

GPCz

V

Oscyloskop

Sieć

Mostek Graetza

GPCz

Rys.10. Schemat obwodu z czterodiodowym prostownikiem dwupołówkowym,
tzw. mostkiem Graetza

Rys.11. Schemat obwodu elektrycznego służącego do obserwacji krzywych Lissajous

Oscyloskop

Generator sygnału
sinusoidalnego

G

2

Generator sygnału

sinusoidalnego

G

1

Ćwiczenie20

10

wmontowany częstościomierz pozwalający na pomiar częstotliwości sygnału

= /2 ).

2.

Zmieniaj stosunek częstotliwości sygnałów

i (np. : =1:1, 1:2, 1:3, itp.) i obser-

wuj pojawiające się na ekranie krzywe Lissajous. Za każdym razem przerysuj je na papier
milimetrowy i zanotuj odczytaną częstotliwość .

4.

Obliczenia

4.1

Wyznaczanie nieznanej częstotliwość sygnału z kształtów krzy-
wych Lissajous

1.

Z kształtu dowolnej, krzywej Lissajous o ustalonym kształcie można określić stosunki czę-
stości drgań harmonicznych, które wykonuje punkt drgający w kierunkach osi i . W
tym celu przecina się krzywą Lissajous prostą równoległą do osi i liczy liczbę N

x

punk-

tów przecięcia prostej z krzywą (punkty przecięcia, przez które krzywa Lissajous prze-
chodzi dwa razy, liczymy podwójnie). Podobnie postępuje się dla prostej równoległej do
osi . Stosunek częstości wyraża się przez odpowiednie liczby punktów przecięcia wzo-
rem:

=

=

-
-

.

Z powyższego wzoru wynika metoda znajdowania nieznanej częstotliwości sygnału, jeśli
znana jest druga częstotliwość, np. f

x

, oraz krzywa Lissajous.

Wyznacz nieznaną częstotliwość sygnału i wyniki wpisz do Tabeli 2.

Tabela 2. Ćwiczenie 20.

Wyznaczanie nieznanej częstotliwość sygnału z

kształtów krzywych Lissajous

Lp.

[Hz]

-

-

[Hz]

1.

2.

3.

5.

Dyskusja wyników

Ustosunkuj się do uzyskanych wyników obserwacji i obliczeń.

Czułość oscyloskopu

., niepewność standardowa czułości / . ,

[działka skali/V]

Zastosowanie oscyloskopu

11

1.

Do czego posłużyła wyznaczona czułość oscyloskopu?

2.

Przeanalizuj wykresy sygnałów z różnymi elementami prostującymi.

3.

Porównaj uzyskane w ćwiczeniu figury Lissajous z figurami w zamieszczonej w Uzupełnieniu
tabeli. Na tej podstawie oceń, jakie było przesunięcie w fazie między sygnałami podanymi na
wejścia oscyloskopu przy danym stosunku częstotliwości.

6.

Uzupełnienia

7.

Literatura

1.

Praca pod red. B.Oleś i M. Duraj: Ćwiczenia laboratoryjne z fizyki, cz.I. wyd.4, Wydawnictwo
PK, Kraków 2008.

2.

H. Szydłowski, Pracownia fizyczna, PWN, Warszawa 1989.

3.

Sz. Szczeniowski, Fizyka doświadczalna, cz. III, PWN, Warszawa 1966.

8.

Jeśli chcesz wiedzieć więcej

8.1

Dlaczego dioda półprzewodnikowa ma właściwości prostujące

Półprzewodniki (np. krzem, german, arsenek galu) cechuje znacznie większy opór elektryczny niż

metale, a w bardzo niskich temperaturach zachowują się nawet jak izolatory. W materiałach tych nie
występują swobodne elektrony i dlatego nie mogą przewodzić prądu elektrycznego, jeśli z zewnątrz

ϕ

= 0

ϕ

= π/4

ϕ

= π/2

ϕ

= π

ω

=

ω

ω

=

2

3

ω

ω

=

1

2

ω

ω

=

1

3

ω

Rys.12. Przykłady figur Lissajous

Ćwiczenie20

12

nie otrzymają pewnej porcji energii. Ze wzrostem temperatury związana jest energia termiczna, dzię-
ki której elektrony walencyjne mogą oderwać się od atomów i zacząć uczestniczyć w przepływie prą-
du (czyli inaczej niż w metalach, gdzie im wyższa temperatura, tym mniejszy prąd!). Na puste miejsce
po elektronie walencyjnym mogą wskoczyć inne elektrony i taki brak elektronu, zwany

dziurą

, za-

chowuje się jak nośnik prądu o ładunku dodatnim. W półprzewodnikach o przewodnictwie elektrycz-

nym decyduje zarówno ilość elektronów jak i dziur, które nazywamy

nośnikami ładunku

.

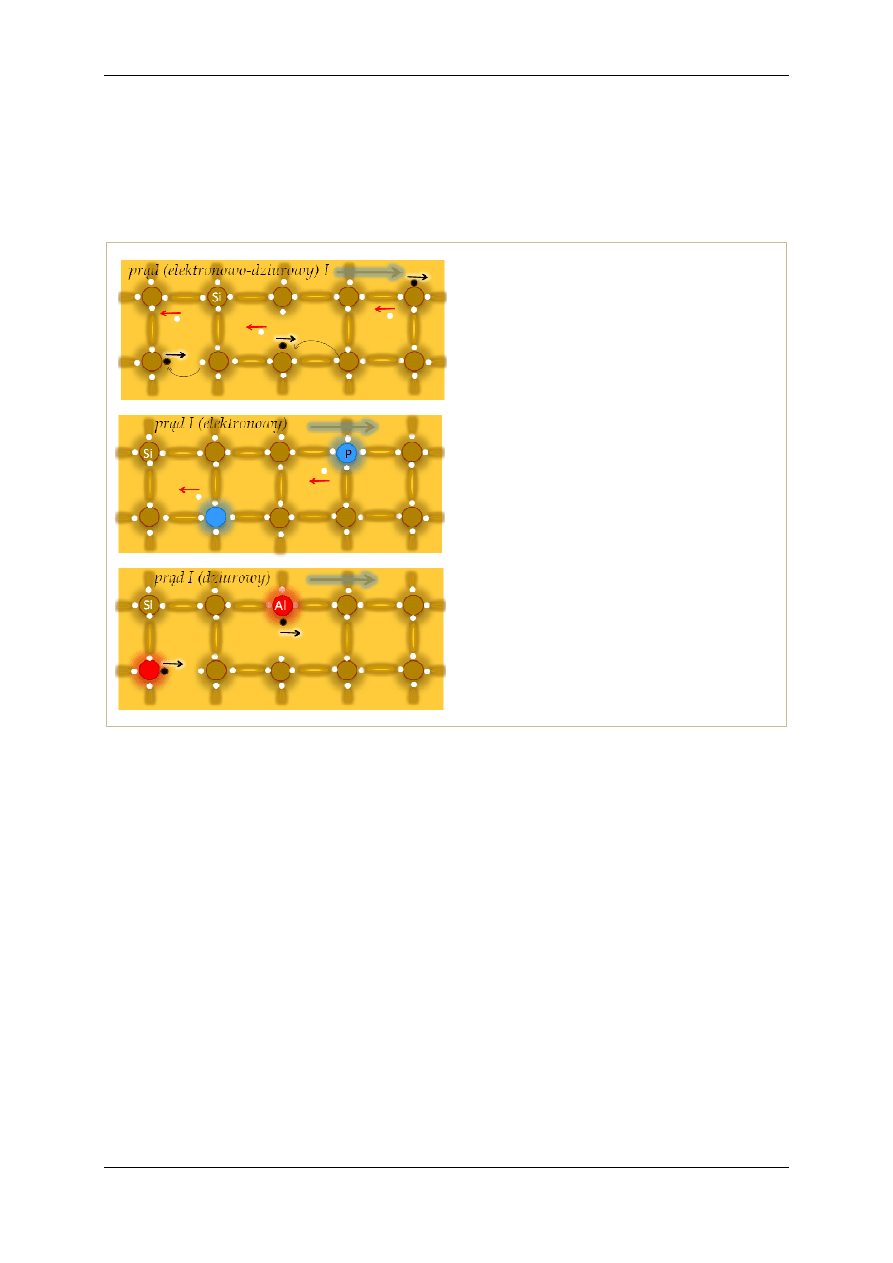
Na rys.13 a przedstawiono schemat sieci krystalicznej krzemu. Każdy atom Si posiada cztery elek-

trony walencyjne (białe kropki) i czterech sąsiadów. Powiązany jest z nimi za pomocą par wspólnych
elektronów walencyjnych, po jednym z każdego atomu. Jeśli elektron odrywa się od atomu, powstaje

dziura

(czarna kropka). Strzałki czerwone pokazują kierunek ruchu elektronów, czarne – dziur, duża

strzałka – kierunek prądu. W czystym półprzewodniku ilość dziur jest taka sama jak ilość elektronów.

Właściwości elektryczne półprzewodników, typ przewodnictwa i opór można zmieniać w szero-

kim zakresie dodając do nich domieszki niewielkich ilości atomów innego pierwiastka. Przykładowo,
przez odpowiednie domieszkowanie krzemu (np. fosforem P, jak na rys.13b) zwiększa się ilość elek-
tronów przewodnictwa i otrzymuje półprzewodnik typu n. Jeśli przez dodanie obcych atomów (np.
glinu Al do krzemu, rys.13c) uzyska się przewagę dziur, to przewodnictwo dziurowe będzie domino-
wało, a półprzewodnik będzie typu p. Domieszki w krzemie typu n posiadają pięć elektronów walen-
cyjnych, w tym jeden elektron nie biorący udziału w wiązaniu i słabo związany. Po dostarczeniu nie-
wielkiej energii staje się on elektronem swobodnym. Takie domieszki określa się mianem

donorów

. W

krzemie typu p atomy domieszek, zwanych

akceptorami

, mają o jeden elektron walencyjny mniej, niż

atomy krzemu. Do utworzenia wiązania brakuje elektronu i powstaje dziura, nośnik ładunku uczestni-
czący w przepływie prądu.

b. W krzemie (Si) typu n jako domieszki wprowa-
dza się atomy arsenu (As), które posiadają pięć
elektronów walencyjnych. Cztery z nich biorą
udział w wiązaniu kowalencyjnym z sąsiednimi
atomami Si, a piąty jest bardzo słabo związany i
łatwo staje się elektronem swobodnym.

c. Jeśli atom krzemu (Si) zastąpimy atomem galu
(Ga), który posiada trzy elektrony walencyjne, to
brakuje jednego elektronu do utworzenia wiąza-
nia i powstaje dziura. Może się ona przemieszczać
w krysztale jak dodatnia cząstka już po dostarcze-
niu niewielkiej energii termicznej.

Rys.13 a. Schemat sieci krystalicznej krzemu (Si).
Każdy atom Si powiązany jest z sąsiadami za po-
mocą par wspólnych elektronów walencyjnych
(białe kropki), po jednym z każdego atomu. Jeśli
elektron odrywa się od atomu, powstaje dziura
(czarna kropka). Strzałki czerwone pokazują kie-
runek ruchu elektronów, białe – dziur, duża ciem-
na strzałka – kierunek prądu.

Zastosowanie oscyloskopu

13

Podstawowym elementem wielu urządzeń półprzewodnikowych jest

złącze p-n

. Stanowi go cien-

ka warstwa (

∼

10

– 4

cm) na granicy między dwoma obszarami tego samego kryształu różniącymi się

typem domieszek. Dziury i elektrony dyfundują w przeciwnych kierunkach poprzez warstwę granicz-
ną i rekombinują, czyli elektron „zapełnia dziurę” i znika para swobodnych nośników ładunku. Proce-
sowi temu towarzyszy emisja porcji energii. W obszarze złącza pojawia się niedobór nośników, po
stronie półprzewodnika typu n powstaje nadmiar jonów dodatnich (donorów), a po stronie p – nad-
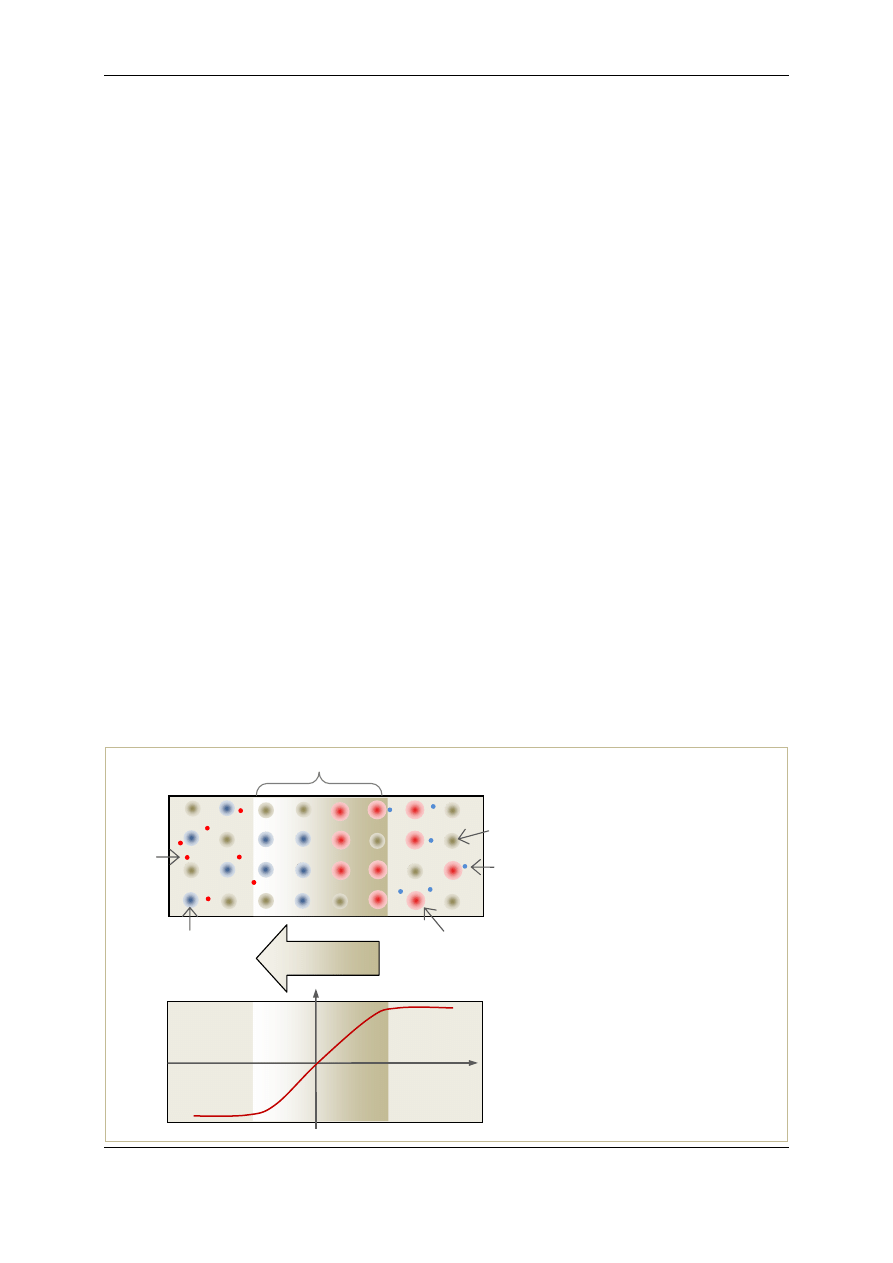
miar jonów ujemnych (akceptorów); sytuację taka przedstawia rys.14. Ta warstwa podwójna

ładun-

ków

wytwarza wewnętrzne pole elektryczne skierowane od obszaru typu n do obszaru typu p, które

powstrzymuje dalszą dyfuzję. Potencjał elektrostatyczny w obszarze złącza zmienia się skokowo two-
rząc

barierę potencjału

(rys.14).

Po przyłożeniu do próbki zewnętrznego napięcia tak, aby plus przyłożony był do obszaru p, minus

do obszaru n, czyli w

kierunku przewodzenia

, wysokość bariery potencjału zmaleje i wzrośnie prąd

nośników większościowych. Zewnętrzne napięcie, które obniża barierę potencjału dla elektronów,
obniża ją również dla dziur. Oznacza to, że z obszaru n do p płynie tak samo dużo elektronów, jak i
dziur w przeciwnym kierunku i natężenia prądów elektronowych i dziurowych dodają się. Prąd nośni-
ków mniejszościowych

&

(czyli generowanych termicznie elektronów z obszaru p i dziur z obszaru n)

pozostanie praktycznie bez zmian. Natężenie prądu szybko rośnie wraz ze wzrostem przyłożonego
napięcia.

Natomiast po przyłożeniu napięcia w

kierunku zaporowym

nastąpi podwyższenie bariery poten-

cjału i odpowiednie zmniejszenie prądu nośników większościowych. Przez złącze popłynie jedynie
słaby prąd nośników mniejszościowych

&

.

Z powyższego widać, że złącze p-n ma własności prostujące, tj. dla polaryzacji w kierunku prze-

wodzenia płynie duży prąd, podczas gdy w kierunku przeciwnym bardzo mały. Wykorzystujemy to
zjawisko w miniaturowych diodach do prostowania prądu przemiennego. Wykres zależności natęże-
nia w funkcji napięcia V, czyli charakterystyka prądowo-napięciowa złącza p-n występującego w
diodzie półprzewodnikowej, przedstawiony jest na rys.3a.

Dziury

+

+

+

+

+

+

+

+

+

+

−

−

−

−

−

−

−

−

−

Kierunek pola
elektrycznego

Półprzewodnik
typu p

Półprzewodnik

typu n

Obszar zubożony

Donory (jony

dodatnie)

Akceptory

(jony ujemne)

Elektrony

Krzem

1

Rys.14. Złącze p-n w krzemie i wy-
kres zmian potencjału 1

w obsza-

rze złącza

Półprzewodnik

typu p

Półprzewodnik
typu n

Obszar zubożony