Ι PRACOWNIA FIZYCZNA U.Ś.
Nr ćwiczenia : 21 temat : wyznacznie WSPÓŁCZYNNIKA LEPKOŚCI CIECZY METODĄ WYPŁYWU . Imię i nazwisko : Wojak Anna , Szałajko Jarosław Rok studiów : Ι kierunek : LFI data wykonania ćwiczenia : 23.03.2000 Ocena :
|
Zagadnienia teoretyczne .
CIECZ IDEALNA - CIECZ RZECZYWISTA .
Ciecz idealna pozostająca w spoczynku jest całkowicie nieściśliwa , a będąc w ruchu spełnia dodatkowo warunek braku lepkości . W przyrodzie nie występuje . Rzeczywiste ciecze występujące w przyrodzie odznaczają się niewielką ściśliwością . Prawo Hooke'a w odniesieniu do cieczy zapisujemy :
![]()
,
gdzie ![]()
nazywamy współczynnikiem ściśliwości cieczy (![]()
dla cieczy doskonałej) . Wskazuje on o jaką część objętości początkowej zmieniła się objętość danej cieczy podczas zmiany ciśnienia o jednostkę .
RÓWNANIE CIĄGŁOŚCI , RÓWNANIE BERNOULLIEGO .
Prędkość cząstek wewnątrz płynu może mieć różne wartości w różnych punktach , chociaż w dowolnym punkcie jest ona równoległa do strugi . Niech prędkość tych cząstek w punkcie P wynosi ![]()
, a prędkość cząstek w punkcie Q-![]()
. Niech ![]()
i ![]()
będą odpowiednio przekrojami strugi w P i Q , prostopadłymi do linii prądu w tych punktach . W czasie ![]()
element płynu przepływa w przybliżeniu odległość ![]()
. Masa płynu ![]()
przenikająca ![]()
w przedziale czasu ![]()
wynosi w przybliżeniu :
![]()
czyli strumień masy ![]()
równa się w przybliżeniu ![]()
. Na to , żeby w tym przedziale czasu ani ![]()
, ani A nie zmieniały się w sposób zauważalny na drodze , po której porusza się płyn , musimy wziąć ![]()
dostatecznie małe . W granicy , gdy ![]()
, otrzymujemy dokładne definicje :
strumienia masy w P : ![]()
oraz
strumienia masy w Q : ![]()
,
gdzie ![]()
i ![]()
są, odpowiednio , gęstościami płynu w punktach P i Q . W szczególności strumień masy w punkcie P musi być równy strumieniowi w punkcie Q :
![]()
,
albo inaczej
![]()
wynik ten wyraża prawo zachowania masy w dynamice płynów .Jeżeli płyn jest nieściśliwy , to równanie przyjmuje prostszą postać :
![]()
lub
![]()
iloczyn ![]()
określa wielkość zwaną często strumieniem objętościowym lub też natężeniem przepływu . Z równania powyższego wynika , że prędkość płynu dla nieściśliwego przepływu ustalonego zmienia się odwrotnie proporcjonalnie do pola powierzchni przekroju i jest większa w węższych częściach strugi . Prawo Bernoulliego . Dotyczy stacjonarnego przepływu nieściśliwej cieczy idealnej . Przepływ stacjonarny to taki , w którym nie ma zawirowań a prędkość cieczy w dowolnie ustalonym punkcie jest stała . W każdym punkcie linii prądu wektor prędkości cieczy jest do niej styczny . Przyjmując powyższe założenia prawo Bernoulliniego dla stacjonarnego przepływu nieściśliwej cieczy idealnej stwierdza , że wzdłuż linii prądu spełniony jest związek :
p+1/2ρv2 +ρgh = const.
gdzie p jest ciśnieniem w danym punkcie cieczy , v prędkością przepływu w tym punkcie , ρ gęstością h wysokością względem wybranego poziomu natomiast g oznacza przyspieszenie ziemskie .
TARCIE WEWNĘTRZNE CIECZY .
Tarcie wewnętrzne zwane lepkością jest siłą , która przeciwstawia się ruchowi . Ciecz przepływająca przez przewody przylega do ścian przewodu tworząc nieruchomą warstwę . W miarę przesuwania się od ścian przewodu do środka prędkości rośnie . W czasie przepływu cieczy mamy do czynienia z przesuwaniem się jednych warstw względem drugich czemu towarzyszy opór . Właściwości różnych cieczy z punktu widzenia ich lepkości charakteryzuje wielkość zwana współczynnikiem lepkości .
WSPÓŁCZYNNIK LEPKOŚCI CIECZY .
Ciecz przepływająca przez przewody przylega do ścian przewodu tworząc nieruchomą warstwę , cylinder z cieczy wewnątrz , którego odbywa się ruch reszty cieczy . W miarę przesuwania się od ścian przewodu do środka prędkość rośnie .
Jeżeli wyodrębnimy dwie warstwy cieczy o powierzchniach S , odległe od siebie o ![]()
poruszające się z prędkościami ![]()
i ![]()
ta siła działająca na górną warstwę i styczna do niej wyraża się wzorem :
![]()
,
gdzie ![]()
jest dynamicznym współczynnikiem lepkości , a ![]()
różnica prędkości obu warstw . Siła lepkości działająca na każde z warstw cieczy jest równa co do wartości sile F. , lecz przeciwnie skierowana . Kierunek jej jest przeciwny do kierunku prędkości względnej danej warstwy . ![]()
wyraża siłę lepkości powstająca przy ruchu względnym dwóch warstw z jednostkowej powierzchni jeśli różnica prędkości między warstwami wynosi ![]()
, a odległość ![]()
.
RUCH LAMINARNY , RUCH BURZLIWY , LICZBA REYNOLDSA .
Ruch laminarny występuje gdy wszystkie cząstki płynu poruszają się po torach równoległych do siebie .
Ruch burzliwy występuje , gdy cząstki wykonują ruchy nieuporządkowane , poruszają się w różnych kierunkach . Towarzyszy temu powstawanie nieregularnych linii prądu i wirów.
Liczba Reynoldsa jest związana z gęstością ![]()
, współczynnikiem lepkości ![]()
, prędkością V oraz średnicą przewodu d :
![]()
,
dla Re<2300 występuje laminarny przepływ cieczy , a dla Re>3000 przepływ burzliwy . Przy jej pomocy można wyznaczyć prędkość krytyczną przepływu płynu po której ruch staje się burzliwy.
PRZEPŁYW LAMINARNY PRZEZ RURĘ - WZÓR POISEUILLE'A .
W takich warunkach wszystkie cząsteczki poruszają się w kierunkach równoległych do
![]()
osi rurki z prędkościami malejącymi wraz z odległością do osi . w płynie można wyróżnić cylindryczne warstwy o stałej prędkości . W idealnym przepływie laminarnym nie zachodzi wymiana cząsteczek przez ścianki tak pomyślanych walców . W rzeczywistości istnieje pewna wymiana cząsteczek , spowodowana ich ruchem cieplnym . Ta wymiana cząsteczek jest czynnikiem działającym na rzecz wyrównania prędkości warstw cylindrycznych , przyspieszającym warstwy wolniejsze a spowalniającym szybsze , leżące bliżej osi .Wzór Poiseuille'a :
gdzie V -objętość cieczy ,która wypływa z kapilary , l -długość kapilary , τ -czas wypływu , g -przyspieszenie ziemskie , ρ -gęstość cieczy , r -promień wewnętrzny rurki kapilarnej , h -średnia wysokość słupa cieczy .
Wykonanie ćwiczenia i opracowanie wyników .
Wartość tablicowa gęstości wody / ρ / w temperaturze / t0 = 200C / :
ρ = 0,9982*103 [kg*m-3]
Mierzymy / h , l / przy pomocy suwmiarki oraz odpisujemy wartość promienia wewnętrznego kapilary z instrukcji przy ćwiczeniu :
h = 0,16 [m] Δh = 0,0001 [m]
l = 13,85 [m] Δl = 0,0001 [m]
r = 0,0025 [m] Δr = 0,0001 [m]
Podstawiamy pustą zlewkę pod wylot rurki kapilarnej ; otwieramy kran [K] i włączamy jednocześnie stoper . Po wypłynięciu objętości / V≅100 [ml] / wody zamykamy kran wyłączając jednocześnie stoper :
początkowa wysokość słupa wody h1 [m] |
końcowa wysokość słupa wody h2 [m] |
czas wypływu τ [s] |
ilość wody wypuszczonej V [m3] |
lepkość cieczy η 10-3 [kg/ms] |
0,3 |
0,294 |
24,39 |
0,000126 |
0,0332 |
0,299 |
0,293 |
27,22 |
0,000126 |
0,0368 |
0,299 |
0,294 |
25,78 |
0,000128 |
0,0344 |
0,299 |
0,294 |
26,43 |
0,000128 |
0,0353 |
0,299 |
0,293 |
25,44 |
0,000126 |
0,0344 |
0,299 |
0,294 |
26,03 |
0,000125 |
0,0356 |
0,3 |
0,294 |
26,57 |
0,000128 |
0,0356 |
0,3 |
0,294 |
26,91 |
0,000127 |
0,0363 |
0,3 |
0,294 |
26,06 |
0,000126 |
0,0354 |
0,299 |
0,293 |
26,45 |
0,000129 |
0,0349 |
Wartości średnie / h1śr , h2śr , τśr , Vśr , ηśr / oraz szacuję niepewności pomiarowe / Δh1śr , Δh2śr , Δτśr , ΔVśr , Δηśr / :
h1śr = 0,2994 [m] Δh1śr = 0,000163 [m]
h2śr = 0,2937 [m] Δh2śr = 0,000153 [m]
τśr = 26,128 [s] Δτśr = 0,254374 [s]
Vśr = 0,000126667 [m3] ΔVśr = 0,0000004 [m3]
ηśr = 0,0352*10-3 [kg/ms] Δηśr = 0,00033*10-3 [kg/ms]
![]()
Δx = 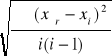
Podstawiamy pod wylot rurki kapilarnej znowu pustą zlewkę ; otwieramy kran [K] i włączamy jednocześnie stoper . Po wypłynięciu objętości / V≅200 [ml] / wody zamykamy kran wyłączając jednocześnie stoper :
początkowa wysokość słupa wody h1 [m] |
końcowa wysokość słupa wody h2 [m] |
czas wypływu τ [s] |
ilość wody wypuszczonej V [m3] |
lepkość cieczy η 10-3 [kg/ms] |
0,30 |
0,289 |
47,06 |
0,000225 |
0,0353 |
0,30 |
0,289 |
45,45 |
0,000225 |
0,0341 |
0,299 |
0,289 |
47,07 |
0,000224 |
0,0353 |
0,299 |
0,29 |
48,78 |
0,000224 |
0,0367 |
0,30 |
0,29 |
49,67 |
0,000223 |
0,0377 |
0,30 |
0,289 |
47,71 |
0,000224 |
0,0359 |
0,299 |
0,289 |
45,37 |
0,000225 |
0,0339 |
0,299 |
0,288 |
45,34 |
0,000227 |
0,0335 |
0,299 |
0,288 |
47,32 |
0,000226 |
0,0351 |
0,299 |
0,288 |
45,88 |
0,000225 |
0,0342 |
Wartości średnie / h1śr , h2śr , τśr , Vśr , ηśr / oraz szacuję niepewności pomiarowe / Δh1śr , Δh2śr , Δτśr , ΔVśr , Δηśr / :
h1śr = 0,2994 [m] Δh1śr = 0,000163 [m]
h2śr = 0,2889 [m] Δh2śr = 0,000233 [m]
τśr = 46,965 [s] Δτśr = 0,471044 [s]
Vśr = 0,0002248 [m3] ΔVśr = 0,0000004 [m3]
ηśr = 0,0352*10-3 [kg/ms] Δηśr = 0,00042*10-3 [kg/ms]
![]()
Δx = 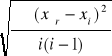
Obliczymy maksymalny błąd bezwzględny / Δηmax / korzystając z metody różniczki zupełnej:
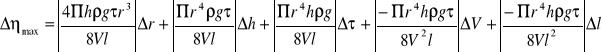
![]()
Δηśr = 0,00042*10-3 [kg/ms]
Δηmax = 0,00607*10-3 [kg/ms]
Podstawiamy pod wylot rurki kapilarnej jeszcze raz pustą zlewkę ; otwieramy kran [K] i włączamy jednocześnie stoper . Po wypłynięciu objętości / V≅300 [ml] / wody zamykamy kran wyłączając jednocześnie stoper :
początkowa wysokość słupa wody h1 [m] |
końcowa wysokość słupa wody h2 [m] |
czas wypływu τ [s] |
ilość wody wypuszczonej V [m3] |
lepkość cieczy η 10-3 [kg/ms] |
0,299 |
0,283 |
105,49 |
0,000327 |
0,0532 |
0,299 |
0,283 |
105,58 |
0,000328 |
0,0531 |
0,299 |
0,282 |
104,44 |
0,000326 |
0,0526 |
0,299 |
0,283 |
105,12 |
0,000325 |
0,0533 |
0,299 |
0,284 |
104,38 |
0,000327 |
0,0528 |
0,299 |
0,282 |
105,15 |
0,000328 |
0,0527 |
0,299 |
0,284 |
106,28 |
0,000328 |
0,0536 |
0,298 |
0,283 |
106,12 |
0,000327 |
0,0533 |
0,298 |
0,284 |
105,23 |
0,000326 |
0,0532 |
0,298 |
0,282 |
104,51 |
0,000325 |
0,0527 |
Wartości średnie / h1śr , h2śr , τśr , Vśr , ηśr / oraz szacuję niepewności pomiarowe / Δh1śr , Δh2śr , Δτśr , ΔVśr , Δηśr / :
h1śr = 0,2987 [m] Δh1śr = 0,000153 [m]
h2śr = 0,283 [m] Δh2śr = 0,000258 [m]
τśr = 105,23 [s] Δτśr = 0,209979 [s]
Vśr = 0,0003269 [m3] ΔVśr = 0,0000004 [m3]
ηśr = 0,0530*10-3 [kg/ms] Δηśr = 0,00011*10-3 [kg/ms]
![]()
Δx = 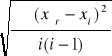
Wnioski .
Maksymalny błąd liczony metodą różniczki zupełnej dla drugiego pomiaru lepkości cieczy wynosi : Δηmax = 0,00607*10-3 [kg/ms] , a błąd statystyczny współczynnika lepkości wynosi : Δηśr = 0,00042*10-3 [kg/ms] . Różnica w błędach to dwa rzędy . Liczenie błędów metodą statystyczną daje w wyniku mniejsze błędy , ponieważ pod uwagę bierze się średnią błędów pojedynczych pomiarów co w sumie musi dać błąd mniejszy od błędu maksymalnego .
Wyniki otrzymane za pomocą powyższych obliczeń świadczą o poprawnym wykonaniu ćwiczenia . Nie mogliśmy ich jednak porównać z danymi tablicowymi ponieważ nie znaleźliśmy podobnych . Błędy wynikają prawdopodobnie z : zanieczyszczenia badanej cieczy , a przede wszystkim związane są z niedoskonałość związana z narządem wzroku (budzące wątpliwości odczytywanie wysokości słupa cieczy) , jak i opóźnienie związane z przekazaniem bodźca wzrokowego z oka do mózgu , a dopiero stamtąd do ręki , która zatrzymuje stoper . Jest to ważne , gdyż pomiary w tym ćwiczeniu polegały w głównej mierze na pomiarze czasu . W doświadczeniu przyjęliśmy temperaturę otoczenia 20°C w rzeczywistości była ona wyższa gdyż stanowisko do ćwiczeń znajdowało się w nasłonecznionym miejscu jak i również badana ciecz była niewiadomego pochodzenia .
7
![]()
![]()
![]()
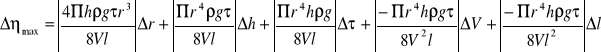
![]()
![]()
Wyszukiwarka
Podobne podstrony:
Fizyka Laborki (cwiczenieS) opracowanie?
Sprawozdanie 4 grupa, studia wsiz, semestr 1 2, fizyka, FIZYKA, Fizyka Laborki cwiczenia Różycki
Fizyka - Laborki (cwiczenie 0) opracowanie dc, AGH, GiG, AGH, fizyka, laborki
Fizyka Laborki (cwiczenie 53) nasze
Ćwiczenie nr 8 [1, inżynieria chemiczna i procesowa, semestr II, fizyka, laborki, 8. ćwiczenie
Fizyka Laborki (cwiczenie 96) nasze
Fizyka Laborki (cwiczenie 96) Jacek G
Fizyka Laborki (cwiczenie 96) Jacek G
Fizyka Laborki (cwiczenie 53) nasze
Fizyka Laborki (cwiczenie 96) Toster
Fizyka Laborki (cwiczenie 96) nasze
103, Studia Politechnika Poznańska, Semestr II, I pracownia fizyczna, LABORKI WSZYSTKIE, FIZYKA 2, F
204pl, Politechnika Poznańska ZiIP, II semestr, Fizyka, laborki fiza, wszystkie laboratoria z 1 prac
Lab fiz 302, Politechnika Poznańska ZiIP, II semestr, Fizyka, laborki fiza, wszystkie laboratoria z
teoria do 109, Politechnika Poznańska ZiIP, II semestr, Fizyka, laborki fiza, wszystkie laboratoria
Ćw109mmm, Politechnika Poznańska ZiIP, II semestr, Fizyka, laborki fiza, wszystkie laboratoria z 1 p
więcej podobnych podstron