13.02.2013

Egzamin nr 2 z Wytrzymałości Materiałów, WILiŚ II, sem.

3

Czas: 150 min.

Nazwisko

Imię

Podpis

Nr albumu

Grupa

Sala

Uwaga. Wypełnić górę w obu formularzach. Wyłożyć dokument do kontroli. Można mieć przy sobie tylko kalkulator i przybory

do pisania/rysowania. Rozwiązania (także brudnopis) zmieścić tylko na otrzymanym formularzu egzaminacyjnym.

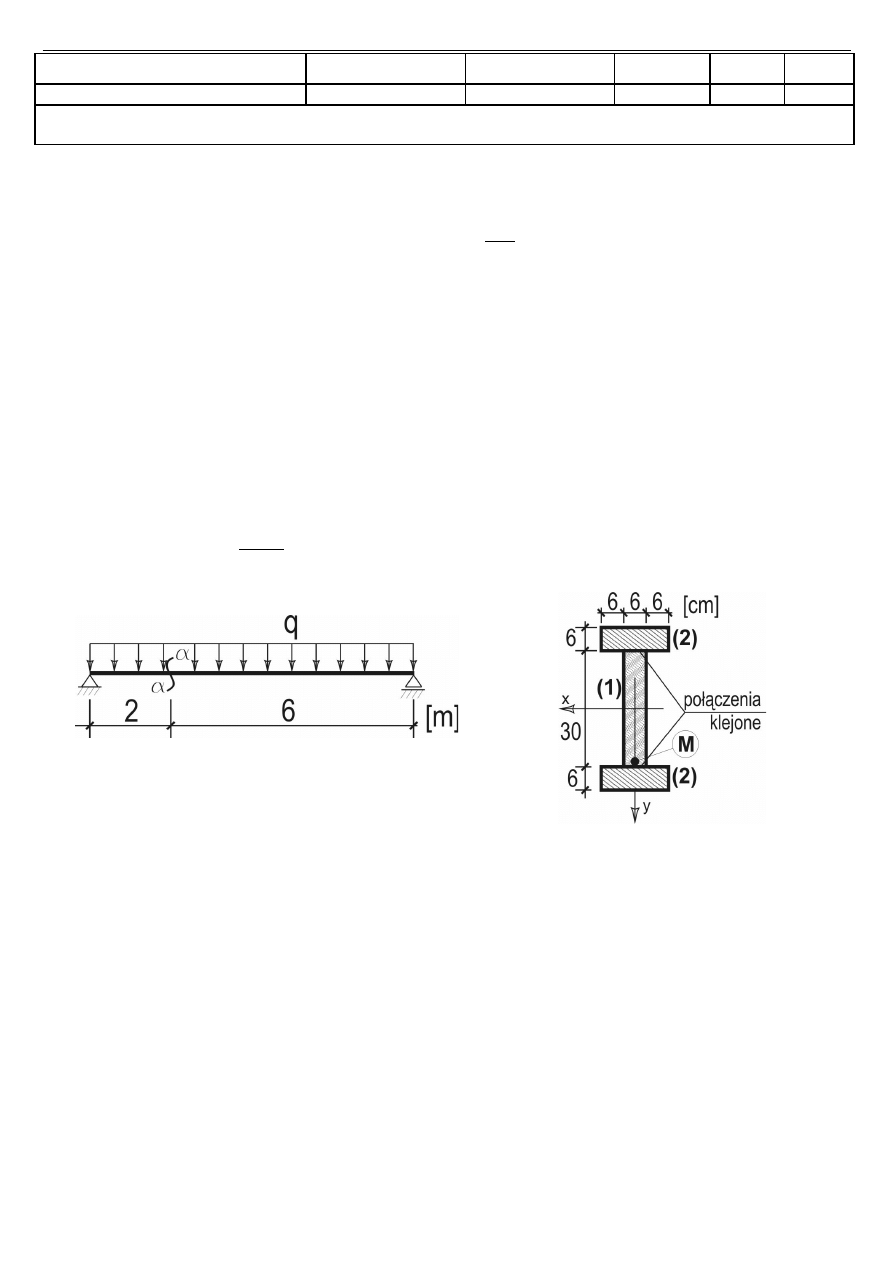
Zadanie 1 (30 punktów)

Dana jest belka o przekroju dwuteowym, swobodnie podparta, pod równomiernym obciążeniem q (rys.).

Ww wszystkich podpunktach, z wyjątkiem 4), przyjąć q =10

kN

m

.

Wariant I – przekrój jednorodny,

E = 60 GPa.

1) Sporządzić wykresy ekstremalnych naprężeń normalnych i stycznych w belce ,
2) Obliczyć naprężenia zredukowane wg hipotezy H-M-H w punkcie M przekroju

α − α

belki,

3) Sprawdzić, czy jest zachowana nośność połączenia klejonego półek ze środnikiem, na całej szerokości

środnika, gdy dopuszczalne naprężenia styczne połączenia klejonego

R

τ

= 2 MPa.

4) Znając granice plastyczności materiału,

R

pl

= 80 MPa, obliczyć dopuszczalną wartość obciążenia

q

dop

w zakresie sprężystym oraz wartość graniczną

q

gr

w stanie całkowitego uplastycznienia przekroju.

W obu przypadkach narysować wykresy naprężeń normalnych w przekroju najbardziej wytężonym.
Ile wynosi plastyczna rezerwa nośności przekroju poprzecznego?

Wariant II – przekrój zespolony, środnik:

E

1

= 60 GPa, półki: E

2

= 90 GPa.

5) Sporządzić wykres ekstremalnych naprężeń normalnych w belce,

6) obliczyć iloraz n =

v (I )

v (II )

maksymalnych ugięć osi belki w obu wariantach.

____________________________________________________________________________________________________________________________________
J.Ch. & W.W. / M.S. & M.G. 2013

Zadania

WM_Egz2ZADANIA_13.doc

13.02.2013

Egzamin nr 2 z Wytrzymałości Materiałów, WILiŚ II, sem.

3

Czas: 150 min.

Nazwisko

Imię

Podpis

Nr albumu

Grupa

Sala

Uwaga. Wypełnić górę w obu formularzach. Wyłożyć dokument do kontroli. Można mieć przy sobie tylko kalkulator i przybory

do pisania/rysowania. Rozwiązania (także brudnopis) zmieścić tylko na otrzymanym formularzu egzaminacyjnym.

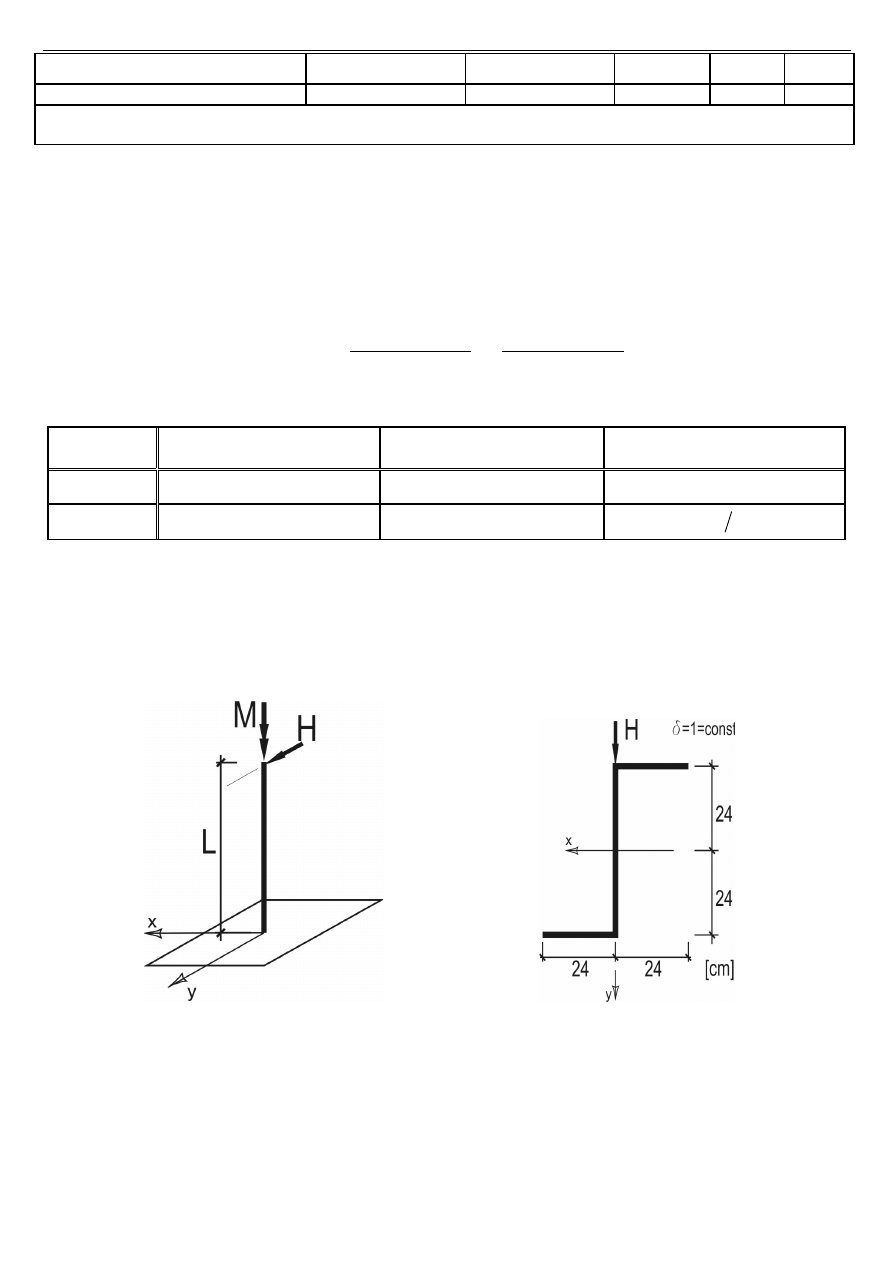
Zadanie 2 (30 punktów)

Słup wspornikowy o wysokości

L = 4 m i przekroju cienkościennym zetowym jak na rys. obciążony jest siłą H

i momentem

M

s

. Dane materiału: E = 200 GPa,

ν

= 0.25

, R

pr

= 200 MPa.

W punktach 1 i 3 przyjąć

M

s

= 0.6 kNm,

H = 5 kN,

1) Podać funkcje i wykresy: osi obojętnej i naprężeń normalnych w przekroju u podstawy słupa.

Przyjąć zwroty osi

x, y wg rysunku.

σ (

x , y )=−

M

y

I

x

+

M

x

I

xy

I

x

I

y

−(

I

xy

)

2

x +

M

x

I

y

+

M

y

I

xy

I

x

I

y

−(

I

xy

)

2

y

2) Wyznaczyć rdzeń przekroju (współrzędne wierzchołków, rysunek)

bok

wierzchołek

i

i

y a x b

=

+

,

a

i

≠ 0,

b

i

≠ 0

y = b

i

≠ 0 – prosta pozioma

x = c

i

≠ 0 – prosta pionowa

i

u

(

) /

i

y

xy

i

a J

J

b A

−

/

xy

i

J

b A

−

/

y

i

J c A

−

i

v

(

) /

i

xy

x

i

a J

J

b A

−

/

x

i

J b A

−

xy

i

J

c A

−

3) Przyjmując założenia skręcania swobodnego obliczyć maksymalne naprężenia styczne związane ze

skręcaniem oraz maksymalny kąt skręcenia pręta.

4) Rozpatrując stan idealnego ściskania osiowego obliczyć siłę krytyczną wyboczenia giętnego pręta,

na rysunku przekroju poprzecznego zaznaczyć ślad płaszczyzny wyboczenia. Sprawdzić warunek
wyboczenia sprężystego.

____________________________________________________________________________________________________________________________________
J.Ch. & W.W. / M.S. & M.G. 2013

Zadania

WM_Egz2ZADANIA_13.doc