Część 2

1. WZORY TRANSFORMACYJNE METODY PRZEMIESZCZEŃ

1

1.



1. WZORY TRANSFORMACYJNE METODY PRZEMIESZCZEŃ

1.1. Wstęp

Podstawowym narzędziem służącym do rozwiązywania zadań metodą przemieszczeń są wzory

transformacyjne. Pozwalają one określić wartości sił przywęzłowych na podstawie parametrów
geometrycznych pręta (sztywność

EJ, długość l) oraz przemieszczeń węzłów pręta (liniowych i obrotowych).

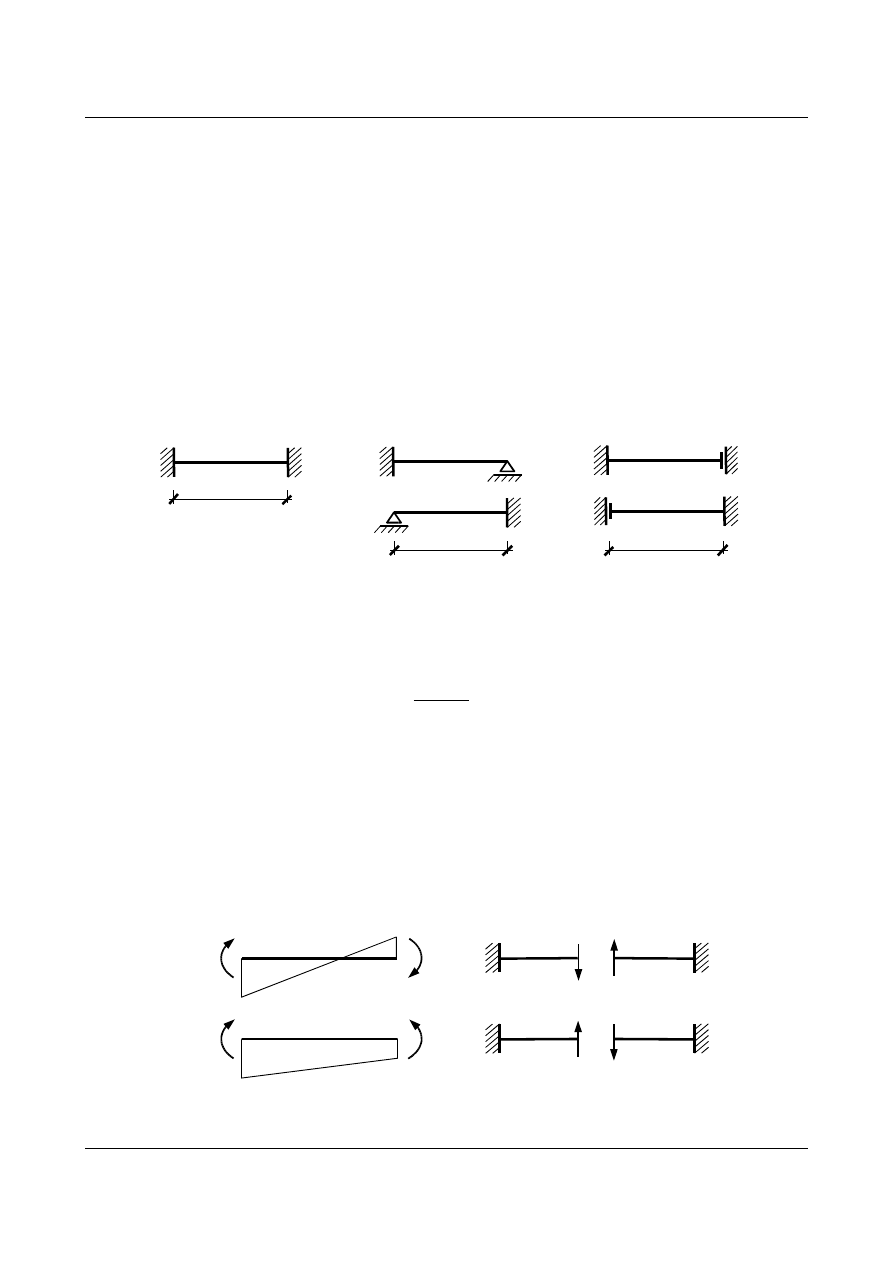
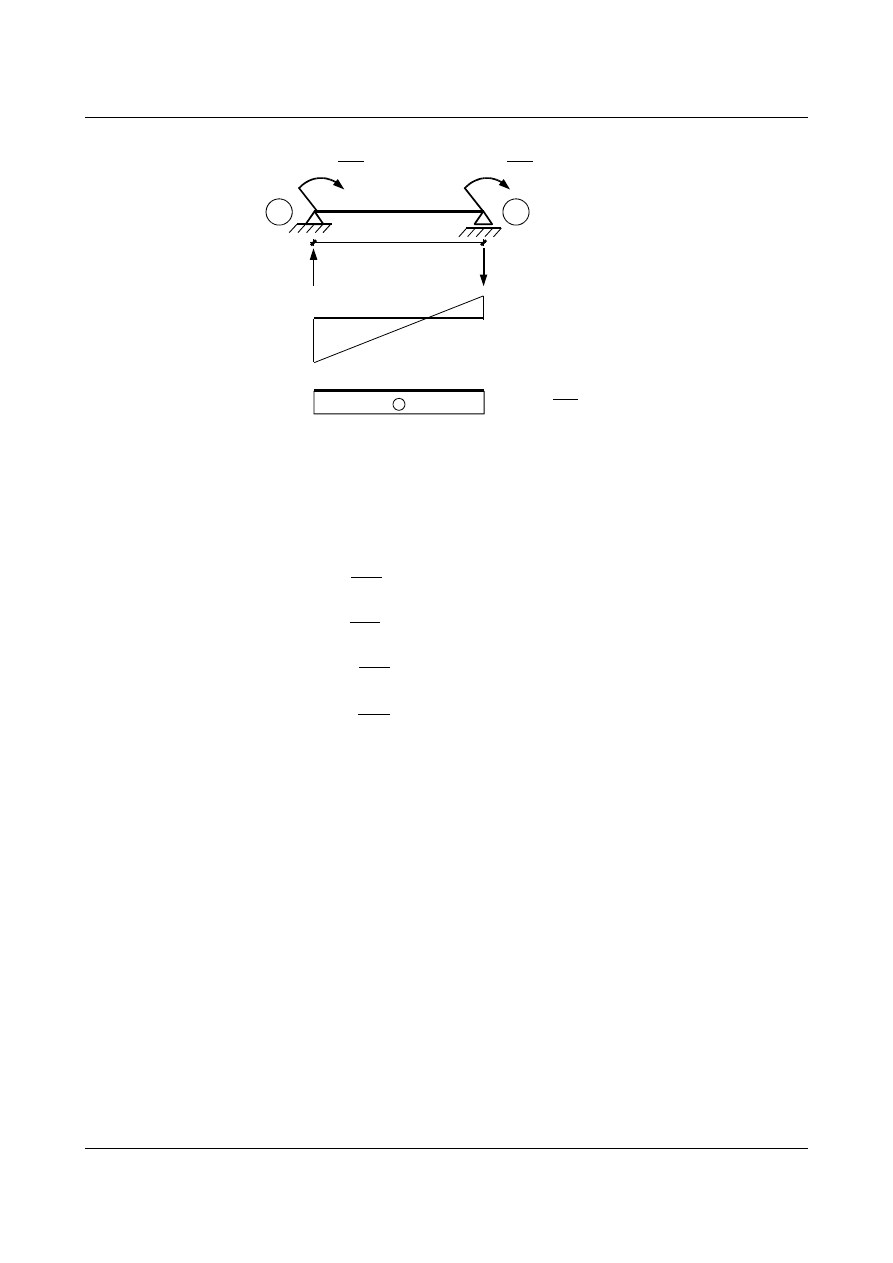
Jeden ze sposobów wyznaczenia wzorów transformacyjnych polega na określeniu reakcji w podporach

belki jednoprzęsłowej. Będą one zależały od typu podpór. Zadanie sprowadza się do rozwiązania belek
statycznie niewyznaczalnych (rys. 1.1) metodą sił. Zakładamy wpływy zewnętrzne w postaci klasycznych
osiadań podpór (przemieszczenia liniowe prostopadłe do osi belki, przemieszczenia kątowe).

a)

c)

b)

l

EJ

EJ

EJ

EJ

EJ

l

l

Rys. 1.1. Schematy belek statycznie niewyznaczalnych

Przed przystąpieniem do obliczeń należy przyjąć umowę dotyczącą znaków poszczególnych wielkości.

Najwygodniejsza dla metody przemieszczeń będzie taka, która uprości obliczenia i wyeliminuje w jak
największym stopniu różnice znaków poszczególnych wyrazów w równaniach.

W związku z tym będziemy traktować jako dodatnie:

•

momenty działające przy węzłach prętów zgodnie z ruchem wskazówek zegara (układ prawoskrętny)
(rys. 1.2),

•

siły poprzeczne obracające odciętą część pręta zgodnie z ruchem wskazówek zegara (rys. 1.2),

•

kąty obrotu przekrojów węzłowych

φ zgodne z ruchem wskazówek zegara (rys. 1.3),

•

przemieszczenia

Δ zgodne z kierunkiem i zwrotem przyjętego układu współrzędnych (rys. 1.3).

Wielkości ujemne będą miały zwroty przeciwne w stosunku do wymienionych. Ponadto tak jak

dotychczas wykresy momentów zginających będziemy odkładać po stronie włókien rozciąganych, czyli od
wypukłej strony osi odkształconej.

T>0

T<0

M>0

M>0

M>0

M<0

Rys. 1.2. Znakowanie momentów zginających i sił poprzecznych

Dobra D., Dziakiewicz Ł., Jambrożek S., Komosa M., Mikołajczak E., Przybylska P., Sysak A., Wdowska A.

AlmaMater

Część 2

1. WZORY TRANSFORMACYJNE METODY PRZEMIESZCZEŃ

2

i

k

k

i

Δ

i

>0

Δ

k

>0

φ

i

>0

φ

k

>0

z

x

Rys. 1.3. Znakowanie kątów obrotu φ i przemieszczeń pionowych Δ węzłów podporowych

Procedurę wyprowadzania wzorów transformacyjnych omówimy analizując różne przypadki podparcia

pręta.

1.2. Belka utwierdzona

Rozpatrzmy belkę obustronnie utwierdzoną o długości

l i sztywności EJ (rys. 1.4), której podpory

doznają przemieszczeń

φ

i

,

φ

k

,

Δ

i

,

Δ

k

.

i

k

Δ

i

Δ

k

φ

i

φ

k

z

x

EJ

l

Rys. 1.4. Schemat belki obustronnie utwierdzonej poddanej przemieszczeniom podpór

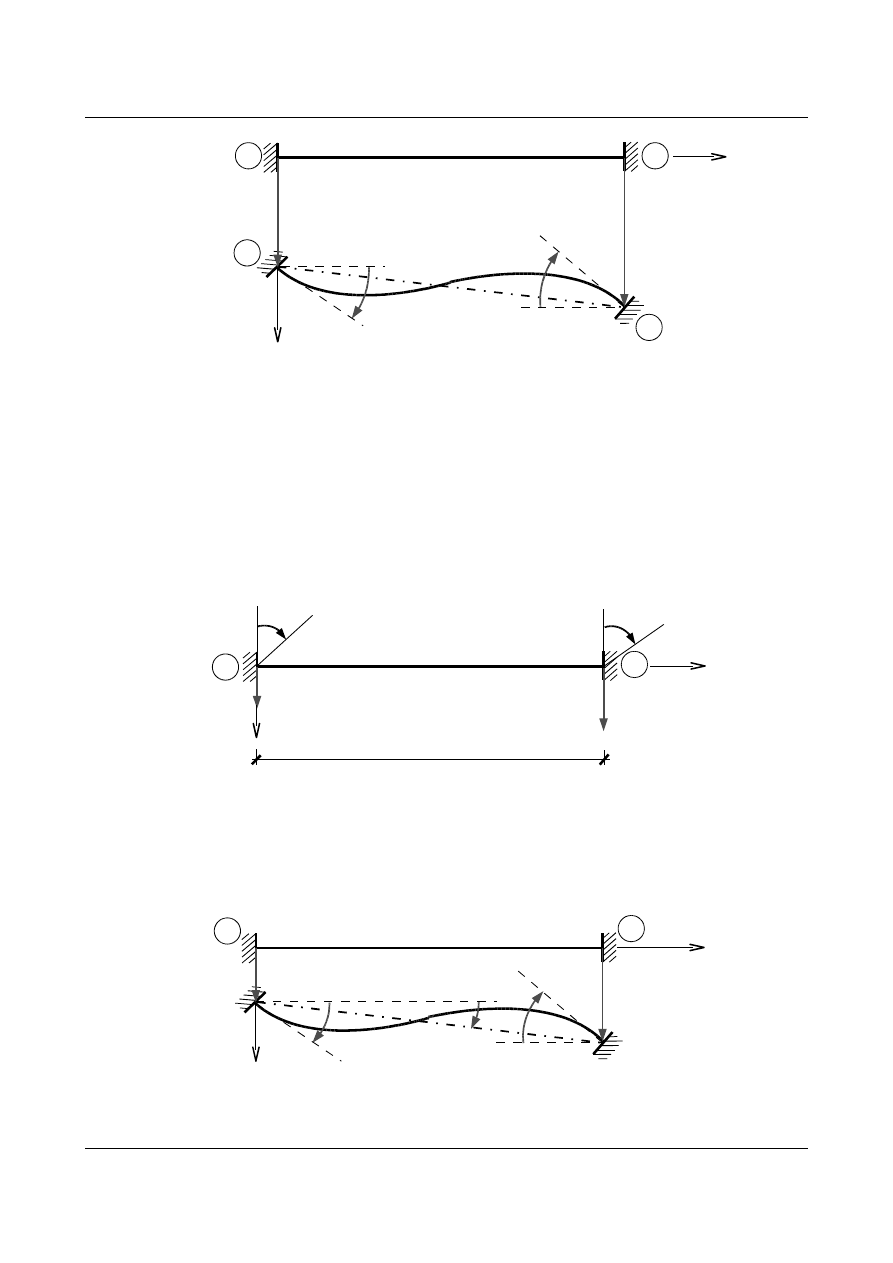
Narysujmy stan po przemieszczeniu podpór

i, k o zadane wartości (rys. 1.5). W rozważaniach

przemieszczenia podpór będą dowolne, lecz z uwagi na czynione uproszczenia przyjmujemy, że ich wartości
są niewielkie (małe w stosunku do wymiarów pręta).

i

k

Δ

i

Δ

k

φ

i

φ

k

z,w

x

Ψ

ik

Rys. 1.5. Stan po przemieszczeniu belki

Dobra D., Dziakiewicz Ł., Jambrożek S., Komosa M., Mikołajczak E., Przybylska P., Sysak A., Wdowska A.

AlmaMater

Część 2

1. WZORY TRANSFORMACYJNE METODY PRZEMIESZCZEŃ

3

Na rys. 1.5 symbol

ψ

ik

oznacza obrót cięciwy wynikający z pionowych przemieszczeń podpór

Δ:

tg



ik

=



k

−

i

l

=



k

l

−



i

l

(1.1)

ponieważ dla małych kątów

tg ψ

ik

≈

ψ

ik

, to możemy zapisać:



ik

=



k

l

−



i

l

=



k

−

i

l

(1.2)

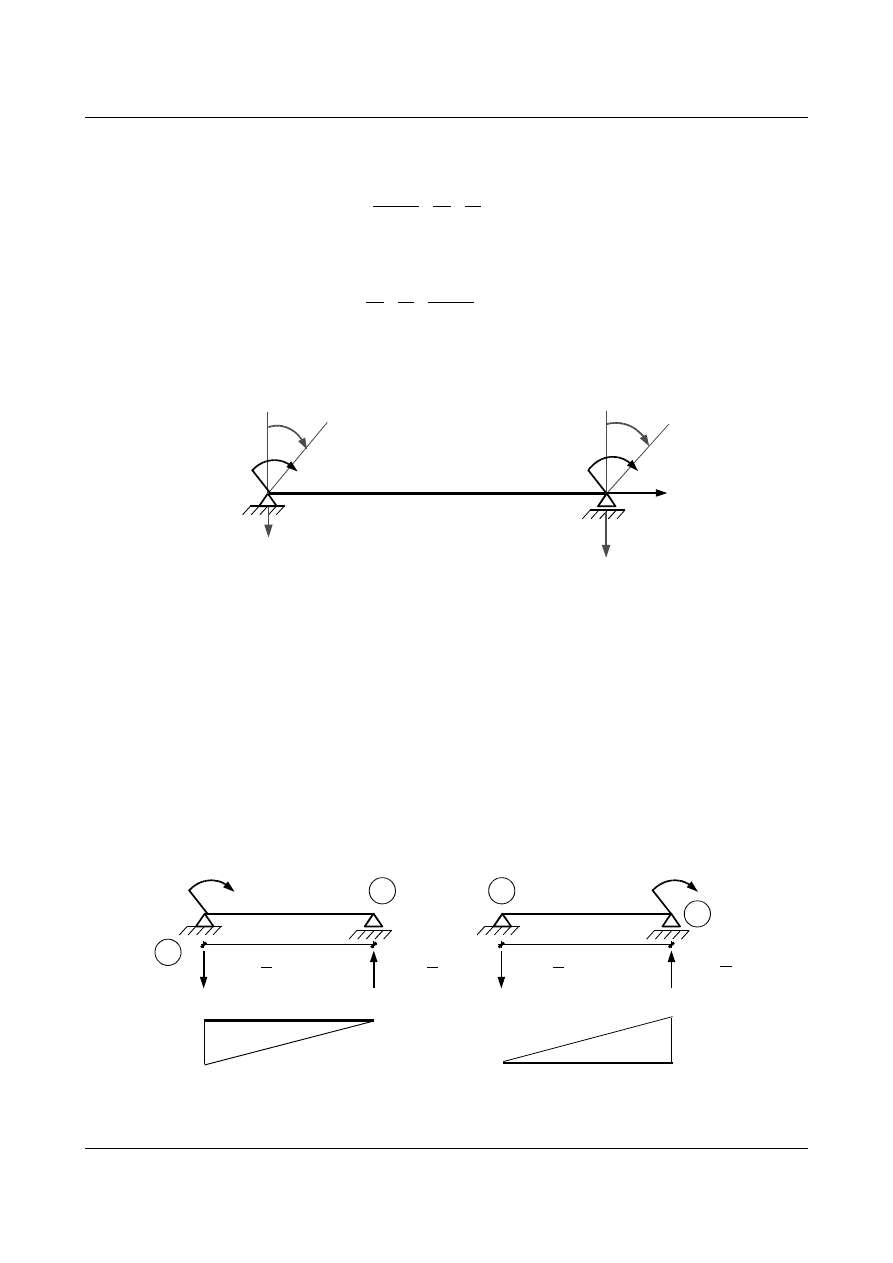
Aby rozwiązać zadanie metodą sił trzeba przyjąć układ podstawowy oraz odpowiadające mu warunki
przemieszczeniowe.

X

1

X

2

Δ

i

Δ

k

φ

i

φ

k

X

3

Rys. 1.6. Układ podstawowy



1

=0



2

=0



3

=0

Ponieważ pomijamy w obliczeniach wpływ sił normalnych współczynniki

δ

3i

(siła

X

3

wywołuje tylko siłę

normalną) będą równe zero, a układ równań kanonicznych ograniczy się do dwóch równań:



11

⋅X

1



12

⋅X

2



1



=0



21

⋅X

1



22

⋅X

2



2



=0

(1.3)

W celu obliczenia przemieszczeń z układu (1.3) narysujemy wykresy momentów w stanach

X

1

= 1 i X

2

= 1.

X

1

=1

H = 0

l

R

k

(1)

=

R

i

(1)

=

1

M

1

[-]

X

2

=1

H = 0

l

R

k

(2)

=

R

i

(2)

=

1

M

2

[-]

i

k

i

k

1

l

1

l

1

l

1

l

Rys. 1.7. Reakcje i momenty zginające w stanach X

1

= 1 i X

2

= 1

Dobra D., Dziakiewicz Ł., Jambrożek S., Komosa M., Mikołajczak E., Przybylska P., Sysak A., Wdowska A.

AlmaMater

Część 2

1. WZORY TRANSFORMACYJNE METODY PRZEMIESZCZEŃ

4

Obliczamy współczynniki macierzy podatności metodą Wiereszczagina-Mohra:



11

=

1

EJ

⋅



1
2

⋅1 ⋅l⋅

2
3

⋅1



=

l

3 EJ



22

=

1

EJ

⋅



1
2

⋅1 ⋅l⋅

2
3

⋅1



=

l

3 EJ



12

=

21

=

1

EJ

⋅



1
2

⋅1 ⋅l⋅

1
3

⋅1



=−

l

6 EJ

A wyrazy wolne

Δ

iΔ

według wzoru:



i



=−

i

−

∑

j

R

j

i 

⋅

j

(1.4)

gdzie:



i

- rzeczywiste, narzucone przemieszczenie zgodne z kierunkiem niewiadomej

X

i

,

R

j

i 

- reakcja w podporze j, w stanie

X

i

= 1,



j

- przemieszczenie narzucone po kierunki reakcji

R

j

i 

.



1



=−

i

−

1

l

⋅

i



1

l

⋅

k

=−

i



ik



2



=−

k

−

1

l

⋅

i



1

l

⋅

k

=−

k



ik

Po podstawieniu otrzymanych wartości równanie kanoniczne (1.3) uzyskuje postać

l

3 EJ

⋅X

1

−

l

6 EJ

⋅X

2



ik

−

i

=0

−

l

6 EJ

⋅X

1



l

3 EJ

⋅X

2



ik

−

k

=0

(1.5)

Rozwiązanie układu (1.5) prowadzi do wartości sił nadliczbowych:

X

1

=

2 EJ

l

⋅2

i



k

−3

ik



(1.6)

X

2

=

2 EJ

l

⋅

i

2 

k

−3

ik



(1.7)

W przyjętym układzie podstawowym siły nadliczbowe

X

i

oznaczają reakcje podporowe, a zarazem

równoważne im wewnętrzne siły przypodporowe (rys. 1.8). Można zapisać:

X

1

=M

ik

X

2

=M

ki

Dobra D., Dziakiewicz Ł., Jambrożek S., Komosa M., Mikołajczak E., Przybylska P., Sysak A., Wdowska A.

AlmaMater

Część 2

1. WZORY TRANSFORMACYJNE METODY PRZEMIESZCZEŃ

5

gdzie:

M

ik

to przęsłowy, przywęzłowy moment zginający w przekroju

i,

M

ki

to przęsłowy, przywęzłowy moment zginający w przekroju

k.

i

k

M

ik

M

ki

M

k

M

i

Rys. 1.8. Momenty podporowe i przywęzłowe momenty zginające

Obliczmy jeszcze reakcje

R

i

i R

k

.

∑

M

i

=0

⇔

2 EJ

l

⋅2

i



k

−3

ik



2 EJ

l

⋅

i

2 

k

−3

ik

R

k

⋅l=0

(1.8)

R

k

=−

6 EJ

l

2

⋅

i



k

−2

ik



(1.9)

R

i

=−

6 EJ

l

2

⋅

i



k

−2

ik



(1.10)

Ponieważ reakcje węzłowe są równoważne wewnętrznym siłom przywęzłowym (rys. 1.9)

R

k

=T

ki

R

i

=T

ik

to siła tnąca wynosi:

T

ik

=T

ki

=−

6 EJ

l

2

⋅

i



k

−2

ik



(1.11)

gdzie:

T

ik

, T

ki

oznaczają przęsłowe, przywęzłowe siły poprzeczne.

i

k

T

ik

T

ki

R

k

R

i

Rys. 1.9. Reakcje podporowe i przywęzłowe siły poprzeczne

Gdy znamy już wartości wszystkich sił, to możemy narysować wykresy rzeczywistych sił wewnętrznych.

Dobra D., Dziakiewicz Ł., Jambrożek S., Komosa M., Mikołajczak E., Przybylska P., Sysak A., Wdowska A.

AlmaMater

Część 2

1. WZORY TRANSFORMACYJNE METODY PRZEMIESZCZEŃ

6

X

1

= (2φ

i

+φ

k

-3Ψ

ik

)

l

R

k

R

i

M[kNm]

i

k

X

2

= (φ

i

+2φ

k

-3Ψ

ik

)

M

ik

M

k i

T[kN]

T

ik

=T

ki

=- (φ

i

+φ

k

-2Ψ

ik

)

-

2EJ
l

2EJ
l

6EJ
l

2

Rys. 1.10. Wykresy rzeczywistych sił wewnętrznych dla belki obustronnie utwierdzonej, obciążonej

przemieszczeniami φ

i

, φ

k

, Δ

i

, Δ

k

Ostatecznie dla belki obustronnie utwierdzonej (rys. 1.4) otrzymaliśmy komplet wzorów

transformacyjnych:

M

ik

=

2 EJ

l

⋅2

i



k

−3

ik



M

ki

=

2 EJ

l

⋅

i

2 

k

−3

ik



(1.12)

T

ik

=−

6 EJ

l

2

⋅

i



k

−2

ik



T

ki

=−

6 EJ

l

2

⋅

i



k

−2

ik



(1.13)

Należy przypomnieć, że wzory transformacyjne metody przemieszczeń zależą od warunków

brzegowych belki i przedstawiają relacje między przęsłowymi, przywęzłowymi siłami wewnętrznymi, a
uogólnionymi przemieszczeniami jej podpór.

1.3. Równanie osi odkształconej

Napiszemy równanie osi odkształconego, obustronnie utwierdzonego pręta (rys. 1.5) poddanego

wpływom osiadań podpór

φ

i

,

φ

k

,

Δ

i

,

Δ

k

(nie obciążonego siłami zewnętrznymi).

Aby rozwiązać to zadanie korzystamy z równania różniczkowego linii ugięcia.

[ EJ w' '  x]' '=q x

Ponieważ nie ma obciążeń zewnętrznych

q x=0

otrzymujemy równanie jednorodne

Dobra D., Dziakiewicz Ł., Jambrożek S., Komosa M., Mikołajczak E., Przybylska P., Sysak A., Wdowska A.

AlmaMater

Część 2

1. WZORY TRANSFORMACYJNE METODY PRZEMIESZCZEŃ

7

[ EJ w' '  x]' '=0

które następnie całkujemy

[ EJ w' '  x]'=c

EJ w' '

 x=cxd

EJ w '

 x=c⋅

x

2

2

dxe

(1.14)

Ostatecznie funkcja osi odkształconej jest wielomianem trzeciego stopnia

EJ w

x=c⋅

x

3

6

d⋅

x

2

2

ex f

(1.15)

Stałe całkowania wyznaczamy z warunków brzegowych, które dla belki przedstawionej na rys. 1.4 wyrazimy
przez wielkości kinematyczne (przemieszczenia):

{

w

x=0=

i

w '

x=0=

i

w

x=l =

k

w '

x=l =

k

(1.16)

Po podstawieniu warunków brzegowych (1.16) do równań (1.14) i (1.15) uzyskujemy układ równań:

{

EJ



i

= f

EJ



i

=e

EJ



k

=

cl

3

6



dl

2

2

el f

EJ



k

=

cl

2

2

dle

Podstawienie dwóch pierwszych związków do dwóch ostatnich równań

{

EJ



k

=

cl

3

6



dl

2

2

EJ 

i

⋅lEJ 

i

EJ



k

=

cl

2

2

d⋅lEJ 

i

po przekształceniach

d

⋅l=EJ 

k

−

cl

2

2

−EJ 

i

Dobra D., Dziakiewicz Ł., Jambrożek S., Komosa M., Mikołajczak E., Przybylska P., Sysak A., Wdowska A.

AlmaMater

Część 2

1. WZORY TRANSFORMACYJNE METODY PRZEMIESZCZEŃ

8

d

=

EJ

l



k

−

cl

2

−

EJ

l



i

EJ



k

=

cl

3

6





EJ

l



k

−

cl

2

−

EJ

l



i



⋅

l

2

2

EJ 

i

⋅lEJ 

i

cl

3

6

−

cl

3

4

=EJ 

k

−EJ 

i

−EJ 

i

⋅l−

EJ

2



k

⋅l

EJ

2



i

⋅l

prowadzi do wartości stałych

c i d:

c

=

6 EJ

l

2

⋅

i



k



12 EJ

l

3

⋅

i

−

k



d

=

EJ

l



k

−

EJ

l



i

−

l

2

⋅

[

6 EJ

l

2

⋅

i



k



12 EJ

l

3

⋅

i

−

k



]

d

=−

2 EJ

l



k

−

4 EJ

l



i

−

6 EJ

l

2

⋅

i

−

k



Równanie osi odkształconej pręta obustronnie utwierdzonego poddanego przemieszczeniu węzłów
podporowych wyraża się funkcją:

EJ w

 x=

[

6 EJ

l

2

⋅

i



k



12 EJ

l

3

⋅

i

−

k



]

⋅

x

3

6



[

−

2 EJ

l



k

2

i

−

6 EJ

l

2

⋅

i

−

k



]

⋅

x

2

2

EJ 

i

x

EJ 

i

w

 x=

[



i



k



2

l

⋅

i

−

k



]

⋅

x

3

l

2



[

−

k

2

i

−

3

l

⋅

i

−

k



]

⋅

x

2

l



i

⋅x

i

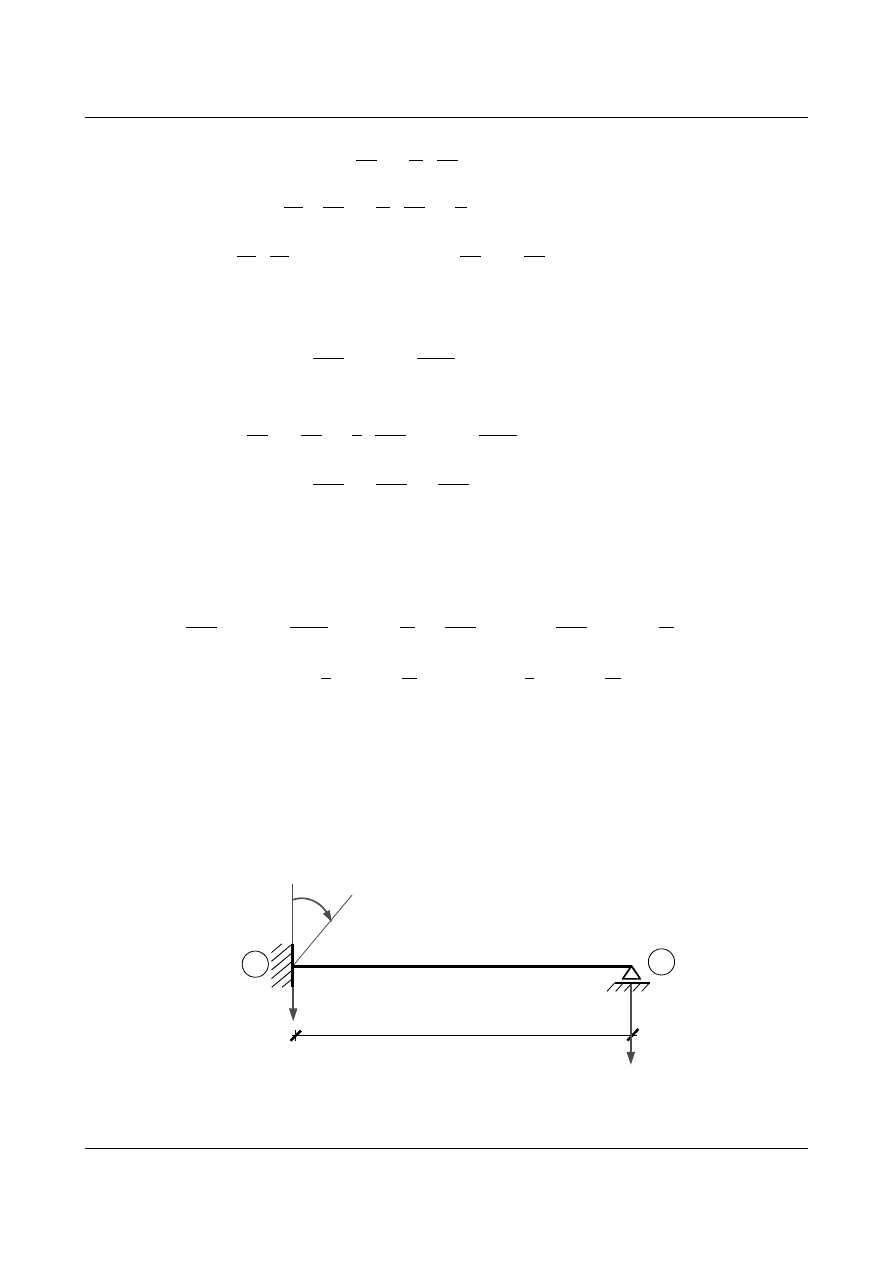
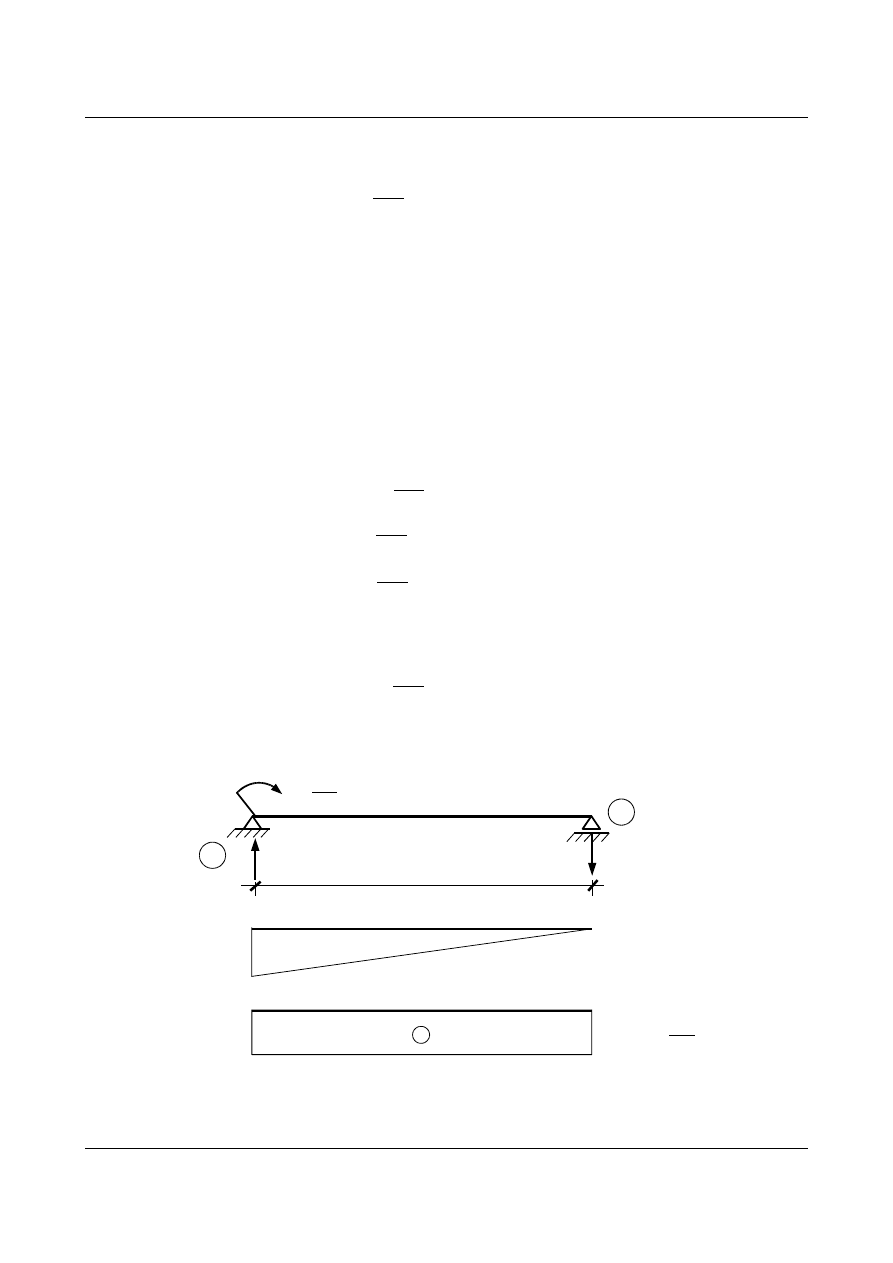
1.4. Belka utwierdzona jednostronnie

Rozpatrzmy belkę utwierdzoną z jednej strony (rys. 1.11), której podpory ulegają przemieszczeniom

φ

i

,

Δ

i

,

Δ

k

. Poniższy przykład rozwiążemy dwoma metodami: metodą sił (analogicznie do punktu 1.2) oraz

korzystając z gotowych wyników otrzymanych w punkcie 1.2 (przyjmując odpowiednie warunki brzegowe).

Δ

i

Δ

k

φ

i

i

k

l

Rys. 1.11. Schemat belki jednostronnie utwierdzonej

Dobra D., Dziakiewicz Ł., Jambrożek S., Komosa M., Mikołajczak E., Przybylska P., Sysak A., Wdowska A.

AlmaMater

Część 2

1. WZORY TRANSFORMACYJNE METODY PRZEMIESZCZEŃ

9

Metoda I – metoda sił

Zgodnie z zasadami metody sił przyjmujemy układ podstawowy

Δ

i

Δ

k

φ

i

i

k

l

X

1

Rys. 1.12. Układ podstawowy

w którym przemieszczenie po kierunku zwolnionego więzu musi być równe zero (

δ

1

= 0). Wynikające z tego

warunku równanie kanonicznych będzie miało następującą postać:



11

⋅X

1



1



=0

(1.17)

Aby obliczyć współczynniki równania narysujemy wykresy momentów w stanie

X

1

= 1 (analogicznie jak na

rys. 1.7).

i

k

l

X

1

=1

H = 0

1

M

1

[-]

1

l

1

l

Rys. 1.13. Reakcje i momenty zginające w stanie X

1

= 1

i wyznaczamy wartości przemieszczeń:



11

=

1

EJ

⋅



1
2

⋅1 ⋅l⋅

2
3

⋅1



=

l

3 EJ



1



=−

i

−

1

l

⋅

i



1

l

⋅

k

=−

i



ik

Po podstawieniu otrzymanych wyników do równania kanonicznego (1.17)

l

3 EJ

⋅X

1



ik

−

i

=0

Dobra D., Dziakiewicz Ł., Jambrożek S., Komosa M., Mikołajczak E., Przybylska P., Sysak A., Wdowska A.

AlmaMater

Część 2

1. WZORY TRANSFORMACYJNE METODY PRZEMIESZCZEŃ

10

uzyskujemy wartość nadliczbowej siły

X

1

=

3 EJ

l

⋅

i

−

ik



(1.18)

Niewiadoma

X

1

jest reakcją podporową, której wartość odpowiada wewnętrznej sile przywęzłowej

X

1

=M

ik

M

ik

to przęsłowy, przywęzłowy moment zginający w przekroju

i. Natomiast przęsłowy, przywęzłowy

moment zginający w przekroju

k jest równy zero (przegub).

M

ki

=0

Obliczmy wartości reakcji

R

i

i R

k

.

∑

M

k

=0

⇔

3 EJ

l

⋅

i

−

ik

R

i

⋅l=0

R

i

=−

3 EJ

l

2

⋅

i

−

ik



(1.19)

R

k

=−

3 EJ

l

2

⋅

i

−

ik



(1.20)

które pokrywają się z wartościami sił tnących (przęsłowych, przywęzłowych)

T

ik

=T

ki

=−

3 EJ

l

2

⋅

i

−

ik



(1.21)

Znając wartość nadliczbowej

X

1

możemy narysować wykres rzeczywistych sił wewnętrznych.

i

k

l

H=0

R

i

M

ik

X

1

= (φ

ik

-Ψ

ik

)

M[kNm]

T[kN]

T

ik

=T

ki

=- (φ

i

-Ψ

ik

)

R

K

-

3EJ
l

3EJ
l

2

Rys. 1.14. Wykresy rzeczywistych sił wewnętrznych dla belki utwierdzonej z jednej strony,

obciążonej przemieszczeniami φ

i

, Δ

i

, Δ

k

Dobra D., Dziakiewicz Ł., Jambrożek S., Komosa M., Mikołajczak E., Przybylska P., Sysak A., Wdowska A.

AlmaMater

Część 2

1. WZORY TRANSFORMACYJNE METODY PRZEMIESZCZEŃ

11

Metoda II

W tej metodzie wzory (1.12), (1.13) potraktujemy jako uniwersalne i po podstawieniu odpowiednich

warunków brzegowych wyprowadzimy wzory transformacyjne dla rozpatrywanego przypadku.

Wiemy, że dla belki (rys. 1.11) utwierdzonej z lewej strony i podpartej prętem ze strony prawej moment

przęsłowy, przywęzłowy

M

ki

= 0, a zatem na podstawie równania (1.12) możemy zapisać:

M

ki

=

2 EJ

l

⋅

i

2 

k

−3

ik

=0

(1.22)

Z równania tego wyznaczamy funkcję kąta obrotu

φ

k



i

2 

k

−3

ik

=0



k

=

3



ik

−

i

2

(1.23)

Po podstawieniu funkcji

φ

k

do równań (1.12), (1.13) otrzymujemy komplet wzorów transformacyjnych dla

belki jednostronnie utwierdzonej (utwierdzenie z lewej strony):

M

ik

=

2 EJ

l

⋅



2



i



3



ik

−

i

2

−3

ik



=

3 EJ

l

⋅

i

−

ik



(1.24)

M

ki

=0

(1.25)

T

ki

=T

ik

=−

6 EJ

l

2

⋅





i



3



ik

−

i

2

−2

ik



=−

3 EJ

l

2

⋅

i

−

ik



(1.26)

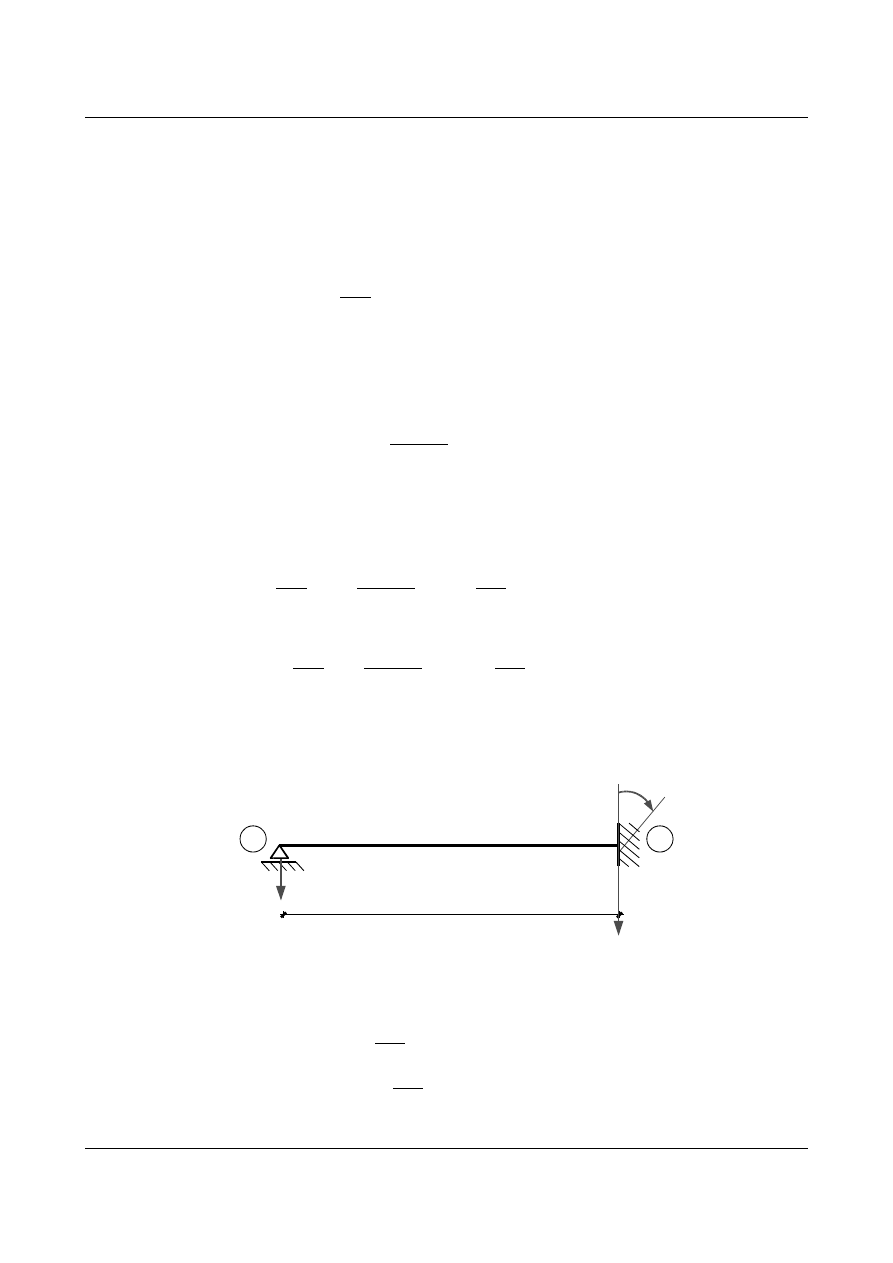
Dla belki o podobnych podporach (rys.1.15) jednak ułożonych przeciwnie, czyli będącej lustrzanym

odbiciem układu z rys. 1.11 można zapisać gotowe wzory transformacyjne.

Δ

i

Δ

k

φ

k

i

k

l

Rys. 1.15. Schemat belki utwierdzonej z prawej strony

M

ik

=0

(1.27)

M

ki

=

3 EJ

l

⋅

k

−

ik



(1.28)

T

ki

=T

ik

=−

3 EJ

l

2

⋅





k

−

ik



(1.29)

Dobra D., Dziakiewicz Ł., Jambrożek S., Komosa M., Mikołajczak E., Przybylska P., Sysak A., Wdowska A.

AlmaMater

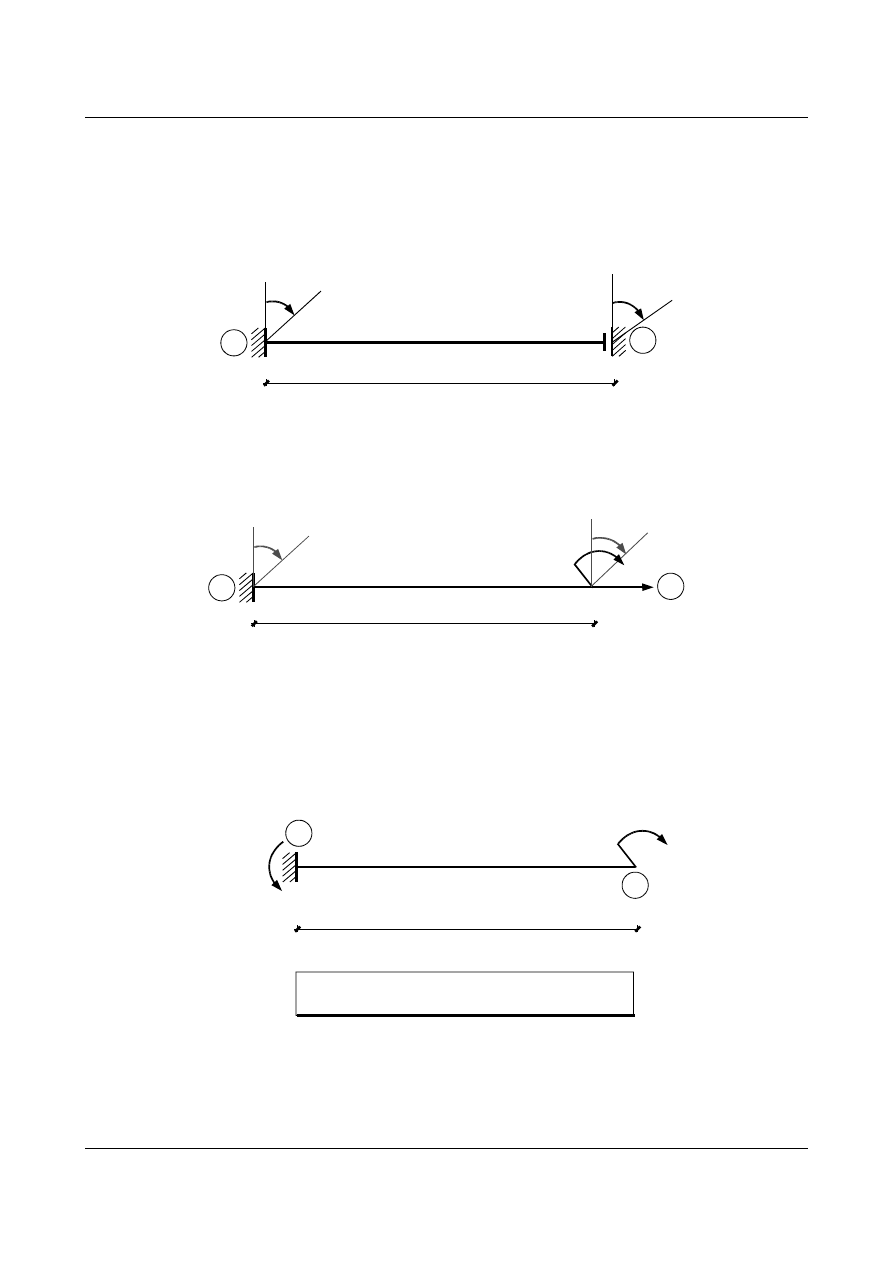
Część 2

1. WZORY TRANSFORMACYJNE METODY PRZEMIESZCZEŃ

12

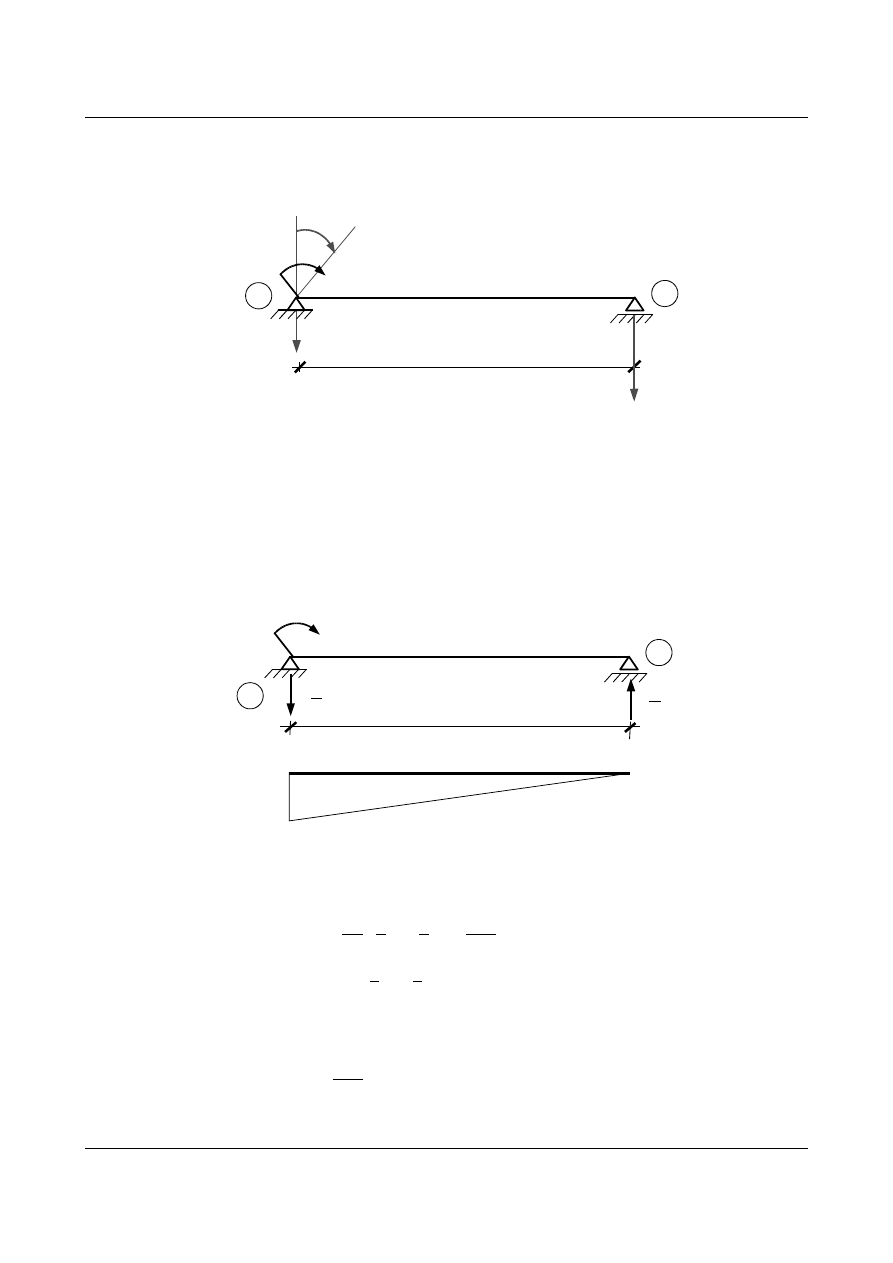
1.5. Belka obustronnie utwierdzona z przesuwem

Rozpatrzmy belkę o schemacie przedstawionym na rys. 1.16, której podpory doznają przemieszczeń

φ

i

,

φ

k

. Przemieszczenie pionowe podpory

i o Δ

i

spowoduje ruch całej belki i nie wywoła sił wewnętrznych, dlatego

ten wpływ pomijamy. Poniższy przykład taj jak poprzednio rozwiążemy dwoma metodami.

i

k

φ

i

φ

k

l

Rys. 1.16. Schemat belki utwierdzonej z przesuwem

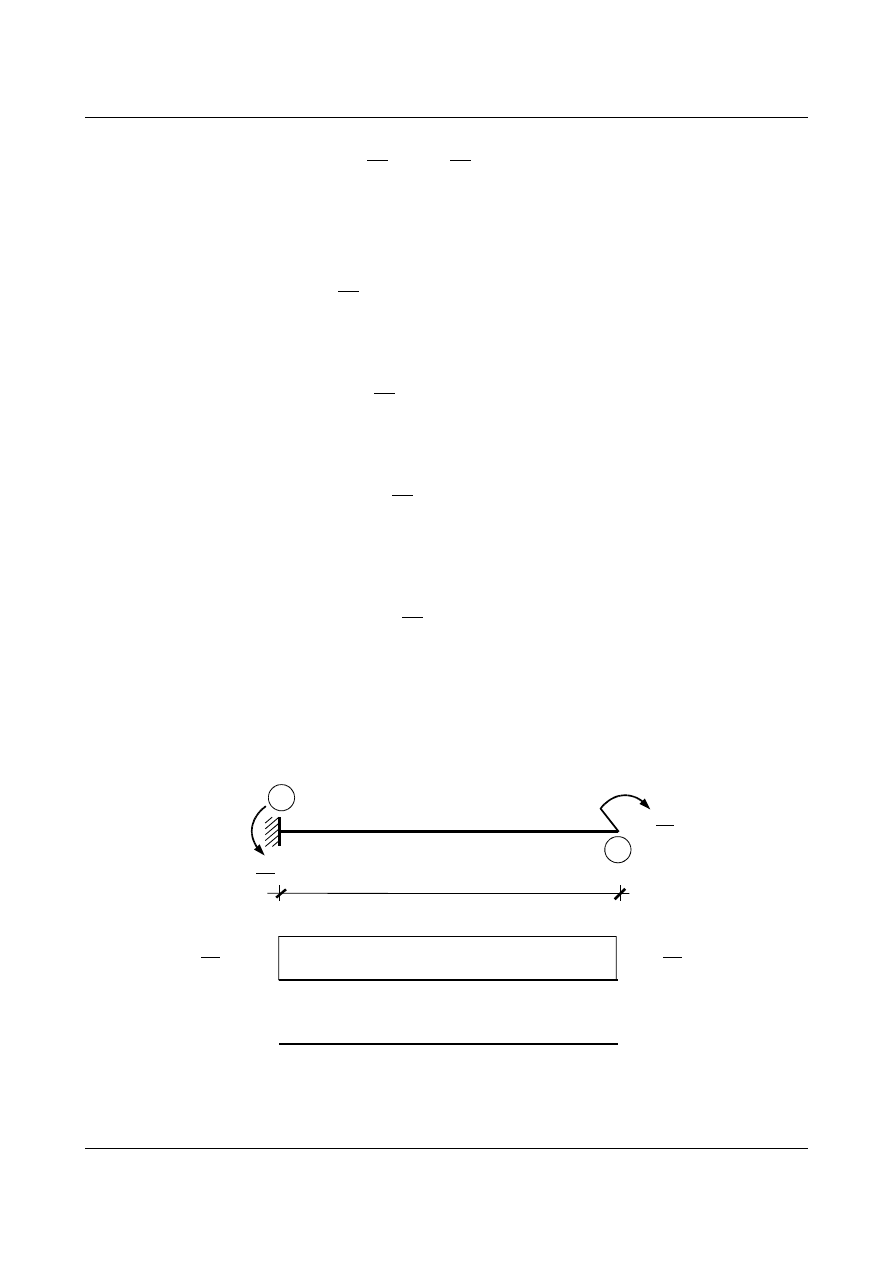
Metoda I – metoda sił

Przyjmujemy układ podstawowy.

i

k

φ

i

φ

k

l

X

1

X

2

Rys. 1.17. Układ podstawowy

i zapisujemy równanie kanoniczne (nie uwzględniamy sił normalnych):



1

=

11

⋅X

1



1



=0

(1.30)

Aby obliczyć współczynniki równania rysujemy wykres momentów w stanie

X

1

= 1.

i

k

l

X

1

=1

M

i

=1

H = 0

R

i

=0

M

1

[-]

1

Rys. 1.18. Reakcje i momenty zginające w stanie X

1

= 1

Obliczamy współczynniki równania kanonicznego.

Dobra D., Dziakiewicz Ł., Jambrożek S., Komosa M., Mikołajczak E., Przybylska P., Sysak A., Wdowska A.

AlmaMater

Część 2

1. WZORY TRANSFORMACYJNE METODY PRZEMIESZCZEŃ

13



11

=

1

EJ

⋅



1

⋅l⋅1



=

l

EJ



1



=−

k



i

Po podstawieniu otrzymanych wyników do równania (1.30)

l

EJ

⋅X

1



i

−

k

=0

(1.31)

Otrzymujemy wartości nadliczbowej siły:

X

1

=

EJ

l

⋅−

i



k



(1.32)

Reakcja w podporze odpowiada momentowi zginającemu w przekroju podporowym:

M

ki

= X

1

=

EJ

l

⋅−

i



k



M

ki

to przęsłowy, przywęzłowy moment zginający w przekroju

k. Natomiast przęsłowy, przywęzłowy

moment zginający w przekroju

i wynosi.

M

ik

=−X

i

=

EJ

l

⋅

i

−

k



Siła tnąca przy braku obciążeń zewnętrznych jest równa reakcji

T

ik

=T

ki

=R

i

=0

(1.33)

Na koniec rysujemy wykresy rzeczywistych sił wewnętrznych.

i

k

l

M[kNm]

X

1

= (-φ

i

+φ

k

)

M

i

= (-φ

i

+φ

k

)

T[kN]

0

EJ
l

EJ
l

M

k i

= (-φ

i

+φ

k

)

EJ
l

M

i k

= (φ

i

-φ

k

)

EJ
l

Rys. 1.19. Wykresy rzeczywistych sił wewnętrznych dla belki obustronnie utwierdzonej,

obciążonej przemieszczeniami φ

i

, φ

k

Dobra D., Dziakiewicz Ł., Jambrożek S., Komosa M., Mikołajczak E., Przybylska P., Sysak A., Wdowska A.

AlmaMater

Część 2

1. WZORY TRANSFORMACYJNE METODY PRZEMIESZCZEŃ

14

Metoda II

Wykorzystujemy wzory (1.12), (1.13) (traktujemy je jako uniwersalne) i podstawiamy odpowiednie

warunki brzegowe. W ten sposób otrzymujemy wzory transformacyjne dla rozpatrywanego przypadku.

Wiemy, że dla belki przedstawionej na rys. 1.16 siły tnące

T

ki

= T

ik

= 0, a zatem na podstawie

równania (1.13) możemy zapisać:

T

ik

=−

6 EJ

l

2

⋅

i



k

−2

ik

=0

(1.34)

Z równania (1.34) wyliczamy

ψ

ik



i



k

−2

ik

=0

(1.35)



ik

=



i



k

2

(1.36)

Jeśli podstawimy

ψ

ik

do równań (1.12), to otrzymamy komplet wzorów transformacyjnych:

M

ik

=

2 EJ

l

⋅



2



i



k

−3 ⋅



i



k

2



=

EJ

l

⋅





i

−

k



(1.37)

M

ki

=

2 EJ

l

⋅





i

2 

k

−

3

⋅

i



k

2



=

EJ

l

⋅



−

i



k



(1.38)

T

ik

=T

ki

=0

(1.39)

Dla belki o schemacie podanym na rys. 1.20 (lustrzane odbicie do rys. 1.16) wzory transformacyjne są takie
same jak w powyższym przykładzie.

i

k

φ

i

φ

k

l

i

k

M[kNm]

X

1

= (φ

i

-φ

k

)

M

k

= (φ

i

-φ

k

)

EJ
l

EJ
l

M

k i

= (φ

k

-φ

i

)

EJ
l

M

i

k

= (φ

i

-φ

k

)

EJ
l

T[kN]

0

Rys. 1.20. Schemat belki

Dobra D., Dziakiewicz Ł., Jambrożek S., Komosa M., Mikołajczak E., Przybylska P., Sysak A., Wdowska A.

AlmaMater

Część 2

1. WZORY TRANSFORMACYJNE METODY PRZEMIESZCZEŃ

15

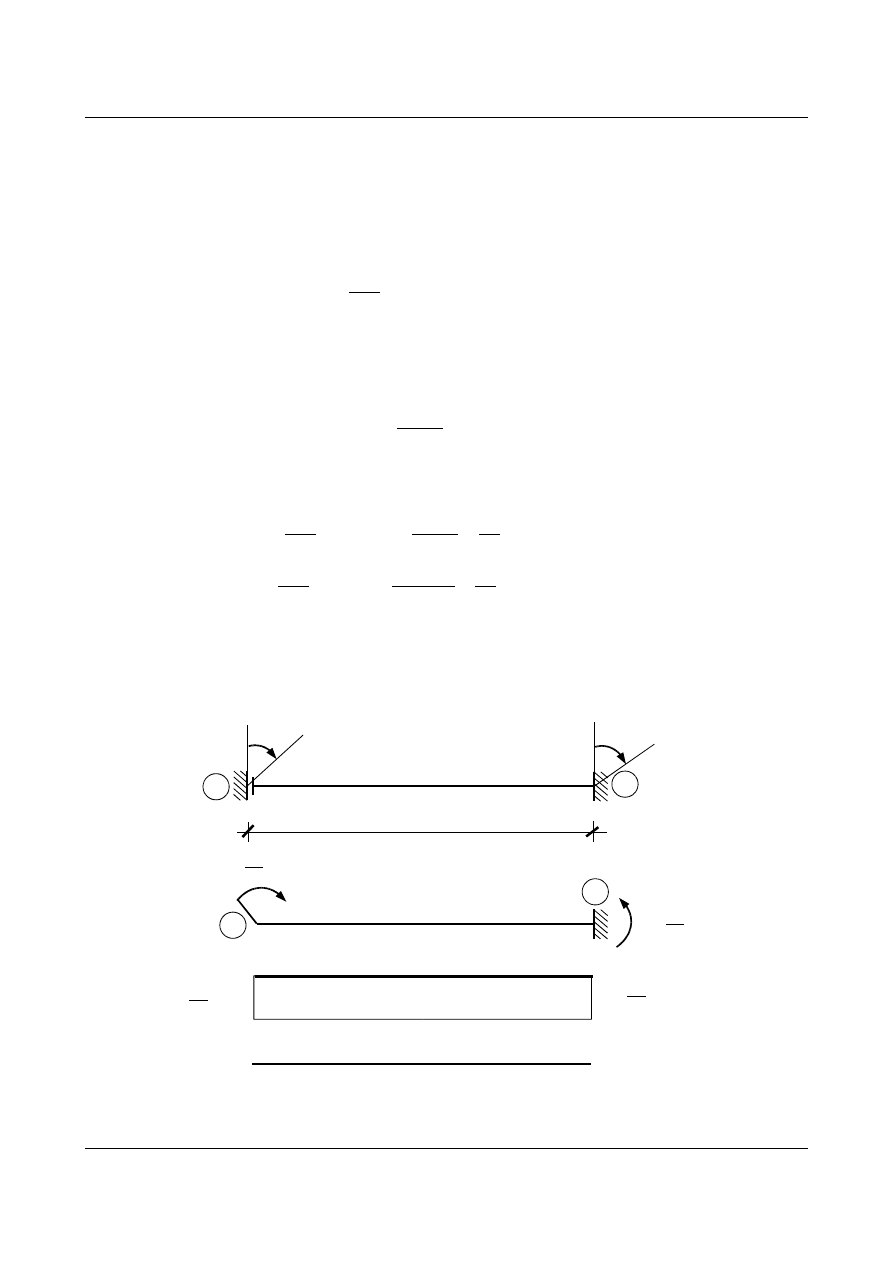
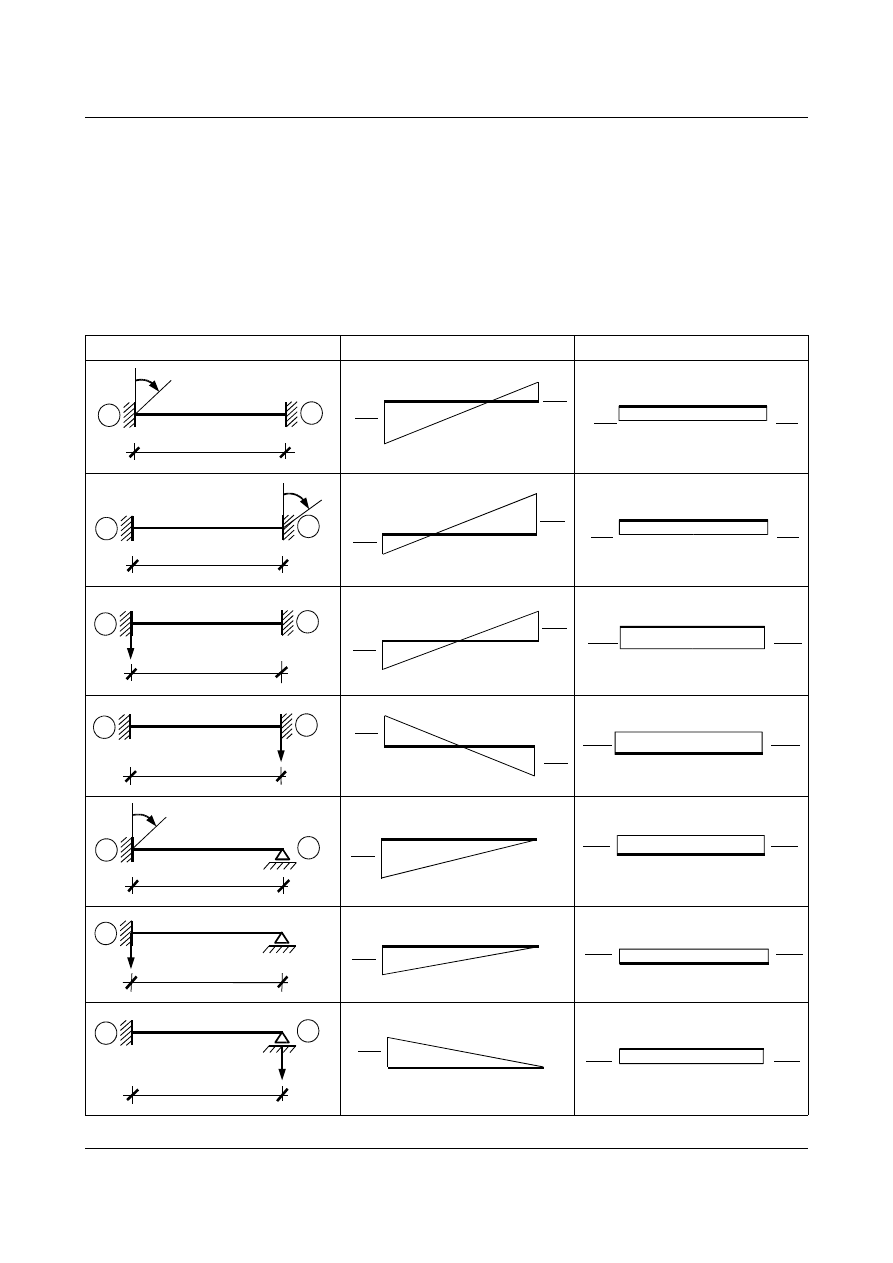
Wyniki rozważań zestawiono w tabeli 1.1. Podano wartości przywęzłowych sił wewnętrznych w

zależności od sposobu podparcia belki wywołane jednostkowymi przemieszczeniami węzłów podporowych.
Natomiast w tabeli 1.2 zestawiono wykresy sił wewnętrznych (przywęzłowych) dla trzech schematów belek od
obciążeń zewnętrznych (przęsłowych).

Uwaga: w tabelach narysowane są wykresy momentów zginających “po inżyniersku”, tzn. wykres po stronie
włókien rozciąganych. Natomiast ich wartości podano zgodnie z zasadami metody przemieszczeń, tzn.
momenty dodatnie działają zgodnie z ruchem wskazówek zegara (prawoskrętnie).

Tabela 1.1. Wykresy momentów zginających i sił poprzecznych od jednostkowych przemieszczeń podporowych

Schemat belki

M

T

i

k

φ

i

=1

l

EJ

4EJ
l

2EJ
l

6EJ
l

-

6EJ
l

-

i

k

φ

k

=1

l

EJ

2EJ
l

4EJ
l

6EJ
l

-

6EJ
l

-

i

k

Δ

i

=1

l

EJ

6EJ
l

2

6EJ
l

2

12EJ
l

3

-

12EJ
l

3

-

i

k

Δ

k

=1

l

EJ

6EJ
l

2

6EJ
l

2

-

-

12EJ
l

3

12EJ
l

3

i

k

φ

i

=1

l

EJ

3EJ
l

3EJ
l

2

3EJ
l

2

i

Δ

i

=1

l

EJ

3EJ
l

2

3EJ
l

3

3EJ
l

3

i

k

Δ

k

=1

l

EJ

3EJ
l

2

-

3EJ
l

3

3EJ
l

3

-

-

Dobra D., Dziakiewicz Ł., Jambrożek S., Komosa M., Mikołajczak E., Przybylska P., Sysak A., Wdowska A.

AlmaMater

Część 2

1. WZORY TRANSFORMACYJNE METODY PRZEMIESZCZEŃ

16

Schemat belki

M

T

i

k

φ

i

=1

l

EJ

EJ
l

EJ
l

-

0

i

k

φ

k

=1

l

EJ

EJ
l

-

EJ
l

0

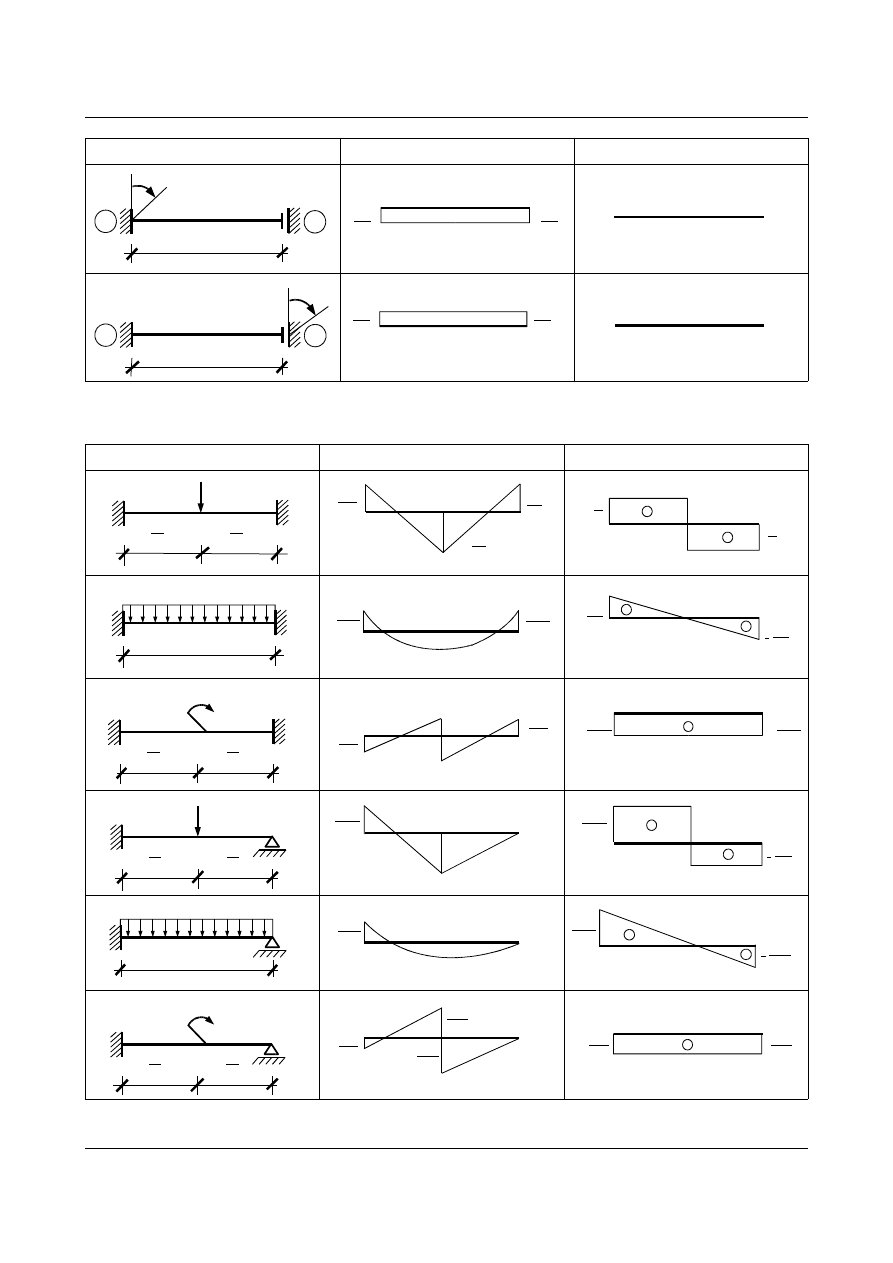
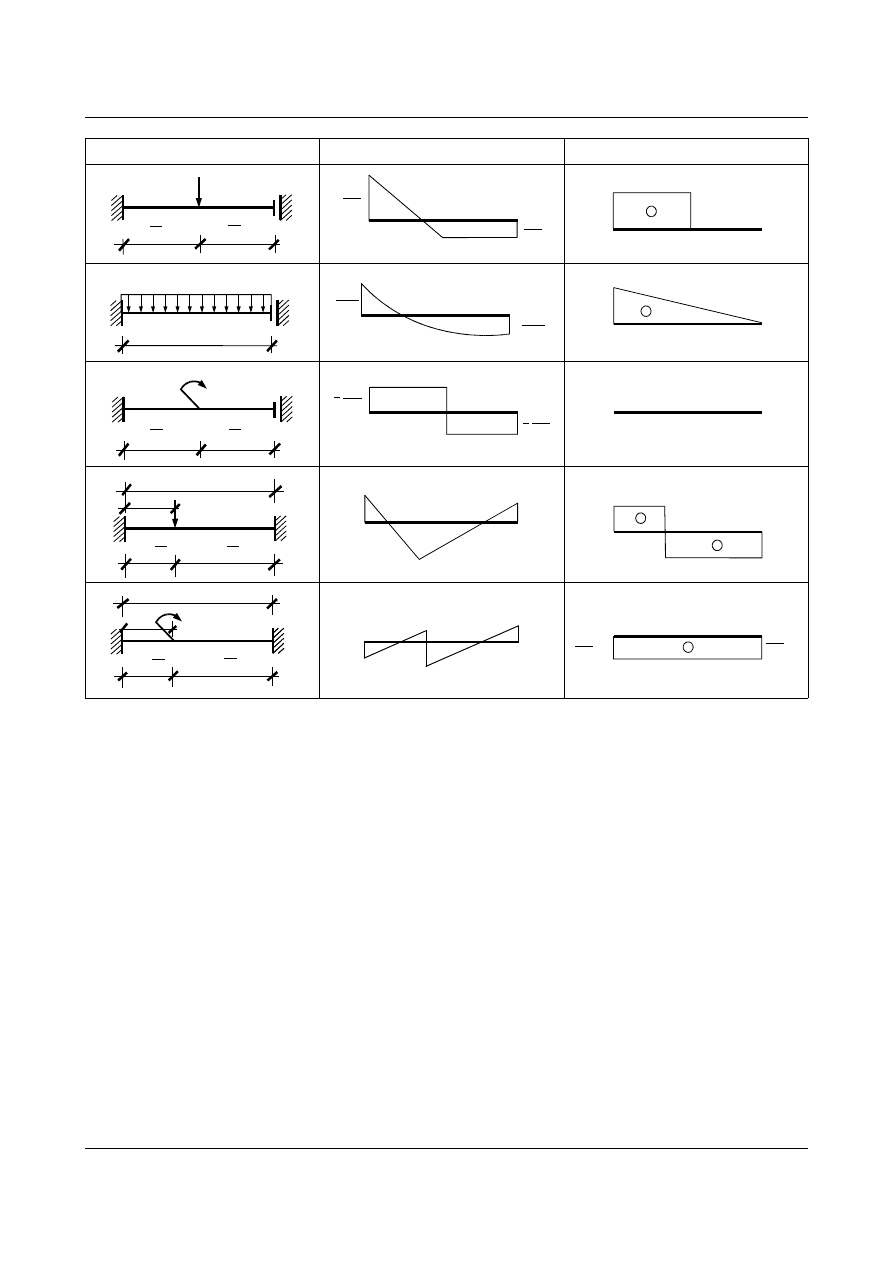
Tabela 1.2. Wykresy momentów zginających i sił poprzecznych od przęsłowych obciążeń

Schemat belki

M

T

P

l

2

l

2

Pl

8

Pl

8

-Pl

8

P

2

-

+

P

2

q

l

ql

2

12

-

ql

2

12

ql
2

-

+

ql
2

M

l

2

l

2

M
4

M
4

3M
2l

-

-

3M
2l

-

P

l

2

l

2

-3Pl

16

0

11P
16

-

+

5P
16

q

l

ql

2

8

-

0

5ql
8

+

3ql
8

-

M

l

2

l

2

M
8

0

9M
16

7M
16

9M
8l

-

9M
8l

-

-

Dobra D., Dziakiewicz Ł., Jambrożek S., Komosa M., Mikołajczak E., Przybylska P., Sysak A., Wdowska A.

AlmaMater

Część 2

1. WZORY TRANSFORMACYJNE METODY PRZEMIESZCZEŃ

17

Schemat belki

M

T

P

l

2

l

2

-3Pl

8

-Pl

8

P

+

q

l

ql

2

3

-

ql

2

6

-

ql

+

M

l

2

l

2

M

2

M

2

0

P

ξ=

x

l

ξ'=

l-x

l

x

l

Plξ'ξ

2

-Plξξ'

2

-Pξ

2

(3-2ξ)

-

+

Pξ'

(1+ξ-2ξ

2

)

ξ=

x

l

ξ'=

l-x

l

x

l

M

Mξ'

(2-3ξ'

)

Mξ(2-3ξ)

-

6M
l

ξξ'

6M
l

ξξ'

Dobra D., Dziakiewicz Ł., Jambrożek S., Komosa M., Mikołajczak E., Przybylska P., Sysak A., Wdowska A.

AlmaMater